Modele macroeconomice cu economie monetara

Modele macroeconomice cu economie monetara

III. 1. Modelul monetarist standard al lui Friedman

Pornind de la conceptia a teoretica privind teoria cantitatii de bani, Friedman a dezvoltat un model în cadrul caruia sunt utilizate ca ipoteze cele patru propozitii prezentate mai u.

Modelul lui Friedman este alcatuit din doua blocuri: un bloc al sectorului economiei reale si unul al sectorului economiei monetare.

Ecuatiile modelului unt urmatoarele:

Sectorul economiei reale

, 0 < c < 1 (3.1.)

, (3.2.)

(3..3.)

Sectorul economiei monetare

(3.4.)

(3.5.)

(3.6.)

Sectorul economiei reale este descris, deci, de o functie de consum (3.1.), o functie a investitiilor (3.2.) si o conditie de echilibru a pietei bunurilor si serviciilor (3.3.). Funcţ 636g65g ;ia consumului (3.1.) arata ca consumul real C / p este proportional cu venitul real Y / p. Functia de investitii (3.2.) exprima faptul ca investitiile reale I / p cuprind o parte autonoma A, reprezentând suma dintre investitiile private si cele publice independente de rata dobânzii si o componenta i_r r care depinde de rata dobânzii. Aici i_r reprezinta parametrul de senzitivitate a investitiilor reale la nivelul ratei dobânzii. El este negativ deoarece între investitii si rata dobânzii exista un raport invers proportional.

Conditia de echilibru (3.3.) spune ca venitul national real este egal cu suma cheltuielilor reale planificate pentru bunuri de consum si investitii.

Sectorul economiei monetare este descris de urmatoarele trei ecuatii. Relatia (3.4.) exprima cererea de bani ca suma a doua componente: cererea tranzactionala m_y Y / p si cererea speculativa, m_r r. Cererea tranzactionala este proportionala, deci, cu marimea venitului national real în timp ce cererea speculativa depinde de nivelul ratei dobânzii. Aici m_y reprezinta parametrul de senzitivitate al cererii reale în timp ce m_r reprezinta senzitivitatea cererii de bani la nivelul ratei dobânzii.

Relatia (3.5.) arata ca oferta de bani M^S este data exogen la nivelul M* în timp ce relatia (3.6.) exprima conditia de echilibru de pe piata monetara.

Modelul contine sase ecuatii dar sapte variabile (C, I, Y, M^D, M^S, p, r) deci este nedeterminat. Astfel de problema este rezolvata în teoria clasica introducând o noua ecuatie care permite determinarea venitului real:

(3.7.)

unde Y* este dat exogen. Aici Y* reprezinta nivelul de echilibru al venitului real sau nivelul de ocupare deplina, si este stabilit prin sistemul walrasian al ecuatiilor cererii si ofertei, precum si al conditiilor de echilibru ale pietei bunurilor si serviciilor.

Daca nivelul venitului real este dat, atunci modelul (3.1.) - (3.6.) pate fi rezolvat recursiv în modelul urmator:

Din ecuatiile (3.1.) - (3.3.) rezulta ca

si de aici:

(3.8.)

care reprezinta ecuatia IS a modelului.

Din ecuatiile (3.4.) - (3.6.) obtinem mai întâi

si de aici:

(3.9.)

Ecuatia (3.9.) reprezinta ecuatia LM a modelului.

Deoarece Y / p = Y* conform (3.7.), putem înlocui valoarea venitului real în (3.8.) si (3.9.) si obtinem:

Din relatiile de mai sus putem obtine, acum, usor rata dobânzii de echilibru r₀ si nivelul preturilor de echilibru p₀:

Se observa ca în timp ce rata dobânzii se determina în sectorul real al economiei, utilizând curba IS, nivelul preturilor decurge din sectorul monetar al economiei, respectiv din curba LM.

Apare, astfel, o dihotomie în determinarea preturilor: preturile relative, inclusiv rata dobânzii sunt determinate de raportul dintre cererea agregata si oferta agregata în timp ce nivelul preturilor este dat de relatia dintre cererea de bani si oferta de bani.

scoala macroeconomica keynesiana a rezolvat aceasta problema facând ipoteza ca nivelul preturilor este determinat în afara sistemului.

Solutia lui Friedman la problema ecuatiei absente este introducerea unei ecuatii prin care este data rata dobânzii.

El propune urmatoarea relatie:

r = r^e + π^e (3.14.)

unde r^e este rata anticipata a dobânzii iar π^e este rata anticipata a inflatiei.

Daca notam cu y^e rata asteptata de crestere a venitului nominal, atunci:

y^e = π^e + x^e (3.15.)

unde x^e este rata asteptata de crestere a venitului real.

Înlocuind π^e = y^e - x^e în ecuatia (3.14.) obtinem:

r = r^e + (y^e - x^e) = (r^e - x^e) + y^e (3.16.)

Friedman a considerat ca diferenta dintre rata asteptarii a dobânzii si rata anticipata de crestere a venitului real este constanta, deci:

r^e - x^e = R₀ (3.17.)

în aceste conditii, obtinem:

r = R0 + y^e (3.18.)

Deci rata dobânzii reprezinta o suma dintre o constanta si rata asteptata de crestere a venitului nominal, variabila care nu este explicitata în cadrul modelului. În continuare, modelul monetarist mai exact blocul monetar al acestuia este modificat în asa fel încât sa poata fi determinat y^e.

Avem:

Ecuatia (3.19.) reprezinta functia cererii de bani, m (r) reprezentând rata de crestere a cererii de bani care variaza invers proportional cu rata dobânzii.

Conform ecuatiei (3.20.), oferta de bani este exogena. Toate variabilele endogene si exogene sunt functii de timp.

Ecuatia (3.21.) este conditia de echilibru a pietei monetare iar ecuatia (3.22.) este ecuatia (3.18.).

Din (3.19.) - (3.21.) obtinem imediat:

(3.23.)

sau

(3.24.)

unde V(t) = 1 / m(t) este viteza de circulatie a banilor.

Ecuatiile (3.22.) si (3.23.) permit determinarea la orice moment de timp t a venitului nominal Y(t).

Friedman ezita sa explice ecuatia sa referitoare la rata dobânzii si sectorului real pentru ca aceasta ar implica o rata reala a dobânzii constanta (mai exact o diferenta constanta între rata reala a dobânzii si rata reala de crestere economica). Cum cererea de bani este influentata în principal de rata inflatiei si de marimea venitului real, ipoteza unei rate reale a dobânzii contante nu denatureaza functionarea sistemului monetar. În sectorul real, însa, o asemenea ipoteza exclude o determinanta economica centrala a comportamentului economiilor si investitiilor. De aceea, Friedman si-a limitat analiza la formularea unei teorii monetare a venitului nominal, lasând nerezolvata problema împartirii acestuia între economii si investitii.

Mai mult, dupa cum a aratat Tobin, modelul monetarist static are anumite proprietati care îl fac mai mult "neokeynesian". Astfel, daca cheltuielile guvernamentale cresc, (deci creste A din curba IS), venitul real Y / p creste cu marimea totala a efectului de multiplicare, în timp ce rata dobânzii ramâne fixata datorita ecuatiei de determinare (3.23.). În schimb, daca oferta de bani M^S creste, curba IS ramâne neschimbata ca si curba LM. În schimb, nivelul preturilor p va creste în acelasi ritm cu M^S astfel încât cererea de bani M^D sa nu fie afectata. De aici concluzia care se regaseste si la neokeynesieni conform careia numai politica fiscala afecteaza productia si ocuparea fortei de munca, în timp ce politica monetara este ineficienta.

III. 2. Modelul monetarist dinamic al lui I. Vanderkamp (1975)

Acest model monetarist include trei componente de baza: ecuatia cantitatii de bani, curba lui Phillips si legea lui Okun. Caracterul monetarist al modelului este dat de faptul ca rata expansiunii monetare influenteaza rata inflatiei, iar prin intermediul curbei lui Phillips se face legatura dintre blocul economiei monetare si cel al economiei reale.

În acest model, un impuls monetar (din o crestere neasteptata a ofertei de bani) genereaza o crestere a ratei de crestere reale peste rata anticipata, ceea ce duce la diminuarea ratei somajului, care determina, mai departe o crestere a ratei inflatiei (legea Okun). La rândul sau rata diminuata a somajului duce la o crestere a ratei inflatiei (curba lui Phillips). Aceasta crestere este egala exact cu diferenta dintre rata de expansiune monetara si rata cresterii reale ponderata cu elasticitatea cererii de bani în functie de venit.

Modelul lui Vanderkamp costa din trei ecuatii:

Ecuatia (3.41.) reprezinta ecuatia monetarista a cantitatii de bani. Aici m_t este rata expansiunii monetare (cresterii cantitatii de bani), x_t reprezinta rata de crestere a venitului real iar π_t - rata inflatiei.

Ecuatia (3.42.) reprezinta o versiune liniarizata a curbei Phillips. Rata inflatiei π_t este legata direct proportional de rata anticipata a inflatiei π^e_t si invers proportional cu diferenta dintre rata somajului u_t si rata naturala (de echilibru) a somajului u^e.

În sfârsit, ecuatia (3.43.) reprezinta legea lui Okun conform careia cresterea ratei de crestere a somajului este invers proportionala cu decalajul dintre rata cresterii reale x_t si rata anticipata a cresterii x^e_t.

Modelul are ca variabile endogene rata cresterii reale x_t, rata inflatiei π_t si rata somajului u_t.

Vanderkamp a dat acestui model o solutie grafica prezentata în continuare (Figura 1).

În cadranul I al graficului, functia R₀ reprezinta o curba Phillips liniara în care asteptarile inflationiste π^e = 0. Intersectia curbei Phillips cu axa Ou determina rata naturala (de echilibru) a somajului u^e .

În cadranul II e reprezinta grafic ecuatia cantitatii de bani.

Figura 1

Dreptele FF_o si FF₁ corespund a doua valori diferite a ratei de crestere a ofertei de bani, m₀ si, respectiv, m₁. Fiecare punct aflat pe dreptele FF exprima, deci, o combinatie posibila (π, x) corespunzatoare unei rate de crestere a cheltuielilor nominale. Dreapta verticala x = x^e este rata constanta de crestere echilibrata a venitului real.

Cadranul IV contine o reprezentare grafica a legii lui Okun. Dreapta OK reprezinta curba Okun în starea initiala. Ea arata ratele somajului care corespund unor rate alternative ale cresterii reale. Cum curba lui Okun este o ecuatie cu diferente de ordinul I, ea se deplaseaza catre stânga atunci când rata somajului scade în urma unei cresteri neasteptate a ratei de crestere a venitului real (în figura 1 distanta ).

Cadranul III transfera valorile lui x din cadranul II în cadranul IV.

În starea stationara, sistemul economic este caracterizat de urmatoarele relatii:

(3.44.)

În acest caz, rata constanta de crestere a ofertei de bani m₀ (apartinând dreptei FF₀) este utilizata complet pentru finantarea cresterii economice reale, x^e_. Rata somajului corespunde ratei naturale u^e aflata, cum am aratat, la intersectia dintre R₀ si abscisa Ou.

Sa presupunem acum ca oferta de bani înregistreaza o accelerare, deci rata de crestere a ofertei de bani sporeste de la m₀ la m₁.

Sa analizam ce se întâmpla în acest caz pe termen scurt cu sistemul economic, "termenul scurt" desemnând aici faptul ca în cursul proceselor de ajustare care se declanseaza nu are loc nici o modificare în rata asteptarilor inflationiste (π^e ramâne tot timpul egal cu zero).

În figura 1, cresterea lui m₀ la nivelul m₁ deplaseaza curba FF din cadranul II de la pozitia FF₀ în pozitia FF₁. Primul efect este o sporire a ratei de crestere a venitului real de la x^e la x_A (mai mare decât x^e corespunzator starii stationare), o reducere a ratei somajului la u_A si o crestere a inflatiei la π_A. Aceasta noua stare este reprezentata în figura prin punctele A, A' si A".

Analizând mai amanuntit aceasta noua stare, observam ca acceleratia monetara (cresterea ratei de crestere a ofertei de bani de la m₀ la m₁), concretizata în deplasarea dreptei FF₀ la FF₁ a produs o acceleratie neanticipata a ratei de crestere reale (a cheltuielilor reale) de marime x_A - xⁱ. Aceasta crestere este transferata în cadranul IV, dând de-a lungul curbei OK a lui Okun, punctul A' corespunzator unei rate a somajului u_A < u^e. În cadranul I, rata mai redusa a somajului duce, prin intermediul curbei lui Phillips la o rata pozitiva a inflatiei, π_A. În cadranul al II-lea, punctul A de pe dreapta FF₁ arata divizarea ratei de crestere a venitului nominal x₁ într-o componenta reala x_A si o componenta inflationista x₁ - x_A = π_A .

Sa dam, în continuare, o exprimare matematica a acestor efecte pe termen scurt.

Se observa ca modelul (3.41.) - (3.43.) poate fi rescris în urmatoarea forma:

sau, sub forma matriceala:

De aici obtinem sistemul de ecuatii liniare cu diferente:

Initial, se presupune ca u_t-1 = u^e ceea ce face ca ultimii termeni din partea dreapta a ecuatiilor (3.48.) - (3.50.) sa fie zero. În aceste conditii, o acceleratie monetara, deci o crestere a ritmului de crestere a masei monetare peste x^e + π^e va determina, simultan, o crestere a lui x_t si π_t si o diminuare a lui u_t .

Noua rata a somajului devine atunci u_t-1 = u_A < u^e , altfel spus în cadranul IV curba lui Okun se deplaseaza spre stânga, corespunzator noii distante de pe ordonata u_A = -a (x - x^e) (vezi figura 2).

În urma noii pozitii a curbei lui Okun noua reprezentare a sistemului economic este dreptunghiul (B,B',B",). În aceasta etapa, noua stare e caracterizeaza printr-o diminuare a diferentialei de crestere pâna la x_B - x^e, printr-o rata sporita a inflatiei π_B (corespunzatoare punctului B' din cadranul al II-lea). Deoarece cresterea ofertei de bani ramâne constanta, inflatia sporita determina o diminuare a ratei de crestere a economiei reale pâna la valoarea x_B (punctul B din cadranul I) si, în consecinta, o rata mai scazuta a somajului, u_B = - a(x_B - x^e).

Acum, curba lui Okun e deplaseaza din nou spre stânga, în pozitia OK₂ , noua reprezentare a sistemului economic fiind dreptunghiul (C, C', C", ), completat cu curba corespunzatoare a lui Okun, OK₂ , unde termenul constant al curbei este dat de rata somajului u_B.

Deplasarea de la A' la G' de-a lungul curbei lui Phillips se realizeaza în conditiile unei rate descrescânde a somajului. Deplasarea corespondenta de la A la G pe dreapta FF₁ reda variatia componentelor ratei nominale de crestere a venitului în favoarea ratei inflatiei.

Figura 2

Dinamica proceselor de ajustare este determinata de deplasarea curbei lui Okun. Atât timp cât aceasta curba se deplaseaza catre stânga nu se poate ajunge la echilibru deoarece se modifica atât rata inflatiei cât si rata somajului. Curba lui Okun va continua sa e deplaseze atât timp cât diferenta x_t - x^e este pozitiva (adica distantele sunt nenule) sau, altfel spus, atât timp cât ritmul de crestere a venitului real manifesta o acceleratie neasteptata.

Vom analiza acum punctele G, G', G", G din figura 2. Din primul cadran putem determina corespondentele ritmului de crestere a venitului nominal (x_G , π_G). Deoarece, acum, x_G - u^e = 0 nu mai avem o acceleratie neasteptata a ritmului de crestere a venitului. În cadranul IV, G" se afla la intersectia curbei lui Okun OK_G cu dreapta x = x^e astfel încât, în acest punct, legea lui Okun nu mai actioneaza si curba lui Okun nu mai ramâne stabila. Punctul G" reprezinta un punct de echilibru pentru piata fortei de munca iar rata corespondenta a somajului u_G nu e mai modifica.

Atunci echilibrul pe termen scurt se caracterizeaza prin urmatoarele relatii:

(3.51.)

Daca asteptarile inflationiste nu sunt revizuite, atunci curba lui Phillips ramâne stabila si predomina un echilibru pe termen scurt. Acest echilibru este caracterizat de o rata mai ridicata a inflatiei, π, o rata mai redusa a somajului, u dar aceeasi rata stabila de crestere reala x^e ca si înaintea impulsului monetar.

Cresterea ratei de crestere a ofertei de bani (sporirea cheltuielilor nominale) determina, deci, o accelerare temporara a cresterii care induce o crestere a ratei inflatiei si o diminuare a salariilor reale. În noua stare de echilibru predomina o rata mai înalta a inflatiei si acelasi ritm al cresterii reale, precum si un nivel mai ridicat al ocuparii fortei de munca si o valoare crescuta a PNB real. Acest echilibru pe termen scurt poate persista numai pâna în momentul în care asteptarile inflationiste (în special cele reflectate de salariile nominale) sunt ajutate la rata efectiva a inflatiei.

Putem presupune, de exemplu, ca procesul de ajustare a asteptarilor este descris de modelul asteptarilor adaptive.

adica rata asteptata a inflatiei variaza proportional cu eroarea de previziune π_t - π^e_t-1.

Pe termen lung, rata asteptata a inflatiei nu poate ramâne zero daca rata efectiva a inflatiei depaseste valoarea zero. Daca s-ar întâmpla acest lucru, ar fi contrazisa ipoteza comportamentului

rational al agentilor economici.

Conform ecuatiei (3.52.), rata asteptata a inflatiei π^e_t va începe sa creasca si va continua sa se mareasca pâna când π^e = π_G . Pe graficul din figura 2, acest proces de ajustare a asteptarilor inflationiste implica o deplasare a curbei lui Phillips de la R₀ la R. În aceasta noua stare stabila, nu vor mai apare surprize si valorile efective ale variabilelor sistemului corespund întocmai valorilor lor anticipate. Starea este descrisa, deci, de relatiile:

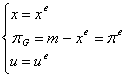(3.53.)

Deosebirea dintre echilibrul pe termen lung, caracterizat de punctul (G, G₁, G₂, ) si echilibrul pe termen scurt (G, G', G", ) consta în faptul ca primul, diferenta de crestere anticipata (x - x^e) cât si efectul real aspra pietei muncii au disparut.

Ca urmare a deplasarii în sus si spre dreapta a curbei lui Phillips, deplasare cauzata de o rata anticipata a inflatiei mai mare, rata somajului creste din nou pâna când, în punctul G₂, rata naturala a somajului, u^e este din nou atinsa. Deplasarea curbei lui Phillips antreneaza si o deplasare a curbei lui Okun, pe care o vom studia în continuare.

La echilibrul pe termen lung, rata inflatiei este complet anticipata si este, ca si în cazul echilibrului pe termen scurt, egala cu diferenta dintre rata de expansiune a ofertei de bani m si ritmul x^e al cresterii reale.

Aceasta analiza arata ca un impuls monetar (diferit ca o deplasare de la FF₀ la FF₁) determina o accelerare neasteptata a cresterii economice care dispare în cursul procesului de ajustare pe termen scurt, prin deplasarile ecuatiei lui Okun.

În timpul procesului de ajustare pe termen lung, care duce la deplasari ale curbelor lui Phillips si Okun, rata somajului creste din nou pâna la nivelul celei naturale.

Spre deosebire de procesul de ajustare pe termen scurt, analizat mai sus, procesul de ajustare pe termen lung implica a deplasare a curbei lui Phillips datorita unei variatii a ratei anticipate a inflatiei, π^e. Trasaturile esentiale ale acestui proces sunt urmatoarele:

a) Pozitia curbei lui Phillips depinde de rata decalata a inflatiei asteptate π^e_-1 si de eroarea de previziune π_-1 - π^e . Daca are loc o accelerare neanticipata a ratei inflatiei, curba lui Phillips se deplaseaza ascendent daca π_-1 - π^e < 0;

b) Pozitia curbei corespondente a lui Okun este data de rata decalata a somajului, u _-1 . Daca rata somajului creste, deci u_-1 > u_-2 , curba lui Okun se deplaseaza catre dreapta; în caz contrar catre stânga;

c) În situatia în care curbele lui Phillips si Okun pentru o anumita perioada sunt determinate de valorile anterioare, rata cresterii reale x (mai precis g = x - x^e ) si curba lui Okun determina atunci rata corespondenta a somajului. Introducând în expresia curbei lui Phillips rata somajului, obtinem rata efectiva a inflatiei.

Traiectoriile de evolutie ale variabilelor endogene π_t , π^e_t si g_t = x_t - x^e sunt determinate de rezolvarea sistemului de ecuatii cu diferente finite (3.48.) - (3.50.) la care e adauga o ipoteza privind formarea asteptarilor inflationiste, de exemplu:

(3.53.)

În plus trebuie specificate asteptarile privind rata somajului, respectiv rata de crestere, u^e si x^e care ramân contante pe orizontul de timp considerat.

Valorile initiale sunt date de echilibrul pe termen scurt, caruia îi corespund anumite valori numerice pentru π_G = π₀; x_G = x^e si u_G = u₀.

În aceste conditii, sistemul compus din ecuatiile (3.48.) - (3.50.) si (3.52.) la care se adauga conditiile initiale poate fi rezolvat, generând traiectoriile de evolutie ale variabilelor endogene amintite.

Se arata usor ca procesul de ajustare este stabil (deci oscilatiile sunt amortizate) daca:

(3.54.)

în timp ce asteptarile inflationiste sunt convergente catre cele date de rata reala a inflatiei daca 0 < θ < 1.

Evolutia oscilanta a variabilelor endogene este determinata de conditia:

(3.55.)

caz în care sistemul de ecuatii cu diferente finite are radacini complexe.

III.3. Modelul monetarist dinamic cu asteptari rationale (Frish, 1982)

Vom introduce, pornind de la modelul lui Vanderkamp, un model dinamic cu asteptari rationale.

Modelul este alcatuit din urmatoarele ecuatii:

Aici g_t = x_t - x^e exprima abaterea ratei reale de crestere a venitului de la valoarea de echilibru iar εⁱ_t, i = 1, 2, 3, sunt variabile aleatoare independente între ele si fata de celelalte variabile ale modelului având media 3^e+0 (E (εⁱ_t) = 0) si dispersie constanta (var (εⁱ_t) = ct.).

Se remarca faptul ca în legea lui Okun (3.58.), termenul u_t-1 este înlocuit cu u^e ceea ce presupune ca o accelerare a cresterii reale poate împinge rata somajului sub valoarea sa naturala de echilibru u^e , în timp ce în modelul lui Vanderkamp rata somajului cobora sub nivelul sa din perioada anterioara.

În modelul (3.56.) - (3.58.) variabilele endogene sunt π_t - rata curenta a inflatiei, g_t - abaterea cresterii reale fata de trend si u_t - rata somajului. Variabilele exogene sunt m_t - rata de crestere a ofertei de bani; π^e_t - rata asteptata a inflatiei, u^e - rata naturala (de echilibru) a somajului, εⁱ_t (i = 1, 2, 3) - variabilele aleatoare si x^e - rata cresterii reale în conditii de echilibru.

Pentru a determina sistemul de ecuatii cu diferente vom pune modelul (3.56.) - (3.58.) sub forma:

(3.59.)

care mai poate fi scris matriceal:

(3.60.)

De aici:

(3.61.)

si efectuând înmultirile:

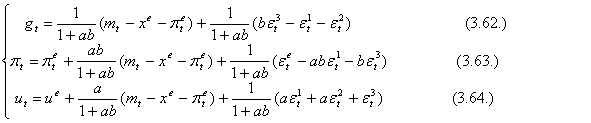
Vom nota termenii aleatori ai ecuatiilor (3.62)-(3.64) cu ω¹_t , ω²_t si, respectiv ω³_t, deci:

(3.65.)

Modelul cu asteptari rationale se scrie:

Se poate observa acum ca variabilele endogene g_t si u_t sunt influentate atât de diferenta (m_t - x^e - π²_t) cât s de termenii aleatori ω¹_t , ω²_t si ω³_t.

Modelul de mai us trebuie completat cu o ipoteza privind generarea ratei de crestere a ofertei de bani m_t. În modelul cu asteptari rationale acest lucru se face prin introducerea unei reguli de politica monetara, de exemplu o regula feed-back liniara de forma:

(3.69.)

Deci m_t depinde de o componenta autonoma μ₀, de abaterea ratei de crestere reala de la rata naturala de crestere, g_t, de rata inflatiei π_t, ambele decalate cu o perioada, precum si de o variabila aleatoare ε_t de medie zero si dispersie contanta.

Primii trei termeni din partea dreapta a ecuatiei (3.69.) formeaza partea sistematica a regulii de politica monetara în timp ce termenul aleator ε_t reprezinta aspectul nesistematic al acestei reguli.

Friedman considera μ₁ = μ₂ = 0, deci recomanda o regula monetara pasiva m_t = μ₀. Alti monetaristi recomandau alegerea lui μ₁ si μ₂ la valori negative, fiind adeptii unei politici monetare anticiclice.

O ipoteza esentiala a teoriei asteptarilor rationale este ca agentii economici cunosc componenta sistematica a ratei de crestere a ofertei de bani si tin cont de ea. Daca notam cu Ω_t-1 informatia totala existenta la nivelul agentilor economici atunci asteptarile acestora în legatura cu m_t pot fi scrise:

(3.70.)

Ecuatia (3.69.) poate fi scrisa sub forma :

(3.71.)

Ecuatia (3.71.) arata ca rata de crestere a ofertei de bani contine o componenta sistematica E(m_t / Ω_t-1) si o componenta aleatoare ε_t care nu poate fi prevazuta.

Sa aratam, în continuare, cum se formeaza asteptarile rationale din cadrul componentei sistematice. Începem cu asteptarile inflationiste. Ţinând seama de faptul ca E(εⁱ_t) = 0, i = 1, 2, 3 si aplicând operatorul de asteptare ecuatiei (3.63.) obtinem:

(3.72.)

De aici rezulta:

(3.73.)

care exprima inflatia anticipata rational π^e_t luând în considerare toate variabilele endogene si exogene precum si interdependentele dintre ele. Rata inflatiei anticipata rational reprezinta, deci, diferenta dintre componenta sistematica a ratei de crestere a ofertei de bani E(m_t / Ω_t-1) si tendinta ratei de crestere a economica reala, x².

O crestere a ratei asteptata de expansiune a ofertei de bani genereaza imediat o crestere a ratei asteptate a inflatiei.

Daca înlocuim, acum, ecuatia (3.73.) în (3.63.) si tinem cont de relatia (3.71.) obtinem:

(3.74.)

Rata curenta a inflatiei π_t ete alcatuita din doua componente: rata anticipata a inflatiei (primul termen din partea dreapta) si o componenta sistematica a ofertei de bani, determinata ca diferenta dintre rata efectiva a ofertei de bani m_t si rata anticipata a acesteia E(m_t / Ω_t-1).

Din ecuatia (3.74.) rezulta imediat:

(3.75.)

Aceasta ecuatie arata faptul ca diferenta dintre rata curenta a inflatiei si rata anticipata a acesteia este dependenta de eroarea de previziune a ofertei de bani, termenul de proportionalitate fiind ab / (1 + ab), la care se adauga si o componenta aleatoare ε²_t .

În continuare sa determinam influenta asteptarilor rationale asupra sectorului economiei reale.

Pentru aceasta vom înlocui ecuatia (3.73.) care da inflatia anticipata în ecuatiile (3.62.) si (3.64.) si obtinem:

Ecuatiile (3.76.) si (3.77.) dau ecuatiile ratei somajului u_t si ratei de crestere a productiei reale g_t. Se poate observa ca amândoua aceste rate sunt influentate de eroarea de previziune a ofertei de bani m_t - E(m_t / Ω_t-1). De exemplu, o diferenta m_t - E(m_t / Ω_t-1) > 0 va determina, prin intermediul unei abateri π_t - π^e_t > 0 coborârea lui m_t sub u^e în ecuatia (3.76.) si cresterea lui g_t în ecuatia (3.77.).

Dar aceste efecte reale sunt influentate si de o componenta sistematica εⁱ_t si de aceea nu pot fi folosite într-o politica economica. Deci sectorul real al economiei este independent de politica monetara anticipata. În cadrul modelului, rata asteptata a inflatiei reflecta perfect orice schimbare a componentei sistematice a cresterii ofertei de bani ceea ce sporeste rata curenta a inflatiei, fara a avea, însa, repercusiuni asupra sectorului real. O astfel de concluzie poarta numele de "teza ineficientei politice" si asupra sa au fost purtate polemici îndelungi între monetaristi si keynesisti.

III.4. Modelul neoclasic cu asteptari rationale al lui McCallum - Whitaker

Înainte de a prezenta modelul este necesar sa precizam anumite caracteristici generale ale asteptarilor rationale. Pentru aceasta ne vom imagina o variabila economica Y ale carei valori sunt determinate de urmatorul proces stochastic, incluzând un element imprevizibil:

(3.78. )

unde λ_t ~ N(0, σ²_λ), iar valoarea sa în perioada t este necunoscuta: nu face parte din I_t-1 (multimea informationala de la momentul t-1).

Este clar ca predictor rational, care se bazeaza pe procesul determinant al lui Y pentru a previziona la sfârsitul perioadei t-1 valoarea lui Y în perioada curenta t, trebuie sa-si formeze o asteptare în privinta valorii pe care o va lua eroarea λ în perioada curenta:

(3.79.)

unde reprezinta asteptarea rationala asupra lui Y_t-1, formata la momentul t-1 si este data de media conditionata a lui Y_t în raport cu informatia disponibila la momentul t-1.

adica:

iar eroarea de asteptare este data de relatia :

(3.80. )

deci de diferenta dintre valoarea reala, la momentul t_1, a lui Y si cea previzionata la momentul t-1.

3.3.1. Caracteristicile generale ale asteptarilor rationale

Mai multe concluzii rezulta din faptul ca daca procesul care îl determina pe Y este înteles, eroarea unei asteptari rationale este aceeasi cu componenta aleatoare a acelui proces:

a)      eroarea medie este zero. Odata ce procesul lui Y este stocastic, asteptarile rationale nu mai au caracteristica implauzibila de a fi exacte în fiecare perioada. În loc de aceasta au caracteristica mai slaba de a fi corecte în medie.

b)      Nu va exista nici un model de comportament pe care sa-l urmeze eroarea asteptarilor rationale. Daca se observa ca ν urmeaza o lege de comportament, de exemplu:

(3.81)

atunci indivizii îsi vor forma asteptarile asupra lui λ în functie de aceasta lege. Rezulta ca asteptarile rationale asupra lui Y vor fi în medie corecte, iar eroarea (acum ε_t) nu va urma nici o lege de comportament.

Ipoteza asteptarilor rationale sugereaza astfel ca, atât timp cât procesul ce determina variabila nu se schimba, nu se va schimba nici metoda de formare a asteptarilor. Altfel, metoda se va schimba odata cu el.

c)asteptarea rationala este, în general, cea mai buna asteptare care se poate forma. λ are varianta finita, ceea ce fixeaza o limita superioara erorii de previziune. Daca avem asteptari rationale, eroarea în fiecare perioada va fi egala cu λ_t . atunci, pentru orice alt model de estimari, acuratetea pe o anumita perioada de timp nu poate sa depaseasca σ_λ² , astfel încât asteptarile rationale sunt cea mai eficienta metoda de previzionare: varianta erorilor de estimare va fi întotdeauna mai mica în acest caz decât orice alt model de previziune.

3.3.2. Descrierea modelului

Modelul utilizat de McCallum si Whitaker este o versiune simplificata a modelului discret Sargent - Wallce (1975).

1.Oferta agregata:

(3.82.)

cu:

y_t reprezentând logaritmul outputului agregat din perioada t

p_t reprezentând logaritmului nivelului pretului agregat din perioada t

E_t-1 p_t = E(p_t/ I_t-1) asteptarea asupra nivelului mediu al pretului în perioada t (p_t), folosind informatia disponibila la momentul t-1.

u_t reprezentând o variabila aleatoare generata de un proces de tip zgomot alb

a₁> 0, 0< a₂ < 1

Termenul al treilea presupune faptul ca deviatiile outputului de la nivelul capacitatii productive determinate de erorile de asteptare pot persista mai multe perioade (datorita costurilor reale de ajustare).

2.Functiile IS si LM:

(IS)

(LM)

unde:

E_t-1 (p_t+1 - p_t) - asteptarea formata la momentul t-1 privind diferenta dintre pretul la momentul t+1 si pretul la momentul t

g_t - logaritmul cheltuielilor guvernamentale

z_t - logaritmul taxelor reale

m_t - logaritmul ofertei de bani

r_t - rata nominala a dobânzii

v_t, e_t - variabile aleatoare generate de procese independente de tip zgomot alb

b₁, b₃, c₂ < 0 iar b₂, c₁ > 0

De notat faptul ca diferenta g_t - z_t reprezinta logaritmul raportului dintre cheltuielile guvernamentale si taxe, astfel încât, daca este pozitiva, ea va implica un deficit bugetar

Aparitia lui z_t în ecuatia curbei (IS) sustine viziunea în care finantarea cheltuielilor guvernamentale cu ajutorul taxelor în loc de obligatiuni va diminua cererea agregata.

Pentru a completa modelul trebuie sa specificam modul în care sunt determinate politicile g_t, z_t si m_t. Astfel, vom presupune ca autoritatea monetara mentine rata taxelor neschimbata în raport cu conditiile economice, astfel încât veniturile din taxe depind doar de outputul curent:

z_t = τ₁ · y_t,

unde:

τ₁ - reprezinta parametrul ratei de taxare (= raportul între rata marginala si rata medie)

τ₁ > 0