Konvoluce, Dirichletovo jádro, Tichonovova regularizace

Konvoluce, numerická konvoluce opakování

Konvoluce je velmi důležitý pojem v teorii integrálních transformací, který se používá k filtraci (vyhlazování) vstupních signálů (dat), při zkoumání přenosových jevů, při řešení inverzních úloh ap. Lze ukázat, že každá integrální transformace - Laplaceova, Fourierova, Hilbertova atd. - je zvláštním případem konvoluce. Tedy konvoluce je operátor a nejobecnější integrální transformace zároveň.

1.1. Konvoluce dvou funkcí.

Definice 1.  Nechť f(t) a g(t) jsou alespoň po částech spojité komplexní funkce reálné proměnné . Konvolucí těchto dvou funkcí, nazýváme funkci h(t), definovanou konvergentním integrálem

Zde t je integrační proměnná. Konvoluci značíme resp. jen

Integrálu ve vztahu (1.1) říkáme konvoluční resp. konvolutorní integrál.

Jsou-li f(t) a g(t) alespoň po částech spojité komplexní funkce reálné proměnné

, pak konvoluce těchto funkcí, je dána konvergentním integrálem

s proměnnou horní mezí: (1.2)

Zde t je integrační proměnná, přitom pro integrand v důsledku principu kauzality (příčina → důsledek). Stačí tedy zapsat, že t se mění v rozmezí .

Postačující podmínkou pro konvergenci konvolučního integrálu je, aby funkce a byli integrovatelné s kvadrátem na R, resp. ohraničenost variace komplexních funkcí a reálné proměnné.

Vlastnosti konvoluce. Z vět o integrálech závislých na parametru plyne:

konvoluce dvou spojitých funkcí a , na R je funkce spojitá,

lineárnost (distributivní zákon vzhledem ke sčítání a násobení konstantou): , kde jsou konstanty,

komutativní zákon: , tj. pro ,

, kde c je konstanta,

,

jsou-li funkce originály (vzory, předměty), tj. existují jejich příslušné integrální obrazy (například Laplaceův, Fourierův ap. ), pak i konvoluce je originál, k němuž lze vytvořit integrální obraz,

věta o součinu obrazů (věta o obrazu konvoluce): jsou-li funkce originály , tj. existují jejich příslušné integrální obrazy (například Laplaceův, Fourierův ap.), pak integrální obraz konvoluce (Laplaceův, Fourierův ap.) se rovná součinu jejich obrazů, tj.. Zde s je parametr jádra transformace.

asociativní zákon, který nám dovoluje vytvořit konvoluci tří a více funkcí:

.

K důkazu prvních 5-ti vlastností postačí jenom definice konvoluce a definice integrální transformace.

Například provedeme důkaz komutativního zákona (3): , zde c je konstanta a funkce i byli integrovatelné s kvadrátem na R.

Sestavíme integrál : ,

Zavedeme substituci:

.  □

K důkazu věty o součinu obrazů zavedeme (pro názornost) konkrétně zvolené jádro integrální transformace .

Pro dvoustrannou Laplaceovu transformaci , pro Fourierovu transformaci , R. Nechť existují dva konvergentní integrály na stejné množině :

a .

Sestavíme -li součin těchto dvou integrálů na této množině, dostaneme:

, zde, stejně jako dříve,

.

Z toho plyne i přímo Borelova věta, která se používá pro jednostrannou Laplaceovu transformaci.

Při důkazu dojde jen ke změně dolní meze a tedy i integrační oblasti D. Oblast D, za podmínky principu kauzality, tj. , znázorněna na obr.1, obr.

Obr.1 Obr

Konvoluce dvou funkcí jako integrální transformace

Na konvoluci dvou funkcí se lze dívat jako na nejobecnější integrální transformaci.

Nechť funkce je originálem, pak integrál (1.1) resp. (1.2) vyjadřuje integrální transformaci s jádrem transformace , které se často zapisuje jenom . Jádro konvolučního integrálu volíme v závislosti na úloze, kterou řešíme.

Lze ukázat, že skoro každá integrální transformace je speciálním případem konvoluce. Ukážeme tuto vlastnost konvolučního integrálu na jednostranné Laplaceově transformaci a na Stieltjesově transformaci.

Laplaceova transformace

Zavedeme do konvolučního integrálu (1.1) substituci:

, s je parametr,

,

Nechť

a) jádro konvolučního integrálu bude ve tvaru , obr.3, potom

a po zavedení uvedené substituce

dostaneme , přitom při ;

b)nechť konvoluce bude ve tvaru pak ,

c) originál označíme: .

Dosadíme teď substituce a uvedené vztahy do konvolučního integrálu (1.1):

, po úpravě dostaneme

. Je zřejmé, že poslední výraz je Laplaceův integrál.

Stieltjesova transformace.

Obdobně při zavedení substituce a jádra , obr. 4, do konvolučního integrálu dostaneme Stieltjesovu transformaci: .

Nechť

a) jádro konvolučního integrálu bude ve tvaru , potom

a po zavedení uvedené substituce dostaneme

,

přitom při .

b) konvoluce bude ve tvaru a po zavedení uvedené substituce

,

c) pro originál zavedeme označení: .

Dosadíme-li substituce a uvedené vztahy do konvolučního integrálu, dostaneme

,

po úpravě dostaneme Stieltjesův integrál

Poznámka. Důležitou vlastností konvolučního integrálu (1.1) při vhodné volbě jádra g(t) bude zmenšení oscilace funkce (originálu, předmětu ,vzoru), tj. výsledná funkce mění své znaménko na intervalu resp. nejvíce tolikrát, kolikrát mění své znaménko .

Jak ukázal Schöenberg I.J. v roce 1947-1948, g(t) bude takovým jádrem jedině tehdy, jestliže

• ,
• a má tvar: ,

kde g je libovolná vertikální přímka, která se nachází v oboru absolutní konvergence dvoustranného Laplaceova integrálu, nazývaného též Fourierův - Laplaceův integrál, tj. Při některých omezeních, například může být .

Funkce má tvar = , (Titchmarsh E.C., 1951).

Zde jsou reálná čísla, přičemž z posloupnosti čísel lze sestavit

konvergentní číselnou řadu .

Funkce se nazývá funkce zpětné transformace resp. reprodukční, přičemž obraz

dvoustranné L - transformace je :.

Vlastnosti uvedených jader jsou:

,

- střední hodnota

< ∞ - disperse

Z těchto vlastností plyne, že g(t) má pravděpodobnostní charakter a je funkcí hustoty rozdělení pravděpodobnosti . Tento typ jader patří ke třídě tzv. „konečných“ jader, jestliže je polynom stupně n s reálnými kořeny. Základní funkce, jejíž pomocí lze obdržet téměř všechna jádra, je :

Všechna „konečná“ jádra lze vytvořit pomocí konečného počtu konvolucí funkcí tvaru . „Nekonečná“ jádra se realizují pomocí nekonečného počtu těchto operací. Je-li alespoň jedna z těchto funkcí finitní, pak nosičem konvoluce () bude .

1. Konvoluce dvou posloupností.

Nechť máme dvě regulární funkce , které lze rozvinout v dvě konvergentní mocninné řady na stejné množině M a se středem v bodě :

,

zde jsou posloupnosti tvořené koeficienty mocninných řad. V oboru konvergence, tj. pro (pro ) lze vytvořit součin těchto dvou řad:

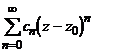= (1.3)

Koeficienty se počítají:

,nebo

,  (1.4)

V tomto případě funkce a lze chápat jako obrazy posloupností a a jako jádro Laurentovy transformace. Obdobně můžeme vytvořit součin dvou Laurentových řad se stejným středem a konvergentních na stejném mezikruží, například při pro :

(1.5)

Zde koeficienty se počítají obdobně: , . (1.6)

Definice 1.18. Posloupnost koeficientů ve vztahu (1.6) se nazývá konvolucí dvou posloupností a . Zapisujeme .

Skutečně, vypočteme- li některé koeficienty ze vzorce (1.6):

.=

dostaneme například:

=

=

=

Definujeme-li: ( viz.jednostranná Z-transformace),

konvoluce dvou posloupností , bude posloupnost koeficientů , vypočtených dle vzorce (1.4) pro .

Ve všech uvedených případech lze říci, že funkce jsou obrazy posloupností , a je obrazem posloupnosti .

Potom ze vzorce (1.7.8) je zřejmé, že jsou -li funkce obrazy posloupností , a je obrazem posloupnosti , pak platí, že obraz konvoluce, tj. obraz posloupnosti , se rovná součinu obrazů posloupností a :

Výpočet konvoluce dvou konečných posloupností.

Nechť posloupnost má N₁ členů: (ostatní jsou nulové) a posloupnost má N₂ členů (ostatní jsou nulové), pak posloupnost bude mít N₁ + N₂ – 1 členů (ostatní budou nulové). Členy této posloupnosti vypočteme: , zde , a, b jsou sloupcové vektory tvořené koeficienty posloupností ,,.

A je matice typu N₁ + N₂ – 1,N₂ tvořená koeficienty posloupnosti ,

B je matice typu N₁ + N₂ – 1,N₁ tvořená koeficienty posloupnosti ,

Příklad

Nechť posloupnost má členů: (ostatní jsou nulové) a posloupnost má členů

(ostatní jsou nulové), pak posloupnost bude mít 10 + 7 – 1 =16 členů (ostatní budou nulové): (-0.45, -1.05, -1, -4.325, -4.05, -725, -1.21, 0.96, 905, 4.74, 5.585, 6.17, 5.34, 59, 1.26, 0.51).

Výpočet periodické (cyklické) konvoluce.

Chceme-li provést vypočet pomocí periodické konvoluce, pak je nutno obě posloupnosti , upravit tak aby obě posloupnosti měli stejnou délku (resp. ):

• doplníme posloupnost :

• doplníme posloupnost :

Chceme-li zdůraznit, že se jedná o cyklickou konvoluce, zapíšeme místo , ale místo křížku v kolečku bude hvězdička v kolečku.

Diskrétní konvoluce lze zapsat ve tvaru soustavy:

,

kde je posloupnost reprezentující vstupní signál f, obsahuje N prvků,

je posloupnost reprezentující výstupní signál y,

je posloupnost reprezentující diskrétní časovou charakteristiku h,

diskrétní „filtr“.

Maticový tvar diskrétní konvoluce bude , zde maticeje dolní trojúhelníková matice , řádu NxN

, jsou vektory-sloupce, obsahující N prvků, tj. , .

Diskrétní dekonvoluce je operace nalezení vstupního signálu f za podmínky, že

tuto operaci nelze !!! napsat ve tvaru ,

ale v maticovém tvaru dostaneme , zde je matice inverzní k H.