MATICE

MATICE

Matice je zkrátka jakási tabulka o n sloupcích a m řádcích, přičemz toto značení řádků a sloupců nemusí být vzdy stejné, na to pozor. V kazdé buňce tabulky je poté nějaké číslo nebo jiný výraz. Matice nemusí být pouze čistě číselná, i kdyz se ze začátku dost pravděpodobně s jinými maticemi nesetkáte. Takze jak asi můze vypadat matice:

Tato matice má dva řádky a tři sloupce. Prvky matice se značí pomocí indexů a namísto velkého písmene se pouzívá malé písmeno: a₁₁ = 0 nebo a₂₃ = 51. První index udává řádek a druhý index sloupec.

Speciální typy matic

Matice mohou mít různé vlastnosti a některé spesl matice mají dokonce své vlastní názvy.

Čtvercová matice je matice, která má stejný počet řádků jako sloupců. a_ij; i = j. Pokud není matice čtvercová, je obdélníková. Příklad čtvercové matice:

Nulová matice je matice, která má na vsech pozicích nuly. a_ij = 0

Jednotková matice je matice, která má na hlavní diagonále jedničky a vsude jinde nuly. Hlavní diagonála je jakoby "úhlopříčka" zleva doprava. Zkrátka jsou to čísla na souřadnicích, kde se i = j

Schodovitá matice je matice, která má nulové řádky na konci (nebo nemá zádné nulové řádky) a kazdý nenulový řádek má na začátku více nul nez předchozí řádek.

Matice transponovaná k matici A je matice A^T, u které platí a_ij = a^T_ji. Zkrátka zaměníte řádk 22122u2022w y matice za sloupce.

Symetrická matice je matice, která se definuje jako A = A^T. Prvky symetrické podle diagonály jsou stejné.

Antisymetrická matice je skoro totéz jako symetrická matice, akorát prvky na druhé straně mají opačné znaménko. A = −A^T

Diagonální matice je matice, která má nuly vsude kromě hlavní diagonály. Přesněji řečeno vsude jinde musí být nuly, co je na hlavní diagonále není specifikováno.

Základní operace s maticemi

Matice můzeme sčítat, můzeme je násobit nějakým číslem a můzeme násobit i matice navzájem.

Sčítání matic je poměrně intuitivní. Pokud jsou matice stejného typu (= stejný počet sloupců a řádků), výsledná matice bude mít na stejných pozicích součty čísel na odpovídajících pozicích v předchozích maticích. Neboli a_ij + b_ij = c_ij

Sčítání matic je zřejmě komutativní a asociativní. A + B = B + A a A + (B + C) = (A + B) + C

Násobení matic číslem je vlastně také intutivní. Vezmete číslo a vynásobíte s ním kazdý prvek matice, nic víc. k · A = k · a_ij

Násobení matic uz je trochu horsí zálezitost, protoze uz není intuitivní, jak by člověk čekal. Nestačí pouze vynásobit odpovídající členy. V prvé řadě musí matice splňovat kritérium, ze počet sloupců první matice musí být stejný jako počet řádků druhé matice. Zbytek můze být libovolný. Nyní uz můzeme nadefinovat součin:

To toho víte, co? Teď to zkusím objasnit i těm méně bystrým :-). Vemete první řádek první matice a první sloupec druhé matice. Nyní vynásobíte první prvek s prvním prvkem a sečtete s násobkem druhého prvku s druhým prvkem a sečtete atd. Tím získáte v nové matici C prvek c₁₁. Úplně nejlepsí bude příklad. Vynásobíme tyto dvě matice:

Nyní vybereme první řádek první matice a první sloupeček druhé matice:

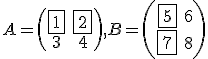
Pro přehlednost zápisu si nově vzniklou matici označíme C. Pokud chceme získat první prvek této matice, musíme vypočítat toto: c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁. Upozorňuji, ze na prvním místě je řádek, poté sloupec. Po dosazení dostáváme: . První prvek má hodnotu 19:

Dalsí prvek, c₁₂, získáme stejným způsobem, pouze vememe první řádek a druhý sloupec. Tímto zdlouhavým výpočtem vzdy získáme ten prvek, který mají společný. První řádek a první sloupec mají společný prvek na souřadnicích c₁₁, první řádek a druhý sloupec zase c₁₂. Hezky to ukazuje následující obrázek:

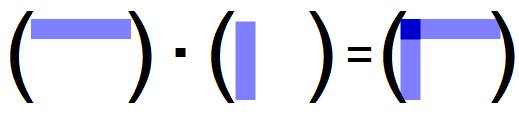Součin matic

Teď uz jen rychle donásobím zbytek matice:

c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ = 1 · 6 + 2 · 8 = 22

c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ = 3 · 5 + 4 · 7 = 43

c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ = 3 · 6 + 4 · 8 = 50

Tato čísla uz jen zapíseme to matice:

Správnost výsledku si můzeme ověřit třeba v Excelu nebo v OpenOffisáckém Calcu, které obsahují funkce pro práci s maticemi.

Teď pár vseobecných informací o násobení matic. Předně násobení matic není komutativní. Obecně neplatí, ze by A · B = B · A, ačkoliv samzořejmě takový případ můze nastat. Ale násobení matic je asociativní. Se sčítáním je dokonce distributivní: A (B + C) = AB + BC. Pokud násobíme dvě matice a_ij · b_mn, pak výsledná matice bude typu i × n (bude mít tolik řádků, kolik má první matice a tolik sloupců, kolik má druhá matice).

Máme dány tyto tři matice:

Proveďte součin matic A · B

Proveďte součin matic B · A

Pozor na to, ze násobení matic není komutativní, takze určitě nemůzeme s jistotou říci, ze výsledek bude stejný jako v předchozím případě. Musíme to zkrátka celé znova vypočítat:

Proveďte součin matic A · C a C · B

Druhý příklad nemůzeme vypočítat, protoze počet sloupců první matice je jiný nez počet řádků druhé matice.

Základní maticové úpravy

Abychom mohli s maticemi efektivně pracovat, musíme si nadefinovat nějaké elementární maticové úpravy. Předně můzeme vynásobit řádek/sloupec matice nějakým číslem různým od nuly. Vynásobení se projeví stejně jako k-násobek matice, ale pouze v onom řádku/sloupci.

Druhá úprava je přičtení k-násobku j-tého řádku k i-tému řádku. Totéz pro sloupce. Zní to trochu strasidelně, ale je to ve skutečnosti jednoduché. Předvedeme si to pro k = 1. Budeme mít tuto matici:

Nyní k prvnímu řádku přičteme druhý řádek. Vememe tedy druhý řádek a čísla na ekvivalentních pozicích přičteme k číslům z prvního řádku. S čísly ze druhého řádku se nic nestane, změní se jen první řádek:

Nyní můzeme v úpravách pokračovat. Teď zkusíme přičíst dvojnásobek prvního řádku ke třetímu řádku. Vytáhneme z této nově vzniklé matice první řádek, vynásobíme ho dvěma a tato čísla přičteme ke třetímu řádek. Opět - první řádek se nezmění, změní se pouze třetí řádek:

Teď přičteme zase ke třetímu řádku součet prvního a druhého řádku. V podstatě to není nic nového, protoze kdyz ke třetímu řádku přičteme nejprve druhý řádek a poté první řádek, musíme dojít ke stejnému výsledku.

A jestě jedna sloupcová úprava (ty se obvykle nepouzívají tak často, protoze nejsou tolik přehledné). Přičteme první sloupec ke druhému sloupci:

A úplně naposledy vynásobíme druhý řádek dvojkou:

Teď si jestě vysvětlíme, co jsou to závislé řádky/sloupce. Řádek je lineárně závislý, pokud tento řádek lze vyjádřit jako lineární kombinací ostatních řádků matice. Zkrátka pokud budete schopni různě posčítat řádky tak, aby vám nakonec vysel hledaný řádek, je tento řádek lineárně závislý. Příklad:

Vezmete-li dvojnásobek prvního řádku a druhý řádek, dostanete řádek třetí. Pokud od třetího řádku odečtete tuto kombinaci, dostanete nulový řádek (řádek obsahující samé nuly). Tento řádek je závislý.

Hodnost matice

Uz známe vsechno potřebné k tomu, abychom si mohli zavést pojem hodnost matice. Hodnost matice je maximální počet lineárně nezávislých řádků/sloupců v matici. Nulová matice má hodnost nula, kazdá jiná matice má hodnost alespoň jedna. Z toho vyplývá, ze matice typu m × n můze nabývat hodnosti maximálně min(m, n)

Teď jak se hodnost matice počítá. No. Je to celkem jednoduché. Musíte matici upravit do takového podoby, ze které uz bude jasně vidět, které řádky jsou lineárně nezávislé. To se nejčastěji provádí tak, ze se matice upraví do schodovitého tvaru (pod diagonálou samé nuly) a pak uz je vidět, jak na tom ta matice je. Supity presto na příklad - máme tuto matici:

A máme zjistit její hodnost. Teď si musíme uvědomit jednu drobnost. Máme-li dva řádky, které jsou plné čísel různých od nuly, mohou být teoreticky lineárně závislé. Museli bychom to počítat. Pokud ale jeden z těch řádků bude mít na nějakém místě nulu, přičemz ten druhý řádek na stejném místě nulu nemá, můzeme s jistotou tvrdit, ze závislé nejsou. Nenajdeme totiz zádné číslo, kterým bychom mohli vynásobit tu nulu (potazmo celý řádek), abychom tam dostali totéz číslo, jako se nachází v druhém řádku. Proto se vzdy budeme snazit upravovat matice do schodovitého tvaru, abychom tam ony nuly dostali.

Postup bývá obvykle takovýto: nejprve dostaneme nuly do prvního sloupce (kromě prvního řádku). Poté upravujeme matici dále tak, abychom dostali nuly ve druhém sloupci, pak třetí atd. atd. atd. az z toho nakonec máme schodovitý tvar. Sečteme nenulové řádky a ejhle tuť hle, máme hodnost matice.

V nasí předchozí matici budeme úpravy provádět takto: Podíváme se, jaký je vztah mezi prvky a₁₁ a a₂₁. Vidíme, ze jsou stejné, takze abychom na místě a₂₁ dostali nulu, musíme přičíst násobek prvního řádku. Let's do it! Přičteme násobek prvního řádku ke druhému řádku (neboli od druhého řádku odečteme první):

Teď máme nulu tam, kde jsme ji chtěli mít. Nyní jestě musíme dostat nulu na pozici a₃₁. Tam je zase jednička, takze jen odečteme první řádek:

Teď uz máme nuly v prvním sloupci, takze se s chutí pustíme na druhý sloupec. Vidíme, ze čísla a₂₂ a a₃₂ jsou opačná, takze stačí řádky sečíst:

HA! A dostali jsme tam jeden nulový řádek. Úpravy jsou jiz hotové, dostali jsme se do schodovitého tvaru. Nyní uz jen sečteme nenulové řádky a máme hodnost. Ta je rovna rank A = 2. Tato matice měla hodnost dva. Teď zkusíme vypočítat hodnost trochu větsí matice:

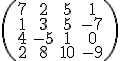
Hodnost matice je maximální počet lineárně nezávislých řádků, takze si můzeme dovolit si v matice rozpřeházet řádky jak je nám libo. Zde by se třeba hodilo mít řádek s jedničkou na začátku úplně nahoře, ať se nám lépe počítá. Můzeme tedy bez obav přesunout první s druhým řádkem:

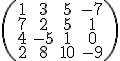
Teď budeme postupovat stejně jako v předchozím příkladě. Musíme v prvním sloupci mít samé nuly (samozřejmě místo prvního řádku), takze k druhému řádku přičteme násobek prvního řádku, ke třetímu násobek a k poslednímu násobek. První řádek zůstane nezměněn:

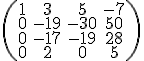
Opět prohodíme řádky, tentokrát bychom měli dostat poslední řádek namísto druhého řádku, kvůli té dvojky na druhé pozici. Prohodíme druhý a čtvrtý řádek:

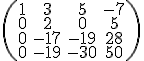
Ale vidíme, ze pod dvojkou máme čísla −17 a −19. Ani jedno z těch čísel není dělitelné dvěma, coz je takové nesikovné, dokonce az mrzké. Proto nyní třetí a čtvrtý řádek vynásobíme dvěma:

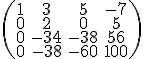
Teď můzeme postupovat v úpravách a ve snaze vynulovat druhý sloupec. Ke třetímu řádku přečteme 17 násobek druhého řádku a ke čtvrtému 19 násobek:

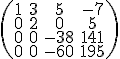
Tak, teď jsme dostali dost - na dalsí úpravu - nesikovná čísla, ale uz jen letmým pohledem zjistíme, ze třetí a čtvrtý řádek závislý není. Z toho vyplývá, ze zadané matice má hodnost čtyři.

Regulární a singulární matice

Matice se nazývá regulární, jestlize má maximální hodnost (tj. pokud se v ní nevyskytuje zádný lineárně závislý řádek) a jestlize je to matice čtvercová. Čtvercová matice se nazývá singulární, jestlize není regulární (tj. jestlize matice obsahuje alespoň jeden lineárně závislý řádek). Tyhle dva pojmy jsou docela důlezité, respektive často na nich stojí nějaké definice. Spousta věcí je definována, jen pokud je matice regulární.

Inverzní matice

Poslední speciální typ matice je matice inverzní. Inverzní matice se můze počítat pouze z matice čtvercové, na obdélníkové matici není inverzní matice definována. Inverzní matice k matici A (značíme A⁻¹) dále existuje jen tehdy, je-li matice regulární. Tato matice je pak určena jednoznačně. Stručně k vlastnostem inverzní matice:

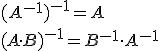
A hlavně nejdůlezitějsí vlastnost inverzní matice (coz je zároveň také definice inverzní matice):

E je jednotková matice.

A teď k metodě výpočtu inverzní matice. Nejjednodussí algoritmus je Gaussova eliminační metoda, která spočívá v tom, ze upravujete matici A do jednotkového tvaru a vedle této matice si napísete jednotkovou matici a na tuto matici provádíte stejné úpravy jako na matici A. Na konci výpočetního procesu máte nalevo matici A upravenou na jednotkovou matici a napravo inverzní matici. Vyzkousejme si to na jednoduchém příkladu:

Letmým kouknutím zjistíme, ze matice je regulární, takze má smysl počítat inverzní matici. Počítáme-li inverzní matici, obvykle to zapisujeme ve tvaru:

Nyní tu levou matici upravíme na jednotkovou matici a identické úpravy budeme provádět na pravé matici. Přičteme násobek prvního řádku ke druhému. Nejprve levá matice:

Teď přičteme násobek první řádku pravé matice k druhému řádku pravé matice

Teď musíme dostat nulu na pozici a₁₂. Stačí, kdyz k prvnímu řádku přičteme druhý řádek. Nyní jiz provedu obě úpravy v jednom kroku:

A teď se zbavíme té minus dvojky tím, ze celý řádek vydělíme minus dvěma:

Výsledná inverzní matice je: