ALTE DOCUMENTE |
Pokud tvořící křivka k lezí v souřadnicové rovině x=0, její parametrické vyjádření je tvaru:
k: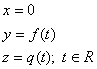 
souřadnicová osa z je osou rotace, pak parametrické vyjádření rotační plochy Q je tvaru:
Q: 
, 
, poloměr r, vznikne rotací přímky k kolem
osy z.
k: 
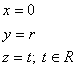Q:
implicitní vyjádření - středová
rovnice válcové plochy: 
, 
, vznikne rotací přímky k kolem osy z.
k: 
Q:
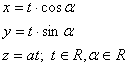
implicitní vyjádření - vrcholová rovnice
kuzelové plochy: 
Jednodílný rotační hyperboloid
, vznikne rotací
hyperboly h kolem její vedlejsí osy.
hlavní osa lezí na souřadnicové ose y, vedlejsí osa na ose z. Velikost hlavní poloosy označme a, velikost vedlejsí poloosy označme b, pak hyperbola je dána rovnicemi
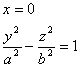
zparametrizujeme-li hyperbolu pomocí
hyperbolických funkcí cosh, sinh, (vyuzijeme vztah 
)dostaneme
h: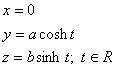 
Q:
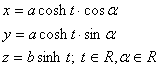
implicitní vyjádření - středová rovnice rotačního jednodílného hyperboloidu je tvaru :
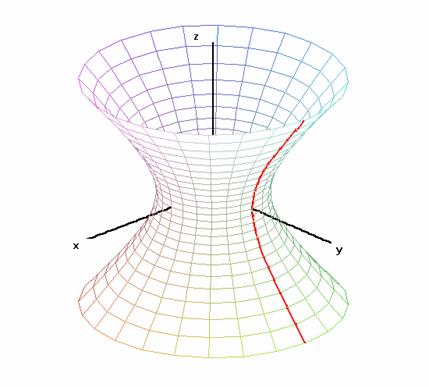
vznikne rotací
hyperboly h kolem její hlavní osy
hlavní osa lezí na souřadnicové ose z, vedlejsí osa na ose y. Velikost hlavní poloosy označme a, velikost vedlejsí poloosy označme b, pak hyperbola je dána rovnicemi
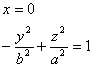
zparametrizujeme-li hyperbolu dostáváme
h: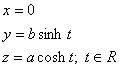 
Q:
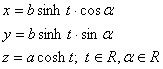
implicitní vyjádření - středová rovnice rotačního jednodílného hyperboloidu je tvaru :
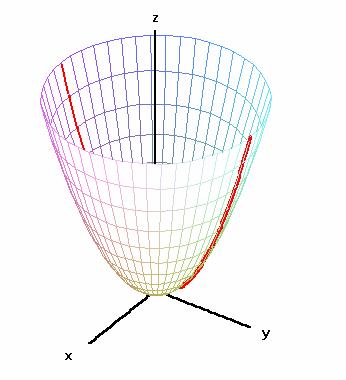
Rotační paraboloid
, , vznikne rotací paraboly 
kolem osy z.
Q:
implicitní vyjádření rotačního
paraboloidu: 
Protáhlý (vejčitý) elipsoid
Vznikne rotací elipsy kolem její hlavní osy.
Hlavní osa lezí na souřadnicové ose z, vedlejsí osa na ose y. Velikost hlavní poloosy označme a, velikost vedlejsí poloosy označme b, pak elipsa je dána rovnicemi
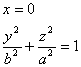
zparametrizujeme-li elipsu pomocí goniometrických funkcí cos, sin, dostáváme
h: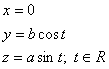 
Q:
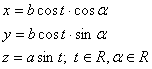
implicitní vyjádření - středová rovnice rotačního protáhlého elipsoidu je tvaru :
|
