ALTE DOCUMENTE
|
|||||||
Introduction to the hard particle paradigm
Conventional physics has always tried to explain mechanics in terms of motion and interaction among particles. At first, everything looked so simple with the introduction of the atom. The Greek root of the word atom, "atomon", means "that which cannot be divided." But it was discovered in the 1930s that these entities are made from even more fundamental particles: a nucleus and electrons, termed elementary particles. Since the nucleus appeared much smaller, solid, and dense, scientists originally thought that the nucleus was the fundamental building block of matter. Later on, they discovered that it was made of protons (p+), which are positively charged, and neutrons (n), which have no charge (although they have the same mass as protons). More recently, physicists have discovered that protons and neutrons are composed of yet smaller particles called quarks. As far as we know, quarks are the most elementary elements, and can be classified as fundamental - simple and structureless elements.
Historically, Isaac Newton derived the laws for forces and motion of masses, Albert Einstein modified them by adding the 'effective mass' factor for relativistic particles, and Niels Bohr complicated the atomic model by proposing that tiny particles (electrons) orbit around a massive nucleus. More recently, scientists have needed to describe more and more particles to explain the particulate nature of the atom. So far, these particles include quarks, gravitons, muons, mesons, kaons, pions - and scientists will surely need to invent more, as long as the real geometric rules of nature remain unknown. The problem here seems to be that, at the subatomic level, the behaviour of matter appears to be radically inconsistent with our daily experience. In fact, the more we examine it, the less and less tangible matter becomes. We cannot help but ask, "Is matter as real as we think it is?" As Feynman said, if we keep picturing electrons and atoms as little steel balls, we're always going to have trouble understanding what is happening at the quantum level.
Many of us have learned about Bohr's atomic model, which postulates electrons orbiting around a central nucleus. Thankfully, conventional physics has taken a step in the right direction by largely abandoning this model. These days, even conventional physics understands that an orbital has little resemblance to the orbit of a planet moving around the sun, but is instead better described as a structure of energy that has a shape, with a probabilistic distribution in space.
|
|
|
|
|
|
As you can obviously conclude from the above electron 'orbitals', the energy shape cannot be accounted for by the path of an orbiting electron. Let's have a look at the simplest type of orbital - the spherically symmetrical type. The Hydrogen atom in its ground state is a very good example of this. Since it is spherically symmetrical, it must have zero total angular momentum. Were we to attempt to interpret this observation in classical terms, we would be forced to conclude that the electron must only move in and out towards the nucleus (radially), while at the same time covering the entire angular range! This, in fact, contradicts the "steel ball" or "classical" interpretations, including Bohr's. So how can an electron possibly produce an orbital path without having an orbit? The only reasonable way to visualise this would be to imagine a spherical balloon being periodically inflated and deflated, but then we cannot talk about orbitals any more, can we? . Undoubtedly these statements will continue to sound strange until we free ourselves from the confines of the 'hard particle' paradigm. I understand that for one to free himself from a 200 years old of non-quantum science, full of assumptions of a world occupied by solid particles, euclidian geometry, and other spoon feeded concepts, it is not an easy thing at all to do. So, before stepping onto new grounds, let's have a further look at what our current knowledge teaches us about matter.
Currently accepted scientific description of an atom
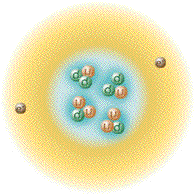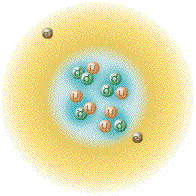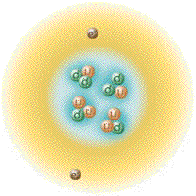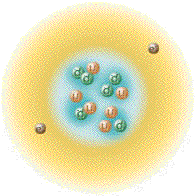
This is the currently accepted atom model.
So, let us first revise how the atom is currently described by modern physics. Electrons are said to be in constant motion around the nucleus, protons and neutrons jiggle within the nucleus, and quarks jiggle within the protons and neutrons. Electrons, protons and neutrons are considered to be 'hard' particles.
This above picture is not to scale. If we drew the atom to scale and made protons and neutrons a centimeter in diameter, then the electrons and quarks would be less than the diameter of a hair and the entire atom's diameter would be greater than the length of thirty football fields! 99.999999999999% of an atom's volume is just empty space! Do you really believe that over 99.99% of the building block of matter is just empty space? If you DO NOT, then you are on the right track. The following is a list describing the currently accepted model of the atom.
At
the center of the atom is a small, dense positively charged nucleus consisting
primarily of protons and neutrons. Protons consist of two up quarks and a down
quark (uud). Neutrons consist of two down quarks and an up quark (ddu).
2. Moving around the nucleus are negatively charged electrons which
account for only 1/5000 of the atom's mass -- the rest of the mass being in the
nucleus. Most of the atom is empty space. The motion of the electrons is not
described.
3. The electrons in an atom are allowed to have only certain energies.
The allowed states are described by a set of "quantum numbers", which
indicate their average distance from the nucleus, their angular momentum and
its direction, and the electrons' spin direction.
4. Light of a specific color is emitted or absorbed when electrons
change from one state to another.
5. The "Heisenberg Uncertainty Principle" states that the
position and momentum of an electron cannot be simultaneously determined. Since
Bohr's orbiting electron model failed to describe the actual orbital
distribution of the electron cloud, it had been concluded that the electrons
motion it not governed by any ordered motion, but is completely random. The
interpretation of the Heisenberg principle is that the atom's structure and the
interactions of its electrons are random and can be discussed only
statistically. The orbitals are therefore just a probabilistic distribution of
such a random motion.
6. Even though the electron's exact position cannot be determined, if
its energy is known, the theory predicts the probability that an electron could
be at a particular place.
7. If the probability location of an electron of known energy is plotted
in space, the plot looks like a fuzzy cloud of varying density, the shape
varying with differences in angular momentum. It always has a definite symmetry
about the nucleus. Some of the clouds or orbitals are spherical,
others are like dumbbells, while others are more complex.
8. In describing an atom with many electrons, the charge clouds of one
shell are superimposed in space with those of other shells.
The big flaws of the currently accepted atom model
Unknown to many of us, it is a fact that Einstein rejected the discrete point particle and stated that matter must be spherical entities extended in space. He writes "Physical objects are not in space, but these objects are spatially extended. In this way the concept "empty space" loses its meaning. Since the theory of general relativity implies the representation of physical reality by a continuous field, the concept of particles or material points cannot play a fundamental part, nor can the concept of motion. The particle can only appear as a limited region in space in which the field strength or the energy density are particularly high." Erwin Schroedinger understood the requirements of particle structure when he wrote in 1937: "What we observe as material bodies and forces are nothing but shapes and variations in the structure of space. Particles are just schaumkommen. (appearances)". He believed that quantum waves were real, not probability distributions with a hidden particle wondering inside. He saw that abolishing the discrete point particle would remove the paradoxes of 'wave-particle duality' and the 'collapse of the wave function'.
No atoms had even remotely been seen visually until 1985, when IBM Research Almaden Labs was the first to use an electron tunneling microscope to actually photograph the organization of molecules of germanium in an ink-blot. Here what we see from this experiment are indistinct, fuzzy spherical objects that appear to have some non-spherical geometric qualities to their shape and are in an extremely geometric pattern of organization, which was definitely a surprise for conventional science. How could the random nature of atoms described by the Heisenberg principle, ever result in such an ordered pattern? Perhaps the probability distributions are not 'distributions' at all. The image shown below was artificially colored orange and green to allow the eye to discriminate between the two types of atom that were seen:

Actual photograph of atoms of germanium in an ink-blot.
Furthermore, when quantum physicists have studied the electrons of the atom, they have observed that they are not actually points at all, not particulate in nature, but rather form smooth, teardrop-shaped clouds where the narrowest ends of the drops converge upon a very tiny point in the center.
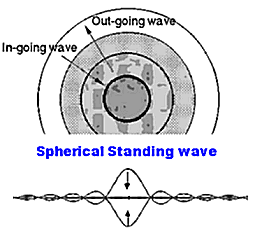
There are no Electron Orbits! Bohr's model, which started the notion of electrons traveling around the nucleus like planets has misled a lot of people and scientists. If you have learned such an idea, forget about it immediately. Instead, all calculations and all experiments show that no satellite-like orbital motion exists in the normal atom. Instead, there are standing wave patterns, very similar indeed to the polar plots of antenna radiation patterns. For example, see the case M=0 and L=0, where the standing wave pattern is entirely spherical, this being equivalent to a pure isotropic antenna radiation plot. Similarly for M=1, L=1, the pattern is exactly the same as that of a half wave dipole, and so on. No one ever asks or requires for an antenna's radiation pattern to be formed of orbiting electrons, and yet we know that the standing wave generated from a typical radio antenna, posseses inertia, and can act upon external matter by means of radiation pressure. The electron path is NOT around and far off the nucleus, nor is the atom made up of 99.999% empty space!. Instead, the center of the electron pattern is also the center of the proton pattern. This is the normal situation of the H atoms in the universe; they have spherical symmetry, not orbits. You see, particulate matter is not requirement to generate the effects known to define matter.
To complicate things further, we have got the particle-wave dual nature enigma. The classical double slit diffraction experiment using a beam of electrons instead of light, shows us that we still get a diffraction pattern. The interpretation of this is that matter travels as a wave. Further more if we arrange a setup for light to enter the slits one photon at a time, or even one electron at a time, in both cases, we still get a build up a diffraction pattern over time. One interpretation of this result is that a single photon or electron goes through both slits and interferes with itself. Thus the common statement accepted by todays textbooks is that "matter acts as both a particle and as a wave." This statement obviously leaves a lot of holes in physics, since no mechanism is defined for how the transformation from one entity to the other is actually done. So, is matter a particle or a wave in nature Actually none of them, both the wave and particle models are flawed and/or incomplete models for subatomic particles as will be shown in this research section.
|
|
|
|
Electron clouds from top-down view (L) and from side view (R). [Courtesy Wolff, 1990] |
|
|
Some of the many
possible spherical harmonics showing |
||
|
|
|
|
|
|2,0,0> |
|2,1,0> |
|2,1,1> |
|
|
|
|
|
|3,0,0> |
|3,1,0> |
|3,1,1> |
|
|
|
|
|
|3,2,0> |
|3,2,1> |
|3,2,2> |
As you can immediately recognise from the above electron distribution probability, electron shells commonly used in chemistry, together with Heisenberg Uncertainty Principle are impossible attempts to describe the above three dimensional atomic standing waves in terms of particles in motion. Now, do you find it surprising that one cannot know both position and momentum of an electron?
 Exploring the Physics of the
Unknown Universe - Milo Wolff
Exploring the Physics of the
Unknown Universe - Milo Wolff
Most of the currently accepted particles have been found by the use of a common basic tool - the particle accelerator. This is a gigantic instrument that detects the effects and products of collisions between very fast moving particles. High speed is necessary so that it is energetic enough to 'crack open' the particles in order to reveal the inner structures that make up the colliding particles. Some of these sub-particles may only exist briefly before they dissapear or change to other form of particles.
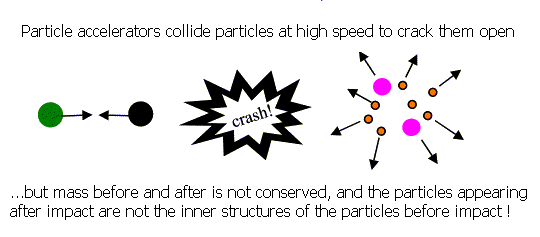
The realities of mainstream science
When two particles collide, or even combine, their total mass is not conserved, and this effect is known as the mass defect. Surely enough, modern science account 141j920b s for this fact, applying the well known Einstein's equation E=mc2, and states that the mass lost or gained is balanced by the change in bonding energy within the formed structure. All particle accelerator experiment results are currently being wrongly interpreted, because the particles appearing after impact are NOT the inner structures of the particles before impact. As we will see, in this theory, a particle is a structure, made up of an elementary unit, and not of an infinite number of a mix of smaller particles. Breaking up a structure of matter, will result in other structures which may not have existed as separate structural entities within the original particle, and the fact that most particles resulting after an impact in a particle accelerator have a very short life strengthens this idea, since how could ever a bigger structure have been formed if the chances of existance of its components are so small or nearly impossible?
The backbone of a new proposed atom model
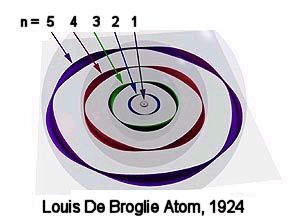

3D attempt for De Broglie model by Kenneth Snelson
It was Louis De Broglie, who for the first time in 1923, proposed that all objects have properties of waves. The lighter the object, the more pronounced the wave effect. An object as small as the electron would act very much like a wave, forming stationary waves around the nucleus. Unfortunately, his was the last of the accepted "physical" models, since just 5 years later, Werner Heisenberg derived his "Uncertainty Principle" which states that it is impossible to determine simultaneously the momentum and position of an electron. Such a principle has been widely accepted and to the present day, science gave up the search for a 'physical' model. De Broglie model is correct in principle, but is too simplistic and cannot account for all the experimental observations done on atoms. For this model to be complete, we first need to transform the 2D Broglie diagram into a 3D spatial equivalent, because we know that an atom occupies a volume. Shown above is one such attempt by Kenneth Snelson to render such a model. Also, Milo Wolff's spherical space resonance model introduced in the 80's, shows us the requirement for incoming and outgoing waves for the production of spherical standing waves.
 Video
interview of Milo Wolff by Geoff Haselhurst about the wave structure of matter
Video
interview of Milo Wolff by Geoff Haselhurst about the wave structure of matter
Here is a list of statements that I believe define a much more accurate model of the atom. This model is fully consistent with all experimental evidence (both wave and particle), the Heisenberg uncertainty principle, as well as quantum mechanics (QM). The backbone of this model is based on Louis De Broglie simple model, which is further elaborated and explored in the following pages. In the following pages we will explore together, refine this model and also solve a few enigmas introduced by this model.
Standing wave theory of matter
1. The universe is not made up of matter and vacuum, but instead
is comprised of standing and travelling electromagnetic (EM) waves. A standing
wave appears to have both momentum and inertia when interacting with another
standing wave, thus giving us the impression of 'hard particles' hitting each
other. The interaction between living organisms (which consist of cells, atoms,
and standing waves) and other standing waves give us the sense of touch - the
most misinterpreted sense of all!
2. All experimental attempts to probe the internal structure of the
electron have proved futile. For that reason, despite its size, the electron is
considered by conventional science to be an elementary particle - a particle
with no internal structure!
3. The substantiality of mass (i.e., its hard particle nature) is redundant
because it can always be converted to electromagnetic energy, which has no
particle properties. This has a serious implication on Newtonian physics, as it
would become merely a redundant branch of science.
4. No theory exists in quantum mechanics that can predict the size of an
electron, its mass, or its charge. Moreover, there is no theory that quantifies
the particle in a meaningful calculation. This implies that QM actually has no
need for a particle concept, because all the calculations are the same whether
or not you believe in hard particles. It is interesting to note that QM
equations still hold true when applied to an electrical entity that can exhibit
momentum and inertia.
5. The atomic nucleus, along with its electron cloud teardrop shapes,
would be also seen if an electron microscope were used to view a resonant
antenna. One would also see different electron wave patterns (or shells) with
different types of antennas, within their nearfield region. But what you see is
not necessarily real and what is real cannot necessarily be seen. If we define
reality, as conventional physics does, as that which is tangible to our senses,
many of our observations become mysterious and unexplainable, which is
precisely the current situation.
6. A 3D standing electromagnetic wave can be thought of as a structured
volume defined by three orthogonal electromagnetic energy vectors, equating to
(T/S)x * (T/S)y * (T/S)z = T3/S3,
the space-time dimensions of mass.
7. A travelling electromagnetic wave alone does not possess the
properties of momentum and inertia, and one EM wave can cross another EM wave's
path with no effect on either. However, a 3D standing EM wave has totally
different characteristics and does have its own momentum and inertia.
Thus momentum or pressure can only be present in the presence of a standing
wave, during that standing wave's interaction with either another standing wave
or with an external travelling EM wave. Momentum is given by P = h / l, where
l is the wavelength of each element forming the standing
wave structure. This means that no motion can exist without standing waves.
This makes a great deal of sense when we consider that no motion can be
observed if there is no particle to be observed.
8. Spherical resonance is what drives the entire observable universe.
Resonance determines the behaviour of the trapped EM waves in the form of
atomic particles. Resonance also determines the behaviour of the electrons in a
hydrogen atom. The various shells of the electron are simply the result of
resonance. Only those orbits that create standing electric waves will be
stable. Non-standing wave orbits disintegrate immediately, as they do in short
half-life isotopes. It is not a matter of some mysterious
"prohibited--permitted" decision; it is a matter of resonance that
can easily be calculated without resorting to quantum theory or the like.
Quantum mechanics' "prohibited orbits" are merely non-standing wave
orbits that cannot exist.
The observed teardrop shape of an electron cloud is exactly what we would expect when seeing a 3D standing wave of vibration. We remember that the hydrogen atom's electron cloud was seen to have a spherical shape, which is the same shape as an isotropic antenna's radiation. So the nucleus is just a 3D structure of oscillating electrical elements, while the electron cloud is the nearfield standing wave of the resulting oscillation, and the point where the teardrop shape of the cloud converges is simply the node of the standing wave. The electron is in fact known to be a Broglie wave (wave of matter) that interferes with itself. The so called 'electron cloud' around the nucleus can only be stable when it meets the condition of a standing wave. As we will see further on, the consequence of all this is that only certain values of radius and energy are permitted.

Mathematical proof that the
electron is a spherical electromagnetic standing wave
Let's find the 'mass' of a spherical standing wave having the same diameter and
charge of the electron:
Starting from the equation for the capacitance of an isolated spherical charge:
C= 4.p e .r
The total internal energy stored in an electromagnetic standing wave = Electric
field energy + Magnetic field energy, where Electric field energy = Magnetic
field energy, hence:
Total internal energy E = 2 * Electric field Energy = 2 * Magnetic field energy
... so it's enough if we solve for one of these to get the total internal
energy for an electron.
Total internal energy E = 2 * Electrical Energy = 2* (1/2QV) = QV ... where
V=Q/C
Total internal energy E = Q2/C ... substitiuting for C, we get
Total internal energy E = Q2/(4.p e .r),
Substitiuting for Q=electron charge=1.602E-19 Coulombs, r=classical electron
radius= 2.8179E-15 m, and e =
permittivity of free space = 8.854E-12 F/m
Total internal energy E = 8.18735E-14 Joules
Using E=mc2, we get
Electron standing wave mass = 9.1096E-31kg ... which is the known electron
mass.
This clearly shows that what we call electron mass is nothing but the
electromagnetic effect of a spherical standing wave.
Synergetics
Replacing the outdated Cartesian system
We are living in a period of such absurdly blind acceptance of the Cartesian system of co-ordinates, based on the cube structure with three axes in 90 degree co-ordination developed more than four centuries ago. Instead, more recently, Buckminster Fuller, came out with a much more natural way of co-ordinate system based on his invention of the geodesic dome, a structure of triangularly-interconnected elements that has the best ratio of weight to enclosed space of any artificial construction so far developed. More recently, Fuller has received much public acclaim for having predicted, with his geometry, the existence of spherical molecules. The experimental discovery of the Buckminster fullerene, a spherical and extraordinarily stable large molecule of carbon, is only a few years old.
|
|
Departing from convention, this geometry replaces the cube with the regular tetrahedron as its principal unit of volume. The four-sided tetrahedron is the simplest possible enclosure, which is why mathematicians call it a "simplex". Drawn as a cage, or wire frame, it has four windows, four corners and six edges. No space-enclosing network has fewer windows (facets) than four. The cube (or hexahedron), by contrast, has six facets, eight corners, and twelve edges.Given the status of the simplex as "simplest space-enclosing network", the decision to use its regular form as a unit of volume makes some sense. As a consequence of this decision, we obtain whole number volumes for other familiar shapes (including for the cube). |
|
Fuller's geometry goes by the name of Synergetics and has been developed by experimentally observing the behaviour of spheres of equal diameter, when packed as close as possible to form regular geometric figures. The basic and most simple stable geometric configuration of synergetic geometry is the tetrahedron, formed by four spheres laying next to each other, in perfect triangular configuration forming four angles of 60 degrees. Other important elements are the octahedron (formed by six closest-packed spheres) and the vector equilibrium, which is the result of twelve spheres nested around a thirteenth, central sphere, in omnidirectional closest-packing, 60 degree co-ordinated configuration. The cube, which is at the basis of our present-day construction methods and of the x-y-z Cartesian co-ordinate system, is not in and by itself a stable configuration. Eight spheres forming a cube are inherently unstable. To gain stability, they must be artificially stabilised by interconnecting them in the way the tetrahedron is connected. In this way, two tetrahedra of four spheres each, joined at their respective centers, form one cube of eight spheres. The cube and dodecahedron are both space-fillers, meaning they fill space without gaps. The tetrahedron and octahedron fill space in complements with twice as many tetrahedra as octahedra. |
|
|
|
It happens that this geometry, as developed by Fuller, is in perfect accord with how crystals grow in their various forms, and that its application in engineering reveals to us the possibility of very efficient structures in terms of economy of raw materials and strength of the resulting construction. |
Now how could the discoveries of Fuller be utilised to
form a co-ordinate system and why should we venture to do such a task, seeing
that the Cartesian x-y-z co-ordinates have done perfect (or almost perfect)
service for such a long time?
For one, Cartesian co-ordinates may be a convenient mathematical construct, but
they do not accord with nature's ways any more than modern chemistry will ever
be able to duplicate the conditions of living organisms.
From waves to particles
by standing waves in space
We have shown that the atom can be perfectly modeled by a standing wave pattern much in common with that of a radio antenna. The problem to visualise matter as being composed of a volume of electromagnetic waves is the fact that matter has got a structure, whilst an EM wave does not. It is true that EM waves have no structure, and are continously vibrating, but EM waves can be 'trapped' within a volume of space, given their dimensions are exact multiples of Planck's half wavelength, forming what is commonly called a standing wave. The nodes within the standing wave form the structure. All objects have a frequency or set of frequencies with which they naturally vibrate when struck, plucked, or somehow given an impulse, these are called the natural frequencies. Each of the natural frequencies at which an object vibrates is associated with a standing wave pattern. When an object is forced into resonance vibrations at one of its natural frequencies, it vibrates in a manner such that a standing wave is formed within the whole object. A standing wave pattern is described as a vibrational pattern created within a medium when the vibrational frequency of a source causes reflected waves from one end of the medium to interfere with incident waves from the source in such a manner that specific points along the medium appear to be standing still. Such patterns are only created within the medium at specific frequencies of vibration; these frequencies are known as harmonic frequencies, with the first harmonic referred to as the fundamental. In our context, this fundamental harmonic is highly related to Planck's length. At any frequency other than a harmonic frequency, the interference of reflected and incident waves results in a resulting disturbance of the medium which is irregular and non-repeating. Our medium is the vacuum through which EM radiation is well known to be able to propagate and vibrate.

Tip of a platinum needle enlarged 750,000 times.
Are those 'hard particles' or standing waves?

Field ion microscope image of a 'single crystal' tungsten
tip.
Are those 'hard particles' or standing waves?

Water standing waves formed with vertical oscillation in a circular dish
On the first two photos, you can see typical images from field ion microscope for platinum and tungsten tips. The bright areas correspond to positions on the tip where the electric field is particularly high, i.e. where the local radius of curvature of the crest of the wave is particularly small. In the lower photo we see water waves formed with 280 Hz vertical oscillation in a 6.3 cm circular dish. The particle like waves travel about independently when a medium strength oscillation is applied. This is very suggestive that atomic particles are similarly formed as standing waves. Some non-linearity is necessary to have stability. In this case it is supplied by the different rate of acceleration applied to the water from above (by gravity) and below (by pressure). Surface tension applies in both directions.
So the natural frequencies of an object are merely the harmonic frequencies at which standing wave patterns are established within the object. These standing wave patterns represent the lowest energy vibrational modes of the object. While there are countless ways by which an object can vibrate (each associated with a specific frequency), objects favor only a few specific modes or patterns of vibrating. The favored modes (patterns) of vibration are those which result in the highest amplitude vibrations with the least input of energy. Objects favor these natural modes of vibration because they are representative of the patterns which require the least amount of energy. Objects are most easily forced into resonance vibrations when disturbed at frequencies associated with these natural frequencies.
|
|
The wave pattern associated with the natural frequencies of an object is characterized by points which appear to be standing still; for this reason, a pattern in 2D is often called a "standing wave pattern", whilst we may call a pattern in 3D, a "standing wave structure". The points in the structure which are at stand-still are referred to as nodal points (in 2D) or vertex positions (in 3D). These positions occur as the result of the destructive interference of incident and reflected waves. Each nodal point is surrounded by anti-nodal points, creating an alternating pattern of nodal and anti-nodal points. A classical two dimensional demonstration utilizes a square metal plate (known as a Chladni plate), a violin bow and salt. The plate is securely fastened to a table using a nut and bolt; the nut and bolt are clamped to the center of the square plate, preventing that section from vibrating. The salt is then sprinkled upon the plate in an irregular pattern. Then the violin bow is used to induce vibrations within the plate; the plate is strummed and begins vibrating. At a certain violin tone, a high-pitched pure tone is sounded out as the plate vibrated; and, remarkably the salt upon the plate begins to vibrate and forms a pattern upon the plate. The pattern formed by the salt on the plate is the standing wave pattern associated with one of the natural frequencies of the Chladni plate. As the plate starts to vibrate, the salt begins to vibrate and tumble about the plate until they reach points along the plate which are not vibrating. Subsequently, the salt finally comes to rest along the nodal positions. The diagrams show two of the most common standing wave patterns for the Chladni plates. The white lines represent the salt locations (nodal positions). Observe in the diagram that each pattern is characterized by nodal positions in the corners of the square plate and in the center of the plate. For these two particular vibrational modes, those positions are unable to move. In a 3D standing waves, a structure, with all charactesitics of a platonic solid, is formed for each standing wave mode. Within an atom, which is the building block of matter, the platonic solid is not formed by salt or known particles, but by electromagnetic waves in vacuum. The final result, the standing wave structure, is one which has a structure, an inertia, a reaction to other standing wave structures, and a reaction to external EM waves, all characteristics of what we use to call 'a particle', which can be felt and seen. As we shall see later on, particles are point effects of the standing wave nodes. |
|
|
|
Both the students of Buckminster Fuller and his protege Dr. Hans Jenny devised clever experiments that showed how the Platonic Solids would form within a vibrating / pulsating 3D sphere. In the experiment conducted by Fuller's students, a spherical balloon was dipped in dye and pulsed with pure sinewave sound frequencies. A small number of evenly-distanced nodes would form across the surface of the sphere, as well as thin lines that connected them to each other. If you have four evenly spaced nodes, you will see a tetrahedron. Six evenly spaced nodes form an octahedron. Eight evenly spaced nodes form a cube. Twelve evenly spaced nodes form the icosahedron and twenty evenly spaced nodes form the dodecahedron. The straight lines that we see on these geometric objects simply represent the stresses that are created by the closest distance between two points for each of the nodes as they distribute themselves across the entire surface of the sphere. |
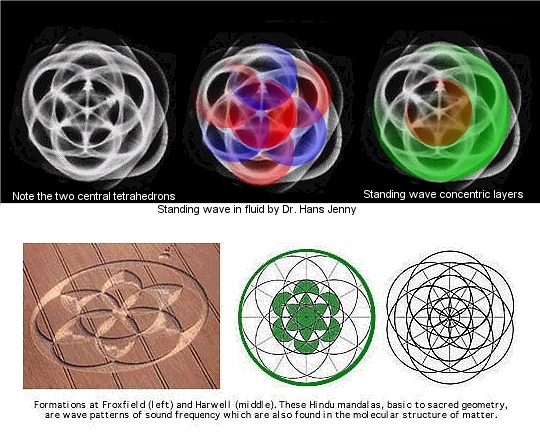
Dr. Hans Jenny conducted a similar experiment, wherein a droplet of water contained a very fine suspension of light-colored particles, known as a colloidal suspension. When this spherical droplet of particle-filled water was vibrated at various diatonic musical frequencies, the Platonic Solids would appear inside, surrounded by elliptical curving lines that would connect their nodes together. As we shall see, these dark points, which are nothing but point of intersections of nodes are the supposed 'point bits of matter'.
From waves to particles
The Oscillon

Photos courtesy of Paul Umbanhowar (
When a bed of dry granular material or fluid is subject to
vertical vibration at certain frequencies, pattern formations start to appear
at the surface when the modulation exceeds a critical value. These waves have a
frequency which is half that of the driving oscillations (the first
sub-harmonic). This effect was first reported by Michael Faraday in 1831.
In ordinary Newtonian fluids, those that do not exhibit shear thickening or
shear thinning, the wave patterns include ones with 1-fold symmetry (stripes),
2-fold symmetry (squares), and 3-fold symmetry (hexagons).
Many of the same patterns seen in the liquid version of Faraday's experiment
are also seen in the granular material. These patterns are in fact the same
phenomena observed on the chladni plates discussed earlier. At lower
frequencies however, a new phenomena has been observed, that of localized
structures called "oscillons". The granular version of this experiment
is done at the
Oscillons can be seen in the image on the lower right of the photographs shown
above. They resemble a splash of water in a puddle, but with one important
difference: instead of spreading out, they slosh back and forth between a state
that resembles a crater and a state that resembles a peak. When one oscillon in
a crater state collides with an oscillon in the peak state, they can form a
bound system, as shown in the image on the lower right.
In shear thinning non-Newtonian liquids, theory suggests that localized
structures analogous to granular "oscillons" should be found. These
have recently been observed in experiments using clay suspensions as shown
below.

Simulating what happens when you shake a box of granular
material such as sand, researchers at the
Particle-like localised excitations in a bed of sand can form into molecules
and even crystals structures. At a certain frequency the energy put into the
system manifests itself as small isolated heaps of sand (about thirty grains in
diameter) which also bob up and down. These heaps, termed
"oscillons," are stable (holding together for thousands of shakings)
and able to slowly drift across the sand bed. This is not like a travelling
wave, were the moving peak is being shaped by different particles, but here the
same grains drift around. And just as with electrical charges, when it comes to
oscillons opposites attract. As long as their centers are within 1.4 diameters
of each other, oscillons of opposite phase (one at its peak height and one at
its shallowest depth) can enter into a dipole state to form a sort of molecule.
This peak-crater pair binding may lead to more complex molecules and even long
chains of oscillons which, under the right conditions, can grow into
extended patterns. Current theories give us no definite answer as to how and
why the oscillons form and interact, but such localized structures may exist in
other dissipative systems (systems which steadily exchange energy), and not
just in granular materials.

Oscillons are a soliton-like phenomenon emerging from
batches of vibrated particles. Basically, researchers are studying them mostly
empirically at this point. They've shown a coupling effect where smaller
oscillons join into larger ones via waves of attraction. These waves of
attraction or repulsion between them propagate through vacuum and seem to be
driven by a force whose aim is to complete a defined pattern.
Schroedinger-wavelike phenomena ensue also. In general oscillons have been
observed when a large number of balls of less than 0.1 millimetres in radius
are vibrated in a tray at between 10 and 100 Hz. They have so far been produced
using a wide range of materials, particle sizes and frequencies of vibration.
Oscillons are very stable and long lived, some having been observed to last for
millions of cycles. Oscillons pulse up and down in the same way as standing
waves in a fluid, such as the water waves discussed in the previous section.
Because these structures attract or repel each other in vacuum as well as in air,
depending on their relatives phases, they appear to
act as charged particles. This is clear evidence that two neighbouring standing
waves show the property of charge attraction & repulsion.
One of the neatest aspects is that the models predict 'mass' for the
fundamental oscillons. I know of no modern physics theory that can claim this.
All other theories assume fundamental particle masses as given constants. So,
again, the 3D standing wave theory is fully compatible with the soliton mass
predictions, because it defines the mass property as a property of space
structure and not as a built in constant of particles. Again, despite continous
research since 1996, oscillons seem to have totally escaped the attention of
mainstream particle physicists as a model or direction of pursuit.
Sonoluminescence
Ionising gas into plasma by resonance
 Sonoluminescence (SL)
was first observed in an ultrasonic water bath in 1934 by H. Frenzel and H.
Schultes at the
Sonoluminescence (SL)
was first observed in an ultrasonic water bath in 1934 by H. Frenzel and H.
Schultes at the
Putterman pursued SBSL, published numerous papers, and
established many of the characteristics which are now taken for granted. Once per
acoustic cycle (1/30kHz), coincident with a sharp
decrease in bubble size, bluey-white light is emitted in a brief flash in the
order of 10 picoseconds in duration, with incredible regularity, and broadband
spectrum, including at least the UV range. The spatial images show a bright
spot in the source with a diameter of about 3 microns, or less, and a larger
diffused region with a diameter of 50 to 100 microns. Scientists
don't even know whether the bubbles emit X rays, a
sign of very high temperatures. Water absorbs X rays, making it futile to try
to detect them from outside the flask. Despite the results that have been
obtained, the actual mechanism by which sound is converted to light remains
elusive, not least because of the difficulty in measuring the conditions inside
a pulsating bubble whose diameter is measured in micro-meters. It is known that
the bubble contracts violently, and at the same time the brief flash is
emitted, after which it expands again and oscillates about its original
equilibrium radius, until it is again stable, ready for another pulse. The
addition of a small amount of noble gas (such as helium, argon, or xenon) to
the gas in the bubble increases the intensity of the emitted light
dramatically. Conventional physics tries to explain SL as the adiabatic compression
of the bubble which leads to very high interior temperatures. The issue is
still hotly debated and possible explanations include shocks, plasmas,
ionisation and photo-recombination, Bremsstrahlung radiation, and even fusion.
Considering one needs just about one watt of audio power to start
observing such effects, sonoluminiscense is to say the least a very efficient
energy converter. As you will see in the 'States of matter' table given below,
the next higher energetic state of a gas is indeed plasma. But how on earth may
one totally ionise a bubble into plasma with just one Watt of power. The trick
is resonance, same as shattering a glass with singing, pulverising a kidney
stone with ultrasonic or collapsing a bridge with resonant wind vibrations.
Once you subject the octahedron structure of a gas to the correct resonance
frequency, you need just enough power to 'get loose' the constituent
tetrahedrons (plasma) from the gas structure. Current estimations for the
bubble temperature and pressure indeed confirm plasma formation. Temperatures
have been estimated to range from 10 to 100eV (1eV = 11,600K or 20,420 degrees
F); that is as hot as the corona of our sun. The pressures are as high as
200Mbar (1Mbar = 1011 Pa) in the core of the imploding bubble. This
pressure is equal to 1.974*108Pa or 19,743,336 atmospheres. The only
state of matter which can exist under these conditions is plasma.
The Glass shattering experiment
Weakening glass' intermolecular structure
 This Quicktime movie shows the classical
shattering of a wine glass when in resonance using a 5 Watt sine wave audio
tone in the range of 800Hz. Play the movie and watch carefully the motion of
the glass rim. You will see that the radius of the rim of the wine glass is
actually deforming by as much as 5 mm!! There is no way that such thing could
be done under non resonant conditions without heating up the glass in a
furnace. At room temperature, the glass is normally so brittle that it would
shatter as soon as the rim is deformed by 1 or 2mm. This 'jellification effect'
indicates that resonance weakened the actual intermolecular force and made them
similar to those within liquids, thus inreasing the elasticity of glass. So,
the audio energy in this experiment is used to modify the solid state of glass
into the next higher state of matter, to give it liquid state characteristics,
making it more elastic. At this point I have to point out that there is no
overunity here.
This Quicktime movie shows the classical
shattering of a wine glass when in resonance using a 5 Watt sine wave audio
tone in the range of 800Hz. Play the movie and watch carefully the motion of
the glass rim. You will see that the radius of the rim of the wine glass is
actually deforming by as much as 5 mm!! There is no way that such thing could
be done under non resonant conditions without heating up the glass in a
furnace. At room temperature, the glass is normally so brittle that it would
shatter as soon as the rim is deformed by 1 or 2mm. This 'jellification effect'
indicates that resonance weakened the actual intermolecular force and made them
similar to those within liquids, thus inreasing the elasticity of glass. So,
the audio energy in this experiment is used to modify the solid state of glass
into the next higher state of matter, to give it liquid state characteristics,
making it more elastic. At this point I have to point out that there is no
overunity here.
In an oscillating system at
resonance, one pours power in small amounts, but the energy thus transferred
gets accumulating in the system (actually in the standing wave). It is a common
misperception to think that with few energy we produce
lots of work. We just keep accumulating slowly the energy, by putting a little
power over a relatively long time, and then we release the same amount of
energy in a relatively short time, giving a tremendous energy per unit time,
that is power. Same applies to sonoluminiscense and all other resonance
phenomena mentioned here.
How to conduct the experiment
This demonstration requires a fair amount of
equipment. A 10Watt stereo amplifier, whose output goes to a horn driver near
the wine glass to be broken, can be switched between a frequency generator,
easily tuned through a broad spectrum, a video camera, and a frequency
synthesizer which can generate a very accurate frequency, at about 0.1Hz steps.
Alternatively, if your frequency generator is of the digital type and accurate
to 0.1Hz and is powerful enough, you can use it instead of the synthesiser. The
response of the wine glass to the sound is monitored with a microphone
connected to an oscilloscope. The first four steps can be prepared before the
lecture, but most instructors like to run through them with the class so the
students can see the entire operation.
Flick the wine glass with you finger to
"ring" it. With the amplifier set at low hearing volume, tune the
frequency generator until you hear a similar pitch.
Watching the response on the scope, tune the
frequency generator until you hit the resonance of the wine glass where the
signal on the oscilloscope becomes much larger.
Read off the approximate resonance frequency from
the frequency counter and enter this number on the frequency synthesizer.
Switch the amplifier over to the frequency synthesizer input.
With the synthesizer in the "edit" mode,
change the frequency one hertz at a time until you hit the resonance again. Now
tune by tenth hertz until you reach the maximum peak.
Move the microphone away from the wine glass and
place the Plexiglas shield in front (to prevent broken glass from spraying into
the class and the video camera).
Start video recording and turn up the amplifier
volume to quite loud and the glass will break. The sound is loud, but not
painful to the operator. At the position of the glass, it is approximately 140
dB. View video in slow motion to see what's happening.
Huge atom structures
From SL micro-metre bubbles to 1 metre Light balls
 Light balls are
sometimes called Ball Lightning which is a misnomer since they do not look like
or relate to lightning. Actually is looks more like a huge sonoluminescent
bubble floating in air. It usually appears as a mysterious glowing sphere which
drifts through the air. It can also appear to bounce along the ground. Light
balls are described as glowing balls of plasma. The phenomena usually lasts for
only 5 seconds, but sometimes remains longer for up to a few minutes. Some of the
balls are blindingly bright, others have almost no
illumination and appeared grayish. The temperature within was evaluated to be a
little bit higher than the solar temperature; 6,500 Kelvin degrees, however
these were also reported to pass through glass and being touched with no
burning effects, and also do not float up as would do a hot object. These
plasmas can suddenly change in size and shape without any change in their
measured temperature.
Light balls are
sometimes called Ball Lightning which is a misnomer since they do not look like
or relate to lightning. Actually is looks more like a huge sonoluminescent
bubble floating in air. It usually appears as a mysterious glowing sphere which
drifts through the air. It can also appear to bounce along the ground. Light
balls are described as glowing balls of plasma. The phenomena usually lasts for
only 5 seconds, but sometimes remains longer for up to a few minutes. Some of the
balls are blindingly bright, others have almost no
illumination and appeared grayish. The temperature within was evaluated to be a
little bit higher than the solar temperature; 6,500 Kelvin degrees, however
these were also reported to pass through glass and being touched with no
burning effects, and also do not float up as would do a hot object. These
plasmas can suddenly change in size and shape without any change in their
measured temperature.
Nominal size of reported light balls being the size of an orange or grapefruit. The diameter of the balls range from a few centimeters to a few meters, with the average around 20 cm. They are sometimes oval, cylindrical, flame, pear, ring, blob shaped or even cornered shapes like a cube. Cylindrical forms can sometimes be flattened, bent, or twisted into a variety forms. Sometimes they have halos, sparks, or radial streamers around them. Some appear to be fibrous. Some are solid in appearance, others are hollow.
|
|
An enlarged picture of the rectangular
plasma formation after changing from a sphere, as well as the corresponding
3-D Point Spread Function (PSF) that is used in order to simultaneously
obtain the peak intensity and the apparent dimension, in pixels, of the
target. |
Various colors of ball lightning have been seen. Sometimes
the colors change as well. The phenomena usually occurs
during or right after a thunderstorm. In most surveys about 70% occured right
after a lightning strike.
Ball lightning has also been seen without any detected electrical storm. In a
shockingly high percentage of cases the balls actually entered in buildings -
through windows and doors. Sometimes they cause no damage to property - yet
other times they burn holes. Balls have been reported as eminating from
tornadoes, cyclones, and hurricanes. In these cases high electric fields are
present.
Light balls have been seen on many occasions traveling along fences or power
lines. Sometimes they appear to roll, spin, hop, or vibrate. Some of them have
been possible to view only under infrared vision and they were observed to
continously flip their shape from spherical to cube.
Some people believe that ball lightning movement is guided by electric fields
EM energies), which might explain their attraction to conductors. There
movement doesn't seem related to wind speed or velocity. Ball lightning
sometimes carries a significant charge, and sometimes no charge. Some witnesses
have reported being seriously shocked and others not at all. People have
sometimes gotten burns similar to those caused by ultraviolet radiation from
touching ball lightning. Most reports show no evidence of radiant heat from the
balls, even at close range. Most researchers agree that ligtning balls are
real, but no one knows exactly what they are. Researchers are also unable to
reproduce free floating ball lightning, however you
may try to create a plasma ball in your microwave oven. More details here.
This experiment shows that plasma balls are real and that energy can be trapped
in a bubble or 3D space. We know that these light balls in general emit light,
and can be considered to be a huge 3 dimensional electromagnetic standing wave
structure. It has the same properties as an unstable mass, in that it radiates
light, and most probably other forms of radiation. Due to it being unstable, it
is very similar to a fast decaying radioactive substance. Unlike a stable atom,
following our atom model, the structure will not be stable, but will break down
slowly from a complex structure (resembling a sphere) to simpler structures
similar to the basic platonics. Once the basic platonic breaks down, the light
ball disappears. This also explains the fact that people saw these light balls
change into cornered shapes before they disappear. In a way, the decay of a
light ball is similar to dismantling a crystal structure back into its
elementary components.
By Engineer Saviour - Blaze Labs
Hutchison Effect
Melting solids into liquids without heat

We know that the state of matter can be changed from one to the other of the four states in the order: Solid - Liquid - Gas - Plasma, by means of increasing or decreasing external energy supplied to the structure. The most common example is water, which when heated changes from liquid to gas and when cooled changes into a solid block of ice. But heating and cooling are just the most inefficient ways to change the state of matter. The state of matter shift occurring with the change of temperature, seems to be only a by-product of the heating, which means that only a part of the energy accumulated in the system is used on weakening the molecular bonds, the most of it going to Brownian kinetic energy in atoms and molecules as large bodies. Therefore, finding the resonance frequency (or harmonics) of the molecular bonds would be indeed a much more efficient way of changing the state of matter.
The Hutchison Effect is a collection of phenomena which were discovered accidentally by John Hutchison during attempts to study the longitudinal waves of Tesla back in 1979. The Hutchison Effect occurs as the result of radio wave interferences in a 3 dimensional zone space volume radiated by two or more high voltage sources, usually a Van de Graff generator, and two or more Tesla coils. The results are levitation of heavy objects, fusion of dissimilar materials such as metal and wood (as shown in the upper right corner of the photo), the anomalous melting (without heating) of metals without burning adjacent material, spontaneous fracturing of metals (which separate by sliding in a sideways fashion), and both temporary and permanent changes in the crystalline structure and physical properties of metals as shown above. The fusion of dissimilar materials, which is exceedingly remarkable, indicates clearly that the Hutchison Effect has a powerful influence on intermolecular forces. Dissimilar substances such as steel and copper or wood can simply "come together," yet the individual substances do not dissociate. A block of wood can simply "sink into" a metal bar, yet neither the metal bar nor the block of wood come apart or carbonise. On the lower left corner of the photo, you may see the imprint left over by coins which were sitting on top of the steel bar during the effect.
The anomalous melting of metal without any evidence of heating, burning or scorching of the adjacent materials (usually wood) can be easily explained if one considers the external high voltage intermediate frequency source to be resonant with the molecular structure of the metal. In such a case, resonance will efficiently use up the external energy to change the metal structure, to the next higher energy level structure which is the liquid state. Thus the metal structure will take over liquid properties, and any foreign solid material, such as wood or different metal, will 'sink' into it. Once the oscillation is switched off, the foreign material will be permanently trapped within the solid structure. The radio wave interferences involved in producing these effects are produced from at least two radio sources, with the correct frequency difference, both operating at low power. However, the zone in which the interferences take place is stressed by hundreds of kilovolts oscillating at the intermediate resonant frequency.
Platonic Solids & States of matter
What's so important about them?
The Platonists symbolised the elements, one with each of the platonic solids. Earth, Water, Air, Fire and Ether are (in sequence of gross to subtle) representative of the basic building blocks of the universe, or states of matter. Although conventional physics refers to solids, liquids, gases, and plasma as the 1st, 2nd, 3rd, and 4th state of matter respectively, it would make more sense to reverse the order, with plasma the first and solids the last, making them ordered in terms of their platonic solid structure complexity. There are ONLY FIVE natural frequency modes for spherical EM standing wave, resulting in the formation of the five Platonic solids shown below. Each platonic would result in the formation of a stable form of matter, anything in between will tend to be unstable, and will degrade to its nearest stable form, giving off its extra elements as EM energy, with radioactive elements being such an example.
|
SHAPE |
ELEMENT |
STATE |
PROPERTIES |
|
Dodecahedron |
Earth |
Solid |
Molecules are limited to vibration about fixed position. Solids have a definitive volume and shape and high density. When energy is applied to a solid (eg heated) the solid becomes a liquid at its melting point. The solid phase is the lowest energy state of matter. See Hutchison effect. Speed of sound in steel is 5960m/s, for glass 5640m/s. |
|
Icosahedron |
Water |
Liquid |
Molecules free to move throughout the liquid but held by intermolecular forces, giving it a definitive volume but no definite shape and a lower density. When energy is applied, evaporation occurs and it becomes a gas at its boiling point. If energy is lowered it becomes a solid at its freezing point. Speed of sound in water is 1482m/s. |
|
Octahedron |
Air |
Gas |
In gas state, molecules are free to move in every direction, and a gas has no definite shape or volume and its density is lower than liquids. When energy is applied, electrons gain enough energy to leave the atom structure and a gas starts getting ionised. When fully ionised it becomes a plasma. See sonoluminescence. If energy is lowered a gas becomes a liquid. Speed of sound in air is approx 343m/s but dependant on pressure, temperature. For Helium it is 965m/s! |
|
Tetrahedron |
Fire |
Plasma |
When a gas is given energy, molecules are torn apart into their component atoms and individual electrons are pulled away. This highly energised mixture of electrons and ions forms the plasma. If energy is lowered, plasma becomes gas. If plasma is given further energy, the atom structure within it is broken into its constituent electromagnetic energy and can no longer be considered a state of matter. Indeed the Plasma phase is the highest energy state of matter. |
|
Cube |
Universe |
Ether |
The ether in itself has no structure, and is not a state of matter. The cube is in fact not a stable structure and symbolises the orthogonal EM wave mechanism, but is also the only space filling shape. Ether is packed with pure electromagnetic energy, which can be organised in a tetrahedron structure to become a basic stable structure - plasma. Ether is energy in its purest form and giving more energy does not change its state. Ether is thus a sea of energy which cannot be detected unless an imbalance is created (example: casimir plates). |
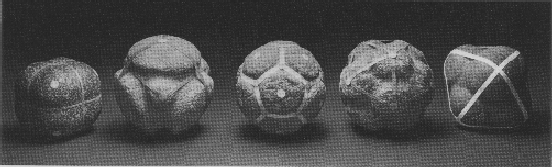
Euclid, 300 BC and the Ancient Greeks, in
their inherited love for geometry, called the five solids shown below, the
atoms of the Universe. In the same way that we today believe
that all matter, is made up of combinations of atoms so the Ancient Greeks also
believed that all physical matter is made up of the atoms of the Platonic
Solids and that all matter also has a mystical side represented by their
connection with earth, air, fire, water and aether. Similar to our conventional
atom model which shows a nucleus surrounded by electrons in orbits creating
spheres of energy, the Greeks felt that these Platonic solids also have a
spherical property, where one Platonic Solid fits in a sphere, which
alternately fits inside another Platonic Solid, again fitting in another
sphere. It is fascinating to see how any one of these solids can fit inside one
another. The concept of one sphere fitting inside another sphere is
surprisingly frequently seen in different cultures. Indeed, the mechanism of
platonic solids is so perfect, that perhaps as we are approaching in this
study, their concept of platonics as being the building blocks of matter, might
be more evolved than our present knowledge of the atom model. As shown in the
photograph below, as in so many other aspects of their science and philosophy,
the Greeks were not the originators of these concepts. The photograph is of a
collection Neolithic stones, unmistakably showing the same basic
"platonic" shapes. These (from the
What's so special about these geometric shapes? Here are the main rules for these geometric solids:
The platonic solids are those polyhedra whose faces are
all regular polygons, which means they have congruent
legs and angles. Leonhard Euler (1707-1783) who was a Swiss mathematician,
noticed that no matter how one cuts a sphere into polygons, sometimes called a
triangulation, there is a quantity which remains constant; in other words,
there is a number related to the sphere independent of the triangulation. This
number is now called the Euler characteristic. Each of the platonic solids is
in fact a triangulation of the sphere into polygons.The Euler characteristic is
given by F-E+V, where F is the number of polygonal faces, E is the number of
edges, and V is the number of vertices in the triangulation. Euler showed that
for any triangulation of the sphere, we get an Euler characteristic equal to 2,
no matter which platonic solid is chosen.
|
|
Each shape can be attached to a multiple number of the same shape or other platonic shape to generate a bigger platonic solid or even a non platonic one, as happens during generation of crystals. In a way, one may regard a crystal lattice structure as a picture of the mechanism within the atom itself. So as you see, this theory works well at quantum level as well as at molecular level, which makes it unique. |
|
Similar to the two-dimensional case of the Chladni plate,
the Platonic Solids are simply representations of waveforms in three
dimensions. Each tip or vertex of the Platonic Solids touches the surface of a
sphere in an area where the vibrations have canceled out to form a node. Thus,
what we are seeing is a three-dimensional geometric image of vibration /
pulsation within a sphere.
This explains why an atom does not necessarily look spherical. It does not
however indicate that an atom is restricted to any particular size, and this
means that an atom mechanism can be 'grown' as much as its spherical boundary
is set. We know, from the art of growing crystals, that a crystal tends to use
up similar atoms to grow up, retaining its original structure.
Sonoluminescence, described earlier, we see how a mechanism in all respects
similar to an atom can be setup to work in the size of a small bubble, many
times greater than any known atom. As we can see, we no longer have to restrain
atoms to a certain size; they are capable of existing on various scales and
maintaining the same properties. Once we fully understand what is going on in
the vibrating sphere, we can design materials that are extremely hard,
extremely light, or extremely unstable at our wish.
As we know, most physics parameters cannot fit in a 3 dimensional space, but in
addition to space, require a further dimension we call time. So, although a 3D platonic may give us a good picture of what an
elementary particle looks like, it will not give us any indication about its
movement in time. As we will see later on, a moving 3D shape can be integrated
over time and be fully described by a stationery 4D
shape. Thus in order to understand the motion of 3D platonics
we need to consider platonics in a higher dimension. In four dimensions,
the five Platonic Solids have six analogues. Interestingly enough higher
dimensions have only three platonic solids, so the 4th dimension is the special
case with the largest variety. In 4D, Polyhedra are called polytopes. The
Simplex and the Hypercube are relatively easy to understand, and illustrated
with projections, as analogues of the Tetrahedron and the Cube.
|
3 Dimensional Platonics |
|||||
|
Polytope |
cells |
vertices |
edges |
faces |
duals |
|
1. Tetrahedron |
triangle |
self-dual |
|||
|
2. Octahedron |
triangle |
cube |
|||
|
3. Cube |
square |
Octahedron |
|||
|
4. Icosahedron |
triangle |
dodecahedron |
|||
|
5. Dodecahedron |
pentagon |
Icosahedron |
|||
|
4 Dimensional "Platonic" Polytopes |
|||||
|
Polytope |
cells |
vertices |
edges |
faces |
duals |
|
1. 5-cell, Pentatope or Simplex |
tetrahedra |
self-dual |
|||
|
2. 8-cell, Tesseract or Hypercube |
cubes |
16-cell |
|||
|
3. 16-cell |
tetrahedra |
8-cell |
|||
|
4. 24-cell |
octahedra |
self-dual |
|||
|
5. 120-cell |
dodecahedra |
600-cell |
|||
|
6. 600-cell |
tetrahedra |
l20-cell |
|||
|
n-Dimensional "Platonic" Polytopes, n > 4 |
||||
|
Polytope |
number of (n-1) D cells |
vertices |
duals |
3-d analogue |
|
1. (n + 1) cell |
n + 1 n-cells |
n |
self-dual |
Tetrahedron |
|
2. 2n-cell |
2n (2n-2)-cells |
2n |
2n-cell |
Cube |
|
3. 2n-cell |
2n n-cells |
2n |
2n-cell |
Octahedron |
Very interesting is the fact that, in ALL dimensions greater than four, there are exactly three analogues to the Platonic Solids. Also these 3 analogues: the Tetrahedron, cube and octahedron, exist in all dimensions. This is, curiously, exactly half the forms we find in 4 dimensions. Also, note that the 3D platonics (or their duals) are found in the cells making up the 4D polytopes. In a way, we can say that the 4 dimensional state, has the highest structural entropy of all, and that is where we live in!. In 1908, a Russian physicist, Minkovsky gave a new concept of space-time continuum, which may be regarded as the geometrical interpretation of the Special Relativity Theory. Minkovsky considered that space and time, being relative, describe a fourth dimension. The space-time is composed of individual events each of which is described by four complex numbers, three space coordinates x, y and z, and one time coordinate t. How does our brain react to 4D space? We tend to see the universe around us as a 3D space, changing in time. What actually our brain is doing, is to take one of the 4D axis as reference (=time) and differenciate (or photograph) the other 3 dimensions with respect to it. This results in a sequence or 3D images over time, but the reference dimension (time) is arbitrarily taken as reference only in our perspective, whilst in reality it is a space dimension in its own right.
The duals
|
Tetra <-> Tetra |
Hexa <-> Octa |
Dodeca <-> Icosa |
|
|
|
|
|
Edge length to circumscribed sphere radius for tetrahedron= 163.3% |
Edge length to circumsribed sphere radius for hexahedron (cube)= 115.47% & octahedron = 141.42% |
Edge length to circumscribed sphere radius for icosahedron = 105.15% and dodecahedron = 71.364% |
|
Inscribed to Circumscribed sphere radius ratio for tetrahedron= 33.33% |
Inscribed to Circumscribed sphere radius ratio for BOTH hexahedron (cube) & octahedron = 57.735% |
Inscribed to Circumscribed sphere radius ratio for BOTH icosahedron and dodecahedron = 92.624% |
|
Inscribed to Circumscribed sphere volume ratio for tetrahedron= 3.7% |
Inscribed to Circumscribed sphere volume ratio for BOTH hexahedron (cube) & octahedron = 19.245% |
Inscribed to Circumscribed sphere volume ratio for BOTH icosahedron and dodecahedron = 79.465% |
|
Inscribed Planck's spherical volume for tetrahedron= 1.8793E-107 m3 |
Inscribed Planck's spherical volume for hexahedron (cube) = 2.762E-106m3 and for octahedron= 1.503E-106m3 |
Inscribed Planck's spherical volume for icosahedron= 9.538E-106m3and dodecahedron = 3.05E-105m3 |
A very interesting characteristic of these five platonic solids, is the so called DUALITY. The dual of a platonic is the shape formed having its vertices at the centre of each face of the parent platonic. The importance of duality is re-confirmed in the 1000 BC old stones shown above, by the presence of white dots, that show the vertices of the dual platonic within each stone. As shown above, you can see that the tetrahedron is the dual of itself, whilst an octahedron is the dual of a hexahedron/cube (and vice versa), and a dodecahedron is the dual of the icosahedron (and vice versa). Thus each platonic can have nested platonics within it of diminishing sizes down to an infinetely small side lengths, and yet every nested structure will still have all characteristics of a platonic solid. In the case of the tetrahedron, where the number of faces is equal to the number of vertices, its dual will be the same shape of its parent platonic shape. From the above calculations, it is shown that the ratios between both radius and volume of any circumcribed sphere to its inscribed sphere is a constant, not only for the case tetra-tetra, but also to the other two dual platonics, even if the platonic shape of the duals is not the same.The limiting edge size of any platonic is equal to half Planck's length (1.616E-35m), since each side of the platonic is vibrating at its fundamental frequency, where node to node distance is equal to half a wavelength.
![]()
This length is the lower limit at which the classical description of gravity ceases to be valid, and below which 'length', and time to travel it, have no meaning. At this value of length, the theories of quantum mechanics and general relativity become incompatible, and so it seems reasonable that it should be at this value that our platonic standing wave should interact with gravity, otherwise it will be, at best, only as good as the present theories. There is a corresponding Planck time associated with the Planck length which is the time required for an EM wave or photon to travel the elementary Planck length at the speed of light, which equates to 5.39E-44 seconds. In the Duals table above, a value named Planck's spherical volume has been worked out for each platonic shape, representing the volume inside the inscribed sphere for the particular platonic shape with edge length equal to half Planck's length. This will later on be shown to be the matter-antimatter interface volume, known in Superstring theories as the light cone.
 Platonic & Archimedian solids -
by Daud Sutton
Platonic & Archimedian solids -
by Daud Sutton
By Engineer Saviour - Blaze Labs
Picturing the standing wave atom model
by visualising rotating platonics
 Now that we know that indeed,
to say the least, there is striking evidence that the atom structure is a
standing wave, we need to describe in terms of this new concept, each
observable conventional particle and picture how the real atom looks like.
Now that we know that indeed,
to say the least, there is striking evidence that the atom structure is a
standing wave, we need to describe in terms of this new concept, each
observable conventional particle and picture how the real atom looks like.
We know that the atom has a high density core at the centre surrounded by a
cloud of electrons. However, even in the case of atoms with a single electron,
we still see a cloud, and never has anyone been able to track any electron
orbiting around. We have also shown that no orbital electrons exist and
therefore electrons can never collide to each other. In this theory there is no
room either for a particulate nucleus or anything else described as particulate
matter within the atom. The whole atom is a standing wave in three dimensions,
and all known effects have to be described by electromagnetic standing wave
geometry. So, where does this leave us with the picture of an atom? Surely we
have got no neutrons, protons or electrons, but our model should still account
for their effects in terms of 3D standing wave geometry.
 It has been already stated
that a sphere has got just five natural frequency modes of vibration, and each
of these frequencies gives rise to the formation of a platonic standing wave
structure. Each 2 dimensional face of these structures is a standing EM wave
node. Here on the left, a tetrahedron is shown. You may notice this shape has
got 4 Vertices, 4 Faces, and 6 Edges. Euler's characteristic, as with the other
four platonics is equal to F-E+V= 4-6+4 =2. It is understood that everything
that we apply for this shape will apply for the other four platonics. Each
platonic, when rotated in all possible angular directions about its centre,
will form two spheres, one inscribed within its faces and one circumsribed by
its vertices, as shown in the diagram. The inscribed sphere,
will in turn be the circumscribed sphere of a smaller nested platonic
structure, and so on, until a point is reached where the actual sides of the
platonic equates to the smallest possible vibrating length in space, relating
to planck length.
It has been already stated
that a sphere has got just five natural frequency modes of vibration, and each
of these frequencies gives rise to the formation of a platonic standing wave
structure. Each 2 dimensional face of these structures is a standing EM wave
node. Here on the left, a tetrahedron is shown. You may notice this shape has
got 4 Vertices, 4 Faces, and 6 Edges. Euler's characteristic, as with the other
four platonics is equal to F-E+V= 4-6+4 =2. It is understood that everything
that we apply for this shape will apply for the other four platonics. Each
platonic, when rotated in all possible angular directions about its centre,
will form two spheres, one inscribed within its faces and one circumsribed by
its vertices, as shown in the diagram. The inscribed sphere,
will in turn be the circumscribed sphere of a smaller nested platonic
structure, and so on, until a point is reached where the actual sides of the
platonic equates to the smallest possible vibrating length in space, relating
to planck length.
The vertices of the internal nested platonic (the dual) will form at the centre of each face of the parent platonic. Curiously enough, this point is shown by dots on the 3,000 year old stones shown previously. This makes the inscribed sphere look very dense, in terms of standing wave structures. Unlike the conventional model, where the space between electron shells is described as a void and empty space, in our model it is the space in between the inscribed and circumscribed spheres, which contain the inward and outward going spherical waves forming up the 3D standing wave shape. Thus such a volume will be less opaque, and less dense than the standing wave shells. This volume, that is the volume trapped between the two spheres is what most call the 'electron cloud'. The internal inscribed sphere is as you might have guessed, what most call the nucleus. To reassure us of such an idea, we have to mention that one stable solution to Maxwell's equations is equivalent to a continuous standing electromagnetic wave arranged concentrically about a point. Standing waves of intermediate sizes explain the Rydberg constant and the fine and superfine structures of spectral lines, and may explain the valency shells of each atom. Since both nucleus and electrons in this model are made up of 3D standing waves, both of them will have common characteristics such as inertia (detected as mass), charge, and magnetic moments. Same characteristics, but not same values, as the energy density of the wave is inversely proportional to the square of the distance from the centre.
If an electric field is sweeping over a sphere, it induces a magnetic field at right angles. Integrating the cross product of the two fields -- over the surface of a sphere -- is equivalent energy divided the speed of light squared -- which is equal to mass. (This is a variation of Gauss's law of gravity.) It follows that the smallest entity which can have all characteristics of a particle should be one the simplest of the basic platonics described above. If this entity is unique, then it must be one whose dual is itself, and which has got its analogue existing in all dimensions. There is just one platonic satisfying this criteria and this is the Tetrahedron (in 3D), called the Simplex in 4D. Of course the atom is not as simple as one tetrahedron and consists of many such elementary particles and so need not be simply composed of nested tetrahedrons, but the above description gives the basic idea of how our model could eventially explain both nuclear and electron shells. Chemists all know about the existence of so called nuclear magic numbers, and atomic magic numbers, and these strongly indicate a kind of geometric structure governing both the built up of the nucleus and that of the electron cloud. A good viewer for 4D shapes is found here 4D Polytope Viewer
|
The TETRAHEDRON is the most basic of
the platonic bodies. It has four corners and four regular triangles as sides.
There are three pairs of othogonal edges, the total
number of edges is six. It may be considered the fundamental platonic shape,
since as shown below, all platonic & archimedian shapes can be
constructed by mathematical functions operating over this shape. |
|
|
|
|
Weyl, Clifford, Einstein, and Schroedinger agreed that the puzzle of matter would be found in the structure of space, not in point-like bits of matter. They speculated, "What we observe as material bodies and forces are nothing but shapes and variations in the structure of space. The complexity of physics and cosmology is just a special geometry." Perhaps it is about time we take such thoughts more seriously.
|
Elementary spherical distribution showing |
|
|
|
|
Schrödinger assumed that the electron's behavior could be
described by a three dimensional standing wave. He derived an equation which
described the amplitude of this wave. The simplest solution for the Schrödinger
Equation for the ground state (1s) energy of a hydrogen atom is:
Y= Ae-Br
where A & B are constants, e is the base of the natural logs, and r is the
radial distance from the nucleus.
The cross product (ExB) of two similar waves gives (Y2) tells the
probability of finding an electron at any given location, or the 'mass'
distribution of the electron cloud.
One may note that the dimension of the nodes is always one less than the dimension of the system. Thus, in a three-dimensional oscillating system the nodes would be two-dimensional rotating surfaces. The square of an electron's wave equation gives the probability function for locating the 'point' electron in any particular region. The orbitals or shells used by chemists describe the shape of the region where there is a high probability of finding a particular electron. Electrons are confined to the space surrounding a nucleus in much the same manner that the standing waves in the platonic are constrained to its surfaces. The constraints of each platonic forces each side to vibrate with specific frequencies, in the case of the tetrahedron each parent platonic will have 3 times the side length of its nested shape. So, an electron, which is equivalent to one of these rotating platonics, can only vibrate with specific frequencies, called eigenfrequencies and the states associated with these frequencies are called eigenstates or eigenfunctions. The set of all eigenfunctions for an electron form a mathematical set called the spherical harmonics. There are an infinite number of these spherical harmonics, but they are specific and discrete. Thus an atomic electron can only absorb and emit energy in specific in small packets called quanta. It does this by making a quantum leap from one eigenstate to another.
|
|
We found a strickingly similar model to the one we are approaching here in Dr. Robert J. Moon's model of the nucleus, a nesting of four of the five Platonic solids similar to that conceived by Johannes Kepler to describe our solar system. Even though this model does not show the tetrahedron as the inner platonic, we know that every cube implies a tetrahedron. Four diagonally opposite vertices of the cube form the vertices of the tetrahedron, and in fact two equal tetrahedrons may be positioned inside a cube, touching all 8 vertices of the cube. The combination of two such tetrahedrons is known as Stella Octangula. |
|
Here is a photograph of a working mechanical model of this nucleus, made for Moon by retired machinist George Hamann in 1986. As we shall discuss later on in this section, the radial distance from the core, represents time, somewhat similar to the concept of measuring distance in light years. As we shall also see, positive time and positive entropy cannot be separated, thus it makes sense, that platonic shapes as time goes forward, will have a higher entropy, which result in a higher number of vertices. |
|
|
|
The periodicity of the atomic volumes of the
elements (the ratio of their atomic weight to density) - a measurement of
structure compactness guided Lothar Meyer in the 19th-century in developing
the periodic table. The maxima in the graph at atomic numbers 3, 11, 19, 55,
and 87 identify the Group 1A elements that begin each period. However, minima
occur in the same graph at or near the atomic numbers 8, 14, 26, and 46,
which mark the completed platonic shapes of this nucleus model. |
Beyond Palladium, a second dodecahedral shell begins to
form as a twin to the first. After 10 of its 20 vertices are
filled at Lanthanum (atomic number 56), a cube and octahedron nesting fill
inside it, accounting for the 14 elements of the anomalous Lanthanide series.
Next, the icosahedron forms around the cube-octahedron structure, completing
its 12 vertices at Lead (atomic number 82), which is the stable, end-point in
the radioactive decay series. Finally the dodecahedron fills up, and the
twinned structure hinges open, creating the instability which leads to the
fissioning of uranium.
The completed shells of the Moon model, correspond to
the elements whose stability is attested by their abundance in the Earth's
crust: Oxygen, Silicon, and Iron. These elements also occur at minima in the
graphs of atomic volume, and of other physical properties (viz.
compressibility, coefficient of expansion, and reciprocal melting point) as
established by Lothar Meyer in the 1870s to 1880s. Palladium, which is an
anomaly in the modern electron-configuration conception of the periodic table
because it has a closed electron shell, but occurs in the middle of a period is not anomalous in the Moon model. Further, all four
closed-shell elements in the Moon model occur at maxima on the graph of paramagnetism
(versus atomic number), as reported by William Draper Harkins.
The Moon model is thus consistent with much of the same experimental data which
underlies the periodic table of the elements, and explains additional features
not explained by the modern, electron-configuration presentation of the
periodic table. However, it seems to be inconsistent with the evidence from
spectroscopy (upon which the electron-configuration conception rests) which
suggests the periods of 2, 8, 18, and 32; it is also not consistent with the
older law of octaves, which was developed to explain the phenomena of chemical
bonding, and was subsumed in Mendeleyev's conception. So, although Moon's model
has introduced important geometric ideas, its accuracy is not good enough to
match with experimental evidence. This means that his basic assumption - that
vertices correspond to particles - may not be quite right.
|
At this point, we may
have a look at what might be happening in a bose-eintein condensate (BEC).
What happens when such a platonic structure is cooled down to zero Kelvin and
screened from all external energies, does the structure collapse? The effect
of external EM radiation, such as heat, on a standing wave structure, is
exchange of momentum. It is a known fact that EM radiation exerts momentum on
matter. Such impacts of heat energy upon the platonic arrives randomly from
its surroundings, but gives the same average momentum impulses to each edge,
which results in rotation of the platonic about its centre. In this way the
platonic vertices will be able to span a whole sphere over time. The whole
integral of momentum over the time taken to span one whole sphere is zero.
Indeed if we lower the temperature to absolute zero, and shield our atom from
all EM radiations, the atom will no longer rotate, and there will be no more
volume of space trapped between any two spheres, hence no
electron cloud, but the structure does not breakdown, it simply becomes one
huge entity made up of stationary platonic standing waves. In 1995, Ketterle
cooled a gas made of sodium atoms to a few hundred billionths of a degree
above absolute zero and created the first Bose-Einstein condensate. In such
condition, the atoms do not need the spherical boundary between them, since
they are not rotating. This means that the atoms will eventually pack side by
side to each other forming a single compact standing wave structure. No
wonder that since all platonic shapes have an even number of vertices, BEC
are only possible with atoms with even number of electrons + protons +
neutrons, normally referred to as bosons. The Bose Einstein plot shown here
(top) shows the distribution of atoms in volume as temperature is decreased
from 400nK to 200nK down to 50nK, in the order from left to right. |
Bose-Einstein Condensate
Fermionic Condensate |

In the above diagram, the cooling down of the gas is shown in three steps. The patterns represent a platonic with its outer circumscribing sphere. When the gas is cooled down, the atoms slow down their rotating movement, impacts due to external travelling EM waves get weaker, as do the impacts with each other, thus reducing their intermolecular distance. Reducing the temperature further, the gas structure will resemble more that of a liquid, with atoms touching each other at their spherical 'shell' that is formed by the slowly rotating platonics inside. Approaching absolute zero, the platonics stop rotating, thus the circumscribed spherical space no longer exists, and they can pack next to each other node to node in the most efficient & compact way. In such condition, the atoms lack their electron cloud, and actually cannot be identified from one another, forming the so called Bose-Einstein condensate or superatom.
By Engineer Saviour - Blaze Labs
Fractional electron charges
Most of the matter we see around us is made from protons
and neutrons, which are each composed of 3 quarks.
There are six quarks, or quark flavours, but physicists usually talk about them
in terms of three pairs: up/down, charm/strange, and top/bottom. Top and bottom
types are the most elementary of them all, and are the ones that make up
protons and neutrons. Quarks have the unusual characteristic of having a
fractional electric charge, unlike the proton and electron, which have integer
charges of +1 and -1 respectively. The up, charm and top quarks have a charge
of +2/3, whilst the down, strange and bottom have a charge of -1/3. Although
individual quarks have fractional electrical charges, they normally combine
into 'hadrons' such that these hadrons have a net integer electric charge.
Protons and neutrons are good examples of quark grouping or hadrons.
Researchers at the Weizmann Institute of Science have provided the first
unambiguous evidence that electrons can behave in an intriguing way that seems
to defy the idea of the electron being an indivisible charged elementary unit.
An electron is by convention considered to be a tiny indivisible hard particle
that carries the smallest negative charge in nature. Yet a daring theory of
physics developed 15 years ago argues that under certain conditions, an
electric current behaves as if it were made up of fractions of electronic
charges. In an experiment described in September 11
issue of Nature, Weizmann Institute physicists measured fractional charges
one-third that of an electron.
"Mind-boggling as this may seem, this phenomenon is real," says study
author Rafael de-Picciotto. "Of course, electrons don't split into
fragments in an electric current, but under certain conditions it is indeed
possible to measure a charge smaller than that of an electron." This
means, that although the electron charge is always the same well known value,
it can no longer be stated that this value is the smallest possible value for
electrical charge.
Almost 100 years ago, ever since American physicist Robert Millikan first
measured the charge of an electron as equal to 1.602E-19C, this value has been
widely regarded as a basic unit of electric charge. Scientists have
consequently come to view electrons that make up an electric current as a flow
of negatively charged, indivisible elementary charged "balls." A
current made up of fractions of an electronic charge, therefore, would seem not
to fit in Millikan's findout.
However, if electrons are always regarded as a "whole" or
fundamental, as understood by current science, it is extremely difficult to
understand and describe their behavior under certain conditions. For example,
some particular instances of this behavior, as in a phenomenon known as the
fractional quantum Hall effect, observed in a strong magnetic field, remain
unexplained.
In 1982, physicist Robert Laughlin of the
In a new experiment, Weizmann Institute scientists designed a sophisticated
system to measure such fractional electric charges, should they exist. The
system makes it possible to measure so-called "shot noise." In
day-to-day environment, this noise results from random variations in the number
and velocity of electrons and causes popping sounds in radio receivers and snow
effects in television pictures. Under special laboratory conditions, "shot
noise" can be analyzed to reveal the make-up of the electric current. This
is possible because the noise has "ripples" left by the flow of
electrons in a conductor. The size of each "ripple" is proportional
to the unit of electric charge: the smaller the ripple, the smaller the charge,
and vice versa.
The scientists passed an electric current through a semiconductor immersed in a
high magnetic field, under conditions in which the fractional quantum Hall
phenomenon is observed. They used sophisticated equipment to eliminate all
extraneous sources of noise. The "shot noise" made by the current was
then amplified and measured. It turned out to be made of charges one-third
that of an electron.So this confirms that an electron is not a fundamental
particle, since such element should be indivisible, simple and structureless.
By Engineer Saviour - Blaze Labs
The search for the elementary particle
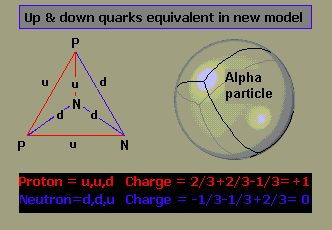
As you see, the one-third electron charge keeps popping up
from every experimental evidence we have. Weyl,
Clifford, Einstein, and Schroedinger once speculated, "What we observe as
material bodies and forces are nothing but shapes and variations in the
structure of space." Our spherical tetrahedron model shown above is indeed
based on this speculation and clearly indicates that the six quarks connecting
up the protons & neutrons are equivalent to the six sides of the spherical
tetrahedron. Protons and neutrons are just the point effects of their points of
intersection, and these types of hadrons can therefore be defined as the
intersection point of 3 standing wave planes.
Remember that the six sides of this tetrahedron are in fact a picture of the
fundamental standing wave nodes which appear on any 3D vibrating sphere. So, if
the sides of our model are the 1 dimensional quarks (6 off), then, each vertex
connecting a group of 3, will define a hadron (a group of 3 quarks). In the
diagram you see the three blue elements are equivalent to down quarks and the 3
red ones to up quarks. By joining together these two frames, a three
dimensional closed platonic structure consisting of two neutrons and two
protons is formed, equivalent to the simplest & strongest stable nucleus of
Helium, namely the Alpha particle. This model also clearly explains why
neutrons and protons never collide within a nucleus, despite being so close.
Once the platonic structure is completed, the protons and neutrons act as a
single entity - the one we call nucleus. It also gives a new meaning to the
strong nuclear bonds, since a tetrahedron is the most stable, and compact
geometric 3D shape.
At first, it might seem a little bit confusing that a 'solid' nucleus, is made
up of a fixed 3D geometric shape of 2D planes and no 3D hard particles, but the
fact that we can now explain a quark in terms of a 1 dimensional nodal string
connection makes sense and reassures us that we really found the most
fundamental elements - simple elements with no structure. The charge on each of
these hadrons is simply the addition of the charges of the quarks, or sides
making up the frame of the particular hadron. This spherical tetrahedron model
has some interesting attributes not the least of which is the fact that spheres
which resonate in phase are known to "attract" one another, while
those with unlike phase angles will repel. We have established that atoms are
EM vibrating spheres and this gives a new more clear meaning to the
gravitational force between atoms. It is known that two spheres vibrating in
phase attract. If all matter in the universe is a differential of the same 4D hyperspherical EM singularity,
then it makes sense that all matter gets attracted to each other since all
matter would be vibrating in phase.
|
|
|||||
|
Polytope |
vertices |
edges |
faces |
duals |
hadron pairs |
|
1. Tetrahedron |
self-dual | ||||
|
2. Tetradual |
Tetrahedron | ||||
|
3. Octahedron |
cube | ||||
|
4. Cube |
Octahedron | ||||
|
5. Icosahedron |
dodecahedron | ||||
|
6. Dodecahedron |
Icosahedron | ||||
Look closely at the hadron pair coloumn: 2,2,4,10.
If we start off with the tetrahedron, and add up shells with the next platonic,
we will get the series: 2 +2+4,2+2+4+10 = 2,2,8,18.
We know that the number of electrons is equal to the number of protons, hence
to the number of hadron pairs. Spectroscopy data gives the sequence 1s, 2s, 2p,
3s, 3p, 4s, 3d or 2,2,6,2,6,2,10,6,2, which may
also be grouped as 2,2,8,18, similar to the shell build up sequence of Tetra,
tetra, cube and dodecahedron.
So we have seen that a simple tetrahedron is the most accurate picture for a
Helium nucleus, which has the strongest nuclear bond of all elements and is
better known the alpha particle. The Alpha particle thus consists of 4 hadrons,
two protons and two neutrons, with a total charge of +2. Protons and neutron
are equivalent to the vertices of the standing wave shapes. We can also extend
the same model to construct the Be4 nucleus, which has a total
binding energy of twice that of 4He2. This is done by fitting
another tetrahedron as shown below to obtain the 8Be4 nucleus, with
its vertices common to a cube, representing its 4 protons and 4 neutrons. Note
that these structures should not be considered as solid structures but as nodes
on spinning spherical surfaces, with each edge element equivalent to a quark,
and each vertex to a nucleon. At all times, tt should be kept in mind that
these shapes are actually 3D standing EM waves, which can also share nodes.
|
|
|
|
The 8Be4 nucleus platonic combination & equivalent spherical standing wave structure. |
|
Even though very light, 8Be is a very stable metal. Its elasticity is larger than that of steel, its strength four times that of aluminum. The melting point at nearly 1600 K is very high. In the gas phase Beryllium is monoatomic.
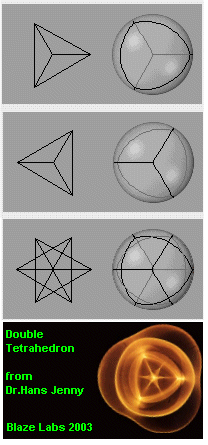 The above structure is the
compound of two tetrahedra called the stella
octangula, discovered by Kepler. The vertices define a cube and the
intersection of the two an octahedron, which shares the same face-planes as the
compound. Thus it is a stellation of the octahedron, and in fact, the only
stellation thereof. The probability of natural existance of such a structure is
fully confirmed by many photos of vibrating fluids taken by Dr. Hans Jenny in
his Cymatics study of sound vibrations in liquids. In this self explanatory
diagram, you can see how two standing wave spherical tetrahedrons combine
within the same 'shell', forming the double spherical tetrahedron structure.
The two tetrahedrons are no longer independent, and any clockwise movement of
one tetrahedron must be accompanied by an anticlockwise movement of its dual so
that the stella octangula moves as a whole body.
The above structure is the
compound of two tetrahedra called the stella
octangula, discovered by Kepler. The vertices define a cube and the
intersection of the two an octahedron, which shares the same face-planes as the
compound. Thus it is a stellation of the octahedron, and in fact, the only
stellation thereof. The probability of natural existance of such a structure is
fully confirmed by many photos of vibrating fluids taken by Dr. Hans Jenny in
his Cymatics study of sound vibrations in liquids. In this self explanatory
diagram, you can see how two standing wave spherical tetrahedrons combine
within the same 'shell', forming the double spherical tetrahedron structure.
The two tetrahedrons are no longer independent, and any clockwise movement of
one tetrahedron must be accompanied by an anticlockwise movement of its dual so
that the stella octangula moves as a whole body.
In ancient times, this shape was given great importance, and was known as
MerKaBa. The Merkaba is a symbol from the sacred geometry and is the symbol
upon which the Star of David is based. The Merkaba has significance in
different ancient cultures around the world. In the Bible's book of Ezekiel, it
is referred to as the chariot of Gods and in Hebrew, Merkaba means chariot.
Some refer to the Merkaba as the 'vehicles of vehicles', or the tool for
ascension. The ancient Egyptian (18th dynasty) meaning is even more interesting
as it stands for MER= counter rotating fields of light in the same space,
KA=spirit and BA=soul. How could ancient Egyptians know of 'counter rotating
fields of light'?
By Engineer Saviour - Blaze Labs
Development of the new model
A proper model has to be compliant with experimental
evidence and so be in perfect agreement with the spectral data for each atom.
It is evident from our previous discussions that each shell is equivalent to a
polyhedra shell, and getting the right sequence of shells is of primary
importance in order to further develop the correct sequence of polyhedra transformations
for each equivalent quantum number. If quantum numbers are unique, it then
follows from our knowledge about the 6 unique basic platonics (5+dual tetra), that all basic elements can be described by no more than 6
pricipal quantum numbers.
Let us first see what the present theory says. Conventionally, the maximum
number of electrons in the set of orbitals, defined by the principal quantum
number n = 1, 2, 3, 4 etc., (also known by their spectroscopic designation K,
L, M, N, etc. is given by the formula Z max = 2n2
and it is presented in table below.
|
Principal |
Number of electrons |
Maximum number of electrons in a shell |
||||||
|
n> |
symbol |
s (l=0) |
p (l=1) |
d (l=2) |
f (l=3) |
g (l=4) |
h (l=5) |
Z max |
|
K | ||||||||
|
L | ||||||||
|
M | ||||||||
|
N | ||||||||
|
O | ||||||||
|
P | ||||||||
Electron configuration
The electron configuration of an atom might be presented by the number of
electrons in each subshell, by the order of filling.
The conventional electron occupancy of the subshells of all atoms is as
follows:
1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f, 5s, 5p, 5d, 5f, 5g,
giving maximum shell capacity sequence 2,8,18,32,50...
etc. Theoretically, with such a theory, additional
subshells such as the g, h and so on, can exist, but they are not required for
any real atoms. See the scheme below:
|
|
1s | ||||||||
|
|
2s |
2p | |||||||
|
|
3s |
3p |
3d | ||||||
|
|
4s |
4p |
4d |
4f | |||||
|
|
5s |
5p |
5d |
5f |
5g | ||||
|
|
6s |
6p |
6d |
6f |
6g |
6h | |||
|
|
7s |
7p |
7d |
7f |
7g |
7h |
7i | ||
|
|
But, by just observing the electron shells
of heavy atoms, one can observe that we soon run into problems, because higher
shells start to be filled up before the respective lower shell has attained
its full capacity. It is a well known nightmare for chemistry teachers, that,
beginning with Z=19, a vivid struggle between normal filling and exeptional
filling of subshells starts. Also, according to the experimental spectral
data, in the ground state, electrons fill the quantum states in the order: |
|
|
1s | ||||||
|
|
2s |
<> |
2p | ||||
|
|
3s |
3p | |||||
|
|
4s |
3d |
4p | ||||
|
|
5s |
4d |
5p | ||||
|
|
6s |
4f |
5d |
6p | |||
|
|
7s |
5f |
6d |
7p | |||
The above table matches the sequence given from spectral data, and also the maximum number of elements of 118 matches the conventional periodic table. But if we try to analyse it in terms of shell build up, there seems to be something still wrong. For example, lets take shell number 7, first we find subshell 7s (l=0), then instead of moving to the next subshells in the order s,p,d,f (l=0,1,2,3..) we see that we are first filling subshell s, and then the remaining subshells in the reverse order f,d,p. It makes sense that higher subshells (lower energy levels) get filled up before the lower subshells (higher energy levels) for each quantum shell number. This means that the table has to be shifted all by one term, in order to move the 's' subshells at the end of each shell build, thus making all shells fill up in the same order f,d,p,s as follows:
|
|
1s | ||||||
|
|
2s | ||||||
|
|
2p |
3s | |||||
|
|
3p |
4s | |||||
|
|
3d |
4p |
5s | ||||
|
|
4d |
5p |
6s | ||||
|
|
4f |
5d |
6p |
7s | |||
|
|
5f |
6d |
7p |
8s | |||
|
|
With the new scheme the quantum numbers will match the lowest energy level subshell of the shell. Quantum number 1 will thus match those subshells with total electron count of 2, quantum number 2 will match those subshells with electron count of 8 and so on. This new quantum numbering scheme now has the same filling order of the subshells and the problem of jumping is totally eliminated during the subshells' filling, with the electrons in full accordance to the present experimental data. In the conventional model, this problem occurs for example at the filling of element with atom no. 19 Calcium, instead of 3d subshell filling, the subshell 4s is filled. The same surprise occurs at the elements with atom no.37 - Rubidium and atom no.55 - Cesium). Also, in contrary to the conventional way of electron shell configuration, with this new scheme, up to 56 basic elements can be contained within the first 6 shells or 3 principle quantum numbers, and up to 120 basic elements can be contained within 8 shells or 4 principle quantum numbers. The new model, apart from being much neater, can thus contain all known elements by using just s,p,d,f shells, without the need to resort to higher shells g,h.. whose existence is not proven. Below is a table summarising the proposed model. |
|
Principal quantum number |
Shell quantum number |
Number of electrons in a subshell |
Maximum number of electrons in a shell |
Maximum number of electrons in a level |
Maximum number of electrons in atom |
||||
|
n |
symbol |
ns |
f (l=3) |
d (l=2) |
p (l=1) |
s (l=0) |
Zsmax |
Zlmax |
Zmax |
|
K | |||||||||
|
L | |||||||||
|
M | |||||||||
|
N | |||||||||
|
O | |||||||||
|
P | |||||||||
|
Q | |||||||||
|
R | |||||||||
This new sequence is totally
in agreement with experimental spectral data sequence:
1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p,
8s ... , which with the new quantum shell renumbering becomes:
1s, 1s', 2p, 2s, 2p', 2s', 3d, 3p, 3s, 3d', 3p', 3s', 4f, 4d, 4p, 4s, 4f',
4d', 4p', 4s' ...
Renumbering the quantum shell levels does not change the original basic
sequence:
2, 2, 6, 2, 6, 2, 10, 6, 2, 10, 6, 2, 14, 10, 6, 2, 14, 10, 6, 2 ...
Note that the sequence is now very simple and no non-sense jumping between quantum
levels is required to agree with experimental spectral data. Also, a new kind
of symmetry now becomes evident. It becomes very noticable the fact that each
principle quantum level is now composed of a paired structure, a double shell,
which must be fully filled before the level can be 'sealed'. Once 'sealed' or
completed, the next quantum level will have no effect on the sealed level
during its growth. Since every two consequtive shells are composed exactly the
same, quantum numbers can now be halved, and each quantum number is given a
property of 'spin' where the first shell of each level shall be arbitrarily be
the positive quantum spin denoted by the usual notations 1s, 2s, etc.. and the second shell will be the negative quantum spin and
is denoted by 1s', 2s', etc.. The new sequence thus becomes:
(1s 1s') (2p 2s, 2p' 2s') (3d 3p 3s, 3d' 3p' 3s') (4f 4d 4p 4s, 4f' 4d' 4p'
4s')
Thus the electron configuration now consists of only four shells, each shell
being a double-structure with twice as many electrons per shell as in the
conventional electron configuration. This double quantum structure is clearly
shown by plotting various physical characteristics for the elements. Similar
graphs for density, ionisation energy, electronegativity, etc
all show the same characteristic of twin quantum
levels, immediately obvious at first glance at the paired curves for each
quantum level. Shown below is the density vs atomic number graph, which makes
it clear that all elements can be built up by nesting 4 paired structures.
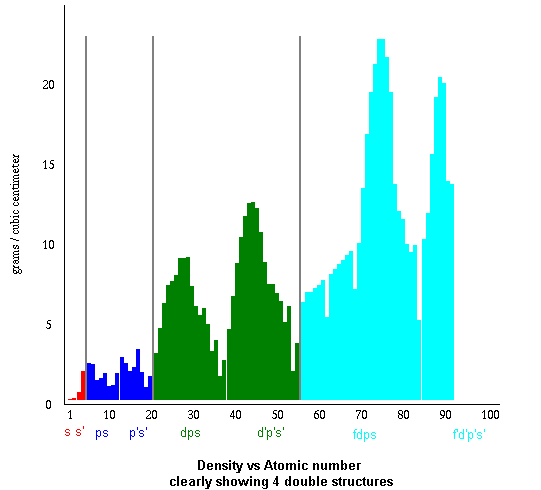
Binding Energy Curve
|
|
This curve shows the nuclear binding energy vs mass (P+N) number. As one can see, the most stable nucleui are those shown at the peaks which are 2He4, 6C12, 8O16 and 28Fe56. Incidentally these are the most cosmic abundant elements. The heaviest most stable element is iron, element number 28, which also sets the divisor between fusion & fission elements. As you will see, in our model this element is achieved when quantum level 3 is fully completed and 'sealed'. |
Nuclear Stability & Hybrid Tetrahedral fractal formation
|
Stable nuclei generally have the same number of protons and neutrons (or Z=N, where Z is the number of protons and N is the number of neutrons in the nucleus). This is more strictly observed for light nuclei with fewer than 20 protons (Z<=20) (see figure on the right). For heavier nuclei with more than 20 protons (Z>20), the nuclear structure takes over more complicated geometry with increasing number of protons. The most common combination of neutrons and protons for stable isotopes is an even number of protons and an even number of neutrons. In a chart of neutrons (N) vs. protons (Z) for stable isotopes, a region of stability (shown in white) can be drawn. The stability line shows that nuclei with Z<=20 have a balanced number of protons and neutrons, and thus indicate a highly symmetric structure. Spatial symmetry, obtained on completion of a quantum level is a possible driving force for structuring the electron configuration in such a way, and also the driving force for chemical reactions and molecular bonds. Atomic build up for Z=20 will follow the growth of shells , or with the new model , . As you may follow in the below diagram, in our model, a 1s shell is a simple tetrahedron (2P+2N), the 1s' (conventional 2s) shell is then a bigger tetrahedron, which inscribes the first tetrahedron. The 2p (conventionally known to contain 6 electrons, 3 upspin and 3 downspin) is actually made up of 3 x 2s tetrahedrons, which together with the original 2s tetrasphere, will pack together into a hybrid tetrahedral formation, to be inscribed in a bigger spherical tetrahedron, which is the 2s shell (conventional 3s). This mechanism will repeat itself in exactly the same way for the opposite spin quantum level. 3s shell will take the place of 2s shown in the diagram, 3p that of 2p, and 4s that of 3s. This hybrid tetrahedron shell build up is no longer followed after shell 4s, where the octahedron will emerge, and that explains why the balance between protons and neutrons is lost for Z>20. Our model, also explains the 'staircase' plot shown in the graph. When Z satisfies the conditions for a complete tetrahedron to form, whether s type or p type, the atom recovers it stability. The last point where the proposed structure touches the stability line coincides to the completion of the pair of hybrid tetrahedrons of quantum level 2. |
|
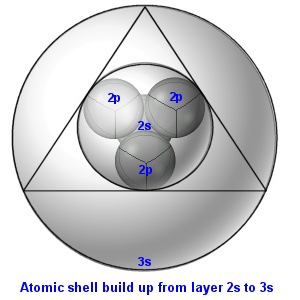
The fundamental hybrid tetrahedral structure
I am now going to explain the
real origin of subshells s,p,d,f and also show that Zmax
for shells g and h are somehow different than those defined for the
conventional theoretic subshells. It is also shown that the empirical equation
for the maximum number of electrons in level n = 2n2 just happens to
give the correct answers only to the first four shells and such equation has no
fundamentals. In fact the conventional equation implies that we can have an
infinite number of subshells s,p,d,f,g,h,i.... whilst our proposed structure
limits the shells to h, at which point the model can handle 412 atomic numbers.
We will also go further to explain why nature abhors the existence of elements
with Z>120.
At this point we no longer need Pauli's exclusion principle to explain
subshells, since the limit of two opposite spin electrons per 'orbit' is built
in the structure of the tetrahedron. In no electromagnetic standing wave
structure could we ever have two vertices touching each other, so this
principle is built inherently in our new definition for matter. In the
preceeding sections I have explained that a tetrahedron, having 4 vertices, is
equivalent to an atom having 2 Protons + 2 Neutrons. We also know that the
number of electrons of such a stable atom will be equal to the number of
protons. So for example, a tetrahedron structure we have 2 electrons. For each
platonic, we can work out the number of electrons which is equal to half the
number of vertices Z/2, as shown in the table below. Note that at each complete
shell stage, that is a formation of a complete platonic shape, one of the
spherical standing wave will always be a complete sphere formed by the previous
higher energy levels. For higher atomic numbers, one of the vertices of each
complete platonic shell will always be formed by a spherical platonic, which in
turn can nest other spherical platonics within it. It's a fractal build up. For
example, in the above diagram, you can see that the inscribed tetrahedron is
made up of 4 spheres, three of which are 2p spheres and one 1s' sphere. So for
the formation of a tetrahedron (4 vertices), you only need to have three extra
spherical tetrahedrons. In general, you will always need the formation of n-1
new spheres which together with the existing complete spherical standing wave,
will form the new platonic with n vertices. The quantum number dictates the
energy level, seperated by s levels, so for example a 3s, a 3p or 3d subshell
spheres will have the same quantum number. In the example shown, we see that
although each of the 4 vertices of the tetrahedron looks electrically the same,
one of them will result in a higher equivalent mass due to its internal
structure. The higher the atomic number, the higher is such imbalance, which
results in deviation of the nuclear stability line from the curve N=Z, as shown
further above. Thus this model accounts for another experimental fact, which is
otherwise unaccounted for in the conventional model. On the last column, Zavail
shows the available electrons for each complete structure. Zavail=
2,10,18,36,54,86 and 118 represent all the noble gases, namely: Helium 2, Neon
10, Argon 18, Krypton 36, Xenon 54, Radon 86, and the still unknown ultimate
element 118. Being complete platonic structures, these are the most inert
elements to exist in nature.
|
Level |
Lowest level Platonic |
Vertices |
No. of inscribed tetrahedrons |
No. of tetrahedron vertices P+N=Z |
Electrons in subshell= Z/2 |
Zsmax |
Zlmax |
Zmax |
Zavail |
|
1 = s,s' |
Tetrahedron + |
2 (s) | |||||||
|
Tetrahedron - |
2 (s) | ||||||||
|
2 = (p,s)(p,s)' |
Dual Tetrahedron + |
6 (p) | |||||||
|
Dual Tetrahedron - |
6 (p) | ||||||||
|
3 = (d,p,s)(d,p,s)' |
Octahedron + |
10 (d) | |||||||
|
Octahedron - |
10 (d) | ||||||||
|
4 = (f,d,p,s)(f,d,p,s)' |
Cube + |
14 (f) | |||||||
|
Cube - |
14 (f) | ||||||||
|
5 = (g,f,d,p,s)(g,f,d,p,s)' |
Icosahedron + |
22 (g) | |||||||
|
Icosahedron - |
22 (g) | ||||||||
|
6 = (h,g,f,d,p,s)(h,g,f,d,p,s)' |
Dodecahedron + |
38 (h) | |||||||
|
Dodecahedron - |
38 (h) |
Why 118 elements not 412 ?
In the above table we see, that we can model all known elements with the proposed fractal structure by just using the first four structures: Tetrahedron, Dual Tetra, Octahedron and Cube. The two 'extra' structures containing icosa & dodeca structures, which could result in a total of 410 elements, seem not to be applied in nature. Why? The answer is quite simple, and you may understand it better as you follow this section. I have hinted in various sections that our reality is just a 'projection' of a unified higher dimensional reality in our 3D vision of the universe. In simple words, those things that cannot be found in higher dimensions, are most probably only man made, unstable and usually abhored by nature. As we have discussed earlier during the introduction to platonics, the icosa & dodeca structures are limited to exist in 3D, whilst the first four, and ONLY the first four structures exist in all dimensions. The fact that no stable elements with Z>118 have ever been found in nature, is in itself a clear indication that atoms, of which the universe is known to be made of, exist as a projection of a higher dimension than 4. So our proposed model gets truncated to the 4th quantum level, and the shaded part of the chart is deleted.
A closer look at the nucleus
The nucleus has been identified by the scattering
experiments of Hans Geiger and Ernest Marsden, carried out under the
supervision of
Let us have a closer look at the nucleus. Assuming closed packing arrangement
for the nucleons, the two protons and two neutrons in the structure of the
nucleus should form a tetrahedron. Calculations of potential model, constrained
by the hadron spectrum for the confinement of the relativistic quark and
colored quark exchange model are also consistent with a tetrahedron formation
of the nucleus. This can be depicted in a very similar way to the nested
platonic model of the electron shells. The resulting orbits form similar
"shells," just as the orbits of electrons. As nucleons are added to
the nucleus, they drop into the lowest-energy shells permitted by the Pauli
Principle which requires that each nucleon has a unique set of quantum numbers
to describe its motion. Again, as soon as one defines a structure, Pauli's
principle is no longer required. For example, if a tetrahedron, with 4 vertices
has been fully filled, the next nucleon cannot be permitted at the same energy
level, and the next spherical standing wave has to start forming.
When a shell is full and the structure is formed (equivalent to saying that the
nucleons have used up all of the possible sets of quantum number assignments),
a nucleus of unusual stability forms, and this makes sense since all platonics
are spherical wave solutions. This concept is similar to that found in an atom
where a filled set of electron quantum numbers results in an atom with unusual
stability, usually an inert gas. When all the protons or neutrons in a nucleus
are in filled shells, the number of protons or neutrons is called a "magic
number." Visualizing the densely packed nucleus in terms of orbits and
shells seems much less plausible than the corresponding shell model for atomic
electrons. You can easily believe that an atomic electron can complete many
orbits without running into anything, but you expect protons and neutrons in a
nucleus to be in a continuous process of collision with each other. Dense-gas
models of nuclei with multiple collisions between particles didn't fit the data, and remarkable patterns like the "magic
numbers" in the stability of nuclei suggested the seemingly improbable
shell structure. In our model, a shell is built up of a structured layer.
"Magic Numbers" in the Nuclear Structure have
been for long been noticed but no plausible explanation for their existance have ever been given. As shown in Figure above,
there are peaks and dips for binding energy, repeating every fourth nucleon.
This periodicity is one clear indication of geometrical structure within the
nucleus. In particular, those nuclei that can be thought of as containing an
exact number of alpha particles, or tetrahedral clusters (two neutrons and two
protons each) are more tightly bound than their neighbors. This effect is more
pronounced for the lightest nuclei, but is still perceptible up to A = 28. For
those nuclei with A > 20, the number of neutrons
exceeds the number of protons, so that they clearly are not just tetrahedral
clusters.
It is found that nuclei with even numbers of protons and neutrons are more stable
than those with odd numbers. This comes from the fact that all 5 platonic shell
structures have an even number of vertices, and no platonic exists with an odd
number of vertices. In particular, there are these specific "magic
numbers" of neutrons or protons which seem to be particularly favored in
terms of nuclear stability:
Note that the shells exist for both protons and neutrons individually, so that
we can speak of "magic nuclei" where any one nucleon type is at a
magic number.
This makes elements with masses:
1+1 (Hydrogen 1st most abundant), 2+2 (Helium 2nd most abundant), 8+8 (Oxygen
3rd most abundant) and 10+10 (Neon 4th most abundant) very stable and abundant
in the universe.
It is found with no exception, that
nuclei which have both neutron number and proton number equal to one of the
magic numbers are particularly highly stable and are called "doubly
magic".
![]()
|
Calcium provides a good example of the
exceptional stability of "doubly magic" nuclei since it has two of
them. The existence of several stable isotopes of calcium may have to do with
the fact that Z=20, another magic number. The two highlighted isotopes have
neutron numbers 20 and 28, also magic numbers. Compared to the binding energy
calculated from the Weizsaecker formula, they both have more than the
expected binding energy.
|
|
Why protons, neutrons & electrons do not collide
within the atom
Compound tetrahedrons (each equivalent to one Alpha particle) can be enclosed
in the same spherical standing wave. The compound tetrahedron although not
defined as a platonic, is still a uniform shape with all its vertices touching
a spherical shell. Since each tetrahedron represents 2 Protons and 2 Neutrons, 2 compound tetra would be equivalent to the stable nucleus
of 4 protons and 4 neutrons, hence the high stability of these even numbered
nuclei.
The evidence for a shell structure in the nucleus was surprising at first,
because according to current physics, a dense collection of strongly
interacting particles should be bumping into each other all the time, resulting
in redirection and perhaps loss of energy for the particles. This idea at first
seems to violate Pauli's exclusion principle but it's not. Keep in mind the exclusion
principle itself has been deviced in the first place due to the lack of
information about the geometrical structure of the electron shells.
If you consider every particle, being it a proton, neutron, or electron, as
being restricted in space relative to its neighbour particle by the shape of a
particular polyhedra (spherical standing wave), there would be no need for any
principle to show how and why these particles can never collide with each
other. We know that collisions between electrons or nucleons in a particle are
very infrequent.
In the nucleus, similar tetrahedrons (Alpha particles) may share the same
spherical wave function with the condition that they maintain a fixed distance
between their vertices and thus form a single compund tetrahedron. This theory
also explains the emission of alpha particles from the nucleus. Many
radio-nuclides achieve increased nuclear stability by emitting an alpha
particle rather than a single proton or neutron. This suggests that many
isotopes contain one or more alpha particles in their nucleus.
What does a non platonic standing wave look like
Till now we have considered filled up shells which equate to a complete
platonic structure such as a simple spherical tetrahedron equivalent to the
Helium nucleus. But what does the standing wave look like when the number of
nodes is not equal to the number of vertices, for example in a Hydrogen
nucleus? Does this result in a non-uniform structure within the spherical
standing wave? How can a spherical wave contain one, two or three nodes?
Chemists just put up the next shell and put the extra particles orbiting
around, but this picture is totally wrong.
Let us assume that a complete shell, say shell '1s' has just been completed and
a spherical tetrahedron has formed. We know that 4 extra nodes (or particles)
are now required until we have enough nodes to create the compound tetrahedron
shell '2s'. The best analogous example to understand this process is using an
oscilloscope trace while increasing frequency. If the wave signal frequency at
its input matches exactly its timebase frequency F, then, the input wave will
appear at a standstill on the screen. If we double the input frequency to 2*F,
we see 2 standstill waves on the screen. But what do we see in between the two
frequencies? If one increases the frequency slowly from F to 2F, the result is
that the wave will start moving across the screen until it slows down again
into the shape of two waves. This is exactly what happens at the nuclear level
as extra nodes are added. This movement of the standing wave results in SPIN of
the shell, until it builds up further nodes and 'slows down' into the new zero
spin complete shells.
All incomplete spherical 3d standing waves have non-zero spin values and are
pictured as various standing wave components as shown. Zero spin and complete
shells are achieved at the same time for the same reason - the number of nodes are equal to the number of nodes of a
spherical platonic. Hydrogen(2) has a spin of 1/2 since it has 1/2 the nodes
required to complete the smallest and simplest spherical tetrahedron, which is
achieved by a minimum of four nodes equivalent to the Helium nucleus, which in
fact has zero spin.
For many years, physicists have known that energy particles spin as they
travel. For example, electrons appear to be continually making sharp 180-degree
turns or half spins as they move through the atom. Quarks are often seen to
make one thirds and two thirds spins when they travel. No one in the mainstream
has provided a truly adequate explanation as to why this is happening. In our
model, spin is just the movement of the spherical standing wave whenever the
number of nodes is not equal to one of the five uniform platonics.
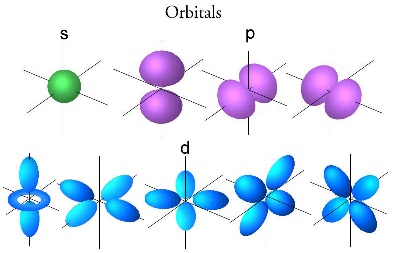
The standing wave shape is called an 'Orbital' - quite a misnomer considering nothing is orbiting inside! We usually learn that these represent the volume of space of probability distribution of an electron in an atom, and whose momentum and position cannot be determined at the same time. This is quite confusing since one would expect any moving object to have both momentum and position. It would all make sense if instead of probability distribution of point particles, we refer to orbitals as the real electromagnetic standing waves.
Building up the nucleus
So is the nucleus just one spherical standing wave, which transforms itself
thoughout the 5 platonic shapes as extra nodes are added? Not
exactly. This mechanism would not be able to generate the huge variety
of atoms in existance. Although the conventional 'bunch of grapes' model of the
nucleus has big flaws, it does give us a good indication of how multiple
spherical waves can combine into another bigger entity, while maintaining
themselves as separate identifiable structures. Evidence for this clustered
structure comes from electron and alpha particle emissions from the atom.

In the conventional 'bunch of
grapes' there is the need for the nuclear binding energy to overcome the
tendency of the nuclear components to fly apart because of the mutual repulsion
of the positive charges. The mass deficiency of atomic nuclei has been
hypotesized as the cause of nuclear binding, and for
this to take place, a new type of strong force has been hypotesized to exists
in the force of 'exchange forces' between nuclear components. To complicate the
issue further, a new type of particle -the meson has been invented to account
for this force exchange mechanism. This hypotises has in fact never been
proved. This model also give no hint to account for
the existance of the nuclear magic numbers and no way to describe its shell
structure.
The below diagram shows how the 'bunch of grapes' may be geometrically arranged
while explaining the shells build up for both nucleus and electron levels. The
singularity shown at the centre will be discussed in more detail later. Shell
1s consists of the most basic spherical tetrahedron formed by 2 Protons and 2
Neutrons. The next shell '2s' is its dual, which inscribes the 1s shell. At
this point, for entropy reasons, the structure does not continue to generate
nested tetrahedron duals but a new spherical tetrahedron, same size as the '2s'
shell, forms, touching at one point on the spherical surface of shell 2s. This
structure is no longer spherical and thus results in a spin factor as discussed
above. Their orbital is in fact the same as the radiation plot of a dipole antenna.
The structure does not get symetrical again, until a total of three 2p orbitals
have been filled up, and stability is fully recovered.
Together with the original 2s shell, they will form a close pack of 4 spherical
waves with their centres forming a tetrahedron structure. At this point, the 2p
shell is said to be complete, and the surfaces of the 4 spherical waves touch a
sphere in which they are contained. This bigger sphere will thus have 4 nodes
so it can be considered as a big spherical tetrahedron. At this point the next
shell is a dual of this tetrahedron which is equivalent to the 3s shell. The
mechanism is repeated in a similar way from shell 3s to shell 4s. The force of
attraction between neighbouring spherical standing waves is not electrostatic
and does not need any mesons to account for it. It is simply the same force
that attracts two objects that vibrate in phase, the same mechanism which
generates gravitational forces between two large bodies in space, the same
mechanism ruling the small vibrating sand particles as described in the
Oscillons page. This force automatically generates clustering and close packing
of spherical standing waves to form nodes of bigger spherical polyhedrons.
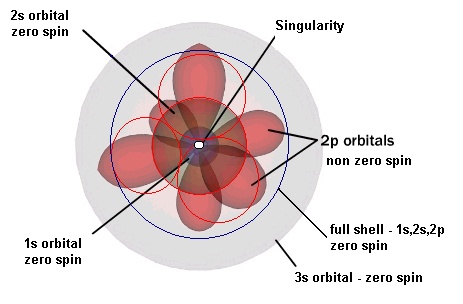

The nucleus - the most basic naturally occuring fractal

As discussed earlier, the above is equivalent to an atom fullfilling its shell 2s, equivalent to atom Be8, which is known to decay in exactly two alpha particles, each of which we explained, take the shape of a tetrahedron. We also know that the second tetrahedron is an exact mirror image of the first one about a central mirror core. Now these two shapes are similar but not the same entity and somehow need to be identified. It's like having to define an uphill from a downhill, so we will call the one with its pointed vertex upwards as the positive tetra and the other as negative tetra. Once the two counter rotating tetrahedrons are summed up in the same spherical space, one gets the geometric shape shown below.
These interactive 3D graphics were created with the help of some Mathematica code written by Robert M. Dickau available on his homepage.
The shape is called the Sierpinski tetrahedron and is the three-dimensional version of the famous Sierpinski gasket. You can rotate this graphic in 3D using your mouse. If you study the shape you will find the the inner shape enclosed between the positive and negative tetrahedrons is in fact a perfect octahedron. This hidden octahedron plays an important role in nature as we shall see later on. For the sake of clarity, the three vertices of the negative tetrahedron are not shown in the 3D diagrams. This fractal is of immense importance as it is probably the key not only to generation of particles but to nature's secret mechanism of growth itself. With the help of this graphic, one can easily understand how nature works out the way from a single entity, in this case the parent tetrahedron (positive), into an opposite parent tetrahedron (negative), and adding them onto the same space coordinates to get three similar structures, each of which have the same 'reproducing' mechanism of their parent structure. Remember that the tetrahedron represents the most basic spherical solution existing in 3D and is thus the best candidate for natures mechanism. Now the wavelength of the EM standing wave generating the structure is equal to twice the distance between vertices, oscillating at a frequency F. What would happen if the structure is twice as energetic? Each positive tetrahedron will replicate itself into its image negative tetrahedron, and four tetrahedrons each oscillating at 2F will take place each parent tetrahedron. Such a mechanism might easily explain the fact that there are peaks and dips of energy per nucleon repeating every fourth nucleon.

|
Doubling the standing wave EM frequency 'mates' each tetrahedron to its opposite polarity tetrahedron and replaces the original with four similar tetrahedrons. The original structure of four tetras is now replaced with sixteen similar tetrahedrons. Doubling the frequency further, gives a structure of 64 positive tetrahedrons as shown on the right. The process of fractal generation does not go for infinity but is restricted by planck's length which defines the shortest wavelength for the distance between vertices of the smallest hidden octahedron. Nature does not in fact set a higher limit for wavelength and that's why we can generate dc (zero frequency currents) in the first place. It is now clear that any possible energy combination within this structure will be a multiple of planck's wavelength represented by the smallest tetrahedron in the fractal structure. |
Black Hole within matter
The matter-antimatter interface core
 Considering
the atom as multiple nesting of 3D platonic solids, all rotating as a single
object, gives us a whole new clearer picture of how the atom looks like, and
explains in a more obvious way many rules which had to be adopted without any
previous plausible reason.
Considering
the atom as multiple nesting of 3D platonic solids, all rotating as a single
object, gives us a whole new clearer picture of how the atom looks like, and
explains in a more obvious way many rules which had to be adopted without any
previous plausible reason.
Each of the outer spherical shells circumscribed by the outer platonics is
analogous to electron energy levels or shells in the conventional model. Inner
spherical shells represent various known (and unknown) conventional particles,
the smaller the shell, the shorter the platonic edge length, the higher the
frequency of its vibration and thus the higher its energy level, frequency and
'mass'.
If one looks closer to this new model however, one can notice that at the very
centre of any atom, there will always exist a platonic whose side lengths are
equal to Planck's length, and whose inscribed spherical volume CANNOT nest any
further platonic shape, in fact it cannot nest anything at all, since units of
wavelength (space) and time are meaningless within such a volume. This is not vacuum, since we know that EM waves CAN be handled in
vacuum. This 3D volume is in fact NOT a space time volume,
it behaves very similarly to a black hole and is NOT REAL. This means that
unlike Wolff's assumption about wavecentres, the ingoing waves never reach to a
single centre point, but a central sphere whose natural resonance wavelength is
equal to plank's length.
We know that a black hole is a region of space whose attractive gravitational
force is so intense that no matter, light, or communication of any kind EXCEPT
GRAVITY can escape. This means that two stars on opposite sides of a black hole
can never 'see' (property of EM radiation) each other but would still 'feel'
(property of gravity) each others gravitational force
A black hole would thus appear black from the outside real world. However, gas
around a black hole can be very bright, indicating an elevated energy level at
its periphery.
Returning back to our atom model, this small 3D sphere, of which one is present
in every standing wave structure (particle), has a very special purpose, and is
the only interface between the real and imaginary components of the standing
wave, will similarly look black, and will be surrounded by the highest energy
level within the atom. As we shall see this spherical core of sub-quantum
dimensions has a special function within matter. But at this point we must
explore the imaginary world of the particle nature.
Most of you have one time or another worked with imaginary terms, or complex
numbers. Conventional physics makes use all the time of imaginary components
for voltage, impedance, currents, permittivity, permeability, refractive index,
but no one ever stops thinking of the consequences of the existence of these
terms, in terms of our restricted 4 dimensional space-time universe.
As with normal travelling EM waves, standing EM waves have an 'imaginary'
component equivalent to an imaginary mass, as in the square-root of (-1), times
its real mass (jm). Imaginary particles are not something new to physics,
although most textbooks barely mention them due to lack of knowledge, and
because they have never been (and can never be) isolated. For example, it is
known that the anti-electron or positron has exactly the same mass as a regular
electron, but has a positive charge and negative entropy, rather than a
negative charge and positive entropy. The anti-proton has the same mass as a
regular proton, but carries a negative electric charge and opposite entropy.
There are also quarks and anti-quarks which carry opposite color-charge, but
otherwise are identical to regular quarks. Anti-neutrinos carry opposite
'neutrino-charge' from ordinary neutrinos. As Feynman correctly described,
these imaginary particles are as real as the real counterparts but travel
backwards in time. This statement may be confusing at first but it's just about
the simplest & best description one could could
come up with for these particles. These antiparticles are not to be found as a
cluster in somepart of the universe. Some people think that such clusters, of
antimatter are being formed elsewhere in the universe, whilst leaving all real
particles clustered in our own universe. This is totally wrong as the anitparticle
is just the mirror image of the particle travelling in a reverse time direction
- something we humans cannot ever experience.
We have no idea how regular matter and 'imaginary' or anti matter interact, but
all forces between real and imaginary matter involving their mass would be
'imaginary', rather than 'real', forces which means that the big chances are
there are no effects from one onto the other, gravitationally. This would not
be true if their interaction is passed through an imaginary function medium, that is a medium which looks like a mirror to both
the imaginary and real sides. In such a case, an imaginary mass through an
imaginary function would result in a real effect on the real mass (j x j x m =
1m), and a real mass through an imaginary function would result in an imaginary
effect on the imaginary mass 1 x j x jm = 1m).
From the Spacetime
conversion table we know that all physics parameters, including
those known to have both real and imaginary components, can be described in
terms of Space (length) and Time. For this to remain mathematically consistent,
both space and time must handle both real and imaginary components. The terms
+j and -j do not mean that the component is orthogonal to the left or right of
the real vector. That is in real 3D space, the vector jx is not equivalent to
either y nor to z. Same applies to time. This means
that our 4D space-time model is not even enough to handle our known physics,
since both space and time are normally being assumed 100% real, which is
definetely not the case.
It is about time, that both mathematical and scientific analysis give more
importance and meaning to all imaginary terms. In multitudes of important
derivations, in both maths and physics, we find imaginary roots and solutions
literally dropped off or disregarded, just because they are not real.
Disregarding imaginary components in the physical world has serious
consequences and is what makes things look to behave weird or showing
overunity. If one does not fully understand that the imaginary components EXIST
as much as the real components, he may be easily tricked, and could never for
example, explain why a seemingly genuine overunity device can never be made
self running.
The implications are rather obvious, an imaginary
space-time dimension has to be defined along with the four real space-time
dimensions to fully represent all physics parameters. This shall upgrade all
physics units into a set of space-time dimensions, one with real and the other
with imaginary, resulting into at least one complex 4 dimension space time. This requires no major change in physics, but from
thereoff, ALL quantities have to be assumed to be complex values, that is, have
BOTH REAL & IMAGINARY COMPONENTS of space-time.

As I have illustrated above, the centre of each particle
of matter cannot be defined as a dimensionless point but one which inscribes a
spherical solution singularity (another platonic), in which real wavelengths
and real time do not fit.
As we have seen in the fractal description of the most inner part of the
nucleus, the mirror core required to perfectly get a mirror image for the
tetrahedron must have the shape of an octahedron. And you must also keep in
mind that such octahedron is in itself a solution of an
incoming and outgoing spherical waves, that is a spherical standing
wave. This octahedron core is illustrated by one of the nice models from Gayla
Chandler which shows the complement shape of the two interlaced tetrahedrons
(the tetrahedron and its reflection, or antiparticle counterpart). The
imaginary component of matter can be visualised as being the exact mirror image
of its real counterpart, being reflected through this interface core. Similarly
to the real side, the imaginary component is made up of imaginary rotating platonics,
and the central interface core has the same size as that in the real matter.
Thus the virtual particle is on one side and the real particle is on the other
side of this spherical volume. Although, the two spheres seem to occupy the
same spherical volume, they are not, and the 'mirror surface' at the centre is
real on the real side and imaginary on the virtual side, it has 3 dimensions of
its own, but it's not a space volume but rather an interface.
Each particle has got this mirror core at the centre, which cannot be defined
in terms of our known space-time dimensions, and so it is independant of both
time and length. Now, we define two different points in space by their
location, and the only way to do that is to define the distance from each other.
If we imagine that each of two independent particle cores are
forming part of a time independent gigantic mirror, how could we measure the
distance between these cores if their dimension is less than any measureable
dimension? You cannot. This means that such mirror cores within two separate
particles cannot be identified from one another, are separated by a
non-measureable distance apart, and from our 4D point of view can thus be
considered as the same entity existing from beginning to end of our time. Also,
the time taken for light to travel from one such core to the other cannot be
measured because light cannot travel without a time dimension.
This has various implications in the real world. It means that all matter in
the universe is interfacing or communicating with its virtual matter through
the same medium, and that all matter in the universe communicates through the
same singularity which has no time dimension. This medium is responsible for
the instantaneous action noticed even at astronomical distances between two
masses, and also for the EPR experimental evidence, and the lack of aberration
of gravitational force. Such theory may finally give significance to the
gravitational constant which seems to depend on the total mass of particles within
the whole universe, which is of course interfacing through this single entity.
Instantaneous (non local) Action
Without violating Causality
 In all textbook physics we
learn that masses, including planets, obey fixed laws of nature. Until the last
decade, these laws were measured properties of nature, no theoretical or
physical origin was known. These measurements indicated that the movement of
energy and information, which are needed to carry out the laws, travel
consistently at the speed of light, and that nothing (no information) can
travel faster than light. This motion satisfied our rule of causality; that is:
Events always occur after their causes.
In all textbook physics we
learn that masses, including planets, obey fixed laws of nature. Until the last
decade, these laws were measured properties of nature, no theoretical or
physical origin was known. These measurements indicated that the movement of
energy and information, which are needed to carry out the laws, travel
consistently at the speed of light, and that nothing (no information) can
travel faster than light. This motion satisfied our rule of causality; that is:
Events always occur after their causes.
 However, some events have
repeatedly seemed to violate the rule of causality. One such force is called
Quantum entanglement. This term is used to describe the way that particles of
energy/matter can become correlated to predictably interact with each other
regardless of how far apart they are.
However, some events have
repeatedly seemed to violate the rule of causality. One such force is called
Quantum entanglement. This term is used to describe the way that particles of
energy/matter can become correlated to predictably interact with each other
regardless of how far apart they are.
Also, events such as gravity pull between planets seem to be transmitted
instantaneously, otherwise it can be shown that any two planets will spiral
into each other. As shown by Sir Arthur Eddington, this means: "If the Sun
attracts Jupiter towards its present position S, and Jupiter attracts the Sun towards
its present position J, the two forces are in the same line and balance. But if
the Sun attracts Jupiter toward its previous position S', and Jupiter attracts
the Sun towards its previous position J', when the force of attraction started
out to cross the gulf, then the two forces give a couple. This couple will tend
to increase the angular momentum of the system, and, acting cumulatively, will
soon cause an appreciable change of period, disagreeing with observations if
the speed is at all comparable with that of light." (Eddington,
1920, p.94).
Evidence of infinite gravitational phase speed at zero frequency has been also
recently observed by a few other researchers by noting the high stability of
earth's orbit about the sun. Light from the sun is not observed to be collinear
with the sun's gravitational force. Astronomical studies indicate that the
earth's acceleration is toward the gravitational centre of the sun even though
it is moving around the sun, whereas light from the sun is observed to be
aberated. If the gravitational force between the sun and the earth were
aberated, then gravitational forces tangential to the earth's orbit would
result, causing the earth to spiral away from the sun, due to conservation of
angular momentum. Current astronomical observations estimate the phase speed of
gravity to be greater than 2x1010c. This value could very well
indicate the limit of the measuring equipment in trying to time a force which
unlike EM waves does not travel, but acts at two distant points at the SAME
TIME regardless of how far apart they are.
Indeed, even
The fact that the gravitational effect is felt before its cause is 'seen' at
the observer does not mean that causality is actually being violated. Instead,
the strange event is merely due to the fact that gravity effect and EM waves
are not travelling through the same medium, or better, through the same spatial dimensions. It is
quite similar (although not really analogous) to the delay between a lightning
flash and its thunder, if one assumes that nothing travels faster than sound,
one would say that the lightning occurred before the strike. The interpretation
of violation of causality is created by our incomplete knowledge of the
Standing Wave Structure of Matter, and of the special energy exchanges taking
place within matters' central sub-quantum core and its periphery. All
electromagnetic communication (radiation & radiation pressure on masses),
detected in 3D space, still travel at c, the speed of light. Action at a
distance can be completely understood if one considers the fourth spatial
dimension. As already discussed here,
the only way we humans get to percieve this 4th spatial dimension is through
the perception of time. Any energy fields in this dimension will appear to us
to be time independent. Our mind normally perceives speed as the rate of change
of a spatial dimension with respect to time, but what happens if we try to
detect the rate of change of time with respect to time itself? Gravitational
forces are taking place in this 4th spatial dimension, which is orthogonal to
all 3D spatial dimensions, the one we normally perceive as 'time' and therefore
the concept of 'travelling' in 3D space makes no more sense for such a force.
The speed of gravity information is still hotly debated, but the EPR experiment
is a well accepted scientific experiment which proves instant action at a
distance. The EPR experiment (named after Einstein, Podolski and Rosen) in
which two quantum particles A and B which were once together fly apart and are
measured at two distant locations A and B. In the Quantum Theory, observer A's
choice of what kind of measurement to make on particle A instantly changes the
state description of particle B--a general feature of quantum theory called
"quantum phase entanglement". In the theory a particle is represented
by possibility amplitudes and relative phases. When the particles separate, so
do the amplitudes, but the phases of particle A remain entangled with the
phases of particle B. Any action on A--such as
reaching the observation sensor--changes not only A's phases but the phases of
B as well. This action of observer A on distant
particle B does not diminish with distance, cannot be shielded and travels
faster than light. This distant influence is unmediated, unmitigated and
immediate. Such quantum connection between two particles once together now
apart is a lot like voodoo--no known force connects particles A and B--just the
fact of their once being together suffices to mingle their phases. Such instant
voodoo influences are called "non-local"; all ordinary
light-speed-limited forces are called "local". All interactions
taking place in the fourth dimension will of course look like voodoo to a 3D
observer, as long as the observer does not recognise TIME as a real SPATIAL
dimension.
This 4th dimension is common to all particles and establishes an interesting
feature in the whole universe : the cosmic wavelength.
The resulting 'heart beat' is the same for all matter, because the homogeneity
of the medium of the waves produces a fixed wave frequency. That's why Planck's
constant is a constant through galaxies light years away from each other, since
for gravity or quantum entanglement, a light year distance and 1 mm make no
difference. The thickness (one planck wavelength or
one timeframe) & homogeneity (G-gravitational constant) of this medium,
sets a standard frequency of vibration for the smallest electric entities
(dielectric entities) across the universe, as well as a relation between them
for their action at a distance. An other interesting
property of this cosmic clock is that it is always in phase at every particle
boundary. This means that if you get two electrons, any two in the whole
universe, their in-going and out-going waves will be EXACTLY in phase. Same
applies for all matter in the universe being it an electron, proton, neutron or
whole particle.
The notion of such universal clock has been suggested by deBroglie. He stated
that the universal frequency of the electron is fe
= mec2/h, and that this will be the same for any electron
that exists anywhere. This frequency standard based on Planck's constant is a
property of the special subquantum core we have defined earlier in this section
and, thus, as we already stated, it is the same for all particles. Similarly
this uniform medium thickness also provides a measure of minimum quantum
length, time interval and speed of light. In a way this medium gives a sense
for the existence of both real and imaginary space-times. Without it, there
would be no boundary limits for the existence of length and time and the
standing wave structures we refer to as the 'elementary building blocks of
matter', and hence no universe, nothing at all. So, how do particles 'feel'
each other within this medium?
The spherical wave structure of particles provides range and location
information for the force laws. Nautical navigation teaches us that the
curvature of a wave front is sufficient to determine the range and position of
the center of the source of the wave fronts. This is the simple mechanism
available to two particles to find their relative range and position. But what
about wavefronts in a time independent medium; they should not exist. That's right,
but since the homogeneity of the medium is constant (G), and all sources have
the same intensity at the interface, the attenuation level would give their
relative position without the requirement of a wavefront.
Time and spherical wave solutions
Perception of time through vortices (CP) asymmetry
 We measure time by clocks, but clocks do
not really measure time. If time slows down, everything will slow down,
including the clock, and we could never detect or feel any change. If time
slows down by a factor of ten, a clock in the same time-frame will still show a
24 hour day. We can only measure the difference between our time-frame and
another. How would we know if time flows backwards. In
the universe the time flow can be noticed by the direction of waves in space,
inward or outwards from a source, outward being the normal positive time.
Similarly, if the real electric and real magnetic fields are in the form of a
spherical standing wave, their real cross product always points to the center
of the sphere, and we call this real mass, which would always be positive. But
how does matter flow through time? We know that when a slight imbalance in
standing wave mechanism occurs, the standing wave will surely but slowly drift
either towards or away from the source. In our real & imaginary spherical
standing wave, the drifting nodes will be the platonic shapes, which will
either drift outwards or inwards the sphere, depending upon the symmetry
imbalance between the real & reflected waves. This effect is perceived by
matter as flowing through time.
We measure time by clocks, but clocks do
not really measure time. If time slows down, everything will slow down,
including the clock, and we could never detect or feel any change. If time
slows down by a factor of ten, a clock in the same time-frame will still show a
24 hour day. We can only measure the difference between our time-frame and
another. How would we know if time flows backwards. In
the universe the time flow can be noticed by the direction of waves in space,
inward or outwards from a source, outward being the normal positive time.
Similarly, if the real electric and real magnetic fields are in the form of a
spherical standing wave, their real cross product always points to the center
of the sphere, and we call this real mass, which would always be positive. But
how does matter flow through time? We know that when a slight imbalance in
standing wave mechanism occurs, the standing wave will surely but slowly drift
either towards or away from the source. In our real & imaginary spherical
standing wave, the drifting nodes will be the platonic shapes, which will
either drift outwards or inwards the sphere, depending upon the symmetry
imbalance between the real & reflected waves. This effect is perceived by
matter as flowing through time.
Wheeler and Feynman (1945) modelled the electron as spherical inward and outward electromagnetic waves, seeking to explain radiation forces, however they failed, because as it was illustrated, the spherical wave is hidden, and is only clearly visible when rotating the standing wave structure. Once you have the standing spherical wave front, you have also got the ingoing and outgoing spherical EM waves and can then account for radiation forces. The major deficiency of the classical force laws is that they have no theoretical or physical mechanism for energy transfer. The formulae contain only constants, "mass" and "charge," - no function & no mechanism. This was an inherent defect of the static point particle model. Einstein, Wheeler and Feynman knew this, recognizing that there must exist a continual dynamic means for forces to transfer energy, and sought it in electromagnetic waves. Unfortunately there are no spherical solutions for the travelling vector e-m wave equation. Hence the mechanism had to await the scalar waves.
|
|
The above diagram shows a 3D view of a
tetrahedron rotated 360 degrees simultaneously about each of its three axis, as viewed from a frozen time axis. This is the
complex vortex one would get from a standing wave structure based on the
tetrahedron. If one had to view such rotation, while giving depth to the
image as time flows, the tetrahedron flowing past time would get smaller and
smaller. The resulting plot of its vertices as viewed from a camera fixed
over one of the vertices, would be exactly as shown
on the left, which happens to be the well known Treble Julia Set crop circle
found overnight in the |
The wave equation must be written in spherical coordinates
because cosmological space has spherical symmetry. Uniform density of the
medium (space) is assumed, which yields a constant speed of the waves (and
'light'). Then the only two solutions describe the charge waves of common
charged particles including the electron, positron, proton, and anti-proton.
They are:
IN-wave amplitude = e(iwt + ikr)
OUT-wave amplitude = e(iwt - ikr)
A= wave amplitude peak
r = radius from wave center
w = 2.pi.f
t = real time
k = mc/h = wave number
Energy = E = hf = mc2.
At the center (the mirror), the in/out waves are joined by rotating the in-wave
to transform it to the out-wave. Superposition of the
two amplitudes to produce a standing wave can occur in two ways depending on
rotation, CW or CCW. One is the electron, the other the positron, with opposite
spins. Writing the rotation operators as CCW or CW ,then
the two resonance amplitudes are:
Rotating standing wave electron = E(-) = CCW
Rotating standing wave positron = E(+) = CW

The above diagram, is equivalent
to the complex vortex diagram, based on the same rotating tetrahedron, but with
the time dimension represented in the shell distance from the core. Thus the
outer shells represent the present and inner ones represent the past. The
diagrams thus represent time reversal.
To perform an entropy or time inversion, change CCW to CW, which converts the
time factor from positive to negative, and the positron into an electron. You
will see that a positron is a mirror image of the electron viewed from the real
space-time. To change a particle to an anti-particle (real to imaginary),
switch the in-waves and the out-waves, it's like
viewing the real particle in the mirror.
If they collide, the electron standing wave structure and anti-particle
(positron) standing wave structure disappear, to leave
only a non-standing (travellling EM wave) energy - an act of mutual
destruction, called annihilation. Experiments have since demonstrated that most
other particles, protons, neutrons, muons and so on, have anti-particles. Note
that in all such cases energy is not destroyed or created, but rather their
structure is destroyed, releasing the energy within it.
When particle and anti-particle meet, a spontaneous burst of pure energy is
produced, such process called annihilation. Let's go a step further. Since
anti-matter is the reflection of matter, and vice-versa, in this central core
black hole or singularity, one would expect that matter and anti-matter exist
in equal amounts, referred to as symmetry. This indicates that way back to the
era when the universe is created, which should have huge energetic conditions,
the amount of matter should be equal to that of anti-matter...but something
unusual happened, which resulted in the existence of space & time itself.
If symmetry had been conserved, why did the anti-matter not completely
annihilate the matter, leaving only energy in the universe? Or why does nobody
ever encounter stable anti-matter or maybe anti-matter planets? At this point
we should know the answer, because anti-matter EXISTS but is NOT REAL - it can
be observed as matter through its reflection in the cetral core of each
elementary particle.
So why do we live and observe the matter side (REAL part) of things, and not
the other. It is believed that there is a breakdown in the symmetry, called the
charge-parity, CP-violation. It is this violation that causes the amount of
matter to be slightly more than anti-matter. For this reason we, and all the
matter around us, can exist, and anti-matter always lags behind matter in time.
If you have read carefully up to this point, you will now understand why action
on a particle will always cause a motion AFTER (NOT before) the force has been
applied. This is the law of causality, and seems quite obvious - but such law
would be reversed if anti-matter leads matter in time, or simply exists in
higher abundance than matter. In such a case, having a CP-violation of the
opposite value, would make us live in and observe an anti-matter universe, but
still exist. 'Existence' shall only stop when time itself stops,
and that can only happen when the CP-violating factor is exactly null.
In 1964, scientists got another anti-matter surprise, when a team of
physicists, studying neutral kaons in experiments at DOE's Brookhaven
Laboratory, discovered a slight but definite assymmetry in the behaviour of the
neutral kaon and its anti-particle - an assymmetry called charge-parity, or CP,
violation. Until that discovery, physicists had believed that particles and
anti-particles behaved symmetrically, like mirror reflections of each other.
At Fermi Labs during 1999, it was announced that epsilon prime over epsilon
equals 28 E -4. Now SLAC is offering a more robust measurement of the
CP-violating parameter, referred to as sine (2beta); the value it reports is
0.59 with an uncertainty of 0.14. From this result we can conclude that there
are less than 3 chances in 100,000 (<0.003%) that the actual, physical
assymmetry could be equal to zero. This is a direct measure confirming charge
parity assymmetry or violation between the real and imaginary components of the
same particle, which is the only measure of the arrow and rate of time -
perhaps the reason why we live on the real side and why real mass exists in
positive time & entropy, whilst virtual particles exist in negative time
& entropy.
In/out waves origin
The Final Enigma
Well, we have seen that both
mathematical evidence and experiments agree with the notion of matter being
made up of a standing wave structure of energetic waves in space. The new model
offers logical mathematical and common sense explanations for many laws which
had previously no origin other than experimental evidence. These include the
conservation of energy, quantum theory, special relativity, origin of charge
and mass,
 Video
interview of Milo Wolff by Geoff Haselhurst about in/out waves
enigma.
Video
interview of Milo Wolff by Geoff Haselhurst about in/out waves
enigma.
According to Milo Wolff, the inwave of a particle must
come from the outwave of another, but the actual origin of the incoming and
final destination of outgoing wave is still unknown, the imaginary part of the
waves is still a confusing issue and this should hold the key to the whole
standing wave model. Personaly, I find Wolff's argument about the ingoing waves
generated by the outgoing waves of other particles not particularly convincing
though, as it implies that no single particle can exist in the absence of
another particle. The standing wave model proves to solve most enigmas in
physics, it explains all paradoxes present in today's modern physics, yet it
seems to suffer the same problem as the chicken & egg paradox - which came
first and from where? I believe, and you shall learn within the following
pages, that things are far more different from what we think they are, but we
are getting closer to the truth.
Let us start to visualise a simple situation, in which a sphere is slowly
immersed in a tray of water.

On the right of the diagram, we see what's 'visible' at the water surface, that is the varying cross sectional area of the sphere being immersed. What we see is the volume of the sphere sliced sequentially into 2D flat disks of varying radii. Now imagine that the original motion consists of immersing the sphere under the water level, and that the part showing it going up again is just a 'reverse playback' of the movie. The time during which the sphere is being immersed is the positive going time, whilst the reversed movie part is the negative going time. If you think about that, you will understand that the cross sectional area at time=t during reverse playback is actually as real as the cross sectional area at time=t during the first playback. There should however be some mathematical way to show which cross sectional area we are refering to. Although they are the same, their motion is opposite to each other, that is during the time the positive time area is expanding the negative time area is contracting and vice versa. We only perceive with our senses the positive time going events, but each negative time going event is there as well since if the negative flat disk slice does not contract back in time, the positive one cannot expand forward in time! It is VERY important you understand this concept. Then you will understand that in such a situation you cannot refer to the positive going part without the knowledge of the negative going counterpart. The whole situation is fully defined only if you describe both the events as happening in both positive and negative time. Whilst the normal playback is showing a cross sectional area coming into existence, the reverse playback is showing the area going out of existence...ingoing, outgoing. At this point you should have guessed what the description of the forward and reverse playback events represent... they do represent the outgoing and incoming waves respectively. Depending whether your mind sees the outgoing wave to represent positive or negative time, will eventually determine which standing wave pattern your mind will select as the REAL and which it selects as IMAGINARY. The imaginary counter part of the standing wave is the virtual particle or antiparticle counterpart of the standing wave and its existence cannot be ignored! For a particle to exist, you need both ingoing and outgoing waves. This implies by logic that you cannot generate an electron without having at the same time generated its imaginary counterpart, the positron. Again this logic deduction is backed by experimental evidence as shown in the bubble chamber photo below.

Part of a bubble chamber picture (Fermilab'15 foot Bubble
Chamber', found at the
The following animation shows how the superposition of both the area flowing
forward in time and the area flowing backward in time, together with their
complex (real + imaginary) superposition which creates the standing EM wave.
The first two animations are the 'playback' and 'reverse playback' of the same
sphere being slowly immersed under the surface of the water.
|
|
|
Concentric spherical standing waves graphics by Gabriel LaFreniere.
If you have problems understanding how the positive and
negative time counterparts can create the above sequence, imagine you are in
the front seat of your car driving inside a tunnel. This will create the effect
shown in the middle animation. Now imagine that you are looking back either
from the rear window or from your mirror, you will see the animation shown on
the left. Both are realities, but we tend to term the one from the front seat
as the real, and the one from the back seat as the imaginary, one cannot exist
if the other ceases to exist, isn't it? If you see the tunnel approaching from
the front seat, and you see no tunnel from the rear window, then it would mean
that the tunnel is being absorbed into the car!! The animation on the right is
just the mathematical addition of both experiences, which therefore contains
all the information of the two separate views. It is interesting to note, that
if at any point in time, the real & imaginary animations are interchanged,
the resultant standing wave will not change at all. So, if we apply this fact
to the above mentioned sphere being immersed in and out of the water surface,
the final standing wave during the whole oscillation will be unchanged. Also,
let's take this one step further, if instead of a moving sphere, you have got a
moving observation plane, the standing wave will still remain unchanged. This
is another important point to understand the universe, since it is not the
ultimate dimension of the universe that is changing but only the observer's
point of view.
Now if you are still with me to this point, you must have one important
question. "How can we have the 'reverse playback' video before we finish
the first playback video, in order to produce the superimposed standing
wave?" Good question which will take us to the next interesting topic. In
order to be able to costruct the above standing wave animation we cheated a
bit. We assumed that both past and future are known already. Does this not
usually make sense to us humans, because we only perceive the positive going
time direction, and thus our mind is capable only of recording the past. But piucture this: if within the next minute you will
be reading the next paragraph, then you can say that one minute in the future
from now you ARE already there reading it, while at the present you are reading
this sentence. Also, it means that if a minute ago you were reading the
previous paragraph, then one minute in the past from
now you ARE reading the previous paragraph. Notice, we are not saying you WERE
and you WILL, but you ARE. I understand this might be puzzling at first, but do
not give up. To re assure you that I am right, I will just mention the name of
the experimental evidence for this: the EPR experiment, in which it is clearly
shown that the particles involved in the experiment know there past and future
during their whole journey from source to detector.
As you will see in the following section, this mechanism can be explained in
terms of differentiating a higher dimensional space. Don't get confused with
the term multidimensional or higher dimensions. Here we are not talking about
science fiction parallel worlds existing independently in different dimensions.
You will soon see, that the existence of higher
dimensions will eventually be the key to solve the ultimate enigma and a few
more that are not yet very clear with the 3D standing wave idea.
If you correctly understood the above diagram, then the answer to the Enigma;
"Where do in/out going waves come from, or go to?" should be quite
straight forward, they come from and go to one space dimension higher than our
observation 3D point of view. Having understood this, you will now find it much
easier to explain how elementary particles are found to pop in and out of the
nothingness into nothingness, as experimental evidence shows. Without the
existence of higher dimensions, the 3D standing wave model on its own is not
enough to explain this hard evidence.
At this point, one can tackle another enigma regarding the origin of the
relativistic energy diagram, which states that
Total energy E2= (Rest mass energy mc2)2 +
(Relative motion energy pc)2
The main enigma here is "why should these two energies use the squares of
each energy term to give the total true energy?" Looking again at our
animated sphere, the answer is quite easy to deduct. The two energies are
orthogonal, not in 3D but in 4D. Thus the true energy is calculated using pythagoras theorem from 475BC as in a right angle triangle
to find the hypotenuse.
We note that if side 'a' represents the relative motion energy in 3D, whilst side 'b' represents the orthogonal 'mass' energy analogous to the above animated sphere penetrating the 2D dimensional plane from a higher dimension, then side 'c' will represent the true total energy of the moving particle. Also, since the speed of light is a property of space, any point on the circular cross sectional area on the surface will see the inwaves of the sphere approaching down at the same speed, whatever relative speed is involved between the two points on the surface. Since the inwaves are EM waves, the speed is always equal to the speed of light 'c'. Despite other expectations from scientists, the verified experimental facts support this concept since if two experimenters measure the speed of light, they always both get the same value for 'c' independent of their relative speed to the source.
Existence of Higher dimensional space & Perception of time
The observation that spatial dimensionality is limited to
three dimensions has been for long a puzzle to scientists. Our mathematics do not limit us to three dimensions. Why are there only
three dimensions? We are 3D observers, and this makes it easy for us to
conceive the observed reality as 3D. We can also quite easily conceive a 2D
universe as a subset of our 3D universe, and we see how complex the explanations
can get in a 2D universe, for events we find simple in our 3-D universe.
The relativity theory made spatial dimensionality elastic. The space-time
continuum was conceived. Four dimensional space-time
was proposed and attempts to visualize a 4-D space, as an extension of our 3-D
world, became popular. We talk about 3-D space being curved around some 4-D
sphere like the atmosphere around the earth.
In science fiction, discussion of alternate planes, or
dimensions of existence, have become ingrained. Religious
"Heaven" has been moved from the stars and galaxies to these
alternate dimensions. In this section I will show you how to scientifically
understand higher dimensions, which will hopefully lead you to better
understand the higher dimensional universe which we all form part of.
Many modern physicists, in their attempts to unify theory, have proposed the
existence of many space dimensions beyond three. The multi-dimensional efforts
at grand unification have indeed mathematically helped describe theory and
predict experimentally observed facts, but attempts at 4D visualization seem
hard indeed. We talk of extra dimensions being curled into minute 3D spaces.
One should keep in mind what we are with respect to the space around us. The
answer is that each one of us is a 3 dimensional spatial observation point in
space, and that dimensionality is not a property of 'reality', but of the
being, the observer. Instead, our spatial dimensionality is a characteristic of
our conceptions, our mind. This means it is a characteristic, or property, of
knowledge rather than of reality. Spatial dimensionality is a property of the
observer rather than of the observed.
 So, is
everything observed around us just an illusion? Not at all, the things around
us will still exist even if no one looked at them. To say spatial
dimensionality is a very powerful tool may be one of the all-time greatest
understatements. However, if spatial dimensionality is a property of our
knowledge, then it is not a complete universal truth, but just a shadow of the
truth (look at the animation to see what I mean). The answer, of course, is
that our spatial dimensionality is based upon what we see. Of
all the senses which a typical person possesss, sight is the one which plays
the greatest role in the perception and conception of reality. The
perception of spatial dimensions does not have to be based upon sight, hearing
or any of the other senses. Our eyes are essentially 2D arrays which sense
light reflected from viewed objects. Therefore, we never actually 'see' three
spatial dimensions. We see (perceive) stereographic 2D pictures. In our mind,
we conceive the existence of a third dimension using two stereographic
pictures. As you see, our mind is already 'too busy' converting 2D sensed data
to reconstruct a 3D observation picture of reality. For humans to visualize a
world in more dimensions than 3D is no trivial task. It may even be impossible,
without physically modifying ourselves. If dimensionality is not a property of
the universe, but of ourselves, then our attempts to 'visualize' 2D and 4D
universes in terms of our 3D abilities is not only futile, it is nonsense. The
reality perceived by a 2D being is the same reality as perceived by a 3D being
and a 4D being. Their methods of description will vary greatly, but they are
each attempting to describe the same thing.
So, is
everything observed around us just an illusion? Not at all, the things around
us will still exist even if no one looked at them. To say spatial
dimensionality is a very powerful tool may be one of the all-time greatest
understatements. However, if spatial dimensionality is a property of our
knowledge, then it is not a complete universal truth, but just a shadow of the
truth (look at the animation to see what I mean). The answer, of course, is
that our spatial dimensionality is based upon what we see. Of
all the senses which a typical person possesss, sight is the one which plays
the greatest role in the perception and conception of reality. The
perception of spatial dimensions does not have to be based upon sight, hearing
or any of the other senses. Our eyes are essentially 2D arrays which sense
light reflected from viewed objects. Therefore, we never actually 'see' three
spatial dimensions. We see (perceive) stereographic 2D pictures. In our mind,
we conceive the existence of a third dimension using two stereographic
pictures. As you see, our mind is already 'too busy' converting 2D sensed data
to reconstruct a 3D observation picture of reality. For humans to visualize a
world in more dimensions than 3D is no trivial task. It may even be impossible,
without physically modifying ourselves. If dimensionality is not a property of
the universe, but of ourselves, then our attempts to 'visualize' 2D and 4D
universes in terms of our 3D abilities is not only futile, it is nonsense. The
reality perceived by a 2D being is the same reality as perceived by a 3D being
and a 4D being. Their methods of description will vary greatly, but they are
each attempting to describe the same thing.
This alternative perspective on spatial dimensionality has offered a rational
answer to the question of why do we conceive the universe to be limited to
three spatial dimensions. The answer is the universe is not limited to 3D, and
most scientific evidence points to higher dimensional universe, but it is we
who are limited, due to our senses. Another dimensionality issue that is
answered is that of the co-existence of multiple dimensions beyond three. This
issue becomes nonsense. An object cannot pass to another plane or dimension of
existence, because these planes or dimensions do not exist. No dimensions exist
except in our minds.
Dimensions are powerful tools which we use to organise, live and understand the
universe. It seems reasonable to believe that a being who can conceive an
"n"*D universe can develop more elegant knowledge that a being who
can only conceive an "n-1"*D universe. In essence, the more dimensions
we can conceive, the more about the universe we can understand. TIME is only a
way to organise information about the n*D universe, for all those mysteries
which we have not been able to fit entirely into our (n-1)D
spatial dimensionality framework. Remember the initial hypothesis was that a
being who perceives "x" dimensions, will conceive the universe in
"x+1" dimensions. We are now expanding the hypothesis to say that a
being who perceives "x" dimensions, will conceive the universe in "x+1"
dimensions where the "+1" is "time." Therefore, as beings
may increase the total number of dimensions in which they perceive and conceive
the universe, there will always be a temporal dimension to the universe for the
beings. In the case of a limited dimensional universe of n*D dimensions, then
the universe (reality) will be the being (the n*D observator) itself and that
is the only possible non-temporal dimension.
If we could increase our perception to 3-D so we could then conceive a 4-D
universe, many phenomena which we now describe as occurring at different times
would then be described as occurring at different spatial locations. The
progressive increase in spatial dimensionality moves explanations from the
infinite reservoir of "time" to spatial locations. However, even
though the number of spatial dimensions may increase without bound, the
conception of "time" remains constant for all beings, from 0D to 3D
to "n"D.
From these ideas one can deduct, that we are 3D spatial observation points
observing a multidimensional universe around us. For us 3D observers, the
"+1" dimension cannot be spatially observed, so our mind perceives
different 3D pictures changing through 'time'. Time being the "+1"
dimension is so embedded in our minds, that subconscious brain functions may be
"hardwired" to better enable its "conception".
Current scientific knowledge is based on a 3D based reality which seems to get
in trouble when small dimensions of length or time are involved. Science is now
talking of energetic particles that randomly pop in and out of existence, which
doesn't make sense if we do not try to understand how higher dimensional
universe may work. It is a fact that at the time of writing, the best candidate
unified theory is fully compatible with this higher dimensional space theory,
namely the supersymmetry.
Supersymmetry is an idea that has been around for decades. It states that every
boson has an associated fermion and vice-versa. So a quark, which is a fermion,
has a supersymmetric imaginary partner called a squark, which is a boson.
Likewise a photon, which is a boson, is teamed up with the photino, a fermion.
None of the proposed supersymmetric particles have ever been detected.
Scientists say this is because current particle accelerators are just not
powerful enough. Science knows that these imaginary components MUST exist, but
will never be able to detect/isolate them with the current methods, for the
simple reason that they are imaginary. Note that the term 'imaginary' is a
mathematical term and does NOT mean 'non-existent'. Any form of matter
interpreted in our space-time dimension can be mathematically expressed as a
complex (Complex = Re+Im) function of space and time. Lately, some evidence
that supersymmetry is real may have emerged from a study of gold and platinum atoms.
Teams from the
Understanding 1 dimensional space
Supersymmetry involves the concept of multidimensional space. In order to understand dimensional spaces higher than three, let's
start with the simplest 1D case, that of a 1D observer - a line. You
might think, well that's quite easy. In fact it is quite easy, but if you
really understand it, you might use your knowledge to understand higher
dimensions. The animation below shows the observer as a grey line, who is
trying to percieve a reality (a 2D circle in this case) in his 1D limited mind. The animated blue line is what he perceives. Note that
the reality, the circle, is not changing in time, its radius, colour and all
other properties are a part of the reality. The observed thing is quite
different from this, it is a blue line varying in
length WITH TIME. For the observer, it remains a mystery as to what happened to
the original full length of line, why and how it changes length and 'pops in
and out' of his 'observed reality'. Also, the 1D observer has no way to find
out whether the oscillating line is due to observing a circle (2D), a sphere
(3D) or hypersphere (D>3). Also, in order for an observation to take place,
we need the grey line (1D) observer, to have a 'thickness'. This thickness is
very small, just enough for the observed image to be projected on, similar to a
projector screen, but has to be greater than zero.

Understanding 2 dimensional space
Let's now start analysing a 2D case, that of the classic Flatland example, in
which a person lives in a 2D universe and is only aware of two dimensions
(shown as the blue grid), or plane, say in the x and y direction. Such a person
can never conceive the meaning of height in the z direction,
he cannot look up or down, and can see other 2D persons as shapes on the flat
surface he lives in.

Now we know that 3D space exists, and can conceive that,
because we see each other in 3D space. So, what does a 3D reality sphere look like
into a 2D plane? The answer is again graphically shown in the animation, which
shows a circle expanding and contracting depending on which slice of the sphere
intersects the 2D observation plane. In the 2D plane, the thickness of the
plane tends to zero, but again, cannot be absolute zero. There must be enough
thickness for the circle to form and be observed. Thus, the 3D sphere is being
differenciated with respect to one of its spatial dimensions (z in our case)
across its diameter. Actually, in the special case of a sphere, it could be
intersecting the plane at any angle to the z axis, and still be perceived as a
perfect circle in 2D. For the person that lives in 2D, the only way to
recognise such a 3D structure is through integrating all the circles he sees,
on top of each other. But here is the problem, he
cannot imagine anything 'on top of each other'. A clever 2D guy has just one
simple way to refer to this z-axis, which is constantly differenciating the 3D
object, and that is TIME.
I admit this concept is quite hard to grasp, especially when one moves on to
describe a 4D universe differenciated by a 3D space, with both real and
imaginary axis. The imaginary space dimensions can be pictured as follows. Just
try to imagine a person in front of a 2D plane surface, but this time a mirror
surface. The person is equivalent to the real part and his image in the mirror
is equivalent to the imaginary part. Imagine also that such a mirror is present
everywhere he can possibly move. So, the person becomes DEPENDENT on the
existence of his imaginary component. That is, if the image is no longer
present in the mirror, then one can deduct that the person can no longer exist
in reality! In fact, beleive it or not, this is a fact. Now this was an example
of a 3D image reflected on a 2D plane (the mirror).
Understanding 4 dimensional space
Recall ages ago, when most people believed that the earth was flat. Some
thought that they would "fall off the edge" of the earth if they went
out too far. No one ever thought, that if they kept on going, they could
possibly end up where they started, having experienced the entire trip as being
in a straight line! No matter how far the subject travels (by boat, train, or
plane), he will never come to a boundary: there is no "edge" to fall
off from!! It is because the earth exists on the surface of a sphere that these
properties hold true. Let us now take this a step further.
Launched from the earth is a rocket ship that is travelling out into space. Its
mission is to continue outward in a straight line in its current direction
until it reaches the "outer edge" of the universe. When will the
rocket ship reach the outer edge of space? In the previous example we find a
similar situation: the concern of "falling off the edge" of a flat
earth - an earth that in reality has no "edge" to fall off from. Now,
if our universe reality is not 3D we will find out that the ship will never
encounter an outer edge. Not only that, but it could also possibly end up where
it started, having experienced the entire trip as being in a straight line! No
matter how far the rocket ship travels through space, it will come across no
boundary of any kind. These properties would hold true if the universe existed
on the surface of a hypersphere in the same way that the earth exists on the
surface of a sphere.
The hypershpere is the 4D analogue to a circle in 2D or of a sphere in 3D. How
would we picture a hypersphere? The key to approaching something of the fourth
dimension is by means of the tool of analogy: we rely upon corresponding
lower-dimensional structures we have studied as the means by which their
4-dimensional analogue is constructed. A solid circle is a 2-dimensional
object. When cut into 1 dimensional slices, you
will see a line, that varies in length between the size of a single dot
to its full length. A solid sphere, as shown above in the flatland animation,
is a 3-dimensional object. When cut into slices, we find that a solid sphere is
in essence an array of 2D solid circles that vary in cross sectional
area. Having obtained the knowledge we have so far, we now possess the
ability to bring these lower-dimensional structures "up a notch"
through analogy to envision a 4D hypersphere.
|
|
We cannot directly visualize a hypersphere for the very reason that it is a 4-dimensional object and goes beyond our senses. What we can visualize, however, is a hypersphere in the form of 3-dimensional slices (as is displayed to the left). A hypersphere is in essence an array of 3 dimensional solid spheres that vary in volume. This would represent our basic conception of the hypersphere, and is shown in the animated picture here. If one superimposes the time reversed animation over this one, a 3D spherical standing wave with 'shells' will result...matter will be formed. Unfortunately we 3D observers can never see the difference between a 4D and a 5D hypersphere, but accepting the knowledge of their existence is a big step. |
As I have said, in 4D space, our 'time' is integrated in a
space dimension, and then action at a distance (gravity being the purest
example), becomes much clearer to us. Just imagine, in the classic 2D example
shown above, that the 2D person is somehow able to impart a force on the circle
he sees on the plane. What would the consequences be? He would eventually move
the whole sphere and would also change the position of the future circles in
the plane. He would also move all points on the circle, as if all points are 'entangled',
and the transmission of this force from the point of action to any other point
on the circle does not depend on the time it takes for the sphere slice to pass
through. So, to the question, is gravity a push, a pull or both, or does
gravity act on a body, or is gravity generated by the mass of a body, there is
no answer if the problem is analysed only in 3D space, as the interaction
between two bodies is just an effect we see due to the interaction on a single
body existing in a higher dimension. The interaction between the two different
dimensions takes place in the 'mirror plane' where the time dimension does not
exist, but is rather a perception of the observer. That also means that issues
like 'the finite speed of gravity' clearly make no sense.
If you try to extend this to our existence and to the existence of all matter,
you will find that all actions (including gravity) are at work at a higher
dimension and we are here in 3D space observing the effects that are being
played at this higher dimension(s). The 4D I am referring to, is quite different from Einstein's 4D Space time, in
that it is a 4D space and no time. The time coordinate comes in as a false
perception of the 4th space dimension, which we are unable to imagine,
analogous to the flatland man who cannot understand height and depth. In this
figure, you can see what a 4D sphere looks like when differenciated in 3D
space. When one differentiates this 4D dimension with respect to an infinitely
small mirror thickness (Plancks length being the best candidate), then you get
the universe we observe, with Plancks time being the time taken for each 3D
slice to pass through the 'thickness' of the mirror, and such universe is
equivalent to Einstein's Space-time.
So, what is the speed of light? The speed of light can now make more sense, it is the thickness of the mirror divided by the time
it takes for the next slice. It is the maximum speed of differenciating the 4D
reality from a 3D spatial point of view. In our context, the value would be equal
to Planck's length/Planck's time which is in fact equal to c, the speed of
light. That's why Einstein's theory of relativity although
correct, CAN NEVER give us all the answers to our questions, because it is NOT
COMPLETE. As Rudolf Steiner stated: "Anything
dead tends to remain within the three ordinary dimensions, while anything
living constantly transcends them". Applying the same rule to
everything, we may modify this statement as "Anything stationary exists in
the ordinary 3D, whilst anything moving is being constantly differentiated in
each 3D plane and hence exists in the fourth dimension". We also know that
matter is made up of waves, and waves cannot be stationary, and this means that
matter requires the existence of a higher dimension in order to exist.Click here for an
excellent site discussing Space in motion.
What's the evidence for the existence of higher
dimensions?
So, are higher dimensions only theoretical? Not at all.
In physics, the inverse square law relation is quite common. This relation is
valid for the gravitational attraction between matter, for the electrical
forces between charges and for magnetic forces between moving charges. A force
that varies with the square of the distance means that the force will increase
with the square of the distance if we reduce the distance, and it will decrease
with the square of the distance if we increase the distance.
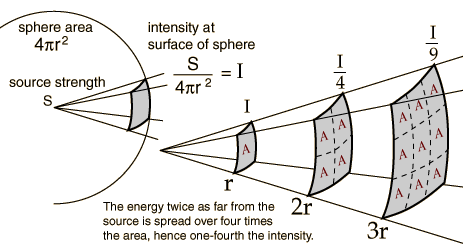
Electromagnetic energy decreases as if it were dispersed over the area of an expanding sphere, 4piR2where radius R is the distance the energy has travelled. The amount of energy received at a point on that 3D sphere diminishes as 1/R2. This clearly shows the origin of the inverse-square law.
Here is a table showing the volume and surface area of hyperspheres of different dimensions:
|
Dimension (n) |
Shape |
Volume |
Surface Area |
|
circle |
π r2 |
2π r |
|
|
sphere |
(4/3)π r3 |
4π r2 |
|
|
4-sphere |
(1/2)π2r4 |
2π2r3 |
|
|
5-sphere |
(8/15)π2r5 |
(8/3)π2r4 |
|
|
6-sphere |
(1/6)π3r6 |
π3r5 |
|
|
7-sphere |
(16/105)π3r7 |
(16/15)π3r6 |
As a result, a force that varies with the square of the distance can be considered as a conventional 1-dimensional force vector (x-axis) that is scattered into 2 additional dimensions (y, z) due to the 3-dimensional nature of space. The square power of the distance indicates the projection of such a force over a 3D spherical surface area. But what happens if the force is also acting in higher order dimensions? What if the originating force is being projected on a higher dimensional surface area? Are there forces which vary to other powers than the inverse square law?
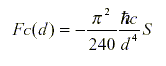
The Casimir force related by
the above equation is known to vary as the inverse d4, which is two
orders of dimensions higher than the more common forces, and coincides with a
force projected over the surface area of a 5D hypersphere (see table above).
Such force that varies with the fourth power of the distance can be thus
considered as a force vector that is scattered in a 5-dimensional space.
Therefore, it is evident that the field that originates the Casimir force is a
5-dimensional field, that it is in fact a hyperspace field that produces the
corresponding effects in our restricted 3D vision of our universe.
Can dimensions be limited, or is the universe really infinite

From our point of view, the
universe seems to be infinite, and it seems that it's not only infinite but
even ever expanding. Now that you should be able to understand how our
seemingly 3D space time universe can all fit in a 4D hypersphere, which in turn
can fit on a surface of a 5D hypershere and so on, where a difference in time
is equivalent to a different point within its volume, you can understand why
the universe as seen by a 3D observing creature/mind has no limits.
Just imagine one of those 2D creatures who cannot understand what is height in the z direction and put him on the surface of a
sphere. He would walk round and round searching for an edge for ever, and
finally he may conclude and even prove that the path is infinite. Same applies
to a 1D creature going round a simple circle, and therefore same applies to us
3D creatures living and travelling around in a 4D universe! In general we can
say that a creature with n*D observation capability, will observe an (n+1)D dimension universe as infinite. We also learn that for an
n*D observer, the only way to observe a universe of a higher dimension than
himself is to 'walk around it' and memorise. A 1D creature cannot understand what is a circle other than observing all the points making it up,
one by one. Similarly a 2D creature cannot understand what is a sphere other by observing the flow of circles making it
up. We see that in all cases, walking around, or observing the flow through
time, is necessary to observe a higher dimensional space.
The question is, how can we know how many dimensions is the universe made up
from. All the arguments mentioned above can be applied to any dimension and
would imply the possibility of an infinite dimension space. However other known
things as the relationship between the gravitational constant and all the
matter in the universe indicate that the universe is closed and limited. Even
mathematics shows us that there are yet unknown reasons for which an ultimate
dimension may be reached. One very interesting curve is the plot of surface
area of hyperspheres of different dimensions, shown below. One would easily
think that as we go higher in dimensions, the surface area of the n-sphere
would increase at each stage, and yet, something very strange occurs, as a maxima in its surface area is reached at the 7th dimension.
This could easily be the reason for the relentless way the energy always seeks
the lowest energy levels. Could this indicate the real ultimate dimension of
the universe Most probably yes.
|
Dimension |
Volume |
Area |
What would an n*D observer see if the universe in which he
lives in is his own n*D dimensions ? - the answer is 'a still, or static (frozen in time) spatial
shape of n*D dimensions'. A 2D creature does not need to move around the
circle to recognise it or know anything else about it, and a 3D creature
does not have to flow through circular slices of a sphere to recognise
a sphere. Note that the actions move and flow both require the
time dimension to make sense, but recognise is an act that reacts to the
shape of a static structure and needs no time. For an n*D observer, the
n-dimensional universe is static, lifeless, and does not change through time,
but has all the knowledge of what's within all lower dimensions. Let's name
this ultimate n*D observer as the universal observer. For the universal
observer, time does not exist, since both himself and the universe are the same
thing and neither himself nor the universe is effected by time in lower
dimensions, and from a lower dimensional observer point of view he can be said
to be existing from eternity to eternity.
For those mathematically minded, let's take a car accelerating in a road. If we
integrate the observed acceleration m/s2 with respect to time we get
a car driving at a velocity measured in m/s. We have thus moved the motion of
the car one dimension up with repect to time. If we integrate further the
velocity with respect to time, we get the total distance covered in metres, no
time. So did the road distance exist before or after the car started
acceleration? As you see the 'road', the time independent dimension is
NECESSARY for all other actions (differentiations with respect to time) to take
place, and hence the universe should be limited in its number of dimensions,
with the highest dimension being time independent, and being the universal
observer itself. This conclusion leads to an inevitable property of space, the
property that seems to drive the whole universe and physics laws the way they
are, which is the property of a SELF OBSERVING SPACE.
Through observation points (central cores of each standing wave), space is
observing itself and in the process move through higher dimensions, with
increasing surface area and lower energy states, until each wavecentre
interface reaches the ultimate time independent dimension.
Unification into a fractal dimension
Conventional science fails to
unify the two seperate backbones of the most recent scientific revolutions:
relativity and quantum mechanics. All our past knowledge seems to assure us is
that 'Nature is simpe', and this should answer our questions as to where these
two important concepts come from and where do they unify into a simple singular
concept. It seems that the answer is beyond any human's mind imagination or
knowledge, but nature offers a lot of clues, which as I will show you, will
eventually let us explain the connection between the macro universe scale and
microphysics, and that enormous simplifications of current science is possible
through such unified concept.
The observations discussed in the previous pages, show that although matter is
made up of standing waves of real and imaginary waves, flowing forward and
backward in time, everything boils down to a single unified dimension in which
time needs no longer to be perceived. Remember that the perception of time is a
requirement in order to observe any dimension higher than the observers'
dimension. This means, that although science shows the existence of waves, and
here we showed that particles are nothing but standing waves, when observed
from the ultimate dimension, we see that the ingoing and outgoing waves, are
not dynamic waves at all, and that 'ingoing' and 'outgoing' no longer apply in
the unified dimension. We will find that the properties of space, and of waves behaviour are built into the SHAPE of the ultimate
space dimension. But what makes the universe so rich in diversity? If the
universe is just a hypersphere, then why are things around us not all
spherical? The answer is partly staring at us in the following curve.

Apart from the fact that the ultimate dimension is approximately 7, we see that the peek of the curve does not occur at an integer value, in fact its maxima can only be approximated by iteration and occurs about 7.25695... which is very different from 7. The consequence of this is very important, as it results in a FRACTAL ULTIMATE DIMENSION. This means that the wave equations and properties can all be described in terms of a FRACTAL SHAPE, yes, it means that reflection, refraction, attenuation and all properties of standing waves (and of the universe) can be described by a complex fractal shape in the 7.25695th dimension. It also means that all things surrounding us, as are solids, liquids, air, plasma, living objects and planets, all obey their underlying fractal equations which are embedded into the hyperdimensional fractal of which they form part. Self-similar replication and harmonic resonance are natural features of fractal structures and organizations. We can finally see how the quantum and macro world can be easily unified. Quit mind boggling, but let us see the clear evidence in nature.


Tungsten needle tip photo ---> Mathematical iteration zn+1
= zn2 modulus n


Platinum needle tip photo ---> Mathematical iteration zn+1
= zn2 modulus n
The above two photos on top and bottom left are actual
field ion microscope images of single crystal tips of Tungsten and Platinum
respectively. The two adjacent plots have been mathematically computed and
plotted by the same fractal function based on the iteration zn+1
= zn2 modulus n.
The plots have been only adjusted in brightness to make the similarity more
obvious, but otherwise are the same. This is fantastic, as it means that the
pattern formed by 3D standing waves obey an underlying iterative function.
Using just a simple iterative function, we do not even need to have any
knowledge of inwaves, outwaves and wave properties such as reflection. This
solves the enigma of which wave (incoming or outgoing) came first. In fact it
explains how neither of them comes first, and although we perceive the standing
wave as a resultant of an incoming and an outgoing wave, both waves are
generated at the same time. This also explains why a wave seems to know its
destination before reaching it... both the positive time going wave and
negative time going wave form part of an underlying static fractal hyper
structure.
In 1904, Swedish mathematician Helge von Koch defined a continuous curve that
could not be differentiated. It was just another example of a discovery first
made some years before by Karl Weierstrass, but it has lead to more general
constructions.

Koch Snowflake fractal
Instead of using the same rule on every step, an element of chance can be introduced by allowing to switch to the opposite orientation. This simple effect leads to more irregular outlines resembling natural coastlines. However, the fractal dimensions of both figures remain the same: approximately 1.262. At first glance one does not notice that a coastline is in fact a fractal. Given a map one can sit down with a ruler and soon come up with a value for the length. The problem is that repeating the operation with a larger scale map yields a greater estimate of the length. If we actually went to the coast and measured them directly, then still greater estimates would result. It turns out that as the scale of measurement decreases the estimated length increases without limit. Thus, if the scale of the (hypothetical) measurements were to be infinitely small, then the estimated length would become infinitely large! Lewis Fry Richardson (quoted in Mandelbrot, 1983) noted this dependence of measured length to the measuring scale used.
Fractal Coastline
Fractals have one special property, self-similarity, which makes them independent of scale. In other words, if you zoom-in on a fractal or magnify a section to view it, it will appear as if you were looking at the original object. A great example of the self-similarity property that can be found in nature is that of the fern. If you examined one of the fronds of a fern, you would see that the frond actually looks like a smaller fern itself. Most fractals in nature however are not as perfectly self-similar as the fern is. Take a cloud for example. If we zoom in on a section of a cloud, cut it out and looked at it from far away, it wouldn't look exactly like the original cloud but would still look like a cloud nonetheless. The importance of the self-similarity property of fractals is therefore not that the magnified portion of the original object looks exactly the same, but that it LOOKS SIMILAR. The intricate patterns embedded in fractals due to the self-similarity property are what make fractals so impressive to the eye. Most impressive is when we find a fractal in nature that is perfectly self-similar like the fern. One sort of fractal is known as the Iterated Function System, or IFS. This fractal system was first explored by Michael Barnsley at the Georgia Institute of Technology in the 1980s. You start with shapes plotted on a graph, and iterate the shapes through a calculation process that transforms them into other shapes on the graph. Starting with four shapes, one of which is squashed into a line segment (this becomes the fern's rachis or stalk), you apply the shapes to the calculation to generate more shapes, feed them back into the calculation process, etc. Eventually a pattern emerges that bears a startling resemblance to a fern, if you choose the right starting shapes and positions. The longer you continue the iteration process, the more intricate the tiny detail in the pattern becomes.


Cloud fractal dimension 2.5
Brownian Motion is an example of a process that has a
fractal dimension of 2. It occurs in microscopic particles and is the result of
random jostling by water molecules (if water is the medium). The path of such a
particle is a "random walk" in which both direction and distance are
uniformly distributed random variables. So in moving from a given location in
space to any other, the path taken by the particle is almost certain to fill
the whole space before it reaches the exact point that is the 'destination'.
Again, for a time dependent observer, it would seem as if each and every
particle has got the knowledge of the path taken of all other particles, very
similar indeed to the enigmatic EPR experiment! Another aspect of brownian motion is its effect on the formation of aggregates
such as crystals. The figure below shows structures formed under different
assumptions about the relative rate of horizontal movement (h) and the
probability (p) of a settling particle sticking to fized particles as it
brushes past. In the figure the following values are shown: (a) h=1, p=0; (b)
h=1, p=1; (c) h=10, p=0; (d) h=10, p=1.

Brownian 'random' motion predicted by fractal function
The most common random signal found in nature is called the 1/f noise. You can
find electronic circuits which let you amplify and hear this naturally
generated background noise. One may think that since nature generates a random
signal, then there are some exceptions to the well regulated fractal concept as
depicted here. But, no, this is no exception, 1/f noise is not chaotic as it
looks like, and is just obeying its higher order fractal function. 1/f noise
can in fact be created using deterministic functions. One such method is a
finite difference equation proposed by I. Procaccia and H. Schuster. It is
simply
xt = (xt-1 + xt-12) mod 1
A section of the time series is illustrated below.
The power spectra is shown below.
We are living in a period of such absurdly blind acceptance of the Cartesian co-ordinate system that we think of all things around us as made up of primitives such as lines, rectangles, polygons, and curves in 2 D or boxes and surfaces in 3D. One of the first lessons present children learn at their primary schools is to build up shapes of various things with such cartesian building blocks. Its not surprising to note that few of them, if any, will be able to build any natural occuring structure in this way, and a high percentage of the students will only be able to replicate other man-made structures as houses, robots, ships, etc.. Even commonly used computer graphic softwares are based on cartesian co-ordinates, and this explains why it is so difficult for anybody to draw for example a fern leave, or landscape or a simple insect with the cartesian based CADs. We often find that these geometric primitives and usual tools for manipulating them, typically prove inadequate when it comes to representing most objects found in nature such as clouds, plants, crystals, waves, or a simple piece of stone. Now we know the reason behind, simply because the universe is unified in a fractal dimension and not in two or three dimensions. Note that when I mention the universe, I am not refering to the stars and galaxies, but to everything from subquantum scale to the macroscale that exists. There has been considerable interest recently in chaos theory and fractal geometry as we find that many processes in the world can be accurately described using that theory. In fact the computer graphics industry is rapidly incorporating these techniques in dedicated graphic rendering CADs to generate stunningly beautiful images as well as realistic natural looking structures.

Fractal computer-generated landscape
At this point, you should realize how the macro and quantum worlds are easily
unified when one considers the fact that the universe we live in, and of which
we are part of, exists in a fractal hyperdimension. All things we observe are
just a small piece of this immense fractal function projected onto our 3D
observation plane. When a fractal function 'separates' from another it is
observed as a seperate entity (in 3D), but actually each one of them still
forms part of one unified function in higher dimension.

Fractal generating 'seperate' entities
Human body computer generated fractal?? See next page...
Sacred Geometry
The link between physics, mathematics & life
|
|
Charles R. Henry ,
professor at the Dept. of Sculpture, |
|
|
|
Close-packed reflective spheres clustered in this concentric shell structure produce an optical distribution network that links the Golden Mean and Pi. The Golden Mean is expressed in the 52 degree angle pyramid structure and Pi is expressed in the ratio of the diameter to the circumference of each sphere of course; but it is also expressed in the ratio of the sizes of spheres in the ten-spheres-within-ten-spheres concentric shell structure that he discovered. This concentric shell structure could continue to expand with many shells and still retain the same ratio between shells. |
|
R. Henry has rediscovered some of what was a highly developed understanding of mankind's relationship to the Universe, and this knowledge was utilized and documented in the geometry of ancient structures, with its origins probably dating back prior the last ice age. Sacred Geometry, the study of the unity of the cosmos, demonstrates relationships between Number and Space and the Human Form. It was used in the construction of ancient glyphs and monuments thereby aiming at preserving the knowledge of these principles of Natural Law for future generations. This construction of reflective spheres may embody the technology that produced the animated images of the deities in the temples of antiquity. |
|
|
|
Here we see a picture of a DNA. Looks familiar doesn't it? One question that becomes obvious to a highly developed human generation, is obviously 'How can we pass over all of our scientific knowledge in case of a cataclysm'. It is believed that such cataclysms have occured more than once in the past, probably wiping off each time whole human generations with all their knowledge. Unfortunately, it is beleived that these generations have either left no signs of their knowledge, or no traces were left of these. However, it is more probable that in our ignorance we are still not able to find and understand their messages, which might have been well visible to us for many years. |
A few years ago Feynman, a great scientist of the past
century, stated that the message he would have passed for the continuation of
all our present knowledge would have been 'all things are made up of atoms-
little particles that move around in perpetual motion, attracting each other
when they are a little distance apart, but repelling upon being squeezed into
one another'. Indeed, such a statement would at the least accelerate the
development of technology in such a situation, but what if we could convey a
message showing the true geometric mechanism of the atom and the whole
universe? Would that convey much more information? The next stage to convey the
message is to convert it into a universal syntax, for generations separated by
thousands of years from each other would certainly not communicate in the same
way or language.
Mathematics is a universal language, and the easiest way to convert any message
into a mathematical format is to change it into a geometric shape. The problem
of any shape surviving a cataclysm has to be well addressed and two obvious
solutions are (a) make the shape as rigid and visible as possible, and (b)
replicate the shape on various parts of the earth's surface.
The pyramid as a model of the mechanism as desribed by my theory, requires us
to visualize an octahedron by a regular pyramid and an inverted pyramid joined
together at the base and surrounded by a sphere. This, in effect, is a 3D
representation of the innermost core as stated in this theory, depicted by the
Hermetic Principle "as above; so below.", a
principle which somehow, mainly through various old religious beleifs, has
survived through the ages. Another fascinating feature of some of the pyramidal
structures is that they contain a broad, thick layer of mica, which had to be
brought from
|