Elements of Zermelo-Fraenkel Theory

Elements of Zermelo-Fraenkel Theory

In the sequel we will try to illustrate how an axiomatic set theory works. In 1909, Ernst Zermelo proposed the former axiomatic system for sets, which was later improved by Abraham Fraenkel and others. Nowadays this system is known as Zermelo-Fraenkel theory of sets, briefly ZF. The main convenience of this theory is the fact that the involved logic is not formalized, i.e. it can be expressed in usual mathematical terms, so that the predicate calculus represents a sufficient logical tool.

Respecting the purpose of the present book, we will limit ourselves to sketch how the ZF theory begins; as a specific feature of the axiomatic set theories, the axioms are progressively introduced (i.e. not all at the very beginning), depending on how many aspects we need to formalize.

1.20. The primary concepts of the ZF theory are the sets and the relation of membership. As usually, we note the sets by Latin capitals A, B, etc., and the membership by . It is tacitly accepted that each set is well described, such that we can always decide whether or . Alternatively, to avoid expressions of the form "set X belongs to set A" by reading , instead of sets we may speak of objects, individuals, elements, etc. For example, we prefer to 21321v2122v say "X is an element of the set A", even if X itself is a set. In addition, if X consists of a single element, that is X = , then and will be considered equivalent ways to say that .

It is interesting to remark that we can introduce a lot of notions and study their properties before introducing the axioms. In fact, if we "borrow" some definitions from the naïve set theory, then we can immediately intuit how to formulate properties of sets even if is free of conditions (compare to the Section devoted to relations). In particular, we start with:

1.21. Definition. We say that A is included (contained, etc.) in B (or, equivalently, B contains A, A is a part (subset) of B, etc.), and we write if the following logical implication holds:

.

We say that A is strictly included in B (respectively A is a strict subset or part of B, etc.), and we write , if , but there exists some such that .

We consider that A equals B, and we note , if they consist of the same elements, i.e.

.

The negation of the above relations are usually noted and . The reversed relations are and , while = is symmetric.

Several remarkable properties of these relations are straightforward:

1.22. Proposition. For arbitrary sets we have:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. , and .

The proof is a recommended exercise.

The first axiom in the ZF theory refers to the replacement by equal sets.

[ZF₁] (The axiom of extensionality) For arbitrary sets X, Y, Z we have

.

It is easy to see that

,

so that in every relation of membership we may replace each of its terms by equal sets.

The second axiom allows the construction of the pairs of sets.

[ZF₂] (The axiom of pairs) For arbitrary distinct sets A, B, , there is a set P, which exactly consists of A and B, i.e.

.

We say that P is the pair set of A and B, and we note . Later on, we avoid the restriction by adding new axioms (see Problem 7).

It is important to distinguish a pair from the union, which is the object of the third axiom.

[ZF₃] (The axiom of union) For every set X, supposed to contain at least two distinct objects (sets), there exists a set U, which exactly consists of the elements of the objects of X, i.e.

.

Obviously, U is completely determined by X, so that we naturally note it

.

In particular, if X consists of two sets, say , , , then we note . It exists by virtue of [ZF₃] applied to the pair , and

.

1.23. Remark. The axiom of union acts in the restrictive case when X has at least two elements. In the remaining cases, when X reduces to one set or even is void, the existence of the union (as well as the intersection) cannot be assured without new axioms, which refer to the subsets of X. The main idea in describing a subset of X is to use monadic predicates on this set, which are functions of the form (compare to Section I.4)

.

We recall that in the spoken language, a predicate results by formulating a property for all the possible elements, so that it reduces to a proposition with variables. In Mathematical Logic, the predicate is defined as function whose values are propositions. In the present context it is very important to stress on the monadic character of the predicate, which takes into account a particular interpretation, such that we can always establish whether the value p(x) is a true or false proposition. For example, the property X = X is valid for all sets, but it is not a monadic predicate because there is no acceptable interpretation (speaking of "set of all sets" leads to antinomies). However, we remain away from paradoxes if we are looking for elements, which are selected by monadic predicates in a previously fixed set.

The next two axioms assure the existence of the subsets of each set X, as well as their concrete construction via predicates.

[ZF₄] (The set of parts) For each set X there exists a set P, whose elements are the subsets of X and only these ones, i.e.

.

As usually, we note P = P (X).

[ZF₅] (The axiom of subsets) For each set X and each monadic predicate

there exists a subset S of X, which exactly consists of those elements Z of X where p is valid, i.e.

.

Most frequently, we note

.

Now, we are able to prove the existence of the void set, noted , which has no elements at all:

1.24. Theorem. There exists , and it is unique.

Proof. Let us first show that each set X contains a subset , which has no elements. In fact, if a predicate p is always false, i.e. p(Z) = 0 at each (for example ), then the corresponding subset (via [ZF₅])

has no elements, since is impossible. If q is another constantly false predicate on X, then

because both these sentences are false. Consequently S_p = S_q , hence there exists a unique element in P (X). To emphasize the dependence on X, we may note it .

Now, let and be constantly false predicates on the different sets X and Y, which correspond to the void sets and . Because the sentences and are simultaneously false, we have

,

hence = .

1.25. Theorem. For each set X there exists another set, noted , which has X and only X as an element.

Proof. We have to distinguish two cases:

Case 1. If X = , then we may take = P (X), which exists according to [ZF₄]. In fact, it is easy to show (compare to Problem 6) that is the only element of P ().

Case 2. If , then according to [ZF₂], there exists the set . If on this set we define the predicate p meaning "Z = X", then [ZF₅] assures the existence of the set

.

Obviously, X uniquely determines the set .

The following theorem extends [ZF₃] to arbitrary sets:

1.26. Theorem (The existence of union) The union exists for an arbitrary set X, and it is defined by

.

Proof. The axiom [ZF₃] states the same fact under the additional condition that X contains at least two different sets. In the remaining cases we have:

(i) If X = , then . In fact, because the assertions

"" and ""

are constantly false, they are logically equivalent. Consequently,

.

(ii) If X consists of a single element, say A, then the predicates

"" and ""

are logically equivalent. In fact, the following implications hold:

"" "" "",

as in the comment to [ZF₁]. Conversely, because the assertion "A = A" is always true (as mentioned in Proposition 1.22/7), we have

"""A = A and " "".

To conclude, there exists the union

,

and it is completely determined by X = .

As usually, the intersection of the sets of a family X exactly consists of the common elements of the sets of this family. However, the existence of the intersection in ZF theory is based on the existence of the union:

1.27. Theorem. (The existence of intersection) For arbitrary non-void set X there exists the intersection

.

Proof. According to Theorem 1.26, the exists the union . On this set we define the predicate p , for which

p(Z) "".

The axiom [ZF₅] assures the existence of the set

,

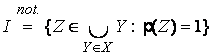so that the proof is accomplished if we justify the equality

.

In fact, "" is obvious in the case when p is always false. Otherwise, if , then p(Z) = 1, i.e. the implication "" is really valid.

Conversely, "" if Z fulfils the condition "", this means that p(Z) = 1, i.e. .

Besides union and intersection, the product of a family of sets is another important operation, which can be realized in at least two different ways, called Cartesian, respectively direct. Both of them represent subsets of the union, but the direct product makes sense only for families of distinct sets, and consists of those subsets of the union, which contain an element and only one from each set of the family. Because the direct product refers to a family X of sets, it is implicitly supposed that the involved sets are pair wise distinct. More exactly, we have:

1.28. Definition. Let X be a set. We say that P is the direct product of the sets , and we note , iff

,

where .

1.29. Examples. 1) If X is a non-void set such that each consists of a single element, then there exists the direct product of the family X, and it consists of a single element too, namely

= .

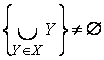In fact, if each reduces to an element, then in the above definition we have , hence . Consequently Z = U is the only element of P.

2) If X consists of a single set, say X = , where , then the direct product exists, and it equals the set of all singletons of A (i.e. sets that contain a single element). More exactly,

= .

The explanation is that U = A (see the proof of the Theorem 1.26), and each element T of A generates a singleton (as in Theorem 1.25), for which .

3) If , then = . In fact, because Y in the above definition is arbitrary, we have once to take , but in this case . Consequently, there is no Z satisfying the condition of the Definition 1.29, which means that P = .

1.30. Theorem. The direct product P = exists for arbitrary set X.

Proof. By definition, the direct product is a subset of the union , which exists according to Theorem 1.26. To select the needed part of U, we define the predicate p:U, such that p(Z) means

.

The existence of P is a consequence of [ZF₅].

In practice, the existence of the direct product, assured by Theorem 1.30, is less important than the fact of being non-void. Because cannot be derived from other properties, we have to state it as an axiom.

The next axiom refers to particular families of sets, namely:

1.31. Definition. We say that X is a disjoined set if holds for all , .

In other words, the elements of X are pair wise disjoint, i.e. they have no elements in common. In particular, is disjoined.

[ZF₆] (The axiom of choice) If X is a disjoined and non-void set, then

.

1.32. Remark. The axiom of choice is much wider known for Cartesian products, in the form of the famous Zorn's lemma: for every collection of nonempty sets there is a function, which chooses an element from each set. In fact, we may describe both products, direct or Cartesian, in terms of functions (if necessary, see the next section for the notion of function).

More exactly, each element Z of the direct product P = defines a choice function

,

which "picks up" an element from every set , i.e. . Conversely, if is a choice function, i.e. for all , then its set of values, , is an element of P.

Similarly, the Cartesian product of the family X = , which is usually noted , consists of all choice functions

,

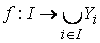where term "choice" stands for at each . Therefore, condition is equivalent to the existence of a choice function.

If there exists some such that , then we obviously obtain . The other cases of void Cartesian products generally ask much more elaboration, but the usefulness of the axiom of choice can be easily seen in many occasions, as for example:

The well ordering Theorem (Zermelo): Every set can be well ordered (i.e. each subset contains its least element);

Every linear space with at least two elements contains a Hamel basis (which is a maximal linearly independent subset);

Each group contains a maximal Abelian (commutative) subgroup.

In 1964, P.J. Cohen has proved that [ZF₆] is an independent axiom.

The next axiom postulates the existence of infinite sets, in particular the existence of N, which are constructed recursively. It is formulated in terms of (Theorem 1.24) and (Theorem 1.25), but other inductive schemes are equally well to generate such sets step-by-step.

[ZF₇] (The axiom of infinity) There exists a set $ such that

(i) $, and

(ii) $ $.

The first important consequence of [ZF₇] is the existence of N:

1.33. Theorem. There exists a unique set, noted N, satisfying (i) and (ii), which is included in every other set of this type (i.e. satisfying (i) and (ii)).

Proof. According to [ZF₄], there exists P($), where $ is specified by [ZF₇]. Let p: P($) be the predicate for which the property p(Z) means that Z $ fulfils (i) and (ii), i.e.

.

By virtue of [ZF₅], there exists the set

N = ,

and it is non-void since Z = $ N. Using Theorem 1.27, there exists

N = ,

which turns out to be the set we have claimed in the theorem. In fact,

N has the properties (i) and (ii), since each Z N does so.

If $* is another set satisfying (i) and (ii), then N $*. This property follows from the simple remark that $ $* N, because

(N $ $*) ($ $* $*) N $*.

N is unique, since for any other set, say M, which fulfils the previous conditions 1, and 2, we have both N M and M N.

To conclude, N is the smallest set that satisfies (i) and (ii).

The next axiom refers to functions, and says that each image f(A) is a set. We derive the notion of function from that of a dyadic predicate, which is a proposition involving two variables, noted p:AxB.

1.34. Definition. We say that the dyadic predicate p is univalent if for each we have p(X, Y) = 1 exactly once. To each univalent predicate we attach a correspondence , called function, which is noted f : AB.

As usually, Y = f(X) stands for p(X, Y) = 1, and expressions like "Y is the value of f at X", "f is defined on A", etc., are naturally accepted.

[ZF₈] (The axiom of function (or substitution)) If p : A x B is a univalent dyadic predicate, then it defines a set

.

In terms of functions, for each f : AB, there exists the subset of B,

.

The last axiom that we discuss guarantees that never holds:

[ZF₉] (von Neumann's axiom) For each non-void set A there exists such that .

1.35. Lemma. The membership never holds.

Proof. The case A = is obvious. Otherwise, if we accept for some set A, then by adding , we find . But A is the only element of , hence there is no other element such that 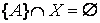, contrarily to [ZF₉].

1.36. Theorem. There is no pair of sets, say , such that and be simultaneously valid.

Proof. The affirmation is obvious (without [ZF₉]) if one of the sets is void, since has no element. The case A = B is solved by the above Lemma. In the remaining cases, let us suppose that both and hold for the non-void sets . Because

,

and

,

we deduce that the property holds for all , which contradicts [ZF₉].