ALTE DOCUMENTE
|
||
a) D. Iordache "Numerical Physics" (in Romanian),
Man-Dely Publishing House,
I. M. Popescu, D. Iordache et al. "Solved Problems
of Physics" (in Romanian), vol.1, Technical Printing House,
§1.7**. Elements of the Similarity Theory
Taking into account that the description of some complex systems (fluids, thermal insulators, some atomic or molecular systems, etc) use similitude numbers (criteria), we will present in following the basic notions of the (physica 939b123j l) similarity theory.
Unlike the mathematical systems (geometrical
figures, symmetry groups, polynomes, etc), whose elements are determined by a given (specific) number of uniqueness
parameters (e.g. the lengths of sides, or the lengths of 2 sides and the angle
between them, for arbitrary triangles), the number 
of uniqueness
parameters 
corresponding to a
physical state (or process) depends on the required accuracy, increasing with
the accuracy level [e.g., the state of the air can be described roughly by the
temperature and pressure, more accurately adding the humidity, with an
increasing accuracy adding also the 
content, etc].
If the physical dimension of a parameter specific to
the studied state (or process) is: 
, (1.7.1)
then the 2 states (or
processes) Σ', Σ" are named
similar if the values of the parameters 
and P corresponding to these states fulfil
the relation [21], [22]: 
. (1.7.2)
In the macroscopic physics [of simple (non-complex)
systems], the similitude indices 
have integer or
semi-integer values, very seldom intervening other rational values (as 2/3 in
the reversed Langmuir law). Some of the uniqueness parameters could be
similitude numbers (criteria), i.e. non-dimensional parameters: [s]=1, with equal values: s' = s"
in all similar states or processes.
According to the first (
(1.7.3)
is a similitude number (criterion) of the physical states (processes) described by relation (1.7.2).
The Π (Buckingham's) theorem of
PST states that: "the number 
of irreducible
similitude numbers (criteria) corresponding to a state (or process) of a
physical system is equal to the difference between the number of independent
uniqueness parameters and the number 
of the active
fundamental physical quantities (e.g. = 2 in kinematics, = 3 in dynamics, etc): 
. (1.7.4)
"
In following, the 2nd (Federman's) theorem of PST states that: "every physical law or relation can be expressed by means of some similitude numbers (criteria) and only by means of similitude criteria".
Finally, the 3rd (Kirpishev-Guhman's)
theorem of PST finds out that: "if for 2 physical states (or processes)
Σ', Σ", all values of irreducible criteria are equal: 
, 
, . 
, then the considered states (processes) Σ', Σ" are
similar".
Finally, it is easy to find [see e.g. relation (1.7.2)] that the geometrical similitude is a particular case of the physical similitude (for the sets of systems that differ only by their geometrical dimensions).
The main applications of the physical similitude theory refer to the possibility:
a) to delimitate the validity field of different physical theories,
b)
to design experimental (laboratory) models of some
inaccessible technical/or physical systems (e.g. of a large energetic network,
of a studied molecule, etc), whose work be similar to that of the considered
inaccessible systems (taking into account the 2nd and 3rd
PST theorems, in this aim it is sufficient to have equal values of all
irreducible similitude criteria: , , . ); we have to mention
also that the experiments on laboratory models can be frequently considerably
cheaper than the corresponding experiments on some studied accessible systems.
Solved Problems
1.7.1*. Consider the vertical launch
(upwards) of a point mass, with the initial velocity 
in a gravitational field of acceleration 
. Check the validity
of the П (Buckingham's), 2nd and 3rd theorems of
PST theory for the motion of the above considered point mass.
Solution: The fundamental
physical quantities active in this problem are: the time and the length (
). The uniqueness
parameters corresponding to the kinetic state of the considered point mass
are: a) v0 , g and t (duration after the point mass launch), or: b) v0
, g and h (the height reached at a certain time), or: c) g , t and h, or . many other equivalent combinations.
The well-known basic equations corresponding to this motion are:
(the velocity
equation) , 
(the space equation)
, and:
(the Galilei's
equation) .
These equations can be written as similitude
relations, by means of the following similitude criteria: 
, 
,
.
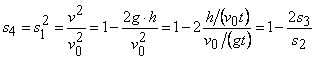From the above equations, one finds that: a) because all similitude criteria (s2, s3, s4, etc can be expressed by means of s1) in this problem there is only 1 irreducible criterion, therefore:
,
i.e. the П
(Buckingham's) theorem is fulfilled, b) all basic equations of the
studied motion can be expressed as relations between similitude criteria,
exclusively, which confirms the validity of the 2nd (Federman's)
theorem of PST; c) if: , then: 
, 
, 
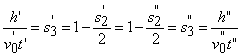, i.e.:
, 
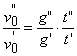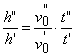, and: 
, i.e. [according to the definition (1.7.2) of the similar states] the kinetic states Σ', Σ" are
similar, which confirms the validity (in this case) of the 3rd
(Kirpishev-Guhman) PST theorem.
1.7.2**. Derive the expression of the similitude criterion, delimitating the: a) relativistic, and the non-relativistic formalisms of Physics, respectively.
Solution: Starting from the
well-known relativistic (Einstein's) energy-mass-velocity equations: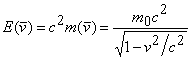 
and the general
(relativistic) definition of the kinetic energy: 
, one obtains the relativistic expression of the kinetic
energy 
of a mass point by
means of its linear momentum p
is: 
, where 
is the rest-mass of
the considered mass point. Dividing
above relation by the rest-energy 
, and defining the
Minkowski's similitude criterion Mi as: 
, one obtains:
.
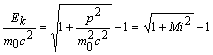One finds easily that if the value of the
Minkowski's similitude criterion is: (i) considerably
less than 1, the previous relation becomes: 
, i.e: 
, which represents exactly the nonrelativistic expression 
; one finds so that
for Mi
<< 1, the relativistic theory particularizes in the nonrelativistic
theory; (ii) of the magnitude order of 1, the relativistic expression of Ek maintains its rather
intricate expression, therefore these values (Mi ~ 1) correspond to the specific validity domain of the
relativistic formalism; (iii) considerably larger than 1, the
relativistic expression of Ek
leads to the relations: 
, which are
specific to the extreme relativistic
field, corresponding to the very highly accelerated particles (v < c, but v ≈ c) and to field particles
(e.g. photons, when 
).
1.7.3**. Consider the propagation of arbitrary pulses s(t) along the direction of the OX axis in non-homogeneous media [where the pulse velocity V(X) depends considerably on the position coordinate X]. Taking into account that the Quantum Physics corresponds to rather strong non-homogeneities, derive the similitude criterion delimitating the: a) classical, and: b) quantum Physics formalisms.
Solution: Because the
expression of the retarded (delayed) time in the observation point of position
coordinate X is: 
(instead of: 
for homogeneous
spaces), the equation of pulses propagation becomes: 
. For harmonic pulses, the equation of pulses
propagation is: 
, where: 
, k(X)
being the wave-vector corresponding to the site X. The nonhomogeneity of the
medium can be neglected if:
.
As
it is well-known, the wave-vector corresponding to (nonrelativistic) quantum
evolutions (the de Broglie's associated wave) is: 
, where E is the total energy, U(X) is the interaction (potential) energy
and: 
is the kinetic energy
of the considered particle. The above
condition becomes: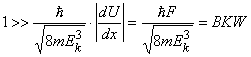 
, where BKW is the similitude criterion of Brillouin-Kramers-Wentzel.
For constant forces, the Maupertuis' mechanical action can be written as:
.
It results that the validity domains of the
classical (nonquantum) Physics, of the
quasiclassical (BKW) approximation and of the quantum Physics (as unique valid
theory), resp. can be defined starting from the values of the Maupertuis'
mechanical action 
and the corresponding
values of the similitude criterion BKW according
to Table 1.7.1.
Table 1.7.1.
Validity domains of some basic Physics formalisms and corresponding values
of the BKW similitude criterion
|
BKW |
|
Magnitude order of |
Larger values or of the magnitude order of 1 |
|
|
>> h |
~ h |
Values less or of the magnitude order of |
|
Valid Physics formalism |
Classical (non-quantum) Physics |
Semi-classical (BKW) approximation |
Quantum Physics |
Consider the motion of a body of dimension d with the velocity v in
a fluid of density ρ and dynamic
viscosity[1]
η. Starting from the expression of the
resistance force opposed to the body motion: 
(where K is the shape coefficient and 
is the maximum area of
a body cross-section transverse to its motion), derive the expression of the
similitude criterion describing this motion.
Solution: According to the
results of problem 1.4.5, the physical dimension: 
, therefore: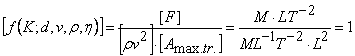 
. Because the correction factor f is
obviously a non-dimensional quantity (a number), while the physical quantities d, v, ρ and η have its specific physical dimensions, it results that the
correction factor has to be expressed as: f=F(K, Re), where Re is a non-dimensional physical
parameter (a number) expressed by means of d,
v, ρ and η. To fulfill this last condition, it is
necessary to have: 
, where: x, y and z are numerical coefficients, suitably chosen to fulfill the
condition: [Re] = 1.
From
the Newton's law expressing the viscous friction forces (see the previous
foot-note), it results that: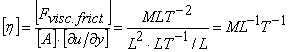 
. Because the physical dimension of the mass
volumic density is: 
, one obtains the condition:
;
in order to obtain a non-dimensional
expression of the above monome, all exponents of the fundamental physical
quantities L, T and M must
be null, therefor the exponents x, y and
z have to fulfill the system of algebraic
equations: 1+ x - 3y - z = 0 , - x - z = 0 , and: y
+ z = 0 . Solving the above system, we obtain the
values of the exponents of the uniqueness parameters: x = y =
1 and: z = -1, therefore the sought
(Reynolds') similitude criterion is: 
.
FURTHER READING
1. R.P. Feynman, R. Leighton, M. Sands "Lectures on Physics" (complete and definitive issue), Pearson, Addison-Wesley, 2nd edition, 2005.
2. R.P. Feynman, M.A. Gottlieb, R. Leighton "Feynman's Tips on Physics: a Problem-Solving Supplement to the Feynman Lectures on Physics", 2005.
3. P.M. Fishbane, S. Gasiorowicz, S.T. Thorton "Physics for Scientists and Engineers", 3rd edition, Englewood Cliffs, Prentice Hall, 2005 (first edition, 1993).
4. a) G.I. Barenblatt "Scaling, Self-Similarity and Intermediate Asymptotics", Cambridge Texts in Applied Mathemmatics, 1996; b) G.I. Barenblatt "Dimensional analysis", Gordon & Breach, 1987.
R.K. Pathria "Statistical Mechanics", Butterworth-Heinemann, 2nd edition, 1996.
K. Hinkelman, O. Kempthorne "Design and Analysis of Experiments", vol. 1 "Introduction to Experimental Design", vol.2 "Advanced Experimental Design", Wiley Series in Probability and Statistics, 1994.
M. Gitterman, V. Halpern "Qualitative Analysis of Physical Problems", Academic Press, New York, 1981, 274 p.
L.D. Landau, E.M. Lifschitz "Statistical Physics" (part 1), Butterworth-Heinemann, 3rd edition, 1980.
9. W. Stegmüller "The Structuralist View of Theories. A Possible Analogue of the Bourbaki Programme in Physical Science", Springer, 1979.
10. A.A. Gukhman "Introduction to the Theory of Similarity", Academic Press, New York, 1965.
10. *** https://www.ericweisstein.com/encyclopedias/books/DimensionalAnalysis.html
|
, delimitating 2 fluid layers in flow with a velocity v(y) continuously changing with the
transverse coordinate y: 
.