Without doubt, all sciences, as well as our everyday language, currently make use of sets. Since many elementary and high schoolbooks contain set theoretical elements, we have to explain why we start again with this topic. The reason is based on the desire to present noncontradictory theories, and to complete the general knowledge with some new specific results, which in particular 656t194g concern the cardinal and ordinal numbers.
§ 1. Noncontradictory set theories
The notion of set is primary, i.e. it has no definition to reduce it to other notions, and represents a product of our everyday experience. There are plenty of examples, which have the common feature (perhaps the only one) of describing several "thought together" objects. More exactly, according to the Cantor's point of view, a set is defined whenever we specify the properties of its constituent elements. Following P. R. Halmos (see [HPR]), this simple approach of sets is frequently qualified as a naïve set theory. The pejorative connotation of the term naïve is due to the fact that in this theory we may encounter paradoxes (antinomies, impossible situations). Facing contradictions in the simplest set theory has generated the famous crisis of mathematics, at the beginning of the 20th century. The presence of some hidden but actual paradoxes in mathematics could equally affect many other sciences, and revoke the entire scientific method of investigation. The simplicity of the most examples of paradoxes has also increased the danger of inconsistency in all branches of knowledge.
The contradictions of the naïve set theory represent logic antinomies of a particular topic, which involves the notion of set. However, many semantic paradoxes can be reformulated in terms of sets. For example, the set of men in a community can be divided into two subsets, according to the capability of waking up by oneself. The watchman's paradox, i.e. the impossibility to decide who shall wake the watchman, becomes a problem of membership to one of these subsets. Of course, there exist more sophisticated paradoxes involving the notion of set, as for example those concerning the "set" of all cardinal (respectively ordinal) numbers (see the subsequent sections).
1.1. Example. The wordy definition of numbers leads to a simple paradox, usually attributed to B. Russell (1902), and later analyzed by H. Poincaré (1913). It appears when we are going to find the smallest natural number n, which cannot be defined by less than 100 words. Trying to solve this problem, we may establish the following facts:
The set of all natural numbers, which can be defined by less than 100 words, is finite, since our vocabulary (dictionary) is so.
N is infinite,
hence there exist numbers that cannot be defined in this way. They form a set M, for which ![]() M
M ![]() N.
N.
n exists because each subset of N has a smallest element.
In the above description of n we have used less than 100 words, when we have said that "n is the smallest natural number that cannot be defined by less than 100 words".
The very definition of n by 13 words contradicts the membership n![]() M.
M.
A deeper analysis of the situation leads to a problem of classification of the numbers based on sorting the sentences used to define these numbers. However, we cannot end the sorting process and then start the classification of the numbers, because some sentences may involve the classification, as in the case of n.
1.2. Example. The quotation paradox is a variant of the watchman's or the barber's paradox, also attributed to B. Russell (1918), and later studied by W.E. Beth (1955) and others. The starting point is that the books of any library (collection, etc.) can be divided into the following categories:
(A) books not quoted in themselves, and
(B) books quoted in themselves (e.g. in supplies lists, bibliography, etc.).
The problem is that we cannot write a book a, where to quote all the books of type (A). In fact, we will be
wrong if we cite a in itself, as well
as if we don't, because in the first case a![]() (A), hence it should be not quoted, while in the second one a
(A), hence it should be not quoted, while in the second one a![]() (A), hence it should be quoted.
(A), hence it should be quoted.
In the other variants, the problem is to identify the set that "contains" the element watchman, respectively barber, etc.
1.3. A set theoretical paradox. If we try to reformulate the
paradoxes from the above examples in abstract terms, we have to discuss the
possibility of accepting the situation ![]() . In mathematics and other sciences, it is not the case,
hence we generally have
. In mathematics and other sciences, it is not the case,
hence we generally have ![]() , as for example a set of numbers is not a number, a set of
electrons is not an electron, etc. However, we may conceive sets, say bizarre, for which
, as for example a set of numbers is not a number, a set of
electrons is not an electron, etc. However, we may conceive sets, say bizarre, for which ![]() holds, e.g. the Universe
holds, e.g. the Universe
U = .
The normal sets, for which ![]() , form a subset of U,
noted
, form a subset of U,
noted
N = .
The paradox rises when we try to establish whether N is normal or bizarre.
In fact, if N is supposed to be
normal, then N ![]() N, hence it has
the property of its elements, and consequently we should have N
N, hence it has
the property of its elements, and consequently we should have N![]() N. On the other hand,
if N is considered bizarre, i.e. N
N. On the other hand,
if N is considered bizarre, i.e. N![]() N, then it must fulfil
the property of its elements, namely N
N, then it must fulfil
the property of its elements, namely N ![]() N. Because N
N. Because N![]() N and N
N and N ![]() N can not be
simultaneously accepted, and tertium non
datur, we must conclude that objects like N
and U should not be considered. In other
words, one source of paradoxes is thinking of "a set of all sets".
N can not be
simultaneously accepted, and tertium non
datur, we must conclude that objects like N
and U should not be considered. In other
words, one source of paradoxes is thinking of "a set of all sets".
1.4. Ways to avoid paradoxes. Among the most frequent methods, which were so far used to avoid paradoxes, we mention the following:
1. The algebra of parts (G.
Boole). In this theory we fix a total
set T, and we restrict ourselves to
operate with parts of T. The algebraic character of the study
is due to the central role of the operations ![]() ,
, ![]() , and by a single axiom, namely:
, and by a single axiom, namely:
![]()
We can formulate other equivalent descriptions of a Boolean algebra in terms of lattices (see the next section).
Besides the properties in proposition 1.6., we may add:
1.10. Proposition. The following properties hold in every algebra of parts:
1. ![]() is a partial order in P (T) (if necessary, see the next section);
is a partial order in P (T) (if necessary, see the next section);
2. = is an equivalence in P (T);
3. A![]() = A, A
= A, A![]() T = A;
T = A;
4. A![]() T = T, A
T = T, A![]() ;
;
5. A![]() B
B ![]() A
A ![]() A
A![]() B;
B;
6. A ![]() B holds iff A
B holds iff A![]() B A,
and equivalently A
B A,
and equivalently A![]() B = B;
B = B;
7. ![]() R
R 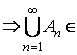 R .
R .
1.14. Proposition. The following properties hold:
Every ring of sets is closed under finite intersections;
Every s-ring of sets is closed under countable intersections;
Every ring of sets is closed under symmetric differences;
![]() R
whenever R
R
whenever R ![]() ;
;
R is an algebra of sets iff T ![]() R .
R .
Proof 1) According to the De Morgan laws, we have
![]()
Similarly to Theorem 1.12, we have:
1.15. Theorem. (M.H. Stone, 1948) Every Boolean ring is isomorphic to a ring of parts.
1.16. Definition. A non-void family F ![]() P (T) is called (proper) filter if
P (T) is called (proper) filter if
[F0] ![]() F
;
F
;
[I0] ![]() F
;
F
;
|