A FIELD-THEORETIC APPROACH
As well as particle theories such as statistical mechanics, classical physics also encompasses field theories such as electrodynamics. The distinction between the two kinds of theory is most obvious when one considers the question of matter and its interactions. The standard view holds that matter is composed of particles which interact via fields of force. Various alternatives have, of course, been propounded and vigorously supported, such as the Boscovichean 'field' theory of matter and the 'action at a distance' view of interactions (usually associated with a 'pure' particle theory of matter), 96 and we acknowledge that the distinction as expressed here is a crude one.
As it stands it is clearly linked to a difference in the underlying ontologies of the theories; in particular as regards their fundamental individuals. In field theories, certain properties are associated with every point of space-time. There are then (at least) two ontologies which are possible. One is to argue that the
end p.51
field is ontologically independent of these points, in much the same way as particles can be said to be, but with some correspondence existing between the points and the field quantities. The other is to regard the field quantities as properties of the space-time points themselves.
Taking the first possibility, fields are then granted the status of indepe 24524c223y ndent, real entities which, furthermore, may be regarded as particulars. The fact that they are 'global' particulars, in the sense of not being localized to a particular region or point of space at a given time, is of course not an issue since the spatial extent of some thing is just another property of that thing and cannot preclude it from being regarded as an individual on this view (in this case, size really doesn't matter!). 97
According to this view, then, a field is an individual and
can be given a label, or proper name, which designates the underlying
substance, for example, or the privileged property of 'thisness'. With regard
to the first option, it may be argued that one of the most striking
developments of late nineteenth- and early twentieth-century physics was the
emancipation of the field concept from the notion of material substance. 98
However, such arguments tend to involve a form of essentialism in the sense
of utilizing a possible answer to the question 'what is the essence of
substance?' in order to justify the exclusion of fields from this category. 99
Thus, one such answer involves impenetrability and since fields are not
impenetrable, they cannot be substances. This is true, but although
impenetrability certainly featured in the characterizations of substance of
Descartes and
end p.52
This response is problematic, however. Relativity theory implies that energy is a conserved quantity only within a given frame of reference and is not itself universally conserved under general coordinate transformations. 104 Although the energy of a system may not vary with time with respect to any chosen frame of reference, it will vary if the reference frame is changed. 105 This pushes against regarding energy as substantial, at least in the sense taken above. 106 The energy of a system cannot always serve to re-identify it because a change of reference frame will produce a change in the observed energy value of the system. Furthermore, it is not the case that Einstein's famous equation represents the acquisition of a substantial nature by energy. What relativity theory requires is that a change in energy corresponds to a change in mass, and vice versa. It does not demand that mass and energy possess the same set of properties and clearly they do not. 107
Of course, one could always take the second option and insist that fields possess primitive thisness. Involving a primitive notion, as it does, there's not a lot that could be said against such a view on the basis of physical considerations such as the above. There's perhaps not a lot that can be said for it either, except that if thisness is understood in terms of self-identity, then a field could be understood as possessing this unique property. But here the issue of metaphysical profligacy looms. The attribution of thisness and indeed non-spatio-temporal individuality in general is redundant, since, like the angels, each field is a kind in itself, individuated in terms of its distinct properties. Thus the properties of the electromagnetic field both distinguish it from the gravitational field and confer individuality upon it. In this case, since the possibility of fields possessing the same 'intrinsic' properties and hence being indistinguishable does not even arise-so that the Identity of Indiscernibles is satisfied, albeit in an uninteresting manner-there is no need to have recourse to any form of TI. 108
end p.53
The alternative is to eschew all talk of fields as individuals entirely and take them to be merely properties of the points of space-time. On this interpretation it is the space-time points which are the primary individuals and which stand in the same relation to the fields as a subject does to its predicates. This shifts the metaphysical focus to the ontological status of these points and, in particular, the issue of whether they can be regarded as individuals. We shall return to this in our discussion of space-time individuality below.
Whatever the ontological status of fields, it turns out that this distinction between particle and field theories does not uniquely and rigidly classify the subject matter of classical physics since it can be shown that classical particle mechanics can, in fact, be rewritten in field-theoretic terms. 109 Each particle is represented by a dichotomic field ψ(r,t) which can possess only two values: . 'Yes' indicates that a particle is present at that particular space-time location and the value 'No' indicates that it is not. Impenetrability is also assumed, so that the fields associated with two different particles cannot have the value 'Yes' at the same space-time point. Now a field is only completely specified if the field amplitude is given for all space-time points (unlike the particle case). Hence, if the field has the value 'Yes' at some point, it must be specified to have the value 'No' everywhere else. A particle will therefore be represented by an infinitesimally thin, sharp spike in the field and its motion will be translated into motion of this spike in the field. 110
For simplicity's sake, let us consider motion in one
dimension, labelled x. We can then construct a kind of 'blip space'
which is represented graphically by taking the x-axis as the real number
line and the y-axis as having two values only, namely 'Yes' and 'No'.
The dichotomic field can now be represented by a mathematical function f(x)
whose domain is the real numbers and whose range is the two member set ; that is, f: ![]() →
. In the particle description, motion is represented in terms of a
particle at time t 1 being at location x 1
and moving at time t 2 to x 2 . In terms of
the dichotomic field in 'blip space', this can be represented as a change in
field configuration from the spike at x 1 to the spike at x
2 , as shown in Fig. 2.2. In this manner, classical particle
mechanics can be rewritten in field-theoretic terms. 111
→
. In the particle description, motion is represented in terms of a
particle at time t 1 being at location x 1
and moving at time t 2 to x 2 . In terms of
the dichotomic field in 'blip space', this can be represented as a change in
field configuration from the spike at x 1 to the spike at x
2 , as shown in Fig. 2.2. In this manner, classical particle
mechanics can be rewritten in field-theoretic terms. 111
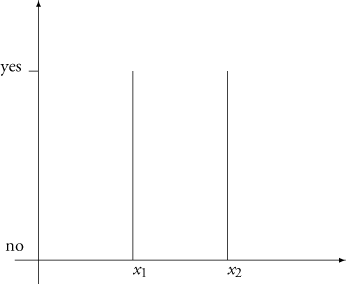
Figure 2.2. The motion of a particle in the field description.
Let us now return, once more, to our philosophically illuminating model of two particles distributed over two boxes. We recall from our historical digression that a justification of the weights given to the various arrangements, or complexions, of balls in boxes, can be attempted by employing some form of ergodic approach together with Liouville's Theorem. In this case, non-spatio-temporal forms of TI must be supplemented with dynamical notions involving spatio-temporal continuity of path in phase space. The alternative would be to insist that the weighting assignments are simply part of the axioms of the theory, with their justification ultimately cashed out in terms of the empirical consequences. In this case, non-spatio-temporal TI would be sufficient for classical statistical mechanics but it turns out that it is not necessary.
We can show this by rewriting the whole theory in field-theoretic terms and representing the particles as dichotomic 'Yes-No' fields as we have just indicated. A two-particle system would then be represented as two 'blips' in 'blip space' which move around in this space as the particles move. Here there is no underlying substance or primitive thisness (since there are no particulars), merely a property-such as impenetrability, for example-passing from one location to another.
end p.55
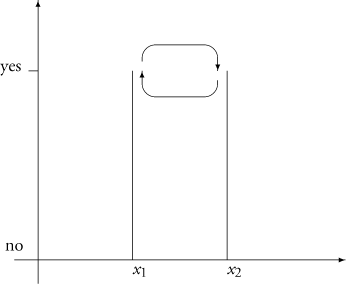
Figure 2.3. The permutation in the 'blip space'.
There is a problem with this representation, however: how can such a 'blip' be re-identified as the same blip through time? We recall from Chapter 1 that a and b are regarded as being identical in the relative sense if a at time t 1 is the same F as b at time t 2 , for some sortal concept F. In this case, the term 'blip' is acting as the sortal concept and the grounds for referring to the 'same' blip at t 1 and t 2 rest on the continuous well-defined spatio-temporal trajectory of such a blip.
Similarly, in our two-particle case, if the two blips are permuted then the change in the situation is revealed through the change in the blips' trajectories in space-time. In our 'blip space' the permutation can be represented as shown in Fig. 2.3, where we have to introduce three dimensions in order to satisfy the impenetrability assumption and allow the particles/blips to actually move around one another. Here it is their spatio-temporal trajectories which confer individuality upon the blips. 112
'Blip space' can be thought of as a form of 'occupation number space', in which one associates with each energy state, or box, the number of particles in that state/box in the particle approach, or one associates with each space-time
end p.56
Figure 2.4. The movement of the point P.
point a value-0 or 1, say-according to whether it is bearing the field property or not. As the system undergoes change, its representative point moves around this occupation number space, which will be multi-dimensional in general, covering the various points available to it, as represented in Fig. 2.4. 113
Now, there are two important points to note about such a representation. The first is that it allows us to recast classical physics in such a manner as to highlight the commonalities with quantum physics. In this way we can avoid getting tied up with apparent metaphysical differences that actually have more to do with the representation than the entities being considered. The second point is that-setting aside the field-theoretic considerations with which we began this discussion and just taking occupation number space on its own-all the considerations of particle permutations and TI appear to have been jettisoned. From the perspective of this representation we are not concerned with issues to do with which particles are in which state but only with how many particles are in which state. This shift in concern has been taken to have a profound impact on the apparent support for haecceitism provided by classical physics. 114
We recall that haecceitism underpins the truth of modal statements by offering an account of individuality articulated in terms of a difference in the de re representation of the individual concerned. 115 If we consider our balls and
end p.57
![]()
Figure 2.5. The arrangement (3).
boxes model again, then the different arrangements that can be obtained, corresponding to different possible states of the system, can be seen as different possible worlds. And, ". the structure in which states are represented by a theory is the structure of the universe of possible worlds postulated by the theory". 116 The question then is, given such an understanding, is haecceitism necessary for classical statistical mechanics? It seems not.
Recalling the distinction between Γ-space and occupation number space above, haecceitism seems to hold in the former but not in the latter. It holds in Γ-space because the two complexions corresponding to the arrangement of Fig. 2.5 are regarded as distinct, even though they are qualitatively indistinguishable, and this distinctness is due to the difference in which the permutations are regarded. This amounts to a difference in de re representation. 117 In occupation number space, however, we are not concerned with which particles are in which states but only in how many particles are in a given state. From this perspective, there aren't two complexions at all, but just arrangement (3) (see Fig. 2.5) corresponding to a single possible world. 118 Haecceistic differences are then simply not possible!
However, before we can conclude that we can do classical statistical mechanics without assuming haecceitism and, more generally, that we can always choose the above field-theoretic representation, we need to show that the phase space and occupation number space representations are relevantly equivalent. In the context of the argument with which we began this chapter, the question immediately arises: from the perspective of occupation number space, how do we get the appropriate weights required for classical statistical mechanics? From the particle perspective, the above arrangement is given the weight of two because it can be achieved in two ways, obtained by permuting the particles. According to the defender of a non-spatio-temporal view of TI, these two ways are ontologically distinguished in terms of the different underlying
end p.58
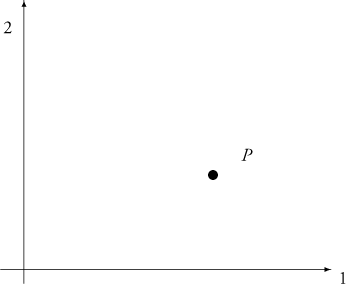
Figure 2.6. The two blip system in a two-dimensional phase space.
substances or primitive thisnesses involved. 119 In the field-theoretic approach the two complexions obtained via a permutation are not distinguished, since in both cases there is just one field property at one point, and another at another point. How, then, can the correct weights be obtained?
There are two ways of addressing this question. The first is to transform from the 'occupation number space' representation of the system to (yet) another space in which the weights can be discovered without having to resort to non-spatio-temporal forms of TI at all. This other space is an r-dimensional phase space, where r is the number of degrees of freedom of the system. Thus, considering more than just two states, our two-blip system can be represented by a point in a two-dimensional phase space as sketched in Fig. 2.6.
Again, the point P representing the system will move around this phase space as the system changes. We can draw a line at 45° through this space to represent the set of points where our blips pass each other as they move about.
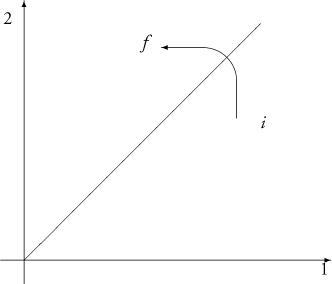
Figure 2.7. The permutation of two blips.
For any point i, there will be a mirror image point f, the reflection of i through this 45° line. The permutation of two blips is then described by the movement of i to f as in Fig. 2.7. 120
Thus, in such a phase space, a permutation of the blips can be represented and distinguished by a continuous trajectory which allows the permuted complexions to be counted as distinct without requiring any non-spatio-temporal form of TI. With regard to such a permutation, when one makes this transformation, the single point in occupation number space is effectively 'exploded' into the two points i and f, as represented in Fig. 2.8. Of course, in the case of n particles, the point P in occupation number space will transform into n! i- and f-type points in phase space. 121
end p.60
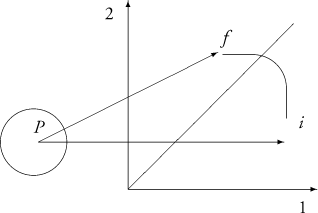
Figure 2.8. The single point 'exploded' into two points.
Alternatively, we can adopt the following strategy. 122 Let us recall Boltzmann's central expression for the permutability:
where the ω i 's are the occupation numbers. If it is assumed that ω i ≤ 1, 123 then we straightforwardly obtain
In other words, as we noted above, our single point in occupation number space explodes out into n! points in phase space. Now, if there are Z points in occupation number space, say, this will correspond to n!Z points in the corresponding phase space. From the perspective of occupation number space, the probability of obtaining a given arrangement, or distribution (corresponding to (3) above), is simply
From the perspective of phase space, this probability is given by
end p.61
where N is the total number of possible arrangements. But as we have just seen, N = n!Z; thus
In other words, the statistics as viewed from the perspectives of occupation number space and phase space are identical. 124
What are the philosophical implications of this result? Recall the point above that Γ-space supports haecceistic differences, whereas occupation number space does not. What the identity of the statistics shows is that haecceitism is not necessary for classical statistical mechanics as we can get the statistics we need on the basis of a representation that does not assume it. As Huggett puts it:
The philosophical pay-off is that statistics do not select one space over the other and hence will not yield conclusions about modal metaphysics. 125
Of course, this result is established on the basis of the above assumption that ω i ≤ 1. How is such an assumption justified? One possibility is to appeal to our old friend, the Impenetrability Assumption:
The key feature . which ensures the agreement of [the phase space and occupation number space representations] is . that no two Newtonian particles ever simultaneously occupy the same point of μ-space. 126
In that case, each such point will either be occupied by one particle, or it will be occupied by none (it will be either monogamous or virginal). More generally, given a finite number of atoms and with position and momentum
end p.62
represented classically in terms of a number line with an infinite number of points, the assumption will also hold. 127 The metaphysical relevance of these considerations is, of course, that they are ultimately spatio-temporal. Impenetrability is explicitly built into STI, as we have seen, but even the less problematic justification hinges on an implicit spatio-temporal representation in terms of space-time points. This is significant, not only for our project as a whole, but also for the issue, noted previously, of the metaphysical utility of haecceitism. That this is not necessary for classical statistical mechanics does not, of course, imply that the particles should not, or cannot, be regarded as individuals. 128 Having established the above conclusion, one needs to pursue the metaphysics further and make clear on what it is that the individuality of the particles is grounded. And by so doing one effectively spells out the terms of the de re representation as we indicated in Chapter 1.
If such a spelling out encompasses non-spatio-temporal forms of TI, involving substances or primitive thisnesses for example, then haecceitism-understood in these terms-is certainly not necessary because one can 'do' the statistics by means of the occupation number space representation. However, insofar as this requires spatio-temporal considerations, whether implicitly or explicitly, the anti-haecceitism conclusion only follows if the spelling out of de re representation is not taken to embrace such considerations. If, alternatively, one were to insist on STI as underpinning trans-world identity of individuals, then a form of haecceitism could be resurrected. The upshot, then, is that casting the discussion in terms of haecceitism is not terribly useful from a metaphysical point of view; what does all the work in taking us to the conclusion regarding particle statistics are the considerations of TI and STI and it is on them that we should be focusing our attention. 129
end p.63
We see then that there are a number of alternative solutions to the problem of how to assign the required classical weights to the states represented by a point in occupation number space. If the axiomatic approach is adopted then it is simply assumed that each such point has a factor n! assigned to it and the appropriate weights for particle permutations are assigned on the basis of some form of non-spatio-temporal TI. If, however, one feels compelled to offer some further justification of these axioms, then one can effect a transformation to the r-dimensional phase space where this point is exploded out, giving the weighting factor without having to resort to this form of TI. The permuted complexion is now regarded as distinct from the unpermuted one on the basis of the system's continuous trajectory in this phase space and individuality is conferred via a form of Space-Time Individuality. Of course, in this latter case, one must still justify the assignment of equal probabilities to the points of this phase space through some form of ergodic hypothesis. Finally, one could stay with occupation number space, resist the transformation to phase space and obtain the appropriate statistics via Huggett's strategy above. Insofar as this depends on an assumption concerning the occupation numbers which is supported either by the Impenetrability Assumption or considerations of the spatio-temporal background, individuality is grounded on STI here too.
Returning to the language of particles, on this account there is no underlying substance conferring individuality or guaranteeing impenetrability. The last is merely one of a set of properties predicated of the particle, moving along a well-defined continuous trajectory in space-time. Of course, some of these properties may change; in particular, 'extrinsic' properties are dependent on the state of the particle. 130 Intrinsic, state-independent properties, such as rest-mass, charge etc., do not change and allow us to re-identify the particle as a particle of the same kind. 131 With regard to reidentifiability, it is these properties which satisfy the sortal constraint by defining the relevant sortal term, such as 'electron' for example. Together with continuity, what we have on this account is nothing more than a set of properties and an underlying sequence of space-time points at which this set is instantiated. Of course, by grounding the individuality of the particle in the points of space-time in this way, this view pushes us to consider the nature of these points themselves and, in particular, their individuality.
|