MATH1052 MATLAB Assignment

MATH1052 MATLAB Assignment

Q1a

x=(-1:0.1:1);

y=(-1:0.1:1);

[X,Y]=meshgrid(x,y);

Z=(X.*Y.^2).*exp(-X.^2+Y.^2);

subplot(2,2,[1 3]);surf (X,Y,Z);

a=(1:0.1:3);

b=(-1:0.1:1);

[A,B]=meshgrid(a,b);

C=((A-2).*(B.^2)).*exp((-A.^2)+(4*A)+(B.^2)-3);

subplot(2,2,[2 4]);surf(A,B,C)

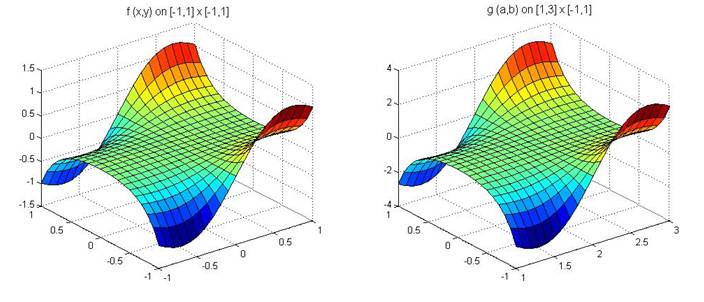
Both curves have the same shape, but different max and mins, shown by the difference in axes

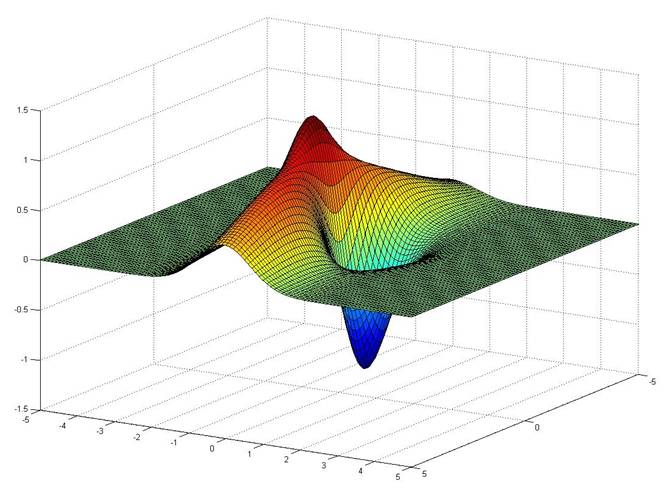
Q1b

x=(0:0.1:2);

y=(0:0.1:2);

[X,Y]=meshgrid(x,y) ;

Z=(X.*Y.^2)*exp(X.^2-Y.^3);

surf (X,Y,Z);

hold;

ezsurf ('2*x^2+6*x-8*x*y+16*y^2-32*y+17'

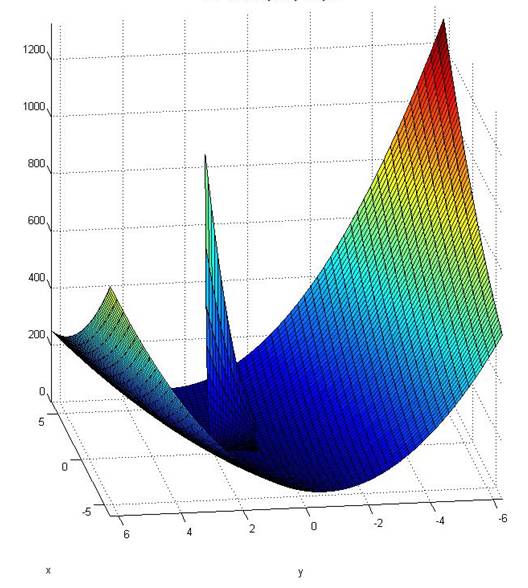
Q1c

x=(-5:0.1:5);

y=(-5:0.1:5);

[X,Y]=meshgrid(x,y);

Z=((X.^2-3*Y)./(1+X.^2)).*exp(-(((X-1).^2)/20)-Y.^2);

surf (X,Y,Z)

Global minimum at (0, 0.7, -1.23)

Global maximum at (0, -0.7, 1.23)

Q2a

x=(0:0.1:3);

k=5

y(1)=k;

for i=1:30

y(i+1)=y(i)+(x(i)^2-y(i)^2)*0.1;

end

y(4)

plot (y)

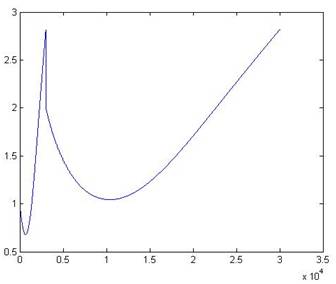
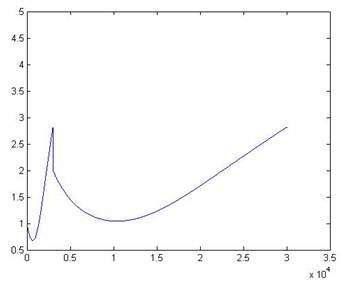
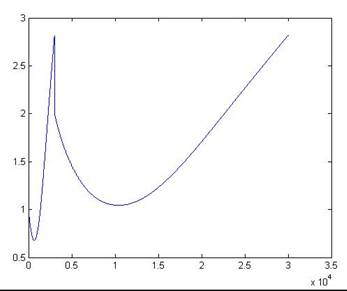k = 1, y(3) = 0.7568 k = 2, y(3) = 1.1681

k = 3, y(3) = 1.3884 k = 4, y(3) = 1.4959

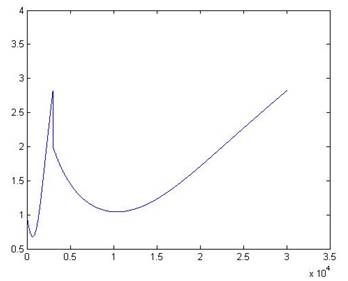
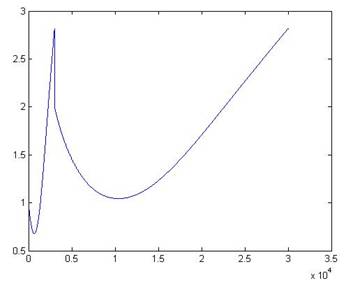
k = 5, y(3) = 1.5281

Q2b

The estimate for y(3) starts to lose accuracy at a step size around 0.01. This is because more samples (smaller step size) will always result in a more accurate answer