Packet Generation Models

729 / 729a

The following table takes into account the limitation of 1ms for the spacing. To further increase the number of users for each case, we can consider Israel's suggestion of generating more than a single packet at a generation instant.

729b Single call

From a study by Wenyu and Schulzrinne (Analysi 616x2316g s of On-Off Patterns in VoIP and their Effect on Voice Traffic Aggregation) we learn that the mean spurt of 729B codec is 362ms and the mean gap is 488ms. To obtain the rate of 8kbits/sec, a frame of 10 bytes is generated every 10ms, meaning that the mean number of frames during a spurt is 36 and the mean number of 'comfort noise' frames that are generated during a gap (assuming they are generated at the same rate as data frames) is 49.

We take a memory-less model for the time a call spends in the spurt period and in the gap period (although the measurements in the paper show that this is only an approximation which is not always good). According to this model, a call can be in one of two states: On (spurt) and Off (gap).

At every instant of packet generation:

1-p

1-q

q

p

If the call is in the On state:

Generate a data packet

With probability 1-p remain in the On state

With probability p move to the Off state

If the call is in the Off state:

Generate a noise packet

With probability 1-q remain in the Off state

With probability q move to the On state

729b Multiple calls

To emulate multiple calls, we assume that each call behaves as described above, and the calls are indistinguishable (i.e., they all have the same parameters).

Assume we want to emulate K calls. Then the system can be in one of K+1 states, where state i (i=0,1,2, .,K) indicates that i calls are in the On state and K-i calls are in the Off state.

If the system is in state i (i=0,1,2, .,K), then a data packet is generated with probability i/K and a comfort noise packet is generated with probability 1-i/K.

In principle the system can move from any state i (i=0,1,2, .,K) to any state j (j=0,1,2, .,K). However, since p and q are rather small, we will assume that transitions from state i can be only to neighboring states, i-1,i,i+1.

The transition probabilities will be:

(a) "move down"

i -> i -1 i p (1-p)^(i-1) (1-q)^(K-i)

(b) "move up"

i -> i+1 (K-i) q (1-q)^(K-i-1) (1-p)ⁱ

(c) "stay"

i -> i 1 - i p (1-p)^(i-1) (1-q)^(K-i) - (K-i) q (1-q)^(K-i-1) (1-p)ⁱ

special cases (I=0 or I=k)

0 -> 1 K q (1-q ^K-1)

0 -> 0 1 - K q (1-q ^K-1)

K -> K-1 K p (1-p ^K-1)

K -> K 1 - K p (1-p ^K-1)

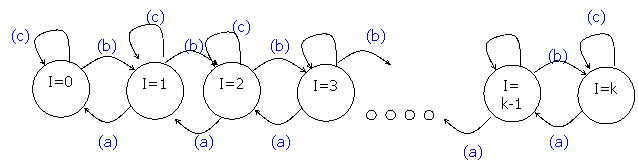These transitions occur at the spacing epochs (every intense of sending a packet)

Excel Table Describing the statistical model above

(G729statisticalModel.xls)

'Probability Scale'

The probabilities will be divided into 3 sections , as illustrated below :

(not necessary in equal size)

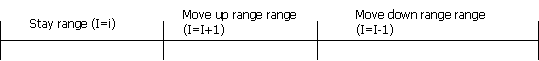
(C) (c) + (b) 1