HOW TO USE SAP90 PROGRAM
I. TRUSS AND FRAMES
Sap90 is an advanced version of Sap series. It performs static and dynamic structural analysis of elastic structures composed of bars, plates, shells, blocks, including soil. Computers and Structures Inc. Berkeley USA have developed the SAP programs during the last 25 years.
Our purpose is to shortly describe how the input data have to be organized and how to interpret the output.
Using Internet has been downloaded a free educational version of SAP2000. For educational purposes the input data will be organized as SAP90 files then the file will be imported by SAP2000, where the output is very user-friendly.
Question 1: How to organize the input data?
Answer 1: A notepad file has to be open. Save the file as text file,
then rename it as an ASCII file. There are 17 distinct blocks or sequences. Some of
them, the underlined ones, are compulsory, depending on the type of analysis.
Each block contains a number of lines and i 19419t196t s separated one to another by one blank line. See the figure, a particular
case applied for framed structures.
STATIC ANALYSIS
DYNAMIC OR MODAL ANALYSIS
Fig. 1b
When both loading types (static and dynamic) were simultaneously applied - the sequences LOADS and COMBO are required.
Suppose that the structural system has been divided and the number of nodes, elements of each type, supports and connections between elements as well as the the sectional area geometric properties and material properties are known. The loads are analysed and their magnitude and position is also known.
Question 2: How may we start in order to perform the static analysis?
Answer 2:
Open a Notepad file and save it with txt extension.
The first line ( 70 characters) contains the TITLE. But you may write commentaries on other lines, marked by letter C on the first column. At the end of an input line commentaries could be added by adding before them :
Question 3. What's SYSTEM?
Answer 3:It is a key word. It is compulsory to write it at the beginning of second BLOCK, containing general information. Let be nld - number of static load cases . SYSTEM has the following syntax:
SYSTEM
L=nld
a blank line
Question 4. How the structural topology is described?
Answer 4. The next block, 3., is named JOINTS. It contains the coordinates for all nodes. The most important facility is the possibility of generating nodes, when their number is very large. Let take first the simplest case, when every node is separately taken. Let be nn a variable representing the current node number, and N the total number of nodes The syntax of the block is:
JOINTS
nn X=xxx Y=yyy Z= zzz
a blank line
Question 5: What's SUPPORTS?
Answer 5: This block describes the restrained degrees of freedom (DOF) at supports. Let's remind that at a point of a deformable body there are associated 3 translational DOF and 3 rotational DOF. The syntax is:
RESTRAINTS
nnr R=r1,r2,r3,r4,r5,r6
a blank line
nnr is the node number where is a restrained DOF
r1 = 0 when the translation along the x-axis is permitted and 1 when it is restrained;
r2 = 0 ...."""........................" the y-axis........."""................'''
r3 = 0 ...."""........................" the z-axis........."""................'''
r4 = 0 when the rotation of the cross -sectional area about x-axis is is permitted and 1 when it is restrained;
r5 = 0 ........""..................'''.......... ..... ...... ....................y-axis ...."""".......... ..... ...... .""""
r6 = 0 ........""..................'''.......... ..... ...... ....................y-axis ...."""".......... ..... ...... .""""
Only restrained nodes (supports on the ground) are considered. When the symmetry is used, on the symmetry axis could appear restrained nodes, whose rotation or translation is 0. Remind from Statics.
A
fixed support is
described as: A SIMPLE SUPPORT in the XOY plane is described as:
nnr R=1,1,1,1,1,1 nnr R=0,1,1,1,1,0
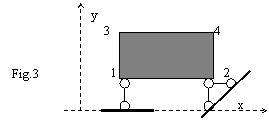A HINGE in the XOY plane
means: AN ELASTIC SUPPORT is not
included in this block, let us see the next block
nnr R=1,1,1,1,1,0
If we refer to Fig. 2, RESTRAINTS block is:
RESTRAINTS
6 R=1,1,1,1,1,1
blank line
If we refer to Fig.3, we have to write:
1 R=0,1,1,1,1,0: Reazem simplu permite deplasarea dupa directia x si rotirea fata de axa normala pe plan, z
2 R=1,1,1,1,1,0 Articulatie plana-permite numai rotirea corpului 1234 in jurul axei z
Question 6: SPRINGS could describe beams on elastic soil or imperfect supports
Answer 6: Yes, ONLY when a structural system or element is modeled as a body resting on deformable ground, or when we want to investigate the soil - structure interaction SPRINGS block has to be filled in.
SPRINGS
n1 n2 D K=KX,KY,KZ,KRX,KRY,KRZ
a blank line
N1 is the first node
elastically restrained; N2 the last one, D is the increment. When only
one node is elastically restrained, do not write N2 and D. The example in Fig.4 is:
Fig.4
N1=1 N2=9 D
KX is the axial stiffness about the x-axis , KY is the axial stiffness about the y-axis, KZ is the axial stiffness about the z-axis (in N/m or N/mm) ,KRX is the rotational stiffness about the x-axis ,KRY the rotational stiffness about the y-axis, KRZ the rotational stiffness about the z axis in N * m/radian or N*mm/rad. Suppose that the axial stiffness of each spring is 30 N/mm .So the block is:
SPRINGS
1 9 1 K = 0,30,0,0,0,0
blank line
Question 7: Does the next block describe the finite elements?
Answer 7: Suppose we refer only to LINEAR BEAM OR TRUSS ELEMENTS.
Question 7: Is any difference between them?
Answer 7: The same block, FRAME, is used. The end releases AND GEOMETRIC CHARACTERISTICS will be different.
Question 8: We start to describe bars or their geometric and elastic properties?
Answer 8: The syntax of the block is:
FRAME:line 1 of Frame block
NM = (1) NL=(2) X= (3), (4),... ,xnld Y= (5),(6)...,ynld Z=(7),(8),...,znld p = (9),(10),..,prnld
np A=a J=JT I=I33, I22 As = A2,A3 E=e G=g W=w M=m TC= a: (every different set of properties should be written on a line, their total number let be NPRO): Information about area, moments of inertia and twisting properties, unit mass and weight, elasticity and shear moduli (I)
ns WL=w1,w2,w3 WG=wx,wy,wz T=t1,t2,t3 PLD=d1,p1,f1,d2,p2,f2,d3,p3,f3,d4,f4 : any different set of external concentrated or distributed loads requires a line containing Information about loads on bars (II)
nel ji jj M=msp LP=n1,n2 LR= r1,r2,r3,r4,r5,r6 RE=ri, rj RZ=z MS=mi,mj NSL=l1,l2,nld G= ng,ninc,g1,g2,g3,g4 : information about bars. Every bar requires a line excepting the case when data are automatically generated (III)
a blank line
REMARKS
The right hand term of equalities have the following significance:
|
|
Abbreviation |
Significance |
||
|
(1)=npro |
Number of distinct geometric and mechanical sets of properties. For example: a straight beam of constant sectional area is made of reinforced concrete, but the central portion contains micro cracks, which modify the elasticity modulus. We take NM=2 |
|||
|
(2)= nbsl |
Number of distinct (magnitude and position ) sets of loads applied to distinct (length and area) finite elements |
|||
|
(3), (4),... ,xnld (5),(6)...,ynld 7),(8),...,znld |
own weight multipliers about X,Y, and Z axes associated to the nld load cases (see pag. 1) |
|||
|
(9),(10),..,prnld |
multipliers of external applied loads associated to the nld load cases (see pag. 1) |
|||
|
np=1,2.....npro |
the current number of a set of geometric and material properties |
|||
|
a// JT// I33, I22 (see Fig. 5) |
Cross-sectional area// Conventional moment of inertia for twisting, according to Strength of Materials theory //The moments of inertia about 22 and 33 axes |
|||
|
A2,A3 (see Fig. 6) |
Shear area associated to a shear force about 22 or 33 direction. 22 and 33 are the principal centroidal axes of the cross-sectional area |
|||
|
e //g |
Young modulus //Shear modulus |
|||
|
w //m //a |
Unit weight ( PER UNIT OF LENGTH kn/m) // Unit mass PER UNIT OF LENGTH)// thermal expansion coefficient (grd-1) |
|||
|
|
ns |
the identification number of a distinct load set (from 1 to nbsl) |
||
|
w1,w2,w3 |
Intensity of uniformly distributed load about the local 1, 2, 3 directions. Remind that 1 is the bar axis, 2 and 3 are the principal centroidal axes as Appendix shows |
|||
|
wx,wy,wz |
Intensity of uniformly distributed load about the X, Y, Z directions. Remind that X,Y, Z are the global axes as SAP90 /or SAP2000 requires |
||||
|
t1,t2,t3 |
temperature gradient about the local directions 1,2,3 |
||||
|
|
Let be pi a concentrated force applied on a beam element, at a distance di from the left end, ji, along direction 2 and fi a concentrated force applied on a beam element, at the same distance di from the left end, ji, along direction 3. Four distinct concentrated loads could be taken when we write a line (II), see above: d1= distance of loads p1,f1 with respect to end ji of the element,d4= distance of loads p4,f4 with respect to end ji |
||||
|
d2/ p2/f2 |
d2=Distance of loads p2, f2 .............................. |
||||
|
d3 /p3/ f3 |
d3=Distance of loads p3, f3 |
||||
|
|
nel |
Current number assigned to a distinct beam finite element. |
|||
|
ji/ jj |
Node i / Node j |
||||
|
msp |
Current number of the material the element is built up ( 1 to npro) |
||||
|
n1, n2 |
nodal numbers necessary to define the local (3) axis . This axis is parallel and has the same positive direction as a global axis when: n1 = 1 n2 =0 PARALLEL TO Z-axis// n1 = 2 n2 =0 PARALLEL TO Y-axis// n1 = 3 n2 =0 PARALLEL TO X-axis// |
||||
|
r1, r2 |
code describing the end conditions at nodes ji and jj related to the possibility of rotation about the local 3 - axis. If r1=0 and r2=0 -the element is fixed at its both ends; if r1=1 and r2=1- the element is double hinged about the 3-axis (as a truss bar) |
||||
|
r3 |
code related to the possibility of axial displacement: if r3=1 ???? |
||||
|
r4, r5 |
code describing the end conditions at nodes ji and jj related to the possibility of rotation about the local 2 - axis. If r1=0 and r2=0 -the element is fixed at its both ends; if r1=1 and r2=1- the element is double hinged (as a truss bar) |
||||
|
r6 |
code related to the possibility of axial twist: if r6=1 ????free torsion?? |
||||
|
ri,rj,z |
when rigid zones have to taken into account- see SAP2000 Tutorial and omit on the contrary . Beginners do not use them |
||||
|
mi, mj |
MASTER nodes (see the above Tutorial) . Beginners do not use them |
||||
|
l1,l2...lnld |
number of load cases that represent the final loading combination of an element. Beginners do not use them |
||||
|
ng |
number of elements that will be generated, similar to the above described element. . Beginners do not use |
||||
|
ninc |
increment of generating FRAME elements. . Beginners do not use |
||||
|
g1, g2 |
increment of generating nodes associated to the elements ends ji and jj . Beginners do not use |
||||
|
g3, g4 |
increment of generating nodes associated to nodes n1 and n2 which are necessary for identification of the local axis 3 . Beginners do not use |
||||
Question 9: Are now all data included in the input file?
Answer 9 : Let us see the figure on the first page. Block 1,2... . No, we didn't fill in the Block LOADS! This block contains information about CONCENTRATED ACTIONS applied at nodes. The syntax is:
loads
j1 j2 inc L= ℓ F=fx,fy,fz,mx,my,mz:
a blank line
The parameters are:
j1/ j2/ inc - the first / last node loaded by a similar action/ the increment
ℓ - loading case number (numarul ipotezei)
fx, fy, fz - concentrated forces applied on the x-y-z-directions (see the following sign convention)
mx,my,mz - concentrated moments .......... ..... ...... ........................
Fig. 5
Sign convention for
concentrated actions
Pay attention! Do not apply an concentrated action upon the direction of a restrained DOF!
Question 10: Is a support settlement an external concentrated action?
Answer 10: Yes, we take into account the nodal displacements into the next block: DISPLACEMENTS
This block helps us to apply known rotations or displacements BUT ONLY ON THE DIRECTION OF A FREE DEGREE OF FREEDOM! Do not apply external loads at a node which undergoes an imposed displacement , on the direction of the same degree of freedom!
The sign convention is the same as for concentrated loads. The syntax of the block is:
displacements
j1 j2 inc L=ℓ U = dx, dy, dz, rx, ry, rz
blank line
Question 11: Is the static analysis accomplished now,?
Answer 11: Yes, but only the output will contain separate load cases. The load superposition according to Romanian Standard or Eurocode, or other, is taken into account by the COMBO block:
COMBO
ncomb c=xc1,xc2,...,xnld D=d : the total number of lines equals to the load combinations
blank line
Example
The truss shown in fig.E1 is made of steel . Bars 1 and 2 have A=100 cm2 and for all remaining bars A= 50 cm2. The Young modulus is E= 2.1 *105 N/mm2 and Poisson ratio , n = 0.25. Only 1 load case should be taken. h= 1 m, a = 0,75 m, P = 10 kN. Use kN and m.
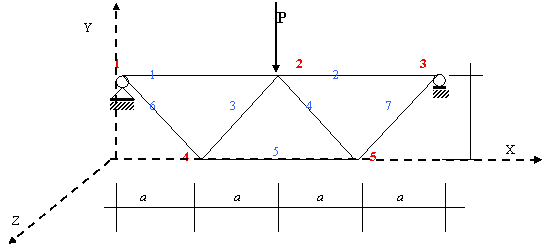
Fig. E1
The file GRZABR
TRUSS
SYSTEM
L=1
RESTRAINT
1,5,1 R=0,0,1,1,1,0
1 R=1,1,1,1,1,0
3 R=0,1,1,1,1,0
JOINTS
1 X=0 Y=1 Z=1
2 X=1.5 Y=1 Z=1
3 X=3 Y=1 Z=1
4 X=0.75 Y=0 Z=1
5 X=2.25 Y=0 Z=1
LOADS
2 L=1 F=0,-10,0
FRAME
NM=2
1 A=1E-2 E=2.1E8 G=2.1E8/2.5
2 A=50E-4 E=2.1E8 G=2.1E8/2.5
1, 1, 2 M=1 LP=1,0 LR=1,1,0,0,0,0
2, 2, 3 M=1 LP=1,0 LR=1,1,0,0,0,0
3, 2, 4 M=2 LP=1,0 LR=1,1,0,0,0,0
4, 2, 5 M=2 LP=1,0 LR=1,1,0,0,0,0
5, 4, 5 M=2 LP=1,0 LR=1,1,0,0,0,0
6, 1, 4 M=2 LP=1,0 LR=1,1,0,0,0,0
7, 3, 5 M=2 LP=1,0 LR=1,1,0,0,0,0
TRUSS comentariul de pe prima linie urmeaza fortele axiale pe bare
F R A M E E L E M E N T F O R C E S
ELT LOAD AXIAL DIST 1-2 PLANE 1-3 PLANE AXIAL
ID COND FORCE ENDI SHEAR MOMENT SHEAR MOMENT TORQ
1 -------- ----- ------ ----------
1 -3.75
2 -------- ----- ------ ----------
1 -3.75
3 -------- ----- ------ ----------
1 -6.25
4 -------- ----- ------ ----------
1 -6.25
5 -------- ----- ------ ----------
1 7.50
6 -------- ----- ------ ----------
1 6.25
7 -------- ----- ------ ----------
1 6.25
J O I N T D I S P L A C E M E N T S
LOAD CONDITION 1 - DISPLACEMENTS "U" AND ROTATIONS "R"
JOINT U(X) U(Y) R(Z)
1 .000000 .000000 .000000
2 -.2679E-05 -.2865E-04 .0000E+00
3 -.5357E-05 .0000E+00 .0000E+00
4 -.8036E-05 -.1533E-04 .0000E+00
5 .2679E-05 -.1533E-04 .0000E+00
R E A C T I O N S A N D A P P L I E D F O R C E S
LOAD CONDITION 1 - FORCES "F" AND MOMENTS "M"
JOINT F(X) F(Y)
1 .0000 5.0000
2 .0000 -10.0000
3 .0000 5.0000
4 .0000 .0000
5 .0000 .0000
TOTAL .0000E+00 .0000E+00
Question 12: How may we take into account a support settlement or rotation?
Answer 12: This case the prescribed value of the known displacement or rotation about a degree of freedom has to be written in the block RESTRAINTS, when we declare the joints and their degrees of freedom.
Suppose that at joint 7 there is a vertical displacement, r3 = -0.05 m (parallel to the global Z-axis , but downwardly directed), and all other degrees of freedom are restrained.
In the RESTRAINTS BLOCK we have to take:
7 R=1,1,-0.5,1,1,1
Question 13: How may we take into account the rigid floor assumption which is very important to the dynamic analysis of multistory frames?
Supplementary very
stiff bars
Answer
13: This
case it is necessary to create a rigid plane that connects the columns top
joints. One possibility is to consider as many very stiff bars as necessary and
to connect them so that a rigid plane would be created (with no in-plane
displacements )
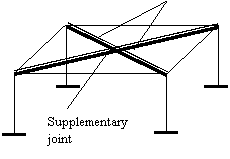
Another possibility is to use the MASTER and SLAVE CONCEPT. (See the SAP2000 educational TUTORIAL)
Question 14: May we start now the modal analysis
Answer 14: The modal analysis does not require the sections LOADS and COMBO. The block SYSTEM contains only the line: L=0 V= nfrequencies , where nfrequencies( the number of frequencies ) means the number of modes to be considered.
The loads applied directly on bars in the static analysis are not required, too.
The two following examples, FRAMED 3D REINFORCED CONCRETE STRUCTURE and STEEL TIMBER BEAM refer both to the static and modal analysis.
|
