MOSFET Differential Amplifier Stage

MOSFET Differential Amplifier Stage

The MOSFET differential amplifier stage is a relatively high-gain stage with grounded dc inputs, which requires no bypass capacitor. The stage also has the important advantage of having two inputs, one inverting and one noninverting. This is essential in operational amplifiers where one or the other (or both) is used, depending on the application. The two inputs also provide for operating the stage in the differential mode, where the input is not referenced to ground. The differential amplifier stage discussed here is an all-resistor circuit with source and drain resistors. In a modern integrated circuit, these are replaced with transistor current sources. However, the principle of operation is the same, and the resistor version can be implemented in our laboratory project.

Various segments of the differential amplifier comprise amplifier stages from all three terminal configurations: the common source, the common gate, and the source follower (common drain). In this unit, a detailed theoretical analysis of all three stages is undertaken (based on Level 1 SPICE). The linear models used include, progressively, the output conductance, g_ds, and the body-effect transconductance, g_mb.

8.1 DC (Bias) Circuit

The equation for the dc circuit (Fig. 8.1) is the same as for the current-source common-source stage except that the bias resistor has current 2I_D as the current from both transistors is flowing through this resistor. For now, the stage will be assumed to be perfectly balanced such that I_D1 = I_D2 = I_D. The bias equation is

Equation 8.1

Figure 8.1. Dc circuit for differential-amplifier stage with resistance bias. Source and body are normally at different potentials. In the project with this circuit, we attach the two sources to the transistor body, which is allowed in a simple circuit.

Note that the threshold voltage is that for V_SB 0 V. The solution can be obtained with the inclusion of the threshold voltage equation, also a function of I_D,

Equation 8.2

In the project on the differential amplifier, we can connect the sources and bodies of the two transistors. This is because only NMOS transistors are used in the circuit, and both transistors have the source connected t 14314k1018o o the same node. In this case, V_tn = V_tno.

8.2 DC Imbalances

In a real transistor, parameters k_n, V_tno, and l_n can be slightly different such that, in general, I_D1 I_D2. The ratio of the currents is given by

Equation 8.3

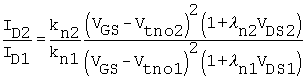
where, in the circuit with the gate of M₁ grounded, V_GS1 = V_GS2 = V_GS. For the specific case of the project on the amplifier, we can assume that V_DS1 V_DS2 such that

Equation 8.4

To simplify the relation, it is advantageous to express parameters in terms of increments. For example, threshold voltage will be expressed as a mean value

Equation 8.5

and a difference between the threshold voltage of the two transistors

Equation 8.6

such that

Equation 8.7

and

Equation 8.8

Using these definitions along with V_eff = V_GS - V_tno, we have

Equation 8.9

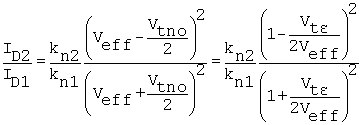
or, approximately,

Equation 8.10

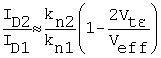
In the differential amplifier project (PMOS), we measure the drain currents along with V_SG over a range of drain current values. These are used to obtain, in the Mathcad project file, k_n1, k_n2, and the threshold voltages and thus, v_t. This will provide a comparison between the measured drain-current ratios and ( ) as a function of V_eff and drain current.

8.3 Signal Voltage Gain of the Ideal Differential Amplifier Stage

This initial assessment of the gain of the differential amplifier neglects the effects of the bias resistor, R_bias, and of the output resistance of the transistors as well as the body effect. These effects are considered below. To generalize the discussion to include the possibility of inverting and noninverting modes of operation, we base the discussion on the circuit (Fig. 8.2) with a drain resistor for both transistors. The inverting and noninverting modes take, respectively, the outputs at V_d1 = V_o1 (a_v1) and V_d2 = V_o2 (a_v2). Also, this is the configuration that is studied in the project on the differential amplifier. Note that the input could arbitrarily be moved to the gate of M₂, in which case the output taken at V_d1 becomes the noninverting mode, and so forth.

Figure 8.2. Circuit for our project on the differential amplifier. The circuit has resistors in both drain branches for comparing the gain from the noninverting and inverting outputs and for sensing the bias drain currents.

Assume for the present that the amplifier is perfectly symmetrical such that, for example, I_D1 = I_D2 and g_m1 = g_m2. A signal voltage V_i is applied to the gate of M₁ as shown in the diagram. The voltage divides between the two transistors (from gate 1 to gate 2) to give

Equation 8.11

Since V_gs1 = |V_sg2| (due to the symmetry of this case), then

Equation 8.12

The negative V_gs2 results from the fact that the total v_GS2 is reduced from bias V_GS2 upon the application of a positive signal voltage, V_i, at the gate of M₁ (i.e., v_GS2 = V_GS2 - V_i/2). It follows that total i_D2 decreases, which leads to a positive signal voltage at the drain, V_d2. Thus, the amplification is noninverting.

As always, the relation between the signal drain current and the signal drain-source voltage is ( ), which is (with g_ds = g_mb = 0)

I_d = g_mV_gs

Eliminating V_gs in ( ), applied to M₂, with ( ), the drain current for M₂ is related to the input voltage, V_i, by

Equation 8.13

Combining ( ) with V_o2 = -I_d2R_D2, the output voltage is related to the input voltage by

Equation 8.14

such that the gain is

Equation 8.15

Note that there is no minus in the relation; that is, this is the noninverting amplifier mode. Also note that the gain for this amplifier is one-half of that for the common-source amplifier. This is a reasonable price to pay for not having a bypass capacitor. The amplification can be viewed as a source-follower stage in cascade with a common-base stage, neither of which is an inverting stage.

The inverting mode of the amplifier is for the output taken at the drain of M₁. For this case, V_o1 = -I_d1R_D1, and from ( ) and ( ) applied to M₁, I_d1 = g_m1V_g/2 and the voltage relationship is

Equation 8.16

This leads to the inverting gain, which is

Equation 8.17

8.4 Effect of the Bias Resistor on Voltage Gain

The results above ignore the effect of resistance, R_bias. When it is included, it is no longer valid to assume that V_gs1 = V_sg2, even with I_D1 = I_D2. The bias-resistor effect is examined here based on a signal equivalent circuit of Fig. 8.3. The resistance at the source of M₁ consists of the bias resistor and the linear-model resistance 1/g_m2 (which neglects 1/g_ds2), looking into the source of M₂.

Figure 8.3. Source circuit as viewed from M₁. Source resistance includes actual resistor R_bias in parallel with input resistance at source of M₂, which is 1/g_m2 for the conditions of this unit.

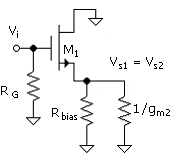
For the noninverting mode, the circuit transconductance, G_m2 = I_d2/V_i, is

Equation 8.18

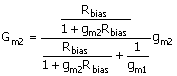
Parameter g_m2 is the transconductance I_d2/V_s2 (i.e., from the source of M₂ to the output V_o2). Note that the fraction is just a voltage divider, V_s2/V_i, since the output resistance at the source of M₁ is 1/g_m1, as noted in connection with ( ). With g_m1 = g_m2, the multiplying fraction assumes the value of ½ for very large R_bias.

The noninverting gain, which includes the effect of the bias resistor, is

Equation 8.19

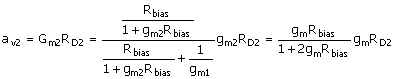
where the right-hand side uses g_m1 = g_m2. The gain result is technically that of the cascade of a source-follower stage (M₁) and a common-gate stage, g_m2R_D2 (M₂). The multiplying fraction is < ½.

The gain for the inverting side can be obtained by using ( ), which is for a common-source amplifier with source resistor. This gives for the inverting-mode gain

Equation 8.20

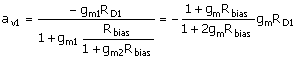
where the right-hand side again uses g_m1 = g_m2. The multiplying fraction is > ½. Note that for both inverting and noninverting gains, the effect of R_bias can be neglected for most purposes, as the multiplying fractions in ( ) and ( ) are both close to ½.

The choice of the input at gate 1 is arbitrary and all of the results obtained here apply equally to the input taken at gate 2. The inverting output is always at the side of the input, and the noninverting output is always at the opposite side.

8.5 Differential Voltage Gain

Suppose that an input voltage, V_g12 = V_g1 - V_g2, is applied between the inputs. Due to symmetry, the voltage magnitudes at the inputs with respect to ground are V_g1 = V_g12/2 and V_g2 = -V_g12/2, respectively. The noninverting output, V_d2, for this case is, by superposition,

Equation 8.21

The gains for the contributions from V_g1 and V_g2 are ( ) and ( ), respectively. This is the case of a pure differential input with resulting gain

Equation 8.22

A similar approach applied to obtain the gain for the output taken as V_d1 produces

Equation 8.23

Assume, for a numerical example, that I_D = 100 mA, R_D1 = 50 KW, and g_m = 200 mA/V (V_effn = 0.5 V). In this case the gain is a_vd1 = -10. This would be consistent with V_DD = |V_SS| = 10 V.

The gain for the case of the differential output, a_vd12 = (V_d1 - V_d2)/(V_g1 - V_g2), can be obtained from (V_d1 - V_d2) = -(1/2)g_m1R_D1V_g12 - (1/2)g_m2R_D2V_g12 and is

Equation 8.24

where g_m1 = g_m2 and R_D1 = R_D2 = R_D. Note that ( ) and ( ) are the same as ( ) and ( ). However, ( ) and ( ) are the limiting forms of ( ) and ( ) for R_bias , whereas ( ) and ( ) apply for a finite R_bias.

8.6 Common-Mode Voltage Gain

The common-mode gain is defined for the same voltage applied simultaneously to both inputs. The output must be the same at either output terminal (again assuming that g_m1 = g_m2 and R_D1 = R_D2). For example, for the output V_d2, the gain can be determined by a superposition of gains, inverting (input, V_g2) and noninverting (input, V_g1), with R_D2 in both equations.

Using ( ) (noninverting) and ( ) (inverting), the gain for finite R_bias is, accordingly,

Equation 8.25

which is

Equation 8.26

The result is that of a common-source stage with source resistance 2R_bias. This is intuitively correct as taken from the half-circuit viewpoint, where the circuit is completely symmetrical. The input from either side looks at a common-source stage except that the opposite side is contributing an equal amount of source current, thus giving an effective source resistance equal to twice the actual value. A valid approximate form for well-designed circuits (in terms of common-mode gain) is

Equation 8.27

The same result applies to the case of the output taken at the opposite drain, with the substitution of R_D1 for R_D2. Using the circuit values following ( ) plus R_bias = 85 kW, a_vcm -0.3. Note that this result in combination with the gain from ( ) would indicate that this is not a particularly good design. The goal is for a_vd >> a_vcm.

8.7 Voltage Gains Including Transistor Output Resistance

In Project 9 we measure the gain of a "balanced" stage with drain resistors for both transistors. The amplifier is the PMOS version of the NMOS amplifier of Fig. 8.2. We obtain an exact Level 1 SPICE solution for the gains for both outputs. The example is used to explore the use of a simulator for obtaining precision results to compare with simple hand calculations.

For larger l_n values (NMOS), the output resistance can influence the gain and complicate the gain expressions considerably. Here we consider the effect due to g_ds1 and g_ds2 while retaining the effect of R_bias. In the following, the gain of the inverting input, a_v1, is obtained again as a common-source stage with source resistance. The effect of g_ds2 on the effective source resistance is included (input at the source of M₂). The effects due to g_ds1 are also taken into consideration.

The gain of the noninverting case, a_v2, is obtained by considering the cascade of the source follower stage (M₁) and the common-gate stage (M₂), as, in effect, was done in the development of ( ). The source-follower gain takes into account effects from g_ds1 and g_ds2, and the gain of the common-gate stage depends on g_ds2.

8.7.1 Gain of the Common-Source Stage with Transistor Output Conductance and Source Resistor

The circuit transconductance for a common-source stage with source resistor, with the inclusion of g_ds, was developed in Unit 4 )]. This will be reviewed and reinforced here in the form of a slightly different approach to the result. The signal circuit for this case is again given in Fig. 8.4. Using the variables of Fig. 8.4, the circuit transconductance is G_m1 = I_d1/V_i. The object is thus to obtain a relation between these two variables.

Figure 8.4. Circuit for obtaining the gain for the inverting output with the transistor output resistance included. R_s includes all resistance contributions at the source.

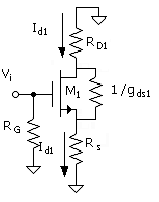
The fraction of the current produced by the intrinsic transistor, g_m1V_gs1, which flows into R_s is

Equation 8.28

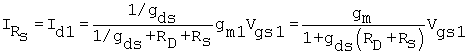
This is the portion of current source g_m1V_gs1, shared between 1/g_ds and R_D + R_s, which flows through R_D + R_s, that is, I_d1. Note that R_D + R_s and 1/g_ds1 are in parallel and shunt the transistor current source.

A relation for V_gs1 in terms of I_d1 follows, which is

Equation 8.29

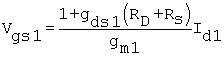
The input Voltage is the sum of V_gs1 and the drop across R_s. That is,

Equation 8.30

Using (8.29) in ( ) gives

Equation 8.31

or

Equation 8.32

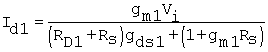
The circuit transconductance follows as

Equation 8.33

The gain for this case is then

Equation 8.34

A discussion of R_s as affected by g_ds2 follows.

8.7.2 Common-Gate Amplifier Stage

The circuit diagram of Fig. 8.5 is for the M₂ portion of the differential amplifier. The input is applied at the source, V_s2, and the output is taken at the drain, V_d2 = V_o2, while the gate is grounded. This is a common-gate configuration. Here we analyze the input resistance, for evaluating the effect on R_s, and gain of the common-gate stage.

Figure 8.5. Circuit that includes the output resistance of M₂. The circuit is for obtaining input resistance at the source of M₂ and the gain of the common-gate stage of M₂

Without g_ds2, the input resistance at the source is just 1/g_m2. With g_ds2 in place, there is a positive feedback from the drain output to the source input. This causes the input resistance to increase. With g_ds2, the current into the source terminal is

Equation 8.35

It is noted that the g_ds2 term reduces the input current, which has the effect of increasing the input resistance. From ( ), the resulting input resistance at the source, R_is2 = V_s2/I_d2, is

Equation 8.36

The input resistance goes to 1/g_m2, as noted above, for g_ds2 = 0. The expression for the equivalent R_s is now R_s = R_bias || R_is2, where R_is2 is ( ). In modern integrated circuits, R_D2 may be replaced with a high-resistance transistor current source, and the input resistance is this case can be much greater than 1/g_m2.

The gain of the common-gate stage is obtained as follows: The output voltage is

Equation 8.37

which gives

Equation 8.38

Note that for g_ds2 = 0, the gain has the same magnitude as the simple case for the common-source stage.

8.7.3 Voltage Gain for the Noninverting Output

The noninverting amplifier gain is based on a cascade of a source-follower stage (M₁) and a common-gate stage (M₂). The source-follower transconductance, I_d1/V_i, is ( ). Using this with V_s1 = I_d1R_s gives

Equation 8.39

Note that the magnitude is about ½. Overall gain is the product of ( ) and ( ), which is

Equation 8.40

The equations from this unit are summarized below in Unit 8.11

Recall from the discussion of MOSFET model parameters that g_ds is given by ( ), which is

Thus, the gain expression depends on parameter l, and especially if l is somewhat large. In Project 9 we measure the gains from the two drains and use the results to find the value of l that makes the theory fit the measurements. In this way, we are getting a signal-derived experimental number to compare with that obtained in the parameter-determination project. This will be done using the PMOS configuration since the value of l_p is large and the effect is significant. All of the gain expressions, which are based on NMOS transistors, apply exactly to the PMOS stage with substitution of subscripts; change n to p (parameters) and reverse the order for dc voltage variables.

For hand calculations, approximate forms must reasonably be used. This applies to approximate forms for device parameters and gain. The basic gain equations are, again, assuming that g_ds = 0 and R_bias = , simply, as given by ( ) and (

with R_D1 = R_D2 and g_m1 = g_m2. In the differential amplifier project, we will compare these with the more precision forms.

8.8 Body Effect and Voltage Gain

In Project 9 we are able to connect the sources of the transistors to the chip body. Certainly, in general this cannot be done such that there is a body effect associated with the differential-amplifier-stage transistors. The necessary alterations to the gain equations are determined in the following. At the end of this unit, we will have the complete, precision-gain calculation equations of Level 1 SPICE. It will be informative to consider numerical results that are based on various degrees of approximations, and this is done below.

8.8.1 Common-Source Stage and Body Effect

With the body effect present, a component of current, g_mb1V_s (Fig. 8.6), is subtracted from g_m1V_gs1 such that ( ) for this case is modified to become

Equation 8.41

Figure 8.6. Circuit for obtaining the inverting gain of the differential stage with body effect included. Body effect is accounted for by the current source added to the transistor signal (linear) equivalent circuit.

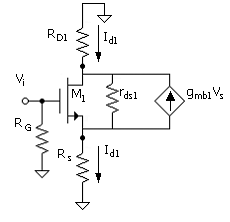
Additionally using V_s = I_d1R_s and V_gs1 = V_i - I_d1R_s ( )] in ( ), a relation between I_d1 and V_i is obtained, which is

Equation 8.42

Solving for I_d1, the circuit transconductance is, for the body-effect case,

Equation 8.43

It follows that the gain for the inverting mode, with the addition of body effect, is

Equation 8.44

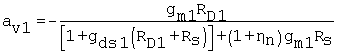
The effect of h_n in the denominator tends to make the gain smaller. However, the body effect, as shown below, will decrease R_s such that the two effects tend to cancel one another.

8.8.2 Common-Gate Stage and Body Effect

The voltage applied to the common-gate stage is V_s2 = V_sg2 (Fig. 8.7). Recall that in the g model for the transistor, as discussed for the common-source mode, current sources g_mbV_sb and g_mV_gs are in parallel but in opposite directions. Thus, the current sources g_mV_sg and g_mbV_sb are, for the common-gate mode, in the same direction since V_sb = V_sg = -V_gs; the common-gate has an effect transconductance of (1 + h)g_m. It follows that the input resistance of the common-gate stage is as obtained before the body effect was included [( )], except for the addition of h_n, as in the following:

Equation 8.45

Figure 8.7. Circuit that includes the voltage-dependent current source due to body effect associated with M₂. Body effect affects the input resistance into the source of M₂ and the gain of the common-gate stage of M₂.

Similarly, the common-gate gain, ( ), is readily modified with the addition of the multiplying factor (1 + h_n This is

Equation 8.46

Note that in the absence of g_ds2, the gain for the common-source stage reduces to a_vcd = g_m2 (1 + h_n)R_D2, where, with body effect, the effective transconductance is, again, (1 + h_n) g_m2.

8.8.3 Source-Follower Stage with Body Effect

The transconductance relation obtained for the common-source stage given by ( ) also applies to the source-follower stage. Combining this with V_s1 = I_d1R_s leads to the source-follower gain associated with M₁, which is

Equation 8.47

The overall gain is again

a_v2 = a_vsf a_vcg

Note that the body effect for the source-follower stage increases the denominator of ( ) while it increases the numerator in the common-gate result, ( ). These tend to cancel, as in the case of the inverting gain.

8.9 Amplifier Gain with Differential and Common-Mode Inputs

For inputs at either or both gates, there exists a common-mode and differential-mode voltage. These are, for applied voltages V_g1 and V_g2, common mode

Equation 8.48

and differential mode

Equation 8.49

Based on these definitions, the output, for example, V_d1, for a given set of inputs is

Equation 8.50

where a_vd1 and a_vcm are ( ) and ( ) (with R_D1), respectively. For the output V_d2, a_vd2 is substituted for a_vd1. V_dm is a pure differential input and is not with respect to ground; the effect from the bias resistor is accounted for in the common-mode gain.

For the case of a single-ended input, for example, V_g1 = V_i and V_g2 = 0, the output is

Equation 8.51

This is identical to ( ). The common-mode contribution can be significant, for example, in a resistance feedback amplifier (Unit 11). In this case, V_dm in ( ) can be very small compared to V_cm.

8.10 Comparison of Numerical Gain Results

Gain calculations were made using k_n = 1000 mA/V², l_n = 0.05 V^-1, R_D = 150 kW, R_bias = 100kW h_n = 0.15, I_D = 50 mA, and V_DS = 5 V. The values are given in Table 8.1. For the comparison, g_m was calculated with the precision form [( l_n 0) for all cases. Possibly a more valid consistency (hand calculation versus precision calculation) would be achieved with the use of the approximate form for g_m up to l_n 0. This would reduce some of the difference in the results. For example, for the first case, a_v1 = -a_v2 = -33.5, with the approximate form for g_m (l_n

It is notable that the various factors do not have a major effect on the results, even though the value of l_n is relatively large. This is especially true for the differential amplifier with resistive load, as considered here. The conclusion can be made that for initial hand-calculation purposes, the simplest form is satisfactory. Precision results can be obtained with a simulator.

8.11 Summary of Equations

8.12 Exercises and Projects