MOSFET Source-Follower Buffer Stage

MOSFET Source-Follower Buffer Stage

High-gain stages in amplifiers are usually some form of differential stage or common-source stage. These are inherently high-output-resistance stages and are not suitable for low-impedance loads. The solution for a requirement to drive low-impedance loads is to insert a buffer stage between the output of the common-source 939b112j stage and the load. The buffer will be a source-follower stage. The name follower comes from the fact that to a good approximation, the output voltage follows the input voltage; that is, it has an open-circuit gain of unity and low output resistance.

Although the output voltage/input voltage relation is sometimes loosely referred to as the gain, it would be more accurate to label it the voltage transfer function, as the "gain" is less than 1. The transfer function is explored in the following for various possibilities of degrees of approximation in the linear circuit.

7.1 DC (Bias) Circuit

The circuit diagram shown in Fig. 7.1 uses for the transistor a symbol that includes the body connection. This is to emphasize the fact that the output (source) of the source follower is generally (and usually) at different dc and signal potentials from the body. In Project 8 we measure the gain for both the connection shown (which we can make for this special case of one transistor on the chip being used) and with the body connected to V_SS, which is signal ground. The latter demonstrates the extent of the influence that the body effect has on the gain when it is not possible to connect the body and source together as shown in Fig. 7.1

Figure 7.1. Source-follower (common-drain) stage (NMOS transistor) with the input at the gate and the output at the source. In this example, the source is connected to the body. Usually, in a circuit, the body will be attached to the power supply V_SS (NMOS).

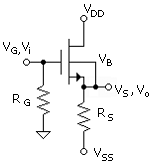
The design of the stage will often consist of setting the dc output at V_O = 0 V (for a dual power supply), as this will be the final (output) stage. Therefore, R_S will be selected based on the design drain current from R_S = |V_SS|/I_D. It is then necessary to determine V_GS in order to determine the V_G = V_GS required (which will be set by the dc circuitry of the preceding circuit).

For the usual practical application, body voltage, V_B = V_SS. With V_S = 0 V, V_SB = |V_SS|. Thus, the threshold voltage, including body effect, will be

Equation 7.1

and the gate bias voltage will be obtainable from

Equation 7.2

If the source and body are connected, as in Fig. 7.1, V_tn is replaced with V_tno.

7.2 Source-Follower Voltage Transfer Relation

A signal circuit is shown in Fig. 7.2, where the dc supplies have been replaced with ground. Also, the internal resistance, r_ds = 1/g_ds, of the transistor has been included in the signal circuit. Note that it is in parallel with R_S since the drain is tied to signal ground. Assume for now that source and body are connected as in Fig. 7.1

Figure 7.2. Signal circuit of the source follower. Body effect is absent since the source and body are assumed connected.

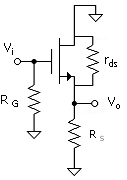
Regardless of the terminal configuration, for infinite output resistance and with the body and source connected, the relationship between the drain current and gate - source control voltage of the transistor is ( ) with g_ds = g_mb = 0, which is [(

In the source-follower circuit, the output resistance of the transistor can be included in the source-follower load and ( ) effectively applies.

The transconductance for the circuit configuration with a source resistor was shown in Unit 4 to be [(

where, for this case, is the source-follower load, which includes the transistor output resistance and is

Equation 7.3

Then using

Equation 7.4

the "gain" (the transfer function is less than unity) is determined to be

Equation 7.5

Ideally, this is a unity gain, as would be the case for . In bipolar transistors, this condition is closely approached. However, in MOSFET source followers, the ideal case is in general not reached. As we will see below, this deficiency is enhanced when the body effect is included.

Note that a_v is

Equation 7.6

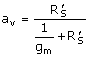
This is the expression for a simple voltage divider. Thus the source follower is the equivalent of a unity-gain circuit with load and output resistance 1/g_m. We can conclude that the transistor viewed from the source has an output resistance of 1/g_m.

Finally, with separated into its component parts, the source-follower gain becomes

Equation 7.7

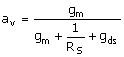
In general, the g_ds parameter can be dropped. The ratio of g_m/g_ds is

Equation 7.8

7.3 Body Effect and Source-Follower Voltage Transfer Relation

Suppose now, as in Fig. 7.3, that the body terminal is connected to V_SS, which is signal ground. Following the definition of the body-effect transconductance, g_mb, the component of I_d due to source-body voltage V_sb is [from (

Equation 7.9

Since the body is at zero potential (signal), this is

Equation 7.10

This component of current can be included in the circuit, as shown in Fig. 7.3, with an additional resistance in parallel with R_S of value 1/g_mb. That is, the body-effect contribution to the drain current is a voltage-dependent current source, where the voltage is the same as that across the current source.

Figure 7.3. Source-follower signal equivalent circuit with body connected to V_SS, which is signal ground. The body effect is taken care of for this case with a resistance of magnitude 1/g_mb placed in parallel with R_S along with r_ds = 1/g_ds.

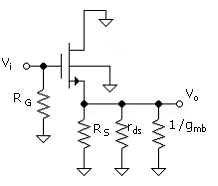
With the body-effect addition, the source-follower gain expression is modified to the following:

Equation 7.11

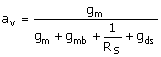
The body-effect parameter is related to g_m by [(

g_mb = hg_m

with

With the substitution of ( ) in ( ), the gain is

Equation 7.12

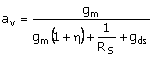
In modern integrated circuits, resistor R_S will be replaced with a current-source output resistance, which is significantly greater than R_S. The source-follower gain is, in this case, approximately (with no external load)

Equation 7.13

Parameter h will typically be in the range 0.1 < h < 0.2.

Note that the body effect degrades the "gain" significantly below the ideal unity. In the project on the source-follower circuit, we measure the voltage transfer function of the source follower for a range of dc drain current with body and source connected and with the body connected to V_SS. The resulting curves will be compared to demonstrate the body effect on the transfer function. A curve fit of the SPICE equation to measured data will provide for an alternative determination of parameter g_n. This value should be close to the value obtained from dc measurements.

7.4 Summary of Equations Threshold voltage VS = 0 zero volts and negative power supply VSS. Source-follower voltage gain with Vsb = 0. Source-follower voltage gain with Vsb = IdRs. gmb = hgm Body-effect transconductance. Source-follower body-effect degradation factor.

7.5 Exercises and Projects