Multiway Trees : B-Tree

Multiway Trees : B-Tree

External information retrieval

B-trees are used in database systems where the tree is kept on a physical disk instead of main memory. The data structures we have considered so far are for internal information retrieval and are kept in high-speed memory (RAM).

Accessing (locating a record) on disk is very expensive process (time required for a single access is thousands of times greater for disk than for RAM). A B-tree takes advantage of the fact that we can read in many records (a page or block at a time) to minimise the number of disk accesses.

Each block becomes a node in our B-tree. The more records we can fit into a block the fewer disk accesses are required to find a record. In practice a B-tree reads from an index file, which indexes a separate data file.

Each index record contains:

• a key value from the data file
• the disk address of the key value's record in the data file
• the disk address of the child node (or block) of the current index record (this will be another block in the index file).

If a complete data structure is in internal storage (e.g. as a binary tree) then there is no advantage in fitting as many keys as possible in a node because moving from one node to another is very fast. However when the retrieval of a node requires a dis 242c21c k access (as in external storage) we want to minimise the number of nodes retrieved. Hence we want to put as many keys as possible in a node. Hence B-trees (and B+-trees).

Because each node in a B-tree has several key values it has several children (unlike a binary tree where every node has one key and two children). Hence it is a multiway tree.

Properties of a B-tree

• The root is either a leaf or has between 2 and m children.
• All non-leaf nodes (except the root) have between [m/2] and m children.
• All leaves are at the same depth.

All data are stored at the leaves. Contained in each interior node are pointers P1, P2, ..., Pm to the children, and values k1, k2, ..., km representing the smallest value found in the subtrees. Some of the pointers can, of course be NULL.

Order:

The order of a B-tree is the maximum number of links that may be contained in a node.

e.g. B-tree of order 4:

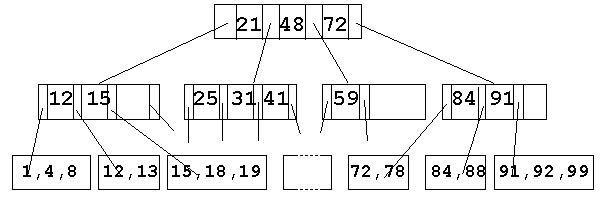
Insertion into a B-tree

A B-tree must (by definition) have all leaves at the same level. This ensures the height of the tree is minimised and so fewer disk accesses are required. However, this also means we cannot just add new leaves on the bottom of the tree (as in a binary tree). Instead the tree must grow from the root.

1. Find the insertion point

This is achieved by adding any new key to the appropriate leaf node (this leaf is found in a similar manner to searching a binary tree as every left sub-tree contains keys that are less than the parent key, and every right sub-tree contains keys that are greater). Once the leaf is found, the new key is added.

2. Node Splitting

If an insertion causes a leaf node to become over-full then it is split and the internal node key value and pointers will need to be changed appropriately. If the internal node then becomes full the process is repeated (ie the parent node is split and the middle value migrates up). This process can continue all the way to the root. If the root becomes full, it is split and the tree gains another level.

As all leaves remain on the same level the tree nodes are always balanced.

Consider the following example:

Example: Insert into a B-tree of order 5 the values

a g f b k d h m j e s i r x

Initially: empty tree

Step 1: insert a g f b k

Step 2: insert d - node full so split

Step 3: insert h m

Step 4: insert j fghkm is full so split

Step 5: insert e s i r

Step 6: insert x jkmrs is full so split

Deletion from a B-tree

As usual deletion poses a more interesting problem than insertion. Instead of expanding the size of the tree at the root, deletion will eventually cause the height of the tree to reduce.

Step 1: Find the key to be deleted

First we find the key value to be deleted. If it is only in a leaf node then it is simply removed. However, if it is also in an internal node we use a similar method as in the AVL tree. We find the successor (or predecessor) of the node to be deleted which must only be in a leaf node. We then replace the deleted key value and record pointers with the successor leaf key, and delete the original successor key value.

Step 2: What if the leaf node has too few keys?

Recall a B-tree node must have at least m/2 key values in all nodes except the root, where m is the order of the tree (this again stops the height of the tree growing unnecessarily). If a deletion causes a node to have too few keys there are two strategies:

Check the adjacent leaf nodes that belong to the same parent. If one of these has spare keys we can move it's smallest key (if to the right of our delete node) or largest key (if to the left) to the 'delete' node so that it now has enough keys.

If taking from the left, that key becomes the new pointer to the 'delete' node in the parent.. If taking from the right, the key pointer to the right node in the parent must be changed to what is now the lowest key in that node.

However, if all adjacent nodes also have too few keys we cannot use the above strategy. Instead we can merge the delete node with one of the adjacent nodes and the key value in the parent node that lies between them. This key value is then removed from the parent.

The process may continue if the parent node now has too few keys. We just repeat the above steps - first we try to move an adjacent key, if this is not possible then we merge nodes. This can continue to the root, and if the root contains only one key the height of the tree will be reduced.

Example: B-tree of order 5

Delete h

Delete r

Need to promote s as low value:

Delete p mn would now contain too few nodes so pull t up, s down, and delete p

The tree now has the following structure:

Now consider Delete t: first we must pull up t's successor u, and delete t in the leaf:

However, when t is deleted this causes u's leaf to have too few nodes. We cannot get another key from the adjacent node because it too would have too few keys. Hence we must merge the two leaf nodes, bringing down u

Now the internal node with m has too few keys and cf does not have a spare key. Hence we must merge the two internal nodes and the root, giving the final tree:

Efficiency

The depth of a B-tree is at most [log_(M/2) N] (i.e. when all nodes have the minimum M/2 keys). If we perform a binary search at each node to find which branch to take then we perform O(log M) operations, but an Insert or Delete operation could require O(M)operations to fix the worst possible scenario.

So the worst possible case for an Insert or Delete operation is:

O(M log_M N) = O((M/log M) log N)

But a find only takes:

O(log N)

Empirically it has been found that M values of 3 or 4 are optimal. If we are only interested in in-memory access there is no point in going to larger values.

However, if we are accessing a B-tree on a disk, then if each node is stored in a single disk block this favours larger M values - the number of disk accesses is equal to the depth of the tree and is therefore:

O(log_M N)

The value of M can then be chosen to be the largest value that can still allow an interior node to fit into one disk block: often 32 <= M <= 256.

In addition, if the higher levels of the B-tree are cached in memory, this can further increase the performance of a disk tree search.