ARBEITSSEMINAR
1.Bestimmen Sie die Ubertragungsfunktionen aller Teilprozesse
a) G1(s) = 
θ(t) = 5 [ ۫ C] = 5 * 1(t) => θ(s) = 5 * 
= 
W(t) = 20 + 0.1 * n [t/h]
W(t) = 20
+ 0.1 * 36 = 23 15315v2111p .6 = 23.6 * 1(t) => W(s) = 23.6 * = 
G1(s) = 
= 
= 0.211
__________ ______ ____ _____
b)
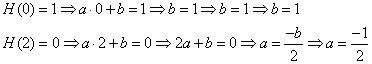
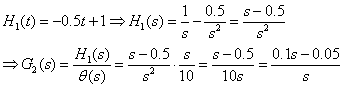
c)
__________ ______ ____ ______________
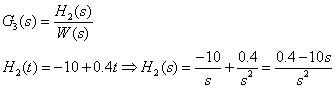
d)
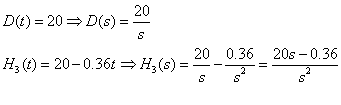
e)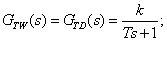
k=Verstarkungsfaktor=Verhaltnis
des Amplituden=
T=Ausgangsfunktion=5+0.01n=5+0.01*36=5.36
GTW(s) = GTD(s) = 
f) GTH(s) = 
= 
= 
= 
g)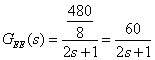
2.Beschreiben Sie die Abhangigkeit Eingang-Asugang fuer diese Teilprozesse durch eine Differentialgleichung mit konstanten Koeffizienten.
ai,bj 
i=0.n
j=0.m
Die Übertragungsfunktion ergibt sich aus der Differentialgleichung in der Form:
G(s)=
nx1 
a)
(s)=0.2427*W(s) (t)=0.2427*W(t)
b)=
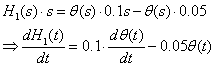
c) 
= 
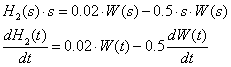
d) =
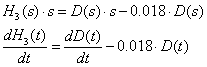
e)
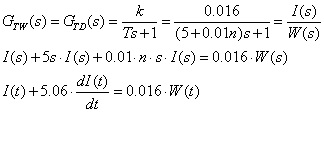
f) 
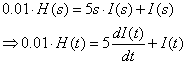
g)
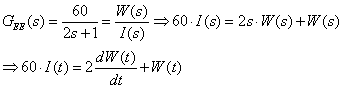
3.Skizzieren Sie die Verteilung der Pole und Nullstellen der Ubertragungsfunktionen der Teilprozesse.
a)
Pole:keine
Nullstellen:keine
b) 
Pole:
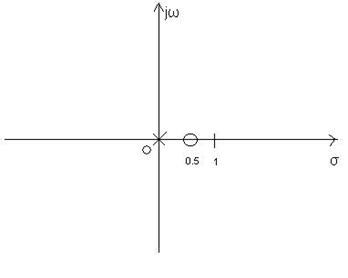
Nulstellen:
c) 
-
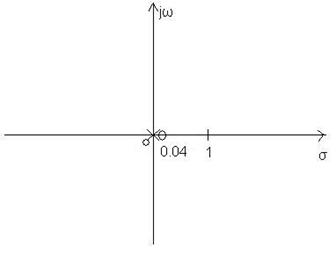
Pole:
- Nullstellen: 
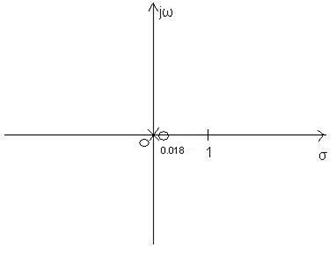
d) 
- Pole:
- Nullstellen: 
e) 
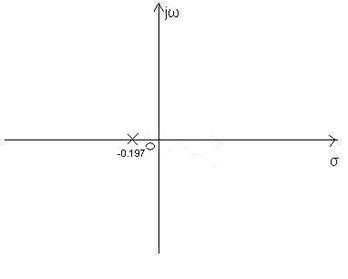
Pole:
- Nullstellen: keine
f)
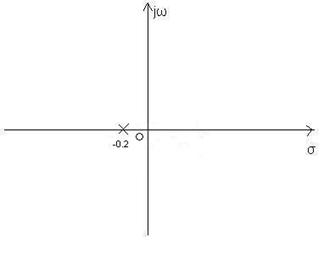
Pole:
Nullstelen:keine
g) 
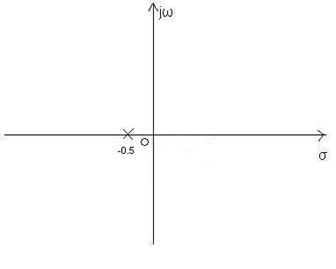
Pole: 
Nullstellen: keine
4. Uberprufen Sie die interne und externe
Stabilitat des Prozesses mit dem Eingang 
und dem
Ausgang 
Prozesse mit dem Eingang
UW und dem Ausgang 
sind die folgenden:
G (s), G (s), G (s), GEE(s) und GTH(s)
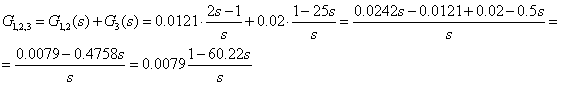
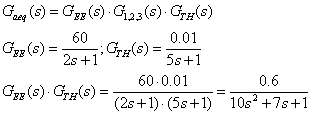
Charakteristischer Polynom:
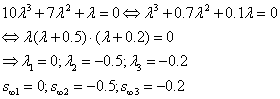
6.Entwerfen Sie (algorithmischer Entwurf) die Regler.
Erwunschte Leistungen sind:
i)
fuer den inneren Regelkreis mit P-Regler
muss der Dampfungsfaktor
=0.7 sein.
;
;
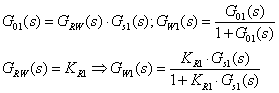
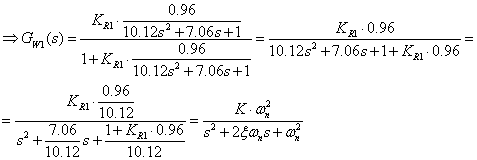
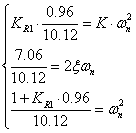
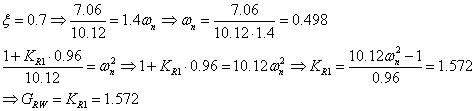
ii) Der aussere Regelkreis mit PI-Regler muss stabil sein.
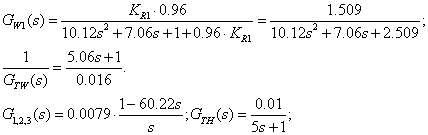
Ubertragungsfunktion
des offenen Regelkreises
Regler
Die Determinanten: Notierung: x=
; y=
1.Grades: m=(45.42x)
Det[m]
45.42 x
Det[45.42 x]
2. Grades:
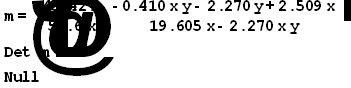
3. Grades:
4. Grades:
5. Grades
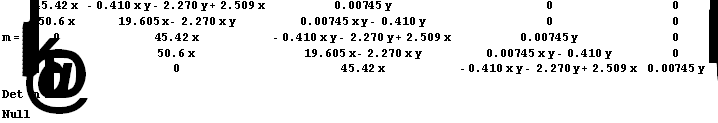
7.a)
; 
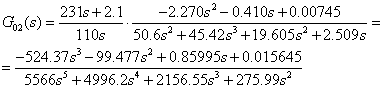
Prufung der Stabilitat mit Bode- und Nyquist-Diagrammen
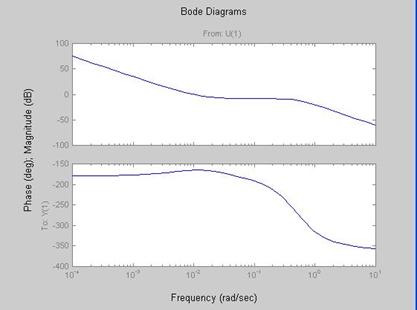
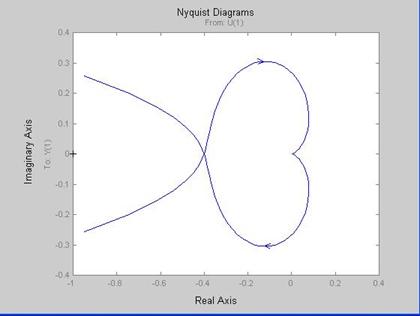
7
b)
=Uberschwingung
-die Zeit des
ersten Maximums: 
-durata regim
tranzitoriu (Dauer...): 
-Indizes der
Oszillation:
-die
Schwingungsdauer:
-die Zahl der Schwingungen: n=3
c)bleibende Differenz=0
9)-innerer Regelkreis:
-ausserer Regelkreis: 
10)
|
