u (x,y,z) = kyz,

(x,y,z) = -kxz,

w (x,y,z) = xy

όπου Κ,Λ σταθερές. Ζητούνται οι παραμορφώσεις και οι τάσεις, η ε 22422s1824w ;παλήθευση των εξισώσεων συμβιβαστού και η εύρεση των μαζικών δυνάμεων. Επίσης ζητούνται οι κύριες τάσεις και διευθύνσεις.

p σημείο Μ (x x x

_ij p _{i j} x_sx_s

x

x

x

με ροπή φορτίο Μ = 12 kNm

i)          

ii)         = 250 .

M

5m

5m

5m 10m 5m

i)           x y

u P x y EI_zz vy EI_zz y GI_zz l EI_zz c GI_zz y

P E vxy I_zz x I_zz xl I_zz l I_zz ]

Poisson και G E

ii)         G l m c = 10 cm t cm

τάσεις στο σημείο

m m

iii Tresa = 200 .

t

P

z c

z c y y

l

cm με τάση διαρροής 220 .

i)          

ii)        

S₁  S₃ m

A

S₂ 2m

0,5m 1m 1m

i)           = 250 ).

ii)         .

iii)       + Μ_Δ) / 2

iv)      

G m

M M

1m 1m 1m 1m

α α

α α

G Poisson ν = 0,3 και τάση διαρροής 220 ( συμπεριφορά).

i)          

ii)         a Mohr x

iii)      

iv)       Tresca

X

50 50

50

90

90

X

50

50 50 1,5 mm

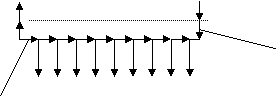
υλικό με = 220 και διατομής Ι με τις διαστάσεις του σχήματος

i)          

ii)         G

iii)      

Μ Μ 80 mm

2 m 2 m

2 mm

80 mm

2 mm

2 mm

Σ

πρόβολος του σχήματος με τάσεις διαρροής = 15 (διάτμηση) και = 150 (εφελκυσμός), που φορτίζεται με τις δυνάμεις F G

i)           F = 10 ΚΝ, Μ = 5 ΚΝm

ii)         x m x m x m x m F

iii)       F

1 cm

x 20cm

F[N]

M[Nm]

P = M[N]

m

ΑΣΚΗΣΗ 10

R _t

i)           A x x u

ii)         d dx const

iii)       τάσης που εμφανίζεται στη δοκό.

x x R

x₂

x₁

x₃ M_t