ΜΑΘΗΜΑΤΙΚΕΣ ΓΝΩΣΕΙΣ

Greaca

 

T

α) κάθε χορδή ισούται με το μισό της αντίστοι` 929e48j 7;ης διαμέτρου.

β) κάθε γωνία εγγεγραμμένη ισούται με την αντίστοι` 929e48j 7;η επίκεντρη που βαίνει στο ίδιο τόξο.

71. Σε κάθε κανονικό πολύεδρο, αν K είναι ο αριθμός των κορυφών του, Ε ο αριθμός των εδρών του και Α ο αριθμός των ακμών του, τότε ισχύει η σχέση:

γ) Το ποσοστό έκπτωσης είναι το ίδιo.

και 2x z x z

h .

h .

h .

h

T

παρακάτω σειρά βρίσκονται ακριβώς πριν από ένα μονό αριθμό και ακρι­βώς μετά από έναν αριθμό με­γαλύτερο του έξι;

81. Ένα παραλληλόγραμμο έχει περίμετρο 44 cm και εμβαδόν 60 cm . Αν η μία πλευρά του είναι 10 cm τότε το ύψος του είναι:

α) 5 cm.

β) 6 cm.

γ) 5 cm ή 6 cm.

Α. Η προετοιμασία των Ολυμπιακών ομάδων αυτών των κρατών ήταν πάντοτε ιδιαίτερα καλή και εντατική.

f x x

xx

x

88. Το εμβαδό Ε_ολ της ολικής επιφανείας κώνου με ακτίνα βάσης R και παράπλευρο ύψος h είναι:

R h R

R h R

R h R

R h R

x x-3=0,

δ) για κ>2 έχει πάντα λύσεις στους πραγματικούς αριθμούς.

93. Αν διπλασιάσουμε την ακτίνα R της βάσης κυλίνδρου, τότε ο όγκος του

ανήκει στην παρακάτω ομάδα;  2, 4, 100, 38, 20, 7 ….

98. Αν διπλασιάσουμε την ακτίνα R της βάσης κώνου τότε ο όγκος του V

0,0026;

.

ημέρα που ενώ το πρωί έβρεξε το βράδυ χιόνισε. Το Σάββατο πάντως και την Τρίτη έβρεχε. Ποια μέρα και έβρεξε και χιόνισε;

Τετάρτη

o

e

και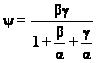

με ΑΒ=6cm cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

cm

δ) 7,2 cm.

112. Έστω οι φυσικοί αριθμοί α και β, με β0 και α < β. Αν αυξήσουμε τον αριθμητή και τον παρανομαστή του κλάσματος κατά 2, δημιουργώ-ντας το κλάσμα

με cm Άρα:

cm

β)   cm

γ)   cm

δ) 5 cm

cm

cm

cm

cm

cm

cm

cm

cm

είναι ίσο με

cm

cm

cm

cm

. Η γωνία

121. Αν διπλασιάσουμε την ακτίνα R της βάσης κυλίνδρου με ύψος υ τότε το εμβαδό Ε_Π της παράπλευρης επιφάνειάς του

cm

cm

cm

cm

cm

cm

cm

cm

cm

είναι ίσο με

128. Στη σειρά αυτή ποιο είναι το επόμενο νούμερο; 2, Α, 9, Β, 6, C, 13, D, …

παίρ­νει καθένας από τούς τρεις συνεργάτες του (πού παίρνουν ίσα μερίδια). Πόσο τοι` 929e48j 2; εκατό από το σύνολο των εισπράξεων παίρνει ο Παπαδόπουλος;

cm

cm

cm

cm

cm

U

134. Το πλήθος των α) διψήφιων αρτίων αριθμών, β) διψήφιων περιττών αριθμών, γ) διψήφιων περιττών αριθμών με διαφορετικά ψηφία και δ) διψήφιων αρτίων αριθμών με διαφορετικά ψηφία, είναι αντίστοι` 929e48j 7;α:

ιππόδρομο, όπου ο Κώστας έχασε 68.000 ευρώ στις πρώτες δύο κούρσες, χάνοντας 6.000 ευρώ περισ-σότερες στη δεύτερη κούρσα απ' ότι στην πρώτη. Στη δεύτερη κούρσα, ο Γιώργος έ­χασε 4.000 ευρώ. περισσότερες απ' ότι ο Κώστας. Πόσα έχασε ο Γιώργος στη δεύτερη κούρσα;

, τότε

x

x

.

β) 1≤ημθ<∞.

152. Ένα κουτί περιέχει 30 καραμέλες με χρώματα κόκκινο, κίτρινο, μπλε. Αν η πιθανότητα να πάρουμε μπλε και κόκκινη καραμέλα από το κουτί είναι 1/6 και 1/3 αντίστοι` 929e48j 7;α, οι κίτρινες καραμέλες είναι:

153. Το εμβαδό Ε σφαιρικής επιφάνειας με ακτίνα R είναι

α) 2πR².

β) 4πR².

γ) 4π²R.

δ) πR².

159. Τρεις αριθμοί είναι ανάλογοι του 7, 8 και 12 αντίστοι` 929e48j 7;α αν το άθροισμά τους είναι 108 τότε δύο από αυτούς έχουν διαφορά

160. Ένα δωμάτιο σχήματος παραλληλεπιπέδου έχει διαστάσεις βάσης 5,3 m αντίστοι` 929e48j 7;α αν το ύψος του είναι 2,5 m τότε ο όγκος του είναι

α) 3,75 m³.

β) 379 m³.

γ) 375 m³.

δ) 37500 lt.

x x

x

x

α) Α΄(-3, 2).

β) Α΄(3, -2).

γ) Α΄(-3, -2).

δ) Α΄(2, 3).

xx

x

xx

f x x

xx

x xx

είναι

x x

cm και ύψος 6 cm. Η πλευρά που αντιστοι` 929e48j 7;εί σε αυτό το ύψος είναι

α) 4 cm.

β) 5 cm.

γ) 3 cm.

δ) 6 cm.

O αριθμός e

cm cm

6.

παραπάνω.

, έχει μήκος:

β) .

206. Αν το εμβαδό Ε_ολ της ολικής επιφάνειας κύβου είναι 54 cm² τότε το μήκος μιας ακμής του α είναι σε cm:

207. Αν το εμβαδό της βάσης ορθογωνίου παραλληλεπιπέδου είναι 4 m² και το ύψος του 2 m τότε ο όγκος του είναι σε m³ :

208. Αν το ύψος υ πυραμίδας διπλασιάζεται, τότε ο όγκος της V

209. Αν τριπλασιάσουμε το ύψος υ κυλίνδρου με ακτίνα βάσης R τότε ο όγκος του

210. Αν υποδιπλασιάσουμε το ύψος υ κυλίνδρου με ακτίνα βάσης R, τότε το εμβαδό Ε_Π της παράπλευρης επιφάνειάς του

της παράπλευρης επιφανείας κώνου με ακτίνα βάσης 2 και παράπλευρο ύψος 3 είναι:

212. Αν διπλασιάσουμε την ακτίνα R σφαιρικής επιφάνειας, τότε το εμβαδό της Ε

cm

cm

β) 10π cm

cm

cm

.

.

Α=9000 €, Β=6.000 €, Γ=4.000 €.

220. Βρείτε το πλήθος των διψήφιων θετικών ακεραίων, τέτοι` 929e48j 9;ν ώστε κάθε ψηφίο να είναι μικρότερο του προηγουμένου ψηφίου:

x

0).

0).

5).

3).

x x

x x

πάντα.

πάντα.

m m m

235. Στη σειρά αυτή ποιο είναι το επόμενο νούμερο; 90, 85, 75, 60, 40, ….

m

m

m

m

να επίπεδο.

είναι 144^ο και η εξωτερική γωνία της είναι 150^ο τότε η γωνία του τριγώνου είναι:

243. Οι κρουνοί (βρύσες) Κ₁ και Κ₂ παρέχουν νερό σε μία δεξαμενή Δ, ενώ ο κρουνός Κ₃ την αδειάζει. Ο Κ₁ έχει παροχή 3 λίτρα το δευτερόλεπτο και ο K₂ έχει παροχή 1,5 λίτρα το δευτερόλεπτο. Ο Κ₃ έχει παροχή 2 λίτρα το δευτερόλεπτο και, όταν η δεξαμενή είναι γεμάτη, την αδειάζει σε μισή ώρα. Αν η δεξαμενή περιέχει νερό κατά τα 2/3 της και ανοίξουμε ταυτόχρονα τους κρουνούς Κ₁ , Κ₂ και Κ₃, πόσος χρόνος απαιτείται για να γεμίσει;

α)  

β)

γ)

.

i ii) 1, 2, 6, 24, οι αριθμοί που έχουν σειρά είναι αντίστοι` 929e48j 7;α :

x x

της παράπλευρης επιφάνειας κύβου ακμής 4 είναι:

266. Τρία παιδιά 5, 8, 10 χρόνων αντίστοι` 929e48j 7;α μοιράστηκαν 46 ευρώ ανάλογα με την ηλικία τους. Τότε

267. Αν διπλασιάσουμε την ακτίνα R της βάσης κώνου και υποδιπλασιάσουμε το παράπλευρο ύψος του h, τότε το εμβαδό Ε_Π της παράπλευρης επιφάνειάς του

268. Έχουμε τη συνάρτηση . Πώς θα μεταβληθεί η συνάρτηση αν διπλασιάσουμε το χ και υποδιπλασιάσουμε το y

x x

, τότε το ισούται με

α) 1980 m.

β) 1950 m.

γ) 1985 m.

δ) 2005 m.

x x x και ψ΄ψ αντίστοι` 929e48j 7;α στα σημεία:

.

ένα χωράφι σε 6 ημέρες. 5 θεριστές σε πόσες ημέρες μπορούν να θερίσουν ένα ίδιο χωράφι;

της προσθέτονται. Από το άθροισμα αυτό αφαιρείται το του και μένει υπόλοιπο 10. Η αρχική ποσότητα είναι:

5.

291. Αν για το θετικό αριθμό x ισχύει: , τότε ο x είναι ίσος με:

292. Ένα τρίγωνο έχει πλευρές 5, 12, 13 cm αντίστοι` 929e48j 7;α. Συνεπώς το τρίγωνο είναι

και είναι άριστες;

f x x

XXVI

Για ποιες τιμές του χ και ψ ισχύει η σχέση: ;

x>-1 και ψ>2.

x

γ) Για .

x και για ψ>2.

Οι Γ και Β δεν αγόρασαν κούρσα.

δεν αγόρασαν μεταχειρισμένα αυτοκίνητα.

2) 8/3 , 3) 2/3 , 4) 21/25 , 5) 4/10 , 6) 2/6, από το μικρότερο προς το μεγαλύτερο είναι:

f x x

cm

. Η γωνία

cm

cm

cm

cm

cm

316. Μια εγγεγραμμένη γωνία φ αντιστοι` 929e48j 7;εί σε τόξο 60^ο. Πόσες μοίρες είναι η γωνία αυτή;

h

h

h

h

319. Ο όγκος V σφαιρικής επιφάνειας με ακτίνα R

R

R

R

R

320. Ο Ιωάννης και ο Θεοφύλακτος βαδίζουν μαζί την ίδια απόσταση. Κάθε τρία βήματα του Θεοφύλακτου, αντιστοι` 929e48j 7;ούν σε τέσσερα βήματα του Ιωάννη. Αν το κάθε βήμα του Ιωάννη είναι ίσο με μισό μέτρο (m), τότε η απόσταση που διανύει ο Θεοφύλακτος κάνοντας 18 βήματα, είναι:

με

είναι ίση με

είναι ίση με

είναι ίση με

327. Ουδέτερο στοι` 929e48j 7;είο της πρόσθεσης είναι

τότε η περίμετρος του τριγώνου είναι:

cm

cm

x x

x x

x x

cm χωράνε σε ένα ισόπλευρο τριγωνικό ταψί πλευράς 30 cm;

Τέσσερις φίλοι, η Άννα, ο Βασίλης, ο Γιώργος και ο Δημήτρης, έκα­ναν σκοποβολή σε τρεις στόχους Α, Β, Γ, που η πετυχημένη βολή στον κα­θένα δίνει διαφορετικό αριθμό πόντων. Ο καθένας έκανε δύο πετυχημέ­νες βο­λές. Η Άννα πέτυχε τους στόχους Α και Β συγκεντρώνοντας 28 πό­ντους, ο Βασί­λης τους στόχους Β και Γ συγκεντρώνοντας 37 πόντους, ο Γιώργος τους στό­χους Α και Γ συγκεντρώνοντας 33 πόντους και ο Δημή­τρης πέ­τυχε δύο φορές το στόχο Α. Πόσους πόντους συγκέντρωσε ο Δη­μήτρης;

Πόσο είναι το 5% του ;

Τέσσερεις αθλητές ο Α, Β, Γ και Δ αγωνίστηκαν στο άθλημα του δρόμου των 1000 μέτρων.

Με την υπόθεση του προηγούμενου ερωτήματος και το δεδομένο ότι ο Α λέει αλήθεια και ο Β ψέματα με ποια σειρά τερμάτισαν ;

Ποιος από τους παρακάτω αριθμούς μπορεί να είναι πιθανό υπόλοιπο στη διαίρεση

Οι ερωτήσεις 341 έως 345 αναφέρονται στην παρακάτω πρόταση: Τέσσερεις φίλοι ο Α, Β, Γ και ο Δ παίρνουν πρωινό που αποτελείται από τυρί φέτα, κασέρι, σαλάμι και αυγό.

Επομένως φέτα και σαλάμι τρώει:

Σαλάμι και αυγό τρώει ο

Φέτα και κασέρι τρώει ο

Κασέρι και αυγό τρώει ο

Φέτα και αυγό τρώει:

346. Πόσες λύσεις έχει η εξίσωση: ;

x z x z

αντίστοι` 929e48j 7;α, δημιουργώντας έτσι στο εσωτερικό του τριγώνου 16 τετράπλευρα ή τρίγωνα.

α) 81 περιοχές.

β) 111 περιοχές.

γ) 121 περιοχές.

δ) 169 περιοχές.

350. Ποιο είναι το άθροισμα της πρόσθεσης:

β) .

353. Ποιο είναι το υπόλοιπο της διαίρεσης

357. Η συνάρτηση

Αν , τότε τα α και β είναι:

361. Το πεδίο ορισμού της συνάρτησης είναι:

α) .

β) .

γ) .

δ) .

362. Αν , τότε

α) .

β) .

γ) .

Aναμιγνύουμε 30 kg κρασί αξίας 2 ευρώ το κιλό με 60 kg

f είναι γνησίως αύξουσα στο , τότε η εξίσωση f x

Aν τότε

α)

β)

γ)

δ)

366. Η απόσταση των σημείων Α(1, 1) και Β(2, -3) είναι

β) .

γ) .

367. Το τετράγωνο ενός περιττού αριθμού και η διαφορά των τετραγώνων δύο διαδοχικών περιττών αριθμών είναι αντίστοι` 929e48j 7;α

β) Α>1.

γ) .

δ) Α<1.

369. Το σημείο τομής των γραφικών παραστάσεων των συναρτήσεων και είναι:

cm

372. Έστω και . Τότε ισχύει:

α)

β)

γ)

x και ψ ισχύει:

x

x

D

D D_x D

D=0 και ( ή ).

375. Η εξίσωση

x

δ) ίση με .

α) 60⁰

β) 90⁰

α) Δύο τρίγωνα είναι ίσα όταν έχουν δύο πλευρές και μια γωνία ίσες.

γ) Δύο τρίγωνα είναι ίσα όταν έχουν τρείς πλευρές ίσες μία προς μία.

385. Ένα τραπέζιο έχει βάση μικρή 5 cm και βάση μεγάλη 11 cm τότε η διάμεσός του είναι:

α) 8 cm

β) 9 cm

γ) 7 cm

386. Ένας χάρτης είναι κατασκευασμένος με κλίμακα 1 προς 500000. Αν δύο πόλεις απέχουν στο χάρτη 5 cm ποια είναι η πραγματική τους απόσταση;

α) 250 km

β) 2,5 km

γ) 25 km

δ) 2500 km

β)

δ)

προέρχεται από ένα πολύ γνωστό θεώρημα της Γεωμετρίας

x 4 τότε τα αυτοκίνητα, τα μηχανάκια και τα τρακτέρ αντίστοι` 929e48j 7;α ήταν;

394. Ποιους αριθμούς με άθροισμα 51 πρέπει να προσθέσω στους αριθμητές των κλασμάτων 2/3, 1/6 αντίστοι` 929e48j 7;α, ώστε το πρώτο κλάσμα αυξημένο κατά 2 να μας δίνει το δεύτερο ελαττωμένο κατά 5;

Ένα φορτηγό ζυγίζει 2 τόνους και ¾ του φορτηγού. Πόσο ζυγίζει το φορτηγό;

t

t

t

t

t

min min

min min

h h

h h

δ) τα στοι` 929e48j 7;εία είναι ανεπαρκή για να συγκρίνουμε τα κεφάλαια.