FIZIKA (MFA101, 3 kp)

Mācību prieksmeta apjoms: lekcijas - 32 st., laboratorijas nodarbības - 16 st., kopa - 48 st.

Kontrole - eksāmens

Prieksmeta saturs.

Ievads. Materiāla punkta kinemātika. Fizikas prieksmets un tā sakars ar citām zinātnēm. Mehāniskā kustība. Atskaisu sistēmas. Materiāls punkts. Trajektorija, pārvietojums un ceļs. Ātrums un paātrinājums. Sakars starp kustību raksturojosiem lineāriem un leņķiskiem lielumiem.

Materiāla punkta dinamika. Ņūtona likumi. Impulss, tā nezūdamības likums. Spēku veidi mehānikā: elastības spēks, berzes spēks, gravitācijas spēks. Jēdziens par spēku lauku. Gravitācijas lauks un tā intensitāte. Smaguma spēka lauks ap Zemi.

Darbs. Mainīga spēka darbs. Jauda. Konservatīvie un nekonservatīvie spēki. Kinētiskā enerģija. Potenciālā enerģija. Sakars starp spēku un potenciālo enerģiju. Lauka potenciāls un tā gradients. Elastīgi deformēta ķermeņa enerģija. Ķermeņu sistēmas pilnā mehāniskā enerģija. Enerģijas nezūdamības likums mehānikā.

Cieta ķermeņa dinamika. Jēdziens par absolūti cietu ķermeni. Ķermeņa translācijas un rotācijas kustība. Cieta ķermeņa masas (inerces) centrs. Spēka moments. Inerces moments. Steinera teorēma. Impulsa moments, tā nezūdamības likums. Ziroskopiskais efekts. Rotējosa ķermeņa kinētiskā enerģija. Spēka momenta darbs rotācijas kustībā.

Mehāniskās svārstības. Periodiska kustība. Harmoniskas svārstības, to raksturojosie lielumi: amplitūda, fāze, frekvence, periods. Harmonisko svārstību vienādojums. Harmonisko svārstību dinamika. Atsperu, matemātiskais un fizikālais svārsts. Harmonisko svārstību kinētiskā, potenciālā un pilnā enerģija. Vienā virzienā vērstu harmonisko svārstību saskaitīsana. Savstarpēji perpendikulāru harmonisko svārstību saskaitīsana. Rimstosas svārstības, rimsanu raksturojosie lielumi. Rezonanse.

Mehāniskie viļņi. Viļņu veidosanās, garenviļņi un sķērsviļņi. Viļņu virsma un viļņu fronte. Heigensa princips. Plakana viļņa vienādojums. Viļņa garums. Superpozīcijas princips. Koherenti viļņu avoti. Viļņu interference. Stāvviļņi. Viļņu enerģija. Umova vektors.

Inerciālas un neinerciālas atskaites sistēmas. Galileja transformāciju formulas. Relativitātes princips mehānikā. Inerces spēks.

Speciālās relativitātes teorijas elementi. Einsteina postulāti. Lorenca transformāciju formulas. Garuma un laika intervāla relativitāte. Ātrumu saskaitīsanas likums. Relatīvistiskā dinamika. Impulsa un enerģijas nezūdamības likumi. Savstarpējais sakars starp masu un enerģiju.

Termodinamiskās sistēmas. Ideālā gāze. Makroskopisku ķermeņu termodinamiskā un molekulāri kinētiskā pētīsanas metode. Sistēmas stāvoklis. Stāvokļa parametri. Līdzsvara un nelīdzsvara stāvoklis. Ideālā gāze, tās stāvokļa vienādojums.

Molekulāri kinētiskās teorijas fizikālie pamati. Gāzu molekulāri kinētiskās teorijas pamatvienādojums. Vienatomu molekulas vidējā translācijas kustības enerģija un tās sakars ar temperatūru. Vidējais kvadrātiskais ātrums. Brīvības pakāpju skaits. Daudzatomu molekulas vidējā enerģija. Ideālās gāzes ieksējā enerģija.

Gāzes molekulu ātrumu sadalījums. Sadalījuma funkcija. Maksvela sadalījums. Molekulu visvarbūtiskais, vidējais aritmētiskais un relatīvais ātrums. Ideālā gāze smaguma spēku laukā. Bocmaņa sadalījums. Maksvela-Bocmaņa sadalījums.

Pārneses procesi. Molekulu savstarpējā sadursme. Molekulu efektīvais diametrs. Molekulu vidējais brīvā ceļa garums. Difūzija, viskozitāte un siltumvadītspēja gāzēs. Difūzijas, viskozitātes un siltumvadītspējas eksperimentālie likumi. Difūzijas, viskozitātes un siltumvadītspējas koeficientu aprēķināsanas molekulāri kinētiskā teorijā.

Termodinamiskie pamati. Līdzsvara un nelīdzsvara procesi. Pirmais termodinamikas likums. Ideālās gāzes siltumietilpība. Izoprocesi. Adiabātisks process. Gāzes veiktais darbs dazādos izoprocesos.

Cikliskie procesi. Siltuma un aukstuma masīnas. Karno ideālas siltummasīnas cikls un tā lietderības koeficients. Otrais termodinamikas likums.

Entropija. Neatgriezeniskie procesi. Entropija. Entropijas izmaiņa atgriezeniskos un neatgriezeniskos procesos. Stāvokļu varbūtība. Entropijas un stāvokļu varbūtības savstarpējais sakars. Otrā termodinamikas likuma statistiskā jēga.

Reālas gāzes. Van der Vālsa vienādojums. Van der Vālsa izotermas. Kristāliskais stāvoklis. Kristāliskie parametri. Reālas gāzes ieksējā enerģija.

Sķidrumi. Sķidrumu struktūra. Siltumkustības raksturs sķidrumos. Sķidrumu virskārta. Virsmas spraigums. Slapināsana. Malas leņķis. Laplasa formula. Kapilaritāte.

Cieti ķermeņi. Kristāliskie un amorfie ķermeņi. Cietu ķermeņu termiskā izplesanās un siltumietilpība. Dilonga un Pti likums. Kvantu oscilators. Einsteina un Debaja siltumietilpības kvantu teorija. Fenoni.

Vielas agregātstāvokļi. Fāze. Fāzu līdzsvara nosacījums. Stāvokļu diagramma. Trīskārsais punkts. I un II veida fāzu pārejas.

Elektriskais lauks vakuumā. Ķermeņu elektriskās īpasības. Elementārlādiņs. Lādiņa nezūdamības likums. Kulona likums. Elektriskais lauks. Lauka intensitāte. Lauku superpozīcijas princips. Intensitātes vektora plūsma. Ostrogradska-Gausa teorēma. Lādētu ķermeņu elektriskā lauka intensitātes aprēķins.

Elektriskā lauka spēka darbs, pārvietojot lādiņus. Lauka intensitātes vektora cirkulācija. Potenciāls. Elektriskā lauka intensitātes un potenciāla savstarpējais sakars. Punktveida lādiņa lauka potenciāls. Elektriskais lauks lādēta vadītāja ieksienē. Lādiņu sadalījums vadītājos.

Vadītāji elektriskajā laukā. Elektriskā lauka enerģija. Vadītāji elektriskajā laukā. Vadītāju elektriskā kapacitāte. Kondensatori. Lādiņu sistēmas enerģija. Lādēta vadītāja enerģija. Lādēta kondensatora enerģija. Elektrostatiskā lauka enerģija, enerģijas blīvums.

Elektriskais lauks dielektriķos. Brīvie un saistītie lādiņi. Elektriskais dipols. Elektriskais dipolmoments. Dipols homogēnā elektriskajā laukā. Polāras un nepolāras molekulas. Dielektriķu polarizācija. Polarizācijas vektors. Elektriskā nobīde. Segnetoelektriķi.

Strāvas stiprums, blīvums. Strāvas eksistences nosacījumi. Potenciālu starpība, elektrodzinējspēks, spriegums.

Homogēns ķēdes posms. Oma likums integrālā un diferenciālā formā.

Oma likums nehomogēnam ķēdes posmam integrālā un diferenciālā formā. Oma likums noslēgtai ķēdei. Sazarotas ķēdes. Kirhofa likumi.

Metālu klasiskā elektronu teorija un tās pielietojamības robezas. Videmana-Franca likums.

Laboratorijas darbi

1. Rotācijas kustības pētīsana ar Oberbeka iekārtu.

2. Rimstoso svārstību pētīsana ar atsperes svārstu.

3. Gāzes siltumietilpību attiecības noteiksana

4. Elektriskā lauka pētīsana.

Literatūra.

Jansone M., Kalnača A., Blūms I., Ķiploka A., Klemenovs I., Medvids M., Knite M. Uzdevumu krājumi vispārīgajā fizikā. R.: RTU, 2000. - 248 lpp.

Jansons L., Zambrāns A., Badūns A., Jansone A. Fizikas praktikums, R.: Zvaigzne, 1979., - 504.lpp.

Klincāre I. Fizikas praktikums tehniskās universitātes studentiem. - R.: RTU, 2001. - 188 lpp

Miglans V. Laboratorijas darbu apraksts. - Rīga: RTU, 2003..- 36 lpp

Uzdevumu krājums fizikā I daļa /Mehānika, mehāniskas svārstības un molekulārfizika./ - Sast. V. Miglans, R.: RTU, 2001. - 52 lpp.

Valters A. Fizika . R.: Zvaigzne, 1992. - 643. lpp.

: T. 1-3. - M

1 kontroldarbs

Uzdevumu numuri un kontroldarbu varianti

2 kontroldarbs

Uzdevumu numuri un kontroldarbu varianti

3 kontroldarbs

Uzdevumu numuri un kontroldarbu varianti

Kinemātika

1-1. Cik ilgā laikā ķermeņa ātrums no 8 m/s var samazināties līdz l m/s ja paātrinājums ir -2 m/s² ? [3.5 s].

1-2. Ar cik lielu paātrinājumu kustas ķermenis, ja kustības sestajā sekundē tā veiktais attālums ir 1.1 m? Cik lielu attālumu sis ķermenis veiks sesās sekundēs? [0.2 m/s²; 3.6 m].

1-3. Cik liels sakuma ātrums vertikāli lejup jāpiesķir lodītei, lai tā no 57 m augstuma nokristu 3 sekundēs? [4 m/s].

1-4. Divas sekundes pēc ķermeņa A krisanas sākuma no tā pasa augstuma uz leju sviez ķermeni B. Cik liels ātrums jāpiesķir ķermenim B, lai tas pēc t sekundēm no sava krisanas sākuma panāktu ķermeni A? .

1-5. Ķermeni sviez vertikāli augsup ar ātrumu 30 m/s. Pēc cik sekundēm ķermenis atradīsies 40 m augstumā, un cik liels tad būs tā ātrums? [2 s; 4 s; 10 m/s].

1-6. Ar cik lielu ātrumu jāsviez ķermenis vertikāli augsup, lai tas 10 m augstumu sasniegtu ar ātrumu 5 m/s? Cik ilgā laikā ķermenis so augstumu sasniedz? Pēc cik ilga laika no izsviesanas mirkļa ķermenis nokritīs zemē? [15 m/s; l s; 3 s].

1-7. Divus ķermeņus izsviez vertikāli augsup ar ātrumu 40 m/s un 30 m/s. Pēc cik ilga laika attālums starp ķermeņiem būs 5 m? [0.5 s].

1-8. Ķermenis A izsviests vertikāli augsup ar ātrumu 30 m/s. Izsviesanas brīdī no punkta, kas atrodas ķermeņa A maksimāla pacelsanās augstumā, sāk krist ķermenis B. Cik augstu no zemes un pēc cik ilga laika ķermeņi sastapsies? [33.75m; 1.5s].

1-9. Laiva kustas perpendikulāri krastam ar ātrumu 7.2 km/h. Straume aiznes laivu 150 m lejup pa upi. Aprēķināt: 1) upes straumes ātrumu un 2) laiku, kas jāpatērē, pārceļoties pāri upei. Upes platums 0.5 km. [1) 0.6 m/s; 2) 250s].

1-10. Vertikāli augsup sviests akmens sasniedz 10 m augstumu. 1) Pēc cik ilga laika tas nokrīt zemē? 2) Kādā augstumā paceļas akmens, ja tā sākuma ātrumu palielina divas reizes? Gaisa pretestību neievērot. [1) 2.9 s; 2) 40 m].

1-11. Ķermenis, kura sākuma ātrums ir nulle, vertikāli krīt no augstuma h = 19.6 m. Cik ilgā laikā ķermenis noiet: 1) sava ceļa pirmo l m; 2) sava ceļa pēdējo l m? Gaisa pretestību neievērot. [1) 0.45 s; 2) 2 s; 0.05 s].

1-12. Ķermeni A izsviez vertikāli augsup ar sākuma ātrumu v/, ķermenis K krīt no augstuma h ar sākuma ātrumu v₂= 0. Atrast ķermeņu A un B attāluma x atkarību no laika t, ja zināms, ka ķermeņi sāk kustēties vienlaicīgi. [h/v₁]

1-13. No torņa, kura augstums H = 25 m, horizontālā virzienā tiek sviests akmens ar ātrumu v₀ = 15 m/s. Aprēķināt: 1) cik ilgi akmens atrodas kustībā; 2) kādā attālumā s no torņa pamata tas nokrīt zemē; 3) ar kādu ātrumu v tas nokrīt zemē; 4) kādu leņķi (p veido akmens trajektorija ar horizontu nokrisanas punktā. Gaisa pretestību neievērot. [1) 2.26 s; 2) 33.9 m; 3) 22.1 m/s; 26.7 m/s; 4) 55°48'].

1-14. Horizontālā virzienā sviests akmens nokrīt zemē pēc 0.5 sekundēm 5 m attālumā no izsviesanas vietas. 1) No kāda augstuma h akmens sviests? 2) Ar kādu sākuma ātrumu v₀ tas sviests? 3) Ar kādu ātrumu v tas nokrīt zemē? 4) Kādu leņķi (p veido akmens trajektorija ar horizontu nokrisanas punktā. Gaisa pretestību neievērot. [1) 1.22 m; 2) 10 m/s; 3) 11.1 m/s; 4) 26°12'].

1-15. Horizontālā virzienā mesta rotaļu bumba atsitas pret sienu, kas atrodas 5 m attālumā no mesanas vietas. Bumbas atsitiena vietas augstums ir par l m mazāks nekā tās vietas augstums, no kuras bumba mesta. 1) Ar kādu ātrumu v₀ bumba mesta? 2) Kādā leņķī φ bumba atsitas pret sienu? Gaisa pretestību neievērot. [1) 11.1 m/s; 2) 68°12'].

1-16. Akmens izsviests horizontālā virzienā. Pēc 0.5 s no kustības sākuma akmens ātruma skaitliskā vērtība ir l .5 reizes lielāka par tā sākuma ātrumu. Aprēķināt akmens sākuma ātrumu. Gaisa pretestību neievērot. [4.4 m/s].

1-17. Akmens izsviests horizontālā virzienā ar ātrumu v_x = 15 m/s. Aprēķināt akmens normālo un tangenciālo paātrinājumu l s pēc kustības sākuma. Gaisa pretestību neievērot. [5.4 m/s²; 8.2 m/s²].

1-18. Akmens izsviests horizontālā virzienā ar ātrumu 10 m/s. Aprēķināt akmens trajektorijas liekuma rādiusu 3 s pēc kustības sākuma. Gaisa pretestību neievērot. [305 m].

1-19. Rotaļu bumbu met ar ātrumu v₀ = 10 m/s virzienā, kas veido ar horizontu leņķi α = 40°. Aprēķināt: 1) kādā augstumā s_y paceļas bumba; 2) kādā attālumā no mesanas vietas bumba sasniedz zemi; 3) cik ilgi tā atrodas kustībā? Gaisa pretestību neievērot. [1) 2.1 m; 2) 10.0 m; 3) 1.3 s].

1-20. Ķermeni izsviez slīpi pret horizontu ar ātrumu v₀. Lidojuma ilgums t = 2.2 s. Atrast sā ķermeņa vislielāko pacelsanās augstumu. Gaisa pretestību neievērot. [5.9 m].

1-21. Akmens izsviests ar ātrumu v₀ = 12 m/s virzienā, kas ar horizontu veido α = 45°, un tas nokrīt zemē attālumā s

no izsviesanas vietas. No kāda augstuma h ar tādu pasu sākuma ātrumu jāsviez akmens horizontālā virzienā, lai tas nokristu tajā pasā vietā? [7.4 m].

1-22. Ķermenis izsviests ar ātrumu v ₀ 14.7 m/s virzienā, kas ar horizontu veido leņķi α = 30°. Aprēķināt ķermeņa normālo un tangenciālo paātrinājumu pēc t = 1.25 s no kustības sākuma. Gaisa pretestību neievērot. [3.52 m/s²; 9.15 m/s²].

1-23. Ķermenis izsviests ar ātrumu v₀ = 10 m/s virzienā, kas ar horizontu veido leņķi α = 45°. Aprēķināt ķermeņa trajektorijas liekuma rādiusu pēc t = l s no kustības sākuma. Gaisa pretestību neievērot. [6.3 m].

1-24. Ķermenis izsviests ar ātrumu v₀ virziena, kas ar horizontu veido leņķi α . Aprēķināt lielumus v₀ un a , ja zināms, ka ķermeņa vislielākais pacelsanās augstums h = 3 m un ķermeņa trajektorijas liekuma rādiuss R trajektorijas augsējā punktā ir 3 m. Gaisa pretestību neievērot. [9.4 m/s; 54°44'].

1-25. No torņa, kura augstums H = 25 m, met akmeni ar ātrumu v₀ = 15 m/s virzienā, kas ar horizontu veido leņķi a = 30°. Aprēķināt: 1) cik ilgi akmens atrodas kustībā; 2) kādā attālumā no torņa pamata tas nokrīt zemē; 3) ar kādu ātrumu tas nokrīt zemē; 4) kādu leņķi (p veido akmens trajektorija ar horizontu nokrisanas punktā. Gaisa pretestību neievērot. [1) 3.16 s; 2) 41.1 m; 3) 26.7 m/s; 4) 61°].

Ķermeņa noietā ceļa i atkarību no laika t izsaka vienādojums s = At- Bt² + Ct³, kur A = 2 m/s, B = 3 m/s² un C = 4 m/s³. Aprēķināt: 1) ātruma v un paātrinājuma a atkarību no laika t; 2) ķermeņa noieto ceļu, ātrumu un paātrinājumu 2 s pēc kustības sākuma. Konstruēt ceļa, ātruma un paātrinājuma grafiku intervālā 0 < t < 3 s pēc katrām 0.5 s. [1) v = (2 - 6t + 12t²) m/s; a = -6 + 24t) m/s²; 2) 24 m; 38 m/s; 42 m/s²].

Ķermeņa noietā ceļa s atkarību no laika t izsaka vienādojums s = A - Bt + Ct², kur A = 6 m, B = 3 m/s un C = 2 m/s². Atrast ķermeņa vidējo ātrumu un vidējo paātrinājumu laika intervālā no l s līdz 4 s. Konstruēt ceļa, ātruma un paātrinājuma grafiku intervālā 0 < t < 5 s pēc katras sekundes. [7 m/s; 4 m/s²].

1-28. Ķermeņa noietā ceļa s atkarību no laika t izsaka vienādojums s = A + Bt + Ct², kur A - 3 m, B = 2 m/s un C = l m/s². Atrast ķermeņa vidējo ātrumu un vidējo paātrinājumu tā kustības pirmajā, otrajā un tresajā sekundē. [3 m/s; 5 m/s; 7 m/s; 2 m/s²; 2 m/s²; 2 m/s² ].

1-29. Ķermeņa noietā ceļa s atkarību no laika t izsaka vienādojums s = A + Bt + Ct² + Dt³, kur C = 0.14 m/s², D = 0.01 m/s³. 1) Pēc cik ilga laika no kustības sākuma ķermeņa paātrinājums ir l m/s²? 2) Kāds ir ķermeņa vidējais paātrinājums sajā laika sprīdī? [1) 12 s; 2) 0.64 m/s²].

1-30. Ass, uz kuras nostiprināti divi diski attālumā l = 0.5 m viens no otra, griezas ar leņķisko ātrumu, kas atbilst frekvencei v = 1600 apgr./min. Lode, lidojot paralēli asij, caursauj abus diskus; pie tam izsautais caurums otrajā diskā attiecībā pret pirmā diska caurumu novirzīts par leņķi (φ = 12°. Aprēķināt lodes ātrumu. [400 m/s].

1-31. Aprēķināt rotējosa riteņa rādiusu, ja zināms, ka lineārais ātrums v_; punktam, kas atrodas uz riteņa aploces, ir 2.5 reizes lielāks par lineāro ātrumu punktam, kas atrodas par 5 cm tuvāk riteņa asij. [8.33 cm].

1-32. Ritenis, rotējot vienmērīgi paātrināti, sasniedz leņķisko ātrumu ω = 20 rad/s pēc N = 10 apgr. no kustība sākuma. Aprēķināt riteņa leņķisko paātrinājumu. [3.2 rad/s²].

1-33. Spararats pēc t = l min. no rotācijas sākuma sasniedz ātrumu, kas atbilst frekvencei v = 720 apgr./min. Aprēķināt spararata leņķisko paātrinājumu un apgriezienu skaitu sajā minūtē. Uzskatīt, ka kustība ir vienmērīgi paātrināta. [1.26 rad/s²; 360 apgr.].

1-34. Bremzējot riteņa griesanos, tā ātrums l min. laikā vienmērīgi palēnināti samazinās no 300 apgr./min. līdz 180 apgr./min. Aprēķināt riteņa leņķisko paātrinājumu un sajā laikā izdarīto apgriezienu skaitu. [-0.21 rad/s²; 240 apgr.].

1-35. Ventilators griezas ar ātrumu, kas atbilst frekvencei 900 apgr./min. Pēc ventilatora izslēgsanas tas turpina griezties vienmērīgi palēnināti un līdz apstāsanās momentam izdara 75 apgriezienus. Pēc cik ilga laika, skaitot no izslēgsanas momenta, ventilators apstājas? [10s].

1-36. Vārpsta griezas ar pastāvīgu ātrumu, kas atbilst frekvencei 180 apgr./min. Sākot ar kādu momentu, vārpstu bremzē un tā griezas vienmērīgi palēnināti ar leņķisko paātrinājumu 3 rad/s². 1) Pēc cik ilga laika vārpsta apstājas? 2) Cik apgriezienu tā izdara līdz apstāsanās momentam? [1) 6.3 s; 2) 9.4 apgr.].

1-37. Punkts kustas pa riņķa līniju, kuras rādiuss R = 20 cm, ar pastāvīgu tangenciālo paātrinājumu a_τ = 5 cm/s². Pēc cik ilga laika no kustības sākuma sā punkta normālais paātrinājums a_n ir; 1) vienāds ar tangenciālo paātrinājumu; 2) divas reizes lielāks par tangenciālo paātrinājumu? [1) 2 s; 2) 2.8 s].

1-38. Punkts kustas pa riņķa līniju, kuras rādiuss R = 10 cm, ar pastāvīgu tangenciālo paātrinājumu a_τ. Aprēķināt punkta tangenciālo paātrinājumu a_τ, ja zināms, ka pēc piektā apgrieziena punkts sasniedz ātrumu v = 79.2 cm/s. [0.1 m/s²].

1-39. Punkts kustas pa riņķa līniju, kuras rādiuss R = 10 cm, ar pastāvīgu tangenciālo paātrinājumu a_τ. Aprēķināt punkta normālo paātrinājumu a_n pēc t = 20 s no kustības sākuma, ja zināms, ka pēc piektā apgrieziena punkta lineārais ātrums v = 10 cm/s. [0.01 m/s ].

1-40. Pirmajā tuvinājumā var pieņemt, ka elektrons ūdeņraza atomā kustas pa riņķveida orbītu ar pastāvīgu ātrumu v. Aprēķināt, ar kādu leņķisko ātrumu elektrons riņķo ap kodolu un kāds ir tā normālais paātrinājums. Pieņemt, ka orbītas rādiuss r = 0.5∙10^-10 m un elektrona ātrums pa so orbītu v = 2.2∙l0^-6 m/s. [4.4∙10^-16 rad/s; 9.7-10²² m/s²].

1-41. Ritenis, kura rādiuss R = 10 cm, griezas ar pastāvīgu leņķisko paātrinājumu ε = 3.14 rad/s². Aprēķināt pirmās sekundes beigās riteņa aploces punkta griesanās: 1) leņķisko ātrumu; 2) lineāro ātrumu; 3) tangenciālo paātrinājumu; 4) normālo paātrinājumu; 5) pilno paātrinājumu un 6) leņķi, ko veido pilnā paātrinājuma virziens ar riteņa rādiusu. [1) 3.14 rad/s; 2) 0.314 m/s; 3) 0.314 m/s²; 4) 0.986 m/s²; 5) 1.03 m/s²; 6) 17°46'].

1-42. Punkts kustas pa riņķa līniju, kuras rādiuss R = 2 cm. Ceļa atkarību no laika izsaka vienādojums s = Ct³, kur C = 0.1 cm/s³. Aprēķināt punkta normālo un tangenciālo paātrinājumu momentā, kad punkta lineārais ātrums v = 0.3 m/s. [4.5 m/s²; 0.06 m/s²].

1-43. Punkts kustas pa riņķa līniju tā, ka ceļa atkarību no laika izsaka vienādojums s = A + Bt + Ct², kur A = 5 m, B = -2 m/s un C = l m/s². Aprēķināt punkta lineāro ātrumu, tā tangenciālo, normālo un pilno paātrinājumu pēc t = 3 s no kustības sākuma, ja zināms, ka pēc t' = 2 s punkta normālais paātrinājums a'_n = 0.5 m/s². [4 m/s; 2 m/s²; 2 m/s²; 2.83 m/s²].

1-44. Aprēķināt riteņa leņķisko paātrinājumu, ja zināms, ka pēc 2 sekundēm no vienmērīgi paātrinātas kustības sākuma aploces punkta pilnā paātrinājuma vektors veido ar sā punkta lineārā ātruma virzienu 60° leņķi. [0.43 rad/s²].

1-45. Ritenis griezas ar pastāvīgu leņķisko paātrinājumu ε = 2 rad/s². Pēc t = 0.5 s no kustības sākuma riteņa pilnais paātrinājums sasniedz a = 13.6 cm/s². Aprēķināt riteņa rādiusu. [6.1m].

1-46. Ritenis, kura rādiuss R = 0.1 m, griezas tā, ka riteņa rādiusa pagrieziena leņķa atkarību no laika izsaka vienādojums φ = A + Bt + Ct³, kur B = 2 rad/s un C = l rad/ s³. Aprēķināt, kāds pēc 2 s no kustības sākuma ir riteņa aploces punktu: 1) leņķiskais ātrums; 2) lineārais ātrums; 3) leņķiskais paātrinājums; 4) tangenciālais paātrinājums; 5) normālais paātrinājums. [1) 14 rad/s; 2) 1.4 m/s; 3) 12 rad/s²; 4) 1.2 m/s²; 5) 19.6 m/s²].

1-47. Ritenis, kura rādiuss R = 5 cm, griezas tā, ka riteņa rādiusa pagrieziena leņķa atkarību no laika izsaka vienādojums φ = A + Bt + Ct² + Dt³, kur D = l rad/s³. Aprēķināt riteņa aploces punktu tangenciālā paātrinājuma izmaiņu Δa_τ katrai kustības sekundei. [0.3 m/s²].

1-48. Ritenis, kura rādiuss R = 10 cm, griezas tā, ka riteņa aploces punktu lineārā ātruma atkarību no kustības laika izsaka vienādojums v = At + Bt², kur A = 3 cm/s un B = l cm/s². Aprēķināt leņķi, ko veido pilnā paātrinājuma vektors ar riteņa rādiusu momentos t = 0, l, 2, 3, 4 un 5 s, skaitot no kustības sākuma. [90°; 72°17'; 30°; 15°32'; 7°58'; 0].

1-49. Ritenis griezas tā, ka riteņa pagrieziena leņķa atkarību no laika izsaka vienādojums φ = A + Bt + Ct² + Dt³, kur B = l rad/s, C = l rad/s² un D = l rad/s³. Aprēķināt riteņa rādiusu, ja zināms, ka kustības otrās sekundes beigās aploces punktu normālais paātrinājums a_n = 3.46-10² m/s². [1.2 m].

1-50. Aprēķināt, cik reizu rotējosa riteņa aploces punkta normālais paātrinājums ir lielāks par tā tangenciālo paātrinājumu tajā momentā, kad sā punkta pilnā paātrinājuma vektors veido ar lineārā ātruma vektoru 30° leņķi. [0.58].

Translācijas kustības dinamika. Darbs, jauda enerģija, impulss

2-1. Cik smags balasts jāizsviez no aerostata, kas vienmērīgi nolaizas, lai tas ar tādu pasu ātrumu sāktu vienmērīgi pacelties? Aerostata svars kopā ar balastu ir 15.68 kN, aerostata cēlējspēks ir 11.76 kN. Pieņemt, ka gaisa pretestība pacelsanās un nolaisanās gadījumā ir vienāda. [7.8∙10³ N].

2-2. Noteikta diametra tērauda stieple iztur 4400 N slodzi. Kāds ir vislielākais paātrinājums, ar kuru var pacelt 3900 N lielu svaru, kas iekārts sajā stieplē, lai tā nepārtrūktu? [l .25 m/s²].

2-3. Diegā iekārts atsvars. Ja so atsvaru paceļ ar paātrinājumu a₁ = 2 m/s², tad diega sastiepuma spēks T ir divreiz mazāks par to sastiepuma spēku, kāds nepieciesams, lai diegs pārtrūktu. Ar kādu paātrinājumu a₂ jāpaceļ sis atsvars, lai diegs pārtrūktu? [13.8 m/s²].

2-4. Automobilis, kura svars ir 10⁴ N, bremzējot apstājas pēc 5 s, sajā laikā vienmērīgi palēnināti noejot 25 m. Aprēķināt: 1) automobiļa sākuma ātrumu; 2) bremzēsanas spēku. [1)10 m/s; 2) 2040 N].

2-5. Kāds spēks jāpieliek vagonam, kas stāv uz sliedēm, lai tas sāktu kustēties vienmērīgi paātrināti un laikā t = 30 s noietu ceļu s = 11 m? Vagona svars P = 15.5 kN. Kustības laikā uz vagonu darbojas berzes spēks, kas ir 0.05 no vagona svara. [8200 N].

2-6. Vilciens, kura svars ir 4.9∙10⁶ N, pēc lokomotīves vilcējspēka izbeigsanās 9.8∙10⁴ N liela berzes spēka iedarbībā apstājas pēc l min. Kāds bija vilciena ātrums? [ 11.75 m/s].

2-7. Vagons, kura masa ir 20 t, kustas ar pastāvīgu negatīvu paātrinājumu, kas skaitliski ir 0.3 m/s². Vagona sākuma ātrums 54 km/h. 1) Cik liels bremzēsanas spēks darbojas uz vagonu? 2) Pēc cik ilga laika vagons apstājas? 3) Kādu attālumu vagons noiet, līdz tas apstājas? [1) 6000 N; 2) 50 s; 3) 375 m].

2-8. Ķermenis, kura masa ir 0.5 kg, atrodas taisnvirziena kustībā, turklāt ķermeņa noietā ceļa i atkarību no laika t izsaka vienādojums s = A - Bt + Ct² - Dl³, kur C = 5 m/s² un D - 1 m/s³. Aprēķināt spēku, kas darbojas uz ķermeni kustības pirmās sekundes beigās. [2 N].

2-9. Pastāvīga spēka F = 9.8 N iedarbībā ķermenis kustas taisna virziena tā, ka ķermeņa noietā ceļa s atkarību no laika t izsaka vienādojums s = A - Bt + Ct². Aprēķināt ķermeņa masu, ja constante C = l m/s². [ 4.9 kg].

2-10. Ķermenis, kura masa m = 0.5 kg, kustas tā, ka ķermeņa noietā ceļa 5 atkarību no laika t izsaka vienādojums s = Asinω∙t, kur A = 5 cm un ω = π rad/s. Aprēķināt spēku F, kas darbojas uz ķermeni, pēc t = 1/6 s no kustības sākuma. [ - 6.123 N].

2-11. Tramvajs uzsāk kustību ar pastāvīgu paātrinājumu a = 0.5 m/s². Pēc t = 12 s no kustības sākuma tramvaja motoru izslēdz, un līdz apstāsanās momentam tramvajs kustas vienmērīgi palēnināti. Visā ceļā koeficients k = 0.01. Aprēķināt 1) tramvaja kustības maksimālo ātrumu, 2) kopējo kustības laiku, 3) tramvaja negatīvo paātrinājumu palēninātajā kustībā, 4) visu ceļu, ko nogājis tramvajs. [1) 21.6 km/h; 2) 73 s; 3) -0.098 m/s²; 4) 218 m].

2-12. Kādu leņķi a ar horizontu veido benzīna virsma automobiļa tvertnē, ja automobilis kustas horizontālā virzienā ar pastāvīgu paātrinājumu a = 2.44 m/s²? [α 14°].

2-13. Pie tramvaja vagona griestiem diegā pakārta lodīte. Vagonu bremzējot, tā ātrums laikā Δt = 3 s vienmērīgi mainās no v_t = 18 km/h līdz v₂ = 6 km/h. Par kādu leņķi α tādā gadījumā novirzās diegs ar lodīti? [6°30'].

2-14. Bremzējot dzelzceļa vagonu, tā ātrums laikā Δt = 3.3 s vienmērīgi mainās no v₁ = 47.5 km/h līdz v₂ = 30 km/h. Kāda var būt berzes koeficienta maksimālā vērtība, lai, vagonu, bremzējot, čemodāns slīdētu pa plauktu? [0.15].

2-15. Automobilis sver 9.8 kN. Kustības laikā uz automobili darbojas berzes spēks, kas ir 0.1 no automobiļa svara. Aprēķināt automobiļa attīstīto vilcējspēku, ja automobilis kustas ar pastāvīgu ātrumu 1) pret kalnu, kura kāpums uz katriem 25 m ir l m, 2) no kalna ar tikpat lielu kritumu. [ 1) 1370 N; 2) 590N].

2-16. Aprēķināt automobiļa motora attīstīto vilcējspēku, ja automobilis brauc pret kalnu ar paātrinājumu l m/s². Kalna kāpums uz katriem 25 m ir l m. Automobiļa svars 9.8 kN. Berzes koeficients 0.1. [2370 N].

2-17. Ķermenis atrodas uz slīpas plaknes, kas veido ar horizontu 4° leņķi. 1) Kāda var būt berzes koeficienta maksimālā vērtība, lai ķermenis slīdētu pa slīpo plakni? 2) Ar kādu paātrinājumu ķermenis slīdētu pa slīpo plakni, ja berzes koeficients ir 0.03? 3) Cik ilgā laikā sādā gadījumā ķermenis var veikt 100 m? 4) Kāds ir ķermeņa ātrums pēc siem 100 m? [1) k < 0.07; 2) 0.39 m/s²; 3) 22.7 s; 4) 8.85 m/s].

2-18. Ķermenis slīd pa slīpu plakni, kas ar horizontu veido leņķi α = 45°. Noejot attālumu s = 36.4 cm, ķermenis sasniedz ātrumu v = 2 m/s. Aprēķināt berzes koeficientu. [0.2].

2-19. Ķermenis slīd pa slīpu plakni, kas ar horizontu veido 45° leņķi. Ķermeņa noietā ceļa i atkarību no laika t izsaka vienādojums s = Ct², kur C = 1.73 m/s². Aprēķināt berzes koeficientu. [0.5].

2-20. Divi atsvari, kuru svars P₁ = 19.6 N un P₂ = 9.8 N savienoti ar auklu, kas pārmesta trīsim. Aprēķināt 1) paātrinājumu, ar kādu kustas atsvari, 2) auklas sastiepuma spēku. Trīsa berzi neievērot. [1) 3.27 m/s²; 2) 13.0 N].

2-21. Trīsis piestiprināts pie galda malas (2-2. Att.). Atsvari A un B, kuru svars P₁ = P₂ = 9.8 N savienoti ar auklu, kas pārmesta trīsim. Atsvara B berzes koeficients k = 0.1. Aprēķināt 1) paātrinājumu, ar kādu kustas atsvari, 2) auklas sastiepuma spēku. Trīsa berzi neievērot. [4.4 m/s²; 2) 5.4 N].

2-22. Trīsis piestiprināts slīpās plaknes virsotnē (2-3. Art.). Atsvari A un B, kuru svars P₁ = P₂ = 9.8 N, savienoti ar auklu, kas pārmesta trīsim. Aprēķināt 1) paātrinājumu, ar kādu kustas atsvari, 2) auklas sastiepuma spēku. Trīsa berzi, kā arī atsvara B berzi neievērot. [1) 2.45 m/s²; 2) 7.35 N].

2-23. Atrisināt ieprieksējo uzdevumu ar nosacījumu, ka atsvara B berzes koeficients k = 0.1. Trīsa berzi neievērot. [ 1) 2.02 m/s²; 2) 7.77 N].

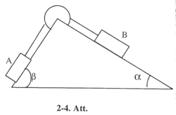
2-24. Trīsis piestiprināts divu slīpo plakņu virsotnē. Plaknes ar horizontu veido leņķus α = 30° un β = 45° (2-4. Att.). Atsvari A un B, kuru svars P₁ = P₂ = 9.8 N, savienoti ar auklu, kas pārmesta trīsim. Aprēķināt 1) paātrinājumu, ar kādu kustas atsvari, 2) auklas sastiepuma spēku. Trīsa berzi, kā arī atsvaru A un B berzi neievērot. [1)1.04 m/s²; 2)5.9 N].

Atrisināt ieprieksējo uzdevumu ar nosacījumu, ka atsvaru A un B berzes koeficienti k₁ = k₂= 0.1. Trīsa berzi neievērot. [0.244 m/s²; 2) 6.0 N].

Impulsa un enerģijas nezūdamības likums

3-1. Lidmasīna, paceļoties augstuma h = 5 km, sasniedz ātrumu v = 360 km/h. Cik reizu darbs, ko veic lidmasīna, pārvarot savu smaguma spēku, ir lielāks par darbu, ko tā veic palielinādama ātrumu? [10 reizes].

3-2. Bumbiņu, kas lido ar ātrumu v₁ = 15 m/s, atsit ar raketi, un tā turpina lidot pretējā virzienā ar ātrumu v₂ = 20 m/s. Aprēķināt bumbiņas impulsa izmaiņu, ja zināms, ka tās kinētiskās enerģijas izmaiņa ΔW = 8.75 J. [-3.5 kg-m/s].

3-3. Automobilis sver 9.8∙10³ N. Kustības laikā uz automobili darbojas pastāvīgs berzes spēks, kas ir 0.1 no automobiļa svara. Cik benzīna jāpatērē automobiļa dzinējam, lai tas 0.5 km garā ceļa posmā palielinātu automobiļa ātrumu no 10 km/h līdz 40 km/h. Dzinēja lietderības koeficients 20%, benzīna siltumspēja 4.6∙10⁷ J/kg. [0.06 kg].

3-4. Aprēķināt automobiļa dzinēja lietderības koeficientu, ja zināms, ka, braucot ar ātrumu 40 km/h, dzinējs patērē 13.5 l benzīna uz katriem 100 km un ka dzinēja attīstītā jauda tādā gadījumā ir 16.3 ZS. Benzīna blīvums 0.8 g/cm³. Pārējie uzdevuma nosacījumi tādi pasi kā ieprieksējā uzdevumā.[0.22].

3-5. 19.6 N smags akmens 1.43 s laikā nokrīt no zināma augstuma. Aprēķināt akmens kinētisko un potenciālo enerģiju sā augstuma viduspunktā. [98.1 J_; 98.1 J].

3-6. Akmens izsviests ar ātrumu v₀ = 15 m/s virziena, kas ar horizontu veido leņķi α = 60°. Aprēķināt akmens kinētisko, potenciālo un pilno enerģiju 1) pēc vienas sekundes no kustības sākuma, 2) trajektorijas augstākajā punktā. Akmens masa m = 0.2 kg. Gaisa pretestību neievērot. [1) 6.67 J, 15.97 J, 22.57 J;2)5.77J, 16.87 J, 22.5 J].

3-7. Darbs, kuru patērē, grūzot lodi leņķī α = 30° pret horizontu, ir A = 216 J. Pēc cik ilga laika un kādā attālumā no grūsanas vietas lode nokrīt zemē? Lodes svars P = 19.6 N. Gaisa pretestību neievērot, [l .5 s; 19. l m].

3-8. Materiāls punkts, kura masa 10 g, kustas pa riņķa līniju ar pastāvīgu tangenciālo paātrinājumu. Aprēķināt tangenciālo paātrinājumu, ja zināms, ka riņķa līnijas rādiuss ir 6.4 cm un otrā apriņķojuma beigās materiālā punkta kinētiskā enerģija sasniedz 8∙10 ^{- 4} J. [0.1 m/s²].

3-9. Pa l m augstu un 10 m slīpo plakni slīd ķermenis, kura masa ir l kg. Aprēķināt kinētisko enerģiju pie plaknes pamata, 2) ķermeņa ātrumu pie plaknes pamata, 3) attālumu, ko noiet ķermenis pa ceļa horizontālo daļu līdz apstāsanās brīdim. Pieņemt, ka berzes koeficients ir 0.05 un visā ceļā pastāvīgs. [1) 4.9 J; 2) 3. l m/s; 3) 10m].

3-10. Cilvēks, kura svars 588.6 N, skrienot ar ātrumu 8 km/h panāk ratiņus un uzlec uz tiem. Ratiņu svars 785 N un to ātrums 2.9 km/h. 1) Ar kādu ātrumu ratiņi turpina ripot? 2) Ar kādu ātrumu ripotu ratiņi, ja cilvēks būtu skrējis tiem pretī? [1)5.14 km/h; 2) 1.71 km/h].

3-11. Slidotājs, kura svars 687 N, stāvot uz ledus, horizontālā virzienā met 29.5 N smagu akmeni ar ātrumu 8 m/s. Aprēķināt, cik tālu tādā gadījumā aizslīd slidotājs, ja zināms, ka slidām, tām slīdot pa ledu, berzes koeficients ir 0.02. [0.3 m].

3-12. Cilvēks, stāvot uz nekustīgiem ratiņiem, sviez uz prieksu horizontālā virzienā akmeni, kura masa ir 2 kg. Ratiņi ar cilvēku aizripo atpakaļ, un pirmajā momentā pēc metiena to ātrums ir 0.1 m/s. Ratiņu svars kopā ar cilvēku ir 980 N. Aprēķināt izsviestā akmens kinētisko enerģiju pēc 0.5 s no kustības sākuma. Gaisa pretestību, akmenim lidojot, neievērot. [49 J].

3-13. Automāts izsauj 600 lodes minūtē. Katras lodes masa 4 g, tās sākuma ātrums 500 m/s. Aprēķināt sausanas vidējo atsitiena spēku. [20 N].

3-14. 19.6 N smags ķermenis kustas ar ātrumu 3 m/s un panāk otru 29.5 N smagu ķermeni, kas kustas ar ātrumu l m/s. Aprēķināt ķermeņu ātrumus pēc sadursmes, ja trieciens ir 1) neelastīgs, 2) elastīgs. Ķermeņi kustas pa vienu taisni. Trieciens ir centrāls. [1) 1.8 m/s; 2) 0.6 m/s; 2.6 m/s].

3-15. Kādai sakarībai jāpastāv starp ieprieksējā uzdevuma ķermeņu masām, lai pirmais ķermenis pēc elastīgā trieciena apstātos? [m₁/m₂= 1/3].

3-16. Lode, lidodama horizontālā virzienā, trāpa bumbu, kas iekārta vieglā stienī, un iestrēdz tajā. Lodes masa m, = 5 g un bumbas masa m₂ = 0.5 kg. Lodes ātrums v₁ = 500 m/s. Cik garam jābūt stienim (attālums no stieņa piekārsanas punkta līdz lodes centram), lai bumba pēc trieciena varētu pacelties līdz riņķa līnijas augsējam punktam? Stieņa masu neievērot [0.64 m].

3-17. Tērauda lodīte, kuras masa m = 20g, krītot no augstuma h₁ = l m uz tērauda plāksni, atlec no tās augstumā h = 81 cm. Aprēķināt: 1) spēka impulsu, kādu iegūst plāksne trieciena momentā; 2) triecienā izdalītā siltuma daudzumu. [ l) 0.17N∙s; 2) 37.2∙10 ^-3J].

3-18. Akmeni, kas iesiets auklā, kuras garums l = 50 cm, vienmērīgi griez vertikālā plaknē. Aprēķināt, kādam jābūt apgriezienu skaitam sekundē, lai aukla pārtrūktu, ja zināms, ka tā pārtrūkst, kad slodze desmitkārt pārsniedz akmens svaru. [2.1 apgr./s].

3-19. 4.9 N smagu akmeni, kas piesiets 50 cm garā auklā, vienmērīgi griez vertikālā plaknē. Riņķa līnijas viszemākajā punktā auklas sastiepuma spēks T = 44 N. Cik augstu paceļas akmens, ja aukla pārtrūkst momentā, kad ātruma virziens vērsts vertikāli augsup? [2 m].

3-20. Kādu darbu veic celtņa motors, lai paceltu 10 kg smagu ķermeni no miera stāvokļa vienmērīgi paātrināti 10 m augstumā ar paātrinājumu 5 m/s², ja dzinēja lietderības koeficients ir 75%? [2∙10 ^-3 J].

3-21. Kāds darbs jāveic, lai 100 kg smagu ķermeni ar paātrinājumu lm/s² paceltu pa slīpo plakni augsup, ja plaknes garums 2 m, bet slīpuma leņķis ar horizontu 30°. Berzes koeficients 0. l. [ l .35 kJ].

3-22. Automasīna, kuras masa 3 t, kustas ar ātrumu 40 km/h. Aprēķināt automasīnas dzinēja jaudu, ja berzes koeficients ir 0.06. [20 kW].

3-23. Kāda ir ūdeņsūkņa jauda, ja 0.5 h tas piepilda 30 m³ tvertni ar ūdeni? Tvertne atrodas 30 m augstumā. Sūkņa lietderības koeficients 80%. [6250 W].

3-24. Diegā iekārts atsvars. Par kādu leņķi no vertikālā stāvokļa jānovirza diegs, lai, atsvaram ejot caur līdzsvara stāvokli, diega sastiepuma spēks būtu 2 reizes lielāks par atsvara smaguma spēku? [60°].

3-25. Pa slīpo plakni no lejas uz augsu ar sākuma ātrumu 2 m/s izslidina ķermeni. Pacēlies kaut kādā augstumā, tas slīd pa to pasu ceļu atpakaļ. Kāds ir ķermeņa ātrums atgriezoties izejas punktā? Berzes koeficients 0.4, plaknes slīpuma leņķis 30°. [0.84 m/s].

Rotācijas kustības dinamika

4-1. Noteikt zemeslodes inerces momentu un impulsa momentu attiecībā pret griesanās asi. [9.7∙10³⁷ kg∙m²; 7∙10³³ kg∙m²/s].

4-2. Divas lodes, kuru rādiusi r₁ = r₂ = 5 cm, piestiprinātas tieva stieņa galos. Stieņa svars ir daudz mazāks par lozu svaru. Attālums starp lozu centriem R = 0.5 m. Katras lodes masa m = l kg. Aprēķināt: 1) sīs sistēmas inerces momentu I₁ attiecībā pret asi, kas iet caur stieņa viduspunktu perpendikulāri tā garumam; 2) sīs sistēmas inerces momentu I₂ attiecībā pret to pasu asi, uzskatot lodes par materiāliem punktiem, kuru masas koncentrētas to centros; 3) relatīvo kļūdu , kas rodas, ja, aprēķinot sis sistēmas inerces momentu, lieluma I₁ vietā ņem lielumu I₂. [1) 63.5∙10 ^-3 kg∙m²; 2) 62.5∙10 ^-3 kg∙m²; 3) 1.6%].

4-3. Pie homogēna diska aploces, kura rādiuss R = 0.2 m, pielikts pastāvīgs tangenciālais spēks F = 98.1 N. Rotējot uz disku darbojas berzes spēku moments M_b = 4.9 N∙m. Aprēķināt diska svaru P, ja zināms, ka disks rotē ar pastāvīgu leņķisko paātrinājumu ε = 100 rad/s². [7.36 kg].

4-4. Homogēns stienis, kura garums l m un svars 4.9 N rotē vertikālā plaknē ap horizontālu asi, kas iet caur stieņa viduspunktu. Ar kādu leņķisko paātrinājumu rotē stienis, ja rotācijas moments ir 9.81∙10 ^-2 N∙m? [2.35 rad/s²].

4-5. Homogēns disks, kura rādiuss R = 0.2 m un svars P = 49.05 N, rotē ap asi, kas iet caur tā centru. Diska rotācijas leņķiskā ātruma atkarību no laika izsaka vienādojums ω= A+ Bt, kur B = 8 rad/s². Aprēķināt tangenciālo spēku, kas pielikts diska aplocei. Berzi neievērot. [4 N].

4-6. Spararats, kura inerces moments I = 63.6 kg∙m², griezas ar pastāvīgu leņķisko ātrumu ω = 31.4 rad/s. Aprēķināt bremzējoso momentu M, kura iedarbībā spararats apstājas pēc t = 20 s. [100 N∙m].

4-7. Pie diskveida riteņa aploces pielikts 980 N liels tangenciālais spēks. Riteņa rādiuss ir 0.5 m un masa m = 50 kg. Aprēķināt: 1) riteņa leņķisko paātrinājumu; 2) pēc cik ilga laika no spēka iedarbības sākuma ritenis iegūst ātrumu, kas atbilst 100 apgr./s. [1) 7.8 rad/s²; 2) l min. 20 s].

4-8. Spararatu, kura rādiuss R = 0.2 m un masa m = 10 kg, savieno ar motoru dzensiksna. Siksnas sastiepuma spēks ir pastāvīgs un ir T = 14.7 N. Cik apgriezienu sekundē izdara spararats pēc 10 s no kustības sākuma? Spararatu uzskatīt par homogēnu disku. Berzi neievērot. [23.4 apgr./s].

4-9. Spararats, kura inerces moments ir 245 kg∙m , griezas, izdarot 20 apgr./s. Pēc vienas minūtes no brīza, kad uz spararatu pārstāj darboties rotācijas moments, tas apstājas. Aprēķināt: 1) berzes spēku momentu; 2) cik apgriezienu izdara ritenis kustības pēdējā minūtē, līdz tas pilnīgi apstājas. [1) 513 N∙m; 2) 600 apgr.].

4-10. Divi atsvari, kuru svars P₁ = 19.6 N un P₂ = 9.8 N savienoti ar auklu, kas pārmesta trīsim. Trīsa rādiuss R = 10 cm un tā svars P = 9.8 N. Aprēķināt: 1) paātrinājumu a, ar kādu kustas atsvari; 2) auklas sastiepuma spēkus T₁ un T₂, pie kuras piekārti atsvari. Trīsi uzskatīt par homogēnu disku. Berzi neievērot. [1) 2.8m/s²; 2) 14 N, 12.6 N].

4-11. Uz veltņa, kura masa M = 9 kg, uztīta aukla, kuras gala piesiets atsvars ar masu m = 2 kg. Aprēķināt atsvara paātrinājumu. Veltni izskatīt par homogēnu cilindru. Berzi neievērot. [3 m/s²].

4-12. Uz veltņa, kura rādiuss R = 0.5 m, uztīta aukla, kurai piesiets atsvars p₁ = 980 N. Aprēķināt veltņa inerces momentu, ja zināms, ka atsvars krīt ar paātrinājumu a = 2.04 m/s². [9.5 kg-m²].

4-13. Uz veltņa, kura rādiuss R = 20 cm un inerces moments I = 0. l kg∙m², uztīta aukla, kurai piesiets atsvars P₁ = 4.9 N. Pirms veltņa griesanās atsvara P₁ augstums virs grīdas h₁ = l m. Aprēķināt: 1) pēc cik ilga laika atsvars nonāk līdz grīdai; 2) atsvara kinētisko enerģiju trieciena momentā pret grīdu; 3) auklas sastiepuma spēku. Berzi neievērot. [1) 1.1 s; 2) 0.81 J; 3) 4.1 N].

4-14. Divi dazāda smaguma atsvari savienoti ar auklu, kas pārmesta trīsim, kura inerces moments I = 50 kg∙m² un rādiuss R = 20 cm. Trīsa berzes spēku moments M_b = 98.1 N∙m. Aprēķināt auklas sastiepuma spēku starpību T₁ - T₂ abās trīsa pusēs, ja zināms, ka trīsis griezas ar pastāvīgu leņķisko paātrinājumu ε = 2.36rad/s². [1080 N].

4-15. Trīsis, kura svars P = 9.8 N, piestiprināts galda galā. Vienāda smaguma atsvari A un B, kuru svars P₁ = P₂ = 9.8 N, savienoti ar auklu, kas pārmesta trīsim. Berzes koeficients, atsvaram B slīdot pa galdu, k = 0.1. Trīsi uzskatīt par homogēnu disku. Berzi trīsī neievērot. Aprēķināt: 1) paātrinājumu ar kādu kustas atsvari; 2) auklas sastiepuma spēkus T₁ un T₂. [1) 3.53 m/s²; 2m 6.3 N, 4.5 N].

4-16. Disks, kura svars 19.6 N bez slīdes ripo pa horizontālu plakni ar ātrumu 4 m/s. Aprēķināt diska kinētisko enerģiju. [24 J].

4-17. Lode, kuras diametrs 6 cm, bez slīdes ripo pa horizontālu plakni, izdarot 4 apgr./s. Lodes masa 0.25 kg. Aprēķināt lodes kinētisko enerģiju. [ 0.1 J].

4-18. Stīpai un diskam ir vienāds svars P, un tie ripo bez slīdes ar vienādu lineāro ātrumu v. Stīpas kinētiskā enerģija W₁ = 39.2 J. Aprēķināt diski kinētisko enerģiju W₂. [29.4 J].

4-19. Lode, kuras masa m = 1 kg, ripojot bez slīdes, atsitas pret sienu un atripo atpakaļ. Lodes ātrums pirms trieciena pret sienu v₁ = 10 cm/s, pēc trieciena v₂ = 8 cm/s. Aprēķināt triecienā izdalīto siltuma daudzumu Q. [2.51∙10 ^-3J].

4-20. Noteikt relatīvo kļūdu, kas rodas, aprēķinot ripojosas lodes kinētisko enerģiju, ja neievēro lodes griesanos. [40%].

4-21. Disks, kura svars 9.8 N un diametrs 60 cm, rotē ap asi, kas iet caur tā centru perpendikulāri diska plaknei, izdarot 20 apgr./s. Cik liels darbs jāpadara, lai disks apstātos? [355 J].

4-22. Vārpsta rotē ar pastāvīgu ātrumu, kas atbilst 5 apgr./s. Tas kinētiska enerģija ir 60 J. Aprēķināt sās vārpstas impulsa momentu. [3.8 kg∙m²/s].

4-23. Aprēķināt riteņbraucēja kinētisko enerģiju, ja tā ātrums v = 9 km/h. Riteņbraucēja un velosipēda kopīgais svars P = 764.4 N, pie tam riteņu svars P_{1 =} 29.4 N. Velosipēda riteņus uzskatīt par stīpām. [253 J].

4-24. Zēns ripina stīpu pa horizontālu ceļu ar ātrumu 7.2 km/h. Cik augstu kalnā uzripo stīpa kinētiskās enerģijas dēļ, ja kalna kāpums uz katriem 100 m ir 10m? [4.1 m].

4-25. Kādam jābūt vismazākajam augstumam H, no kura jāuzsāk brauciens riteņbraucējam, lai inerces dēļ (bez berzes) izbrauktu "nāves cilpu", kuras rādiuss R = 3 m, neatraujoties no cilpas augsējā punkta. Riteņbraucēja un velosipēda kopīgā masa m = 75 kg, pie tam riteņu masa m₁ = 3 kg. Velosipēda riteņus uzskatīt par stīpām. [7.56 m].

4-26. Vara lode, kuras rādiuss R = 10 cm rotē ap asi, kas iet caur tās centru. Rotācijas ātrums v atbilst 2 apgr./s. Cik liels darbs jāpadara, lai rotācijas leņķisko ātrumu palielinātu divas reizes. [34.1 J].

4-27. No slīpās plaknes, kura ar horizontu veido 30° leņķi, bez slīdes ripo: 1) lode; 2) disks un 3) stīpa. Aprēķināt to smaguma centru lineāros paātrinājumus, ja visu so ķermeņu sākuma ātrums ir nulle. 4) Salīdzināt atrastos paātrinājumus ar ķermeņa paātrinājumu, kas bez berzes slīd pa so slīpo plakni. [1) 3.5 m/s²; 2) 3.27 m/s²; 3) 2.44 m/s²; 4) 4.9 m/s²].

4-28. No slīpās plaknes bez slīdes ripo: 1) lode; 2) disks un 3) stīpa. Aprēķināt to smaguma centru lineāros ātrumu, ja slīpās plaknes augstums h = 0.5 m un visu ķermeņu sākuma ātrums ir nulle. 4) Salīdzināt atrastos ātrumu ar ķermeņa ātrumu, kas bez berzes slīd pa so slīpo plakni. [1) 2.65 m/s; 2) 2.56 m/s; 3)2.21 m/s; 4) 3.13 m/s].

4-29. Ir divi cilindri: alumīnija (blīvs) un svina (dobs). Abiem cilindriem ir vienāds rādiuss R = 6 cm un vienāds svars P = 4.9 N. Cilindru virsmas nokrāsotas vienāda krāsā. 1) Kā var atsķirt cilindrus, novērojot to translācijas kustības ātrumu pie slīpās plaknes pamata? 2) Aprēķināt so cilindru inerces momentus. 3) Cik ilgā laikā katrs cilindrs bez slīdes noripo no slīpās plaknes? Slīpās plaknes augstums h = 0.5 m, plaknes slīpuma leņķis a = 30°. Katra cilindra sākuma ātrums ir nulle. [2) 9-10 ^-4 kg∙m², 15.9∙10 ^-4 kg∙m²; 3) 0.88 s].

4-30. Riteni bremzējot, tas griezas vienmērīgi palēnināti un vienā minūtē samazina griesanās ātrumu no 300 apgr./min. līdz 180 apgr./min. Riteņa inerces moments ir 2 kg∙m². Aprēķināt: 1) riteņa leņķisko paātrinājumu; 2) bremzējoso momentu; 3) bremzēsanas darbu; 4) riteņa apgriezienu skaitu sajā minūtē. [1) -0.21 rad/s²; 2) 0.42 N∙m; 3) 630 J; 4) 240 apgr.].

4-31. Ventilators griezas ar ātrumu, kas atbilst 900 apgr./min. Pēc izslēgsanas ventilators turpina griezties vienmērīgi palēnināti un līdz apstāsanās momentam apgriezas 75 reizes. Bremzēsanas spēku darbs ir 44.4 J. Aprēķināt 1) ventilatora inerces momentu; 2) bremzēsanas spēku momentu. [1) 0.01 kg∙m²; 2) 9.4∙10 ^-2 N∙m].

4-32. Spararats, kura inerces moments I = 245 kg∙m², izdara 20 apgr./s. Kad uz riteni pārstāj darboties spēku rotācijas moments, tas vēl apgriezas 1000 reizu un tad apstājas. Aprēķināt: 1) berzes spēku momentu; 2) laiku, kurā spararats izdara pēdējos 1000 apgriezienus. [1) 308 N∙m; 2) 100 s].

4-33. Uz skriemeļa, kas nostiprināts uz kopīgas ass ar spararatu, uztīta aukla, kuras galā piekārts 9.8 N smags atsvars. Cik zemu jānoslīd atsvaram, lai spararats ar skriemeli iegūtu ātrumu, kas atbilst 60 apgr./min.? Spararata un skriemeļa inerces moments ir 0.42 kg∙m², skriemeļa rādiuss 10 cm. [0.865 m].

4-34. Spararats sāk griezties ar pastāvīgu leņķisko paātrinājumu ε = 0.5 rad/s un pēc t₁ = 15 s no kustības sākuma sasniedz impulsa momentu L = 73.5 kg∙m²/s. Aprēķināt spararata kinētisko enerģiju pēc t₂ = 20 s no griesanās sākuma. [490 J].

4-35. Spararats griezas ar pastāvīgu ātrumu, kas atbilst v = 10 apgr./s; tā kinētiskā enerģija W_k = 7.4 kJ. Cik ilgā laikā spēku rotācijas moments M = 50 N∙m, kas pielikts sim spararatam, palielina tā leņķisko ātrumu divas reizes? [5 s].

4-36. Diska aplocei pielikts pastāvīgs tangenciālais spēks F = 19.6 N. Diska masa m = 5 kg. Kāda ir diska kinētiskā enerģija pēc Δt = 5 s no spēka iedarbības sākuma? [1.92kJ].

4-37. Homogēns stienis piekārts pie horizontālas ass, kas iet caur stieņa augsējo galu. Par kādu leņķi stienis jāatvēz, lai, ejot caur līdzsvara stāvokli, stieņa apaksējā gala ātrums būtu 5 m/s? Stieņa garums l m. [81 °22'].

4-38. 85 cm gars homogēns stienis piekārts pie horizontālas ass, kas iet caur stieņa augsējo galu. Kāds vismazākais ātrums jāpiesķir stieņa apaksējam galam, lai tas izdarītu pilnu apgriezienu ap asi? [7.1 m/s].

4-39. Uz galda vertikāli nostādīts zīmulis apgāzas. Kāds leņķiskais un lineārais ātrums krisanas beigās ir zīmuļa: 1) vidum; 2) augsējam galam? Zīmuļa garums 15 cm. [1) 14 rad/s, 1.05 m/s; 2) 14 rad/s; 2.1 m/s].

4-40. Horizontāla platforma, kuras masa 100 kg, griezas ap vertikālu asi, kas iet caur platformas centru, izdarot 10 apgr./min. Uz platformas malas stāv cilvēks, kura svars 588.6 N. Ar kādu ātrumu sāk griezties platforma, cilvēkam pārejot no platformas malas uz tās centru? Platformu uzskatīt par apaļu, homogēnu disku, bet cilvēku par punktveida ķermeni. [22 apgr./min.].

4-41. Kādu darbu padara cilvēks, pārejot no platformas malas uz tās centru, ja ir spēkā ieprieksējā uzdevuma nosacījumi. Platformas rādiuss 1.5 m. [162 J].

4-42. Horizontāla platforma, kuras svars 784 N un rādiuss l m, griezas ar leņķisko ātrumu, kas atbilst 20 apgr./min. Platformas centrā stāv cilvēks un izplestās rokās tur atsvarus. Cik apgriezienu minūtē izdara platforma, ja cilvēks nolaizot rokas, samazina savu inerces momentu no 2.94 kg∙m² līdz 0.98 kg∙m²? Platformu uzskatīt par apaļu, homogēnu disku. [21 apgr./min.].

4-43. Cik reizu palielinās platformas un cilvēka kopīgā kinētiskā enerģija, ja ir spēkā ieprieksējā uzdevuma nosacījumi? [l .05 reizes].

4-44. Cilvēks, kura svars 588 N, atrodas uz nekustīgas platformas. Cik apgriezienu minūtē izdara platforma, ja cilvēks virzās ap griesanās asi riņķa līniju, kuras rādiuss ir 5 m? Cilvēka kustības ātrums attiecībā pret platformu ir 4 km/h. Platformas masa 100 kg un rādiuss 10 m. Uzskatīt platformu par homogēnu disku, bet cilvēku par punktveida ķermeni. [0.49 apgr./min.].

4-45. Homogēns stienis izdara nelielas svārstības vertikālā plaknē ap horizontālu asi, kas iet caur augsējo galu. Stieņa garums l = 0.5 m. Aprēķināt stieņa svārstību periodu. [1.16s].

4-46. Aprēķināt ieprieksējā uzdevumā dotā stieņa svārstību periodu, ja rotācijas ass iet caur punktu, kas atrodas 10 cm attālumā no stieņa augsējā gala. [1.07s].

4-47. Vertikāla stieņa galos piestiprināti divi atsvari, kuru smaguma centrs atrodas 5 cm zem stieņa viduspunkta. Stienis kopā ar atsvariem izdara nelielas svārstības ap horizontālu asi, kas iet caur stieņa centru. Aprēķināt stieņa garumu, ja so svārstību periods T = 2 s. Stieņa svaru neievērot. [0.446 m],

4-48. Stīpa, kuras diametrs ir 56.5 cm, pakārta uz naglas, kas iedzīta sienā, un izdara nelielas svārstības plaknē, kas paralēla sienai. Aprēķināt so svārstību periodu. [1.5 s].

4-49. Diegā iekārta homogēna lodīte, kuras diametrs D = 4 cm. Kāds ir diega vismazākais pieļaujamais garums L, lai, nosakot lodītes mazo svārstību periodu, to varētu uzskatīt par matemātisko svārstu? Turklāt pielaistā kļūda nedrīkst pasniegt l%. [6.9 cm].

4-50. Homogēna lodīte iekārta diegā, kura garums ir vienāds ar lodītes rādiusu. Cik reizu sā svārsta mazo svārstību periods ir lielāks par matemātiskā svārsta mazo svārstību periodu, ja matemātiskā svārsta piekārsanas punkta attālums no tā smaguma centra ir tāds pats? [l .05 reizes].

Statika. Hidrostatika.

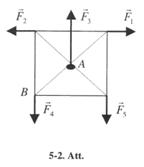
5-1. Plakanam ķermenim, (5.-2. Atī) kuram ir kvadrāta forma, pielikti spēki: F, = F₂ = F₃ = 2N, F₄ = F₅=l N. Kvadrāta malas garums 2 m. Aprēķināt spēku summāro momentu attiecībā pret punktiem A un B. Kā kustas sis ķermenis? [0].

5-2. Uz zemes guļ lauznis, kura smaguma spēks 100 N. Cik liels spēks jāpieliek, lai paceltu vienu lauzņa galu? [50 N].

5-3. Divi strādnieki nes 5 m garu cauruli, kuras masa 40 kg. Pirmais strādnieks tur cauruli l m attālumā no gala, otrs - aiz caurules otra gala. Aprēķināt, ar kādu speķu caurule iedarbojas uz pirmā un otra strādnieka roku. [250 N; 150 N].

5-4. Homogēns baļķis, kura garums l un masa 100 kg, guļ horizontāli uz 2 atbalstiem. Attālums no baļķa labā gala līdz tuvākajam atbalstam l/3, no kreisā - 1/4. Ar kādu spēku baļķis spiez uz atbalstu? Kādu minimālo spēku jāpieliek baļķa labajam galam, lai to paceltu? [400 N; 600 N].

5-5. Homogēns stienis, kura masa l kg, guļ uz horizontāla galda tā, ka 1/3 no stieņa garuma ir pāri galda malai. Aprēķināt masu, kas jāpiekar labajam stieņa galam, lai kreisais gals tiktu pacelts augsup? [0.5 kg].

5-6. Uz galda novietots lineāls, tā, ka uz galda atrodas 4/5 daļas no lineāla garuma, bet 1/5 karājas pāri malai. Ja lineālu grib novietot vertikāli, pieliekot spēku tā brīvajam galam, tad - kā so spēku ir izdevīgāk pielikt? Cik reizu atsķirsies minimālais spēks no maksimālā? [3/2 P; 1/2 P].

5-7. 10 m gara sija, kuras masa 50 kg, ar vienu galu atbalstās pretī horizontālu grīdu. Otru sijas galu notur virve tā, ka virve un sija veido taisnu leņķi, bet sija un grīda 60° leņķi. Aprēķināt virves sastiepuma spēku. [125 N].

5-8. Trīs konteineri, kuru svars, skaitot no augsas, ir 1500 N, 1600 N un 1700 N, novietoti vertikāli viens virs otra. Aprēķināt, cik liela papildu slodze pielikta katram konteineram un ar cik lielu spēku visi trīs kopā spiez uz pamatu. [1500 N; 3100 N; 4800 N].

5-9. Piekrautu liellaivu velk divi traktori, vienmērīgi pārvietojoties gar abām kanāla malām. Cik liels ir ūdens pretestības spēks, ja troses ir sastieptas ar 10000 N lielu spēku, bet leņķis starp trosēm ir 60°? [17.3 kN].

5-10. Stieplē iekārtu 200 N smagu atsvaru velk uz sāniem. Aprēķināt stieples saspiepuma spēku brīdī, kad tā veido 26° lielu leņķi ar vertikāli. [225 N].

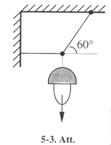
5-11. Apgaismosanas armatūra (5-3. Art.) piekārta trosē un atvilkta sānis ar horizontālu atsaiti. Aprēķināt troses un atsaites sastiepuma spēku, ja armatūras svars ir 5 N. [5.8 N].

 

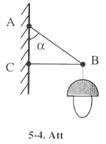
5-12. Kronsteinam (5-4. Att.) piekārta armatūra, kuras svars ir 100 N. Aprēķināt spēkus stieņos AB un BC, ja leņķis α = 60°. [200 N; 173 N].

5-13. Atsvars, kura masa m = 0.5 kg, iekārts divās atsaitēs AB un BC (5-5. Att.). Vai var nostiept atsaiti AB horizontāli, bet BC tā, lai leņķis α būtu 150°, ja atsaite BC iztur maksimālu slodzi 15 N? Ja var, tad cik liels būs atsaites BC sastiepuma spēks? [9.8 N].

5-14. Dēļa garums 3.2 m. Kādā maksimālā augstumā var pacelt tā vienu galu, lai 35 N spēks, kas vērsts paralēli dēļa virsmai, noturētu uz tā kravu, kuras svars 140N? [0.8m].

5-15. Cik lielam jābūt optimālam leņķim α (5-6. Att.), lai stumtu no sāniem automasīnu ar spēku F, ja berzes koeficients rokām pret automasīnu ir 0.8? [32°].

 

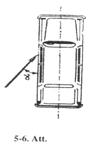
5-16. Cik liels spēks F, jāpieliek āmura kātam, lai izrautu naglu no dēļa? Naglas pretestības spēks F₂ = 160 N, roktura garums l₁ = 32 cm, bet attālums no āmura pieta līdz naglai l₂ = 8.0 cm (5-7. Att.). [40 N].

5-17. Klucis, kura masa 10 kg, jāapgāz ap sķautni O (5-8. Att.). Cik liels spēks jāpieliek, ja kluča platums 50 cm, bet augstums 75 cm? [33 N].

5-18. 10 N smaga un 0.6 m gara homogēna stieņa galos piekārti 10 N un 20 N smagi atsvari. Kurā vietā stienis jāatbalsta, lai tas atrastos līdzsvarā? [37.5 cm].

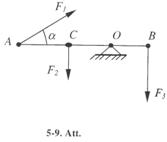
5-19. Stienis AB, kura garums ir 0.8 m, atbalstīts punktā O (5-9. Att.). Triju spēku iedarbībā stienis atrodas līdzsvarā, pie tam F/ = 6.7 N, F₂ - 3 N, F₃ - 4 N, OB = 0.2 m, CO = 0.4 m un leņķis a = 30°. Aprēķināt stieņa smaguma spēku, ja stieņa smaguma centrs ir tā vidū. [8 N].

5-20. 10 N smaga un 0.6 m gara homogēna stieņa galos piekārti 10 N un 20 N smagi atsvari. Aprēķināt pielikto spēku plecus un spiediena spēku, kas darbojas uz atbalsta punktu, ja stienis atrodas līdzsvarā. [0.2 m; 0.4 m; 30 N].

5-21. Četras homogēnas lodes, kuru masas ir m₁ = l kg, m₂ = 5 kg, m₃ = l kg, m₄ = 3 kg, nostiprinātas uz stieņa tā, ka to centri atrodas attālumā d = 0.2 m viens no otra. Noteikt sistēmas smaguma spēka pieliksanas punktu. Stieņa smaguma spēku neievērot. [0.25 m].

5-22. Sadalīt 5 N lielu spēku divos paralēlos un pretēji vērstos spēkos, kuru pieliksanas punkti atrodas no dotā rezultējosā spēka attālumā 3 m un 4 m. [20 N; 15 N].

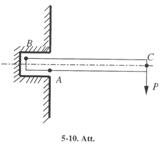
5-23. Smaga sija ar vienu galu ielaista sienā un atbalstās punktos A un B (5-10. Att.), bet otrā galā C piekārta 2∙10³ N smaga krava. Pieņemot, ka visu slodzi uzņem atbalsta punkti A un B, aprēķināt spiediena spēku, kas darbojas uz atbalstu punktā A, un sijas svaru. Sijas garums 2 m, bet sienā iestiprinātās daļas garums 0.5 m. Uz atbalstu punktā B darbojas spiediena spēks F_B = 8∙10³ N. [ 12kN; 2kN ].

5-24. Divas homogēnas lodes, kuru smaguma spēks 3 kgf un 5 kgf, savienotas ar stieni. Stieņa smaguma spēks 2 kgf un garums 30 cm. Noteikt kopējā smaguma centra atrasanās vietu, ja pirmās lodes rādiuss R₁ = 5 cm, bet otrās -R₂ = l cm. [0.25 m].

5-25. 100 N smags dzelzs lauznis guļ uz zemes. Cik liels spēks jāpieliek, lai paceltu tā vienu galu? [50 N].

Hidro- un aerodinamika

6-1. Aprēķināt dzīvsudraba līmeņu starpību divos savienotajos kapilāros, kuru kanālu diametri l mm un 3 mm, ja Hg blīvums 1.36 l0⁴ kg/m³, virsmas spraiguma koeficients 0.47 N/m, brīvās krisanas paātrinājums 9.8 m/s². [4.5 mm].

6-2. Savienotajos traukos iepildīts sķidrums, kura blīvums ρ₁ un sķidruma stabiņa augstums h₁. Savienoto trauku augstums H. Pēc tam vienā caurulītē ielej sķidrumu, kura blīvums ρ₂ > ρ₁. Cik augstam jābūt sī sķidruma stabiņam, lai otrā caurulē sķidrums sasniegtu caurules augsgalu? [2h₁ > H].

6-3. Kubiskas formas trauks, kura sķautnes garums 10 m, līdz malām piepildīts ar ūdeni. Aprēķināt spiediena spēku uz trauka dibenu un sānu virsmu, j a atmosfēras spiediens ir normāls. [6∙l0⁷ N].

6-4. Glāzē, kura ir pilna ar ūdeni, ieliek ķermeni, kura masa 20 g un blīvums 800 kg/m³. Cik ūdens izlīst? [20 g].

6-5. Ar plostu, kas sastāv no 20 vienādiem baļķiem, var pārvadāt kravu, kuras maksimālā masa 1800 kg. Aprēķināt koksnes blīvumu, ja katra baļķa tilpums ir 0.3 m³. [700 kg/m³].

6-6. Doba cinka lode (ρ = 7.1∙10³ kg/m³), kuras ārējais tilpums ir 2∙10 ^-4 m³, ūdenī peld tā, ka puse lodes ir ūdenī. Aprēķināt lodes dobuma tilpumu. [1.86∙10 ^-4 m³].

6-7. Taisnstūrveida pontona masa 100 kg, tā izmēri: garums 5 m, platums 3 m, augstums 0.7 m. Aprēķināt pontona iegrimi bez slodzes un maksimālo celtspēju, ja bortu augstums virs ūdenslīnijas ir 0.2 m. [6.8∙10³ kg].

6-8. Ķermenis gaisā sver 3 N, ūdenī.1.8 N, sķidrumā, kura blīvums nav zināms, - 2.04 N. Aprēķināt sķidruma blīvumu. [800 kg/m³].

6-9. Baļķis, kura garums 3.5 m un sķērsgriezuma laukums 0.04 m³ peld ūdenī. Baļķa blīvums 500 kg/m³, ūdens - 2 reizes lielāks. Uz baļķa uzkāpj cilvēks. Aprēķināt cilvēka maksimālo masu, lai baļķis to noturētu virs ūdens. [70 kg].

6-10. Homogena lode peld līdz pusei iegrimusi ūdeni. Aprēķināt lodes tilpumu, ja uz to darbojas 2 N Arhimēda spēks. [4∙10 ⁴ m³].

6-11. Metāliska cilindra tilpums ir 400 cm³, to nosvēra gaisā un ogļskābajā gāzē. Svaru starpība 28∙10 ^-3 N. Aprēķināt ogļskābās gāzes un gaisa blīvumu, ja to attiecība ir 20/13. [2 kg/m³; 1.3 kg/m³].

6-12. Ķermenis, kura masa ir 2 kg un tilpums 1000 cm³, atrodas ezerā 5 m zem ūdens. Cik liels darbs jāveic, lai to paceltu 5 m virs ūdens? [150 J].

6-13. Koka lodīte krītot no 20 cm augstuma, iegrimst ūdenī par 60 cm. Cik augstu sī lodīte "izlēks" virs ūdens, ja ūdens pretestība nemainās, gaisa neievērot. Koka blīvums 800 kg/m³. [0.1 m].

6-14. Korķa lodīte ir vienu metru zem ūdens. Lodīte atbrīvota, tā uzpeld un "izlec" 0.5 m virs ūdens. Aprēķināt vidējo ūdens pretestības spēku lodītes kustībai. Gaisa pretestības spēku neievērot, lodītes masa 100 g, korķa blīvums 200 kg/m³. [3.5 N].

6-15. Homogēns stienis, kura viens gals nostiprināts tā, kā paradīts 6-2. attēlā, atrodas līdzsvarā, ja puse no tā iegremdēta petrolejā. Aprēķināt stieņa materiāla blīvumu, ja petrolejas blīvums ir 800 kg/m³. [600 kg/m³].

6-16. U veida caurulītes labajā pusē ieliets dzīvsudrabs, kura staba augstums h₁ = l cm. Virs tā uzlietā ūdens staba augstums h₂ = 2 cm (6-3. Att.). Cik augstu jāielej ūdens caurulītes kreisajā pusē, lai līdzsvarotu so abu sķidrumu radīto spiedienu? [24 cm].

6-17. Traktora hidrauliskajā sistēma var radīt 3∙10⁵ Pa lielu eļļas spiedienu. Cik lielu spēku var attīstīt sī palīgiekārta, ja eļļa darbojas uz virzuli, kura diametrs ir 10 cm? [23.6 kN],

6-18. Dzelzs riteni iepresē tērauda gredzenā ar 500 kN lielu spēku, ko] attīsta hidrauliskā spiede. Spiedes lielā virzuļa laukums ir l m², bet mazā - 2 cm². Cik liels spēks jāpieliek mazajam virzulim? [100 N].

6-19. Savienotajos traukos ieliets dzīvsudrabs, bet virs tā vienā traukā ielieta eļļa augstumā h₁ = 48 cm, otrā - petroleja augstumā h₂ = 20 cm. Aprēķināt dzīvsudraba līmeņu starpību abos traukos. [Δh = 2 cm].

6-20. Koka gabals peld ūdenī, iegrimstot par 3/4 sava tilpuma. Aprēķināt sā koka blīvumu, [ρ = 0.75 g/cm³].

6-21. Uz ūdens virsmas peld trauks, kura dibena laukums S₀ (6-4. Art.). Traukā ielietā ūdens līmeņa augstums h₀ un trauka iegrime H₀. Kā mainīsies augstumi h₀ un H₀, ja traukā ievietos koka klucīti, kura smaguma spēks P? [P/dS].

6-22. Gumijas bumba, kuras rādiuss R = 10 cm, peld ūdenī tā, ka tās centrs; atrodas 9 cm virs ūdens virsmas. Cik liels darbs jāveic, lai bumbu iegremdētu ūdenī līdz diametra plaknei? [0.74 J].

6-23. Lodi, kuras rādiuss R = 6 cm, ārējs spēks notur zem ūdens tā, ka tās augsējais punkts pieskaras ūdens virsmai. Lodes materiāla blīvums ρ = 500 kg/m³. Cik lielu darbu padara izgrūdējs spēks, ja lodi atbrīvo no ārējā spēka un ļauj tai brīvi peldēt? [0.17 J].

6-24. Lode, kuras diametrs D = 35 cm, peld ūdenī. Cik liels darbs jāpadara, lai iegremdētu lodi vēl par h = 5 cm dziļāk ūdenī? Lodes materiāla blīvums ρ = 500 kg/m³. [4.6 J].

6-25. Ledus gabals, kura sķērsgriezuma laukums S = l m² un augstums H = 0.4 m, peld ūdenī. Cik liels darbs jāpadara, lai ledus gabalu pilnīgi iegremdētu ūdenī? [7.84 J].

Mehāniskās svārstības un viļņi

7-1. Uzrakstīt harmonisko svārstību vienādojumu, ja svārstību amplitūda 5 cm, l min notiek 150 svārstības un svārstību sākumfāze ir 45°. Konstruēt so svārstību grafiku.

7-2. Uzrakstīt harmonisko svārstību vienādojumu, ja svārstību amplitūda 0.1 m, periods 4 s un sākumfaze ir nulle.

7-3. Harmonisko svārstību amplitūda ir 50 mm, periods 4 s un sākumfaze π/4. 1) Uzrakstīt so svārstību vienādojumu; 2) Aprēķināt svārstību punkta novirzi no līdzsvara stāvokļa laika momentos t = 0 un t = 1.5 s; 3) Konstruēt so svārstību grafiku. [2) 35.2 mm; 0].

7-4. Uzrakstīt harmonisko svārstību vienādojumu, ja svārstību sākumfaze ir l) 0; 2) π/2; 3) π; 4) 3π/2; 5) 2π. Svārstību amplitūda ir 5 cm un svārstību periods 8 s. Konstruēt svārstību grafiku visiem siem gadījumiem.

7-5. Konstruēt vienās koordinātu asīs divu harmonisko svārstību grafikus, ja so svārstību amplitūdas ir vienādas (A₁ = A₂ = 2 cm) un ir vienādi periodi (T_t = T₂ = 8 s), bet ir dazādas fāzu starpības: 1) π/4; 2) π/2; 3) π; 4) 2π.

7-6. Pēc cik ilga laika no kustības sakuma harmoniski svārstosa punkta novirze no līdzsvara stāvokļa sasniedz pusi no amplitūdas? Svārstību periods 24 s un sākumfaze ir nulle. [2 s].

7-7. Harmonisko svārstību sākumfaze ir nulle. Kāda daļa no svārstības perioda būs pagājusi, kad punkts būs sasniedzis pusi no maksimāla ātruma? [T/6].

7-8. Punkta harmoniskas svārstības nosaka vienādojums x = 7sin0.5π.t. Cik ilgā laikā no kustības sākuma punkts noiet ceļu no līdzsvara stāvokļa līdz maksimālai novirzei? [1s].

7-9. Harmonisko svārstību amplitūda ir 5 cm un periods 4 s. Aprēķināt svārstosa punkta maksimālo ātrumu un maksimālo paātrinājumu. [7.85·10 ^-2 m/s; 12.3·10 ^-2 m/s²].

7-10. Punkta kustības vienādojums ir x=2sin(πt/2+ π/4)cm. Aprēķināt: 1) svārstību periodu; 2) punkta maksimālo ātrumu; 3) tā maksimālo paātrinājumu. [1) 4 s; 2) 3.14·10 ^-2 m/s; 3) 4.93·10 ^-2 m/s²].

7-11. Punkta kustības vienādojums ir x=sin(πt/6). Aprēķināt laika momentus, kuros punkts sasniedz maksimālo ātrumu un maksimālo paātrinājumu. [3, 9, 15 s ...].

7-12. Punkts svārstās harmoniski. Svārstību periods 2 s, amplitūda 50 mm, sākumfaze ir nulle. Aprēķināt punkta ātrumu laika momentā, kad punkta novirze no līdzsvara stāvokļa ir 25 mm. [0.136 m/s].

7-13. Uzrakstīt harmonisko svārstību vienādojumu, ja punkta maksimālais paātrinājums ir 49.3 cm/s², svārstību periods 2 s un punkta novirze no līdzsvara sākummomentā ir 25 mm.

7-14. Harmonisko svārstību sākumfaze ir nulle. Kad punkta novirze no līdzsvara stāvokļa ir 2.4 cm, punkta ātrums ir 3 cm/s, bet, kad novirze ir 2.8 cm, ātrums ir 2 cm/s. Aprēķināt so svārstību amplitūdu un periodu. [3.1·10 ^-2 m; 4.1 s].

7-15. Materiāla punkta svārstību vienādojums ir x =0.1sin(πt/8 + π/4)m; sā punkta masa m = 1.6·10 ^-2 kg. Attēlot grafiski atkarību, kāda pastāv starp spēku F, kas darbojas uz punktu, un laiku t (viena perioda robezās). Aprēķināt maksimālā spēka vērtību. [24.6·10 ^-5 N].

7-16. Materiāla punkta svārstību vienādojums ir x = 5sin(πt/5 + π/4)cm; sā punkta masa 10 g. Aprēķināt maksimālo spēku, kas darbojas uz punktu, un svārstosā punkta pilno enerģiju. [19.7·10 ^-5 N; 4.93·10 ^-6 J].

7-17. Materiāla punkta svārstību vienādojums ir x = 2sin(πt/4 + π/4)cm; sā punkta masa 16 g. Attēlot grafiski punkta kinētiskas, potenciālas un pilnās enerģijas atkarību no laika (viena perioda robezās).

7-18. Kāda ir harmoniski svārstosa punkta kinētiskās un potenciālās enerģijas attiecība laika momentos: 1) t = T/12 s; 2) t = T/8 s; 3) t = T/6 s. Svārstību sākumfaze ir nulle. [1) 3; 2) 1; 3) 1/3].

7-19. Kāda ir harmoniski svārstosa punkta kinētiskās un potenciālās enerģijas attiecība laika momentos, kad punkta novirze no līdzsvara stāvokļa ir: 1) x = A/4 ; 2) x = A/2 ; 3) x = A ; A - svārstību amplitūda. [1) 15; 2) 3;

7-20. Harmoniski svārstosa ķermeņa pilnā enerģija ir 3·10 ^-5 J, maksimālais spēks, kas darbojas uz ķermeni, ir 1.5·10 ^-3 N. Uzrakstīt sā ķermeņa kustības vienādojumu, ja svārstību periods ir 2 s un sākumfaze 60°.

7-21. Materiāla punkta harmonisko svārstību amplitūda A = 2 cm, svārstību pilnā enerģija W = 3·10 ^-7 J. Cik liela ir svārstosa punkta novirze no līdzsvara stāvokļa, kad uz to darbojas spēks F = 2.25·10 ^-5 N? [1.5·10 ^-2 m].

7-22. Ja matemātiskā svārsta garumu samazina par 10 cm, tad tā frekvence izmainās 1.2 reizes. Cik liels ir svārsta sākuma garums? [33 cm].

7-23. Viens svārsts izdara 30 svārstības, bet otrs tajā pasā laikā 15 svārstības. Abu svārstu garumu starpība ir 3 m. Cik gars ir katrs svārsts? [l m; 4 m],

7-24. Lifts pārvietojas vertikāli augsup ar paātrinājumu 2 m/s². Pie lifta griestiem l m garā diegā piekārta lodīte. Aprēķināt svārsta svārstību periodu. Cik liels būs sī svārsta periods, ja lifts pārvietosies lejup ar paātrinājumu 2 m/s²? [l.8s; 2.2s].

7-25. Ar cik lielu paātrinājumu un kādā virzienā vertikālā plaknē jāpārvietojas liftam, lai pie tā griestiem piestiprināta l m gara svārsta svārstību Periods būtu 2.3 s? [2.6 m/s²].

7-26. Uzrakstīt tādas kustības vienādojumu, kas rodas, summējoties divām vienāda virziena harmoniskām svārstībām, kam vienādi 8 s periodi un vienādas 0.02 m amplitūdas. Fāzu starpība starp sīm svārstībām ir Sākumfāze vienai no sīm svārstībām ir nulle.

7-27. Aprēķināt amplitūdu un sākumfazi harmoniskai svārstībai, kuru iegūst, saskaitot divas vienāda virziena svārstības: x₁ = 0.02sin(5πt + π/2) m un x₂ = 0.03sin(5πt + π/4) m. [4.6·10 ^-2m; 62⁰46'].

7-28. Saskaitot divas vienāda virziena harmoniskās svārstības, kuru periodi vienādi un vienādas amplitūdas, iegūst rezultējoso svārstību ar tādu pasu periodu un tādu pasu amplitūdu. Aprēķināt saskaitāmo svārstību fāzu starpību. [2π/3].

7-29. Uzrakstīt rezultējosās svārstības vienādojumu, ko iegūst, saskaitot divas savstarpēji perpendikulāras svārstības ar vienādu frekvenci v₁ = v₂ = 5 Hz un vienādu sākumfazi φ₁ = φ₂ = 60°. Vienas svārstības amplitūda A₁ = 0.10 m, otras A₂ = 0.05 m.

7-30. Punkts piedalās divās svārstībās, kuru periodi un sākumfazes ir vienādas. Svārstību amplitūda A₁ = 3 cm un A₂ = 4 cm. Aprēķināt rezultējosās svārstības amplitūdu, ja: 1) svārstības notiek vienāda virzienā; 2) svārstības ir savstarpēji perpendikulāras. [1) 7 cm; 2) 5 cm].

7-31. Punkts vienlaicīgi piedalās divās savstarpēji perpendikulārās svārstībās x = 2sinω·t m un y = 2cosω·t m. Aprēķināt punkta kustības trajektoriju.

7-32. Punkts vienlaicīgi piedalās divās savstarpēji perpendikulārās svārstības x = cosπt un y = cos(πt/2). Aprēķināt punkta rezultējosās kustības trajektoriju.

7-33. Punkts vienlaicīgi piedalās divās savstarpēji perpendikulārās svārstībās x = sinπt un y = 2sin(πt + π/2). Noteikt punkta kustības trajektoriju un konstruēt tas grafiku, ievērojot mērogu.

7-34. Punkts vienlaicīgi piedalās divas savstarpēji perpendikulāras svārstībās x = sinπt un y = 4sin(πt + π). Noteikt punkta kustības trajektoriju un konstruēt tās grafiku, ievērojot mērogu.

7-35. Rimstosu svārstību periods ir 4 s, rimsanas logaritmiskais dekrements 1.6, sākumfāze ir nulle. Punkta novirze ir 4.5 cm, ja t = T/4 . 1) Uzrakstīt so svārstību vienādojumu. 2) Konstruēt so svārstību grafiku divu periodu robezās.

7-36. Rimstoso svārstību vienādojums ir x = 5e ^{- 0.25t}sin(πt/2) m. Aprēķināt svārstosā punktā ātrumu sādos laika momentos: 0, T, 2T, 37 un 47. [7.85 m/s; 2.88 m/s; 1.06 m/s; 0.39 m/s; 0.14 m/s].

7-37. Matemātiskā svārsta rimsanas logaritmiskais dekrements ir 0.2. Aprēķināt, cik reizu samazinās svārstību amplitūda viena perioda laikā. [1.22].

7-38. Kāds ir matemātiska svārsta rimsanas logaritmiskais dekrements, ja vienā minūtē svārstību amplitūda samazinās divas reizes? Svārsta garums l m. [0.023].

7-39. 24.7 cm gars matemātiskais svārsts svārstās rimstosi. Pēc cik ilga laika svārsta svārstību enerģija samazinās 9.4 reizes? Uzdevumu atrisināt, pieņemot, ka rimsanas logaritmiskais dekrements: 1) X =0.01 un 2) X = 1. [1) 120s; 2) 1.22s].

7-40. Matemātiskais svārsts svārstās rimstosi. Rimsanas logaritmiskais dekrements ir 0.2. Cik reizu samazinās svārsta pilnais paātrinājums tā malējā stāvoklī vienas svārstības laikā? [1.22 reizes].

7-41. Matemātiskā svārsta rimstoso svārstību amplitūda vienā minūtē samazinās divas reizes. Cik reizu tā samazinās trijās minūtēs? [8 reizes].

7-42. 0.5 m gars matemātiskais svārsts, izvirzīts no līdzsvara stāvokļa, pirmajā svārstībā novirzās par 5 cm, bet otrajā svārstībā (tajā pasā virzienā) par 4 cm. Aprēķināt relaksācijas laiku, t. i., laiku, kurā svārstību amplitūda samazinās e reizes, kur e - naturālo logaritmu bāze. [6.4 s].

7-43. Vertikālā atsperē iekārts smagums, tāpēc atspere pagarinās par 9.8 cm. Pavelkot smagumu uz leju un palaizot vaļā, tas sāk svārstīties. Kādam jābūt rimsanas koeficientam 8, lai: 1) svārstības izbeigtos pēc 10 s (pieņemt, ka svārstības ir izbeigusās, ja to amplitūda samazinājusies līdz 1% no sākotnējās vērtības); 2) smagums aperiodiski atgrieztos līdzsvara stāvoklī; 3) rimsanas logaritmiskais dekrements būtu 6? [1) 0.46 s ^-1; 2) 10 s ^-1; 3) 6.9 s ^-1].

7-44. Aprēķināt svārstību viļņa garumu, ja to periods ir 10 ^-14s. Svārstību izplatīsanās ātrums 3·10⁸ m/s. [3·10^-6 m].

7-45. Skaņas svārstības, kuru frekvence v = 500 Hz un amplitūda A = 0.25 mm, izplatās gaisā. Viļņa garums A = 70 cm. Aprēķināt: 1) svārstību izplatīsanās ātrumu; 2) gaisa daļiņu maksimālo ātrumu. [1) 350 m/s; 2) 0.785 m/s].

7-46. Nerimstosu svārstību vienādojums ir x = 10sin0.5πt cm. 1) Sastādīt viļņa vienādojumu, ja svārstību izplatīsanās ātrums ir 300 m/s. 2) Uzrakstīt un attēlot grafiski punkta svārstību vienādojumu, ja punkts atrodas 600 m attālumā no svārstību avota. 3) Uzrakstīt un attēlot grafiski viļņa punktu svārstību vienādojumu momentā t = 4 s pēc svārstību sākuma.

7-47. Nerimstosu svārstību vienādojums ir x = 4sin600πt cm. Aprēķināt punkta novirzi no līdzsvara stāvokļa 0.01 s pēc svārstību sākuma, ja punkts atrodas 75 cm attālumā no svārstību avota. Svārstību izplatīsanās ātrums ir 300 m/s. [0.04 m].

7-48. Nerimstosu svārstību vienādojums ir x = sin2.5πt cm. Aprēķināt punkta novirzi no līdzsvara stāvokļa, tā ātrumu un paātrinājumu momentā t = l s pēc svārstību sākuma, ja punkts atrodas 20 m attālumā no svārstību avota. Svārstību izplatīsanās ātrums ir 100 m/s. [0; 7.85·10 ^-2 m/s; 0].

7-49. Kāda ir fāzu starpība divu punktu svārstībām, ja punkti atrodas attiecīgi 10 m un 16 m attālumā no svārstību avota? Svārstību periods 0.04 s un svārstību izplatīsanās ātrums 300 m/s. [n].

7-50. Aprēķināt fāzu starpību divu punktu svārstībām, ja punkti atrodas uz stara 2 m attālumā viens no otra un viļņa garums ir l m. [4n].

Ideālās gāzes stāvokļa vienādojums. Daltona likums

8-1. Kāda temperatūra ir 2 g slāpekļa, ja tas aizņem 820 cm³ tilpuma pie 2 atm spiediena? [280 °K],

8-2. Kādu tilpumu aizņem 10 g skābekļa, ja tā spiediens ir 750 mm Hg un temperatūra 20° C? [7.6·10 ^-3 m³].

8-3. Balons, kura tilpums 12 l, piepildīts ar slāpekli, kura spiediens 8.l.10⁶ N/m² un temperatūra 17° C. Cik daudz slāpekļa atrodas balonā? [1.13 kg].

8-4. Gaisa spiediens blīvi noslēgtā pudelē l atm un temperatūra 7° C. Pudeli sildot, izsprāgst korķis. Aprēķināt, līdz kādai temperatūrai pudele tika sasildīta, ja zināms, ka korķis izsprāgst tad, kad gaisa spiediens pudelē sasniedz 1.3 atm. [364°K].

8-5. Kāds ir vismazākais balona tilpums, kurā var iepildīt 6.4 kg skābekļa, ja balona sieniņas 20° C temperatūrā iztur 15.68·10 ⁶ N/m² lieli spiedienu? [3.1·10 ^-2 m³].

8-6. Balonā atrodas 10 kg gāzes, pie 10⁷ N/m² liela spiediena. Aprēķināt, kāds gāzes daudzums izlaists no balona, ja beigās spiediens ir 2.5·10 ⁶ N/m² Gāzes temperatūru uzskatīt par pastāvīgu. [7.5 kg].

8-7. Aprēķināt sēra gāzes (SO₂) masu, ja tā aizņem 25 l tilpuma pie 760 mm Hg spiediena un tās temperatūra ir 20° C. [0.065 kg].

8-8. Aprēķināt gaisa masu auditorijā, kuras augstums 5 m un grīdas laukums 200 m². Gaisa spiediens 750 mm Hg, telpas temperatūra 17° C. (Pieņemot, ka viena kilogrammola gaisa masa ir 29 kg/kmol.). [1200 kg].

8-9. Cik reizu tā gaisa svars, kas piepilda telpu ziemā (7 °C) ir lielāks par gaisa svaru vasarā (37 °C)? Spiediens vienāds. [1.1 reizi].

8-10. Uzzīmēt 0.5 g ūdeņraza izotermas temperatūrām: 1) 0°C, 2) 100°C.

8-11. Uzzīmēt 15.5 g skābekļa izotermas temperatūrām: 1) 29° C un 2) 180° C.

8-12. Cik kilogrammolu gāzes atrodas balonā, kura tilpums 10 m³, ja gāzes spiediens 720 mm Hg un temperatūra 17° C? [0.4 kmol].

8-13. 5 g slāpekļa atrodas slēgtā traukā, kura tilpums 4 l, skābekli sasilda no 20° C līdz 40° C temperatūrai. Aprēķināt gāzes spiedienu pirms un pēc sildīsanas. [1.08·10 ⁵ N/m²; 1.16·10 ⁵ N/m²].

8-14. Atsūknētā un no abiem galiem aizlodētā horizontāla kapilāra vidū atrodas dzīvsudraba stabiņs, kura garums l = 20 cm. Nostādot kapilāru vertikāli, dzīvsudraba stabiņs pārvietojas par attālumu Ai = 10 cm. Līdz kādam spiedienam atsūknēts kapilārs? Kapilāra garums L = l m. [375 mm Hg].

8-15. Kādam jābūt bērnu gaisa balona apvalka svaram, lai balona rezultējosais cēlējspēks būtu nulle, t. i. , lai balons atrastos līdzsvara stāvoklī? Balons piepildīts ar ūdeņradi un tā diametrs 25 cm. Gaiss un ūdeņradis atrodas normālos apstākļos. Spiediens balonā ir vienāds ar ārējo spiedienu. [0.096 N].

8-16. Piesātinātu ūdens tvaiku spiediens 50° C temperatūrā ir 92.5 mm Hg. Kāds sajā gadījuma ir ūdens tvaiku blīvums? [0.083 kg/m³].

8-17. Aprēķināt ūdeņraza blīvumu, ja tā temperatūra ir 15° C un spiediens 730 mmHg. [0.081 kg/m³].

8-18. Gāzes blīvums 10° C temperatūrā pie 2·10 ⁵ N/m² spiediena ir 0.34 kg/m . Cik liela sīs gāzes viena kilogrammola masa? [4 kg/kmol].

8-19. Kāds ir gaisa blīvums traukā, ja trauks atsūknēts līdz vislielākajam retinājumam, kādu var iegūt mūsdienu laboratorijas apstākļos (p = 10 ¹¹ mm Hg)? Gaisa temperatūra 15° C. [1.6·10 ^-14 kg/m³].

8-20. 12 g gāzes 7° C temperatūrā aizņem 4·10 ^-3 m³ tilpuma. Pēc gāzes sasilsanas pie pastāvīgā spiediena tās blīvums sasniedz 6·10 ^-4 g/cm³. Līdz kādai temperatūrai gāze sasildīta? [1400° K].

8-21. 10 g skābekļa, kura temperatūra 10° C, atrodas zem 3 atm spiediena. Sildot pie pastāvīga spiediena, skābeklis izplesas un aizņem 10 l tilpuma. Aprēķināt 1) gāzes tilpumu pirms izplesanās; 2) gāzes temperatūru pēc izplesanās; 3) gāzes blīvumu pirms izplesanās; 4) gāzes blīvumu pēc izplēsanās. [1) 2.4·10 ^-3 m³; 2) 1170° K; 3) 4.14 kg/m³; 4) l kg/m³].

8-22. Aizlodēta trauka atrodas ūdens, kas aizņem pusi no trauka tilpuma. Aprēķināt ūdens tvaiku spiedienu un blīvumu 400° C temperatūrā, zinot, ka sajā temperatūrā viss ūdens pārvērsas tvaikos. [1.55·10 ⁸ N/m²; 500 kg/m³].

8-23. Attēlot grafiski skābekļa blīvuma atkarību 1) no spiediena, ja temperatūra T = const = 390° K (0 < ρ < 4 at, ik pēc 0.5 at) un no temperatūras, ja ρ = const = 4 at (200° K ≤ T ≤ 300° K, ik pēc 20°). [ p = ρ·μ / RT ja T =const, lielums ρ =Ap, t. i., ρ ir tiesi proporcionāls p, bet, ja p - const, lielums ρ = B/T, t. i., ρ ir apgriezti proporcionāls lielumam T.]

8-24. Slēgtā traukā, kura tilpums l m³, atrodas 0.9 kg ūdens un 1.6 kg skābekļa. Aprēķināt spiedienu traukā 500° C temperatūrā, zinot, ka sajā temperatūrā viss ūdens pārvērsas tvaikos. [6.4·10 ⁵ N/m²].

8-25. 6 g ogļskābās gāzes (CO₂) un 5 g slāpekļa oksīda (N₂O) piepilda, trauku, kura tilpums 2·10 ^-3 m³. Kāds ir kopīgais spiediens traukā 127° C temperatūrā? [4.15·10 ⁵ N/m²].

Molekulu termiskās kustības enerģija un siltumietilpības

9-1. Aprēķināt 1) ūdeņraza un 2) hēlija atoma masu. [1) 1.67·10 ^-27 kg; 2) 6.65·10 ^-27 kg].

9-2. Slāpekļa molekula ar ātrumu 600 m/s atsitas perpendikulāri pret trauka sieniņu un elastīgi atlec no tās, nezaudējot ātrumu. Aprēķināt spēka impulsu, ko iegūst trauka sieniņa trieciena brīdī. [5.6·10 ^-23 Nּs].

9-3. Argona molekula, lidodama ar ātrumu 500 m/s, elastīgi atsitas pret trauka sieniņu. Molekulas ātruma virziens veido ar trauka sieniņas normāli 60° leņķi. Aprēķināt spēka impulsu, ko iegūst trauka sieniņa trieciena brīdī. [3.3·10 ^-23N∙s].

9-4. Slāpekļa molekula lido ar ātrumu 430 m/s. Aprēķināt sās molekulas kustības daudzumu. [2·10 ^-23 kg∙m/s].

9-5. Cik molekulu satur l g ūdens tvaiku? [3.3·10 ²²].

9-6. Traukā, kura tilpums 4 /, atrodas l g ūdeņraza. Cik molekulu ir sā trauka l cm³? [7.5·10 ¹⁹ cm^-3].

9-7. Cik molekulu atrodas istabā, kuras tilpums 80 m³, temperatūra 17° ^c un gaisa spiediens 750 mm Hg? [2·10 ²⁷].

9-8. Cik molekulu ir trauka vienā kubikcentimetrā 10° C temperatūrā, ja trauks atsūknēts līdz vislielākajam retinājumam, kādu var iegūt mūsdienu laboratorijas apstākļos (p = 10 ^-11 mm Hg)? [3.4·10 ⁵ cm ^-3].

9-9. Lai stikla traukā iegūtu labu vakuumu, atsūknējot nepieciesams sasildīt trauka sieniņas, lai tās atbrīvotu no adsorbētās gāzes. Aprēķināt, par cik var paaugstināties spiediens sfēriska traukā, kura rādiuss r = 10 cm, ja adsorbētās molekulas pāriet no sieniņām traukā. Pieņemt, ka molekulas sķērsgriezuma laukums ir 10 ^-15 cm² un kārta ir monomolekulāra. Temperatūrai = 300° C. [1.8·10 ^-2 mm Hg].

9-10. Traukā atrodas 10 ^-10 kmol skābekļa un 10 ^-6 g slāpekļa. Maisījuma temperatūra 100° C. Pie tam spiediens traukā ir 10 ^-3 mm Hg. Aprēķināt; 1) trauka tilpumu; 2) skābekļa un slāpekļa parciālo spiedienu; 3) molekulu skaitu sā trauka l cm³. [1) 3.2·10 ^-3 m³; 2) 7.37·10 ^-4 mm Hg, 2.63·10 ⁴ mm Hg; 3) 2.6·10 ¹³ cm^-3].

9-11. Aprēķināt gaisa molekulu vidējo kvadrātisko ātrumu 17° C l temperatūrā, uzskatot gaisu par viendabīgu gāzi, kuras viena kilogrammola masa µ = 29 kg/kmol. [500 m/s].

9-12. Atrast hēlija un slāpekļa molekulu vidējo kvadrātisko ātrumu attiecību, ja abām gāzēm ir vienāda temperatūra. [2.65].

9-13. Aprēķināt ūdeņraza molekulu skaitu vienā kubikcentimetrā, ja tā spiediens 200 mm Hg, bet molekulu vidējais kvadrātiskais ātrums sajos apstākļos ir 2400 m/s. [4.2·10 ¹⁸ cm^-3].

9-14. Kādas gāzes blīvums ir 6·10 ^-2 kg/m³, tās molekulu vidējais kvadrātiskais ātrums 500 m/s. Aprēķināt, ar kādu spiedienu gāze spiez uz trauka sieniņām. [5·10 ³ N/m²].

9-15. Cik reizu puteklīsa, kas suspendēts gaisā, vidējais kvadrātiskais ātrums ir mazāks par gaisa molekulu vidējo kvadrātisko ātrumu? Puteklīsa masa 10 ^-8 g. Gaisu uzskatīt par viendabīgu gāzi, kuras viena kilograīnmola masa ir 29 kg/kmol. [1.44·10 ⁷ reizes].

9-16. Aprēķināt ūdeņraza molekulas kustības daudzumu 20° C temperatūrā. Uzskatīt, ka molekulas ātrums ir vienāds ar vidējo kvadrātisko ātrumu. [6.3·10 ^-24 kg·m/s].

9-17. Traukā, kura tilpums 2 l, atrodas 10 g skābekļa zem 680 mm Hg spiediena. Aprēķināt: 1) gāzes molekulu vidējo kvadrātisko ātrumu; 2) molekulu skaitu traukā; 3) gāzes blīvumu. [1) 230 m/s; 2) 1.9·10²³; 3) 5.0 kg/m³].

9-18. Gumiguta daļiņas, kuru diametrs D = l µm, piedalās Brauna kustībā. Gumiguta blīvums p = 1 g/cm³. Aprēķināt gumiguta daļiņu vidējo kvadrātisko ātrumu, ja t = 0° C. [4.6·10 ^-3 m/s].

9-19. Kādas gāzes molekulu vidējais kvadrātiskais ātrums ir 450 m/s. Gāzes spiediens 5·10 ⁴ N/m². Aprēķināt gāzes blīvumu sajos apstākļos. [0.74 kg/m³].

9-20. 1) Aprēķināt molekulu vidējo kvadrātisko ātrumu gāzei, kuras blīvums pie 750 mm Hg spiediena ir 8.2·10 ^-5 g/cm³; 2) cik liela ir sās gāzes viena kilogrammola masa, ja tas blīvums dots 17° C temperatūra? [1) 1900 m/s; 2) 2 kg/kmol].

9-21. Kādas gāzes molekulu vidējais kvadrātiskais ātrums normālos apstākļos ir 461 m/s. Cik molekulu satur sās gāzes 2 g? [l .88·10²²].

9-22. Cik liela ir 20 g skābekļa termiskās kustības enerģija 10° C temperatūrā? Kāda daļa no sīs enerģijas tiek patērēta translācijas kustībai un kāda daļa - rotācijas kustībai? [3.7·10³ J, 2.2·10³ J un 1.5·10³ J].

9-23. Aprēķināt viena grama gaisa molekulu termiskās kustības kinētisko enerģiju 15° C temperatūrā. Gaisu uzskaitīt par viendabīgu gāzi, kuras viena kilogrammola masa ir 29 kg/kmol. [210 J].

9-24. Aprēķināt l kg slāpekļa molekulu rotācijas kustības enerģiju 7° C temperatūrā. [8.3·10⁴ J].

9-25. Cik liela ir divatomu gāzes molekulu termiskās kustības enerģija, ja gāze atrodas noslēgtā traukā, kura tilpums 2 l, zem spiediena 1.5·10⁵ N/m²? [750 J].

9-26. Balonā, kura tilpums 0.02 m³, atrodas slāpeklis. Slāpekļa molekulu translācijas kustības kinētiskā enerģija ir 5·10³ J, bet to vidējais kvadrātiskais ātrums 2·10³ m/s. Aprēķināt: 1) slāpekļa daudzumu balonā; 2) zem kāda spiediena atrodas slāpeklis. [1) 2.5·10 ^-3 kg; 2) 1.67·10⁵ N/m²].

9-27. Kādā temperatūrā hēlija atomu termiskās kustības vidējā kinētiskā enerģija ir pietiekama, lai hēlija atomi pārvarētu Zemes gravitāciju un uz visiem laikiem atstātu Zemes atmosfēru? Atrisināt līdzīgu uzdevumu, attiecinot to uz Mēnesi. [1) 20000° K; 2) 900° K].

9-28. l kg divatomu gāzes atrodas zem spiediena p = 8·10⁴ N/m². Tās blīvums p = 4 kg/m³. Aprēķināt gāzes molekulu termiskās kustības enerģiju sajos apstākļos. [5·10⁴ J].

9-29. Kāds skaits divatomu gāzes molekulu aizņem tilpumu V = 10 cm³, ja spiediens p = 40 mm Hg un temperatūra t = 21° C? Kāda ir so molekulu termiskās kustības enerģija? [l .3·10¹⁹; 0.133 J].

9-30. Noteikt īpatnējo siltumietilpību, 1) ja V = const un 2) ja p = const. [1) 650 J/kg·deg; 2) 910 J/kg·deg].

9-31. Noteikt īpatnējo siltumietilpību pie pastāvīga spiediena sādām gāzēm: 1) hlorūdeņradim; 2) neonam; 3) slāpekļa oksīdam; 4) oglekļa oksīdam un 5) dzīvsudraba tvaikiem. [1) 800 J/kg·deg; 2) 1025 J/kg·deg; 3) 970 J/ kg·deg; 4) 1040 J/kg·deg; 5)103 J/kg·deg].

9-32. Kāda ir skābekļa īpatnējās siltumietilpības pie pastāvīga spiediena attiecība pret īpatnējo siltumietilpību pie pastāvīga tilpuma? [l .4],

9-33. Kādas divatomu gāzes īpatnēja siltumietilpība pie pastāvīga spiediena ir 3.5 cal/g·deg. Cik liela ir sās gāzes viena kilogrammola masa? 1 kg/kmol].

9-34. Cik lielas ir divatomu gāzes īpatnējās siltumietilpības c_v un c_p, ja sās gāzes blīvums normālos apstākļos ir 1.43 kg/m³? [650 J/kg·deg; 910 J/kg·deg]

9-35. Noteikt kādas gāzes īpatnējās siltumietilpības c_v un c_p, ja zināms, kaļ sās gāzes viena kilogrammola masa µ = 30 kg/kmol un attiecība c_p/c_v = 1.41 [693 J/kg·deg; 970 J/kg·deg].

9-36. Cik reizu sprāgstosās gāzes siltumietilpība ir lielāka par ūdens tvaika siltumietilpību, kurs rodas, so gāzi sadedzinot? Uzdevumu atrisināt sādiem gadījumiem: 1) V = const un 2) p = const. [1) 1.25; 2) 1.31].

9-37. Noteikt īpatnējo siltumietilpību pie pastāvīga spiediena gāzu maisījumam, kas sastāv no 3 kmol argona un 2 kmol slāpekļa. [685 J/kg·deg].

9-38. Aprēķināt attiecību c_p/c_v gāzu maisījumam, kas sastāv no 8 g hēlija un 16 g skābekļa. [1.59].

9-39. Gāzu maisījums sastāv no viena kilogrammola skābekļa un daziem kilogrammoliem argona. Sī maisījuma īpatnējā siltumietilpība pie pastāvīga tilpuma ir 430 J/kg·deg. Cik daudz argona atrodas gāzu maisījumā? [60 kg].

9-40. 10 g skābekļa atrodas zem spiediena 3·10⁵ N/m². Skābekļa temperatūra 10° C. Pēc sildīsanas pie pastāvīga spiediena gāze aizņem 10 l lielu tilpumu. Aprēķināt: 1) siltuma daudzumu, ko saņem gāze; 2) gāzei molekulu termiskās kustības enerģiju pirms un pēc sildīsanas. [1) 7.9·10³ J; 2) 1.8·10³ J, 7.6·10³ J].

9-41. 12 g slāpekļa , kura temperatūra 10° C, atrodas slēgtā traukā. Trauka tilpums 2 l. Pēc sildīsanas spiediens traukā sasniedz 10⁴ mm Hg. Kādu siltuma daudzumu saņem gāze sasilstot? [4.15·10³ J].

9-42. 2 l slāpekļa atrodas zem spiediena 10⁵ N/m². Kāds siltuma] daudzums jāpievada slāpeklim, lai 1) pie p = const tā tilpums palielinātos divas reizes, 2) pie V = const spiediens palielinātos divas reizes? [1) 700 J; 2 500 J].

9-43. Slēgtā traukā atrodas 14 g slāpekļa zem spiediena 10⁵ N/m². Slāpekļa temperatūra 27° C. Pēc sildīsanas spiediens traukā palielinās 5 reizes. Aprēķināt: 1) līdz kādai temperatūrai gāze sasildīta; 2) trauka tilpumu; 3) kādu siltuma daudzumu saņēmusi gāze? [1) 1500° K; 2) 12.4·10 ^-3 m³; 3) 12.4 kJ].

9-44. Kāds siltuma daudzums jāpievada 12 g skābekļa, lai pie pastāvīga spiediena to sasildītu par 50°? [545 J].

9-45. 40 g skābekļa sasildīsanai no 16° C līdz 14° C patērētas 150 cal. Kādos apstākļos gāze sildīta? (Pie pastāvīga tilpuma vai pie pastāvīgai spiediena?) [20.8·10³ J/kmol·deg; (pie pastāvīga tilpuma)].

9-46. Slēgtā traukā, kura tilpums 10 l, atrodas gaiss pie spiediena 10⁵ N/m². Kāds siltuma daudzums jāpievada gaisam, lai spiediens traukā palielinātos 5 reizes? [10⁴J].

9.47. 1) Cik daudz ogļskābās gāzes var sasildīt no 20° C līdz 100° C, ja pievadītais siltuma daudzums ir 222.6 kJ? 2) Par cik tādā gadījumā izmainās vienas molekulas kinētiskā enerģija? Sildīsanas laikā gāze izplesas, ja p = const. [l) 3.7·10 ^-3 kg; 2) 3.3·10 ^-21J].

9.48. Slēgtā traukā, kura tilpums V = 1 l, atrodas slāpeklis, kura blīvums p = 1.4 kg/m³. Kāds siltuma daudzums g jāpievada slāpeklim, lai sajos apstākļos to sasildītu par Δt = 100° C? [208 J].

9-49. Slāpeklis atrodas slēgtā traukā, kura tilpums 3 l. Slāpekļa temperatūra 27° C un spiediens 3 at. Pēc sildīsanas spiediena traukā palielinās līdz 25 at. Noteikt: 1) slāpekļa temperatūru pēc sildīsanas; 2) slāpeklim pievadīto siltuma daudzumu. [1) 2500° K; 2)16.3 kJ].

9-50. Lai sasildītu noteiktu daudzumu gāzes par 50° pie pastāvīga spiediena, jāpatērē 670.4 J siltuma. So pasu gāzes daudzumu atdzesējot par 100° pie pastāvīga spiediena, izdalās 1006 J. Kāds ir sīs gāzes molekulu brīvības pakāpju skaits? [6].

Molekulu sadalījums pēc ātrumiem. Barometriskā formula.

10-1. 10 g slāpekļa atrodas slēgta trauka 7° C temperatūra. 1) kāds siltuma daudzums jāpievada slāpeklim, lai tā molekulu vidējais kvadrātiskais ātrums palielinātos divas reizes? 2) Cik reizu pie tam palielinās gāzes temperatūra? 3) Cik reizu palielinās gāzes spiediens uz trauka sienām? [1) 6.25 kJ; 2) 4T₁; 3) 4 p₁ ].

10-2. Slēgtā traukā, kura tilpums 2 l atrodas hēlijs. Tā temperatūra 20° C i spiediens 10⁵ N/m². 1) Cik daudz siltuma jāpievada hēlijam, lai tā temperatūru paaugstinātu par 100°? 2) Kāds ir tā molekulu Vidējais kvadrātiskais ātrums jaunajā temperatūrā? 3) Kāds ir spiediens? 4) Kāds ir hēlija blīvums? 5) Kāda ir tā molekulu termiskās kustības enerģija? 6) 102 J; 2) 1.57·10³ m/s; 3) 1.33·10⁵ N/m²; 4) 0.164 kg/m³].

10-3. Slēgtā traukā, kura tilpums 2 l, atrodas m gramu slāpekļa un m gramu argona normālos apstākļos. Cik daudz siltuma jāpievada, lai so gāzu maisījumu sasildītu par 100°? [155 J].

10-4. Gāzes blīvums pie 300 mm Hg spiediena ir 0.3 g/l. Aprēķināt sās gāzes molekulu vidējo aritmētisko, vidējo kvadrātisko un visvarbūtīgāko ātrumu. [579 m/s; 628 m/s; 513 m/s].

10-5. Kādā temperatūrā slāpekļa molekulu vidējais kvadrātiskais ātrums ir par 50 m/s lielāks nekā to visvarbūtīgākais ātrums? [83° K].

10-6. Kādai skābekļa molekulu daļai piemīt ātrumi no 100 m/s līdz 110 m/s, ja tā temperatūra 0° C? [0.4%].

10-7. Kādai slāpekļa molekulu daļai piemīt ātrumi no 300 m/s līdz 325 m/s, ja tā temperatūra 150° C? [2.8%].

10-8. Kādai ūdeņraza molekulu daļai piemīt ātrumi no 2000 m/s līdz 2100 m/s, ja tā temperatūra 0° C? [4.5%].

10-9. Kādai slāpekļa molekulu daļai piemīt ātrumi, kas atrodas intervālā v_v + ∆v, kur ∆v = 20 m/s, ja tā temperatūra T? Uzdevumu atrisināt sādām temperatūrām: 1) T= 400° K un 2) T= 900° K. [1) 3.4%; 2) 2.2%].

10-10. Kādai slāpekļa molekulu daļai piemīt ātrumi, kas atrodas intervālā no v₁ = 300 m/s līdz v₂ = 800 m/s, ja tā temperatūra T= 150° C? [70%].

10-11. Kādai molekulu daļai no kopīgā molekulu skaita N piemīt ātrumi, kas 1) lielāki par visvarbūtīgāko ātrumu un 2) mazāki par visvarbūtīgāko ātrumu? [1) 57%; 2) 43%].

10-12. Balonā atrodas 2.5 g skābekļa. Noteikt skābekļa molekulu skaiti! kuru ātrumi pārsniedz vidējo kvadrātisko ātrumu, [l .9∙10²²].

10-13. Traukā atrodas 8 g skābekļa, kura temperatūra 1600° K. Kādam skaitam skābekļa molekulu piemīt translācijas kustības kinētiskā enerģija, kas pārsniedz vērtību W₀ = 6.65∙10 ^-20J? [1.8∙10²²].

10-14. Kosmiskā stacija atrodas Armēnijā, Alageza kalnā 3250 m virs jūras līmeņa. Aprēķināt gaisa spiedienu sajā augstumā. Gaisa temperatūru uzskatīt par pastāvīgu, un tā ir 5° C. Pieņemt, ka gaisa kilogrammola masa ir 29 kg/kmol. Gaisa spiediens jūras līmenī ir 760 mm Hg. [510 mm Hg].

10-15. Kādā augstumā gaisa spiediens ir 75% no gaisa spiediena jūras līmenī? Temperatūru uzskatīt par pastāvīgu, un tā ir 0° C. [2.3 km].

10-16. Pasazieru lidmasīna lido 8300 m augstumā. Lai pasazieri nebūtu jāapgādā ar skābekļa maskām, ar kompresoru kabīnēs uztur pastāvīgu spiedienu, kas atbilst 2700 m augstumam. Aprēķināt starpību starp spiedienu kabīnes iekspusē un ārpusē. Uzskatīt, ka ārējā gaisa vidējā temperatūra ir 0⁰ C. [0.36 at].

10-17. Aprēķināt ieprieksējā uzdevumā, cik reizu gaisa blīvums kabīnē l lielāks par gaisa blīvumu ārpus tās, ja ārējā temperatūra ir -20° C, bet temperatūra kabīnē +20° C. [1.7 reizes].

10-18. Cik sver l m³ gaisa 1) pie Zemes virsmas; 2) 4 km virs Zemes virsmas? Uzskatīt, ka gaisa temperatūra pastāvīgi ir 0° C. Gaisa spiediens pie Zemes virsmas ir 10⁵ N/m². [1) 12.54 N; 2) 7.65 N].

10-19. Kādā augstumā virs jūras līmeņa gāzes blīvums ir 50% no tās blīvuma jūras līmenī? Temperatūru uzskatīt par pastāvīgu, un tā ir 0° C. Uzdevumu atrisināt: 1) gaisam; 2) ūdeņradim. [1) 5.5 km; 2) 80 km].

10-20. Aprēķināt ogļskābās gāzes molekulu brīvā noskrējiena vidējo garumu 100° C temperatūrā pie 0.1 mm Hg spiediena. Pieņemt, ka ogļskābās gāzes molekulas diametrs ir 3.2∙l0 ^-8 cm. [ 8.5∙l0 ^-4 m].

10-21. Ar jonizācijas manometru, kas bija uzstādīts tresajā padomju Zemes mākslīgajā pavadonī, konstatēts, ka 300 km augstumā virs Zemes virsmas vienā atmosfēras kubikcentimetrā ir apmēram miljards gāzes daļiņu. Aprēķināt gāzes daļiņu brīvā noskrējiena vidējo garumu sajā augstumā. Pieņemt, ka daļiņu diametrs ir 2∙10 ^-10 m. [5.6 km].

10-22. Aprēķināt gaisa molekulu brīvā noskrējiena vidējo garumu normālos apstākļos. Pieņemt, ka gaisa molekulas diametrs ir 3∙10 ^-8 cm. [9.3∙10⁸ m].

10-23. Aprēķināt ogļskābās gāzes molekulu vidējo sadursmju skaitu l sekundē 100° C temperatūrā, ja brīvā noskrējiena vidējais garums sajos apstākļos ir 8.7∙10 ^-2 cm. [4.9∙10⁵ s^-1].

10-24. Aprēķināt slāpekļa molekulu vidējo sadursmju skaitu l sekundē, ja temperatūra t = 27° C un spiediens p = 400 mm Hg. [2.47∙10⁹ s^-1].

10-25. Traukā, kura tilpums 0.5 l, normālos apstākļos atrodas skābeklis. Aprēķināt skābekļa molekulu kopējo sadursmju skaitu sajā traukā l sekundē. [3∙10³¹].

Pārneses procesi.

11-1. Aprēķināt ūdeņraza difūzijas koeficientu normālos apstākļos, ja molekulu brīvā noskrējiena vidējais garums sajos apstākļos ir 1.6∙10 ^-7 m [0.91∙10 ^-4 m²/s].

11-2. Aprēķināt hēlija difūzijas koeficientu normālos apstākļos. [8.4∙10 ^-5 m²/s].

11-3. Grafiski attēlot ūdeņraza difūzijas koeficienta atkarību no temperatūras intervālā 100° K < T < 600° K pēc katriem 100° pie pastāvīga spiediena p = const. = 2 at. .

11-4. Aprēķināt slāpekļa daudzumu, kas difūzijas rezultātā 10 sekundēs izplūst caur 100 cm² lielu laukumu, ja blīvuma gradients laukumam perpendikulārā virzienā ir 1.26 kg/m⁴. Slāpekļa temperatūra 27° C; slāpekļa molekulu brīvā noskrējiena vidējais garums ir 10 ^-5 cm. [2∙10 ^-6 kg].

11-5. Divi trauki A un B savienoti ar caurulīti, kuras diametrs d = 1 cm un garums l = 1.5 cm. Ja caurulītes krāns ir aizgriezts, tad gaisa spiediens traukā A ir p; trauks B atsūknēts līdz spiedienam p₂ << p₁ Aprēķināt, cik daudz gaisa difundē no trauka A traukā B pirmajā sekundē pēc krāna atgriesanas. Uzskatīt, ka gaisa temperatūra abos traukos ir vienāda un tā ir 17° C; gaisa molekula diametrs σ =3∙10 ^-10 m. [9.7∙10 ^-8 kg].

11-6. Aprēķināt hēlija molekulu brīvā noskrējiena vidējo garumu 0°C temperatūrā pie 760 mm Hg spiediena, ja sajos apstākļos ieksējās berzes koeficients (dinamiskā viskozitāte) ir 1.3∙10 ^-4 g/cm∙s. [1.84∙10 ^-7 m].

11-7. Aprēķināt slāpekļa ieksējās berzes koeficientu normālos apstākļos, ja tā difūzijas koeficients sajos apstākļos ir 0.142 cm²/s. [1.78∙10⁵ N∙s/m²].

11-8. Aprēķināt skābekļa molekulas diametru, ja zināms, ka 0° C temperatūrā skābekļa ieksējās berzes koeficients η = 18.8∙10 ^-6 N∙s/m². [3∙10 ^-10 m].

11-9. Grafiski attēlot slāpekļa ieksējas berzes koeficienta atkarību no temperatūras intervālā 100° K < T < 600° K pēc katriem 100°. [].

11-10. Aprēķināt gaisa difūzijas koeficientu un tā ieksējās berzes koeficientu 10° C temperatūrā pie 760 mm Hg spiediena. Pieņemt, ka gaisa molekulas diametrs ir 3∙10 ^-10 m. [1.48∙10 ^-5 m²/s].

11-11. Cik reizu skābekļa ieksējās berzes koeficients ir lielāks par slāpekļa ieksējās berzes koeficientu? Gāzu temperatūras ir vienādas. [1.07 reizes].

11-12. Noteiktos apstākļos ūdeņraza molekulu difūzijas un ieksējas berzes koeficienti attiecīgi ir D = 1.42 cm²/s un η = 8.5∙10 ^-6 N∙s/m². Aprēķināt sajos apstākļos ūdeņraza molekulu skaitu vienā kubikcentimetrā, [ 1.8∙10²⁵ m^-3].

11-13. Skābekļa difūzijas un ieksējās berzes koeficienti attiecīgi ir 1.22∙10 ^-5 m²/s un η = 1.95∙10 ^-5 kg/m∙s. Aprēķināt sajos apstākļos: 1) skābekļa blīvumu; 2) tā molekulu brīvā noskrējiena vidējo garumu un 3) tā molekulu vidējo aritmētisko ātrumu. [1) 1.6 kg/m³; 2) 8.35∙10 ^-8 m; 3) 440 m/s].

11-14. Kādu vislielāko ātrumu var sasniegt lietus piliens, kura diametrs ir 0.3 mm? Pieņemt, ka gaisa molekulas diametrs ir 3∙10 ^-10 m; gaisa temperatūra 0° C. Uzskatīt, ka lietus pilienam ir spēkā Stoksa likums. [2.72 m/s].

11-15. Lidmasīna lido ar ātrumu 360 km/h. Uzskatot, ka gaisa kārta, kas apņem lidmasīnas spārnu viskozitātes dēļ, ir 4 cm, atrast tangenciālo spēku, kas darbojas uz spārna virsmas katru kvadrātmetru. Pieņemt, ka gaisa molekulas diametrs ir 3∙10^-8 cm. Gaisa temperatūra 0° C. [0.045 N].

11-16. Telpa starp diviem koaksiāliem cilindriem piepildīta ar gāzi. Cilindru rādiusi attiecīgi ir r = 5 cm un R = 5.2 cm. Ieksējā cilindra augstums h = 25 cm. Ārējais cilindrs rotē ar ātrumu, kas atbilst v = 360 apgr./min. Lai ieksējais cilindrs paliktu nekustīgs, tam jāpieliek tangenciālais spēks F = 1.38∙10 ^-3 N. Uzskatot pirmajā tuvinājumā to par plaknes gadījumu, aprēķināt pēc sā eksperimenta lielumiem viskozitātes koeficientu gāzei, kas atrodas starp cilindriem. [1.8∙10 ^-5 N∙s/m²].

11-17. Aprēķināt ūdeņraza siltumvadītspējas koeficientu, ja zināms, ka tā ieksējās berzes koeficients sajos apstākļos ir 8.6∙10 ^-6 N∙s /m². [0.090 W/m∙deg].

11-18. Aprēķināt ūdeņraza siltumvadītspējas koeficientu 10° C temperatūrā pie 10⁵ N/cm² spiediena. Pieņemt, ka gaisa molekulas diametrs ir 3∙10⁸ cm. [13.2∙10 ^-3 W/m∙deg].

11-19. Grafiski attēlot ūdeņraza siltumvadītspējas koeficienta atkarību no temperatūras intervālā 100° K < T < 600° K pēc katriem 100°. [].

11-20. Traukā, kura tilpums V = 2 l, atrodas N = 4∙10²² divatomu gāzes molekulas. Gāzes siltumvadītspējas koeficients K = 0.014 W/m∙deg. Aprēķināt gāzes difūzijas koeficientu sajos apstākļos. [2∙10 ^-5 m²/s ].

11-21. Ogļskābā gāze un slāpeklis atrodas vienādā temperatūrā pie vienāda spiediena. Aprēķināt so gāzu: 1) difūzijas koeficientu attiecību; 2) ieksējās berzes koeficientu un 3) siltumvadītspējas koeficientu attiecību. So gāzu molekulu diametrus uzskatīt par vienādiem. [1) 0.8; 2) 1.25; 3) 0.96].

11-22. Starp Djuāra trauka sieniņām, kuru attālums 8 mm, atrodas gaiss Kādam jābūt spiedienam, lai, atsūknējot gaisu, tā siltumvadītspēja sāktu samazināties? Gaisa temperatūra 17° C. Pieņemt, ka gaisa molekulas diametrs ir 3∙10 ^-7mm. [1.26N/m²].

11-23. Cilindrisks termoss, kura ārējais rādiuss r₂ = 10 cm, ieksējais rādiuss r₁ = 9 cm un augstums h = 20 cm, piepildīts ar ledu. Ledus temperatūra 0° C; ārējā gaisa temperatūra 20° C. 1) Kādai jābūt gaisa spiediena robezvērtībai starp termosa sieniņām, lai siltuma vadītspējas koeficients vēl būtu atkarīgs no spiediena? Pieņemt, ka gaisa molekulas diametrs 3∙l0 ^-8 cm; uzskatīt, ka gaisa temperatūra starp sieniņām ir vienāda ar ledus un apkārtējās telpas temperatūru vidējo aritmētisko. 2) Aprēķināt starp termosa sieniņām ieslēgtā gaisa siltumvadītspējas koeficientu pie spiedieniem: a) 760 mm Hg, b) 10 ^-4 mm Hg (µ = 29 kg/mol). 3) Kāds siltuma daudzums siltumvadītspējas dēļ izplūst vienā minūtē caur termosa sānu virsmu, ja vidējais rādiuss 9.5 cm? Uzdevumu atrisināt sādiem spiedieniem: a) 760 mm Hg un b) 10 ^-4 mm Hg. [1) 7.6∙10 ^-3 mm Hg; 2)a) 13.1∙10^-3 W/m∙deg, b) 17.8∙10 ^-5 W/m∙deg ; 3) a) 188 J, b) 25.5 J].

11-24. Cik daudz siltuma katru stundu aizplūst caur sakarā ar to, ka gaisam starp loga rāmjiem piemīt siltumvadītspēja? Katra rāmja laukums 4 m²; attālums starp rāmjiem 30 cm. Telpas temperatūra 18° C, ārējā gaisa temperatūra - 20° C. Pieņemt, ka gaisa molekulu diametrs ir 3∙10 ^-8 cm, bet gaisa temperatūra starp rāmjiem ir vienāda ar telpas un ārējā gaisa temperatūru vidējo aritmētisko. Spiediens ir 760 mm Hg. [5.7 kcal].

11-25. Starp divām plāksnēm, kuras atrodas l mm attālumā viena no otras, atrodas gaiss. Starp plāksnēm pastāv temperatūru starpība ∆T = 1°. Katras plāksnes laukums 5 = 100 cm². Kāds siltuma daudzums siltumvadītspējas dēļ pāriet no vienas plāksnes uz otru 10 minūtēs? Uzskatīt, ka gaiss atrodas normālos apstākļos. Pieņemt, ka gaisa molekulas diametrs ir 3∙10 ^-10 m. [78 J].

Pirmais termodinamikas likums. Izoparametriskie un adiabātiskie procesi

12-1. 10 g skābekļa atrodas 10° C temperatūrā zem 3∙10⁵ N/m² spiediena. Pēc sildīsanas pie pastāvīga spiediena gāze aizņem 10 l tilpuma. Aprēķināt: 1) siltuma daudzumu, ko iegūst gāze; 2) gāzes ieksējās enerģijas izmaiņu; 3) darbu, ko gāze padara izplesoties. [1) 7.92∙10³ J; 2) 5660 J; 3) 2.26∙10³ J].

12-2. Ūdeņradis, kura masa 6.5 g un temperatūra 27° C, divkārt palielina tilpumu pie p = const, tāpēc ka no ārienes tiek pievadīts siltums. Aprēķināt: 1) izplesanās darbu; 2) gāzes ieksējās enerģijas izmaiņu; 3) siltuma daudzumu kas pievadīts gāzei. [1) 8.1∙10³ J; 2) 20.2∙10³ J; 3) 28.3∙10³ J].

12-3. Slēgtā traukā atrodas 20 g slāpekļa un 32 g skābekļa. Aprēķināt sā gāzu maisījuma ieksējās enerģijas izmaiņu, ja to atdzesē par 28°. [1000 J].

12-4. 2 kmol ogļskābās gāzes pie pastāvīga spiediena sasilda par 50°. Aprēķināt: 1) gāzes ieksējās enerģijas izmaiņu; 2) izplesanās darbu; 3) siltuma daudzumu, kas pievadīts gāzei. [1) 2500 kJ; 2) 830 kJ; 3) 3330 kJ].

12-5. Divatomu gāzei pievadītas 500 cal siltuma. Tādēļ gāze pie pastāvīga spiediena izplesas. Aprēķināt gāzes izplesanās darbu. [600 J].

12-6. Divatomu gāze, izobāriski izplesoties, padara 156.8 J darbu. Cik daudz siltuma pievadīts gāzei? [550 J].

12-7. Gāze aizņem 5 t tilpuma, tās temperatūra 17° C un spiediens 210 N/m². Sildīsanas rezultātā gāze izobāriski izplesas. Izplesoties gāze padara 196 N darba. Par cik grādiem gāze tiek sasildīta? [57 °].

12-8. Brīvas izplesanās apstākļos 7 g ogļskābās gāzes sasildīti par 10°. Aprēķināt gāzes izplesanās darbu un tās ieksējās enerģijas izmaiņu. [13.21 39.6 J].

12-9. l kmol daudzatomu gāzes sasildīts par 100° brīvas izplesanās: apstākļos. Aprēķināt: 1) siltuma daudzumu, kas pievadīts gāzei; 2) tās ieksējās enerģijas izmaiņu; 3) izplesanās darbu. [1) 3.32∙10⁶ J; 2) 2.49∙10⁶ J; 3) 8.31∙10⁵ J].

12-10. Trauka zem virzuļa atrodas l g slāpekļa. 1) Cik daudz siltuma jāpatērē, lai slāpekli sasildītu par 10°? Cik augstu tādā gadījumā paceļas vizulis? Virzuļa svars 9.8 N, tā sķērsgriezuma laukums 10 cm². Spiediens virs virzuļa l at. [1) 10.4 J; 2) 2.8 cm].

12-11. Trauka zem virzuļa atrodas sprāgstosa gāze. Aprēķināt, cik daudz siltuma izdalās, sai gāzei sprāgstot, ja zināms, ka gāzes ieksējā enerģija sprādzienā izmainās par 80.2 cal un virzulis paceļas par 20 cm. Virzuļa svars 196 N, tā sķērsgriezuma laukums 10 cm². Virs virzuļa atrodas gaiss normālos apstākļos. [360 J].

12-12. 10.5 g slāpekļa -23° C temperatūra izotermiski izplesas, pamazinoties spiedienam no p₁ = 2.5 at līdz p₂ = l at. Aprēķināt darbu, ko gāze padara izplesoties. [720 J].

12-13. 10 g slāpekļa, kura temperatūra 17° C, izotermiski izplesoties, padara 860 J darba. Kā izmainās slāpekļa spiediens, tam izplesoties? [2.72 reizes].

12-14. 10 g gāzes izotermiski izplesoties no tilpuma V₁ līdz tilpumam V₂ = 2V₁, tiek padarīts 575 J darba. Aprēķināt gāzes molekulu vidējo kvadrātisko ātrumu sajā temperatūrā. [500 m/s].

12-15. Vienam litram hēlija, kas atrodas normālos apstākļos, no ārienes tiek pievadīts siltums. Tā rezultātā hēlijs izotermiski izplesas, aizņemdams 2 l tilpuma. Aprēķināt: 1) darbu, ko gāze padara izplesoties; 2) gāzei pievadītā siltuma daudzumu. [1) 70 J; 2) 16.8 cal].

12-16. 2 m³ gāzes izotermiski izplesoties, spiediens izmainās no p₁ = 5 at līdz p₂ = 4 at. Aprēķināt darbu, ko gāze padara izplesoties. [2.2∙10 J].

12-17. Līdz kādai temperatūrai atdziest gaiss, kura temperatūra 0° C, ja tas adiabātiski izplesas no tilpuma V, līdz tilpumam V₂ = 2V₁ ? [-66° C].

12-18. 7.5 l skābekļa adiabātiski saspiez līdz l l tilpuma, pie tam saspiesanas beigās spiediens sasniedz 1.6∙10⁶ N/m². Kāds bija gāzes spiediens Pirms saspiesanas? [9.5∙10⁴ N/m² ].

12-19. Ieksdedzes dzinēja cilindros gaiss tiek saspiests adiabātiski, un tā rezultātā gaisa spiediens izmainās no p₁ = l at līdz p₂ = 35 at. Gaisa sākuma temperatūra 40° C. Aprēķināt gaisa temperatūru saspiesanas beigās. [865° K].

12-20. Gāze adiabātiski izplesas, un tās tilpums palielinās divas reizes, bet temperatūra (absolūtā) samazinās 1.32 reizes. Kāds ir sās gāzes molekulu brīvības pakāpju skaits? [5].

12-21. Divatomu gāzi, kuras temperatūra 27° C un spiediens 2∙10⁶ N/m², adiabātiski saspiez no tilpuma V/ līdz tilpumam V₂ = 0.5 V₁. Aprēķināt sās gāzes temperatūru un spiedienu pēc saspiesanas. [123° C; 52.8∙10⁵ N/m² ].

12-22. Traukā zem virzuļa atrodas sprāgstosa gāze, kas normālos apstākļos aizņem 10 ^-4 m³ tilpuma. Strauji saspiezot, gāze uzliesmo. Aprēķināt sprāgstosas gāzes uzliesmosanas temperatūru, ja zināms, ka saspiezot padarīti 46.4 J darba. [780° K].

12-23. Traukā zem virzuļa atrodas gāze normālos apstākļos. Attālums starp trauka dibenu un virzuļa dibenu ir 25 cm. Uzliekot uz virzuļa 196 N smagu atsvaru, virzulis noslīd uz leju par 13.4 cm. Uzskatot, ka gāzi saspiez adiabātiski, aprēķināt tai attiecību c_p/c_v. Virzuļa sķērsgriezuma laukums 10 cm²; virzuļa svaru neievērot. [1.4].

12-24. Divatomu gāze aizņem tilpumu V₁ = 0.5 l pie spiediena p₁ = 0.5 at. Gāzi saspiez adiabātiski līdz tilpumam V₂ un spiedienam p₂ un pēc tam, nemainot tilpumu V₂, to atdzesē līdz sākotnējai temperatūrai. Tā rezultātā gāzes spiediens kļūst p₀ = l at liels. 1) Attēlot so procesu grafiski; 2) Aprēķināt tilpumu V₂ un spiedienu p₂. [2) 0.25 l; 1.32 at].

12-25. Gāze adiabātiski izplesas tā, ka tās spiediens samazinās no 2 at līdz l at. Pēc tam, nemainot tilpumu, to sasilda līdz sākotnējai temperatūrai, līdz ar to tās spiediens pieaug līdz 1.22 at. 1) Noteikt sai gāzei attiecību c_p/c_v.2) Konstruēt sā procesa grafiku, [l.4].

Otrais termodinamikas likums. Karno cikls. Entropija.

13-1. l kg gaisa, kura temperatūra 30° C un spiediens 1.5 atm, adiabātiski izplesas, tā rezultātā gaisa spiediens samazinās līdz l atm. Aprēķināt: 1) izplesanās pakāpi; 2) beigu temperatūru; 3) darbu, ko gāze padara izplesoties. [1) 1.33; 2) 270°K; 3) 2.3∙10⁴J].

13-2. Noteikts daudzums skābekļa, kura temperatūra t₁   = 27° C un spiediens p₁ = 8.2∙10⁵ N/m², aizņem tilpumu V₁ = 3 l. (13-2. Att.). Gāzei otrajā stāvoklī ir sādi parametri: V₂ = 4.5 l un p₂ = 6∙10⁵ N/m² . Aprēķināt: 1) siltuma daudzumu, ko iegūst gāze; 2) darbu, ko gāze padara izplesoties; 3) gāzes ieksējās enerģijas izmaiņu. Uzdevumu atrisināt gadījumiem, kad gāze pāriet no pirmā stāvokļa otrajā: 1) pa ceļu ACB un 2) pa ceļu ADB. [1) 1.55 kJ, 0.92 U, 0.63 U; 2) 1.88kJ, 1.25 kJ, 0.63 kJ].

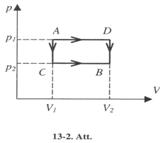
13-3. Ideāla siltummasīna, strādādama pēc Kārno cikla, katrā ciklā saņem no sildītāja 600 cal. Sildītāja temperatūra 400° K, dzesinātajā temperatūra 300° K. Aprēķināt darbu, ko masīna padara viena cikla laikā, un siltuma daudzumu, ko saņem dzesinātājs sajā laikā. [630 J, 1880 J].

13-4. Ideāla siltummasīna strādā pēc Kārno cikla. Noteikt cikla lietderības koeficientu, ja zināms, ka viena cikla laikā padarīts 2.94 kJ darbs un dzesinātājs saņēmis 3.2 kcal. [18 %].

13-5. Ideāla siltummasīna strādādama pēc Kārno cikla, viena cikla laikā padara 7.35∙10⁴ J darba. Sildītāja temperatūra 100° C, dzesinātajā temperatūra 0° C. Aprēķināt: 1) masīnas lietderības koeficientu; 2) siltuma daudzumu, ko masīna saņem no sildītāja viena cikla laikā; 3) siltuma daudzumu, ko saņem dzesinātājs viena cikla laikā. [1) 26.8 %; 2) 27.4∙10⁴ J; 3) 20.0∙10⁴ J].

13-6. Ideāla siltummasīna strādā pēc Kārno cikla. Pie tam 80 % siltuma ko masīna saņem no sildītāja, tiek atdoti dzesinātajam. No sildītāja saņemtas 1.5 cal siltuma. Aprēķināt: 1) cikla lietderības koeficientu; 2) darbu, ko masīna padara pilna cikla laikā. [1) 20 %; 2) 1.26∙10³ J].

13-7. Ideāla siltummasīna strādā pēc Kārno cikla ar sakarsētu gaisu, kura sākuma temperatūra 127° C un spiediens 7 atm. Gaisa sākotnējais tilpums 2∙10 ^-3 m³. Gaisam izplesoties izotermiski, tas aizņem 5 l tilpumu; izplesoties adiabātiski, tā tilpums sasniedz 8 l. Aprēķināt: 1) izotermu un adiabātu krustosanās koordinātes; 2) padarīto darbu katrā cikla posmā; 3) pilno darbu, kas padarīts visa cikla laikā; 4) cikla lietderības koeficientu; 5) siltuma daudzumu, ko viena cikla laikā atdod sildītājs; 6) siltuma daudzumu, ko vienā cikla laikā saņem dzesinātājs. [1) 2 l, 7 atm, 5 l, 2.8 atm, 8 l, 1.44 atm; 3.22 l, 3.6 atm; 2)1300 J, 620 J, -1070 J, -620 J; 3) 230 J; 4) 17.5 %; 5) 312 cal; 6) 256 cal].

13-8. Ideālas gāzes viens kilogrammols veic ciklu, kas sastāv no divām izohorām un divām izobārām. Pie tam izmainās gāzes tilpums no V₁ = 25 m³ līdz V₂ = 50 m³ un spiediens no p_l = l atm līdz 2 atm. Cik reizu darbs, kas padarīts sajā ciklā, ir mazāks par darbu, kas padarīts Kārno ciklā, kura izotermas atbilst vislielākajai un vismazākajai apskatāmā cikla temperatūrai, ja zināms, ka, gāzei izotermiski izplesoties, tās tilpums palielinās divas reizes? [2.1 reizi].

13-9. Ideāla aukstuma masīna, strādādama pēc apgrieztā Kārno cikla, viena cikla laikā padara 3.7∙10⁷ J darba. Turklāt tā ņem siltumu no ķermeņa, kura temperatūra ir -10° C, un atdod siltumu ķermenim, kura temperatūra +17° C. Aprēķināt: 1) cikla lietderības koeficientu; 2) siltuma daudzumu, ko atdod aukstais ķermenis viena cikla laikā; 3) siltuma daudzumu, ko saņem siltais ķermenis viena cikla laikā. [1) 0.093; 2) 360 kJ; 3) 397 kJ].

13-10. Tvaikmasīna, kuras jauda 14.7 kW, l stundā patērē 8.1 kg ogles, kuru siltumspēja 3.3∙10⁷ J/kg. Katla temperatūra 200° C, dzesinātajā temperatūra 58° C. Aprēķināt masīnas faktisko lietderības koeficientu η₁ un salīdzināt to ar ideālas siltummasīnas lietderības koeficientu η₂, ja tā strādā pēc Kārno cikla tajās pasās temperatūras. [20 % un 30 %].

13-11. Aprēķināt entropijas izmaiņu, ja 10 g ledus, kura temperatūra -20° C, pārvērs tvaikā, kura temperatūra 100° C. [88 J/deg].

13-12. Aprēķināt entropijas pieaugumu, ja l g ūdens, kura temperatūra 0° C, pārvērs tvaikā, kura temperatūra 100° C. [7.4 J/deg].

13-13. Aprēķināt entropijas izmaiņu, izkausējot l kg ledus, kura temperatūra 0° C. [ 1230 J/deg].

13-14. 640 g izkausēta svina kusanas temperatūra izliets uz ledus, kura temperatūra 0° C. Aprēķināt entropijas izmaiņu sajā procesā. [62 J/deg].

13-15. Aprēķināt entropijas izmaiņu 8 gramiem skābekļa, pārejot no 10 l tilpuma un 80° C temperatūras uz 40 l tilpuma un 300° C temperatūras. [5.4 J/deg].

13-16. Aprēķināt entropijas izmaiņu 6 gramiem ūdeņraza pārejot no 20 l tilpuma un 1.5∙10⁵ N/m² spiediena uz 60 l tilpuma un 1∙10⁵ N/m² spiediena. [71.0 J/deg].

13-17. 6.6 g ūdeņraza izobāriski izplesas, līdz tā tilpums divkārsojas. Aprēķināt sīs izplesanās entropijas izmaiņu. [66.3 J/deg].

13-18. Aprēķināt entropijas izmaiņu, 8 g hēlija izobāriski izplesoties no tilpuma V₁ = 10 l līdz tilpumam V₂ = 25 l. [38.1 J/deg].

13-19. Aprēķināt entropijas izmaiņu, 6 g ūdeņraza izotermiski izplesoties no 10⁵ līdz 0.5∙10⁵ N/m². [17.3 J/deg].

13-20. 10.5 g slāpekļa izotermiski izplesas no tilpuma V₁ = 2 l līdz tilpumam V₂ = 5 l. Aprēķināt entropijas pieaugumu sajā procesā. [2.9 J/deg].

13-21. 10 g skābekļa sasilda no t₁ = 50° C līdz t₂ = 150° C. Aprēķināt entropijas izmaiņu, ja skābekli silda: 1) izohoriski un 2) izobāriski. [1) 1.76 J/deg; 2) 2.46 J/deg].

13-22. Sildot l kmol divatomu gāzes, tās absolūtā temperatūra palielinās 1.5 reizes. Aprēķināt entropijas izmaiņu, ja gāzi silda: 1) izohoriski un 2) izobāriski. [1) 8.5∙10³ J/deg; 2) 11.8∙10³ J/deg].

13-23. Sasildot 22 g slāpekļa, tā absolūtā temperatūra palielinās 1.2 reizes, bet entropija par 4.19 J/deg. Kādos apstākļos slāpeklis sildīts (pie pastāvīga tilpuma vai pie pastāvīga spiediena)? [Sildīsana notika pie pastāvīga spiediena].

13-24. Aprēķināt entropijas izmaiņu, gāzei pārejot no stāvokļa A stāvoklī B, ievērojot 13-2. uzdevuma nosacījumus, ja pāriesana notiek: 1) pa ceļu ACB un 2) pa ceļu ADB (sk. zīm. 13-1). [5∙45 J/deg].

13-25. Viens kubikmetrs gaisa, kura temperatūra 0° C un spiediens 196 kPa, izotermiski izplesas no tilpuma V₁ līdz tilpumam V₂ = 1V₁;. Aprēķināt entropijas izmaiņu sajā procesā. [≈500 J/deg].

Siltuma bilances vienādojums

14-1. Svina lode, lidojot ar ātrumu 300 m/s, caururbj koku un lido tālāk ar ātrumu 200 m/s. Par cik grādiem sasila lode, ja 30 % no patērētās enerģijas patērēta lodes sasildīsanai? [60° C].

14-2. Misiņa ieksēja enerģija pieaug par 200 J, ja to sasilda par 10° C. Cik liela ir misiņa masa? [50 g].

14-3. Par cik kelviniem jāsilda 0.2 kg svina, lai ieksēja enerģija pieaugtu par 260 J? [10K].

14-4. Svina lode, kas ar ātrumu 430 m/s, caursauj svinu un lido tālāk ar ātrumu 200 m/s. Kāda daļa lodes masas izkūst? Sākuma temperatūra lodei 80° C; sasildīsanai patērēti 50 % no tās kinētiskās enerģijas izmaiņas. [20 %].

14-5. Kolbā, kuras siltumietilpību neņem vērā, atrodas 600 g ūdens pie temperatūras 80° C. Kāds ledus daudzums pie -15°C jāpievieno ūdenim, lai maisījuma beigu temperatūra būtu 50° C? [0.13 kg].

14-6. Par cik grādiem paaugstinājās ūdens temperatūra, kas ņemts pie 10° C, ja tajā ielēja 1.5 kg izkausēta svina pie tā kusanas temperatūras? Svina kusanas temperatūra 327° C. [34° C].

14-7. Ledus gabalu ar masu 2 kg un temperatūru -20° C sasildīja, pievadot tam 10⁶ J siltuma. Noteikt vielas temperatūru pēc sasildīsanas. [30° C].

14-8. 20 kg ledus pie -20° C temperatūras iemests ūdenī, kura masa 20 kg, temperatūra 70° C. Vai viss ledus izkusīs? [15 kg].

14-9. Cik liels darbs jāpadara, lai berzējot vienu gar otru divus ledus gabalus, izkausētu l g ledus pie 0° C?

14-10. Kāds siltuma daudzums patērēts, pārvērsot 2 kg ledus pie -10 ° C tvaikā pie temperatūras 110° C? Ūdens tvaika īpatnējo siltumietilpību temperatūras intervālā no 100 līdz 110° C pieņemt vienādu 1.675 kJ/kg∙K. [≈6∙10⁶J].

14-11. Viss siltuma daudzums, kas izdalās, kondensējoties l kg tvaika pie 100° C un atdziestot iegūtam ūdenim līdz 0° C, tiek iztērēts ledus kusanai pie 0° C. Cik ledus izkusa? [8 kg].

14-12. Dzelzs detaļa ar masu 0.5 kg, sasildīta līdz 800° C, iegremdēta 5 l ūdens pie temperatūras 19° C. Rezultātā radās kaut kāds tvaika daudzums un ūdens temperatūra paaugstinājās par vienu grādu. Cik ūdens pārvērtas tvaikā? [0.06 kg].

14-13. Traukā atrodas 1.5 kg ūdens, kura temperatūra 0° C. Ūdenī iemeta 0.5 g ledus, kura temperatūra -20° C. Cik daudz tvaika, kura temperatūra 100° C, ir jāievada ūdenī, lai pēc siltumapmaiņas ūdens temperatūra paaugstinātos līdz 30° C?

14-14. Kalorimetra ir 200 g ūdens, kura temperatūra -20° C. Cik daudz ūdens atradīsies kalorimetrā pēc siltumapmaiņas? Kalorimetra siltumietilpība 150J/K.

14-15. Dzelzs gabalu, kuram ir kuba forma, sasildīja līdz 200° C un uzlika ∙uz ledus. Cik dziļi dzelzs kubs iegrima ledū, ja ledus temperatūra 0° C? Siltuma zudumus neievērot. Kuba malas garums 2 cm. [≈ 4.8 mm].

14-16. 10 g ledus, kura temperatūra -10° C, atrodas kalorimetrā. Kas atradīsies traukā un kāda būs vielas temperatūra pēc siltumapmaiņas, ja traukā ielaidīs 5 g ūdens tvaika, kura temperatūra 100° C?

14-17. Uz elektriskās plītiņas 15 minūtes ūdens, kura temperatūra 20° C, uzvārījās. Cik ilgā laikā ūdens iztvaikos, ja plītiņa netiks izslēgta? [≈ 110 min].

14-18. Ar kādu spēku divsantīmu monēta jāpiespiez virsmai, lai, pārvietojot monētu 6 m attālumā, tā sasiltu par 12 K? Berzes koeficients starp monētu un virsmu ir 0.4. Monētas materiāla īpatnēja siltumietilpība 400 J/kg∙K. [4N].

14-19. Sajauc 300 g ūdens, kura temperatūra 10° C, un 400 g ledus, kura temperatūra -20° C. Aprēķināt maisījuma temperatūru. No kādiem komponentiem sastāv maisījums? Aprēķināt so komponentu masu.

14-20. Cik daudz siltuma jāpatērē, lai 8 kg ledus, kura temperatūra -30° C, sasildītu līdz kusanas punktam, izkausētu un iegūto ūdeni sasildītu līdz 60° C temperatūrai? [5.2∙10⁶J].

14-21. Alumīnija kalorimetrā, kura masa 0.2 kg un kurā ielieti 0.34 kg ūdens ar 23.5° C temperatūru, iegremdēja 81.5 g ledus ar 0° C temperatūru. Viss ledus izkusa. Aprēķināt ūdens beigu temperatūru kalorimetrā. [5.4° C].

14-22. Stikla traukā, kura masa 1.2 kg, atrodas 3 l ūdens ar 80° C temperatūru. Sis ūdens jāatdzesē līdz 5° C temperatūrai, iegremdējot ledus gabaliņus, kuru temperatūra 0° C. Aprēķināt, cik daudz ledus nepieciesams. [2.9 kg].

14-23. 20 kg ledus pie temperatūras -20° C iemests 20 kg ūdens, kura temperatūra 70° C. Vai viss ledus izkusa? [15 kg].

14-24. Misiņa kalorimetrā, kura masa 100 g, atrodas 5 g ledus ar temperatūru -10° C. Kalorimetrā ielej 30 g izkausēta svina pie kusanas temperatūras. Kas būs kalorimetrā pēc siltuma līdzsvara iestāsanās? Kāda beigu temperatūra? [0.5 g ledus; 4.5 g ūdens; 30 g svins; 0° C].

14-25. Ar kādu minimālo ātrumu zemes atmosfērā jāielido dzelzs meteoram, lai tas sakārstu, izkustu un pārvērstos tvaikā? Pieņemot, ka meteora sākuma temperatūra atrodas tuvu absolūtajai nullei. [2.2 km/s].

Kulona likums, elektriskā lauka intensitāte un potenciāls

15-1. Aprēķināt pievilksanas spēku starp ūdeņraza atoma kodolu un elektronu. Ūdeņraza atoma rādiuss ir 0.5∙10 ^-8 cm, kodola lādiņs pēc lieluma vienāds, bet pēc zīmes pretējs elektrona lādiņam. [F = 9.23∙10 ^-8 N]

15-2. Divi punktveida lādiņi, atrazdamies gaisā 20 cm attālumā viens no otra, savstarpēji iedarbojas ar noteiktu spēku. Cik tālu viens no otra jānovieto sie lādiņi eļļā, lai iegūtu to pasu mijiedarbības spēku? [r = 8.94∙10 ^-2 m].

15-3. Grafiski attēlot divu punktveida lādiņu mijiedarbības spēka atkarību no attāluma starp tiem intervālā 2 < r < 10 cm pēc katriem 2 cm. Lādiņi attiecīgi ir 2∙10 ^-8 C un 3∙10 ^-8 C.

15-4. Cik reizu Ņūtona pievilksanās spēks starp diviem protoniem ir mazāks par Kulona atgrūsanās spēku? Protona lādiņs skaitliski ir vienāds ar elektrona lādiņu. [ 1.25∙10³⁶ reizes].

15-5. Aprēķināt elektrostatisko atgrūsanās spēku starp nātrija atoma kodolu un protonu, kas to bombardē, pieņemot, ka protons atrodas 6∙10 ^-12 cm attālumā no nātrija atoma kodola. Nātrija kodola lādiņs ir 11 reizes lielāks par protona lādiņu. Nātrija atoma elektronu čaulas ietekmi neievērot. [F = 0.7 N].

15-6. Katrā kvadrāta virsotnē atrodas 2.33∙10 ^-9 C liels lādiņs, bet tā centrā novietots negatīvs lādiņs. Aprēķināt sā lādiņa lielumu, ja rezultējosais spēks, kas darbojas uz katru lādiņu, ir nulle. [q = -2.23∙10 ^-9 C].

15-7. Divas vienāda rādiusa un vienāda svara lodītes iekārtas divos diegos tā, ka to virsmas saskaras. Cik liels lādiņs jāpiesķir lodītēm, lai diega sastiepuma spēks būtu 0.098 N? Attālums no piekārsanas punkta līdz lodītes centram 10 cm. Katra lodīte sver 0.05 kg. [q = 1.1∙10 ^-6 C].

15-8. Divas vienāda rādiusa un vienāda svara lodītes iekārtas divos diegos tā, ka to virsmas saskaras. Uzlādējot lodītes ar lādiņu q₀ = 4∙10 ^-7 C, tās atgrūzas viena no otras, izveidodamas 60° leņķi. Aprēķināt lodīsu svaru, ja attālums no piekārsanas punkta līdz lodītes centram ir 20 cm. [P = 0.157 N ].

15-9. Aprēķināt 15-8. Uzdevumā doto lodīsu materiāla blīvumu, ja zināms, ka, iegremdējot sīs lodītes petrolejā, starp diegiem izveidojas 54° leņķis. [p₁ = 2550 kg/m³].

15-10. Divas uzlādētas vienāda rādiusa un vienāda svara lodītes, kas iekārtas vienāda garuma diegos, iegremdētas sķidrā dielektriķī, kura blīvums ir ρ₁ un dielektriskā caurlaidība £ Kādam jābūt lodīsu materiāla blīvumam ρ_, lai leņķis starp diegiem gaisā un dielektriķī būtu vienāds? [].

15-11. 15-6. attēlā AA ir uzlādēta bezgalīga plakne un B - ar vienādas zīmes lādiņu uzlādēta lodīte, kuras svars P = 4∙10 ^-6 N un lādiņs q = 6.67∙10 ^-4 C. Diega sastiepuma spēks, kurā karājas lodīte, F = 4.9∙10 ^-4 N. Aprēķināt virsmas lādiņa blīvumu uz plaknes AA. [a = 7.8∙10 ^-6 C/m²].

15-12. Noteikt divu lodīsu savstarpējās atgrūsanās spēkus, ja katra lodīte uzlādēta līdz 600 V potenciālam, katras lodītes diametrs l cm un attālums starp lodīsu centriem ir 20 cm. [F = 2.5∙10 ^-8N].

15-13. Atrast divu svina lodīsu pievilksanas spēku ja katram vienas lodītes atomam ir atņemts viens elektrons un pārnests uz otru lodīti. Lodīsu diametrs l cm un attālums starp lodītēm l m. [6.9∙10⁶ N].

15-14. Divi vienādi punktveida lādiņi q = 1.1∙10 ^-9 C atrodas 17 cm attālumā viens no otra. Kāds spēks un kādā virzienā darbojas uz pozitīvu vienības lādiņu, ka atrodas 17 cm attālumā no abiem lādiņiem? [ 0.6∙10^-6 N].

15-15. Divas vienādas metāla uzlādētas lodes atrodas attālumā 60 cm. Lozu atgrūsanas spēks 70 mkN. Pēc tam, kad lodes savienoja un atgrieza sākuma attālumā, atgrūsanas spēks pieauga līdz 160 mkN. Atrast lozu lādiņus pirms kontakta. Pieņemt, ka lozu diametrs ir niecīgs, salīdzinājuma ar attālumu starp tām. [ q₁ = 0.14 µC, q₂ = 20 µC].

15-16. Divas vienādas metāla uzlādētas lodes atrodas attālumā 30 cm. Lozu atgrūsanas spēks 90 N. Pēc tam, kad lodes savienoja un atgrieza sākuma attālumā, atgrūsanas spēks pieauga līdz 160 µN. Atrast lozu lādiņus pirms kontakta. Pieņemt, ka lozu diametrs ir niecīgs, salīdzinājumā ar attālumu starp tām. [q₁ = 0.09 µC, q₂ = 0.01 µC].

15-17. Ūdens piliens ar 10² cm diametru ir uzlādēts ar lādiņu q₀ un tā elektriskā laukā intensitāte uz piliena virsmas ir 6 10⁵ V/m. Kādai ir jābūt vertikālā lauka intensitātei lai pilienu atturētu no krisanas? [3∙10⁴ V/m].

15-18. Aprēķināt paātrinājumu a, kuru viens elektrons piesķir otram, kas atrodas r = l mm attālumā no tā. [2.5∙10⁸ m/s²].

15-19. Kādai ir jābūt protona masai m', lai gravitācijas pievilksanas spēks kompensētu elektrostatiskās atgrūsanas spēku? [1.86∙10 ^-9kg].

15-20. Divu vienādu pilienu (rādiuss 0.1 mm) gravitācijas pievilksanas spēku kompensē elektrostatiskās atgrūsanas spēks. Noteikt pilienu lādiņu. [0.361 aC].

15-21. Vienādmalu trīsstūra virsotnē atrodas vienādi pozitīvi lādiņi q = 2nC. Kādu negatīvu lādiņu q₁ ir jānovieto trīsstūra centrā, lai atgrūsanās spēki starp lādiņiem q būtu kompensēti ar pievilksanās spēkiem. [1.15 nC].

15-22. Svina lodīte ar diametru 0.5 cm iemērcēta glicerīnā. Noteikt lodītes lādiņu, ja homogēnā elektrostatiskajā laukā lodīte atrodas līdzsvarā. Elektrostatiskā lauka intensitāte ir vērsts vertikāli augsup un tā intensitāte E = 4 kV/cm. [1.61 nC].

15-23. Salīdzināt elektriskās mijiedarbības spēku F_E ar gravitācijas spēku F_g: 1) divām homogēnām lodēm ar masām m₁ = m₂ = 100 kg, ja uz katras no tām atrodas lādiņs q = 5∙10 ^-9 C; 2) diviem elektroniem. [0.34; 4.2∙10⁴²].

15-24. Trīs vienādi lādiņi q novietoti vienādmalu trīsstūra virsotnēs. Kāds lādiņs jānovieto trīsstūra centrā, lai sistēma būtu līdzsvarā? Vai sis līdzsvars būs stabils? [].

15-25. Vienādmalu trīsstūra virsotnēs novietoti vienādi punktveida lādiņi q₁ = q₂ = 2∙10 ^-9 C. Aprēķināt, kāds spēks F uz katru no tiem darbojas, ja trīsstūra malas garums a = 10 cm. [6.23∙10 ^-6 N].

Superpozīcijas princips.

15-26. Attālums starp diviem punktveida lādiņiem q₁ = 7.5∙10 ^-9 C un q₂ = -14.7∙10 ^-9 C ir 5 cm. Aprēķināt elektriskā lauka intensitāti punktā, kas atrodas 3 cm attāluma no pozitīvā lādiņa un 4 cm attālumā no negatīvā lādiņa. [E = 1.12∙10⁵ V/m].

15-27. Aprēķināt spēku, kas darbojas uz 0.7∙10 ^-9 C lielu lādiņu, ja tas novietots l) 2 cm attālumā no uzlādēta diega, kura lineārā lādiņa blīvums 2∙10 ^-9 C/cm, 2) uzlādētas plaknes laukā, kuras virsmas lādiņa blīvums 2∙10 ^-9 C/cm², 3) 2 cm attālumā no uzlādētas lodes virsmas; lodes rādiuss 2 cm un virsmas lādiņa blīvums 2∙10 ^-9 C/cm². Vides dielektriskā caurlaidība visos trijos gadījumos ir 6. [1) 2∙10 ^-5 N; 2) 12.6∙10 ^-5 N; 3) 6.28∙10 ^-5 N].

15-28. Ar cik lielu spēku uzlādētas bezgalīgas plaknes elektriskais lauks iedarbojas uz katru sajā laukā novietota uzlādēta bezgalīgi gara diega metru? Lineārā lādiņa blīvums uz diega ir 3∙10 ^-8 C/cm un virsmas lādiņa blīvums uz plaknes ir 2∙10 ^-9 C/cm². [F = 3.4 N].

15-29. Divi ar vienādu zīmju lādiņiem uzlādēti gari diegi atrodas attālumā a = 10 cm viens no otra. Lineārā lādiņa blīvums uz diegiem τ₁ = τ₂ = 10 ^-7 C/cm. Aprēķināt rezultējosā elektriskā lauka intensitātes vērtību un virzienu punktā, kas atrodas 10 cm attālumā no katra diega. [E = 3.12∙10 ⁶ V/m].

15-30. Vara lode, kuras diametrs l cm, ievietota eļļā. Eļļas blīvums p = 800 kg/m³. Cik liels ir lodes lādiņs, ja homogenā elektriskā laukā lode eļļā atrodas līdzsvara stāvoklī? Elektriskais lauks vērsts vertikāli uz augsu un tā intensitāte E = 36000 V/cm. [q = 1.1∙10 ⁸ C].

15-31. Plakanā horizontāli novietotā kondensatorā uzlādēts dzīvsudraba piliens atrodas līdzsvara stāvoklī, ja elektriskā lauka intensitāte E = 600 V/cm. Piliena lādiņs ir 0.8∙10 ^-9 C. Aprēķināt piliena rādiusu, [r = 0.44∙10 ^-3 m].

15-32. Tievs stienis ar 10 cm garumu vienmērīgi uzlādēts ar pozitīvu lādiņu 10 ^-7 C. Noteikt ar kādu spēku stieņa radītais lauks iedarbosies uz punktveida lādiņu 2∙10 ^-9 C, kurs atrodas attālumā 20 cm no stieņa gala (stieņa turpinājuma virzienā). [3.0∙10 ^-5 N].

15-33. Dotie no 15-32. Noteikt elektriskā lauka intensitātes atkarību no attāluma x (līdz stieņa galam).

15-34. Tievs stienis ar garumu 12 cm uzlādēts ar lineāro lādiņa blīvumu 200 nC/m. Atrast elektriskā lauka intensitāti punktā uz vidus perpendikula attālumā 5 cm no stieņa. [55.7 kV/m].

15-35. Tievs stienis ar garumu 2a ir uzlādēts ar konstantu lineāro lādiņa blīvumu τ un atrodas vakuumā. Noteikt intensitātes E moduļa atkarību no attāluma r punktiem, kas atrodas uz taisnes, kura ir perpendikulāra stieņa asij un iet caur stieņa centru. r - attālums līdz stienim. Izpētīt gadījumu a→∞. [].

15-36. Pa tievu garu diegu ar garumu l ir sadalīts pozitīvs lādiņs ar lineāro blīvumu τ Noteikt lauka intensitāti punktā uz vidus perpendikula attālumā r no diega. [].

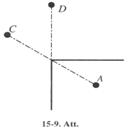
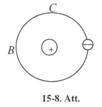
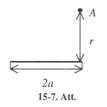15-37. Tievs diegs ar garumu 2a ir vienmērīgi uzlādēts ar lineāro blīvumu τ. Noteikt lauka intensitāti punktā A (sk. Att. 15-7.)

15-38. Ar cik lielu speķu (uz garuma vienību) atgrūzas divas ar vienādzīmju lādiņiem uzlādētas bezgalīgas plaknes, ja lādiņa blīvums uz abām ir 3∙10 ^-8 C/cm²? [5.1∙10 ³ N/m²].

15-39. Attālums starp diviem punktveida lādiņiem q₁ = 9q un q₂ = q ir 8 cm. Kādā attālumā no lādiņa q₁ atrodas punkts, kurā lauka intensitāte ir vienāda ar nulli? Kā mainīsies sis attālums, ja q₂ būs negatīvs? [6 cm, 12 cm].

15-40. Pieņemot, ka protons un elektrons, kuri veido ūdeņraza atomu ir punktveida lādiņi attālumā 5∙10 ^-9 viens no otra, noteikt intensitāti punktos B un C (sk 15-8. Att.). [4.3∙10 ¹¹ V/m, 4.2∙10 ¹¹ V/m].

15-41. Tievs, bezgalīgi gars diegs veido taisnu leņķi (sk. 15-9. Att.). Atrast lauka intensitāti punktos A un C, kuri atrodas uz bisektrises un punktā D, kurs atrodas uz vienas diega daļas turpinājuma. Attālums no leņķa virsotnes līdz katram punktam ir R.[; ; ].

15-42. Noteikt elektrostatiska lauka intensitāti punkta A, kas atrodas uz lādiņus q₁ = 10 nC un q₂ = 10 nC savienojosās taisnes viduspunktā. Attālums starp lādiņiem l = 20 cm. [0].

15-43. Noteikt elektrostatiska lauka intensitāti punktā A, kas atrodas uz lādiņus q₁ = 10 nC un q₂ = -10 nC savienojosās taisnes attālumā r = 4 cm no negatīvā lādiņa. Attālums starp lādiņiem l = 10 cm. [81.25 kV/m].

15-44. Ar kādu spēku (uz garuma vienību) atgrūzas divas ar vienādzīmju lādiņiem lādētas stieples (lādiņa blīvums τ₁ = τ₂ = 3 µC/m), kuras atrodas attālumā b = 20.0 mm viena no otras? [8.1 N/m].

15-45. Noteikt elektrostatiska lauka intensitāti punktā A, kas atrodas uz lādiņus q₁ = 10 nC un q₂ = -8 nC savienojosās taisnes attālumā r = 8 cm no negatīvā lādiņa. Attālums starp lādiņiem l = 20 cm. [10.1 kV/m].

15-46. Divi punktveida lādiņi q₁ = 4 nC un q₂ = -2 nC atrodas attālumā 60 cm viens no otra. Noteikt lauka intensitāti viduspunktā. Cik liela būs lauka intensitāte, ja lādiņs q₂ būs pozitīvs? [0.6 kV/m, 0.2 kV/m].

15-47. Noteikt lauka intensitāti, ko veido dipols ar momentu p = 10 ^-9 Cm attālumā r = 25 cm no dipola centra, dipola asij perpendikulārā virzienā. [576 V/m].

15-48. Attālums l starp lādiņiem q = ± 2 nC ir 20 cm. Noteikt lauka intensitāti E punktā, kas atrodas attālumā r₁ = 15 cm no pirmā un r₂ = 10 cm no otrā lādiņa. [2.14 kV/m].

15-49. Kvadrāta virsotnēs atrodas vienādi pozitīvi lādiņi q = 2 nC. Kvadrāta mala - 5 cm. Noteikt elektrostatiska lauka intensitāti 1) kvadrāta centrā; 2) vienas malas viduspunktā. [1) 0; 2) 1.03 kV/m].

15-50. Gredzens no tievas stieples ar rādiusu r = 5 cm vienmērīgi uzlādēts ar lineāro blīvumu τ = 14 nC/m. Noteikt lauka intensitāti uz ass, kura iet caur gredzena centru attālumā a = 10 cm no gredzena centra. [2.83 kV/m].

Elektriskā lauka intensitāte un potenciāls

15-51. Aprēķināt lauka potenciālu punktam, kas atrodas 10 cm attālumā no uzlādētas lodes centra; lodes rādiuss l cm. Uzdevumu atrisināt sādiem gadījumiem: 1) virsmas lādiņa blīvums uz lodes 10 ^-11 C/cm²; 2) lodes potenciāls 300 V. [1) 11.3 V; 2) 30 V].

15-52. Lodīte, kuras masa l g un lādiņs 10 C, pārvietojas no punkta A, kura potenciāls 600 V, uz punktu B, kura potenciāls nulle. Cik liels lodītes ātrums punktā A, ja punktā B tas ir 20 cm/s? [16.7∙10 ^-2 m/s].

15-53. Kāda lauka intensitāte ir , kur E - konstante. Uzrakstīt izteiksmi lauka potenciālam φ. [φ = -Ex + const].

15-54. Elektrostatiska lauka intensitātei , kur E₁,   E₂ un E₃ - konstantes, a) Vai dotais lauks ir homogēns? b) Uzrakstīt izteiksmi lauka potenciālam, [a) Jā; b). ].

15-55. Elektrostatiska lauka intensitāti nosaka vienādojums kur a - konstante, a) Vai dotais lauks ir homogēns? b) Uzrakstīt izteiksmi lauka potenciālam. [a) Ne; b) ].

15-56. Kāda elektrostatiska lauka potenciālu nosaka vienādojums φ = φ(x² + y² + z²). a) Vai lauks ir homogēns? b) Atrast vektora E moduli punktā x, y, z. [a) Nē; b) ].

15-57. Lauka potenciāls, kuru veido kāda lādiņu sistēma, apraksta vienādojums φ = a(x² + y² )+ b∙ z², kur a un b - pozitīvās konstantes. Noteikt lauka intensitāti un moduli E. [a) ; b) ].

15-58. Lauka potenciālu, kuru veido kāda lādiņu sistēma, apraksta vienādojums φ = a(x² + y² ) - b ∙ z², kur a un b - pozitīvās konstantes. Noteikt lauka intensitāti   un moduli E. [a) ; b) ].

15-59. Vakuumā novietotais stienis ar garumu 2a ir vienmērīgi lādēts ar lādiņa lineāro blīvumu τ. Noteikt lauka intensitātes moduli punktiem, kas atrodas uz vidus perpendikula, ka attāluma funkciju. [].

15-60. No tievas stieples pagatavots gredzens ar rādiusu r = 5 cm ir vienmērīgi uzlādēts ar lādiņu q = 10 nC. Noteikt elektrostatiskā lauka potenciālu: a) gredzena centrā; b) uz gredzena ass, attālumā a = 10 cm no gredzena centra, [a) 1.8 kV; b) 805 V].

15-61. Metāliskai lodei ar rādiusu 5 cm ir piesķirts lādiņs q = 10 nC. Noteikt elektrostatiskā lauka potenciālu φ: 1) uz lodes virsmas; 2) attālumā a = 2 cm no lodes virsmas. [1) 1.8 kV; 2) 1.29 kV].

15-62. Elektrostatisko lauku veido pozitīvs punktveida lādiņs. Noteikt potenciāla gradienta skaitlisko vērtību un virzienu, ja attālumā r = 10 cm no lādiņa potenciāls ir vienāds ar φ = 100 V. [l kV/m].

15-63. Elektrisko lauku veido bezgalīga plakne, kura ir uzlādēta ar virsmas lādiņu a = 5 mC/m². Noteikt dotā lauka potenciāla gradienta skaitlisko vērtību un virzienu. [282 V/m].

15-64. Elektrisko lauku veido bezgalīgs vienmērīgi uzlādēts ar lineāro blīvumu τ = 50 pC/cm diegs. Noteikt potenciāla gradienta skaitlisko vērtību un virzienu attālumā r = 0.5 m no diega. [180 V/m].

15-65. Elektrostatisko lauku veido bezgalīga plakne, kura ir uzlādēta ar virsmas blīvumu σ = 1 nC/m². Noteikt potenciālu starpību starp punktiem, kuri atrodas attālumam x₁ = 20 cm un x₂ = 50 cm no plaknes. [16.9 V].

15-66. Elektrostatisko lauku veido sfēra ar rādiusu R = 5 cm. Sfēra ir vienmērīgi uzlādēta ar virsmas blīvumu σ = l nC/m². Noteikt potenciālu j starpību starp punktiem attāluma r₁ = 10 cm un r₂ = 15 cm no sfēras centra. [0.94 V].

15-67. Elektrostatisko lauku veido vienmērīgi uzlādēta lode ar rādiusu R = l m un kopējo lādiņu q = 50 nC. Atrast potenciālu starpību punktiem, kas j atrodas attālumos: 1) r₁ = 1.5 m un r₂ = 2 m; 2) r₁'= 0.3 m un r₂'= 0.8 m no lodes centra. [1) 75 V; 2) 124 V].

15-68. Elektrisko lauku veido lode ar rādiusu R = 8 cm. Lode uzlādēta ar telpisko blīvumu ρ = 10 nC/m³. Noteikt potenciālu starpību starp punktiem,] attālumos r₁ = 10 cm un r₂ = 15 cm no lodes centra. [0.64 V].

15-69. Elektrostatisko lauku veido lode ar rādiusu R = 10 cm. Lode vienmērīgi uzlādēta ar telpisko blīvumu ρ = 20 nC/m³. Noteikt potenciālu starpību starp punktiem lodes ieksienē attālumos r₁ = 2 cm un r₂ = 8 cm no tās centra. [2.26 V].

15-70. Pieņemot zemi par vadosu lodi ar rādiusu R = 6400 km, aprēķināt Zemes lādiņu un potenciālu, zinot, ka elektriskā lauka intensitāte Zemes tuvumā ir E = 100 V/m. (ε = 1). [4.5∙10⁵ C; 6.4∙10⁸ V].

15-71. Divās pretējās kvadrāta virsotnēs atrodas lādiņi q = 0.2∙10 ^-6 C. Aprēķināt potenciālu otrās divās virsotnēs, ja malas garums a = 30 cm. [12 kV].

15-72. Zināms, ka Zemes elektriskā lauka potenciāla gradients uz Zemes virsmas ir 130 V/m un vērsts uz Zemes centru. Aprēķināt Zemes virsmas lādiņa blīvumu. [-1.15∙l0 ^-9 C/m²].

15-73. Elektrisko lauku veido bezgalīga vienmērīgi uzlādēta ar blīvumu σ = 4∙10 ^-10 C/m² plakne. Aprēķināt potenciālu starpību ∆φ starp diviem punktiem, kas atrodas attālumos r₁ = 15 cm un r₂ = 20 cm no plaknes. [112V].

15-74. Starp Zemes elektriskā lauka diviem punktiem, kas pa vertikāli atrodas 0.5 m attālumā, ir 60 V liela potenciālu starpība. Aprēķināt Zemes elektriskā lauka intensitāti (pieņemot, ka tā ir homogēna) pie Zemes virsmas. Kāds ir lauka potenciāls attiecība pret Zemi 10 m augstumā? [120 V; 1.2 kV].

15-75. Homogēna parafīna lode, kuras rādiuss R = 10 cm, vienmērīgi uzlādēta ar lādiņa tilpuma blīvumu ρ = 10 ^-6 C/m³. Aprēķināt elektriskā lauka potenciālu lodes centrā un uz tās virsmas. Uzzīmēt grafiku φ = f (r). [472 V; 377 V].

Lādētu daļiņu kustība elektrostatiskajā laukā

16-1. Attālums starp plakana kondensatora platēm 4 cm. No negatīvās plates uzsāk kustību elektrons tajā momentā, kad no pozitīvās plates uzsāk kustību protons. Kādā attālumā no pozitīvās plates tie sastopas? [0.022 mm],

16-2. Attālums starp plakana kondensatora platēm l cm. No vienas plates vienlaikus uzsāk kustību protons un α daļiņa. Kādu attālumu noiet α daļiņa laika sprīdī, kurā protons noiet visu ceļu no vienas plates līdz otrai? [0.5 cm].

16-3. Elektrons, noiedams plakanā kondensatorā ceļu no vienas plates līdz otrai, iegūst ātrumu 10⁸ cm/s. Attālums starp platēm 5.3 mm. Aprēķināt 1) potenciālu starpību starp platēm; 2) elektriskā lauka intensitāti kondensatorā; 3) virsmas lādiņa blīvumu uz platēm. [1) 2.8 V; 2) 530 V/m; 3) 4.7∙10 ^-9 C/m²].

16-4. Elektrisko lauku veido divas paralēlas plates, kas atrodas 2 cm attālumā no otras; potenciālu starpība starp tām 120 V. Cik lielu ātrumu iegūst elektrons lauka iedarbības rezultātā, pārvietojoties 3 mm pa spēka līniju? [2.53∙10⁶ m/s].

16-5. Elektrons, kas atrodas homogēna elektriskā laukā, iegūst 10¹⁴ cm/s² lielu paātrinājumu. Aprēķināt 1) elektriskā lauka intensitāti; 2) ātrumu, kādu elektrons iegūst, atrazdamies kustībā 10 ^-6 sekundes, ja tā sākuma ātrums ir nulle; 3) elektriskā lauka spēku darbu sajā laikā; 4) potenciālu starpību, kādu pārvarējis sajā gadījumā elektrons. [1) 5.7 V/m; 2) 10⁶ m/s; 3) 4.5∙10 ^-19 J; 4) 2.8 V].

16-6. Elektrons lido no vienas plakana kondensatora plates uz otru. Potenciālu starpība starp platēm 3 kV; attālums starp platēm 5 mm. Aprēķināt 1) spēku, kas darbojas uz elektronu; 2) elektrona paātrinājumu; 3) ātrumu, ar kādu elektrons nonāk pie otras plates; 4) virsmas lādiņa blīvumu uz kondensatora platēm. [1) 9.6∙10 ^-14 N; 2) 1.05∙10¹⁷ m/s²; 3) 3.24∙10⁷ m/s; 4) 5.3∙10 ^-6 C/m²].

16-7. Elektrons ar kādu sakuma ātrumu v₀ ielido plakanā kondensatorā paralēli platēm vienādā attālumā no tām. Kondensatora platēm pielikta potenciālu starpība U = 300 V. Attālums starp platēm d = 2 cm, kondensatora garums l = 10 cm. Cik liels drīkst būt sākuma ātrums v₀, lai elektrons neizlidotu no kondensatora? So pasu uzdevumu atrisināt α daļiņai. [3.64∙10⁷ m/s; 6∙10⁵ m/s].

16-8. Elektrons ielido plakanā horizontālā kondensatorā paralēli platēm vienādā attālumā no tām. Attālums starp platēm d = 4 cm, elektriskā lauka intensitāte kondensatorā E = l V/cm. 1) Pēc cik ilga laika no elektrona ielidosanas kondensatorā, tas nonāk uz vienas no platēm? 2) Kādu attālumu elektrons noiet kondensatorā, līdz tas nokļūst uz plates, ja paātrinājumu tam piesķir 60 V potenciālu starpība? [1) 4.8 ∙10 ^-7 s; 2) 22 cm.].

16-9. Elektrons ielido plakanā horizontālā kondensatorā paralēli platēm ar ātrumu 9∙10⁶ m/s. Aprēķināt elektrona pilno, normālo un tangenciālo paātrinājumu pēc 10 ^-8 s no elektrona kustības sākuma kondensatorā. Potenciālu starpība starp platēm ir 100 V, attālums starp platēm l cm. [15.7∙10¹⁴ m/s²; 8∙10¹⁴m/s²; 17.6∙10¹⁴ m/s²].

16-10. Protons un a daļiņa, kustēdamies ar vienādu ātrumu, ielido plakanā kondensatorā paralēli platēm. Cik reizu kondensatora laukā protona novirze lielāka par α daļiņas novirzi? [2 reizes].

16-11. Protons un a daļiņa, kurus paātrinājusi vienāda potenciālu starpība, ielido plakanā kondensatorā paralēli platēm. Cik reizu kondensatora laukā protona novirze lielāka par a daļiņas novirzi? [Protona un a daļiņas novirze ir vienāda].

16-12. Elektrons ielido plakanā horizontālā kondensatorā paralēli platēm ar ātrumu v_x = 10⁷ m/s. Kondensatorā lauka intensitāte E = 100 V/cm, kondensatora garums l = 5 cm. Aprēķināt elektrona ātruma skaitlisko vērtību un virzienu, tam izlidojot no kondensatora. [1.33∙10⁷ m/s; 41°20'].

16-13. Elektronu kūlis, kam paātrinājumu piesķīrusi potenciālu starpība U = 300 V, izejot caur uzlādētu horizontālu plakanu kondensatoru paralēli tā platēm, rada spīdosu plankumu uz fluorescējosa ekrāna, kas novietots attālumā l = 12 cm no kondensatora gala. Uzlādējot kondensatoru, plankums uz ekrāna pārvietojas par y = 3 cm. Aprēķināt kondensatora platēm pielikto potenciālu starpību U₁. Kondensatora garums l = 6 cm un attālums starp tā platēm d = l .4 cm. [28 V].

16-14. Elektrons kustas plakanā horizontālā kondensatorā paralēli tā platēm ar ātrumu 3.6∙10⁴ km/s. Lauka intensitāte kondensatorā 37 V/cm. Kondensatora plasu garums 20 cm. Par cik novirzās elektrons vertikālā virzienā elektriskā lauka iedarbībā pa kustības laiku kondensatorā? [0.01 m].