Ciklo sakiniai. Lentelių ir diagramų komponentai

3.1. Ciklo sakinys while

Ciklams C++ kalboje uzrasyti skirta keletas sakinių. Dazniausiai vartojamas ciklo sakinys while. Sio sakinio struktūra yra tokia:

while (sąlyga) ciklo_sakinys;

Vykdymo tvarka:

patikrinama sąlyga. Jei ji lygi true, atliekami 2 etapo veiksmai, priesingu atveju - 3 etapo veiksmai.

įvykdomas ciklo_sakinys ir grįztama prie 1 etapo;

vykdomas uz ciklo while esantis sakinys.

Jeigu ciklo viduje reikia įvykdyti ne vieną sakinį, o sakinių grupę, tai grupė bus rasoma skliaustuose. Jei pries pradedant vykdyti ciklą sąlyga yra false, tai sakinys nevykdomas nė karto. Ciklas bus vykdomas be galo daug kartų, jei sąlyga niekada neįgaus reiksmės false.

#include <iostream.h>

main ()

cout <<" Skaičių sudaro "<<kiekis<<" skaitmenų";

cout <<" Norėdami baigti, paspauskite bet kokio simbolio klavisą";

cin >> k;

}

1. Parasykite programą, skaičiuojančią įvesto natūraliojo skaičiaus lyginių ir nelyginių skaitmenų sumas bei formuojančią įvesto natūraliojo skaičiaus atbuląjį skaičių.

2. Palūkanos. Pristigo zmogus pinigų ir nuėjo pasiskolinti jų is prekybininko. Tas sutiko paskolinti, bet paprasė grązinti juos kitą mėnesį sitaip: pirmąją mėnesio dieną - 1 litą, antrąją - du litus, trečiąją - keturis litus, t.y. kiekvieną dieną du kartus daugiau negu pries tai buvusią. Tą dieną, kai skola galės būti padengta, reikės atiduoti ir visą tos dienos normą. Tai, kas bus atiduota virsaus, ir bus prekybininko palūkanos. Parasykite programą, kuri suskaičiuotų, kiek palūkanų litais gaus prekybininkas uz paskolintus n litų. Pavyzdziui, jei zmogus pasiskolino litus, prekybininkas gaus litus palūkanų.

3. Fibonačio skaičiai sudaro eilutę 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .... Kiekvienas sios eilutės narys, pradedant trečiuoju, yra lygus dviejų pries jį einančių narių sumai. Parasykite programą visų Fibonačio skaičių, ne didesnių uz duotą natūralųjį skaičių M, sumai rasti.

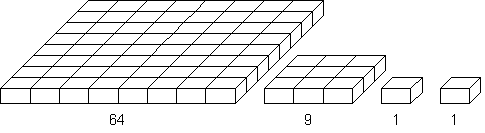
Is n kvadratinių plytelių reikia sudėlioti vienos plytelės storio kvadratų eilę. Pirmiausia sudedamas didziausias galimas kvadratas. Is likusių plytelių - vėl didziausias ir t. t. Parasykite programą, kuri isskaidytų duotą plytelių skaičių į dalis, reikalingas kiekvieno kvadrato statybai. Pavyzdziui, kai n 75, tai rezultatas turi būti: 64, 9, 1, 1.

5. Parasykite programą, skaičiuojančią dviejų natūraliųjų skaičių maziausią bendrą kartotinį.

6. Daugyba ą la russe. Ą la russe - tai daugybos algoritmas dviems teigiamiems sveikiesiems skaičiams (pazymėkime juos N ir M) sudauginti. Aprasysime jį. Pradzioje tarpinei sandaugai priskiriamas nulis.

Jei pirmasis daugiklis nelyginis, tuomet antrasis daugiklis pridedamas prie tarpinės sandaugos, jei lyginis - tarpinė sandauga nekeičiama. Po to pirmasis daugiklis padalinamas is dviejų (imama sveikoji dalis), o antrasis - padvigubinamas pridedant jį patį prie jo paties.

Veiksmai kartojami. Kai pirmasis daugiklis tampa lygus vienam, veiksmai atliekami paskutinįjį kartą, o gautoji tarpinė sandauga tampa lygi skaičių N ir M sandaugai.

Pavyzdziui, sudauginkime skaičius 325 ir 6874.

Pirmasis daugiklis  Antrasis daugiklis Tarpinė sandauga

6874 6874

162 13748 6874

81 27496 34370=6874+27496

40 54992 34370

20 109984 34370

10 219968 34370

5 439936 474306=34370+439936

2 879872 474306

1 1759744 2234050=474306+1759744

Gauname: 325 6874 2234050;

Parasykite programą, kuri siuo būdu sudaugintų du skaičius. Reikia spausdinti visas skirtingas tarpines bei galutinę sandaugos reiksmes. Auksčiau pateikto pavyzdzio pradiniai duomenys būtų , o rezultatą sudarytų keturi skaičiai: .

Įdomi seka. Seka formuojama tokiu būdu. Pirmasis sekos narys yra bet kuris nelyginis natūralusis skaičius didesnis uz vienetą. Kiekvienas tolesnis sekos narys lygus:

p div 2 jei p yra lyginis;

3p+1, jei p yra nelyginis;

čia p yra pries tai buvęs sekos narys. Seka uzbaigiama, kai gaunamas vienetas.

Pavyzdziui, pirmasis sekos narys lygus 7. Tuomet gaunama tokia seka:

Spėjama, kad tokia seka visuomet yra baigtinė. Tačiau dar nė vienam mokslininkui nepavyko to įrodyti.

Uzduotis. Duotas pirmasis sekos narys p (3 p<30000). Parasykite programą, kuri suskaičiuotų koks bus sekos ilgis. Jei seka turi daugiau nei 300 narių, reikia isspausdinti pranesimą, kad sekos pabaiga nepasiekta.

Pavyzdys. Jei pradinis duomuo lygus , rezultatas turėtų būti lygus

Skaičiaus saknis. Natūraliojo skaičiaus skaitinė saknis apskaičiuojama taip: sudedami visi skaičiaus skaitmenys ir gaunamas naujas mazesnis skaičius, tuomet vėl sudedami naujojo skaičiaus skaitmenys ir veiksmai kartojami tol, kol gaunamas vienzenklis skaičius.

Yra greitesnis būdas siai sakniai apskaičiuoti. Jį pailiustruosime pavyzdziu. Apskaičiuosime skaičiaus 87345691 skaitinę saknį. Pirmiausia sudedame skaitmenis 8 ir 7. Gauname 15. Kadangi suma didesnė uz 10, atimame 9 (kitaip sakant, sudedame 5 ir 1) 15-9 5+1. Gauname 6. Pridedame trečią skaitmenį: 6+3 9. Prie gautos sumos pridedame ketvirtą skaitmenį: 9+4 13; Vėl atimame 9 (arba sudedame abu skaitmenis) 13-9 4. Ir taip kartojame veiksmus, kol gauname rezultatą:

Ieskoma skaitinė saknis lygi 7. Duotas teigiamas sveikasis skaičius. Parasykite programą, kuri čia aprasytu būdu suskaičiuotų sio skaičiaus skaitinę saknį.

3.2. Ciklo sakinys for

Ciklas for yra bendriausia ciklo forma. Sio ciklo antrastėje yra nustatomos ciklo kintamųjų pradinės reiksmės, tikrinama ciklo pabaigos sąlyga, keičiami ciklo parametrai. Ciklo for konstrukcija:

For (NebūtinaiIsraiska1; NebūtinaiIsraiska2; NebūtinaiIsraiska3) CikloSakinys;

Ciklo sakiniu gali būti ir sudėtinis sakinys skliaustuose. Kiekvieną is trijų skliausteliuose nurodytų israiskų galima praleisti, tačiau būtina padėti kabliataskį. Paprastai pirmoji israiska taikoma indekso nustatymui, antroji - ciklo pabaigos sąlygos tikrinimui, trečioji - indekso reiksmės keitimui.

Formaliai ciklo for veiksmai aprasomi taip:

Jeigu NebūtinaiIsraiska1 vartojama, tai ji skaičiuojama;

Skaičiuojama NebūtinaiIsraiska2, jei ji vartojama. Jei sios israiskos rezultatas yra lygus false, tai ciklas nutraukiamas, priesingu atveju - tęsiamas;

Vykdomas CikloSakinys;

Skaičiuojama NebūtinaiIsraiska3, jei ji vartojama;

Grįztama į 2 punktą.

Is pirmo zvilgsnio ciklas for yra panasus į kitų programavimo kalbų ciklus, tačiau yra zymiai uz juos lankstesnis. Lankstumą uztikrina trijų israiskų vartojimas ciklo antrastėje:

Galima praleisti vieną ar kelias israiskas. Į ciklą būtinai turi būti įtraukti veiksmai, apibrėziantys ciklo baigimo sąlygas;

Pirmoji israiska nebūtinai turi suteikti kintamajam pradinę reiksmę. Tai gali būti bet koks sakinys. Reikia įsidėmėti, kad sis sakinys bus vykdomas vieną kartą - pries įeinant į ciklą;

Ciklo kintamasis gali keistis bet kokiu zingsniu. Kintamojo reiksmės skaičiavimo israiskoje galima naudoti bet kokias aritmetines operacijas.

#include <iostream.h>

# include <math.h>

main ()

#include <vcl.h>

#include <math.h>

#pragma hdrstop

#include "Unit1.h"

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

void __fastcall TForm1::Button1Click(TObject *Sender)

1 pav. Programos, spausdinančios trizenklius Amstrongo skaičius, darbo langas

Nagrinėdami programą, parasytą C++ Builder 5, atkreipkite dėmesį į tai, kaip uzrasomas rezultatų isvedimas etiketės (Label) komponente:

Label1->Caption = Label1->Caption + "  " + IntToStr(sk);

Kiekvienas naujas įrasas gaunamas, pries tai buvusį įrasą nuo būsimo atskiriant tarpu ir konvertuojant naujai rastą Amstrongo skaičių į eilutės tipo kintamąjį.

Nagrinėdami sį pavyzdį, ismoksime naudoti du naujus komponentus is Additional komponentų grupės. Tai lentelės komponentas StringGrid ir diagramų komponentas Chart (2 pav.).

2 pav. Grupės Additional komponentai

Sie komponentai į programos darbo langą įkeliami kaip ir dauguma kitų.

Pagrindinės lentelės komponento StringGrid savybės, kurias turėsime pakeisti - eilučių (RowCount) ir stulpelių (ColCount) skaičius. Sios savybės keičiamos objektų inspektoriaus lange (3 pav.). Stulpeliai ir eilutės numeruojami pradedant nuline reiksme. Todėl norėdami automatiskai įvardinti, kur bus x ir y reiksmės, turime tai nurodyti sakiniais:

StringGrid1->Cells[0][0] = "x";

StringGrid1->Cells[1][0] = "y";

Sie sakiniai nurodo, kad x reiksmė bus nulinio stulpelio nulinėje eilutėje, o y - pirmo stulpelio nulinėje eilutėje.

Komponento nulinis stulpelis ir nulinė eilutė is likusių komponentų issiskiria tuo, kad jie yra pilkos spalvos, o likusieji - baltos.

3 pav. Lentelės komponento savybių keitimas

Diagramų komponento pagrindinė paskirtis - piesti duomenų lentelių arba funkcijų diagramas ir grafikus. Reikia pasirinkti norimą diagramos formą ir perduoti atvaizdavimui skirtus duomenis. Duomenis galima grupuoti ir vienoje diagramoje parodyti kelių duomenų sekų grafinius vaizdus.

Pagrindiniai veiksmai, atliekami įkėlus diagramų komponentą į programos darbo langą:

Pasirinkti diagramos tipą;

Pasirinkti diagramos pavadinimą;

Pasirinkti, rodyti ar nerodyti asis, komentarus (legendas), rėmelius, foną ir kitus diagramos redagavimo veiksmus. Sie pasirinkimai labai panasūs į pasirinkimus, atliekamus kuriant Microsoft Excel diagramas.

Duomenys į diagramą nukreipiami sakiniu:

Series1->AddXY(x koordinatė, y koordinatė, x asies duomenys, spalva);

Programos kodas:

#include <vcl.h>

#pragma hdrstop

#include "Unit1.h"

#pragma package(smart_init)

#pragma resource "*.dfm"

TForm1 *Form1;

__fastcall TForm1::TForm1(TComponent* Owner)

: TForm(Owner)

void __fastcall TForm1::Button1Click(TObject *Sender)

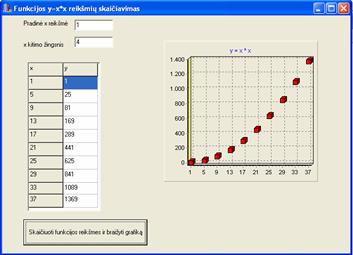
Rasant sią programą panaudotas ciklo sakinys for. Programos darbo langas pateiktas 4 pav.

4 pav. Programos, skaičiuojančios funkcijos y = x² funkcijos reiksmes ir braizančios sios funkcijos grafiką, darbo langas

9. Pakeiskite 3 pavyzdzio programą taip, kad ji skaičiuotų funkcijos y = x² reiksmes, kai x ir z kintamieji gali įgyti bet kokias realias reiksmes ir braizoma tiesinė zalios spalvos diagrama (pavyzdyje pateikta taskinė diagrama, kurioje taskai yra raudonos spalvos).

10. Parasykite programą, skaičiuojančią natūraliųjų skaičių eilutės

1 * 3 + 3 * 5 + 5 * 7 + ... + n * (n + 2), kur n - nelyginis skaičius, sumą. Sumos kitimą kintant n reiksmėms, pavaizduokite tiesine mėlynos spalvos diagrama.

11. Papildykite 2 uzduoties programą, kad būtų skaičiuojama ir eilutės 2 * 4 + 4 * 6 + 6 * 8 + ... + n * (n + 2), kur n - lyginis natūralusis skaičius, suma. Diagramą papildykite taip, kad joje matytųsi abiejų eilučių sumų kitimas kintant n reiksmėms.

12. Sudarykite programą, kuri rastų ir isspausdintų intervalo [2;100] skaičių, turintį daugiausiai daliklių. Jei intervale yra keli skaičiai, turintys po daugiausiai daliklių, tai pakanka atspausdinti didziausią is jų.

Sakoma, kad skaičiai, gauti pagal formulę x² + x + 17, kai 0, yra pirminiai. Parasykite programą, patikrinančią, ar sis teiginys yra teisingas intervalo [1; 10000] skaičiams.

14. Duotas natūralusis skaičius a. Parasykite programą, randančią artimiausią, einantį po a, pirminį skaičių. Pvz., jei a - 9, tai rezultatas turi būti 11, jei a - 23, rezultatas - 29.

15. Pradinis duomuo - natūralusis skaičius. Parasykite programą, kurios rezultatas būtų skaičius, gautas pasalinus is pradinio duomens visus nelyginius skaitmenis.

16. Sudarykite programą, tikrinančią, ar įvestą natūralųjį skaičių galima isreiksti trejeto laipsniu. Jei taip, būtina nurodyti laipsnio rodiklį.

17. Skaičiai 55 ir 66 įdomūs ne tik tuo, kad  susideda is vienodų skaitmenų, bet ir tuo, kad juos galima isreiksti pirmųjų is eilės einančių natūraliųjų skaičių suma:

Galbūt yra ir daugiau tokių skaičių, pasizyminčių minėtomis savybėmis? Sudarykite programą, kuri rastų visus intervalo [1; 10000] sveikuosius skaičius, sudarytus is vienodų skaitmenų ir lygius kokios nors sekos 1 + 2 + 3 + ...+ N sumai.

Įdomūs penkiazenkliai. Ar galite rasti visus penkiazenklius skaičius, kurie yra tam tikro skaičiaus kvadratas ir kurių dviejų pirmųjų skaitmenų bei dviejų paskutiniųjų skaitmenų sudaromų dvizenklių skaičių suma yra taip pat kvadratas? Parasykite programą, randančią visus tokius penkiazenklius skaičius. Skaičius reikia isspausdinti po vieną eilutėje. Toks skaičius, pavyzdziui, yra 19881, nes 141² 19881 ir 19+81=100, o 100

240 minučių trukmės vaizdajuostė kainuoja 10 litų 90 centų, 180 minučių trukmės vaizdajuostė kainuoja 9 litus 15 centų. Tomas perziūrėjo Baltijos televizijos savaitės programą ir panorėjo įsirasyti n laidų. Zinoma kiek valandų ir kiek minučių trunka kiekviena laida. Reikalui esant, bet kuri laida gali būti suskaidyta į dalis ir įrasyta į dvi ar daugiau vaizdajuosčių, o į vieną vaizdajuostę gali būti rasomos kelios laidos. Deja, Tomas neturi nei vienos tusčios vaizdajuostės. Parasykite programą, kuri suskaičiuotų, kiek maziausiai pinigų (litų bei centų) reikės isleisti Tomui, norint nusipirkti tiek vaizdajuosčių, kad jų uztektų norimoms laidoms įrasyti.

Dangoraizis. Naujame dangoraizyje yra n kabinetų, sunumeruotų nuo 1 iki n. Prie kiekvieno kabineto durų reikia prikalti lenteles su to kabineto numeriu. Ant vienos lentelės uzrasytas tik vienas skaitmuo. Jei kabineto numeris nevienzenklis skaičius, tai prie durų kalamos kelios lentelės. Parasykite programą, kuri suskaičiuotų, kiek reikės lentelių su kiekvienu skaitmeniu atskirai, norint prikalti numerius prie visų dangoraizio kabinetų durų. Pavyzdziui, jei n 6, tai rezultatai turėtų būti , čia pirmasis skaičius reiskia lentelių su skaitmeniu 0 skaičių, antrasis - lentelių su skaitmeniu 1 skaičių ir t. t. Paskutinysis skaičius reiskia lentelių su skaitmeniu 9 skaičių.

Amstrongo skaičiai. n-zenklis (n>1) skaičius vadinamas Amstrongo skaičiumi, jeigu jis lygus savo skaitmenų n-ųjų laipsnių sumai.

Pavyzdziui, skaičius 371 yra Amstrongo skaičius: 371 = 3³+7³+1³; Sudarykite programą, kuri rastų didziausią Amstrongo skaičių, nevirsijantį m.

Seka 153. Pirmasis sekos narys - natūralusis skaičius, kuris dalosi is 3. Kiekvienas tolesnis sekos narys lygus pries tai buvusio nario skaitmenų kubų sumai.

Įdomu tai, kad skaičius 153 būtinai yra tokios sekos narys. Ir visi tolimesni sekos nariai sutampa: 153

Uzduotis. Duotas pirmasis sekos narys. Nustatykite, kelintas sekos narys bus skaičius 153.

Duomuo skaitomas is ekrano ir rezultatas pateikiamas ekrane.

Pavyzdziui, jei pirmasis sekos narys lygus 33, tai seka bus tokia:

s₁

s₂

s₃

s₄

s₅

s₆

s₇

Taigi rezultatas turėtų būti lygus 7.