Skaitmeniniai elektroniniai įtaisai
Teorijos pagrindai
ĮVADAS
0.1. Skaitmeniniai įtaisai. Teoriskai nagrinėjant skaitmeninius informacijos apdorojimo įtaisus, diskretiniai jų signalai zymimi dvejetainiais simboliais, kurie gali įgyti loginio vieneto (1) arba loginio nulio (0) reiksmes. Jei įtaisas turi keletą įėjimų ar isėjimų, tai sie signalai reiskiami elementarių dvejetainių signalų rinkiniais:
 (1)
(1)
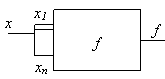
Elementarių signalų skaičius diskretiniame signale vadinamas kanalu, arba skilčių, skaičiumi. Tuomet skaitmeninis įtaisas, turintis m įėjimo kanalų ir n isėjimo kanalų, tampa (m, n) poliu (1 pav.), m skilčių įėjimo signalą X= keičiančiu į n skilčių isėjimo signalą Y=.
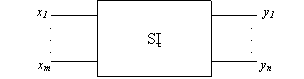
1 pav. Skaitmeninis įtaisas
0.2. Diskretinis laikas. Nagrinėjant skaitmeninius įtaisus, svarbi diskretinio laiko sąvoka. Įprasta laikyti, kad įtaiso darbo laikas yra suskaidytas į diskretinius intervalus, kurie kartais vadinami taktais. Pagal diskretinių laiko intervalų trukmės nustatymo būdą įtaisai skirstomi į sinchroninius ir asinchroninius. Sinchroniniams įtaisams diskretinio laiko intervalo trukmę nurodo specialus sinchronizavimo (taktavimo) signalas, o asinchroniniams įtaisams - įėjimo signalas: laikoma, kad pakitus nors vienai sio signalo skilčiai, taktas t pasibaigė ir prasidėjo kitas taktas (t+1).
Nors pereinamieji procesai, vykstantys kintant signalams, yra labai svarbu, nagrinėjant įtaisų veikimo dėsnius (algoritmus), vertinamos tik nusistovėjusios signalo reiksmės. Tokiais atvejais įprasta laikyti, kad įėjimo bei isėjimo signalai viso takto metu yra pastovūs ir kinta tik intervaluose tarp taktų.
0.3. Kombinaciniai įtaisai ir automatai. Kita svarbi skaitmeninių įtaisų skiriamoji ypatybė - rysys tarp jų įėjimo ir isėjimo signalų. Siuo poziūriu skaitmeniniai įtaisai skirstomi į kombinacinius įtaisus ir sekvencinius įtaisus, arba automatus.
Kombinacinių įtaisų isėjimo signalas Y= priklauso tik nuo tuo metu (nagrinėjamiems takte t ) veikiančio įėjimo signalo X =
Y(t)=f(X(t)) (2)
Norint issamiai apibūdinti kombinacinio įtaiso veikimą, reikia kiekvienai galimai įėjimo signalo X reiksmei nurodyti isėjimo signalo Y reiksmę. Matematiskai tokios priklausomybės uzrasomos Bulio funkcijomis. Todėl sios funkcijos ir taikomos kaip matematinė kombinacinių įtaisų modelis.
Automatuose isėjimo signalo reiksmė Y takto t metu apskritai priklauso nuo visų anksčiau duotų įėjimo signalų:
![]() (3)
(3)
Kito takto metu, davus naują įėjimo signalą X(t+1) , automatas duos kitą isėjimo signalą Y(t+1)=f(X(t+1), X(t)). Taip į kiekvieną įėjimo signalų seką (X(0), X(1), ..., X(t)) automatas reaguos atitinkama isėjimo signalų seka (Y(0), Y(1), ..., Y(t)). Todėl automatai dar vadinami sekų arba sekvenciniais įtaisais. Norint issamiai aprasyti automato veikimą (algoritmą), reikia nurodyti kiekvieną galimą įėjimo signalų seką atitinkančią isėjimo signalų seką (automato reakciją). Kadangi apskritai įėjimų signalų sekos ilgis, tuo pačiu ir galimų skirtingų sekų skaičius, gali būti labai didelis, net begalinis, toks automato aprasymas nekonstruktyvus ir praktikoje sunkiai pritaikomas.
0.4. Automato struktūra. Automato isėjimo signalą (3) uzrasysime taip:
Y(t)=f(X(t), j(X(t-1), X(t-2), ..., X( (4)
Pazymėję
j(X(t-1), X(t-2),..., X(0))=A(t) (5)
turėsime
Y(t)=f(X(t), A(t)) (6)
Čia A(i) - automato atmintis, arba vidinė būsena (įprasta laikyti, kad ankstesnes signalo X reiksmes automatas įsimena pereidamas į tam tikras vidines būsenas). 959j921j
Automato vidinė būsena A(t) laiko momentu t priklauso nuo visų ankstesnių signalo reiksmių pradedant taktu (t-1). Takto (t+1) metu vidinė būsena jau priklausys ir nuo signalo X(t) takto t metu.
A(t+1) = f(X(t), A(t)) (7)
Panaudojus atminties, arba vidinės būsenos, sąvoką ir remiantis israiskomis (6) ir (7), automatą galima pavaizduoti struktūrine schema (2 pav.), kurioje LK loginis keitiklis, o A - atminties blokas. Sis automatas veikia taip: takto t metu loginis keitiklis formuoja isėjimo signalą Y(t). ir grįztamojo rysio signalą R(t), priklausančius nuo įėjimo signalo reiksmės X(t) ir vidinės būsenos A(t). Grįztamojo rysio signalo R(t) paskirtis - kito, (t+ I) takto metu pervesti automatą į naują vidinę būseną A(t+1).
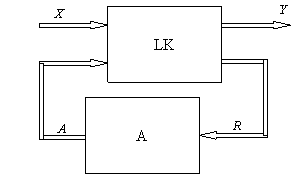
2 pav. Automato struktūrinė schema
Paprastai automatuose signalai X, Y, R yra daugiaskilčiai dvejetainiai. Automato vidinę būseną taip pat atitinka daugiaskiltis dvejetainio atminties bloko isėjimo signalas A=. Taigi automato loginis keitiklis yra kombinacinis įtaisas, kuris formuoja signalus Y ir R, priklausančius nuo signalų X ir A reiksmių,
Atminties blokas turi turėti atmintį arba bent pakankamą signalo vėlinimą: loginiam keitikliui. suformavus signalą R(t), atminties bloko isėjimo signalas A(t) turi islikti nepakitęs iki takto pabaigos. (Tiksliau priesingai - kitas automato darbo taktas prasideda pakitus vidinės būsenos signalui). Taigi automato atminties blokas apskritai pats turi būti automatas. Kad toks aiskinimas nebūtų "rekursyvus" (automatui sudaryti reikalingas automatas), pazymėsime, kad automatu (įtaisu su atmintimi) tampa kombinacinis įtaisas, jei į jį įvedami grįztamieji rysiai: dalis jo isėjimo kanalų prijungiama prie įėjimo. Taigi bet kurioje automato schemoje turi būti grįztamieji rysiai, o kombinaciniams įtaisams jie nebūtini.
Atminties elementai automatuose dazniausiai būna elementarūs automatai - trigeriai. Matematinis automato modelis yra abstraktus automatas.
Kartais automatais vadinami visi skaitmeniniai įtaisai. Tuo atveju kombinaciniai įtaisai priskiriami prie automatų be atminties, o sekvenciniai įtaisai - prie automatų su atmintimi. Savo ruoztu pastarieji gali turėti baigtinę arba begalinę atmintį. Automatai, turintys begalinę atmintį, dar vadinami masinomis.
. BŪLIO FUNKCIJOS
1.1. Būlio funkcijos ir jų pateikimo būdai
1.1.1. Būlio funkcijos ir kombinaciniai įtaisai. Loginėmis, arba Būlio (pagal jas tyrinėjusio anglų matematiko G.Boole pavardę), vadinamos funkcijos, kurios įgyja I arba 0 reiksmę ir priklauso nuo argumentų, taip pat įgyjančių tik I arba 0 reiksmes:
![]() (1.1)
(1.1)
Taigi tai yra dvejetainės dvejetainių argumentų funkcijos. Sugretinę Būlio funkcijos reiksmę su kombinacinio įtaiso isėjimo signalu, o jos argumentus su įėjimo signalais, pastebime, kad Būlio funkcija ir kombinacinis įtaisas yra analogiski. Kiekvienas kombinacinis įtaisas su vienu isėjimo kanalu ir m įėjimo kanalų gali būti aprasomas m argumentų Būlio funkcija. Kombinacinio įtaiso (1 pav.) su m įėjimo kanalų ir n isėjimo kanalų modelis yra m Būlio funkcijų, priklausančių nuo n argumentų, sistema:
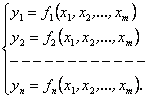 (1.2)
(1.2)
1.1.2. Argumentų rinkiniai. Kombinacinio įtaiso įėjimo signalą sudaro vienu metu veikiančių elementarių dvejetainių įėjimo signalų rinkinys. Būlio funkcijos reiksmę taip pat lemia jos argumentų rinkinys (X1, X2, ..., Xk). Konkreti jo israiska yra k ilgio vienetų ir nulių eilutė, pavyzdziui, 10110101. Kiekviena baigtinė simbolių 1 ir 0 seka dvejetainės skaičiavimo sistemoje reiskia skaičių. Pavyzdziui, 10110 reiskia 22, 1001 - 9. Skaičius, dvejetainėje sistemoje isreikstas argumentų rinkimui, vadinamas rinkinio numeriu.
Imant k dvejetainių
skilčių, galima uzrasyti skaičius nuo 0 iki 2K-1. Taigi esant k argumentų, gali būti 2 skirtingų jų
rinkinių. Taip Būlio funkcijų argumentų rinkinių; skaičius visuomet yra
baigtinis. Toks yra ir skirtingų Būlio funkcijų
skaičius. Jeigu kiekvienos k
argumentų Būlio funkcijos reiksmė yra apibrėzta esant
visiems 2K galimiems argumentų rinkiniais, skirtingų
tokių funkcijų skaičius yra ![]() (1.1 lentelė).
(1.1 lentelė).
1.1 lentelė
k argumentų Būlio funkcijų skaičius
|
Argumentų skaičius k | |||||
|
Skirtingų funkcijų skaičius |
1.1.3.Nevisiskai apibrėztos funkcijos. Būlio funkcijos kurių reiksmės apibrėztos visiems galimiems argumentų rinkiniams, vadinamos visiskai apibrėztomis, o tos, kurių reiksmės apibrėztos ne visiems argumentų rinkiniams (zymima X arba * ), - nevisiskai, arba dalinai apibrėztomis. Argumentų rinkiniai, kuriems funkcijos reiksmė neapibrėzta, vadinami neesminiais rinkiniais.
Kombinaciniuose įtaisuose neesminiai būna negalimi signalų rinkiniai (kai realių galimų signalų skaičius mazesnis uz 2K) arba tokie, kuriuos davus į įėjimą taikomuoju poziūriu nesvarbi isėjimo signalo reiksmė.
1.1.4. Funkcijos reiksmių lentelė. Būlio funkcijos gali būti pateikiamos (uzrasomos) įvairiais būdais. Jie pasirenkami priklausomai nuo turimų pirminių duomenų ir funkcijos pateikimo tikslo.
Paprasčiausia - sudaryti funkcijos reiksmių lentelę.
Čia pateikiamas issamus sąrasas argumentų rinkinių ir juos atitinkančios funkcijos reiksmės. Kartais toje pat lentelėje gali būti keleto funkcijų reiksmės. Stai 1.2 lentelėje nurodomos funkcijų y1 ir y2 reiksmės. Funkcija y1 yra visiskai, o y2 - nevisiskai apibrėztos. Kartais rasomi ne argumentų rinkiniai, o tik jų numeriai.
1.2. Lentelė
Funkcijų y1 ir y2 reiksmių lentelė
|
x1 |
x2 |
x3 |
y1 |
y2 |
|
X X X |
Reiksmių lentelės dazniausiai taikomos, kai pirminis formalus funkcijos ar įtaiso aprasymas sudaromas analizuojant visus galimus kintamųjų rinkinių variantus.
1.1.5. Reiksmių sritys. Funkcija pateikiama kaip sąrasus ar sąrasai argumentų rinkinių, kuriems esant, ji įgyja vienokią ar kitokią reiksmę. Sąrasas argumentų rinkinių, kuriems esant funkcija y lygi 1, vadinamas jo vienetų sritimi D1(y), o kai si reiksmė lygi 0, - nulių sritimi D0(y). Nevisiskai apibrėztos funkcijos dar turi neapibrėztumo sritį D*(y).
Visiskai apibrėztų funkcijų pakanka nurodyti vieną sritį, dazniausiai - D1(y).2?/ (&/ . Nevisiskai apibrėztų - dvi sritis, paprastai D1(y) ir D0(y). Sąrasuose isvardijami patys rinkiniai arba tik jų numeriai. Pavyzdziui, 1.2 lentelėje pateiktų funkcijų reiksmių sritys yra tokios:

1.1.6.Karno diagramos. Jos dar vadinamos Karno kortomis arba Karno lentelėmis (pagal jas pasiūliusio Karnough pavardę). Tai specialus funkcijos reiksmių lentelės uzrasymo kvadratinėse (arba 1x2 formato, jei kintamųjų skaičius nelyginis) lentelėse būdas (I.I pav.). Kiekvienas sių lentelių langelių atitinka vieną argumentų rinkinį, kurio reiksmė yra langelio koordinatės, uzrasytos prie isorinių lentelės krastinių. Kiekviename lentelės langelyje įrasoma funkcijos reiksmė 1, 0 arba * (jei funkcija nevisiskai apibrėzta).
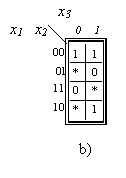
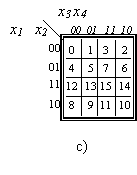
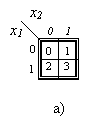
l.l pav. Karno diagramos 2, 3 ir 4 argumentų funkcijai uzrasyti. Diagramose a) ir c) langeliuose nurodyti juos atitinkančių argumentų rinkiniai ar numeriai. Diagramoje b - funkcijos y2 (zr. 1.2 lentelę) reiksmės.
Karno diagramos langeliai (zr.1.2 pav.) isdėstomi taip, kad kiekvienus du gretimus (gretimais laikomi ir langeliai, esantys toje pat eilutėje ar stulpelyje prie priesingų lentelės krastų) atitiktų gretimi, tai yra besiskiriantys tik vienos skilties reiksme argumentų rinkiniai.
Funkcijos kartais pateikiamos Veičo diagrama (1.2 pav.), kuri nuo Karno lentelės skiriasi kiek kitokiu argumentų rinkinių uzrasymu, o kartais ir isdėstymu.
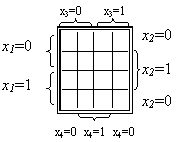
Karno diagramos lengvai sudaromos, kai argumentų skaičius ne didesnis kaip 4. Jas galima sudaryti ir kai argumentai yra 5 ar 6. Tuomet diagramą reikia įsivaizduoti kaip 2 ar 4 vieną ant kitos padėtas keturių argumentų funkcijos lenteles, kurių kiekviena turi skirtingas argumento x5 (penkių argumentų funkcija) arba argumentų x5x6 reiksmių poras (sesių argumentų funkcija) ir kurios isdėstomos taip, kad gretimi ne tik lentelių, bet ir sluoksnių langeliai atitiktų gretimus argumentų rinkinius.
1.2 pav. Keturių argumentų funkcijų Veičo diagrama.
Kai argumentų daugiau kaip 6, Karno diagramomis naudotis sunku arba net neįmanoma.
Karno diagramos plačiai taikomos paprastinant Būlio funkcijas bei sintezuojant kombinacinius įtaisus.
1.1.7. Geometrinis vaizdavimas. Sis Būlio funkcijos pateikimo būdas dar vadinamas pateikimu kubu kompleksais, arba intervalais. Čia n argumentų rinkinys interpretuojamas kaip n-matis vektorius, arba kaip taskas n-matėje erdvėje. Kadangi visos vektoriaus koordinatės yra dvejetainės, tai sis taskas visada sutampa su viena is n-mačio kubo n-matėje erdvėje virsūnių.
Aiskinimą iliustruosime trijų argumentų funkcija, vaizduodami ją trimačiu kubu. Kiekvienos is astuonių sio kubo virsūnių koordinatės sutampa su vienu is trijų kintamųjų funkcijų argumentų rinkinių. Pazymėję, pavyzdziui, ryskesniu tasku tas kubo virsūnes, kurias atitinkantiems argumentų rinkiniams esant funkcijos y reiksmė lygi 1, gausime geometrinį jos vaizdavimą (1.3 pav.).
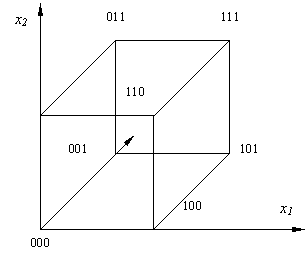
1.3 pav. Geometrinis trijų argumentų funkcijos vaizdavimas
Kai kintamųjų skaičius daugiau kaip trys, geometriskai funkciją pavaizduoti sunku. Tuomet vaizdavimas isplečiamas į algebrinį vaizdavimą kubais, arba intervalais: daugiamatėje erdvėje nagrinėjamo daugiamačio kubo elementai - 0-matė virsūnė, vienmatė briauna, dvimatė siena ir didesnio matmenų skaičiaus dariniai - vadinami n-mačiais kubais, arba n-mačiais intervalais.
Sąrasas 0-mačių kubų, kuriems esant funkcijos reiksmė lygi 1, vadinama 0-mačiu funkcijos kubų kompleksu
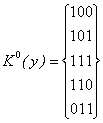
Funkcijos pateikimas kubų kompleksu K0 yra issamus, tačiau gana gremėzdiskas. Pazymėsime, kad kai kurios funkcijos komplekso K0 kubų poros yra toje pat briaunoje. Tokių kubų aprasymai skiriasi tik viena koordinate (skiltimi). Sujungsime tas 0-mačių kubų poras į 1-mačius kubus (geometriskai - į briaunas) ir uzrasysime juos taip: koordinačių, bendrų abiem 0-mačiam kubam, nekeisime, o tą vienintelę koordinatę, kuri visame kube lygi 1, kitame - 0, pazymėsime X - tai reiskia, kad ji gali būti visokia. Pavyzdziui,
![]()
Visų galimų funkcijos vienmačių kubų sąrasą sudaro funkcijos kubų kompleksą K1.
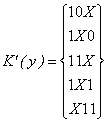
Pazymėsime, kad funkcijos uzrasymas vienmačių kubų kompleksu gali būti ir neissamus: gali būti tokia izoliuota virsūnė (0-matis kubas), per kurią neina nė viena briauna, turinčios kitą funkcijos 1 reiksmę atitinkančią virsūnę. (Nagrinėjamame pavyzdyje tokios virsūnės nėra). Be to, aprasymas kompleksu K1 gali būti ir perteklinis, nes kai kurie 0-mačiai kubai įeina į daugiau kaip vieną 1-matį kubą.
Analogiskai dvi gretimas briaunas (I-mačius kubus) galima sujungti į 2-matį kubą - sieną. Pavyzdziui, kubai 10X ir 11X sujungiami į dvimatį kubą 1XX; taip pat ir kubai 1X0 ir 1X1. Nagrinėjamos funkcijos dvimačių kubų kompleksą sudaro vienintelis kubas:
K2(y)=
Turint daugelio kintamųjų funkcijų aprasytuosius sujungimus galima tęsti sudarant 3-mačius, 4-mačius ir t.t. kubus.
Funkcija kubais uzrasoma issamiai, kai sujungiami visi kubų kompleksai.
![]() (1.3)
(1.3)
Aisku, toks aprasymas yra perteklinis. Jei kuris nors mazesnis kubas įeina į kitą didesnį kubą (sakoma, toks didesnis kubas dengia mazesnį), pirmasis kubas funkcijos aprasyme nebūtinas. Funkcijai, vaizduojamai 1.3 pav., aprasyti pakanka, pavyzdziui, kompleksų
![]()
Funkcijos uzrasymas kubų kompleksais yra gana ekonomiskas, ypač kai funkcija yra daugelio argumentų.
1.1.8. Analizinis uzrasymas. Tai Būlio funkcijų uzrasymas formulėmis. Formulės sudaromos taikant elementariųjų Būlio funkcijų superpoziciją.
Elementariosioms priskiriamos visos vieno ir dviejų argumentų Būlio funkcijos. Vieno argumento funkcijos yra keturios (1.3 lentelė). Is jų dvi, konstanta 0 ir konstanta 1, yra issigimusios (trivialios).
Dviejų argumentų funkcijų yra sesiolika (1.4 lentelė), is kurių Sesios (lentelėje pazymėtos *) issigimusios.
Superpozicija - tai vienos funkcijos argumentų pakeitimas kitomis funkcijomis. Taip is vieno ar dviejų argumentų funkcijų sudaromos daugelio argumentų funkcijos. Pavyzdziui, y1=x1·x2, y2=x3Vx4 ir z=y1 y2; sudarome z=x1x2 (x3Vx4). Arba is y1=x1x2, y2x2x3 ir z=y1y2 gauname z=x1x2x3;
Taikant elementariųjų Būlio funkcijų superpoziciją, galima sudaryti norimo sudėtingumo formules. Būlio funkcijų teorijoje įrodoma /8/, /10/, /4/, kad elementariųjų funkcijų superpozicija galima isreiksti bet kokią Būlio funkciją.
Rinkinys funkcijų, kurių superpoziciją galima isreiksti bet kokią pasirinktos klasės funkciją, vadinamos tos klasės funkcijų pilnąja sistema, arba baze. Taip elementariosios Būlio funkcijos sudaro Būlio funkcijų bazę.
Tačiau,
reikia pazymėti, kad taip sudaryta bazė yra perteklinė. Sudarant
sudėtingesnių funkcijų formules, nebūtina imti visas
elementariąsias funkcijas, nes daugelį jų galima isreiksti
kitomis. Pavyzdziui, 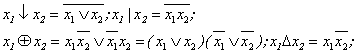
1.3 Lentelė
Vieno kintamojo elementariosios funkcijos
|
Funkcijos reiksmė esant argumento reiksmei |
Zymėjimas |
Pavadinimas |
|
|
x |
x |
||
|
y= y=x y= x y= |
Konstanta 0 TAIP NE Konstanta 1 |
||
1.4 lentelė
Dviejų argumentų elementariosios funkcijos
|
Funkcijos reiksmė esant argumentų x1x2 reiksmei |
Zymėjimas |
Pavadinimas |
||||
|
y= y=x1x2=x1&x2 y=x1Dx2 y=x1 y=x2Dx1 y=x2 y=x1 x2 y=x1Vx2 y=x1 x2 y=x1~x2 y=x2 y=x1 x2 y= x1 y=x2 x1 y=x2|x1 y= |
Konstanta 0 IR, konjunkcija, loginė daugyba x2 draudimas, bet ne x2 x1 kartojimas x1 draudimas, bet ne x1 x2 kartojimas Neekvivalentiskumas sudėtis moduliui 2 ARBA. Disjunkcija, loginė sudėtis. Pirso operacija, ARBA-NE Ekvivalentiskumas x2 neigimas Implikacija jeigu x1 tai x2 x1 neigimas Atvirkstinė implikacija jeigu x2 tai x2 Seferio operacija IR-NE Konstanta 1 |
|||||
Funkciją, kurią galima isreiksti kitomis tos bazės funkcijomis, galima is bazės pasalinti. Taip nuosekliai jas salindami gausime minimalią bazę, tai yra tokių funkcijų sistemą, kuri, pasalinus nors vieną funkciją, tampa nepilnąja.
Is elementariųjų Būlio funkcijų galima sudaryti keletą skirtingų minimalių bazių. Tokios, pavyzdziui, yra funkcijų sistemos
IR, NE
ARBA, NE
Neekvivalentiskumas, IR.
Dvi elementariosios funkcijos: Seferio
operacija: ![]() ir Pirso funkcija
ir Pirso funkcija ![]() - pačios vienos
sudaro pilnąją sistemą. Tokios funkcijos (tuo pačiu ir
bazės) vadinamos universaliosiomis.
- pačios vienos
sudaro pilnąją sistemą. Tokios funkcijos (tuo pačiu ir
bazės) vadinamos universaliosiomis.
Sudarant loginius įtaisus, plačiausiai taikomos sios bazės:
IR, NE,
ARBA, NE,
IR, ARBA, NE.
Bazė IR, ARBA, NE vadinama logikos, arba Būlio algebros baze. Nors ji nėra minimali, bet plačiai taikoma kombinaciniams įtaisams sintezuoti, nes Būlio algebros teorija yra gana isplėtota.
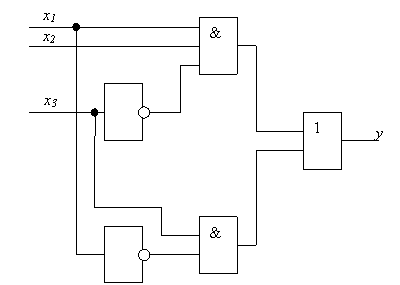
1.1.9. Loginės schemos. Pazymėję elementariąsias funkcijas tam tikru elemento zymeniu (1.4 pav.), kiekvieną Būlio funkcijos formulę galėsime pavaizduoti grafiskai logine schema (1.5 pav.). Ir atvirksčiai, kiekvienai loginei schemai galima uzrasyti Būlio funkcijos formulę. Pakeitę elementų zymenis konkrečiais loginiais elementais, gausime schemą kombinacinio įtaiso, realizuojančio ta formule uzrasytą Būlio funkciją.

1.4 pav. Kai kurių loginių funkcijų zymenys
![]() ;
;
1.5.pav. Loginių schemų pavyzdziai
1.2. Būlio algebra
1.2.1. Bazės funkcijos. Jau buvo minėta, kad trijų elementariųjų Būlio funkcijų IR, ARBA ir NE rinkinys sudaro Būlio bazę. Sistema, kurioje įvairios formulės sudaromos ir veiksmai tarp jų atliekami taikant tik sias funkcijas, vadinama Būlio algebra.
Funkcija IR. Ji yra dviejų ar daugiau argumentų ir lygi nuliui, jei nors vienas jos argumentas lygus nuliui, bei lygi vienetui, jei visi argumentai lygūs siai reiksmei. Ji dar vadinama konjunkcija arba logine sandauga. Zymima zenklais: &, L, tasku arba nezymima: y=x1&x2=x1Lx2=x1x2.
Funkcija ARBA. Ji yra dviejų ar daugiau argumentų ir lygi vienetui, jei siai reiksmei lygus nors vienas argumentas, bei lygi nuliui, kai visi argumentai lygūs nuliui. Ji dar vadinama disjunkcija, arba logine sudėtimi. Zymima zenklu V, kartais +, nors sis nerekomenduojamas: y =x1Vx2=x1+x2.
Funkcija NE. Ji yra vieno argumento funkcija, dar vadinama neigimu, arba inversija. Zymima brūksniu virs kintamojo ar israiskos arba specialiu zenklu pries juos: y= x x Funkcijos reiksmė priesinga pazymėto argumento ar israiskos reiksmei.
1.2.2. Pagrindinės taisyklės ir aksiomos. Būlio algebroje veiksmai tarp funkcijų israiskų (formulių) ar kintamųjų atliekami laikantis 1.5 lentelėje pateiktų arba is jų isvestų taisyklių.
1.5 lentelė
Būlio algebra. Pagrindinės taisyklės
|
Taisyklė |
Pavadinimas |
|
xVx=x; 1V1=1 x·x=x; |
Tapatumo |
|
(x1Vx2)Vx3=x1V(x2Vx3) (x1·x2)x3=x1(x2·x3) |
Asociatyvumo |
|
x1Vx2=x2Vx1 x1·x2=x2·x1 |
Komutatyvumo |
|
xV1=1; x·1=x xV0=x; x·0=0 |
Sujungimo ir susikirtimo |
|
|
Papildymo |
|
|
Distributyvumo |
|
|
Absorbavimo |
|
|
Dvigubo neigimo |
|
|
Derinimo |
|
|
de Morgano |
Plačiau aptarsime de Morgano taisyklę, gana daznai taikomą sintezuojant loginius įtaisus. Ji isplėtojama ir didesniam argumentų skaičiui:
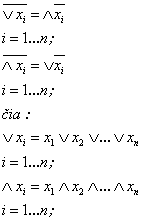 (1.4)
(1.4)
De Morgano taisyklė Būlio algebroje apibendrinama dalumo dėsniu: kiekvienos sudėtinės israiskos (formulės), kurių argumentai arba jų inversijos susiję operacijomis IR bei ARBA, inversija gali būti isreiskiama ta pačia formule, visus argumentus pakeitus jų inversijomis, o operacijas IR ir ARBA sukeitus vietomis. Pavyzdziui,
![]()
Kaip matyti is pateiktų taisyklių ir pavyzdzių, ta pati Būlio funkcija gali būti uzrasoma gana įvairiomis formulėmis. Panagrinėsime kai kurias standartines Būlio funkcijų israiskas.
1.2.3. Nariai. Būlio algebroje nariais vadinamos elementariosios loginės gumos arba sandaugos.
Elementarioji konjunkcija. arba minimalus narys - tai vieno ar kelių argumentų arba jų inversijų loginė sandauga, į kurią kiekvienas argumentas įeina tik vieną kartą. Pavyzdziui, x, x, x1x2, x1 x3, x1x2x5x7
Analogiskai vieno ar kelių argumentų bei jų inversijų loginė suma vadinama e1ementariąja disjunkcija arba maksimaliu nariu. pavyzdziui, x, x, x1Vx2, x1V x2Vx5.
Nario argumentų skaičius vadinamas nario rangu.
Su nariu yra siejami tam tikri jį sudarančių argumentų rinkiniai. Su elementaria konjunkcija siejamas rinkinys, kurio neinvertuotos konjunkcijoje argumentas lygus 1, invertuotas lygus 0. Pavyzdziui, su elementaria konjunkcija x1, x2, x3, x4, x1V siejamas rinkinys 10110. Jei sią konjunkciją laikysime funkcija y= x1, x2, x3, x4, x1; tai ji bus lygi vienetui tik esant su ja susijusių argumentų rinkiniui, o esant visiems kitiems narį sudarančių argumentų rinkiniams bus lygi nuliui. Su elementaria disjunkcija siejamas rinkinys, kurio neinvertuota disjunkcijoje argumentas lygus 0, o invertuotas lygus 1. Elementari disjunkcija x1V x2Vx3 siejama su rinkiniu 010. Elementari disjunkcija lygi nuliui tik esant su ja susijusių kintamųjų rinkiniu ir lygi vienetui esant visiems kitiems sį narį sudarančiais argumentų rinkiniais.
1.2.4. Normalinės formos. Vienos is plačiausiai Būlio algebroje taikomų formulių - Būlio funkcijų normalinės formos. Jos yra dvi: disjunkcinė ir konjunkcinė,
Disjunkcinė normalinė forma
(DNF) - tai baigtinio skaičiaus elementarių konjunkcijų
disjunkcijos (elementarių sandaugų suma). Pavyzdziui, israiskos y=x,
y2=x1 x2, y3=x1x2V x2x4Vx1x3x5
yra funkcijų DNF. Israiskos y4=x1(x2x3V x2x3) arba
![]() nėra normalinės formos.
nėra normalinės formos.
Konjunkcinė normalinė forma (KNF) - tai baigtinio skaičiaus elementarių disjunkcijų konjunkcija (elementarių sumų sandauga). Pavyzdziui, israiskos y1=x, y2=x1Vx2, y3=(x1V x3)· (x2V x4Vx5) yra Būlio funkcijų KNF.
Funkcijos normalines formas sudarančių narių rangai gali būti nevienodi, tačiau niekada ne didesni uz argumentų skaičių, nuo kurio priklauso pati funkcija. Normalinės formos narių skaičius vadinamas formos ilgiu.
Kiekviena Būlio funkcija gali būti uzrasyta ir KNF ir DNF pavidalu, be to, - isreiskiama daugeliu skirtingų KNF ir DNF.
Reikia pazymėti, kad funkcijoms uzrasyti bei analizuoti DNF taikoma dazniau negu KNF.
1.2.5. Tobulosios normalinės formos. Tobulosiomis, arba kanoninėmis, vadinamos tos normalinės formos, kurių visų narių rangai yra vienodi ir lygūs skaičiui argumentų, nuo kurių priklauso funkcija. Taip kiekvieną sios formos narį sudaro visi, tiesioginiai arba invertuoti, funkcijos argumentai.
Tobulosios normalinės formos gali būti sudarytos isplečiant paprastas. Kiekvienas normalinės formos narys, kuris neturi argumento xi keičiamas dviem nariais, is kurių vienas turi xi , o kitas - xi. Procedūra kartojama, kol visų narių rangai tampa maksimalus. Sudarant tobuląsias disjunkcines normalines formas (TDNF), tai atliekama taikant taisyklę:
![]() (1.5)
(1.5)
čia W - nuo argumento xi nepriklausantis konjunkcinis narys. Analogiskai tobulosios konjunkcinės normalinės formos (TKNF) sudaromos pagal taisyklę:
![]() (1.6)
(1.6)
čia W - nuo argumento xi nepriklausantis disjunkcinis narys.
Dar paprasčiau funkcijų tobulosios normalinės formos sudaromos taikant jų reiksmių lenteles. Pirmiausia sudarysime funkcijos TDNF. Pastebėsime, kad ji lygi vienetui tik tada, kai siai reiksmei lygus koks nors vienas jos narys. Du nariai esant tam pačiam argumentų rinkiniui negali būti lygus vienetui, nes kiekvienas narys siai reiksmei lygus tik vienam argumentų rinkiniui, o normalinėje formoje dviejų vienodų narių nėra. Kad TDNF būtų lygi vienetui tik tiems argumentų rinkiniams, kuriems lygi vienetui uzrasoma funkcija, kiekvieną argumentų rinkinį, kuriam esant funkcija lygi vienetui, TDNF turi atitikti vienas su tuo rinkiniu susijęs narys (1.6 pav.).
|
X1 |
X2 |
X3 |
Y |
![]()
1.6 pav. Funkcijos lentelė ir TDNF
1.2.6. Rysys tarp funkcijos DNF ir jos kubų komplekso. Aptarus rysį tarp funkcijos reiksmių lentelės ir jos TDNF, taip pat tarp lentelės ir kubų komplekso K0, rysys tarp funkcijos TDNF ir komplekso K° tampa akivaizdus: kiekvieną komplekso K0 0-matį kubą TDNF atitinka narys, kurio argumentas neinvertuotas, jei kube jo reiksmė 1, ir invertuotas, jei kube reiksmė 0.
Vienmačiai komplekso K1 kubai gaunami sujungus du 0-mačius kubus, kurie skiriasi viena koordinate. Analogiskas elementarių loginių sandaugų (DNF narių) jungimas vadinamas lipdymu. Jei normalinė forma turi du narius, kurie skiriasi vienu argumentu, tai yra narius Wxi ir W xi, (W elementari sandauga, nepriklauso nuo xi ), tuomet juos galima pakeisti vienu nariu - sulipdyti:
![]() (1.7)
(1.7)
Taigi lipdant du nariai Wxi ir W xi, sulipdomi į vieną narį W, kurio rangas vienetu mazesnis uz lipdomų.
Taip vienmatį kubą funkcijos kubų komplekse tos funkcijos DNF-ą atitinka narys, kuris neturi argumento kube pazymėto X. Lipdydami narius arba jungdami kubus, pastebėsime, kad, atliekant kiekvieną tokią operaciją, nario rangas vienetu sumazės, o kubo dimensija vienetu padidės. Todėl funkcijos didesnės dimensijos kubus, kuriuose yra keletas zenklų X, jos normalinėje formoje atitiks narys, neturintis argumentų, kube pazymėtų X. Pavyzdziui:
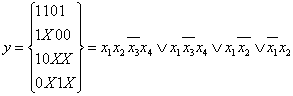
Funkcijos k-matį kubą (k-kubą) sudaro 2K virsūnių (0-mačių kubų), kuriuose funkcijos reiksmė lygi 1. Sakoma, kad k-kubas dengia sias 2k virsūnes.
Jei turime n kintamųjų funkcijos DNF k-tojo rango narį (sandaugą), jis lygus vienetui vieninteliam argumentų rinkiniui. Sulipdzius du tokius narius, gaunamas (n-1) rango narys bus lygus vienetui dviem argumentų rinkiniams, n-kintamųjų funkcijos r rango narys (r ≤ n) bus lygus vienetui 2(n-r) argumentų rinkiniams. Čia paprastai sakoma, kad narys tuos argumentų rinkinius dengia.
Du normalinės formos nariai gali būti sujungti ne tik lipdant, bet ir absorbuojant pagal taisyklę:
![]() (1.8)
(1.8)
Analogiskai, jei funkcijos kubų komplekse yra du kubai, sutampantys visu, isskyrus vieną koordinatę, kuri viename kube yra X, o kitame 1 arba 0, aisku, kad pastarasis kubas įeina į pirmąjį ir yra jo dengiamas. Lengva pastebėti, kad jei vienas narys ar kubas absorbuoja kitą, absorbuojantysis visiskai dengia absorbuojamąjį ir pastarasis funkcijos aprasyme nebūtinas.
1.3. Būlio funkcijų minimizavimas
1.3.1. Minimizavimo uzdavinys. Jau buvo minėta, kad kiekvieną Būlio funkcijos formulę atitinka konkreti loginė schema. Pakeitę funkcijų zymenis konkrečiais loginiais elementais ir įvertinę jų kainą (atsizvelgdami į realizuojamą funkciją ir įėjimų skaičių), galėsime apskaičiuoti įrenginio, realizuojančio pasirinktą Būlio funkcijos formulę, kainą. Aiskiai matyti, kad tarp visų sios funkcijos formulių tikslinga ieskoti tokios, kurią atitinkančio įrenginio kaina būtų minimali. Tai ir yra Būlio funkcijų minimizavimo uzdavinys.
1.3.2. Kenoninis minimizavimo uzdavinys. Formalizuoti minimizavimo uzdavinį nėra lengva dėl dviejų priezasčių. Pirma, sunku tai daryti taikant realias elementų kainas, kurios priklauso nuo daugelio aplinkybių ir nuolat kinta. Antra, sunku pasiūlyti kitokį negu visų 'galimų' variantų analizės metodą, kai ieskomai minimaliai funkcijos israiskai netaikomi jokie apribojimai.
Kad uzdavinys būtų paprastesnis, kainos formalizuojamos. Viena is plačiausiai taikomų yra formali kaina C, isreiskiama bendru visų naudojamų elementų įėjimų skaičiumi. Si kaina funkcijos normalinei formai, kurios ilgis (narių skaičius) m ir narių rangai (kintamųjų skaičius naryje) ri, isreiskiama:
![]() (1.9)
(1.9)
Israiska (formulė), arba schema, kurios kaina C minimali, vadinama minimalia pagal Kvainą. (Kvainas - matematikas, pasiūlęs nagrinėjamus Būlio funkcijų minimizavimo metodus).
Siekiant isvengti visų galimų variantų analizės taikomi įvairūs supaprastinti bei asimptotiniai (artutiniai) metodai. Populiarus kanoninis metodas, atliekamas dviem etapais: pirmiausia randama minimali funkcijos normalinė forma (paprastai DNF), o vėliau, jei reikia, ji paprastinama sudarant suskliaustas formas.
1.3.3. Minimali disjunkcinė norma. Paprastosios implikantės. Minimizavimo uzdavinys dazniausiai spendziamas ieskant funkcijos minimalios disjunkcinės normalinės formos (MDNF), nors jį isspręsti galima ir minimizuojant KNF.
DNF minimizuojamas atliekant lipdymo (1.7) ir absorbavimo (1.8) operacijas. Tos kartojamos tol, kol israiskoje likę nariai daugiau tarpusavyje nebelimpa ir vienas kitą neabsorbuoja. Gauta supaprastinta DNF vadinama akląja DNF, bet tai nebūtinai minimali normalinė forma. Narius pradėjus lipdyti kita tvarka, galima gauti kitą akląją DNF, kurios kaina gali nesutapti su kitaip gautos aklosios formos kaina. Minimali normalinė forma bus ta akloji forma, kurios kaina C (1.9) bus minimali.
Normalinę formą minimizuoti paprasčiau pagal minimizavimo metodą, grindziamą teiginiu: funkcijos DNF yra minimali tik tada, kai visi jos nariai (elementarios sandaugos) yra paprastosios implikantės. Pries įrodydami sio teiginio teisingumą, apibrėsime paprastos implikantės sąvoką.
Būlio funkcijos f implikante vadinama funkcija g, lygi vienetui tik esant tokiems argumentų rinkiniams, kuriems esant ir funkcija f lygi vienetui. Tai galima uzrasyti tokia sąlyga:
![]() (1.10)
(1.10)
Funkcijos implikantė, pavyzdziui, yra bet kuria jos DNF narys, arba keleto jos narių loginė suma.
Paprastąja, arba pirmine funkcijos implikante vadinama elementari konjunkcija (loginė sandauga), esanti tos funkcijos implikantė, kurios jokia dalis jau nėra tos funkcijos implikantė. Kitaip tariant, tai yra tokia elementarios konjunkcijos pavidalo funkcijos implikantė, kuri, pasalinus nors vieną jos argumentą (dauginamąjį), jau nebebus tos funkcijos implikantė, o dengs bent vieną argumentų rinkinį, kuriam funkcijos reiksmė yra nulis.
Interpretuodami geometriskai, nustatysime, kad implikantė gali būti kiekvienas funkcijos kubų komplekso kubas, o paprastoji implikantė yra maksimalus kubas, apimantis (dengiantis) tik vienetines virsūnes (0-mačius kubus), tai yra toks kubas (briauna, siena ir t.t.), kurį sujungę su bet kuriuo gretimu tokio pat matmens kubu, būtinai apimsime ir virsūnes, kuriose funkcijos reiksmė yra nulis.
Dabar galime pagrįsti teiginį, kad funkcijos DNF bus minimali tik tada, kai visi jos nariai bus paprastosios implikantės. Jeigu kuris nors narys nėra paprastoji implikantė jį dar galima absorbuoti kitu nariu (arba su juo sulipdyti) ir gauti mazesnės kainos DNF. Vadinasi, DNF, kurios bent vienas narys nėra paprasta implikantė, nėra minimali.
Būtina, kad visi DNF nariai būtų paprastosios implikantės, tačiau to nepakanka, kad DNF būtų minimali. Is paprastosios implikantės apibrėzimo bet sudarymo matyti, kad tas pats argumentų rinkinys (virsūnė) gali būti padengtas ne vienintele paprastąja implikante. Tuo tarpu, kad DNF atitiktų funkcijos reiksmę, pakanka, kad visi argumentų rinkiniai, kuriems funkcijos reiksmė yra I, būtų padengti implikantėmis bent po kartą. Taigi 4 funkcijos MDNF nebūtinai turi įeiti visos paprastosios jos implikantės.
1.3.4. Kanoninis minimizavimo metodas. Siuo metodu funkcijos MDNF randama dviem etapais. Pirmuoju - randamos visos minimizuojančios funkcijos paprastosios implikantės, antruoju - sudaromas minimaliom kainom paprastųjų implikančių komplektas, dengiantis visus vienetinius funkcijos argumentų rinkinius.
1.3.5. Nevisiskai apibrėztų funkcijų minimizavimas. Kaip kombinacinių skaitmeninių įtaisų modelį taikant nevisiskai apibrėztas Būlio funkcijas, jų reiksmes argumentų rinkiniams, kuriems funkcija neapibrėzta, reikia apibrėzti papildomai, nes kombinacinio įtaiso isėjimo signalas negali būti neapibrėztas. Sia papildomas funkcijos apibrėzimas jos modeliuojamam įtaisui esminės įtakos neturi, nes, kaip jau buvo minėta, argumentų rinkiniai, kuriems funkcijos reiksmė neapibrėzta, kombinaciniame įtaise atitinka negalimus arba neesminius signalus.
Minimizuojant nevisiskai apibrėztą funkciją, laikomasi sios taisyklės. Ieskant funkcijos paprastų implikančių, visos neapibrėztos funkcijos reiksmės prilyginamos vienetui. Todėl galima sudaryti daugiau zemesnio rango (dengiančių daugiau rinkinių) implikančių. Sudarant galutinį minimalios kairios paprastų implikančių komplektą, padengiam tik tie argumentų rinkiniai, kuriems funkcijos reiksmė apibrėzta ir lygi vienetui, o į kitus, kuriems funkcijos reiksmė neapibrėzta, nekreipiama dėmesio.
Yra sudaryta daug algoritmų, realizuojančių kanoninį minimizavimo metodą. Jie skiriasi sudėtingumu ir ESM taikymo galimybe, čia pateiksime porą populiaresnių.
1.3.6. Minimizavimas Karno diagramų metodu. Minimizuojama funkcija uzrasoma Karno diagrama. Ieskoma gretimų (taip pat ir esančių prie priesingų krastinių) langelių, kuriuose būtų įrasyti vienetai. Tokie langeliai atitinka gretimus kintamųjų rinkinius, o esant funkcijos tobulajai DNF - du nariai besiskiriančius vienu argumentu. Siuos narius galima sulipdyti, gaunant vieną, jau nepriklausanti nuo argumento, kuriuo skyrėsi lipdomi nariai. Grafiskai lipdoma tuos du gretimus langelius apimant uzdaru kontūru.
Jei sulipdzius dvi poras narių, gaunami du nauji vienu kintamuoju besiskiriantys, juos galima vėl lipdyti pagal tą pačią taisyklę. Karno diagramoje tai bus stačiakampis (2x2 arba 4 x 1), susidedąs is keturių langelių. Du gretimus tokius stačiakampius vėl galima jungti į 8 langelių stačiakampį ir t.t. Jei didesnio stačiakampio, neįjungiant langelio, kuriame įrasytas 0, sudaryti jau negalima, vadinasi, turimas stačiakampis yra paprastoji implikantė. Uzrasysime formatų minimizavimo, taikant Karno diagramas algoritmą.
Minimizuojama funkcija uzrasoma Karno diagrama. Langeliai, kuriuose įrasyti vienetai, sujungiami į maksimalaus dydzio stačiakampius, sudarytus is 2k langelių (k=0, 1, 2, ...}. Taigi leistinas stačiakampio langelių sakaičius - 1, 2, 4, 8, ... Stačiakampiai gali susikirsti, tie patys langeliai gali priklausyti ne vienam stačiakampiui. Reikia visus langelius, kuriuose įrasytas 1, apimti stačiakampiais. Stengiamasi, kad stačiakampių skaičius būtų minimalus, o kiekvienas stačiakampis apimtų kiek galima daugiau langelių. Po to uzrasoma funkcijos MDNF. Joje kiekvieną, darytą stačiakampį, atitinka narys (elementari sandauga), kurio rangas (argumentų skaičius) bus dydziu k mazesnis uz funkcijos argumentų akaičių. Stačiakampį, atitinkąs, narys turi tuos argumentus kurių, kaip langučių koordinačių, reiksmės yra vienodos visam stačiakampiui. Be to, jei koordinatės reiksmė I, argumentas į sandaugą įeina neinvertuotas, o jei reiksmė 0 - invertuotas.
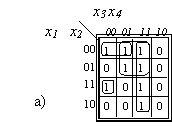
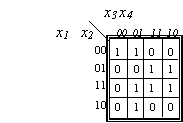
Pailiustruokime metodą keletu pavyzdzių (I.7 pav.). Pavyzdyje a) minimizuojama 4 argumentų funkcija. Dviejų langelių stačiakampį atitinka trečio rango narys, keturių langelių -antro, vieno langelio - ketvirto. Keturių langelių stačiakampiai yra 2x2 ir 1x4. Jie atkerta, todėl kai kurie langeliai uzdengiami daugiau kaip po kartą.
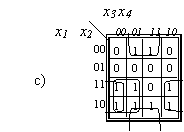
Pavyzdyje b) minimizuojama trijų argumentų funkcija. Ji turi vieną (apibrėztą punktyru) perteklinę paprastąją implikantę x2,x3 , MDNP neįeina, nes abu jos dengiamus langelius dengia kitos implikantė.
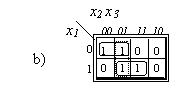
Pavyzdziuose e) ir d) į stačiakampius Jungiami prie priesingų krastinių esantys langeliai. Gaunamas vienas ir astuonių langelių stačiakampis, kurį atitinkantį narį sudaro vienas argumentas.
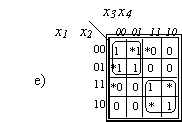
Pavyzdyje e) minimizuojama nevisiskai apibrėzta funkcija. Sudarant stačiakampius, kad jie būtų didesni, įjungiami ir x pazymėti langeliai. Tačiau nebūtina įjungti visų tokių langelių. Būtina jungti visus 1 pazymėtus langelius ir negalima dengti pazymėtų 0. Salia * pazymėti 1 ar 0 rodo, kaip funkcija papildomai buvo apibrėzta minimizuojant.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
1.7 pav. Minimizavimas naudojant Karno kortas
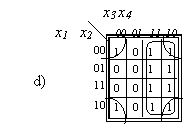
Karno diagramų metodu galima sudaryti ir funkcijos minimalią konjunkcinę normalinę formą. Plačiau neaiskindami, uzrasysime sudarymo taisyklę ir pailiustruosime pavyzdziu (1.8 pav.).
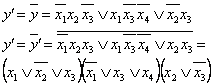
1.8 pav. Funkcijos MKNF sudarymas
1.
Į stačiakampius jungiami langeliai, kuriuose įrasyti - 0.
Sudaromos funkcijos y', inversinės funkcijai ![]() DNF.
DNF.
2.
Sudarytai israiskai taikome de Morgano taisyklę ![]() ir gauname funkcijos
MKNF.
ir gauname funkcijos
MKNF.
Vadinasi, funkcijos minimali KNF sudaroma Karno diagramoje į stačiakampius jungiant 0 pazymėtus langelius. Kiekvienam stačiakampiui rasomas su juo susijęs disjunkcijos narys - elementari suma, kurią sudaro sujungtų langelių invertuotos bendrosios koordinatės: jei bendroji koordinatė 1 - argumentas invertuotas 0, jei koordinatė 0 - neinvertuotas.
Minimizuoti taikant Karno diagramas yra gana paprasta, vaizdu ir patogu, kai argumentų skaičius ne didesnis kaip 4. Kai argumentų skaičius 5, 6, sį metodą taip pat galima taikyti jungiant ir gretimus gretimų kortų langelius. Plačiau apie Karno diagramų taikymą daugelio argumentų funkcijoms minimizuoti rasoma /2/, /7/.
1.3.7. Minimizavimas Kvaino-Mak-Klaski metodu. Tai algebrinis metodas, tinkantis bet kokio argumentų skaičiaus Būlio funkcijoms minimizuoti. Minimizuojama funkcija uzrasoma kubais.
Minimizuojama sudarant visų funkcijos implikančių sąrasą ir vėliau ieskant minimalaus padengimo komplekso - funkcijos minimalios DNF atitikmens.
Paprastų implikančių sąrasas sudaromas taip:
a) funkcija pateikiama kubų kompleksu K0 - sąrasu argumentų rinkinių, kuriems funkcijos reiksmė yra 1;
b) tarpusavyje lyginami visi 0-mačiai kubai. Jei du kubai skiriasi tik viena koordinate, sudaromas 1-matis kubas, kuriame vietoj sios koordinatės rasoma X, 0-mačiai kubai, sujungti į 1-matį kubą, zymimi, pvz., "varnele";
c) tarpusavyje lyginami visi sudaryti 1-mačiai kubai. Du kubai, kurie turi bendrą nepriklausomą (pazymėtą X) koordinatę ir skiriasi tik viena koordinate, sujungiami į vieną bendrą 2-matį kubą, o sujungtieji pazymimi. Jungiant aukstesnius nei 0-mačius kubus, kartais dvi ar daugiau porų n-mačių kubų sujungiami į vienodus (n─1)-mačius kubus. Taip gautas kubas rasomas tik vieną kartą arba baigus tos eilės kubų sujungimus, visi pasikartojantys kubai isbraukiami paliekant tik po vieną);
d) jungimo operacija kartojama su naujai sudarytais aukstesniais kubais, kol eiliniame i-tame komplekse jų lieka tik vienas arba gaunamų kubų sujungti negalima;
e) kubų kompleksuose K0 ... Ki nepazymėti (nesujungti) kubai sudaro nagrinėjamos funkcijos visų paprastų implikančių rinkinį.
Kadangi į aukstesnį kubą galima sujungti tik kubus, kuriuose vienetų skaičius skiriasi vienu, rekomenduojama visus vienodo rango kubus sugrupuoti, į. k-tąją grupę jungiant kubus, turinčius lygiai K vienetų. Tuomet lyginti reikia ne visus to rango, o tik k-tosios ir k 1-osios grupės kubus.
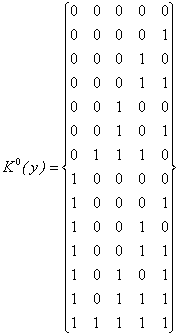
Pailiustruosime, kaip sudaromas paprastų implikančių sąrasas funkcijai, pateiktai kubų kompleksu:
|
0 kubai |
1 kubai |
2 kubai |
3 kubai |
|||||||||||||||||||||||
|
X |
X |
X |
X |
X |
X | |||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X |
X |
X | ||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
|
X | ||||||||||||||||||||||||||
Nepazymėti "varnele" kubai sudaro paprastų implikančių rinkinį.
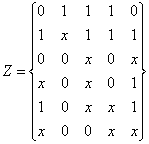
Ieskant minimalaus dengimo kubų komplekso, pirmiausia sudaroma funkcijos dengimo lentelė (zr. 1.6 lentelę). Jojo kiekvienai paprastai funkcijos implikantei skiriama eilutė, o kiekvienam argumentų rinkiniui (virsūnei), kuriam funkcijos reiksmė yra 1, ─ stulpelis. Eilutės ir stulpelio susikirtimo vieta zymima (1, + , V), jei sios eilutės implikantė dengia stulpelio virsūnę (0-matį kubą). (Implikantė dengia 0-matį kubą, kai sutampa visos jų koordinatės, isskyrus implikantėje pazymėtas x). Minimalus funkcijos dengimas yra toks minimalios kainos C paprastų implikančių rinkinys, kuris garantuotų bent po vieną zymę kiekviename dengimo lentelės stulpelyje. Analizuojamų variantų skaičių mazėjant, dengimo lentelė paprastinama atliekant tris veiksmus.
1.6 1ente1ė
Funkcijos dengimo lentelė
[Trūksta]
1. Esminiu implikančių isskyrimas. Jei kuriame nors stulpelyje tėra viena zymė, tai paprasta implikantė, atitinkanti eilutę, kurioje yra ta zymė, yra esminė, Ji būtinai turi įeiti į minimalų dengimą, antraip virsūnė, atitinkanti stulpelį su vienintele zyme, liks nepadengta.
Isskirta esminė implikantė įtraukiama į minimalaus dengimo implikančių sąrasą, o dengimo lentelėje isbraukiama ją atitinkanti eilutė ir visi jos padengtas virsūnes atitinkantys stulpeliai. Likę neisbraukti stulpeliai toliau tikrinami, ar jiems neegzistuoja esminės implikantės. Nagrinėjamame pavyzdyje (1.6 lentelė) paprastos implikantės X00XX, 00X0X, 01110, 1X111 yra esminės.
2. Nereikalingu stulpeliu isbraukimas. Jei isbraukus esmines implikantes ir jų dengiamus stulpelius tarp neisbrauktųjų liko stulpelių, turinčių zymes tose pačiose eilutėse, tai vieną jų palikus, kitus galima isbraukti, nes padengus paliktų - jį bus padengti ir isbrauktieji.
3. Nereikalingu implikančių isbraukimas. Jei tarp likusių neisbrauktų implikančių yra tokių, kurių eilutėse visos zymės isbrauktos (visas jų dengiamas virsūnes dengia esminės implikantės), sios implikantės (eilutės) isbraukiamos kaip nereikalingos.
Po to sudaroma nauja supaprastinta dengimo lentelė, į kurią įtraukiamos tik neisbrauktos eilutės ir neisbraukti stulpeliai. Sudaromas minimalus jos dengimas ir, prijungus prie jo funkcijos esmines implikantes, gaunamas minimalus funkcijos dengimas.
Nagrinėjamame pavyzdyje supaprastintą lentelę sudaro dvi eilutės ir vienas stulpelis.
1.7 1entelė. Supaprastinta funkcijos dengimo lentelė
|
X |
X | ||||||||
|
X |
X | ||||||||
Į padengimą pakanka įtraukti bet kurią vieną implikantę, nes jų kainos vienodos. Pavyzdziui, X0X01. Tuomet minimalus funkcijos dengimas
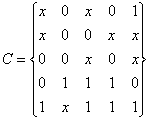
ir jį atitinka funkcijos minimali DNF
![]() .
.
Paskutiniajame etape supaprastinta dengimo lentelė daznai būna nedidelė ir minimalų dengimą galima rasti euristiskai. Kartais galimi keli, kainos poziūriu ekvivalentiski dengimo variantai.
Jei supaprastinta lentelė tebėra sudėtinga, tenka analizuoti visus galimus dengimo variantus. Kad si procedūra būtų paprastesnė ir nepadarytume klaidų (nepraleistume neisanalizavę visų galimų variantų), tenka taikyti įvairius formalius perrinkimo algoritmus, is kurių minėtini sakojimosi algoritmas ir Petriko metodas /7/.
Sakojimosi algoritmas pagrįstas bandymu sudaryti dengimo variantus įjungiant ir neįjungiant pasirinktą implikantę. Toliau įjungiama arba neįjungiama kita implikantė. Sakojimasis tampa hierarchiskas. Pradedant analizuoti nuo kitų implikančių, gaunami kiti variantai. Metodas tinkamesnis minimizavimui taikant ESM.
Petriko metodas - tai algebrinis metodas visiems galimiems dengimo variantams nustatyti. Naudojamasi Bulio algebros (matematinis logikos) aparatu. Pazymėkime supaprastintoje dengimo lentelėje likusias implikantes didziosiomis raidėmis A, B, C, D, G, o nepadengtas virsūnes - mazosiomis a, b, c. Pavyzdziui, supaprastinta dengimo lentelė yra tokia:
|
Virsūnės |
a |
b |
c |
|
Implikantės | |||
|
A | |||
|
B | |||
|
C | |||
|
D | |||
|
B |
Kadangi
turi būti padengta kiekviena virsūnė, jų visų dengimo
sąlygą uzrasysime kaip atskirų virsūnių dengimo
sąlygų sandaugą. Savo ruoztu virsūnė a bus dengta, jei
į dengimą bus įjungta implikantė A arba B, tai yra (![]() ). Analogiskai virsūnės b dengimo sąlyga - (
). Analogiskai virsūnės b dengimo sąlyga - (![]() ). Visų virsūnių padengimo sąlygą
uzrasysime KNF:
). Visų virsūnių padengimo sąlygą
uzrasysime KNF:
![]()
Pertvarkysime
KNF į DNF panariui sudauginę elementarias sumas, sutraukdami vienodus
narius ir absorbuodami visus galimus didesnio rango narius mazesnio rango
nariais (pvz., ![]() ). Gauname:
). Gauname:
![]() .
.
tai rodo, kad galimi tokie funkcijos dengimai
![]()
Apskaičiavę kiekvieno sio dengimo kainą, randame minimalų dengimą.
1.3.8. Funkcijų sistemos minimizavimas. Panagrinėsime trijų funkcijų, priklausančių nuo keturių argumentų, sistemą
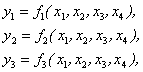
1.9 paveiksle pateiktą sių funkcijų jų Karno diagramomis. Minimalios sių funkcijų DNF yra:
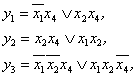
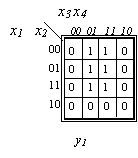
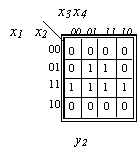
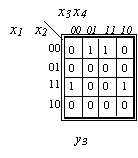
1.9 pav. Funkcijų y1,y2,y3 Karno diagramos
Pagal sias israiskas sudarytos loginės schemos (1.10 pav.) kaina C=18.
Tačiau sią sistemą galima uzrasyti ir neminimaliomis DNP.
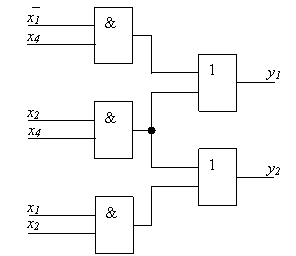
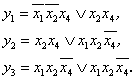
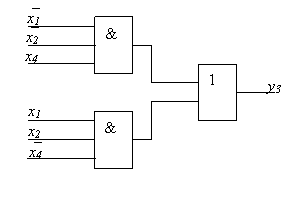
1.10 pav. Loginė schema, sudaryta pagal minimalias DNF
Gaunamą israiską atitiks 1.11 pav. vaizduojama loginė schema, kurios kaina C=14 s
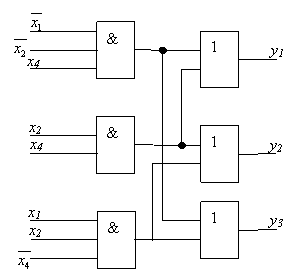
1.11 pav. Minimali sistemos loginė schema
Jau sis mazas pavyzdys rodo, jog, minimizuodami kiekvieną sistemos funkciją atskirai, neturime garantijų, kad gausime minimalią sistemos israiską, ir todėl būtina globalinė minimizacija.
Funkcijų sistemų minimizavimo metodai taip pat dazniausiai pagrįsti Kvaino metodo principais: randamos visos funkcijų sistemos paprastosios implikantės ir sudaromas minimalus jų rinkinys, dengiantis visų sistemos funkcijų visus argumentų rinkinius (virsūnes), kuriems tos funkcijos reiksmė yra 1. Čia būtina pabrėzti, kad visų sistemos funkcijų paprastųjų implikančių rinkinys dar nesudaro viso funkcijų sistemos paprastųjų implikančių rinkinio. Įrodoma /9/, kad sistemos implikantės dar yra visų sistemos funkcijų visų galimų loginių sandaugų (po dvi, po tris, ir t.t.) paprastosios implikantės. Taip gaunamos paprastosios implikantės nėra implikantės kiekvienai sistemos funkcijai, o tik toms, is kurių jos sudarytos. Todėl sudaryti minimalų sistemos dengimą gerokai sunkiau. Funkcijų sistemoms minimizuoti yra sukurti specialūs metodai. Is tokių galima paminėti funkcijų sistemos keitimo bei zymių metodus /7/.
Kiti minimizavimo metodai bei algoritmai. Kai funkcijos argumentų skaičius didesnis kaip 6...8, dėl didelio skaičiavimų masto funkcijų minimizavimui taikomos ESM. Tam yra sudaryti įvairūs algoritmai, dazniausiai pagrįsti Kvaino metodu. Is jų minėtinas plačiai taikomas Roto algoritmas /7/.
Kai kintamųjų skaičius yra kelios desimtys arba kai minimizuojamos funkcijų sistemos skaičiavimų mastai per dideli net ESM. Tuomet taikomi įvairūs apytikriai (dazniausiai euristiniai) metodai. /3/, /10/, kuriuos taikant yra didelė tikimybė gauti israiskas, gana artimas minimalioms.
Skliaustinės BF formos
Kiekvienai Būlio funkcijai galima sudaryti daug formulių, kurios nėra normalinės funkcijų formos. Kai kurios specifinės sių funkcijų formos taikomos sintezuojant bei minimizuojant kombinacinius įtaisus, Čia pateiksime tris is dazniau taikomų,
Funkcijų skaidymas. Turime n
argumentų Būlio funkciją ![]() Pazymėsime f1
i ir f0 i(n-1) argumento
Būlio funkcijas, gaunamas is funkcijos f, joje i-tąjį argumentą Xi pakeitus
konstantėmis ir 0:
Pazymėsime f1
i ir f0 i(n-1) argumento
Būlio funkcijas, gaunamas is funkcijos f, joje i-tąjį argumentą Xi pakeitus
konstantėmis ir 0:
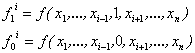 (1.11)
(1.11)
Tuomet funkcijos f skaidymu pagal argumentą Xi vadinamas jos pateikimas tokia forma;
![]() (1.12)
(1.12)
Panagrinėsime rysį tarp
israiskos ir funkcijos f
reiksmių. Pavyzdziui, kuriam nors argumentų rinkiniui ![]() , kai Xi=1, f=1. Tuomet f1i=1, pirmoji
israiskos komponentė Xi
f1i=1 ir visos israiskos reiksmė yra
Jei esant tam pačiam argumentų rinkiniui Xq kai Xi=1, f=0, gausime, kad ir f1i Dėl to komponentė Xi f1i
ir antroji komponentė
, kai Xi=1, f=1. Tuomet f1i=1, pirmoji
israiskos komponentė Xi
f1i=1 ir visos israiskos reiksmė yra
Jei esant tam pačiam argumentų rinkiniui Xq kai Xi=1, f=0, gausime, kad ir f1i Dėl to komponentė Xi f1i
ir antroji komponentė ![]() , nes
, nes ![]() , kai Xi=1. Taigi israiskos reiksmė lygi
, kai Xi=1. Taigi israiskos reiksmė lygi
Jei esant argumentų rinkiniui Xq kai Xi=0, f=1, gausime, kad ir f0i ![]() ir komponentė
ir komponentė ![]() , o tuo pačiu ir israiska
(1.12) lygi vienetui. Jei tomis pačiomis sąlygomis f = 0,
tuomet f0i = 0 ir
, o tuo pačiu ir israiska
(1.12) lygi vienetui. Jei tomis pačiomis sąlygomis f = 0,
tuomet f0i = 0 ir ![]() , o pirmoji komponentė Xi fi1
taip pat lygi 0 nes Xi=0. Tuo pačiu ir visos israiskos reiksmė lygi
, o pirmoji komponentė Xi fi1
taip pat lygi 0 nes Xi=0. Tuo pačiu ir visos israiskos reiksmė lygi
Taip isanalizavę visus galimus variantus įsitikinome, kad skaidymas teisingas.
Savo ruoztu, remdamiesi israiska (1.12), funkcijas (1.11) ![]() vėl galėsime skaidyti pagal kurį nors
kitą kintamąjį Xj :
vėl galėsime skaidyti pagal kurį nors
kitą kintamąjį Xj :
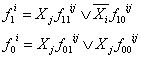 (1.13)
(1.13)
čia ![]() (s=0,1) gauname is f vietoj
argumentų xi, xj įstatę
konstantes 0 ar 1, kaip nurodyta apatiniuose indeksuose. Įstatę
(1.13) į (1.12), gauname funkcijos f skaidymą pagal du
kintamuosius:
(s=0,1) gauname is f vietoj
argumentų xi, xj įstatę
konstantes 0 ar 1, kaip nurodyta apatiniuose indeksuose. Įstatę
(1.13) į (1.12), gauname funkcijos f skaidymą pagal du
kintamuosius:
![]() (1.14)
(1.14)
Taip funkcijos skaidymą galima tęsti pagal norimą kintamųjų skaičių k, (k ≤ n) ir isreiksti 2 komponenčių logine suma:
![]() (1.15)
(1.15)
čia ![]() (pasirinkus
indeksą i: jei si=1, tai
(pasirinkus
indeksą i: jei si=1, tai ![]() ir jei si=0,
tai
ir jei si=0,
tai ![]() ).
).
Funkcijos galima skaidyti ne tik loginių sandaugų sumą (1.12), bet ir loginių sumų sandaugomis:
![]() (1.16)
(1.16)
Normalinių formų faktorizavimas Tai nuoseklus bendrų konjunkcijų (sandaugų) dalių iskėlimas pries skliaustus vėliau loginėje schemoje juos realizuojant bendri elementu. Tai pailiustruosime pavyzdziais (kad būtų paprasčiau, argumentus zymėsime ne X su indeksu, o skirtingomis raidėmis):
 (1.17)
(1.17)
Faktorizuotas funkcijų y1 ir y2 israiskas atitinka loginės schemos, pateikiamos 1.12 pav.
Faktorizuojant kartais (bet ne visuomet) gaunamos paprastesnės, mazesnės kainos loginės schemos visuomet sumazėja reikiamas elementų įėjimų skaičius paveiksle visi elementai yra dviejų įėjimų, nors realizuojant funkcijų y1 ir y2 normalines formas reikėtų ir elementų su penkiais įėjimais. Sudarant skaitmeninius įtaisus taip redukuoti elementų įėjimų skaičių, kartais labai pageidautina. Tačiau įtaisuose, sudarytų pagal faktorizuotas israiskas signalas nuosekliai turi pereiti daugiau elementų, todėl jis daugiau vėlinamas.
Faktorizavimo sėkmė ir faktorizuotos israiskos paprastumas labai priklauso nuo argumentų ar jų grupių iskėlimo pries skliaustus tvarkos. Pavyzdziui, funkcija y2 gali būti faktorizuojama:

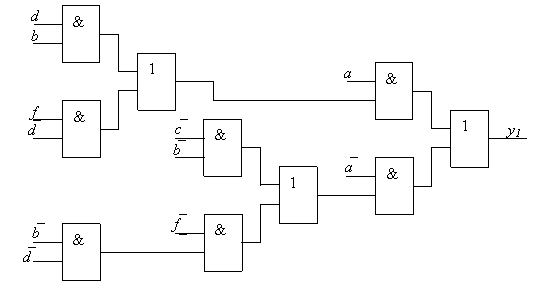
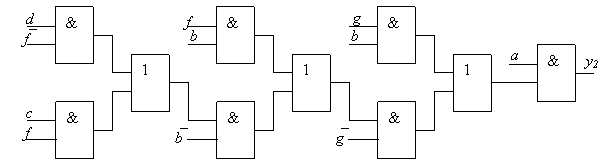
pav. Funkcijų y1 ir y2 loginės schemos
Kad faktorizuojant būtų gaunama paprastesnė israiska, reikia stengtis pirmiausia iskelti pries skliaustus didziausią bendrą dalį is didziausio sandaugų skaičiaus, tačiau ne visuomet aisku, kaip tai padaryti. Todėl paprasčiausioms arba joms artimoms israiskoms gauti yra sukurti formalūs atskirų funkcijų bei funkcijų sistemų faktorizavimo algoritmai. Keleto tokių algoritmų aprasymus galima rasti /7/, /1/.
1.4.3. Funkcijų dekompozicija. Tai funkcijos pateikimas kitų dviejų funkcijų kompozicija;
f(X)=j j(U), V). (1.17)
Čia X= aibė argumentų, nuo kurių priklauso funkcija f o
![]() ir
ir
yra tokie aibės X poaibiai, kad U V=X
Jei funkcijos j ir j priklauso nuo skirtingų argumentų, t.y. jei aibės X poaibiai U ir V bendrų narių neturi U V tokia dekompozicija vadinama paprasta nesusikertančiąja, o priesingu atveju susikertančiąja.
Dekompozicija leidzia funkcijos loginę schemą isreiksti dviem blokais (1.13 pav.), kurie abu kartu gali būti maziau sudėtingi negu bendras blokas, tiesiogiai realizuojąs funkciją /7/, /10/.
Dekompozicija yra gana efektyvi priemonė prastinant Būlio funkcijoms ar jų sistemoms, tačiau is visų minimizavimo metodų , ji maziausiai formalizuota.
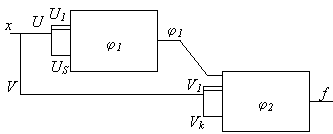
pav. Funkcijos dekompozicija
Praktikoje dazniausiai taikomi euristiniai dekompozicijos metodai, pagrįsti analize ne tiek dekomponuojamų funkcijų, kiek objekto, kurio modelis yra ta Būlio funkcija.
AUTOMATAI
Baigtiniai automatai
Abstraktus automatas. Matematinis skaitmeninio automato (2.1pav.) modelis yra abstraktus automatas.
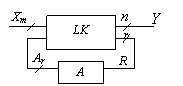
pav. Automato struktūrinė schema: LK loginis keitiklis, A atmintis.
Abstraktus automatas S tai algebrinė struktūra:
S (2.1)
čia
A vidinių būsenų aibė,
x= - įėjimo signalų aibė,
y= isėjimo signalų aibė.
d perėjimų funkcija, įėjimo signalo x(t) ir vidinės būsenos A(t) porai laiko momentu t priskirianti gretimo laiko momento vidinę būseną A(t+1):
A(t+1)=d(A(t), x(t))
l isėjimų funkcija, įėjimo signalo x(t) ir vidinės būsenos A(t) porai laiko momentu t priskirianti automato isėjimo signalą y(t) tuo pačiu laiko momentu t:
y(t)=l(A(t), x(t)) (2.3)
A pradinė automato vidinė būsena, nuo kurios automatas pradeda veikti.
Abstraktus automatas veikia taip: laiko momentu t būdamas vidinėje būsenoje Ai ir jo įėjime veikiant įėjimo signalui xj jis duoda isėjimo signalą yk(yk=l(Ai,xj)) nusakomą isėjimų funkcija l ir pasiruosia gretimame takte (t+1) pereiti į vidinę būseną Al(Al = d(Ai, xj), nusakomą perėjimų funkcija d
Abstraktūs automatai, kurių vidinių būsenų aibė A yra baigtinė, vadinami baigtiniais Toliau nagrinėsime tik baigtinius automatus.
Automatų perėjimų ir isėjimo funkcijų d ir l argumentai yra įėjimo signalo ir vidinės būsenos pora. Tuo pačiu laiko momentu esančių automato įėjimo signalo xi ir vidinės būsenos Aj pora mij vadinama automato pilnąja būsena. Jei automatas turi R vidinių būsenų ir jam galima paduoti M skirtingų įėjimo signalų, didziausias jo būsenų skaičius yra R M.
Automatai, kurių perėjimų ir isėjimų funkcijos d ir l apibrėztos visoms galimoms vidinių būsenų A ir įėjimo signalų x poroms (visoms pilnosioms būsenoms m vadinami visiskai apibrėztais, priesingu atveju nevisiskai apibrėztais, arba daliniais.
Neapibrėztumo poziūriu funkcijos d ir l nėra ekvivalentinės. Dalinio automato būsenos m kurioms perėjimų funkcija d neapibrėzta, vadinamos nenaudotomis. Jei automatas patenka į nenaudotą būseną, visas tolesnis jo funkcionavimas tampa neapibrėztas. Jei nenaudotai būsenai papildomai apibrėsime funkciją d tai nuo sio apibrėzimo priklausys visas tolesnis automato funkcionavimas.
Dalinio automato pilnosios būsenos kurioms perėjimo funkcija d apibrėzta, vadinamos naudotomis Jei kuriai nors naudotai būsenai mi isėjimų funkcija l neapibrėzta, tai tą būseną atitinka neesminis įėjimo signalas. (Kartais neapibrėztas gali būti ne visas isėjimo signalas y=, o tik kuri nors viena ar kelios jo skiltys yi). Jei automato isėjimų funkciją l papildomai apibrėsime būsenai mi tai sis apibrėzimas bus lokalus, nes turės įtakos automato funkcionavimui tik toje būsenoje.
2.1.2. Sinchroniniai ir asinchroniniai automatai. Kaip jau buvo minėta, sinchroniniai ir asinchroniniai įtaisai skiriasi diskretinių laiko intervalų formavimu. Automatai siuo poziūriu skiriasi kiek daugiau, ir tai čia trumpai aptarsime.
Sinchroniniuose automatuose yra taktinių impulsų generatorius, generuojantis sinchronizavimo signalą C, kuris automatą valdo. Priklausomai nuo to, kurį automato struktūrinį bloką pav.) sis signalas valdo ir kaip, automatas gali funkcionuoti kiek skirtingai, todėl projektuojant konkrečius įtaisus į tai būtina atsizvelgti.
Techniskai paprasčiau realizuoti sinchronizuojamą atmintį (blokas A 2.1 pav.). Naudojant sinchronizuojamus atminties elementus (trigerius) sinchronizavimo signalu C isskiriami laiko intervalai, kuriais atminties elementai reaguoja į grįztamojo rysio signalą R, ir kuriais, pakitus atminties elemento būsenai, duodamas jo isėjimo signalas A. Nagrinėjant automato veikimą, teoriskai patogiau laikyti, kad sinchronizuojamas loginis keitiklis (blokas LK pav.),
Pavyzdziui, loginis keitiklis sudarytas taip, kad jis reaguoja įėjimo signalus x ir A tik sinchronizacijos impulso metu, o pauzėje tarp impulsų jo isėjimo signalai nekinta. Be to, garantuojama, kad sio impulso metu įėjimo signalai nekis. Toks automatas funkcionuos stabiliai, jei sinchronizavimo impulsų trukmę Ti ir jų pasikartojimo periodą T parinksime taip, kad atminties elemento vėlinimo laikas t būtų patikimai didesnis uz impulso trukmę Ti, bet patikimai mazesnis uz pasikartojimo periodą T (2.2 pav.). Tuomet, pakitus kuriai nors įėjimo signalo skilčiai xi loginis keitiklis į jį sureaguos tik gavęs sinchronizavimo impulsą C, ir tik tada pakis grįztamojo rysio signalas, pavyzdziui, jo skiltis rj . O atitinkama atminties skiltis aj pakis tik praėjus laikui t bet pries gaunant kitą sinchronizavimo impulsą.
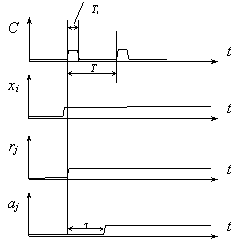
pav. Sinchroninio automato darbo laikinės diagramos.
Kadangi sinchroninių automatų įėjimo signalas gali islikti nepakitęs keletą taktų, jų isėjimo signalas y ir vidinė būsena A taip pat gali būti keletą taktų nepakitę. Tačiau jei įėjimo signalas xi pervedęs automatą į vidinę būseną Aj vėl turi ją keisti, t.y. d taip pat bus nestabili ir prasidės antras nestabilus taktas. Taip tęsis tol, kol po eilinio būsenos pakitimo automatas pereis į tokią vidinę būseną Ar kad d(Ar,xi)=Ar. Būsena mir= bus stabili ir prasidėjęs stabilus taktas tęsis iki įėjimo signalo kito pokyčio.
Kai automatas is vienos stabilios būsenos į kitą pereina per k nestabilių taktų minimali nekintančio įėjimo signalo trukmė Tmin turi būti didesnė uz k maksimalių atminties elementų vėlinimo laikų: Tmin>ktmax
Asinchroniniame automate įėjimo signalas, sukėlęs vidinės būsenos kitimą, lieka nepakitęs, kol nusistovi nauja stabili būsena. Todėl stabilus takto metu vidinė asinchroninio automato būsena nusakoma praeito takto vidine būsena ir to paties takto įėjimo signalu:
A(t)=d(A(t─1),x(t)) ,
arba:
![]() (2.5)
(2.5)
Taigi sinchroninio (2.4) ir asinchroninio (2.5) automatų perėjimų funkcijos nesutampa.
Pagrindinis nesinchronizuojamų automatų trūkumas pereinamojo proceso nestabilumas (gali susidaryti nevienareiksmės situacijos) kai vienu metu turi kisti ne viena signalo x arba A skiltis. Sinchronizuojamuose automatuose sinchronizavimo signalu isskiriami laiko intervalai, kada signalai gali kisti ir kada jų nusistovėjusias reiksmes gali priimti kiti blokai ar įtaisai. Todėl pastaruoju metu asinchroniniai automatai taikomi vis rečiau, nors jie yra ir paprastesni, ir jų greitaveika gali būti didesnė.
Siame leidinyje toliau bus nagrinėjami sinchroniniai automatai.
Mylio ir Mūro automatai. Dazniausiai naudojami dviejų tipų baigtiniai automatai: Mylio ir Mūro, taip vadinami pagal juos tyrinėjusių amerikiečių mokslininkų G.H.Meale ir E.P. Moore pavardes.
Mylio automato funkcionavimas nusakomas perėjimų ir isėjimų funkcijomis:
![]() (2.6)
(2.6)
Taigi būsima būsena ir isėjimo signalas priklauso nuo esamos vidinės būsenos ir įėjimo signalo, tai yra nuo esamos pilnosios būsenos.
Mūro automato perėjimų ir isėjimų funkcijos:
![]() (2.6)
(2.6)
Taigi sie automatas nuo Mylio automato skiriasi tuo, kad jo isėjimų funkcija priklauso tik nuo vidinės būsenos ir nepriklauso nuo įėjimo signalo. Tačiau, įvertindami, kad
A(t)=d(A(t─1), x(t─1)),
gauname:
y(t)=l d(A(t─1), x(t─1)))=l' (A(t─1), x(t─1)). (2.8)
Taigi Mylio automatą galima laikyti ir Mūro automatu, kurio isėjimo signalai vienu taktu atsilieka:
![]() (2.6)
(2.6)
2.1.4. Automatu pateikimo būdai. Abstraktus automatas bus isasmiai aprasytas, jei, be vidinių būsenų, įėjimų ir isėjimų signalų aibių A, X, Y, apibūdinsime ir jo perėjimų bei isėjimų funkcijos d ir l. Tai galima padaryti įvairiai, tačiau plačiausiai taikomi standartiniai automatų pateikimo būdai lentelėmis arba grafu.
Pirmuoju atveju pateikiama perėjimų ir isėjimų lentelėmis.
Perėjimų lentele (2.4 pav. pateikiama perėjimų funkcija A(t+1)= d(A(t), x(t)). Čia kiekvienam įėjimo signalui skiriama eilutė, o vidinei būsenai stulpelis. Eilutės ir stulpelio susikirtimo vietoje įrasoma vidinė būsena, į kurią automatas pereina is stulpelį atitinkančios būsenos veikiant eilutę atitinkančiam įėjimo signalui x .
|
A1 |
A2 |
A3 |
A4 |
A1 |
A2 |
A3 |
A4 |
|||
|
x1 |
A2 |
A3 |
A4 |
x1 |
A2 |
A3 |
A4 | |||
|
x2 |
A3 |
A2 |
A3 |
A3 |
x2 |
A3 |
A2 |
A3 |
A3 |
|
|
x3 |
A1 |
A2 |
A2 |
A1 |
x3 |
A1 |
A2 |
A2 |
A1 |
pav. Automato perėjimų (a) ir isėjimų (b) lentelės
Isėjimų lentelėje analogiskai uzrasoma funkcija y(t)=l(A(t), x(t)).
Jei kuri nors automato būsena yra nenaudota arba jos isėjimas neapibrėztas, atitinkamuose langeliuose dedamas brūksnys.
Siuo būdu galima pateikti ir Mylio, ir Mūro automatus. Tačiau Mūro automatui, kurio isėjimo signalai priklauso tik nuo vidinės būsenos, visuose to paties stulpelio langeliuose tektų įrasyti tą patį isėjimo signalą y. Todėl jam aprasyti naudojama viena, zymėtoji lentelė, kurioje virs vidines būsenas aprasančių langelių yra dar viena eilutė, su įrasytais isėjimo signalais (2.5 pav.).
Mylio automatas taip pat gali būti aprasytas viena sutapatintąja lentele, kurios langeliuose Įrasoma pora: būsima būsena tr isėjimo signalas (2.6 pav.).
Ir sinchroninio ir asinchroninio automato lentelės is principo yra vienodos. Tačiau pastarųjų lentelėse kartais papildomai zymimos stabiliosios būsenos m(A,x jas atitinkančiuose langeliuose įrasytas vidines būsenas apibraukiant apskritimu.
|
y2 |
y1 |
y3 |
y2 |
|
|
A1 |
A2 |
A3 |
A4 |
|
|
x1 |
A1 |
A2 |
A3 |
A4 |
|
x2 |
A2 |
A1 |
A2 |
A1 |
|
x3 |
A4 |
A3 |
A4 |
A2 |
pav. Mūro automato zymėtoji lentelė.
|
A1 |
A2 |
A3 |
A4 |
|
|
x1 |
A2,y1 |
A3,y2 |
A4,y2 | |
|
x2 |
A3,y2 |
A2,y4 |
A3,y3 |
A3,y3 |
|
x3 |
A1,y3 |
A2,y3 |
A2,─ |
A1,y1 |
pav. Sutapatintoji Mylio automato, pateikiamo 2.4 pav. lentelė.
Panagrinėkime asinchroninį automatą, kurio sutapatinta lentelė pateikiama 2.7 pav. Pavyzdziui, automatas yra stabilioje būsenoje m = ir jo įėjime signalas pakinta į signalą x3. Tuomet pirmiausia automatas pereina į nestabilų taktą vėliau, kaip nurodyta lentelėje, į vidinę būseną A3 Tačiau būsena m = taip pat nestabili, nes d A3, x3)= A2, ir automato vidinė būsena tuojau pat pakinta A2 Būsena m = jau yra stabili ir pereinamasis procesas baigiasi.
Kadangi nestabilios būsenos tėra tam tikros pereinamojo proceso fazės, asinchroninių automatų isėjimo signalai paprastai nurodomi tik stabilioms pilnosioms būsenoms, o nestabiliųjų laikomi neesminiais.
Lengva pastebėti, kad stabilios būsenos m yra tos, kai vidinė būsena Ai yra įrasyta siai būsenai skirtame stulpelyje.
|
A1 |
A2 |
A3 |
A4 |
|
|
x1 |
|
|
|
A3 |
|
x2 |
A4 |
A4 |
|
|
|
x3 |
A3 |
|
A2 |
A2 |
|
x3 |
A1 |
|
A1 |
pav. Asinchroninio automato sutapatintoji lentelė
Aprasant automatą grafu, sudaromas orientuotas grafas, kurio virsūnės sutapatinamos su automato vidinėmis būsenomis Ai. Jei automatas gali tiesiogiai pereiti is būsenos Ai į būseną Aj, - jei yra įėjimo signalas xk, kuris jį perveda is būsenos Ai į būseną Aj sias dvi vidines būsenas atitinkančios virsūnės sujungiamos lanku-rodykle, nukreipta is Ai į Aj Įėjimo signalas xk sukeliantis būsenos pasikeitimą, uzrasomas prie lanko. Jei koks nors įėjimo signalas automato vidinės būsenos nekeičia, lankas prasideda ir pasibaigia toje pat virsūnėje (sudaro kilpą). Mylio automato isėjimo signalas rasomas prie lanko po įėjimo signalo, o Mūro automato salia virsūnės arba pačioje virsūnėje (2.8 pav.).
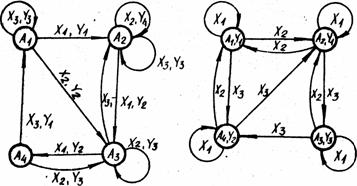
pav. a) Mylio automato (2.6 pav. lentelė) grafas. b) Mūro automato pav. lentelė) grafas
Pagal grafą nesunkiai galima patikrinti, ar automatas sudarytas teisingai. Teisingai sudarytame neturi būti aklaviečių ir nepasiekiamų vidinių būsenų.
Aklavietėmis vadinamos būsenos, kurias patekęs automatas negali iseiti. Grafe yra tik nukreiptos tokias virsūnes rodyklės. Nepasiekiamomis vadinamos būsenos, į kurias automatas pereiti negali. Grafe is tokios virsūnės rodyklės tik iseina. Kartais pirmoji būsena gali būti ir nepasiekiama, jei į ją automatas grązinamas ne įėjimo signalu, o kitomis priemonėmis.
Mylio ir Mūro automatu rysys. Du automatai SA ir SB realizuojantys tą pačią funkcionavimo taisyklę (algoritmą), laikomi ekvivalentiniais SA SB (tiksliau automatų ekvivalentiskumas apibrėziamas kitame skyriuje). Ekvivalentiniai gali būti ir Mylio bei Mūro automatai. Dar daugiau, kiekvienam Mūro automatui galima sudaryti ekvivalentinį Mylio automatą, ir atvirksčiai. Tai daryti patogiausia, kai automatas pateikiamas grafu. Kadangi ekvivalentinių automatų SA= ir SB= isorinės funkcionavimo sąlygos tapačios jų isėjimų ir įėjimų signalų aibės sutampa: xA=xB=x1, yA=yB=y Taigi, sudarant automatui SA ekvivalentinį automatą SB tenka sudaryti pastarojo vidinių būsenų aibę B ir reikiamu būdu transformuoti funkcijas d ir l
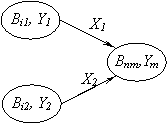
Keičiant Mylio automatą Muro automatu, kiekviena Mylio automato būsena Ai generuoja Mūro automato būsenų poaibį Bij (j=1, 2, ..., k, čia k į Mylio automato būseną Ai ateinančių lankų, zymimų skirtingais isėjimo zodziais, skaičius). Taigi pora AiYl atitinka Mūro automato būsena Bil zymimą isėjimo signalu Yl Jei Mylio automate buvo pereinama is būsenos Ai į būseną An duodant signalą Ym
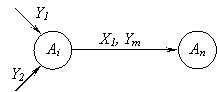
tai ekvivalentiniame Mūro automate visos būsenos Ai generuotosios būsenos Bik sujungia su būsena Bnm, atitinkančią BnYm porą.
Jei Mylio automate yra būsena, į kurią neateina joks lankas (tokia gali būti tik pradinė automato būsena), Mūro automate ją atitinka viena būsena su neapibrėztu isėjimo signalu. Pradine Mūro automato būsena laikoma bet kuri pradinio Mylio automato būsenos generuotoji būsena.
Panagrinėsime Mylio automato S1 (2.9 pav.) keitimo Mūro automatu S2 pavyzdį.
|
A1 |
A2 |
A3 |
|
|
x1 |
A2,y1 |
A3,y3 |
A2,y3 |
|
x2 |
A3,y2 |
A2,y1 |
A1,y1 |
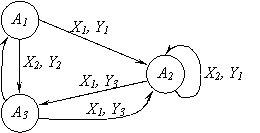
2.9 pav. Mylio automato S1 lentelė ir grafas
Mylio automate į būseną A1 ateina vienintelis lankas, zymimas isėjimo signalu Y1 Vadinasi, Mūro automate bus generuojama vienintelė būsena B11 zymima signalu Y1. Į būseną A2 ateina trys lankai, zymimi dviem skirtingais isėjimo signalais Y1 ir Y3. Vadinasi, ji generuos Mūro automato būsenas B21 ir B Analogiskai būsena generuos būsenas B ir B33. Visose būsenose Bij antrasis indeksas j reiskia isėjimo signalo, kuriuo turi būti pazymėta si būsena, indeksą.
Sudarysime perėjimų funkciją dB Automate S1 is būsenos A2 pereinama būseną A3 veikiant signalui X1 ir isduodant signalą Y2 Vadinasi, automate S2 bus perėjimas į būseną B33 is būsenos A2 generuotųjų būsenų B21 ir B23 veikiant signalui X1 pav.). Analogiskai, sudarant automato S1 perėjimo ekvivalentus automate S2, sudaromi ir likusieji automato S2 perėjimai. Sudarius S2 perėjimų funkciją (grafo lankus), dvigubos būsenų indeksacijos galima atsisakyti ir sunumeruoti jas eilės seka. Tokie "naujieji" būsenų pavadinimai pav. pazymėti grafe salia virsūnių ir įrasyti lentelėje.
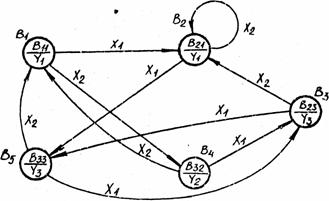
|
Y1 |
Y2 |
Y3 |
Y4 |
Y5 |
|
|
B1 |
B2 |
B3 |
B4 |
B5 |
|
|
X1 |
B2 |
B5 |
B5 |
B3 |
B3 |
|
X2 |
B4 |
B2 |
B2 |
B1 |
B1 |
pav. Mūro automato S2 ekvivalentisko Mylio automatui S1 grafas ir lentelė
Keičiant Mūro automatą Mylio automatu vidinės būsenos lieka tos pačios ir jų skaičius nekinta, tai yra A B. Kiekvieną perėjimą Mūro automate is būsenos Ai į būseną Aj zymimą signalu Yk veikiant signalui Xl Mylio automate
![]()
atitinka perėjimas is būsenos Bi į būseną Bj veikiant tam pačiam signalui Xl ir duodant signalą Yk:
![]()
Taigi keičiant Mūro automatą Mylio automatu, pirmojo grafas lieka nepakitęs, tik isėjimo signalai, kuriais zymimos grafo virsūnės, pereina prie rodyklių, nukreiptų į tą virsūnę. Pagal ekvivalentinio automato grafą nesunkiai galima sudaryti ir jo lenteles.
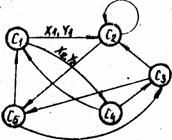
Pagal aprasytas taisykles sudarytas Mylio automatas. S3=, ekvivalentiskas Mūro automatui S2=, pateikiamas 2.11 pav.
Kadangi Mylio automatas S1 ekvivalentinis Mūro automatui S2(S1 S2), o Mūro automatas S2 ─ Mylio automatui S3(S2 S3) remiantis ekvivalentiskumo santykio tranzistyvumu galima daryti isvadą, kad Mylio automatai S1 ir S3 taip pat ekvivalentiniai (S1 S3). Tačiau jie nevienodai sudėtingi: automatas S1 turi tris būsenas, automatas S3 - penkias. Is sio nedidelio pavyzdzio matyti, kad tą patį funkcionavimo algoritmą realizuojantį automatą gali atitikti įvairūs modeliai baigtiniai automatai Taigi ekvivalentiskai automatą transformuojant, galima kelti uzdavinį sudaryti tam tikrų savybių turinį automatą. Vienas is dazniausių tokio tipo uzdavinių automato minimizavimas
|
C1 |
C2 |
C3 |
C4 |
C5 |
|
|
X1 |
C2, Y1 |
C2, Y1 |
C5, Y3 |
C3, Y3 |
C5, Y5 |
|
X2 |
C4, Y2 |
C5, Y3 |
C2, Y1 |
C1, Y1 |
C1, Y1 |
pav. Mylio automato S3 ekvivalentinio Mūro automatui S2(S1 S2) ir Mylio automatui S1(S3 S1), grafas ir sutapatintoji lentelė
2.2. Automatų minimizavimas
Baigtiniu automatu minimizavimo uzdavinys. Is automato modelių baigtinių automatų, realizuojančių tą patį, algoritmą (funkcionavimo taisyklę), reikia pasirinkti tokį, pagal kurį sudarytas automatas (įtaisas) būtų paprasčiausias. Tai nėra paprasta, nes tą patį, baigtinį - automatą gali realizuoti įvairaus sudėtingumo skaitmeniniai įtaisai priklausomai nuo jo vidinių būsenų kodavimo, atminties elementų ir sinchronizavimo būdo parinkimo. Tačiau tarp baigtinio automato struktūros ir jį realizuojančio skaitmeninio įtaiso sudėtingumo rysys yra; jis isreiskiamas baigtinio automato vidinių būsenų skaičiumi. Mat tą patį algoritmą realizuojančių baigtinių automatų įėjimo X ir isėjimo Y signalų aibės sutampa (nes tik sugretinus siuos signalus galima patikrinti, ar automatas realizuoja tą patį algoritmą) ir vienintelė kiekybinė charakteristika, kuria tokie baigtiniai automatai gali skirtis vienas nuo kito, yra jų vidinių būsenų skaičius. Taigi minimalių baigtiniu automatu is tą pati algoritmą realizuojančių baigtinių automatų laikomas toks, kurio vidinių būsenų skaičius yra maziausias.
Pilnųjų (visiskai apibrėztų) ir dalinių (nevisiskai apibrėztų) automatų minimizavimo uzdavinys sprendziamas kiek skirtingai.
Pilnųjų automatų perėjimų funkcija d yra apibrėzta visoms galimoms įėjimo signalų ir vidinių būsenų poroms, tai yra visoms pilnosioms būsenoms m=. Pilnajam automatui galima duoti bet kokią įėjimo signalų seką, ir ją visuomet atitiks konkreti isėjimo signalų seka automato reakcija. Du automatai S1 ir S2 kurių, nustačius juos į pradines būsenas ir davus tas pačias įėjimų signalų sekas, reakcijos (isėjimo signalų sekos) tarpusavyje sutampa, laikomi neatskiriamaisiais, arba ekvivalentiskais. Tai zymima S1 S2 Minimizuojant pilnąjį, baigtinį automatą, minimalaus automato ieskoma tarp visų, jam ekvivalentiskų baigtinių automatų.
Daliniai automatai turi pilnųjų būsenų, kurioms perėjimo funkcija neapibrėzta, vadinamų nenaudotomis. Į sią būseną patekusio automato tolesnis veikimas tampa neapibrėztas. Įėjimo signalų seka, jį pervedanti į sią būseną, vadiname tam automatui neleistinąja. Ir priesingai, leistinoji įėjimo signalų seka yra tokia, kuri automato į nenaudotą būseną neperveda. Davus leistiną įėjimo signalų seką, automatas duoda konkrečią isėjimo signalų seką (kurioje kai kurios reiksimės gali būti neapibrėztos) ir, jai pasibaigus, sustoja konkrečioje, apibrėztoje vidinėje būsenoje.
Kadangi daliniams automatams gali būti paduotos ir leistinos ir neleistinos įėjimo signalų sekos, jų ekvivalentiskumo tiksliai apibrėzti negalima.
Pavyzdziui, turime du automatus S1 ir S2 is kurių bent S1 dalinis. Tuomet is to, kad su visomis automatui S1 leistinomis įėjimo signalų sekomis automatų S1 ir S2 isėjimo signalų sekos sutampa arba nėra priestaringos (sutampa visur, kur abi apibrėztos) dar negalima daryti isvados, kad automatai S1 ir S2 ekvivalentiniai, nes gali būti, kad automatui S2 dar yra leistinos ir tos sekos, kurios neleistinos automatui S1 (kai kurios nenaudotos automato S1 būsenos yra naudotos automate S2 Kitaip tariant, gali būti, kad "automatas S2 daro viską ką automatas S1 ir dar kai ką daugiau". Tuomet laikoma, kad automatas S2 dengia automatą S1.
Minimizuojant dalinius baigtinius automatus minimalaus automato ieskoma tarp visų jį - dengiančių.
Dalinį automatą galima minimizuoti ir kaip pilnąjį, jei apibrėsime jo nenaudotų būsenų bent perėjimų funkciją. Bet tuomet minimizavimo rezultatas priklausys nuo papildomo apibrėzimo: nenaudotų būsenų funkciją apibrėzę kitaip, gausime kitą, paprastesnį ar sudėtingesnį automatą. Nors taip minimizuojant dalinius automatus ir galima pasiekti neblogų rezultatų, įrodoma /4/, kad net isanalizavus visus galimus papildomo apibrėzimo variantus negarantuojama, jog bus rastas minimalus ekvivalentiskas automatas. Tarp dengiančių automatų gali būti ir turintis (maziau vidinių būsenų.
Apskritai dalinių automatų minimizavimo teorija yra gana sudėtinga. Dėl vietos stokos jos čia nenagrinėsime. Besidomintys ją gali rasti /1/, /5/.
Pilnųjų automatu minimizavimas Sis procesas pagrįstas ekvivalentiskumo santykiu. Ekvivalentiniai gali būti ne tik automatai, bet ir atskiros to paties ar skirtingų automatų vidinės būsenos.
Įvedus ekvivalenčių būsenų sąvoką, galima pateikti konstruktyvesnį automatų ekvivalentiskumo apibrėzimą: du automatai SA ir SB yra ekvivalentiniai, jeigu kiekviena automato SA vidinė būsena turi bent vieną ekvivalentinę būseną automate SB , o kiekviena automato SB vidinė būsena - bent vieną ekvivalentinę būseną automate SA
Pilnieji automatai minimizuojami tarpusavyje ekvivalentines būsenas keičiant viena bendra.
Ekvivalentinės automato būsenos Dvi automato būsenos yra ekvivalentinės, jeigu davus bet kokią įėjimo signalų seką, isėjimo signalų seka nepriklausys nuo to, kurią is sių būsenų laikysime pradine. Minimizuojant automatą, tenka isaiskinti (atpazinti) visas tarpusavyje ekvivalentines būsenas. Todėl svarbu turėti konstruktyvesnį būsenų ekvivalentiskumo apibrėzimą ir jo galimybę jį patikrinti. Pateiksime tokį apibrėzimą.
Automato vidinės būsenos Ai ir Aj yra ekvivalentinės (Ai Aj), jeigu bet kokiam įėjimo signalui Xk Xk X
būsenų Ai ir Aj isėjimo signalai sutampa:
l(Ai, xk)=l(Aj,xk)
is būsenų Ai ir Aj bus pereinama į tą pačią arba tarpusavyje ekvivalentines vidines būsenas:
d(Ai, xk)= d(Aj, xk)
arba
d(Ai, xk) d(Aj, xk) (2.11)
T.y. būsenos arba turi sutapti, arba būti ekvivalentinės.
Pirmuoju atveju (2.10) būsenos laikomos ekvivalentinėmis besąlygiskai. Jei baigtinis automatas pateikiamas lentelėmis, sias būsenas atpazinti nesunku: jas atitinkantys stulpeliai yra vienodi. Pavyzdziui, pav., pateiktame automate S1 būsenos A3 A5 ir A4 A6 ekvivalentinės besąlygiskai. Ekvivalentiniame automate S2 jos sujungtos pazymint (A3 A5)=A35=A3 ir (A4 A5)=A45=A4.
|
S1 |
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
S2 |
A1 |
A2 |
A3 |
A4 |
|
|
X1 |
A3,Y1 |
A5,Y1 |
A5,Y2 |
A1,Y1 |
A5,Y2 |
A1,Y1 |
X1 |
A3,Y1 |
A5,Y1 |
A5,Y2 |
A1,Y1 |
|
|
X2 |
A4,Y1 |
A6,Y1 |
A3,Y2 |
A6,Y1 |
A3,Y2 |
A6,Y1 |
X2 |
A4,Y1 |
A6,Y1 |
A3,Y2 |
A1,Y1 |
pav. Ekvivalentiniai automatai S1 ir S2.
Besąlygiskai ekvivalentines būsenas tikslinga isaiskinti ir sujungti pries atliekant tolesnius minimizavimo veiksmus, nes taip įdedama maziau darbo minimizuojant automatą. Jungiant kelias tarpusavyje ekvivalentines būsenas, isbraukiami visi, isskyrus vieną, jas atitinkantys stulpeliai, o likusioje lentelėje visos isbrauktos būsenos pakeičiamos joms ekvivalenčia paliktąja (2.12 pav.).
Jei būsenos nėra ekvivalentinės besąlygiskai, tikrinti sudėtingiau, nes vienos būsenos poros ekvivalentiskumas tampa priklausomas nuo kitos poros ekvivalentiskumo, kuris taip pat dar gali būti neįrodytas. Tada ekvivalentiskumui tikrinti taikomi įvairūs iteraciniai metodai /1/, /7/, /5/, dazniausiai trikampės lentelės metodas.
Trikampės lentelės. Minimizuojant trikampių lentelių metodu, automatas "turi būti pateikiamas lentelėmis (geriau sutapatintosiomis) (2.13 pav.). Nubraizoma trikampė (n─1) (n─1) lentelė (2.54 pav.), kurioje kiekvienai būsenų porai skiriamas langelis. čia n - automato vidinių būsenų skaičius. Lentelė uzpildoma tikrinant visų būsenų ekvivalentiskumą (nuosekliai taikant jo apibrėzimą
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
A8 |
|
|
X1 |
A3,Y1 |
A1,Y1 |
A3,Y1 |
A4,Y1 |
A5,Y1 |
A5,Y1 |
A3,Y1 |
A3,Y2 |
|
X2 |
A2,Y1 |
A6,Y1 |
A5,Y2 |
A6,Y2 |
A1,Y1 |
A2,Y1 |
A6,Y1 |
A7,Y2 |
pav. Sutapatintoji automato S3 lentelė
|
A2 |
|
||||||
|
|||||||
|
A3 |
X |
X |
|
||||
|
A4 |
X |
X |
|
||||
|
|||||||
|
A5 |
X |
X |
|
||||
|
A6 |
X |
X |
|
||||
|
|||||||
|
A7 |
X |
X |
|
||||
|
|||||||
|
A8 |
X |
X |
X |
X |
X |
X |
X |
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
|
pav. Automato S3 trikampė lentelė
Zenklu x isbraukiami langeliai, atitinkantys būsenų poras, kurios negali būti ekvivalentinės dėl to, kad nors vienai įėjimo signalo reiksmei (nors vienoje eilutėje) isėjimo signalai yra skirtingi. "Kandidatais" į ekvivalentines būsenų poras lieka neisbraukti langeliai.
Neisbrauktuose langeliuose įrasomos poros būsimų būsenų, į kurias automatus pereina is langelį atitinkančių būsenų, veikiant tam pačiam įėjimo signalui (tai yra poros būsimų būsenų, kurios turėtų būti ekvivalentinės, kad langelį, atitinkančios būsenos būti ekvivalentinės). Kadangi tikrinama pagal kiekvieną įėjimo signalą atskirai, kiekviename langelyje gali tekti įrasyti tiek būsenų porų, kiek yra skirtingų įėjimo signalų. (Į langelį būsenų pora nerasoma, jei tokia pora ten jau įrasyta kitai įėjimo signalo reiksmei arba jei is abiejų būsenų pereinama į tą pačią) Jei tokių porų nėra (abi būsimos būsenos sutampa), dedamas zenklas V, reiskiantis jog būsenos ekvivalentiskos besąlygiskai. Taupant vietą, paprastai rasoma ne būsenų pora Ai Aj, o tik jų numeriai (indeksai i, j).
Isbraukiami langeliai, kuriuose yra įrasyta nors viena pora neekvivalentiskų būsenų pagal 1 punkto rezultatus (atitinka jau isbraukytų langelių poras).
Isbraukiami langeliai, kuriuose yra įrasytos poros, isbrauktos vykdant 3 ar punktą. punktas kartojamas tol, kol daugiau nieko negalima isbraukti.
Likę neisbraukti langeliai reiskia, kad juos atitinkančios būsenų poros yra ekvivalentinės,
Toliau sudaromos sutapatinamų vidinių būsenų grupės. Paprasčiausiai tam naudoti būsenų santykio grafą. Kiekviena būsena sutapatinama su viena grafo virsūne, ir ekvivalentinės būsenos sujungiamos lanku (2.15 pav.).
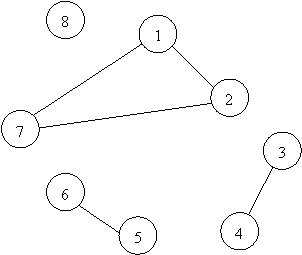
2.15 pav. Automato S3 būsenų santykio grafas
|
A1 |
A3 |
A5 |
A8 |
|
|
X1 |
A3,Y1 |
A3,Y1 |
A5,Y1 |
A3,Y2 |
|
X2 |
A5,Y1 |
A5,Y2 |
A1,Y1 |
A1,Y2 |
pav. Minimalaus automato, ekvivalentinio automatui S3, lentelė.
Kadangi būsenų ekvivalentiskumo santykis yra tranzistyvus (is Ai Aj ir Aj Ak seka Ai Ak pilnojo automato būsenų santykio grafas susideda is tiek atskirų pilnųjų pografių ir izoliuotų virsūnių, kiek vidinių būsenų bus minimaliame automate, o kiekviename pografyje visos virsūnės tarpusavyje paporiu sujungtos. Minimizuojamame automate S3 isskirtos tokios ekvivalentiskų būsenų grupės ir niekam neekvivalentiskos būsenos = A1,= A3,= A5 ir A8. Sudaryto minimalaus automato, ekvivalentinio automatui S3, lentelė pateikiama pav.
Panagrinėtame pavyzdyje buvo minimizuojamas Mylio automatas. Mūro automatas gali būti minimizuojamas analogiskai, pazymėtą Mūro automato lentelę keičiant sutapatintąja jam ekvivalentinio Mylio automato lentelę, o jį, minimizavus, atlikti atvirksčią ekvivalentinį pakeitimą.
Automatų sintezės principai
Pačią bendriausią automato struktūrinę schemą (2.1 pav.) sudaro du blokai: kombinacinis įtaisas loginis keitiklis (LK) ir atminties blokas (A). Automato atminčiai sudaryti dazniausiai parenkami standartiniai elementai. Tuomet pagrindinis automato struktūros sintezės uzdavinys jo loginio keitiklio sintezė.
Sintezuojant automatas pirmiausia koduojamas, parenkami jo atminties elementai, po to sudaromos loginio keitiklio lygtys.
2.3.1. Automato kodavimas. Abstraktaus automato signalai ir vidinės būsenos yra zymimos abstrakčiais simboliais. Koduojant abstraktus automatas transformuojamas į struktūrinį. Jame signalai ir būsenos yra uzkoduotos dvejetainiais kodais.
Sudarant automatą, įėjimo bei isėjimo signalų projektuotojui koduoti dazniausiai nereikia, nes jie būna uzkoduoti jau formuojant uzduotį. Vidines automato būsenas visuomet tenka koduoti jį sintezuojant.
Jei automatas turi N būsenų, jo atminčiai koduoti reikia ne maziau kaip n=]log2N[ skilčių (čia ]x[ reiskia artimiausią skaičiui X sveiką skaičių, ne mazesnį uz x). Paprasčiausia automato vidines būsenas sunumeruoti ir kiekvienai jų priskirti jos numerį atitinkantį. n-skiltį dvejetainių skai8ių. Taip kartais ir daroma, nors sis būdas nėra pats geriausias. Nuo automato vidinių būsenų uzkodavimo labai priklauso loginio keitiklio sudėtingumas. Asinchroniniuose automatuose specialiu kodavimo būdu garantuojamas stabilumas pereinamųjų procesų metu. Bet tai yra specialūs automatų sudarymo klausimai, ir čia nenagrinėsime, o pateiksim, tik paprastą automato kodavimo pavyzdį.
|
d |
A1 |
A2 |
A3 |
A4 |
l |
A1 |
A2 |
A3 |
A4 |
|
|
X1 |
A1 |
A4 |
A4 |
X1 |
Y2 |
Y1 |
Y3 | |||
|
X2 |
A3 |
A1 |
X2 |
Y3 |
Y1 | |||||
|
X3 |
A2 |
A2 |
A3 |
X3 |
Y1 |
Y4 |
Y2 |
2.17 pav. Automato S lentelės
Turime abstraktų automatą S, pateiktą perėjimų ir isėjimų lentelėmis (2.17 pav.). Keturioms jo vidinėms būsenoms uzkoduoti reikia dviejų skilčių , o trims įėjimo ir keturiems isėjimo signalams taip pat po dvi skiltis , . Koduojama, pavyzdziui, taip, - kaip rodoma pav. lentelėse.
|
Ai |
a1 |
a2 |
Xi |
x1 |
x2 |
Yi |
y1 |
y2 |
||
|
A1 |
X1 |
Y1 | ||||||||
|
A2 |
X2 |
Y2 | ||||||||
|
A3 |
X3 |
Y3 | ||||||||
|
A4 |
pav. Automato kodavimo lentelės
Tuomet uzkoduotos abstraktaus automato S lentelės pav. tampa struktūrinio automato S lentelėmis pav.).
A=(a1a2); Y=
|
|
| |||||||||
pav. Struktūrinio automato 3 perėjimų (a) ir isėjimų (b) lentelės
Atminties elementų parinkimas Kad sintezuojamas automatas funkcionuotų teisingai, jo vidinė būsena, tam tikrame takte neturi priklausyti nuo loginio keitiklio signalo pav.) to -takto metu. Tai yra atminties isėjimo signalas A, kuris dalyvauja formuojant atminties elemento įėjimo signalą R to paties takto metu "neturi veikti pats save", o turi priklausyti tik nuo A reiksmės ankstesnio takto metu. Taip funkcionuoja Mūro automatas, todėl atminties elementas gali būti tik jis.
Sudarant automatus, kaip atminties elementai paprastai naudojami paprasčiausi įvairių tipų automatai trigeriai. Jie turi dvi stabilias būsenas (koduojamas ir ir vieną arba du įėjimo signalus (be sinchronizacijos) Kiekvienai dvejetainės atminties skilčiai realizuoti skiriamas vienas trigeris. Tuomet atminties blokui sudaryti reikia tiek trigerių, kiek skilčių reikia atminčiai uzkoduoti. Savo ruoztu atminties valdymo signalui R reikės tiek kanalų (skilčių), kiek yra atminties trigerių (arba du kartus daugiau, priklausomai nuo to, ar trigeriai turi vieną ar du įėjimo signalus). Čia nagrinėsime trigerius, turinčius vieną valdymo įėjimą, todėl signaluose A ir R bus vienodas skilčių skaičius.
3. Funkcinio keitiklio sudarymas. Kai automato signalai bei būsenos uzkoduotos ir parinkti atminties elementai, galima sudaryti loginio keitiklio logines lygtis. Automato loginis keitiklis tai kombinacinis įtaisas, realizuojantis (m+r) Būlio funkcijas, priklausančias nuo (n+l argumentų.
Sių funkcijų kintamieji yra n įėjimo signalo skiltys xi= ir l vidinių būsenų atminties (kartais dar vadinamos antriniais įėjimo signalais) skiltys Ai=. Kombinacinis įtaisas realizuoja (m+r) isėjimo funkcijų, atitinkančių m isėjimo signalo A=skilčių:

ir atminties zadinimo funkcijų, atitinkančių r atminties valdymo signalo R= skilčių:

Isėjimo funkcijos sunkiai sudaromos pagal struktūrinio automato isėjimų lentelę (2.19 pav. b). Si lentelė yra savitos formos isėjimo funkcijos reiksmių lentelė: jos eilučių ir stulpelių "pavadinimuose" surasyti argumentų rinkiniai, o langeliuose funkcijos reiksmės (panasiai kaip Karno diagramoje). Laikoma, kad kintamųjų rinkinius, kuriems isėjimo reiksmė neapibrėzta arba kurių lentelėje nėra, atitinka neapibrėztos signalų y reiksmės. Įprastine forma perrasyta funkcijų y1 ir y2 reiksmių lentelė ir jų Karno diagramos pateikiamos pav.
|
a1 |
a2 |
x1 |
x2 |
y1 |
y2 |
|
|
|||||
pav. Isėjimų funkcijų reiksmių lentelė ir Karno diagramos
Jas atitinka loginės lygtys:
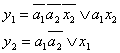 (2.12)
(2.12)
Atminties zadinimo funkcijoms sudaryti reikalinga struktūrinio automato atminties zadinimo lentelė pav.). Jos eilutės atitinka įėjimo signalus, stulpeliai vidines būsenas, o langeliuose rasomi atminties zadinimo signalai R, kurie reikalingi automatui pervesti į būseną Al d(Ai, xj), atitinkančią stulpelio pirminę būseną Ai ir eilutės signalą xj. Kitaip tariant, atminties zadinimo lentelė tai automato perėjimų lentelė, kurios langeliuose vietoje būsenos Al į kurią automatas turi pereiti, įrasomas signalas R, reikalingas automatui į ją pervesti.
Taip perkoduojant automato perėjimų lentelę, reikia naudoti parinkto atminties elemento įėjimų lentelę.
Atminties elemento įėjimų lentelėje uzrasoma jo įėjimų funkcija
Ril g(Ai, Al);
kuri rodo, kokį signalą reikia paduoti atminties elemento įėjimą, kad jis is būsenos Ai pereitų būseną Aj. Kada kaip atminties elementai naudojami trigeriai, realizuojantys vieną atminties skiltį jų įėjimų lentelė sudaroma taip pat vienai skilčiai ir turi tik, keturis langelius. Populiariausių vieno įėjimo (T, D) ir dviejų įėjimų (RS, JK) trigerių įėjimų lentelės pateikiamos 2.21 pav.
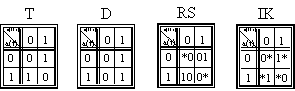
pav. Trigerių T, D, RS ir JK įėjimų lentelės (* - signalas neapibrėztas)
Sudarysime automatui S, kurio struktūrinė perėjimų lentelė pateikiama 2.19 pav., atminties zadinimo lentelę pav.) kada kaip atminties elementai naudojami T trigeriai. Analizuodami jo įėjimų lentelę pav.), pastebėsime, kad sio trigerio būsenai pakeisti (perėjimai 0 1 arba 1 0) įėjimo signalas turi būti vienas (T=1) arba, kai būsenos keisti nereikia perėjimai 0 0 arba 1 1, nulis (T=0). Toliau analizuojame automato struktūrinę perėjimų lentelę. Jei, pavyzdziui, automatas esant jo būsenai a1,a2 ir veikiant įėjimo signalas x1,x2=1,0, turi pereiti būseną a1,a2 , į atminties elementus turi būti duodami signalai R1,R2=T1,T2=1,0. Analogiskai uzpildoma visa lentelė pav.),
Jei kaip atminties elementai būtų naudojami dviejų įėjimų trigeriai (RS, JK), kiekviename atminties zadinimo lentelės langelyje tektų įrasyti po keturis signalus po du kiekvienai skilčiai.
Automato atminties zadinimo lentelė nurodo atminties zadinimo funkcijų reiksmes, kaip ir struktūrinė isėjimų lentelė - isėjimo funkcijų reiksmes. Todėl analogiskai sudaroma ir jos įprastinės formos lentelė bei Karno diagramos (2.23 pav.), is kurių gauname atminties zadinimo funkcijų lygtis:
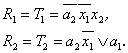 (2.13)
(2.13)
|
| ||||
pav. Automato S struktūrinė atminties zadinimo lentelė
Sujungę lygtis (2.12) ir (2.13) į bendrą sistemą, gauname automato loginio keitiklio bloko logines lygtis.
|
a1 |
a2 |
x1 |
x2 |
T1 |
T2 |
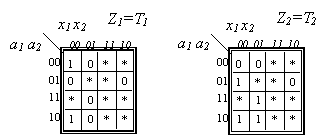
pav. Atminties zadinimo funkcijų lentelė ir Karno diagramos
LITERATŪRA
|