A Klein-féle kancsó

Klein német matematikusról kapta a nevét. A Möbius-szalag egyfelületű és egy éle van. A Klein-féle kancsó szintén egyfelületű test, s mint ilye 717t194h n, külső és belső felülete nem különböztethető meg, nem festhető két különböző színre.

Leírás:

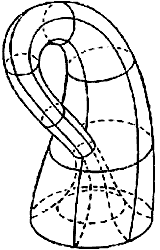
Önmagába visszatérő üvegcső, melyet folytonos felület alkot (a külső felület és a belső folyamatosan megy át egymásba.)

Előállítás:

1. Ha egy gömbön lukat vágunk és Möbius szalaggal befoltozzuk, elvileg Klein-féle kancsót kapunk.

2. Ugyanezt érhetjük el máshogy: Kiindulunk egy mindkét végén nyitott csőből, amelynek egyik elkeskenyedő végét átdugjuk a csőnek a falán. Ezután a csőnek a két végét összeragasztjuk, a belsőnek kifelé a külsőnek befelé való nyújtásával.

A természetben ritkán jönnek létre Möbius szalag és Klein-kancsó elvű felületek (pl.: ha az elefánt az ormányát a szájába veszi, topológiailag Klein-féle kancsónak tekinthető) Ilyen jellegű felületek poétikus, tisztán szellemi alkotások, melyekben magának a tudatnak az elve manifesztálódik. E ténynek jelentősége abban áll, hogy az autonóm, a tapasztalattól független szellemi világban pusztán játékos.

Hogy még szemléletesebb képet kapjunk a Klein-féle palackról, vágjuk ketté egy vízszintes síkkal. A felület két Möbius szalagra esik szét.