A rend fogalma igen átfogó és távolról sem lehet azonosítani a matematikai renddel, még a logikaival sem. Nagyon jól érzékeljük a rendet ott is, ahol nincs szó matematikai fogalmakkal leírható, vagy egyáltalán logikusan vizsgálható dolgokról. Ez egy sajátos rend, amin csodálkozni valóban lehet, alapvető elvként elfogadni és ebből a meghatározott szemszögből látni mindent azonban merész vállalkozás. A matematikusok gyakran azzal érvelnek, hogy egyre több olyan tárgyat tudunk matematikával vizsgálni, ezek számára matematikai alapokat találni, amelyekről régebben ezt el sem lehetett képzelni. Kérdés, hogy meddig lehet eljutni ezen a téren, a vélemények igen eltérőek vele kapcsolatban.
"Az évszázadok során a matematikusok kollektív tudata megalkotta saját univerzumát. Hogy ez hol van, nem tudom - s gondolom, a 'hol' szó itt értelmét is veszti , de biztosíthatom az olvasót: ez a matematikai univerzum nagyon is reális annak a számára, aki benne él. Az emb 16316e47q eriség éppen a matematika révén hatolt be legmélyebben környező világa rejtelmeibe."
Ian Stewart
Fontos itt is megemlíteni a matematika elvont, absztrakt voltát, mert ez a fajta, bizonyos szempontból tökéletes rend nagymértékben ezért lehetséges egyáltalán, a csupán szellemi létezőket tudja szellemünk elrendezni igazán.
"A rend - mégpedig az intellektuális rend - megteremtése a legnagyobb emberi adottságok egyike, és elfogadott ténynek számít, hogy a matematika a teljes intellektuális rend tudománya."
Philip J. Davis - Reuben Hersh
"A matematikai tudományok különösen a rendet, a szimmetriát és a határt mutatják meg: és ezek a szépség legkiemelkedőbb formái."
Arisztotelész
A rendet szoktuk akkor is értékelni, amikor már meglévő ismereteink kerülnek új, átláthatóbb megvilágításba, s akkor is amikor szinte reménytelen összevisszaságból tudunk értékelhető szabályosságot felszínre hozni. Az utóbbira példa a következő:
Az természetes számok tulajdonságait
vizsgálva újra és újra felbukkannak a prímszámok. Ezek bizonyos szempontból
alapstruktúráját alkotják a természetes számoknak, mert kettőtől
fölfelé minden számot felírhatunk prímek szorzataként. A prímek látszólag mégis
mindenféle szabály nélkül helyezkednek el ebben a számsorban, ez vizuálisan is
szembetűnő, ha a sorban leírt természetes számok között külön
jelöljük a prímeket. Alapvető fontosságuk miatt sokan szerettek volna
mondani valamit a prímek elhelyezkedésével kapcsolatban, sokáig kerestek
például abban irányban, hogy minden n természetes
számra megmondják, hogy n-ig hány
prím van. Ilyen 
képletet senkinek sem
sikerült találnia máig sem, viszont Gauss megsejtette, majd később be is
bizonyították, hogy asszimptotikusan
egyenlő 
-el, vagyis a hányadosuk
1-hez közelít, ha n-et egyre
nagyobbra választjuk. Másként felírva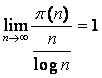 
.
Szabályosságot tehát ilyen formában sikerült felfedezni. További érdekessége e képletnek, hogy vajon miért éppen a logaritmus szerepel benne, van-e ennek mélyebb oka is?
Egy tetszőleges sokszögből kiindulva képezzünk újabb és újabb sokszögeket úgy, hogy az eredeti sokszög oldalfelező pontjai legyenek az új sokszög csúcspontjai. Így majdnem minden esetben a kiindulási zűrzavarból egy ellipszisszerű alakzatot kapunk:
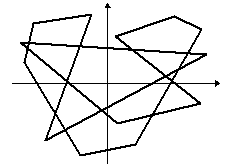
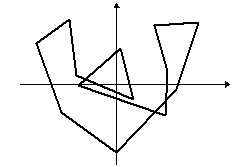
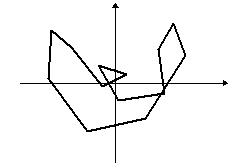
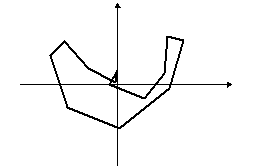
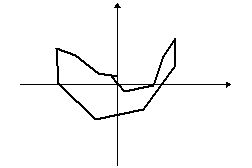
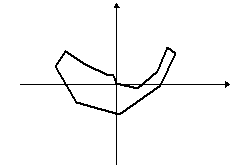
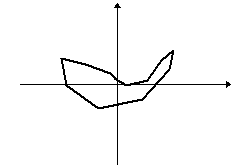
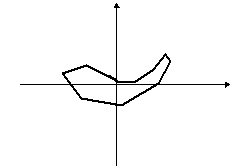
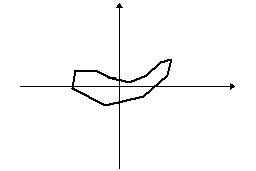
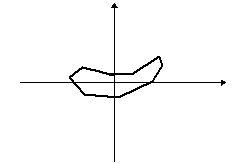
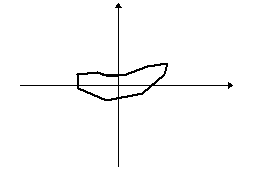
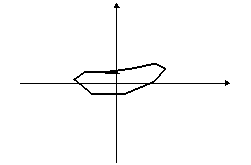
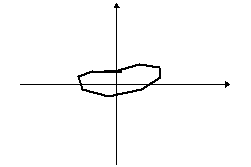
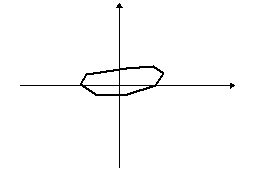
A rend fogalma a matematikán belül is változik, kibővül, az utóbbi időkben például néhány olyan fizikai jelenséget sikerült matematikával megragadni, amelyeknél erre régebben kevés esély volt, igaz a matematikai leírás fogalmát is ki kellett kitágítani hozzá. Ilyenek például az időjárás, egy falevél mozgása a szélben, az ún. kaotikus jelenségek.
Mindennapjainkban nem a matematikában szokásos szigorú rend szerint viselkedünk, ez teljesen nyilvánvaló. Senkit sem zavar, ha nem definiálunk pontosan mindent, amiről beszélünk. A matematikai szigor megtartása mellett kétséges, hogy tudunk e mondani valami lényegeset a világról, avagy elveszünk a részletek tisztázásában. A fizikusok közül sokan mondják, hogy milyen nehéz szavakba önteni, megvilágítani azokat az összefüggéseket, amelyeket megsejtenek, még akkor is ha matematikailag le tudják írni.
"Ez a mosogatás is olyan, mint a nyelv. Piszkos a vizünk, piszkos a törlőruhánk, valahogy mégis megtisztítjuk az edényt meg a poharakat. Így állunk a nyelvvel is: tisztázatlan fogalmakkal dolgozunk, és olyan logikát használunk, amelynek nem ismerjük a pontos érvényességi körét; ennek ellenére reménykedünk, hogy mégiscsak tisztaságot teremtünk a természet megértésében."
Niels Bohr
"Egyre nyilvánvalóbbá vált azonban, hogy a természet másképpen működik. Alapvető törvényei nem úgy szabályozzák működését, ahogyan az a mi képzeteinkben közvetlenül megjelenik, ehelyett egy, a jelenségek mögött rejlő valamit irányítanak, amelyről nem tudunk képet alkotni oda nem tartozó dolgok bevezetése nélkül."
Paul Dirac
Nagyon sok automatikus elem működik tevékenységeinkben, a világról alkotott képünk is számos olyan elemből épül fel, amelyeket nem ellenőrzünk le állandóan, nem kötjük magunkat abszolútnak gondolt szabályokhoz, lehetőségünk sem lenne bizonyos dolgokat véghezvinni, ha egy, a matematikában használatos határozottan körvonalazott szabályrendszerhez igazodnánk. A rendet megszokásból rendszerint ott is feltételezzük, szemünk egyből megtalálja ott is, ahol később, hosszasabb szemlélődés után kiderül, hogy egyáltalán nem az van, amit először feltételeztünk, ilyen a következő rajz is:
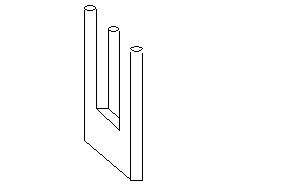
"A szívnek megvannak a maga indokai, amelyeket az indokló értelem nem ismer."
Blaise Pascal
Megemlítésre érdemes, hogy nemcsak ez ember alkotja meg a matematikát, hanem a tapasztalatok szerint az is visszahat az emberre. Ha sokat foglalkozunk vele elvont rendje, légköre, szemlélet- és gondolkodásmódja hat ránk. Egyesek szinte teljes mértékben matematikus szemmel látnak minden jelenséget, másoknál csak időnként bukkan ez nyíltan a felszínre, s van, aki éppen ennek a negatívját tarja üdvözítőnek, módszeresen elhárítva minden gyanút arra vonatkozóan, hogy bármi köze lenne az egészhez. Nem születünk eleve ilyennek vagy olyannak, személyiségünkben nagyon sok a tanult, felvett elem, így az is meghatározó, hogy mivel foglalkozunk intenzíven. Egy szemléletmód részünkké válhat, vagy elhatárolódásként negatív részünkké. A matematika látásmódja elég szuggesztív ahhoz, hogy bizonyos szempontból rajta keresztül lássuk a világot. A hangsúlyok nagymértékben különbözhetnek, egy igazi matematikus máshogy lát mindent, mint egy igazi színész. A végletességtől azonban ezzel kapcsolatban ugyanúgy óvakodni érdemes, mint bármilyen más véglettől.
A megértés azért fontos tényező a matematika megítélésében, mert bizonyos szempontból itt vagyunk képesek elérni a lehető legteljesebb mértékben. Ha valamit megértünk, ez gyakran felemelő élményt jelent számunkra. Akik szeretnek matematikával foglalkozni, azok közül mindenki átélte a megértés örömét. Furcsa érzés ez, mert ilyen élményünk máshol nemigen lehet, nem maradnak kételyek bennünk, érvényességi köre nem korlátozott, mondhatjuk, hogy teljesen megértettünk valamit. Magyarázható ez azzal, hogy az itteni fogalmakat szellemünk teljes mértékben körül tudja járni, az itteni létezőknek nincsen zavaró fizikai megjelenése, minden elvont, egynemű, csupán szellemi. Kiegészítve ezt még azzal a feltevéssel, hogy a matematika saját alkotásunk, még érthetőbbé válik, hogy jobban értjük, hisz tekinthető ez a világ szellemünk rendező, egyértelműségre, logikai tisztaságra törekvő hajlamának megnyilatkozásaként, létrehozásakor tapasztalatunkat addig csupaszítjuk, az egyértelmű elemeket addig emeljük ki, s hagyjuk el a viszonylagosakat, az új területeket addig elemezzük, míg minden világossá nem válik számunkra. Itt nem függ semmi ellenőrizhetetlen, rajtunk kívül álló tényezőktől, ahogyan ezzel legtöbbször szembesülnünk kell. A valós viszonyokat jobban jellemzi az M.C. Escher képe által sugárzott összefonódás, egymásba nyúlás, a döbbenetes és szoros ôsszetartozás, egymás determinálása, s ugyanakkor a kibogozhatatlan kapcsolatok, a fogalmak, képek ellenôrizhetetlen gomolygása, a tisztánlátás hiánya.
M.C. Escher: Mozaik II
A legtöbb esetben, amikor valaminek a megértéséről beszélünk, akkor azt inkább felfogjuk, mint önmagunkon kívüli létezőt, amit máshogyan is el tudnánk képzelni, a matematikán belül megértett viszont annyira a sajátunk, hogy annak más formában történő megvalósulása nagyon különös lenne számunkra.
Nem mindenki számára jelent sokat, nem mindenki fogékony a matematika által nyújtott megértésre, többek szerint igazából csak az érzelmi, az átélt megértés számít szemben a pusztán szellemivel. Egyik meghatározó eleme ez annak, hogyan is viszonyulunk a matematikához. A matematikusok általában érzelmileg is kötődnek ehhez a fajta megértéshez, amelyet mások értetlenül szemlélnek.
Már volt róla szó, de ide itt is meg kell említeni, hogy a természettudományokban a megértéshez szorosan hozzátartozik a matematikával való leírhatóság. Érdekes különbség van a matematikusok és egyéb természettudósok hozzáállása között ezen a téren, például a fizikusok sokkal szabadabban kezelik, eszköznek, néha szinte formálható anyagnak, tekintik a matematikát, amit felhasználnak a magyarázat érdekében, míg a matematikusok minden téren ragaszkodnak a precízséghez, mindenféle bizonytalanság elkerüléséhez.
Magunkban mindenről kialakítunk egy belső képet, tudatosan, vagy ösztönösen az új információkat állandóan összevetjük a már meglévő elképzeléseinkkel, értelmezzük azokat, s ha valami nem illik bele a már meglévő rendszerünkbe, akkor az lehet érdekes, vagy megrázó élmény, attól függően milyen mélyen érint bennünket. A matematikában is érhetnek meglepetések, de itt kizárólag szellemi szinten. Hétköznapi szemléletünk számára és speciálisan a matematikai létezők rendszeréről kialakított mentális képünk számára is akadnak különösnek tűnő megállapítások. Matematikával foglalkozás közben ugyanis az itteni sajátos objektumokat és ezek egymáshoz való viszonyát is elképzeljük valahogyan, s elmondható, hogy ez a rendszer sokban különbözik egyéb rendszereinktől. Érdekességének jelentős eleme, hogy ezen a tiszta szellemi szinten is tud meglepetéssel, váratlan fordulatokkal szolgálni, olyan eredményekkel, amelyek valamiért nem illenek a tárgy eddig elképzelt belső struktúrájába. Ezek gyakran új, felderítésre váró irányokba mutatnak.
Különös, hogy egyszerűen megfogalmazható kérdéseink közül, amelyek között első ránézésre nem látszik nehézségbeli különbség, egyesek valóban könnyen megválaszolhatóak, másokra pedig több mint száz éve történt felvetésük óta senkinek sem sikerült választ adnia. Ezt talán csak a matematika világában tűnik meglepőnek, hiszen nem csodálkozunk különösebben azon, hogy a "Miért öltözünk fel télen jobban, mint nyáron?" és a "Miért van egyáltalán valami, ahelyett, hogy ne lenne semmi?" kérdések közül, amelyeket nyelvtanilag körülbelül egyforma nehézséggel tudunk megfogalmazni, az egyikre természetesnek tűnő választ tudunk adni, a másik azonban zavarba ejtő, nem igen tudjuk, hogyan adhatnánk választ rá, esetleg nem is tudjuk pontosan, mire vonatkozik a kérdés. Egy tetszőleges, egynél nagyobb egész szám és kétszerese közötti egészeket vizsgálva mindig találunk prímszámot, ezt sikerült bebizonyítani és ez a bizonyítás nem is olyan nagyon nehéz, míg az eddig megfigyelt esetek mindegyikében egy pozitív szám négyzete és a tőle eggyel nagyobb szám négyzete között, tehát két szomszédos négyzetszám között is mindig volt prímszám, de senkinek sem sikerült ezt belátnia általánosan, tehát hogy ez mindig szükségszerűen így van.
Nem tudjuk biztosan azt sem, hogy végtelen sok ikerprím van-e, vagyis, hogy végtelen sok olyan két szomszédos páratlan szám van-e, ahol mindkettő prím?
Szokatlan, amikor világosan, egyértelműen, matematikai precizitással megmutatkozik konkrét jelenségek adott szempontú rangsorolásának lehetetlensége. Például nézzük a következő módon elkészített dobókockákat:
Az első: négy lapján 2-2 pont, a fennmaradó kettőn 5-5 pont van.
A második: minden lapján 3-3 pont van.
A harmadik: két lapján 1-1 pont, a többi négyen 4-4 pont van.
Próbáljunk meg sorrendet felállítani a nyerési esély szerint, ha két kockával dobunk és az nyer, amelyiknél több pont van legfelül. Kipróbálható, de ki is számolható, hogy a kockák a következő viszonyban vannak egymással:
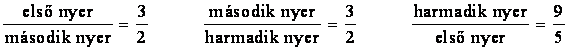
Vagyis az első kocka jobb, mint a második, a második jobb, mint a harmadik és a harmadik jobb, mint az első. Elindulunk egy irányban, s mindig felfelé haladva egyszer visszajutunk a kiindulóponthoz, ahogyan M.C. Escher képén a katonák is teszik.
M.C. Escher: Emelkedés és ereszkedés
Van olyan irracionális a
szám, amelynél a 
kifejezés - ahol a-t a 3n-edik hatványra emeljük, majd az így kapott szám egész részét
vesszük - minden n természetes szám
esetében prímszámot ad eredményül, viszont nincs olyan egész együtthatós
polinom, amely minden egész számra ugyanezt tenné. Az 
másodfokú polinom
értéke például n=1-től 79-ig
prím, de 80-nál már nem.
Hétköznapi szemléletünknek meglepő tény tárul fel a következő feladat kapcsán: Egy koordinátarendszer kezdőpontjából elindul valaki és minden másodpercben egy olyan vektorral lép arrébb, amelynek mindkét koordinátája racionális szám, de ezt a vektort mi nem ismerjük. Ennek ellenére, ha minden másodpercben valahová ledobhatunk egy bombát, akkor tudunk-e olyan stratégiát mondani, amellyel előbb-utóbb biztosan eltaláljuk? A válasz igen, sőt akkor is, ha nem tudjuk azt sem, hogy honnan indult el.
|
