Teoria gier-można

1. Wstęp

Teoria gier-można ją określic opisowo jako teorie podejmowania decyzji w szczególnych interaktywnych warunkach, w których konsekwencje działań podejmowanych przez poszczególnych uczestników, nazywanych graczami, zależą od działań pozostałych uczestników. Teoria gier jest teorią normatywną oznacza to, że bada możliwe zachowania i decyzje uczestników (nie muszą to być pojedyncze osoby, lecz również grupy osób koordynujących swoje działania, nazywane na ogół koalicjami, organizacje, a nawet z 19319n1313t wierzęta, rośliny lub komputery) w sytuacjach częściowego lub pełnego konfliktu interesów między nimi i poszukuje takich wyborów, jakich powinni dokonac racjonalni uczestnicy tych sytuacji oraz rozwiązań, które powinni zaakceptowac. Teoria gier pozwala również przewidywac rozwiązania sytuacji konfliktowych w przypadkach, gdy założenia o racjonalności uczestników tych sytuacji są spełnione. Teoria gier ma zastosowanie w wielu dziedzinach, przede wszystkim w ekonomii i w naukach politycznych, a także w biologii, naukach wojskowych, psychologii społecznej, socjologii, filozofii, statystyce. Za datę narodzin teorii gier przyjmuje się często rok 1944, w którym opublikowana została monografia Johna von Neumanna i Oskara Morgensterna Theory of Games and Economic Behavior. Natomiast autorstwo matematycznego modelu konfliktu interesów przypisuje się Johnowi von Neumannowi (1928).

Charakterystyka gry, która jest uproszczonym, matematycznym modelem sytuacji konfliktowej, wymaga między innymi określenia liczby uczestników tej sytuacji( graczy); możliwości postępowania każdego z graczy (strategii); reguł gry, które z jednej strony określają informacje dostępne graczom, możliwości porozumiewania się i zawierania wiążących umów, a z drugiej uporządkowują wyniki gry (wypłaty) zbiorom strategii zastosowanych przez poszczególnych graczy; oceny indywidualnie możliwych wyników gry(użyteczności); opis stopnia sprzeczności interesów poszczególnych graczy itp.

W zależności od zastosowanego kryterium można wyróżnic rodzaje gier. Istotne znaczenia ma liczba graczy. Z tego punktu widzenia dzieli się gry na dwuosobowe i wieloosobowe. Zasadnicza różnica między nimi polega na możliwości tworzenia koalicji, pod warunkiem że zakładamy możliwośc komunikowania się graczy. Drugim znaczącym kryterium jest stopień sprzeczności interesów graczy. Z tego punktu widzenia dzieli się gry na ściśle konkurencyjne i częściowo konkurencyjne. Gry ściśle konkurencyjne charakteryzuje pełny konflikt interesów graczy. Oznacza on brak możliwości poprawy sytuacji jednego gracza bez pogorszenia sytuacji innego lub innych graczy (są to tzw. gry o sumie zerowej). W grach częściowo konkurencyjnych występują wyniki, które są korzystniejsze od innych wyników dla jednego, kilku lub nawet wszystkich graczy bez pogorszenia sytuacji pozostałych. Nazywa się je grami o sumie niezerowej. W tych przypadkach możliwa staje się kooperacja między graczami. Aby kooperacja była możliwa, reguły gry muszą dopuszczac porozumiewanie się graczy i zawieranie przez nich wiążących umów.

2. Równowaga Nasha

Równowaga Nasha jest to profil strategii teorii gier, w którym strategia każdego z graczy jest optymalna, przyjmując wybór jego oponentów za ustalony. W równowadze żaden z graczy nie ma powodów jednostronnie odstępować od strategii równowagi. W tym sensie równowaga jest stabilna. Każda gra ma przynajmniej jedną równowagę Nasha, niekoniecznie w strategiach czystych. Z reguły równowaga Nasha nie jest efektywna w sensie Pareto(optimum Pareta, optimum w sensie Pareto termin opracowany przez włoskiego ekonomistę Vilfreda Pareta, oznacza taki podział dóbr, którego nie można już poprawić nie pogarszając jednocześnie sytuacji któregokolwiek z podmiotów. Klasycznym przykładem tej nieefektywności jest paradoks znany jako 'Dylemat Więźnia' pochodzący od wybitnego matematyka Alberta W. Tuckera.)

Rozważmy grę dwuosobową. Równowagą Nasha jest to następujący wybór: wybór gracza A jest optymalny dla wyboru gracza B i wybór gracza B jest optymalny przy danym wyborze A. Inaczej: Wybieram to, co jest dla mnie najlepsze, gdy ty robisz to, co robisz. Ty robisz to, co jest dla ciebie najlepsze, gdy ja robię to, co robię.

3. Teoria negocjacji Nasha

Przyjmujemy założenie o grze o sumie niezerowej oraz przyjmujemy, że gracze mają możliwośc porozumiewania się. Mamy graczy, którzy dyskutują ze sobą o tym jaki wynik byłby uzasadniony ( czy też sprawiedliwy), oraz gotowych na zaakceptowanie uzgodnionego wyniku. Gracze mogą też postanowic, że racjonalny i sprawiedliwy wynik zostanie wskazany przez bezstronnego arbitra- i jego decyzji zobowiązują się podporządkowac. Regułami jakimi powinni kierowac się gracze lub też arbiter, oraz kwestią możliwości określenia co jest racjonalnym lub sprawiedliwym wynikiem gry zajęli się jako pierwsi von Neumann i Morgenstern. Stwierdzili oni, że dopuszczalne rozwiązanie arbitrażowe gry o sumie niezerowej musi spełniac następujące warunki:

Musi byc optymalne w sensie Pareto: nie może być żadnego wyniku, który byłby lepszy dla obu graczy lub lepszy dla jednego, a nie gorszy dla drugiego,

Wypłaty obu graczy powinny być nie niższe niż ich poziomy bezpieczeństwa. Żadnego z graczy nie można zmusic do zaakceptowania rozwiązania, w którym jego wypłata jest niższa niż ta, którą może on sobie zagwarantowac, grając nie kooperacyjnie.

Zbiór wyników (czystych lub mieszanych), spełniających oba powyższe kryteria, nazywamy zbiorem negocjacyjnym lub obszarem negocjacji. Pojawia się pytanie czy w tym przedziale dopuszczalnych wyników możemy wskazac pojedynczy najsprawiedliwszy wynik. Sposób rozwiązania tego problemu zaproponował John Nash. Przed Nashem powszechnie uważano, że niemożliwe jest stworzenie formalnego modelu negocjacji prowadzonych przez ludzi. Obawy te brały się z podzielanego przez ekonomistów poglądu, iż negocjowanie w sposób naturalny zależy od czynników, które trudno sprecyzować, jak na przykład niejasne pojęcie umiejętności negocjacyjnych. Stąd też przypuszczano, że znajdują się one poza sferą wszelkiej racjonalnej analizy ekonomicznej. W cyklu artykułów naukowych, napisanych w latach 50-tych ubiegłego wieku, Nash pokazał, jak można podejść do problemu negocjacji w sposób konsekwentny i racjonalny Od tego czasu teoria negocjacji stała się centralnym obszarem badań ekonomistów i teoretyków gier, a jej zastosowanie pomaga lepiej zrozumieć wiele występujących w rzeczywistości zjawisk związanych z negocjowaniem. Pomogło także teoretykom gier położyć fundament pod teorię gier kooperacyjnych.

Pomysł Nasha był następujący. Przypuśćmy, że dwaj uczestnicy negocjacji (zwani dalej graczami 1 i 2) chcą osiągnąć porozumienie w sprawie podziału jakiegoś obiektu. Niech p [0, 1] oznacza prawdopodobieństwo pomyślnego zakończenia negocjacji, podane a priori dla rozważanego problemu (p można zinterpretować jako strategiczną zmienną gracza i. W tym przypadku p wybiera gracz wnoszący sprzeciw, przez co ustala on, że w procesie negocjacyjnym będzie "dokładać wszelkich starań", aby prawdopodobieństwo niepowodzenia wynosiło 1-p). Zdefiniujmy sprzeciw gracza i wobec porozumienia a* jako inne możliwe porozumienie a zgodnie z następującą interpretacją: a jest alternatywnym porozumieniem, które proponuje gracz i a 1 - p jest prawdopodobieństwem załamania się negocjacji, jeśli gracz i będzie obstawać przy swoim sprzeciwie. Gracz i wniesie taki sprzeciw wobec a* tylko wtedy, gdy będzie ściśle preferować wynik a (pomimo niepewności, jaką p wnosi do procesu negocjacyjnego mającego na celu wprowadzenie w życie a) nad a*. Gracz j może wnieść kontr-sprzeciw wobec a, jeśli j jednoznacznie woli a* (w warunkach niepewności wniesionej przez p do procesu dalszych targów mającego na celu wdrożenie a* zamiast a) od a. Przyjąwszy powyższe definicje sprzeciwów i kontr-sprzeciwów, rozwiązaniem Nasha dowolnego problemu negocjacyjnego jest zbiór wszystkich porozumień a* charakteryzujących się tym, że wobec każdego sprzeciwu któregokolwiek gracza w odniesieniu do a*, drugi gracz może wnieść kontr- sprzeciw.

Można wykazać, że rozwiązanie to daje w rezultacie zbiór wszystkich porozumień, które maksymalizują iloczyn funkcji użyteczności von Neumanna-Morgensterna obu graczy. Rozwiązanie to spełnia też pewne pożądane, a co za tym idzie, istotne aksjomaty, a mianowicie efektywność w sensie Pareto (Porozumienie a jest efektywne w sensie Pareto, jeżeli dla każdego innego możliwego do osiągnięcia porozumienia a' zawsze istnieje co najmniej jeden gracz, który woli a od a'), symetrię (porozumienie przypisane symetrycznemu problemowi negocjacyjnemu - tj. takiemu, w którym gracze i i j są nie do rozróżnienia - nie rozróżnia pomiędzy graczami i i j.) oraz niezależność od alternatyw nieistotnych(jeżeli porozumienie a* przetrwa pomimo sprzeciwów wnoszonych przez gracza i w ramach danego problemu negocjacyjnego, musi ono też przetrwać w innym problemie negocjacyjnym, w którym ten sam gracz i jest mniej skory do wnoszenia takich samych sprzeciwów).Co ważniejsze, jest jedynym rozwiązaniem o tych własnościach. Inną ważną cechą rozwiązania Nasha jest to, że gracz uzyskuje tym gorsze wyniki, im większą wykazuje awersję do ryzyka.

4. Schemat arbitrażowy Nasha i rozwiązania kooperacyjne.

Na początku określmy, jakie właściwości posiada kompromis. Aby go wyznaczyć, najpierw trzeba ustalić jakie jest faktyczne status quo. W tym celu pożyteczne są wiadomości uzyskane spoza kręgów oddziaływań zwaśnionych stron. Każda z nich, aby zmienić propozycję kompromisu będzie usiłowała fałszować rzeczywisty obraz sytuacji. Zobaczmy to na następujących przykładach. Stanowisko Polski wobec przyjęcia konstytucji Unii Europejskiej streszczało ostatecznie stwierdzenie Jana Rokity "Nicea albo śmierć". Zaostrzenie stanowiska negocjacyjnego miało na celu maksymalne przybliżenie ostatecznego rezultatu konferencji międzyrządowej do najbardziej korzystnego dla Polski stanowiska: nicejskiego systemu liczenia głosów. Jak się okazało, faktyczne stanowisko polskiego rządu było o wiele mniej drastyczne. Innym przykładem zafałszowanego wizerunku przed przystąpieniem do negocjacji może być stwierdzenie pracodawcy wobec strajkującej załogi zakładu: jeżeli nie zaniechacie roszczeń, zostaniecie zwolnieni z pracy. Chociaż faktyczny koszt zwolnienia wszystkich strajkujących pracowników często jest większy (koszt przyuczenia do zawodu nowych, przestój w produkcji itp.) niż koszt spełnienia postulatów, zarządowi firmy chodzi o takie skierowanie gróźb wobec pracowników by końcowe ustępstwa były jak najmniejsze. Zaczynamy od ustalenia jakie jest status quo. Potem określamy skalę użyteczności graczy. Przykładowo podwyżka o 1 zł za godzinę pracy będzie równa dla pracowników użyteczności +10, dla pracodawcy -3, a likwidacja przerwy na kawę dla pracowników -1, a dla pracodawcy +2. Jeżeli na tych skalach status quo ma współrzędne SQ=(a,b), to rozwiązaniem konfliktu jest taki punkt N = (x,y) że N należy do zbioru negocjacyjnego, a jego współrzędne maksymalizują wartość iloczynu W=(x-a)(y-b). Do zbioru negocjacyjnego zaliczamy natomiast takie rozwiązania konfliktu, że: po pierwsze są one paretooptymalne, a po drugie dla każdego gracza ich rezultat jest niegorszy niż ten, który mógłby on sobie zapewnić bez negocjacji. Przyjmiemy, że status quo oznacza dla każdego gracza użyteczność równą zeru. Wtedy musimy zmaksymalizować iloczyn W=xy lub dla n graczy W=x[1]*x[2]*...*x[n].

Konkretny przykład takiej sytuacji przytoczę za artykułem     "Rozwiązywanie konfliktów. Schemat arbitrażowy Nasha" J. Kotlarz

Dyrekcja firmy negocjuje nowe warunki pracy z organizacją zrzeszającą pracowników (np. związek zawodowy). Konflikt powodują cztery projekty:
A: Likwidacja refundacji pracownikom kosztów przejazdów służbowych
Z: Przejście z umów o pracę na samo zatrudnienie pracowników
P: Podwyżka wynagrodzenia o 1 zł za godzinę
G: Unormowanie (zmniejszenie) czasu pracy.
SQ: Stan status quo (ewentualnie)

Badając użyteczności dyrekcji firmy i pracowników nie oczekujemy, że będą one dla konkretnych projektów równe co do wartości bezwzględnych. Przykładowo to, że dla pracowników zrealizowanie postulatu P daje użyteczność sytuacji +2 nie oznacza, że zmniejsza ono użyteczność dyrekcji do -2. Nie oczekujemy tutaj gry o sumie zerowej. Gdyby tak było jedynym rozwiązaniem byłby status quo i negocjacje byłyby zbędne. Cały pomysł Nasha polega na tym, że różnice w wartościach bezwzględnych użyteczności konkurujących graczy, dają pole do manewru i ustalenia nowej sytuacji - korzystniejszej dla wszystkich.

Niech użyteczności wyglądają następująco:

Przekształcenie tych wartości liniowo w dowolny sposób nie będzie miało wpływu na dalsze rozważania, ponieważ schemat Nasha jest od przekształceń liniowych niezależny. W tym przykładzie użyteczności kompromisów (wszystkich możliwych w strategiach czystych) kształtują się następująco:

Rysunek przedstawia wielobok wypłat dla wszystkich kompromisów. Przyjmując SQ=(0,0) otrzymujemy rozwiązanie - punkt Nasha równy N=(3,2). Dla żadnego innego punktu tego wieloboku iloczyn jego współrzędnych nie będzie większy niż 3*2=6 i nie będzie należał do zbioru negocjacyjnego.

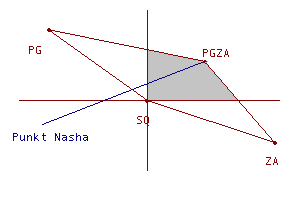
Powyższy punkt N=(3,2) odpowiada przyjęciu wszystkich postulatów, a więc
- likwidacji refundacji kosztów przejazdów
- przejściu z umów o pracę na samo zatrudnienie pracowników
- podwyżki wynagrodzenia o 1 zł za godzinę i
- zmniejszenie czasu pracy.

Ta sytuacja - zgodnie z deklaracjami użyteczności pracowników i pracodawcy - będzie lepsza dla obu stron niż obecna. To rozwiązanie powinien zaproponować negocjator. Oczywiście po drodze można natrafić na kilka problemów. Po pierwsze: czy użyteczności są dla graczy addytywne. To znaczy, czy uzyskując podwyżkę o złotówkę wartość regulacji czasu pracy będzie miała nadal dla pracowników taką samą wartość jak przed podwyżką. Jeżeli nie - sytuacja staje się nieco bardziej skomplikowana. Po drugie, co zrobić gdy wynikiem Nasha jest strategia mieszana, przykładowo 1/2 A i 1/2 Z? Tutaj musimy wykazać się dobrą interpretacją. 1/2 A można zinterpretować jako obniżkę refundacji podróży o 50%. Po trzecie. Co zrobić, jeśli żadne z rozwiązań nie jest lepsze niż status quo? Czy rekomendować w tej sytuacji pozostanie przy zastanym stanie? Istnieje możliwość zwiększenia - paradoksalnie - przedmiotu konfliktu o "coś jeszcze" co sprawi że będziemy mieli lepsze pole manewru. Allen proponuje, by spodziewając się tej sytuacji negocjacje rozpoczynać od znanej "burzy mózgów". Po czwarte. Musimy zadać sobie pytanie, czy strony negocjują w przyjaznej atmosferze czy też w atmosferze konfliktu. Obie strony mogą przekazywać fałszywe informacje o swoich użytecznościach. Zaskakujące jest to, że przekazując arbitrowi kłamstwa - spodziewając się lepszych wyników dla siebie - strony (nawet obie) mogą uzyskać dla siebie gorsze wyniki niż punkt N, lub nawet SQ. Pokażmy tą sytuację na przykładzie.

Załóżmy, że dyrekcja firmy postanowiła w celu uzyskania lepszego dla siebie wyniku kłamać. Jedną z form nacisku będzie zafałszowanie oceny poszczególnych kompromisów. W ten sposób dyrekcja przekazuje informację, że oczekuje większych ustępstw niż w rzeczywistości. Załóżmy, że dyrekcja podwaja wszystkie swoje ujemne użyteczności: dla P (-4) a dla G (-6). W wyniku oszustwa dyrekcji część punktów na wykresie zostanie przesunięta na lewo. Obszar obustronnie korzystnego kompromisu zmniejszy się, a punkt N wyniesie N=(1, 1/2). Najciekawsze jest to, że ten punkt można teraz zinterpretować dwojako: jako 1/2 PZ, 1/2 GZA. Przeliczając to na sytuację niezafałszowaną otrzymujemy rozwiązanie korzystniejsze dla dyrekcji. Pracownicy zostają oszukani. Lecz Arbiter może również zinterpretować punkt N jako 3/4 PZ, 1/4 Z. Wtedy wygrywają pracownicy. W wyniku oszustwa dyrekcji pracownicy uzyskują lepszą sytuację końcową.
Ogólnie rzecz biorąc kłamstwo nie popłaca jeżeli kłamią obie strony. Jeżeli kłamie tylko jeden gracz - sprawa jest bardziej złożona.

Rozwój teorii gier.

Teoria gier rozwija się obecnie głównie na potrzeby nauk ekonomicznych. Wielu ekonomistów otrzymało już Nobla za osiągnięcia w tej dziedzinie. W roku 2005
nobliści z dziedziny ekonomii ,Robert J. Aumann i Thomas C. Schelling, zostali nagrodzeni właśnie za wzbogacenie teorii gier strategicznych. Zajmowali się oni przede wszystkim analizą sytuacji, w której gra nie jest jednokrotna, lecz się powtarza, często nie wiadomo nawet, ile razy. Thomas Schelling stosował teorię gier do analizy negocjacji międzynarodowych w okresie "zimnej wojny". Analizował takie zagadnienia, jak: polityka wzajemnych ustępstw, gróźb, zastraszania. Tę analizę można zastosować również do negocjacji prowadzonych przez firmy. Robert Aumann zajął się matematyczną analizą gier powtarzanych. Okazuje się, że inna jest optymalna strategia w przypadku gry powtarzanej, a inna w przypadku gry rozgrywanej jednokrotnie. Aumann zajmował się także problemami bankructwa. Zbudował matematyczny model zagadnienia pochodzącego z Talmudu (jest głęboko wierzącym Żydem), kiedy to majątek zmarłego - lub po prostu bankruta - nie wystarcza na pokrycie jego zobowiązań. Powstaje problem, jak podzielić ten majątek. Po równo? Proporcjonalnie? A może więcej dać tym, których przyszłość jest uzależniona od zwrotu długu?

Bibliografia:

Kotlarz J, Rozwiązywanie konfliktów. Schemat arbitrażowy Nasha www.teoriagier.emaus.waw.pl

Malawski M, Wieczorek A, Sosnowska H, Konkurencja i kooperacja- teoria gier w ekonomii i naukach społecznych, PWN, Warszawa 1997

Osborne M, Rubinstein A, A course in game theory, The MIT Press Cambridge, Massachusetts 1999

Straffin Philip, Teoria gier, Wydawnictwo Naukowe Scholar Warszawa 2001

https://teoriagier.blox.pl/html