Постановка и решение задач

состоит в получении определенных результ 414t1921e 72;тов. Это относится к работе, жизни или учебе: сдача экзаменов, написание сочинений, выполнение чертежей, изготовление приборов, инструментов и машин, сбор урожая, накопление капитала - все это получение результ 414t1921e 72;тов.

Ключом к любой задаче является способ решения, дающий необходимые результ 414t1921e 72;ты. Знание способов решения и умение их применять для решения практических задач - важнейшая характеристика профессиональной квалификации.

Результ 414t1921e 72;ты правильные, если они отвечают требованиям решаемых задач. Однако если требования неизвестны или сформулированы недостаточно четко, то нельзя однозначно судить о правильности полученных результ 414t1921e 72;тов.

Результ 414t1921e 72;ты неправильные, если они противоречат заданным требованиям. Как однозначно определить правильность результ 414t1921e 72;тов? Ответ: для этого необходима точная постановка задач с четким выделением требований.

Ответ на первый вопрос - что требуется? - точное определение требуемых результ 414t1921e 72;тов. При отсутствии требований к конечным целям оценка полученных результ 414t1921e 72;тов может быть неоднозначной.

Ответ на второй вопрос - что дано? - определение исходных условий, при которых требуется получить результ 414t1921e 72;ты. Неоднозначность в определении исходных условий может привести к получению неправильных результ 414t1921e 72;тов.

если он дает правильные результ 414t1921e 72;ты. Для определения правильности способов решения задач необходима четкая постановка решаемых задач, в которых должны быть строго определены требуемые результ 414t1921e 72;ты.

если его применение приводит к получению неправильных результ 414t1921e 72;тов либо вовсе не дает никаких результ 414t1921e 72;тов. Использование неправильных способов решения может вообще не давать результ 414t1921e 72;тов.

b

x₀ = -b/а.

b = 1 дает решение x₀ = -b/а = -1/2, которое нам уже известно как правильное.

b 0 можно убедиться подстановкой формулы x₀ = -b/а в само уравнение:

a x₀ + b = a (-b/a) + b = -b + b

решить уравнение а ∙ х + b = 0.

Дано: а, b - коэффициенты уравнения.

если он дает правильные результ 414t1921e 72;ты для любой задачи данного класса. Применение таких методов гарантирует правильность результ 414t1921e 72;тов для любой задачи данного класса.

если можно указать конкретную задачу данного класса, для которой применение метода даст неправильные результ 414t1921e 72;ты либо не даст результ 414t1921e 72;тов вовсе.

+ b = 0 формула х = -b/а не дает результ 414t1921e 72;та при а = 0. Но при значении а = 0 уравнение превращается в соотношение b = 0, что говорит о недопустимости этого значения. Следовательно, условием допустимости данных в рассматриваемой задаче будут значения а ≠ 0.

Правильность методов решения можно и нужно проверять на конкретных примерах, подтверждающих правильность получаемых результ 414t1921e 72;тов. Однако достаточно привести хотя бы один контрпример, чтобы утверждать о неправильности метода решения в целом.

И все-таки демонстрация правильности результ 414t1921e 72;тов на двух-трех конкрентных примерах не может служить достаточным основанием для утверждений о правильности метода или способа решения в целом.

правильности методов решения дает только исчерпывающий анализ результ 414t1921e 72;тов, получаемых для любой из задач данного класса. Пример - приведенное выше обоснование общего метода решения линейных уравнений.

В общем случае обоснование правильности обобщенных методов решения требует исчерпывающего математического исследования получаемых результ 414t1921e 72;тов и математического доказательства их правильности для всех конкретных случаев.

s₁

{s_k = s_k-1 (k-l) / k x_k / k, (k n)

s_n

k

s₁

k

s₂ = s₁ (2 - 1) / 2 s₁ / 2 x₁ / 2 2 = (x₁ + х₂

Для k = 3 из этой же рекуррентной формулы получим:

s₃ = s₂ 3 + x₃ 3 = s₃ 2/3 + x₃ 3 = (x₁ + x₂) + x₃ 3 = (х₁ + х₂ + x₃)

На основе приведенных формул можно сделать заключение о том, что для произвольного k будет выполняться соотношение

s_k ... + х_k) k.

k-1:

s_k-1 x_k-1) / (k-1)

s_k = S_k-1(k - l) / k + х_k / k [(x₁ x₂ x_k-1) / (k - l)] (k - l) / k x_k / k (x₁ x₂ x_k-1) / k x_k / k x₂ + ... + х_k-1 + x_k) / k.

Таким образом, на каждом шаге k = 1, 2, 3, ... рекуррентная формула дает среднее арифметическое значение обработанной последовательности чисел. Тогда на основании математической индукции можно утверждать, что на последнем шаге вычислений при k = n будет вычислено среднее арифметическое значение:

1. Когда результ 414t1921e 72;ты правильные?

2. Когда результ 414t1921e 72;ты неправильные?

b

d y = f

D_x / D y = D_y / D

D_x e d b f D_y a f b e

D a d b c

а) суммирование чисел СУММ (x₁, x₂, ..., x_n) = х₁ + х₂ + ... + x_n

s₀

{s_k s_k-1 + x_k , (k = 2, 3, ., n)

СУММ (x₁, x₂, ..., x_n) = s_n

б) максимальное значение МАКС (x₁, x₂, ..., x_n) = mах (x₁, x₂, ..., x_n)

mх₁ = х,

mx_k mах(mx_k-1, х_k), (k = 2, 3, ..., n)

МАКС (x₁, x₂, ..., x_n) = mх_n

в) минимальное значение МИН(x₁, x₂, ..., x_n) = min(x₁, x₂, ..., x_n)

mn₁ = х₁

mn_k = min(mn_k-1, х_k) , (k = 2, 3, ..., n)

МАКС(x₁, x₂, ..., x_n) = mn_n

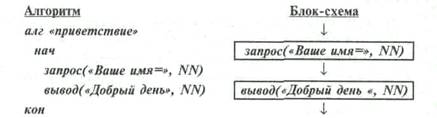
Программа

' приветствие

сls

uмя=»,NN) input «Ваше имя=»,NN$

eнь»,NN) print «Добрый дeнь»,NN$

end

Программа

10 ' приветствие

20 сls

uмя=»,NN) input NN$

»,NN) 40 print день»,NN$

50 end

алгоритмов и программ для вычислительных машин - однозначность, результ 414t1921e 72;тивность, правильность и массовость. Этими свойствами алгоритмы отличаются от различного рода расплывчатых и неоднозначных предписаний, инструкций и кулинарных рецептов, которые могут толковаться и исполняться многими способами.

алгоритмов - это однозначность правил их выполнения. Следствием этого свойства алгоритмов является однозначность результ 414t1921e 72;тов их выполнения в одинаковых начальных условиях. Это не всегда верно для кулинарных рецептов, когда разные исполнители в одних и тех же условиях могут придавать различный вкус и пикантность одним и тем же блюдам.

Результ 414t1921e 72;тивность - это завершение выполнения алгоритмов определенными результ 414t1921e 72;тами. Результ 414t1921e 72;тивность - наиболее важное свойство алгоритмов и программ, предназначенных для решения прикладных задач. Алгоритмы и программы, не дающие результ 414t1921e 72;тов или ведущие к сбоям и отказам, никому не нужны.

определяется-правильностью результ 414t1921e 72;тов, получаемых с их помощью. По этой причине правильность алгоритмов и программ является относительным понятием. Оценка правильности может проводиться только при наличии требований к конечным результ 414t1921e 72;там.

считается правильным, если он дает правильные результ 414t1921e 72;ты при любых допустимых начальных условиях. Правильность алгоритмов гарантирует правильность результ 414t1921e 72;тов их выполнения.

содержит ошибки, если его выполнение может привести к отказам, сбоям или неправильным результ 414t1921e 72;там либо вовсе не дает никаких результ 414t1921e 72;тов. Эти ошибки называются алгоритмическими. Алгоритмы и программы, содержащие такие ошибки, могут нанести вред или ущерб тем, кто захочет ими воспользоваться.

алгоритмов и программ необходимо уметь оценивать результ 414t1921e 72;ты выполнения составляющих их действий и конечные результ 414t1921e 72;ты их выполнения в целом.

машинных операций - операции присваивания. С помощью присваиваний в алгоритмах описываются вычисления в программах для ЭВМ. Рассмотрим примеры операций присваивания и описания результ 414t1921e 72;тов их выполнения.

Результ 414t1921e 72;ты:

а = 0

b b

b b+1 b" b' + 1

b := b+1 - «переменной b присвоить значение b+1».

Записи в колонке результ 414t1921e 72;тов читаются так:

b' = b+1 - «значение b' равно b+1».

Здесь а и b - программные переменные - область машинной памяти, в которой хранятся их значения а и b. В отличие от обычных математических переменных программные переменные могут получать новые значения. В частности, присваивание b := b+1 записывает в программную переменную b новое значение b', равное величине b+1, где b прежнее значение переменной b.

Для описания результ 414t1921e 72;тов выполнения алгоритмов и программ могут и должны использоваться спецификации. Спецификации -

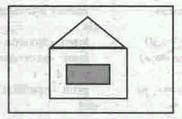
Решение - следующие алгоритм и программа, результ 414t1921e 72;том работы которых должен быть приведенный выше рисунок:

Программа

' Домик

screen

line(150,40)-(

line(150,40)-(200,100),8

line(100,100)-(200,200),15,b

line(130,120)-(170,160),3,b

end

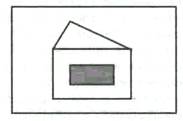
Однако результ 414t1921e 72;том выполнения приведенных алгоритма и программы будет следующий рисунок:

Программа

' расчет прибыли

сls

=»,d) input =»,d

=»,r) input r

р := d - r р = d - r

print

end

<d>

расходы =? <r>

прибыль = <р>

r

d

d = r

d > 0.

Для оценки правильности полученных результ 414t1921e 72;тов нужно сверить расходы и прибыль с доходами. В нашем случае это должно быть 700 + 300 = 1000, что выражает правильный конечный результ 414t1921e 72;т при указанных данных.

Для оценки правильности алгоритма и программы в целом необходимо рассмотреть конечные результ 414t1921e 72;ты их выполнения при произвольных значениях данных d и r. Вычисляемая величина р по алгоритму будет равна:

Результ 414t1921e 72;т

p:= d - r = d - r

d = r + p = r + (d- r) = d -

Таким образом, при любых значениях исходных данных результ 414t1921e 72;ты выполнения приведенного алгоритма будут правильными.

4. Что такое результ 414t1921e 72;тивность алгоритмов?

г) украинского флага;

д) французского флага;

е) британского флага.

д) автомобиля;

е) усадьбы;

ж) цветка;

з) птицы.