Обобщенный алгоритм Евклида

ктов, касающихся алгоритмов. Давайте рассмотрим следующее обобщение алгоритма 23223v211x ; Евклида.

m b d b am bn d

E l

а' b а b с d n

q r d

qd r r < d

r = 0, то выполнение алгоритма 23223v211x ; прекращается; в этом случае имеем

am bn d

d d r t а' а t qa t b b b b t qb

Если изъять из алгоритма 23223v211x ; переменные а, b b m n d, то получим старый алгоритм Е (см. параграф 1.1). В новой версии алгоритма 23223v211x ; выполняется немного больше вычислений, так как необходимо определить коэффициенты a b m n

Алгоритм Е дает правильное решение для заданного n m b b

а'т + b am bn d

то очевидно, что алгоритм работает правильно, поскольку его работа заканчивается на шаге ЕЗ в первом же цикле и мы получаем верный результат. Это происходит всегда, когда n = 1. Поэтому остается провести доказательство для случая, когда п > 1 и т не является кратным п. В такой ситуации в первом цикле осуществляется переход к шагу Е4 и выполняются операции присвоения с d r r < п, по индукции можно предположить, что окончательное значение d r и d m n am bn d

b справедливы, и на этом основании докажем справедливость утверждения Р 1)», мы будем говорить просто «Теперь докажем утверждение Р что P k k < n

Если хорошо вдуматься и посмотреть на все вышесказанное с несколько иной точки зрения, то перед нами предстанет общий метод доказательства корректности любого алгоритма 23223v211x ;. Идея состоит в том, чтобы взять блок-схему некоторого алгоритма 23223v211x ; и к каждой стрелке добавить примечание о текущем состоянии дел в тот момент, который соответствует стрелке. На рис. 1.4 эти примечания (мы их будем называть также утверждениями) обозначены через Al A В утверждении А даются первоначальные предположения о входных данных алгоритма 23223v211x ;, а в А формулируется положение о том, что мы хотим доказать по поводу выходных значений а, b d

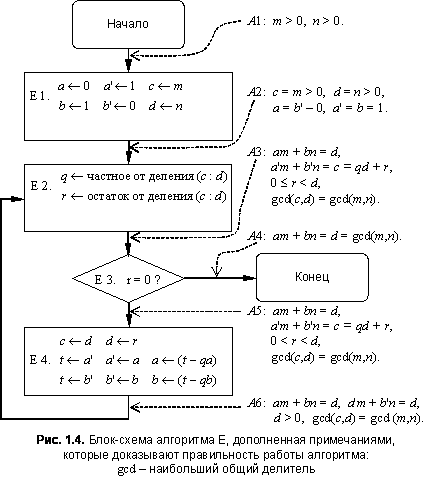
либо А то после выполнения этого шага верно A (В данном случае утверждение А является более сильным, чем А т.е. из А следует А Поэтому нам достаточно доказать, что выполнение А шага Е2 влечет за собой выполнение A после этого шага. Заметим, что условие d > для того, чтобы операция Е2 имела смысл.) Нужно показать также, что из A (при условии, что ) следует А из A (при условии, что ) следует А и т.д. Все это доказывается очень просто.

(1.10) для каждого блока, то все примечания к стрелкам будут верны в любом случае выполнения алгоритма 23223v211x ;. Теперь мы можем применить индукцию по числу шагов, т. е. по числу стрелок в блок-схеме. При прохождении первой стрелки (той, которая выходит из блока «Начало») утверждение А1 верно, поскольку мы всегда исходим из предположения, что входные значения удовлетворяют заданным условиям. Таким образом, утверждение, которое соответствует первой стрелке, верно. Если утверждение, которое соответствует n n

Исходя из этого общего метода доказательство правильности заданного алгоритма 23223v211x ;, очевидно, сводится к нахождению правильных утверждений, соответствующих стрелкам блок-схемы. Как только данное начальное препятствие будет преодолено, останется лишь рутинная работа, связанная с доказательством того, что каждое утверждение на входе в блок влечет за собой утверждение на выходе из блока. В действительности после того как вы придумаете самые трудные из этих утверждений, найти все остальные уже не составит труда. Скажем, если даны утверждения А1, А4 и А уже понятно, какими должны быть утверждения А В нашем примере самых больших творческих усилий потребует доказательство утверждения А все остальное, в принципе, должно получиться автоматически.

Этот подход к доказательству корректности алгоритма 23223v211x ; имеет и другой, еще более важный аспект: он отражает способ нашего понимания алгоритма 23223v211x ;. Нужно проверять работу алгоритма 23223v211x ; на примере одного-двух наборов входных данных. И это не случайно, так как пробная «прогонка» алгоритма 23223v211x ; поможет вам мысленно сформулировать утверждения, соответствующие стрелкам на блок-схеме. Уверенность в корректности алгоритма 23223v211x ; приходит только тогда, когда мысленно сформулированы все утверждения, приведенные на рис. 1.4. Отсюда следуют важные психологические выводы, касающиеся передачи алгоритма 23223v211x ; от одного лица к другому. Речь идет о том, что, объясняя алгоритм кому-либо другому, всегда следует явно формулировать основные утверждения, которые трудно получить автоматически. Например, в случае алгоритма 23223v211x ; Е нужно обязательно упомянуть утверждение А

Но бдительный читатель, конечно, заметил явный недостаток в нашем последнем доказательстве алгоритма 23223v211x ; Е. Из доказательства нигде не следует, что алгоритм обладает свойством конечности, т.е. рано или поздно его выполнение завершится. Мы доказали только, что если алгоритм конечен, то он дает правильный результат!

m n d r

v

Переменные q b b должны по-прежнему принимать целые значения. Если, например, на вход подать значения и , то на выходе будет получен «наибольший общий делитель» и коэффициенты a b до А остаются в силе. Следовательно, на любом этапе выполнения этой процедуры все утверждения верны. Но если начать со значений m = 1 и , то вычисления никогда не закончатся (см. упражнение 1.15). Следовательно, из доказательства утверждений А1

Итак, мы уже дважды доказали правильность алгоритма 23223v211x ; Е. Чтобы быть последовательными до конца, нам следовало бы попытаться доказать, что первый алгоритм в этом разделе, а именно - алгоритм I I I

n либо равно 1, либо может быть получено, если взять 1 за исходное значение и последовательно прибавлять по единице. Этого достаточно, чтобы доказать правильность алгоритма 23223v211x ; I

нужно доказать для всех неотрицательных целых чисел, т.е. для n n

a - любое положительное число. Для всех целых положительных чисел п имеем .

Если п = 1, то . По индукции, предполагая, что теорема верна для 1, 2, ..., п, имеем

;

n

Следующее доказательство по индукции выглядит корректным, но по непонятной причине для п = 6 левая часть уравнения дает , а правая дает . В чем же ошибка? «Теорема.

Докажите, что числа Фибоначчи удовлетворяют не только соотношению (1.6), но и неравенству .

большее единицы, которое делится только на 1 и на само себя. Используя данное определение и метод математической индукции, докажите, что любое целое число, большее единицы, можно записать как произведение одного или нескольких простых чисел. (Для удобства будем считать, что простое число это «произведение» одного простого числа, т.е. его самого.)

. Докажите по индукции, что если 0 < a < 1, то .

по индукции, что если п > 10, то .

Покажите, как можно обобщить алгоритм Е, чтобы, как было указано в тексте, для него допускались входные значения вида , где и и v - это целые числа, и вычисления по-прежнему выполнялись элементарным образом (т.е. не выражая иррациональное число бесконечной десятичной дробью). Докажите, что при т = 1 и выполнение алгоритма 23223v211x ; никогда не закончится.

счетчик выполненных шагов.)

Предположим, что первоначальное значение Т равно нулю, поэтому утверждение А на рис. 1.4 примет вид m > 0, n > 0, Т = 0. Аналогично к А следует добавить дополнительное условие Т = 1. Покажите, как добавить к утверждениям дополнительные условия таким образом, чтобы из любого утверждения А ..., А следовало, что Т < 3n n