КОНТРОЛЬ И ОЦЕНКА КАЧЕСТВА ПРОДУКЦИИ

Решение проблемы дефектных изделий через усиление контроля их качества равносильно ув 17517e415r еличению расходов, то есть сокращению прибыли, росту цены товара, снижению уровня конкурентоспособности.

Качество продукции зависит от многих факторов, потому формы, виды, методы и объекты контроля качества весьма разнообразны. Наиболее распространенные формы отражены на рис. 8.1.

Критерием готовности предприятия к выпуску продукции требуемого качества является наличие, как минимум, следующих свидетельств результатов контроля []:

называется уровень дефектности в принятой партии или потоке продукции, поступающей за определенный интервал времени. Математическое ожидание выходного уровня дефектности в принятых и забракованных партиях (в которых после сплошного контроля все обнаруженные дефектные изделия заменены годными) называется средним выходным уровнем дефектности (AOQ)

Так как входной контроль нивелирует и высокий, и низкий входной уровень дефектности, то существует максимальное для каждого плана контроля значение среднего выходного уровня дефектности, которое носит название пределом среднего выходного уровня дефектности (AOQL)

средний выходной уровень дефектности AOQ

предел среднего выходного уровня дефектности AOQL

В ГОСТ 18242-72 на статистический приемочный контроль по альтернативному признаку приведены коэффициенты, которые могут служить точной оценкой значения AOQL для выбранного плана контроля при умножении их на (1 - n / N). Если n (выборка) мала по сравнению с объемом партии N, то выражение в скобках незначительно отличается от единицы, и тогда сами коэффициенты являются достаточно точной оценкой AOQL.

Допустим, на контроль поступает продукция партиями по 1000 единиц. Для контроля выбран одноступенчатый, нормальный план с приемочным уровнем дефектности AQL = 4%, уровнем контроля - 2. По таблице 1 ГОСТа 18242-72 находим код объема выборки - J. Требуется определить предел среднего выходного уровня дефектности AOQL.

Из таблицы 31 в ГОСТе 18242-72 по коду объема выборки J и AQL = 4% находим n = 80 и AOQL = 5,6%. Это значение является достаточно точной оценкой AOQL, так как объем выборки составляет 80/1000 = 0,08, т.е. 8% от объема партии. Точное значение AOQL определяется по формуле:

AOQL ∙ (1 - n / N) = 5,6 ∙(1 - 0,08) = 5,15%.

Следовательно (так как 5,15 < 5,6), выбранный план контроля с AQL = 4% гарантирует, что в принятых партиях продукции в среднем будет не больше 5,15% дефектной продукции.

Приемочным уровнем дефектности (AQL)

Браковочным уровнем дефектности (LQ)

В ГОСТ 18242-72 приведены таблицы, позволяющие определить риск потребителя β, браковочный уровень LQ, приемочный уровень AQL и объем выборки n. В указанном стандарте риск потребителя

Основной характеристикой партии изделий при контроле по альтернативному признаку является генеральная доля дефектных изделий q:

q = M / N

где M - число дефектных изделий в партии объемом N.

Как правило, в практике статистического контроля генеральная доля q неизвестна и ее следует оценивать по результатам контроля ряда случайных выборок объема n изделий, из которых m дефектных.

, согласно которым если среди n случайно отобранных изделий число дефектных m окажется не больше приемочного числа с (m ≤ c), то партия принимается; в противном случае партия бракуется.

, согласно которым, если среди n₁ случайно отобранных изделий число дефектных m₁ окажется не больше приемочного числа c₁ (m ≤ c₁), то партия принимается; если m₁ ≥ d₁, где d₁ - браковочное число, то партия бракуется. Если же c₁ < m₁ < d₁, то принимается решение о взятии второй выборки объемом n₂. Тогда если суммарное число дефектных изделий в двух выборках (m₁ + m₂) ≤ c₂, то партия принимается, в противном случае партия бракуется по данным двух выборок.

являются логическим продолжением двухступенчатых планов. Первоначально берется выборка объемом n₁ и определяется число дефектных изделий m₁. Если m₁ ≤ c₁, то партия принимается. Если m₁ ≥ d₁ (d₁ > c₁ + 1), то партия бракуется. Если же c₁ < m₁ < d₁, то принимается решение о взятии второй выборки объемом n₂. Пусть среди n₁ + n₂ изделий имеется m₂ дефектных. Тогда если m₂ ≤ c₂, где c₂ - второе приемочное число, то партия принимается; если m₂ ≥ d₂ (d₂ > c₂ + 1), то партия бракуется. При c₂ < m₂ < d₂ принимается решение о взятии третьей выборки. В дальнейшем контроль проводится по аналогичной схеме, за исключением последнего k-го шага, при котором если m_k ≤ c_k, то партия принимается, если же m_k > c_k, то партия бракуется. При этом обычно принимается, что объем выборок одинаков.

фактически сводится к статистической проверке гипотезы о том, что доля дефектных изделий q в партии равна допустимой величине q₀. Задача правильного выбора плана статистического контроля состоит в том, чтобы сделать ошибки первого рода (риск поставщика) и второго рода (риск потребителя) маловероятными.

. Этот метод можно отнести к методам статистического управления качеством. В его основу положена идея, что для любых технологических процессов необходимо обеспечить индекс воспроизводимости Cp ≥ 2.

Этому условию на рис. 8.2 отвечала бы центральная кривая нормального распределения, если верхняя и нижняя границы допуска находятся на расстоянии 6 σ от центра кривой. Строгое выполнение этого условия приводит к уровню дефектности 2ррВ, то есть 2 дефекта на миллион изделий.

способные сдвинуть центр кривой на 1,5 σ влево или вправо от центра поля допуска. Такое условие расположения кривой распределения в поле допуска соответствует индексу воспроизводимости Ср = 1,5. В этом случае уровень дефектности составит 3,4 ррВ. Это значение и принимается в качестве норматива для метода «6 σ». Из данных таблицы 8.1 видно, как увеличивается дефектность от уменьшения расстояния между центром распределения и границей допуска [].

Метод «6 σ» впервые был применен на фирме «Motorola». Именно специалисты этой фирмы на основании собственного опыта скорректировали первоначальные жесткие условия метода, предложив возможность сдвига центра распределения на 1,5 σ под действием постоянных причин. Результаты внедрения метода «6 σ» на практике превзошли все ожидания. Так, компания «Allied Signal» (США) сообщила об экономическом эффекте в 800 млн. долларов, полученных за три года применения метода, а компания «General Electric»

[] успех внедрения метода «6 σ» связан с применением важнейших аспектов современного менеджмента, таких как лидерство, приверженность изменениям, «прорывное мышление», командная работа, обучение и т.д. Фирма «Motorola» раньше других осознала преимущества статистического мышления и сумела разработать системную концепцию его внедрения. Чтобы по достоинству оценить громадную работу, проделанную фирмой по внедрению метода «6 σ», следует отметить, что только программа обучения статистическим методам управления качеством составляла 150 часов. Вместе с этим внедрение концепции «6 σ» требует от руководства и персонала фирмы значительных напряжений, и ее реализация возможна в комплексе с сильной директивной культурой управления.

В соответствии с традиционным подходом оценки потерь качества, часто используемым при статистических методах контроля процессов, потери качества принимаются равными нулю, если измеряемый параметр попадает в пределы поля допуска. При выходе параметра за пределы поля допуска Т потери качества считаются недопустимо большими, что приводит к браку продукции или ее переработке (рис. 8.3). В этом случае на границах поля допуска (в точках А и С) имеет место разрыв функции потерь (ломаная кривая 1).

Ф(R) = сR2

где R - разность между истинным и номинальным значением параметра;

Допустим, что в поле допуска Т параметра Х, номинальное значение которого равно X₀, вписано поле рассеивания измеряемых значений этого параметра, в результате реализации какого-то процесса, подчиняющегося нормальному закону распределения со среднеквадратическим отклонением σ (рис. 8.4). При этом координаты середины поля допуска и середины поля рассеивания совпадают с номинальным значением параметра. Очевидно, что T = 6 σ с вероятностью 99,73%. Выберем симметричный диапазон значений параметра АВ (АО = ОВ) относительно X₀ и определим вероятность попадания значений параметра Х в этот диапазон P(АВ):

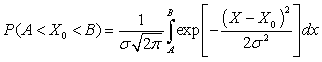
Постепенно ув 17517e415r еличивая диапазон АВ, определим значения вероятности P (X - X₀), пока АВ не станет равным полю допуска Т.

Покажем на конкретном примере, что указанная вероятность P (X - X₀) имеет отношение к функции потерь качества в поле допуска.

Допустим, что для параметра с номинальным значением 100,00 мм определен симметричный допуск по 8 квалитету точности равный ± 27 мкм. Предположим, что поле рассеивания реального параметра, распределенного по закону Гаусса, укладывается в поле допуска с вероятностью 99,73% и координата середины поля допуска совпадает с серединой поля рассеивания. Разметим все поле допуска (а значит, и поле рассеивания) на симметричные относительно номинала диапазоны, соответствующие диапазонам всех квалитетов точности до восьмого включительно (табл. 8.2). Определим по уравнению (8.2) вероятности попадания значений параметров в поле допусков указанных квалитетов точности и результаты занесем в таблицу 8.2. Изобразим по результатам расчетов на рис. 8.3 две ветви кривой вероятности P (X < X₀) попадания значений параметров, расположенных во все возрастающем поле допусков соответствующих квалитетов точности.

Значения P(X<X₀) и Ф(Х) для различных квалитетов точности

Если допустить, что все значения измеряемого параметра совпадают с его номинальным значением X₀, то суммарное качество этих значений равно 1 (по 0,5 с каждой стороны симметричного допуска). Назовем симметричной функцией потерь качества Ф(Х) разность между 0,5 и вероятностью P (Х - X₀), то есть:

Ф(Х) = 0,5 - P (Х - X₀)

1. Чем ближе случайные значение параметра Х к точке номинала X₀, тем к более высокому квалитету точности относится изготовленное изделие с этим значением параметра, а значит, тем выше его качество изготовления. Приближение значения параметра к границам максимального допуска соответствует его переходу во все более «грубые» квалитеты и, тем самым, снижает его точность и увеличивает потери качества изделий, изготовленных с этими квалитетами точности. Таким образом, потери качества заложены в самой структуре распределения параметра внутри допуска.
2.