Основы искусственных нейронных сетей

Искусственные нейронные сети чрезвычайн&# 22122c219w 1086; разнообразны по своим конфигурациям. Несмотря на такое разнообразие, сетевые парадигмы имеют много общего. В этой главе подобные вопросы затрагиваются для того, чтобы читатель был знаком с ними к тому моменту, когда позднее они снова встретятся в книге.

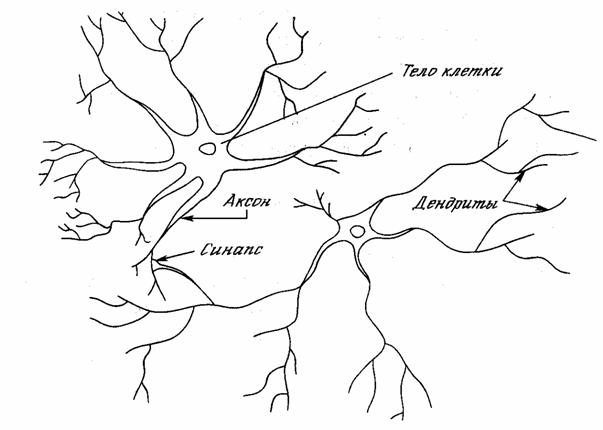
x x ., x_n, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w w w_n Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET.

NET = XW.

NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT.

OUT = K(NET),

OUT = 1, если NET > T, OUT = 0 в остальных случаях,

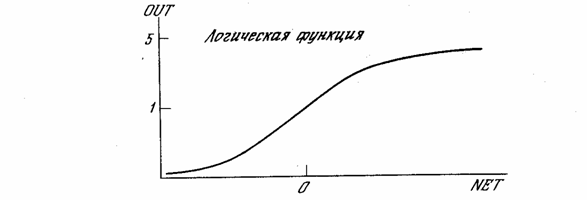
F, NET OUT. Если блок F сужает диапазон изменения величины NET NET OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция, показанная на рис. 1.4а. Эта функция математически выражается как F(x) ^x

.

OUT NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Гроссберг (1973) обнаружил, что подобная нелинейная характеристика решает поставленную им дилемму шумового насыщения. Каким образом одна и та же сеть может обрабатывать как слабые, так и сильные сигналы? Слабые сигналы нуждаются в большом сетевом усилении, чтобы дать пригодный к использованию выходной сигнал. Однако усилительные каскады с большими коэффициентами усиления могут привести к насыщению выхода шумами усилителей (случайн&# 22122c219w 1099;ми флуктуациями), которые присутствуют в любой физически реализованной сети. Сильные входные сигналы в свою очередь также будут приводить к насыщению усилительных каскадов, исключая возможность полезного использования выхода. Центральная область логистической функции, имеющая большой коэффициент усиления, решает проблему обработки слабых сигналов, в то время

OUT = th(x).

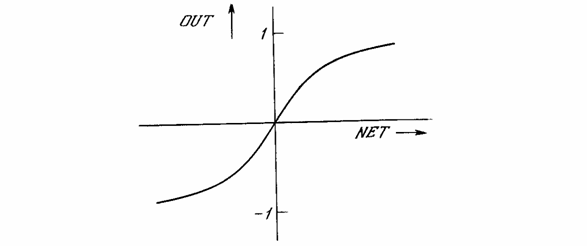
Подобно логистической функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET OUT

Несмотря на эти ограничения, сети, построенные из этих нейронов, обнаруживают свойства, сильно напоминающие биологическую систему. Только время и исследования смогут ответить на вопрос, являются ли подобные совпадения случайн&# 22122c219w 1099;ми или следствием того, что в модели верно схвачены важнейшие черты биологического нейрона.

W m n w N OUT нейронов, сводится к матричному умножению N = XW, где N и Х - векторы-строки.

(XW₁)W₂

X W W

Сеть обучается, чтобы для некоторого множества входов давать желаемое (или, по крайн&# 22122c219w 1077;й мере, сообразное с ним) множество выходов. Каждое такое входное (или выходное) множество рассматривается как вектор. Обучение осуществляется путем последовательного предъявления входных векторов с одновременной подстройкой весов в соответствии с определенной процедурой. В процессе обучения веса сети постепенно становятся такими, чтобы каждый входной вектор вырабатывал выходной вектор.

w_ij n+1) = w(n) + αOUT_i OUT_j,

w_ij(n) - i j w_ij(n+1) - значение веса от нейрона i к нейрону j OUT_i i j OUT_j j

Grossberg S. 1973. Contour enhancement, short-term memory, and consistencies in reverberating neural networks. Studies in Applied Mathematics 52:217,257.

Hebb D. 0. 1961. Organization of behavior. New York: Science Edition.

Kohonen T. 1984. Self-organization and associative memory. Series in Information Sciences, vol. 8. Berlin: Springer Verlag.

Rosenblatt F. 1962. Principles of neurodynamics. New York: Spartan Books. (Русский перевод: Розенблатт Ф. Принципы нейродинамики. - М.: Мир., 1965.)

Widrow В. 1959. Adaptive sampled-data systems, a statistical theory of adaptation. 1959 IRE WESCON Convention Record, part 4, pp. 88-91. New York: Institute of Radio Engineers.

Widrow В., Hoff М. 1960. Adaptive switching circuits. I960 IRE WESCON Convention Record, pp. 96-104. New York: Institute of Radio Engineers.