Решение задач на ЭВМ

Следу& 656v212g #1102;щий этап - определение способа решения задачи. Способ решения - это набор действий, позволяющих получить требуемое из исходного:

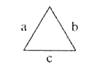
Дано: а, b, с - длины сторон.

S

a > 0, b > 0, с > 0,

a < b + c, b < a + c, c < a + b.

Для надежности программ такого рода ситуации (когда нет решений) должны быть преду& 656v212g #1089;мотрены в сценарии диалога. В этих случаях в сценарий необходимо включить сообщения с диагностикой причин отказов: отсутствие решений, недопустимость данных, некорректность команд, противоречивость фактов и т. п.

Программа

' площадь треугольника

сls

? «площадь треугольника»

? «длины сторон:»

a) input «a=»,a

(«b=», b) input «b=»,b

input «c=»,c

если не (а > 0 и b > 0 и с > 0) то if a<=0 or b<=0 or c<=0 then

инес не (а < b + с и b < а c elseif not (a < b and b < а + с

и с < а + b) то and с < а + b) then

else

+ b + с)/2  р = (а+b+с)/2

S := S = sqr (p*(p-a)*(p-b)*(p-c))

вывод («площадь=», S) ? «площадь=», S

end if

end

определение среднего арифметического последо­вательности из N чисел _N

Дано: N - количество чисел, среднее N чисел

x₁, х₂, .., х_N - числа,  <N>

s - среднее N чисел.  *

Где: s = (х , + х₂ +...+ х_N N <х₁>

При: N > 0.  2: <х₂>

N: <х_N>

S₀ <s>

S_k S_k-1 + х_k

[k N] недопустимо N

s = S_N / N

Обратите внимание: метод вычисления среднего N чисел здесь описан через подсчет суммы чисел. Правильность метода может быть проверена по отношению к требованиям постановки задачи.

cls

вывод («среднее N чисел») ? «среднее N чисел»

N) input «чисел=», N

S S = 0

если N <= 0 то if N <= 0 then

вывод («недопустимо N») ? «недопустимо N»

инеc N > 0 то elseif N > 0 then

от k = 1 до N цикл for k = 1 to N

(k, k,

(x) input x

S S x S S x

next k

s S/N s S/N

s) s

end if

end

определение самого легкого из учеников по данным из таблицы, содержащей N строк:

рост вес

Сценарий

(D₁, D_N) - Данные об учениках

D [Fam, R,V] - фамилия вес

Fam R - рост, V -вес

Fam_m <Fam₁> <V₁> *

m: V_m Min (V₁ V_N).   . .

При: N > 0.  <Fаm_N> <V_N>

самый легкий:

Min (V1,.. Vn): <Fam m > <Vm >

min = V₁

k

V_k < min dan:

min: = V_k data

data

Выбранному сценарию, методу решения и представлению дан­ных соответствуют следу& 656v212g #1102;щие алгоритм и программа на Бейсике.

cls

N: n = 0

do

(Fam, r, v) read fam, r, v

Fam if fam$ then exit do

(Fam, v) fam$, v, r

N:=N+1 n n+1

если N = 1 или V < Vmin if n=l or v < vmin then

Vmin: V  vmin v

Fmin: Fam  fmin$ fam$

end if

loop

(Fmin, Vmin) ? fmin$, vmin

end

задача способы

постановка методы

алгоритмы

ЭВМ программа

A_nxm:

<N> <M>

a₁₁ . a_1N)  < a₁₁> ... < a_1N >

Anxm

(a_Ml a_MN)  < a_Ml > . < a_MN >

(S₁ S_N) <S₁> <S_N>

S_i = а_i1 + ...+ а_iM

i = (1. N)]

При: N > 0, М > 0.

sk0 matr: Anm:

s_k1 a_k1 ⁺ s_k1-1 data

M)] data I,

S_k = S_kN data

[k = N)] data

data. В первом из этих операторов записаны размеры, а в каждом последу& 656v212g #1102;щем операторе - строки матрицы:

cls

read n, m

если п > 0 и т > 0 то if N > 0 and М > 0 then

dim A (N,M)

S[1:n] dim S(n)

gosub vvod

gosub sum

от k for k= 1 to n

(s[k]) s[k]

next k

end if

end

sum:

от k = 1 до N цикл for k to n

s k] s[k]

l for I to m

s k s k A[k,l s[k] s[k] a[k,l]

next I

next k

return

vvod:

вывод («Матрица», N, «х», М) m; m

от k = 1 до N цикл for k to n

I for l = 1 to m

(A [k,l]) read A (k,l)

(A [k,l]) A (k,l)

next

next k

return

_N

а) самого высокого ученика;

б) самого низкого ученика;

в) самого тяжелого ученика;