В экзаменационной работе используются три & 656c22g #1090;ипа заданий. Задание Части 1 (с выбором ответа) считается выполненным верно, если в «Бланке ответов» отмечена цифра, которой обозначен верный ответ. Верный ответ в заданиях Части 2 (с кратким ответом) – некоторое число. Такое задание считается выполненным верно, если в «Бланке ответов» записано именно это число. Проверка выполнения этих двух типов заданий осуществляется с помощью компьютера. За каждое верно выполненное задание выставляется 1 балл.

.

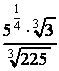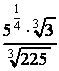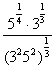= = = = 5 = 5= 5.

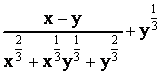, если = 27, у = 25.

== =

.

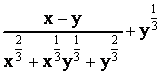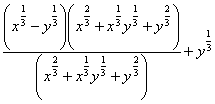= log log log log

.

= sinαsin cosαcos sinα cos ) – sinα = cosα sinα

.

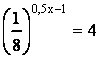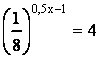. (2^-3)^0,5x x x

Номер ответа – 2).

;

Так как логарифмическая функция с основанием меньше 1 убывающая, то

x x >0). Отсюда x x < 4; . 

.

^{x – 3} – 1 ≥ 0.

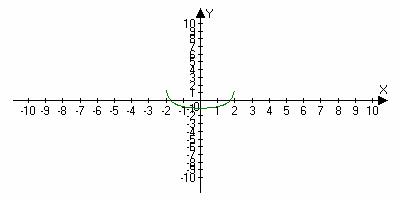
у = ( ) задана графиком на отрезке [– 4; 2]. Найдите область ее значений.

Область значений – это множество значений, которые принимает функция на данной области определения. Наименьшее значение функции – 2 при = -2, а наибольшее значение функции 1 при = 1. Область значений от у = -2 до = 1.

Укажите функцию, производная которой в точке а равна

А11. Найдите значение производной функции в точке .

.

F x f x F x f x F^’(x) = (2x + cosx)^’ = (2x)^’+ (cosx)^’ = 2 – sinx.

sin x cosx

p p

sin x cosx sinxcosx cosx 2cosx(sinx cosx sinx

= 2). У первого уравнения общий вид решения , а второе решения не имеет т.к. |sinx принадлежит промежутку [2π; 3 ] при n

= . Номер правильного ответа – 2)

f x x + x – x

f x) = (

равна нулю, то функция в этой точке имеет максимум, минимум или это точка .

x x x x x x x x x + )=0.

x x x

Если производная на промежутке больше нуля, то на этом промежутке функция возрастает, поэтому минимум функции будет в точке, где знак производной меняется с минуса на плюс. f^’= - x(x -1)(x+0,5)

f (x) + - + -

f x -0,5 0 1

Можно сделать вывод, что минимум функции при = 0 и значение функции в этой точке тоже равно нулю т.к. f(0) =

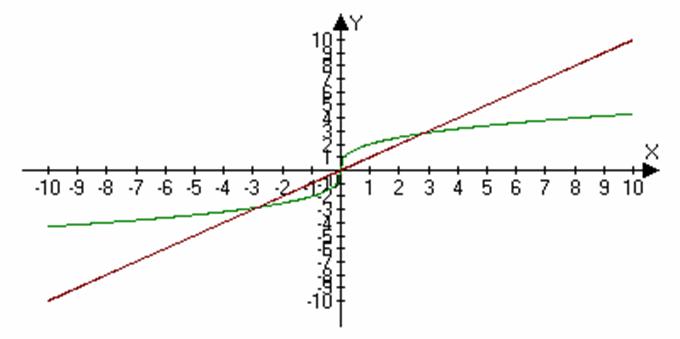
Вычислите площадь фигуры, расположенной в первой координатной четверти и ограниченной линиями y y x

Построим схематично графики заданных функций в одной системе координат. Вычислим абсциссы точек пересечения графиков этих функций:

Возведем обе части уравнения в куб x x x

x =

y y x , значит площадь фигуры будет находится по формуле =

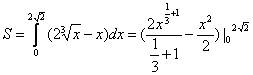Сколько решений имеет уравнение

cos x

cos x x = 0). Из первого получаем

x x x ≥ 0, а значит только такие, которые находятся в промежутке [-1; 1]. Это может быть при ,

. Можно выбрать только два . Значит корни уравнения будут следующие

Верный ответ будет 4 корня.

возрастает на всей числовой прямой?

f x a a

Пусть (x y ) – решение системы уравнений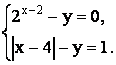

Найдите произведение x y

При ≥ 0 получаем систему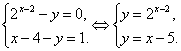

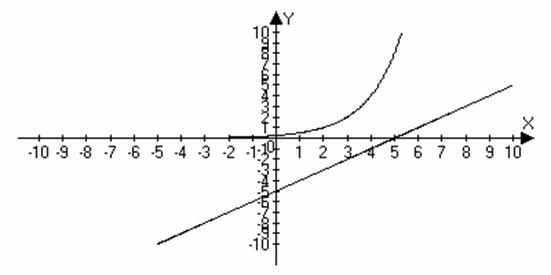
При < 0 получаем систему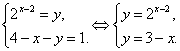

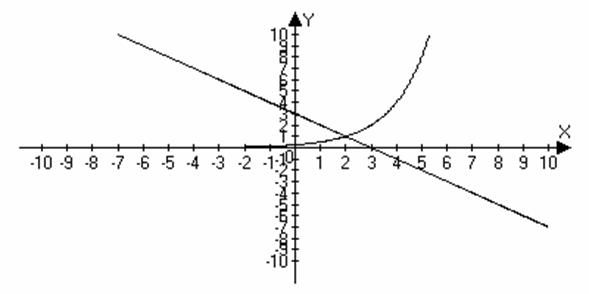
Из графика видно, что графики пересекаются при х₀ = 2, а значение у₀=2^2-2=

Значит Верный ответ равен 2.

Найдите значение выражения .

=

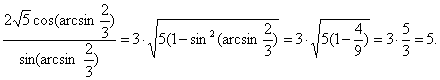
Найдите наименьшее значение функции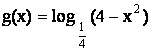

x >0 x x+2)<0 -2 < x < 2

g x

g x 2x x = 0. Значит в точке = 0 экстремум или это точка перегиба. Исследуем производную:

g (x) +

0

g x

Значит в точке = 0 функция принимает минимальное значение и значение

g log

A

R

x

L M

r

D O R

r

C B

r E y

D L E – точки касания вписанной окружности со сторонами треугольника. По свойству касательных к окружности AD AL BE BL CD CE. Значит AD BE AL LB AB AB R AD x BE y. Составим уравнении

x y

AC² + CB² = AB² ; CD = CE = r = 2. x y

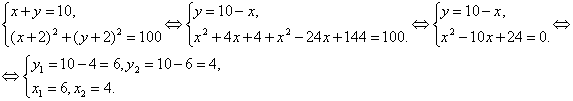
Значит площадь прямоугольного треугольника равна: .

В9. В прямоугольном параллелепипеде ABCDA B C D АВ = 6 м, ВС = 8 м,  м. Найдите площадь сечения параллелепипеда плоскостью, параллельной прямой АС и содержащей прямую .

D₁  C₁

x L 10-x

A₁ B₁

D C

A B

A C AC параллельна плоскости треугольника А₁ВС₁. В нём А₁С₁=АС ==10, ВС₁=

ВА₁=.

16,4² – х² = 296,96 -(10 – )², 268,96 –х² = 296,96 – 100 +20х – х², 20х =72, = 3,6.

BL

LB

С1. Найдите количество целых чисел, принадлежащих множеству значений

f x) = .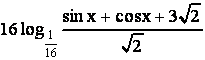

е и е.

Так как sinx cosx sin x ], а для всей дроби – это отрезок [2;4]. Так как функция является монотонно убывающей и непрерывной, то множество значений данной функции – это отрезок [16]. Вычислив значения логарифмов, получаем , что множеством значений функции f x) является отрезок [– 8; – 4]. Этому отрезку принадлежат ровно пять целых чисел: – 8; – 7; – 6; – 5; – 4.

Найдите наибольшее значение а, при котором уравнение

x x ax b с целыми коэффициентами имеет три & 656c22g #1088;азличных корня, один из которых равен – 2.

е и е.

Подставим = – 2 в левую часть уравнения.

–8 + 20 – 2а + b = 0 Þ b a

2) Так как = – 2 является корнем, то в левой части уравнения можно вынести общий множитель x + 2. Производим тождественные преобразования, выделяя общий множитель (x

x x ax b x x x ax a x x x x x ax

+ (2a – 12) = x²(x + 2) + 3x(x + 2) + (a – 6 x + 2) – 2(a – 6) + (2a – 12) =

= (x² + 3x + (a – 6))(x + 2).

D a a > 0  Þ a < 8,25.

Подставим а = 8 в исходное уравнение

x x ax b x x x + 4 = (x x + 2)( + 2) = ( + 1)( + 2)²

Тогда уравнение имеет только два различных корня. Подставим а = 7 в исходное уравнение

x x ax b x x x x x + 1)( + 2)

D = (–3)² – 4 = 5 > 0 . Эти корни – иррациональные, так как иррационален . Значит, у уравнения есть три различных корня.

Ответ: 7.

С3. При каком x I значение выражения

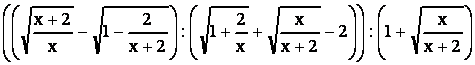
е и е.

После тождественных преобразований данного выражения, учитывая, что принимает только натуральные значения, получаем

= = = = =

= .

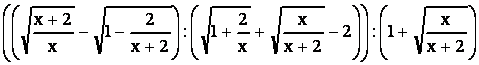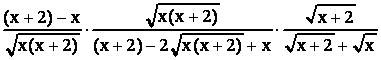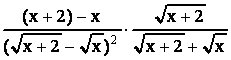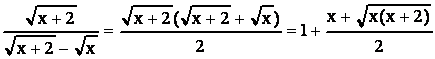Оценим подкоренное выражение x x + 2) сверху и снизу.

x < x x + 2) < (x

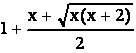1 + < < 1 +

Значит, исходное выражение больше, чем 1 + x и меньше, чем 1 + x + 0,5. Поэтому, при x = 72 значение этого выражения в интервале (73; 73,5).

При ³ 73 все значения этого выражения больше 74, а при x £ 71 все значения меньше 72,5.