Интерполяция многочленами

y(x), то это озна&# 23123g67x 1095;ает, что любому допустимому зна&# 23123g67x 1095;ению сопоставлено зна&# 23123g67x 1095;ение у. Но нередко оказывается, что нахождение этого зна&# 23123g67x 1095;ения очень трудоёмко. Например, у( ) может быть определено как решение сложной задачи, в которой играет роль параметра или у( ) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу зна&# 23123g67x 1095;ений функции, но прямое нахождение функции при большом числе зна&# 23123g67x 1095;ений аргумента будет практически невозможно. Функция у( ) может участвовать в каких-либо физико­-технических или чисто математических расчётах, где её приходится многократно вычислять. В этом случае выгодно заменить функцию у( ) приближённой формулой, то есть подобрать некоторую функцию j( ), которая близка в некотором смысле к у( ) и просто вычисляется. Затем при всех зна&# 23123g67x 1095;ениях аргумента полагают у( ) j( ).

Существуют 3 класса или группы функций, широко применяемых в численном анализе. Первая группа включает в себя линейные комбинации функций 1, , х², , хⁿ, что совпадает с классом всех многочленов степени n cos a_ix, sin a_ix. e^-az

Что касается критерия согласия, то классическим критерием согласия является «точное совпадение в узловых точках». Этот критерий имеет преимущество простоты теории и выполнения вычислений, но также неудобство из-за игнорирования шума (погрешности, возникающей при измерении или вычислении зна&# 23123g67x 1095;ений в узловых точках). Другой относительно хороший критерий - это «наименьшие квадраты». Он озна&# 23123g67x 1095;ает, что сумма квадратов отклонений в узловых точках должна быть наименьшей возможной или, другими словами, минимизирована. Этот критерий использует ошибочную информацию, чтобы получить некоторое сглаживание шума. Третий критерий связывается с именем Чебышева. Основная идея его состоит в том, чтобы уменьшить максимальное отклонение до минимума. Очевидно, возможны и другие критерии.

Цель задачи о приближении (интерполяции): данную функцию у( ) требуется приблизительно заменить некоторой функцией j( ), свойства которой нам известны так, чтобы отклонение в заданной области было наименьшим. интерполяционные формулы применяются, прежде всего, при замене графически заданной функции аналитической, а также для интерполяции в таблицах.

Один из подходов к задаче интерполяции - метод Лагранжа. Основная идея этого метода состоит в том, чтобы прежде всего найти многочлен, который принимает зна&# 23123g67x 1095;ение 1 в одной узловой точке и 0 во всех других. Легко видеть, сто функция

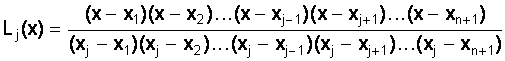
n x=x_j x=x_i, i j L_j(x) y_j принимает зна&# 23123g67x 1095;ения y_i i й узловой точке и равен 0 во всех других узлах. Из этого следует, что 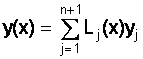есть многочлен степени n n+1 x_i, y_i).

Другой подход - метод Ньютона (метод разделённых разностей). Этот метод позволяет получить аппроксимирующие зна&# 23123g67x 1095;ения функции без построения в явном виде аппроксимирующего полинома. В результате получаем формулу для полинома P_n f(x)

P(x)=P(x₀)+(x-x₀)P(x₀,x₁)+(x-x₀)(x-x₁)P(x₀,x₁,x₂)+.+

(x-x₀)(x-x₁).(x-x_n)P(x₀,x₁,.,x_n)

-

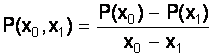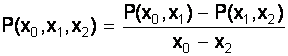- разделённая разность 2-го порядка и т.д.

P_n(x) в узлах совпадают со зна&# 23123g67x 1095;ениями f(x)

[a b] [x_i, x_i+1] с большой первой производной. Сплайновая интерполяция напоминает тем, что требует только зна&# 23123g67x 1095;ения в узлах, но не её производных.

n x_i=x+e_i (i=1, 2, ., n) e_i это ошибки (или шум) измерений, а - истинное зна&# 23123g67x 1095;ение. Метод наименьших квадратов утверждает, что наилучшее приближённое зна&# 23123g67x 1095;ение есть такое число, для которого минимальна сумма квадратов отклонений от

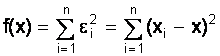
n x_i, y_i) (i=1, 2, ., n) m<n

y(x)=a₀+a₁x+a₂x²+.+a_mx^m

Вычисленная кривая у( ) в некотором смысле даёт сложное множество зна&# 23123g67x 1095;ений у_i. Метод наименьших квадратов утверждает, что следует выбирать многочлен, функцию.

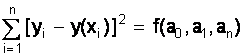
a_k

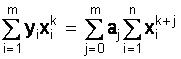
Определитель этой системы отличен от нуля и задача имеет единственное решение. Но система степеней не ортогональна, и при больших зна&# 23123g67x 1095;ениях n

T_n(x)=cos(n arccos(x))

T₀(x)=cos(0)=1,

T₁(x)=cos(q)=x,

T₂(x)=cos(2q)=cos²(q)-sin²(q)=2x

соотношение, связывающее T_n+1(x), T_n(x) T_n-1(x)

T_n+1(x)=cos(nq q)=cos(nq)cos(q)-sin(nq)sin(q

T_n-1(x)=cos(nq q)=cos(nq)cos(q)-sin(nq)sin(q

T_n+1(x)+T_n-1(x)=2cos(nq)cos(q)=2xT_n(x);

T_n+1(x)=2xT_n(x)-T_n-1(x).

(x)=2xT₂(x)-T₁(x). Подставляя зна&# 23123g67x 1095;ения T₂( ) и Т₁( ) имеем Т₃( )=2х(2х²-1)- =4х³-3х. Графически первые 10 полиномов Чебышева изображены ниже. Последующие полиномы по-прежнему колеблются между +1 и -1, причём период колебания уменьшаются с ростом порядка полинома.

q arccos(x) x_j многочленов T_n(x)

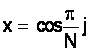, (j=0, 1, 2, .,N-1

T_n(x) cos(nq функциями, и так как они многочлены, то обладают всеми свойствами ортогональных многочленов.

Чебышев показал, что из всех многочленов Р_n(x) n старшим коэффициентом 1, у многочлена 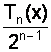точная верхняя грань абсолютных зна&# 23123g67x 1095;ений на интервале -1 x T_n(x)=1, óêàçàííàÿ

Ниже представлена таблица коэффициенты первых 12-и полиномов Чебышева, а также таблица коэффициентов перед полиномами Чебышева, выражающие первые 12 степеней .

I.   

a₀, a₁, ., a_n T(x) a_i

j=2, 3, ., n k=n, n-1, ., j

a_k-1=a_k-2-a_k

a_k=2a_k

P_n(x)

II. P_n(x) T_n(x)

P_n(x) - _i

j=n, n-1, ., 2 k=j, j+1, ., n в первом случае спускаясь, а во втором поднимаясь, проводим преобразование коэффициентов по следующим формулам:

a_k=a_k/2

a_k-2=a_k-2+a_k

ñ) a₀=2a₀

В результате получим коэффициенты полинома Т_n(x). Любопытно было бы узна&# 23123g67x 1090;ь, какую ошибку мы получаем при разложении степенной функции по полиномам Чебышева. Для этого, используя выше описанные алгоритмы, я сначала  представлял функцию y=xⁿ n T_n разложение снова превращал в многочлен. Выполнив эти операции, я получил достаточно интересные результаты. Для нечётных n x⁰ x⁰ y=x² y=x¹⁰ T₀ x .

y=sin x/3) . Для её написания был использован следующий алгоритм:

I. f(x)

n T_n(x) [a; b] f(x)

i=0, 1, ., n формируем сетку оптимальных зна&# 23123g67x 1095;ений аргумента в узлах чебышевской интерполяции:

.

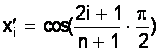Переводим [a; b]

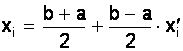и вычисляем f(x_i)

k=0, 1, ., n è i=0, 1, ., n

.

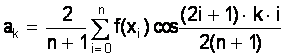a₀, a₁, ., a_n T( f(x)

II. Вычисление зна&# 23123g67x 1095;ений T(x)

a_k n+2 b_k b_n+2=0, b_n+1=0

Задаём зна&# 23123g67x 1095;ения x [a; b]

.

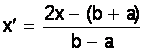k=n, n-1, ., 1 b_k=a_k-b_k+2+2xb_k+1

T()=a₀/2 - b₂ +xb₁

sin( x/3) график его приближения полиномами Чебышева и график, построенный с помощью разложения в ряд Тейлора, я получил очень точное совпадение. Визуально нельзя различить три кривых. Рассмотрим график ошибок. В соответствии с теорией ошибка Чебышева зна&# 23123g67x 1082;опеременна и распределена более или менее равномерно по всему интервалу. Ошибка же Тейлора небольшая около 0 и сильно увеличивается при приближении к 1 (заметим, что в этом и в других случаях ряд Тейлора содержит те же степени x ). Рассмотрим приближение на этом же интервале полиномом более высокой степени (T₁₁) , мы увидим, что приближение с помощью рядов Тейлора очень хорошее в середине интервала, но сильно отклоняется от эталона на концах. Сравним ошибки приближения и приближения с помощью рядов Тейлора. При этом сравнении ясно проявляются свойства полиномов Чебышева - максимальная ошибка меньше, чем при использовании ряда Тейлора.

степенного ряда может применяться для повседневного программирования.