Вероятность (probability)

Вероятност 313r175d ;ь (probability)

Теория вероятност 313r175d ;ей имеет большое значение для психологии, поскольку служит теорет. фундаментом стат., а последняя служит необходимым инструментарием для проведения эмпирических исслед.

Предположим, что событие Е может появиться в М случаях и не может - в N случаях. При условии, что случаи М и N являются равновозможными, вероятност 313r175d ;ь успеха (т. е. появления события Е) будет равна:

Вероятност 313r175d ;ь неуспеха (т. е. непоявления события) соответственно равна:

Отсюда:

и

q = 1 - p.

Теорема сложения. Вероятност 313r175d ;ь суммы двух несовместных событий равна сумме вероятност 313r175d ;ей этих событий:

Pr = Pr + Pr

Теорема умножения. Вероятност 313r175d ;ь произведения двух независимых событий равна произведению вероятност 313r175d ;ей этих событий:

Pr = Pr Pr

Выборка с возвращением и без возвращения

Два важных понятия - выборка с возвращением и выборка без возвращения. В ситуации выборки с возвращением возможност 313r175d ;и наступления всех событий ост 313r175d ;аются пост 313r175d ;оянными, так как никакой случай не происходит вслед за появлением любого предыдущего события. В ситуации выборки без возвращения появление определенного события исключает для него возможност 313r175d ;ь произойти вновь, поскольку данный случай не повторяется. Выборка с возвращением обычно допускает применение теорем сложения и умножения. При выборке без возвращения вероятност 313r175d ;ная картина существенно меняется и распределение вероятност 313r175d ;ей принимает форму и свойства гипергеометрического распределения. Его вероятност 313r175d ;и вычисляются по следующей формуле:

,

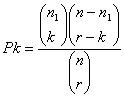где n - число элементов множества, п₁ - число элементов подмножества, k - численност 313r175d ;ь группы k, r - численност 313r175d ;ь группы r.

Распределения вероятност 313r175d ;ей

Встречающиеся в стат. распределения частот принято считать распределениями вероятност 313r175d ;ей, выражаемыми в общей форме как (р + q)ⁿ. Хотя распределение вероятност 313r175d ;ей является дискретным, оно сглаживается до приемлемо непрерывного распределения при увеличении п, т. е. когда п -> Если р = q = 1/2, то при п -> распределение вероятност 313r175d ;ей, как доказал Бернулли еще в начале XIX в., аппроксимируется нормальной кривой.

См. также Доверительные границы, Выборочное исследование, Статистика в психологии

П. Ф. Меренда