TOC \o "1-4" \h \z \u Uvod PAGEREF _Toc196560993 \h

Teoretična analiza PAGEREF _Toc196560994 \h

Delovanje rotorja vetrne turbine PAGEREF _Toc196560995 \h

Tokovna cev in pretvorba kinetične energije v mehansko PAGEREF _Toc196560996 \h

Betzova meja PAGEREF _Toc196560997 \h

Aerodinamika rotorja PAGEREF _Toc196560998 \h

Tip rotorja PAGEREF _Toc196560999 \h

Premer rotorja PAGEREF _Toc196561000 \h

Stevilo lopatic PAGEREF _Toc196561001 \h

Hitrostno stevilo PAGEREF _Toc196561002 \h

Aerodinamični profil lopatice PAGEREF _Toc196561003 \h

Bernoullijev zakon PAGEREF _Toc196561004 \h

Aerodinamika profila lopatice PAGEREF _Toc196561005 \h

Hitrostne razmere na lopatici PAGEREF _Toc196561006 \h

Geometrija lopatic rotorja PAGEREF _Toc196561007 \h

Pojav zračnega vrtinca PAGEREF _Toc196561008 \h

Teorija o ohranitvi gibalne količine PAGEREF _Toc196561009 \h

Teorija elementa lopatice PAGEREF _Toc196561010 \h

Teorija elementa in spremembe gibalne količine lopatice PAGEREF _Toc196561011 \h

Faktor izgube na konicah lopatic PAGEREF _Toc196561012 \h

Tokovne razmere PAGEREF _Toc196561013 \h

Karakteristika rotorja PAGEREF _Toc196561014 \h

Model rotorja vetrne turbine PAGEREF _Toc196561015 \h

Zasnova PAGEREF _Toc196561016 \h

Dimenzioniranje PAGEREF _Toc196561017 \h

Izbira profila PAGEREF _Toc196561018 \h

Optimalna geometrija PAGEREF _Toc196561019 \h

Linearizacija geometrije PAGEREF _Toc196561020 \h

Izvedba in opis PAGEREF _Toc196561021 \h

Preliminaren izračun moči PAGEREF _Toc196561022 \h

Numerična iteracija PAGEREF _Toc196561023 \h

Metoda 1 PAGEREF _Toc196561024 \h

Metoda 2 PAGEREF _Toc196561025 \h

Karakteristična krivulja PAGEREF _Toc196561026 \h

Primerjava PAGEREF _Toc196561027 \h

Zaključek PAGEREF _Toc196561028 \h

Viri: PAGEREF _Toc196561029 \h

Seznam uporabljenih simbolov

Uvod

Vetrne turbine sodijo v eno od pomembnih panog na področju obnovljivih virov energije. Raziskave, ki trenutno potekajo, so usmerjene k izboljsanju aerodinamike rotorjev in njihovih materialov. Tehnologije, ki so posledica razvoja, pričajo o visoki ravni napredka, kar se kaze v aplikaciji sodobnih materialov na izvedbe in stalnem visanju mej aerodinamičnih izkoristkov, predvsem v praksi. Cilj znanstvenih raziskav je v izrabi energije vetra na najučinkovitejsi mozni način ter s tem priblizevanje k teoretično podani meji. Omejitev je definirana z Betzovo mejo pri 59,3% in je podana za idealne pogoje natekanja zračnega toka na rotor v obliki homogenega diska.

Obseg raziskav je v svetu zelo razsirjen in pusča odprto ozko področje ekonomsko se upravičenih projektov. Stroski razvoja ne dopusčajo mnogo sprememb zasnov prototipa in ponovitev meritev karakteristik. S tem namenom je uvedeno računalnisko podprto modeliranje in analiza rotorjev. Ena od metod, ki dovoljuje tak pristop, je razvita posebej za rotorje vetrnih turbin in temelji na teoriji spremembe gibalne količine in elementa lopatice (BEM). Posebno trzno niso predstavljajo vetrne turbine manjsih moči, do 20kW. Izvedba modela je iz tega razloga zasnovana z namenom mnozične proizvodnje in tehnolosko nezahtevne izdelave končne izvedbe.

V nalogi je potrebno izvesti izračun matematičnega modela rotorja aksialne vetrne turbine. Smisel izračuna je v napovedi karakteristike za dano geometrijo rotorja v sirsem intervalu delovanja. Pri tem sta relevantna parametra aerodinamičnega izkoristka in hitrostnega stevila, ki popisujeta karakteristiko rotorja. Resitev problema je v fleksibilni metodi analize geometrije, glede na potrebe večkratnih ponovitev izračunov, ki jih pogojuje numerična metoda iteracijskega resevanja algoritmov. S tem namenom skusam skozi nalogo izvesti računalnisko podprto analizo rotorja, ki je primerna tudi za dimenzioniranje in optimizacijo aksialnih vetrnih turbin. Postopek temelji na teoriji spremembe gibalne količine in diferencialni analizi geometrije lopatic. Program se izvede v okolju MS Excel, v obliki tabelarično podanih parametrov. Vstopne podatke matematičnega modela se določi iz načrtovane moči, hitrostnega stevila in aerodinamičnih lastnosti profila lopatic. Vzporedno se izvede primerjava karakteristik z meritvenim modelom, čigar meritve karakteristike rotorja so bile predhodno izvedene v vetrovniku instituta KGH-Hidria Godovič. Geometrija in postavitev lopatic je identična matematičnemu modelu, za kar se izvedejo meritve geometrije na meritvenem modelu rotorja.

Teoretična analiza

Namen vetrnih turbin je v pridobivanju električne energije z izkorisčanjem energije premikajočih se zračnih mas, torej vetra. Iz strokovnega vidika gre za tehnično dovrseno izvedbo naprave, ki med delovanjem na najboljsi mozen način pretvarja različne oblike energij v univerzalno obliko. S spremembo gibalne količine zračnega toka, se pretvori kinetična energija zračnega toka v rotacijsko. Nato se preko različnih oblik mehanskih prenosov, ki so potrebni za delovanje naprave, pretvori s principom indukcije v električno energijo. Moč turbine je odvisna od neposrednega stika ali interakcije rotorja z zračnim tokom, zato ga označimo kot sredisče naprave. Med delovanjem se kinetična energija, ki jo ima veter zaradi hitrosti premikajočih se zračnih mas, pretvori v mehansko energijo. Pri procesu nastajajo zaradi načina izvedbe konstrukcije in fizikalnih principov izgube, ki jih je potrebno pri načrtovanju turbine upostevati. Delovanje vsakega sklopa naprave je popisano z enačbami, mehanskih in aerodinamičnih zakonitosti, kar je pogoj za optimalno delovanje naprave pri zelenih obratovalnih pogojih. Tako lahko določimo nazivno moč in ostale potrebne parametre za začetek dimenzioniranja rotorja naprave. Na začetku se osredotočimo na pretvorbo kinetične energije v obliki pridobljene moči s pomočjo enostavnega modela, s katerim lahko določimo vpliv okolice na delovanje rotorja in obratno. Velik vpliv na delovanje rotorja in posledično njegovo obliko, ima aerodinamika. Osnovne principe iz navedenih področij, obravnavamo v poglavju teoretične analize delovanja vetrne turbine.

Delovanje rotorja vetrne turbine

Tokovna cev in pretvorba kinetične energije v mehansko

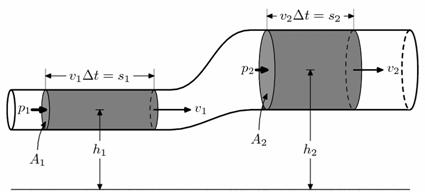
Za popis razmer na rotorju, ki se pojavljajo med delovanjem turbine, uporabimo model tokovne cevi (1.1). Z njeno pomočjo definiramo obnasanje rotorja, njegove lastnosti in določimo teoretično moč ali izkoristek vetrne turbine. Pri analizi predpostavimo, da ima tok skozi volumen majhno hitrost, zato je gostota zraka konstantna, tokovnice so homogene, med njimi ni upora zaradi trenja. Predvidimo tudi, da je statični tlak daleč za in pred rotorjem enak atmosferskemu. Oblika rotorja je idealna, poenostavljena z neskončnim stevilom lopatic in ni omejena na določen tip rotorja. Definirana je kot enotna ravnina, ki poganja turbino in je razlog za spremembo tlaka v cevi. Zanemarimo viskozni upor skozi lopatice ter zračni vrtinec, ki nastane za rotorjem.

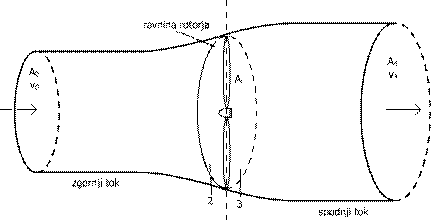
Slika 1.1

Tokovna cev je tako sestavljena iz ravnin, ki so pravokotne na zračni tok: A₀,A_r,A₄ in definirajo kontrolni volumen. Tukaj je moč spremljati parametre volumna, tlaka in hitrosti zraka za določen interval tokovne cevi. Energija, ki je na voljo se nahaja v odseku cevi med A₀ in A_r, ki jo imenujemo zgornji tok. Najdemo jo v obliki kinetične energije premikajoče se zračne mase (1.1).

(2 . )

Povezava s povrsino rotorja A_r, kamor nateka zračni tok na časovno enoto, nam poda moč vetrne turbine.

(2 . )

Iz enačbe je razvidno, da ima vpliv na moč turbine, njena povrsina rotorja, hitrost in gostota zračnega toka. Enačba velja za idealne pogoje opisane zgoraj. To je v primeru idealnega plina, ki ga poznamo za zrak, pri visokih temperaturah, ko ne vsebuje vlage. V povezavi z gostoto zraka, je parameter merodajen pri realnih pogojih, kot funkcija temperature in tlaka, kar izrazimo v enačbi (1.6). Iz plinske enačbe

(2 . )

in gostote zraka,

(2 . )

izpeljemo iz enačb (1.3) in (1.4) gostoto kot funkcijo temperature in tlaka:

(2 . )

Za izračun gostote zraka na predvideni lokaciji turbine, je potrebno poznati lokalne vrednosti za visino h in temperaturo T, kar vstavimo v enačbo (1.6):

(2 . )

Glede na argument eksponenta vidimo pomembno lastnost enačbe, da z visino in prav tako s temperaturo, vrednost gostote zraka pada. Izračun lokalne gostote zraka se uporablja v primeru večjih turbin, kjer vplivajo na samo gostoto zraka velike dimenzije rotorjev, kar je potrebno upostevati pri konstruiranju naprave. Navadno je zadovoljivo uporabiti vrednost za gostoto zraka pri 1.225 kg/m3

Pomembnejsi parameter s stalisča pridobivanja energije je hitrost. Celotna energija, ki je na voljo za opravljanje dela, je potemtakem funkcija hitrosti na tretjo potenco, enačba (1.2). V primeru spremembe hitrosti vetra za 5%, se pogonska energija poveča za 15% ali iz praktičnega vidika, pri enaki moči turbine, lahko zmanjsamo velikost rotorja za 15%. V praksi se pretvorba energije zmanjsa za več kot polovico, saj gre preostali del energije mimo rotorja. Pojav je značilen eksplicitno za vetrne turbine in ga definiramo z aerodinamičnim izkoristkom rotorja vetrne turbine ηp.

Betzova meja

Znano je, da se tokovnice ob ravnini, ki jo opisuje rotor, odklonijo zaradi same fizične ovire rotorja, kar je prikazano na sliki (1.1). Vpliv rotorja na zračni tok v tokovni cevi povzroči prekinitev tlaka. Hkrati se pretvori pri natekanju zraka na lopatice manj kinetične energije v mehansko delo, kot jo je sprva na voljo, kar izrazimo z teoretičnim aerodinamičnim izkoristkom rotorja turbine η_p. Pojav imenujemo Betzova meja in velja splosno za vse vrste vetrnih turbin. Izhaja iz razlike hitrosti pred in za ravnino rotorja, torej razlike gibalne količine.

Zrak ki se odkloni, ima zaradi ohranitve masnega toka, enačba (1.2), manjso hitrost kot zrak, ki potuje skozi ravnino rotorja A₀, zato se mu postopoma poveča volumen. Velja ohranitev masnega toka, ki ga zapisemo v primeru laminarnega toka z enačbo:

(2 . )

Sunek sile, ki deluje na rotor, je posledica spremembe gibalne količine, ki nastane zaradi natekajočega se zračnega toka.

(2 . )

z upostevanjem (1.7), zapisemo:

(2 . )

Gibalno količino lahko izrazimo tudi z razliko tlakov v zgornjem in spodnjem toku. Zapisemo Bernullijev zakon za dane pogoje ob upostevanju, da je p₀=p₄ in v₂=v₃.

(2 . )

(2 . )

Iz enačb (1.10) in (1.11) izrazimo p in dobimo:

(2 . )

Ob upostevanju, da je sila produkt tlaka in povrsine, lahko izrazimo sunek sile v aksialni smeri, t.i. normalni sili, ki deluje na rotor zaradi spremembe gibalne količine vetra (1.14):

(2 . )

Z uporabo enačb (1.8) in (1.14) vidimo, da je povprečna hitrost na lopaticah enaka:

Kljub natekajoči se relativno veliki hitrosti zračnega toka na rotor, je tam hitrost srednja vrednost hitrosti v zgornjem in spodnjem toku. Porazdelitev hitrosti in tlaka je podana v diagramu (), ki je nadaljevanje slike () in popisuje tlačne in hitrostne razmere v tokovni cevi. Zaradi ohranitve mase, se v blizini ravnine rotorja premer tokovnega polja poveča. Posledica je povečanje tlaka proti ravnini in nenaden padec na sami ravnini, kar prispeva k navoru vrtečega se rotorja.

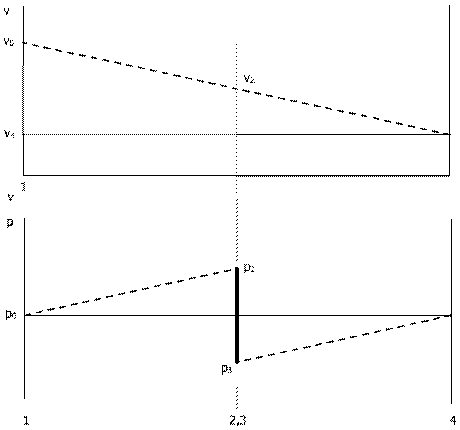
Diagram ()

Za nadaljnjo analizo uvedemo parameter aksialnega indukcijskega količnika, ki ponazarja stopnjo, s katero turbina v zgornjem delu zračnega toka zmanjsuje hitrost natekajočega se zračnega toka.

(1.17)

Iz enačb (1.16) in (1.17),

(1.18)

(1.19)

Po enačbah (),() in () lahko zapisemo sunek sile v obliki, ki vsebuje aksialne indukcijske kolčinikov:

(1.26)

In z upostevanjem enačb (1.5), (1.6), zapisemo:

Izrazimo hitrosti v₂ in v₄ z enačbama (1.18) in (1.19) in podamo teoretično moč vetrne turbine s parametri aksialnih količnikov:

(1.21)

Zadnja člena enačbe definirata aerodinamični izkoristek rotorja:

(1.22)

Izkoristek rotorja η_p je definiran kot del energije, ki jo absorbira vetrna turbina, glede na celotno razpolozljivo energijo v referenčnem volumnu tokovne cevi. Enačbo izenačimo z 0, odvajamo po a in dobimo ekstremno vrednost za največji aerodinamični izkoristek turbine imenovan Betzova meja, ki znasa 59,3%, enačba (1.23). Iz diagrama (1.2) je razvidno, da krivulja doseze svoj maksimum pri v₂/v₀=1/3:

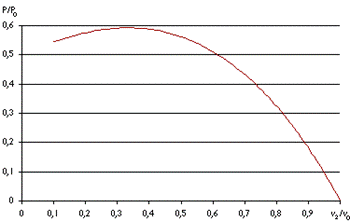
Diagram (1.2)

Betzova meja predstavlja karakteristiko ali kvaliteto vetrne turbine podane z aerodinamičnim izkoristkom moči pri pretvorbi kinetične energije zračnega toka. Teoretično velja maksimum pri 59,3% dovedene energije, kar je iz praktičnega vidika tezko dosegljivo, saj se količniki pri sodobnih turbinah v praksi, kljub optimalni obliki konstrukcije ter sodobnih materialih, gibljejo pri 44%. Vzrok lezi v dodatnih izgubah, ki nastajajo med obratovanjem in sicer:

viskoznost zraka na lopaticah, ki se s hitrostjo povečuje in predstavlja upor pri vrtenju

vrtinčenje zraka na obodu lopatic in rotacija toka v spodnjem delu cevi, ki ga povzroči vrtenje samega rotorja

končno stevilo lopatic

mehanske izgube pri prenosih obremenitev, ki se kazejo v segrevanju materiala

Aerodinamika rotorja

V poglavju so predstavljeni različni tipi rotorjev in njihove glavne značilnosti. Delitev je za lazjo predstavo prikazana v obliki diagrama. Poudarek je na aerodinamiki rotorja kot glavnem pogonskem elementu v interakciji z zračnim tokom. Definiran je pomen osnovnih gabaritov z relacijo med stevilom lopatic, močjo in vrtilnim momentom rotorja. Podane so primerjave različnih oblik rotorja in ovrednotene z vrednostmi izkoristka rotorja. Opisano je delovanje aerodinamično oblikovanih profilov lopatic, dopolnjeno s teorijo elementa lopatice, po kateri je definirana, s preračuni in iteracijami, končna oblika lopatice. Posledično je opisan postopek za izračun rotorja, za načrtovano turbino v podpoglavju o poteku snovanja rotorja.

Tipi vetrnih turbin

Obstaja več vrst turbin, ki jih delimo glede na njihove skupne lastnosti in so pogojene s tipom, postavitvijo rotorja ter načinom delovanja turbine, diagram (1.1). Za medsebojno argumentirano primerjavo je podana vrtilna frekvenca in aerodinamični izkoristek rotorja, ki sta merodajna parametra pri nadaljnji izbiri rotorja vetrne turbine.

a) Turbine z vertikalno osjo (VAWT) in horizontalno osjo (HAWT) vrtenja.

V splosnem je razlika v postavitvi gredi glede na smer vetra, kar prinese zaradi različnih izvedb postavitve in geometrije rotorja drugačno vrsto obremenitev na lopaticah in gredi. V primeru vertikalne osi se pojavi v podporah v navpični smeri aksialna obremenitev zaradi mase konstrukcije in vrtilne količine, ki nastopi med obratovanjem. Centrifugalna sila nastopi zaradi vrtenja mase samega rotorja. Pri tem se v lopaticah pojavi natezna napetost, ki je trdnostno manj kritična v primerjavi z upogibno napetostjo lopatic turbine s horizontalno osjo vrtenja. Ne prihaja tudi do utrujanja materiala zaradi vpliva gravitacije na vrtenje rotorja. V primeru horizontalne turbine je situacija drugačna, saj se utrujenost lopatic povečuje s hitrostjo in dimenzijami, se posebej pri vzgonskih tipih kjer so hitrosti velike in oblika lopatic trdnostno neugodna. Potrebno je tudi dodatno krmiljenje, ki ga je moč izvesti na več načinov. Namen je v ohranjanju optimalnega stevila vrtljajev, kar se posledično odraza v večjem izkoristku turbine, konstantni izhodni frekvenci električne napetosti in ohranjanjanju integritete konstrukcije. Pomanjkljivost je v potrebnem zagotavljanju dodatne funkcije naprave in s tem povezanih stroskov pri vzdrzevanju in proizvodnji. Druge prednosti so v ohranjanju konstantne velikosti navora, kar je pri vertikalnih tipih neizvedljivo zaradi simetrične oblike rotorja in s tem povezanim konstantnim gibanjem lopatic proti in stran od smeri vetra. Samozagon je običajna praksa za začetek delovanja HAWT turbine z indukcijskim generatorjem, pri vertikalnih tipih je za obratovanje potrebna dodatna energija.

b) Vzgonski in uporovni tip.

Vzgonski tip rotorja je v praksi znan po velikih obratovalnih hitrostih. Delovanje pogojuje dodatna vzgonska sila na lopaticah, zato je njegova hitrost na obodu nekajkrat večja od hitrosti samega vira. Največjo vrednost doseze tako tudi izkoristek moči turbine, ki se se najbolj pribliza teoretičnemu maksimumu. V primerjavi z uporovnim tipom je moč, ki jo proizvede turbina pri isti povrsini lopatic kar nekajkrat večja. Za uporovni tip veljajo nizje obratovalne hitrosti, saj obodna hitrost rotorja v večini primerov ne doseze hitrosti vetra. Z znatno večjim navorom in manjsim izkoristkom se uporablja  predvsem za črpane vode. Vzgonski tip z velikim izkoristkom in velikim stevilom vrtljajev pa za pridobivanje električne energije.

c) Rezimi obratovanja

Obstajata dva načina krmiljenja turbin z namenom doseganja maksimalnih vrednosti pridobljene količine energije povezane z aerodinamičnimi izkoristki in močmi, ki se relativno spreminjajo s hitrostjo vetra ter manjsanjem operativnih in vzdrzevalnih stroskov kot posledice manjsih obremenitev. Rezim s spremenljivo in stalno vrtilno frekvenco obratovanja. Prvi način vzdrzuje konstantno hitrostno stevilo, pri maksimalnem aerodianmičem izkoristku rotorja ne glede na hitrost vetra. Drugi način postopoma doseze svojo maksimalno vrednost za načrtovano točko obratovanja, je ne preseze ne glede na moč vetra ter ohranja maksimalno nazivno moč turbine. Ta način obratovanja ni racionalen razen za načrtovano hitrostno stevilo, saj turbine na splosno dosezejo največji izkoristek pri za njih načrtovani moči, ki je iz diagrama karakteristike turbine definiran v ekstremu parabole. Krmiljenje je moč izvesti mehansko, na lopaticah rotorja s spreminjanjem njihovega naklona, z zračnimi zavorami, z naklonom ene od osi rotorja ali v drugem primeru, z določitvijo zgornje meje vrtljajev s porusitvijo vzgona. Obratovalna hitrost je pomembna pri pretvorbi mehanske energije v električno. Električno omrezje deluje pri frekvenci 50Hz pri neposrednem vklopu, za kar je potrebno enakomerno vrtenje gredi generatorja, ki jo je potrebno krmiliti. Turbine večjih moči delujejo s stalno obratovalno hitrostjo zaradi enostavnejsega priklopa na omrezje saj je prav tu frekvenca na izhodu generatorja konstantna. Pri spremenljivi hitrosti obratovanja je krmiljenje potrebno do te mere, da se v vseh obratovalnih pogojih ohranja maksimalen izkoristek moči turbine, ob tem pa ne sme priti do porusitve konstrukcije. Sama električna napetost in frekvenca se krmili z asinhronskim generatorjem preko navora, ki navadno presezek odvaja preko toplotnih izgub. Prednosti tovrstnega obratovanja so v doseganju večjih izkoristkov zaradi večjih obodnih hitrostih, diagram (1.4). Manjse so tudi mehanske obremenitve na nosilno konstrukcijo, saj se rotor prosto vrti.

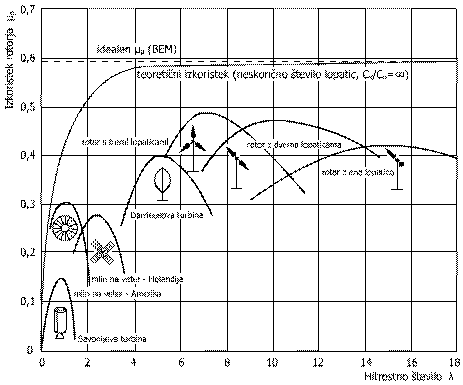
Diagram (1.4)

Iz navedenih lastnosti za posamezen tip rotorja je razvidno, da je glede na izkoristek turbine poznana optimalna oblika rotorja, ki proizvede maksimalno količino električne energije pri nazivni moči, t.j. rotor s profiliranimi lopaticami in horizontalno osjo vrtenja s spremenljivo hitrostjo obratovanja. Obstajajo tudi turbine s se večjim izkoristkom, z dvema rotorjema (dvostopenjske), pozicioniranima eden za drugim. Po teoretičnih izračunih se Betzova meja dvigne na 64%. Raziskave v tej smeri trenutno potekajo na Fakulteti za strojnistvo, laboratorij za vodne in turbinske stroje LVTS.

Premer rotorja

Kot prvo je potrebno podati dejstvo, da je premer rotorja povezan z močjo turbine in sicer proporcionalno s kvadratom povrsine rotorja. V praksi to pomeni, da v primeru podvojitve dolzine lopatic, lahko pričakujemo stirikrat več moči. Neomejen premer je na eni strani odvisen zgolj od lastnosti materiala, kar pogojuje njegova mehanska trdnost. Na drugi strani pa se porajajo argumenti proti neomejeni velikosti, saj se z velikostjo poveča masa rotorja, obremenitve se med obratovanjem povečajo in z navedenim tudi cena, ki je prav tako v kvadratni odvisnosti. Optimalno dimenzijo izbrano glede na omenjene omejitve podamo z enačbo za gostoto rotorja, podano z razmerjem povrsine vseh lopatic in povrsine rotorja.

(1.30)

Gostota rotorja je eden pomembnejsih parametrov pri določanju učinka rotorja in geometrije lopatic. Nanasa se na splosno obliko rotorja, tako za gabaritne mere, kot za samo obliko, kar je pojasnjeno v naslednjem poglavju. Turbine z majhno gostoto se izkazejo za bolj efektivne. S tem je pogojena večja vrtilna hitrost pri enaki relativni hitrosti vetra in manjsi vrtilni moment. Meja hitrosti vetra za zagon in vklop turbine se pri omenjeni lastnosti zvisa.

Stevilo lopatic

Največkrat vidimo v uporabi rotorje s tremi kraki, ki hkrati v splosnem simbolizirajo vetrne turbine. To ni tako nenavadno saj je njihova uporaba zaradi praktično teoretičnih lastnosti najpogostejsa. V nadaljevanju bomo videli, da je povezava hitrostnega stevila (λ) in stevila lopatic, funkcija moči in njenega izkoristka. Če se osredotočimo na samo stevilo lopatic, ugotovimo, da z večanjem stevila lopatic povečujemo izkoristek moči turbine, zato je največkrat izbrano stevilo lopatic za pridobivanje električne energije ne manj kot tri. Navedeno trditev je moč podkrepiti z enačbo (1.31), ki popisuje diagram (1.5) za različno stevilo lopatic.

(1.31)

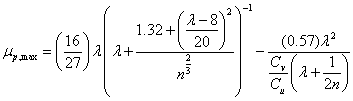
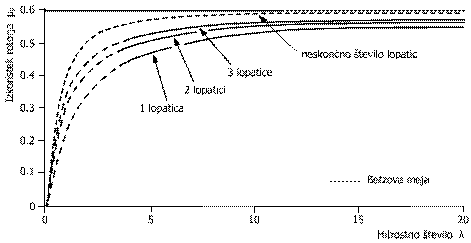
Diagram (1.5)

Maksimalna moč za optimalno obliko rotorja in s končnim stevilom lopatic, je leta 1976 izračunal Wilson. Zgornja enačba je veljavna za hitrostno stevilo od 4 do 20 (del neprekinjene krivulje), razmerje aerodinamičnih koeficientov od 25 do neskončno in stevilo lopatic od 1 do 3. Pomanjkljivost enačbe je v ne nedoslednem upostevanju razmerja aerodinamičnih koeficientov, bolj natančno aerodinamičnega upora. Vidimo, da povečevanje hitrosti rotorja na eni strani zvisuje izkoristek vendar na drugi strani ugotovimo, da se z večanjem stevila lopatic povečuje koeficient upora rotorja ter da prihaja do aerodinamičnih izgub na konicah lopatic. Zato primerjava po teoretičnih izračunih med dvo ali tro krakim rotorjem privede do minimalne razlike ob upostevanju optimalnih obratovalnih pogojev za večje vrednosti λ. Dejansko stanje, ki uposteva razmere aerodinamičnih koeficientov za primer rotorja s tremi kraki sledi v diagramu (1.6).

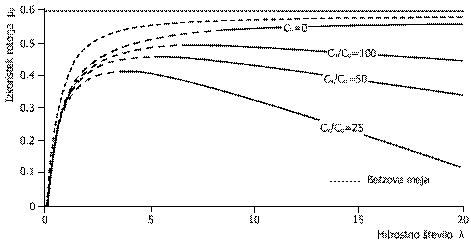
Diagram (1.6)

Po vsem tem je jasno, da pri snovanju rotorja izberemo aerodinamični profil z visokim razmerjem Cv, Cu. Obstaja tudi moznost za enostavnejsi način izbire pri določanju stevila lopatic v obliki tabele (1.1), s priporočenimi vrednostmi za različne vrednosti razmerij hitrosti konic.

Tabela (1.1)

V zaključku poglavja je v tabeli (1.2) podana primerjava optimalno oblikovanih rotorjev z različnim stevilom lopatic in ostalimi parametri, potrebnimi za določitev oblike.

Primerjava optimalnih oblik rotorjev, za različne izvedbe, pri enakih obratovalnih pogojih in parametrih, potrebnih za objektivno ovrednotenje določenih oblik, je podana v tabeli (1.2). Empirično definirane oblike rotorja so dane za različno stevil lopatic in razmerje hitrosti konic rotorja. Parametri, ki se pri tem spreminjajo, sirina lopatice c, radij rotorja R, kot zračnega toka φ, temeljijo na teoretično definiranih relacij (BEM), z upostevanjem izgub zaradi zračnega vrtinca.

Tabela (1.2)

Primer prve turbine z velikim stevilom lopatic, je rotor z nizko vrtilno hitrostjo in dvanajstimi lopaticami po obodu. Stolpec z razmerjem sirina/radij pokaze na obliko posamezne lopatice, ki je v tem primeru od srednjega dela proti obodu priblizno konstantne sirine in se proti korenu tanjsa. Lopatice imajo v tem primeru izrazitejso torzijsko obremenitev po dolzini v primerjavi z ostalima. Ostala rotorja z dvema ali tremi lopaticami, imata prav tako torzijsko obliko ukrivljenosti, vendar v veliko manjsi meri. Porazdelitev ukrivljenosti je zgolj funkcija razmerja hitrosti konic lopatic, zato je najhitreje vrteč se rotor, najmanj ukrivljen. Tako so lopatice rotorja z dvema krakoma tudi glede povprečne sirine najtanjse, saj je vpadni kot relativne hitrosti zračnega toka majhen in nateka na samo dve lopatici. Splosna oblika hitro vrtečih se rotorjev je ravno nasprotna kot pri počasnih. Koren lopatice je sirok in se ozi proti konici, kar kaze na trapezasto obliko.

Hitrostno stevilo

Je parameter, ki je prisoten v večini enačb potrebnih za konstrukciji rotorja, kar kaze na njegovo relevantnost. V praksi je oblika rotorja izvedena s pomanjkljivostmi, saj je daleč od optimalno teoretično definirane oblike. Ze sama poenostavitev s končnim stevilom lopatic po definiciji Betzove meje nas pripelje v praksi do omejitve, ki jo izvedemo z izvedbo rotorja s končnim stevilom lopatic. Zajemanje energije je odvisno od relativne hitrosti natekajočega se zraka na rotor in hitrostnega stevila, ki je funkcija oblike rotorja. Pri istem stevilu lopatic analizirajmo dva načina obratovanja. Za prvi primer določimo, da se rotor turbine vrti zelo počasi ter, da je hitrost natekajočega se vetra zelo velika. Pri teh pogojih gre del zračnega toka mimo lopatic, kar ima za posledico del neizkorisčene energije. Podobno nastane problem pri prehitro vrtečem se rotorju. Del zračnega toka se zaradi turbulence, ki jo ustvarja rotor in zračnega vrtinca za lopaticami odkloni, kar privede do izgub. Relacija oblike rotorja in natekanja vetra, je zato popisana z razmerjem hitrosti konic lopatic in hitrosti zračnega toka vetra, torej s hitrostnim stevilom λ.

(1.32)

Glede na navedeno dejstvo, obstaja optimalno razmerje za dan rotor, pri katerem je aerodinamični izkoristek maksimalen. Zapisemo enačbo za aerodinamičen izkoristek rotorja po (1.2),

(1.33)

saj je:

(1.34)

Sedaj lahko izrazimo hitrostno stevilo z razmerjem izkoristkov moči in navora, da določimo optimalno hitrostno stevilo.

(1.35)

Tabela () predstavlja pregled veličin za maksimalne vrednosti μ_p, kot funkcijo hitrostnega stevila λ, za ustrezne vrednosti aksialnih indukcijskih količnikov na konicah lopatic.

Tabela ()

Rezultat tabele za primer praktičnega rotorja iz tabele, priča o delovanju rotorjev v splosnem. Ugotovimo, večje kot je hitrostno stevilo, večji je aerodinamični izkoristek, kar sovpada z teoriji o ohranitvi gibalne količine in Betzovo mejo.

Aerodinamični profil lopatice

Bernoullijev zakon

Obnasanje aerodinamičnih teles v tekočini je odvisno od vpliva hitrosti in tlaka tekočine na telo, zato je potrebno predstaviti fizikalni zakon, omenjenega v prvem poglavju, ki nastopa pri pretvorbi kinetične energije v mehansko, t.i. Bernuollijev zakon ali zakon o ohranitvi energije. Gre tudi za relacijo rotorja, hitrosti in tlaka tekočine v opazovanem volumnu tokovne cevi. Definicija Bernuollijeve enačbe se glasi, da je vsota vseh energij v vsakem prerezu tokovne cevi za stacionarni tok idealnega nestisljivega fluida konstantna, slika (1.3). Enačba (1.39) popisuje razmere v tokovni cevi za nestisljiv plin ter velja pri določenih pogojih. Tok tekočine je homogen, za Re < 1000. Je nestisljiv kar pomeni, da je gostota konstantna. Zanemari se tudi viskoznost tekočine, kar priča da velja v navedeni obliki za idealne pogoje.

(1.39)

Za opazovani povrsini iz slike (1.3), sledi enačba (1.40):

(1.40)

Slika (1.3)

Z večanjem hitrosti tekočine se sočasno zmanjsuje tlak. Navedba je kontradiktorna s stalisča splosnega opazanja pojava. Primer za to je delovanje vetrnice, ki deluje na principu upora vetra, v tokovnem stanju mlina na veter. Vrtenje rotorja nastane zaradi večjega tlaka na lopaticah, relativno s hitrostjo vetra. Večja kot je hitrost, večji je tlak in s tem povezan upor rotorja, kar je tudi pravilna ugotovitev. Ta stavek je tukaj kar tako in je vzet iz konteksta. Vendar se zakon ne nanasa na hitrost zraka pravokotno na povrsino telesa, kot v danem primeru, ampak na hitrost, ki obteka povrsino telesa. Temu primerno so tudi oblikovane lopatice. Izkaze se pomembna lastnost aerodinamično oblikovanih lopatic rotorja in sicer pojav podtlaka in nadtlaka na povrsini lopatice.

Aerodinamika profila lopatice

Aerodinamično oblikovane lopatice imajo mnogo prednosti pri snovanju vetrnih turbin namenjenih za pridobivanje električne energije. Njihova uporaba je kljub drazji izvedbi smotrna, na kar kazejo teoretične analize in praktične izkusnje po podatkih navedenih v diagramu (1.4), kar kaze na njihovo rentabilnost. Dodatne negativne lastnosti so zahtevnejse vzdrzevanje, krmiljenje, konstruiranje ter izdelava, v primerjavi z uporovnimi tipi. Obstaja tudi srednja pot, ki zmanjsa proizvodnje stroske izdelave rotorja in hkrati omogoča masivno proizvodnjo. Resitev je v enostavnejsem aerodinamičnem profilu, ki je trdnostno manj odporen, posledično omejen na moči velikosti manjsih turbin in doseze slabsi aerodinamični izkoristek. Profil ima obliko ukrivljene plosče, z oznako GOE 417A, kar omogoča enostavno proizvodnjo lopatic.

Kako pomemben faktor dimenzioniranja rotorja je aerodinamika, nam priča dejstvo, da je geometrija lopatic, dolzina, sirina in nenazadnje moč turbine, pogojena z aerodinamičnimi lastnostmi profilov. Navadno je oblika lopatice tipa HAVT aerodinamične oblike, ki spominja na krilo sodobnega jadralnega letala. Ne gre za naključje, saj gre za identičen princip delovanja, s pomočjo vzgonske sile, ki je posledica Bernuollijevega zakona. Tako kot krilo ima lopatica v prerezu, slika (1.4), sprednji del odebeljen (A), na koncu pa se zozi (B), pri tem je zgornji del močneje ukrivljen, v primerjavi s spodnjim. V točki A se plast zraka, ki nateka na profil v t.i zastojni točki loči na zgornji in spodnji del, nato potuje ob konturi profila in na koncu profila zopet zdruzi v točki B. Med tem opravi zaradi različne ukrivljenosti profila ali spremembe naklona profila, bolj natančno različnih dolzin poti in posledično spremembe tlaka, zgornja plast zraka daljso pot. Pri tem se hitrost zraka zaradi ohranitve mase poveča. Kot smo ze omenili, z relacijo tlaka in hitrosti po Bernuolliju, nastopi padec tlaka na zgornji strani profila in povisanje na spodnji, kar privede do tendence premikanja lopatice v x smeri, glede na zračni tok, paradoksalno torej proti smeri vetra.

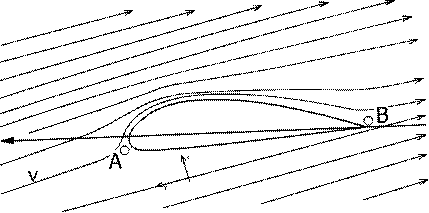
Slika (1.4)

Tlačne razmere na profilu ponazorimo z dvema silama in momentom za statično določen element profila lopatice, slika (1.5). Rezultanta sil je sestevek trikotnika sil F_u in F_v. Sila upora je definirana kot vektor F_u, ki je vzporeden s tokovnicami zraka in je pravokoten na smer vzgonske sile. Njena velikost je zazeleno čim manjsa. S tem dosezemo večjo vrednost rezultante, ki opravlja koristno delo v smeri vrtenja. Relacija z vzgonsko silo je podana z razmerjem brezdimenzijskih aerodinamičnih koeficientov.

(1.40)

kar je za idealen primer, kjer silo upora zanemarimo enako 0. Vzgonska sila ima glede na navedene argumente lastnost koristne sile in je definirana pravokotno na smer tokovnic zraka. Zadnja veličina, ki vpliva na delovanje lopatice je moment M_ac. Definiran je kot moment aerodinamičnega centra lopatice in je podan relativno na določeno točko na tetivi profila, pri c/4 od začetka odebeljenega dela profila. Pomemben je pri načrtovanju trdnosti lopatic ter turbinah krmiljenih s spremenljivim nagibom lopatic.

Slika (1.5)

Matematična definicija sil in momenta, ki delujejo na profil v zračnem toku:

(1.41)

Veličine so odvisne od kinetičnega tlaka, tlorisne povrsine profila in brezdimenzijskega količnika. Z drugimi besedami vpliva na velikost in smer posameznih komponent oblika konture, vpadni kot tokovnic in relativna hitrosti vetra. Primer debelejsih profilov z manjso ukrivljenostjo, ima v sami osnovi hidromehanike teles, pričakovano večji delez upora in manjsi delez vzgona. Torej imajo pri konstrukciji vetrne turbine za njen aerodinamični izkoristek rotorja poglavitni vpliv geometrijski parametri profila. Geometrija profila je definirana z radijem začetnega odebeljenega roba, srednjo linijo komor, največjo odebeljenostjo, porazdeljenostjo debeline in kotom izhodnega robu. Količnike, ki definirajo karakteristike profilov, se določi z meritvami ali izračuna, za vsako izpeljanko aerodinamičnega profila posebej in veljajo pri določenem Reynoldsovem stevilu.

(1.42)

Podatke za določeno obliko je moč najti v bazi profilov univerze UIUC, na spletni strani katalogov aerodinamičnih profilov^[5] ali z numeričnimi izračuni računalniskih programov, kjer je moč določiti optimalno obliko profila. Simetrični profili podobnih oblik imajo v idealih pogojih podobne teoretične aerodinamične količnike, ne glede na velikost. Iz tega sledi ugotovitev, da se s spremembo naklona telesa z znano obliko spremeni absolutna geometrija telesa glede na tokovnice. Aerodinamični koeficienti se spreminjajo ne samo zaradi same oblike ampak tudi zaradi naklona lopatice. Vrednosti koeficientov so z narasčanjem vpadnega kota tokovnic do ekstremne vrednosti v linearni odvisnosti, za tem se razmere spremenijo, nastopi prevoj, diagram (1.7). Obnasanje je splosno za linijska telesa z aerodinamičnim profilom.

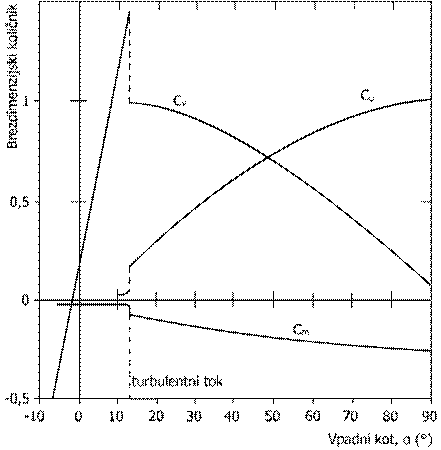
Diagram (1.7)

Zrak obteka profil pri vpadnem kotu α, ki je definiran s smerjo zračnega toka in tetivo profila. Vpadni kot je funkcija porazdelitve tlaka na aerodinamičnem profilu kar je v neposredni relaciji z vzgonskim količnikom, diagram (1.7). Z njegovo spremembo, torej naklonom lopatice, določimo izhodne vrednosti rotorja. Pri vrednosti α=0° imamo na zgornji in spodnji strani profila laminaren tok, do točke na odebeljenem delu, kjer preide v turbulentno stanje. Laminaren tok se ohrani do konca profila, zato ne prihaja do vrtinčenja zraka na samem profilu. Z večanjem naklona pri α=6° se mejna plast turbulentnega stanja odlepi in nastopi vrtinčenje zraka, na ozjem delu profila, kar je vzrok za večji upor lopatice. Iz diagrama razberemo, da nastane pri vrednosti α=13° nenadna sprememba aerodinamičnih lastnosti, količnikov. Mejna plast se odlepi čisto na začetku odebeljenega dela profila, kar povzroči porusitev vzgona (stall). Na zgornjem delu profila nastane čisti turbulentni tok in posledično zaustavitev rotorja. Porusitev vzgona je eden od načinov krmiljenja turbine. Maksimalno obratovalno hitrost turbine določimo pri načrtovani hitrosti vetra in preprečimo nastanek deformacij ali celo porusitve konstrukcije. Pri spremembi vpadnega kota, ki ga povzroči povečanje hitrosti zračnega toka v soodvisnosti s tangencialno komponento, se vzgonski količnik linearno povečuje, do maksimalne vrednosti C_vmax, ki jo doseze pri kritičnem vpadnem kotu α_kr. Pri nadaljnjem večanju nastopi padec vzgona, porast upora in popolna zaustavitev sistema.

Z uporabo komornega profila, pri majhnih naklonih vpadnega kota lopatice, dosezemo optimalne pogoje delovanja. Značilnost komornega profila je, da ima pri α=0° aerodinamični koeficient vzgona vrednost večjo od nič, kar je za popolnoma čelno dotekanje zraka po pričakovanjih nemogoče. Povečanje naklona, posledično vzgona povzroči hkratno zmanjsanje upora. Obnasanje velja v intervalu velikem za nekaj stopinj, pri α=0° in se z blizanjem proti α_kr vrne v normalno stanje, ki je skupno vsem aerodinamično oblikovanimi telesom. Prednost v primerjavi s simetričnim profilom je v zagonu pri nizkih hitrostih vetra in večjem navoru pri omenjenih pogojih. Zato najraje uporabljamo to vrsten tip aerodinamičnih profilov, ki po klasifikaciji NACA spada v serijo 4 mestnih profilov.

Hitrostne razmere na lopatici

Pomen vpadnega kota smo sedaj pojasnili, vendar pride njegova vloga do izraza v relaciji z vektorjem relativne hitrosti zraka, ki definira gonilno silo rotorja ter posledično vrtilni navor. Podamo tetivo profila, ki je definirana s samo geometrijo profila, kot referenca profila. Drugi parameter, ki določa postavitev lopatice glede na smer vetra je relativna hitrost vetra. Definicija zahteva natančnejso analizo hitrostnih razmer na lopatici, njegovih komponent ter ostalih geometrijskih parametrov, ki so relevantni za optimalno delovanje rotorja za kar upostevamo razmere iz slike (1.7). Smer tokovnic na profil definiramo z vektorjem relativne hitrosti vetra, ki je sestavljen iz vsote aksialne in tangencialne komponente. Aksialna hitrost je posledica pravokotnega natekanja zračnega toka na ravnino rotorja enačba (1.18) medtem, ko za prisotnost tangencialnega dela odgovarja vrtenje rotorja in zračnega vrtinca v nasprotni smeri na izstopu rotorja. Tangencialna hitrost je podana z vsoto kotne hitrosti rotorja in srednjo vrednostjo kotne hitrosti zračnega vrtinca, poglavje 1.2.6:

(1.44)

Lopatico prerezemo na razdalji r in opazujemo razmere na samem elementu profila. V tezisču profila določimo referenčno točko in postavimo vektorje hitrosti v aksialni in tangencialni smeri slika (1.7). Podamo kote, ki nastopajo v relaciji tetive profila z okolico in z vektorsko vsoto določimo za dan element rezultanto relativne hitrosti vrel. Vpadni kot je označen z α, naklonski kot prereza z β in kot zračnega toka φ.

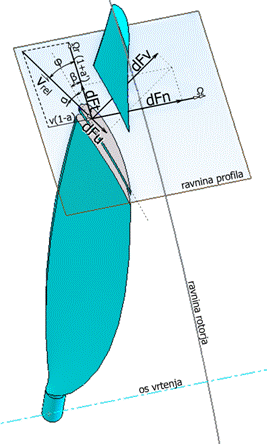
Slika (1.7)

Definiramo relativno hitrost kot rezultanto delujočih hitrosti na posamezen element:

(1.45)

Iz geometrije na sliki in ob uporabi kotnih funkcij zapisemo enačbi za relacije med relativno hitrostjo in absolutnima.

(1.46)

(1.47)

(1.48)

In se, da je vsota vpadnega kota in naklonskega kota prereza enaka kotu relativne hitrosti:

(1.49)

Geometrija lopatic rotorja

Oblikovanje lopatic ima v fazi dimenzioniranja rotorja dve funkcionalno neizbezni, nasprotujoči si zahtevi. Na eni strani je potrebno določiti konturo, ki bo s svojim obratovanjem zagotovila maksimalno količino električne energije na letni ravni. Na drugi strani je ta ista oblika potrebna za regulacijo turbin krmiljenih s porusitvijo vzgona, kar je izključno pogojeno z geometrijo lopatic. Pridobljeno delo se v tem primeru občutno zmanjsa. Segment načrtovanja je iz teh razlogov zahteven. Sestavljen je iz aerodinamičnega dela, ki pokriva geometrijski del (tip, dolzino profila, porazdelitev torzije in debeline) in mehanskega dela (izbira materiala, izvedba polnila). Da bi dosegli optimalno obliko, ki bi bila zadovoljiva tako s stalisča trdnosti kot aerodinamike, je potrebno vzeti v precep lastnosti iz obeh panog in jih racionalno uporabiti v obliki kompromisa. Poglaviten kriterij, ki vpliva na načrtovanje je način obratovanja turbine in sicer s stalno ali spremenljivo frekvenco vrtenja. Načrtovanje je potrebno za vsako turbino posamezno in je edinstveno za vsak primer posebej.

Tendenca v aerodinamični domeni je k obliki profila s tanjso debelino zaradi manjse občutljivosti na hrapavost v povezavi s čim nizjimi vrednostmi upora. Zaradi trdnosti lopatice je aerodinamični profil ob korenu odebeljen, kar radikalno ne spremeni aerodinamičnih lastnost in doprinosa energije na letni ravni. Pomemben aspekt je načrtovanje oblike lopatice pri turbinah krmiljenih s stalno hitrostjo obratovanja torej turbinah krmiljenih s porusitvijo vzgona. Profil korena lopatice je v tem primeru celo okrogle oblike tudi zaradi kasnejsih dodatnih nastavitev naklona lopatic za praktično ujemanje obratovalnih parametrov z načrtovanimi. Dobro oblikovane lopatice imajo načrtovano porusitev vzgona pri visanju hitrosti postopoma. Prehoden efekt, ki predstavlja izgube pri pojavu dinamičnega zastoja zaradi turbulentnega obnasanja zračnega toka, naj bi bil čim manjsi ali celo ničen. Natančnejsi potek snovanja oblike lopatice sledi v teoriji elementa lopatice.

Problem oblike pri vrtenju rotorja z aerodinamično oblikovanimi lopaticami je v spreminjanju obodne hitrosti z radijem. To pomeni, da bi v primeru konstantnega naklona lopatice po celotni dolzini, prihajalo proti korenu lopatice do čedalje večjih aerodinamičnih izgub, saj je obodna hitrost tam najmanjsa, vpadni kot pa je glede na vektorsko vsoto hitrosti premajhen za normalno delovanje. S tem je večina dela lopatice v neprimerni legi glede na smer relativne hitrosti vetra. Optimalno aerodinamično obliko lopatice, torej naklon okoli njene dolzinske osi, določimo glede na oddaljenost opazovanega prereza od glavne vrtilne osi in naklonskim kotom β glede na relativno hitrost vetra. Na sliki (1.6) je prikazana optimalna oblika lopatice v narisnem pogledu, poleg desno, je prerez lopatice v srednji in skrajnih legah. Moč je opaziti spreminjajoč se naklonski kot β, ki je ob konici lopatice enak 0, kar definiramo z vsoto kotov torzije prereza β_t in naklonom lopatice β₀.

(1.43)

Pomembno za torzijo lopatice je, da ohranimo konstanten vpadni kot zračnega toka α po celotni dolzini, kar pogojuje optimalni geometriji lopatice. Kot ze rečeno se z manjsanjem radia zmanjsuje obodna hitrost, kar se kaze v spreminjanju velikosti tangencialne komponente v_t, ki pojema proti korenu lopatice. Z vektorsko vsoto se posledično pri konstantni aksialni hitrosti 2/3 v_a, po enačbi (1.18) za a=1/3, zmanjsa vrednost relativne hitrosti v_rel in poveča njen tangens kota, iz slike (1.7).

(1.43)

Kot relativne hitrosti se zato spreminja in veča s smerjo relativne hitrosti in je vsota kotov rezultante relativne hitrosti vetra φ ter vpadnega kota α. Če sledimo s tetivo profila smeri relativne hitrosti, nastane geometrijska oblika spirale ali torzije lopatice.

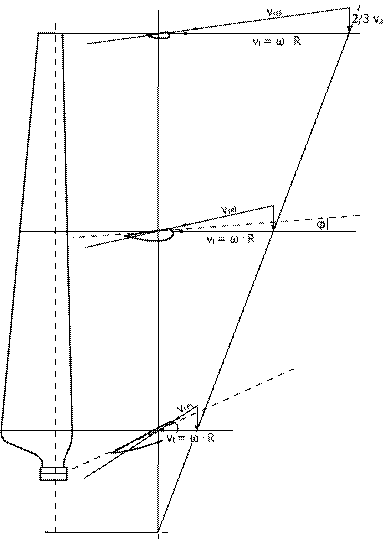
Slika (1.6)

Geometrija lopatice je definirana posebej za rezim obratovanja turbine s stalno ali spremenljivo hitrostjo delovanja rotorja. V nasem primeru se bomo osredotočili na tip s stalno rotacijsko hitrostjo, ki velja za optimalnega le pri nazivnem hitrostnem stevilu λ.

Pojav zračnega vrtinca

Zračni vrtinec, ki se pojavi za rotorjem nastane iz znanega fizikalnega dejstva, osnovnih zakoni kinetike (Newtonovi zakoni), da akcija sile na telo povzroči reakcijsko silo z enako velikostjo, v nasprotni smeri. Opisana situacija se dogaja v primeru vrtečega se rotorja, ki preko vrtilnega momenta gredi rotorja, ki ga povzroča magnetno polje generatorja na lopaticah, povzroča upiranje zračnemu toku, kar se kaze v manjsem izkoristku turbine. Posledica reakcije je zračni vrtinec, ki nastane pri prehodu skozi rotor in ima nekoristno smer rotacije nasprotno od rotacije rotorja. Pretvorba rotacije iz zračnega toka poteka izključno po sirini rotorja. Komponenta hitrosti vrtinca se razdeli v aksialno in tangencialno smer, vendar je tangencialni del tisti, ki nasprotuje vrtenju turbine in manjsa delez koristne kinetične energije. Sprememba tangencialnega dela hitrosti je popisana v obliki ze omenjenega tangencialnega indukcijskega količnika enačba (1.24), ki smo jo izpeljali iz zakona o ohranitvi gibalne količine.

Slika (1.2)

Kot lahko razberemo iz slike (1.2) je hitrost v zgornjem toku, tik pred vstopom v rotor, točka 2, slika (1.1), enaka 0. Takoj po izstopu, točka 3, ima tangencialna hitrost vrednost 2Ωra'= ωr ter na sredini, srednjo vrednost obeh skrajnih Ωra'. Trikotnik vsote vektorjev hitrosti se proti izstopu povečuje. Z radiem pa se spreminja tudi tangencialni indukcijski količnik, kar je upostevano na koncu poglavja o Betzovi meji.

Teorija o ohranitvi gibalne količine

Do sedaj smo s pomočjo Betzove meje in ostalih lastnosti horizontalnih vetrnih turbin, podali osnovne principe aerodinamičnega delovanja rotorja, vendar so bila omenjena dejstva posplosena in zgolj v pomoč nadaljnjemu razumevanju. Omenili smo ze, da naletimo pri opazovanju delovanja rotorja vetrne turbine na zanimiv pojav, ki ga lahko opazimo pri potovanju plovila na mirujoči vodni gladini. Potovanje plovila pusti za seboj na vodni gladini sled, ki jo imenujemo vodni razor in je posledica turbulence tekočin predela ob konturi trdnega telesa. Iz enakega razloga, nastane pri obremenitvi rotorja preko navora gredi generatorja zračni vrtinec, ki deluje na turbino z značilno aerodinamično obliko vrtinca za horizontalne vetrne turbine. Zračni vrtinec rotorja, aerodinamični upor in vrtinci ob konicah lopatic, povzročajo aerodinamične izgube, kar se kaze v manku energije in manjsi nazivni moči turbine. Za natančnejso analizo je potrebna dodatna razlaga pri kateri upostevamo navedena dejstva in s katerimi nadgradimo teorijo Betzove meje s predpostavko, da deluje rotor na tok z radialno komponento v nasprotni smeri vrtenja. Pojavi se nov parameter količnika učinka hitrosti v radialni smeri, t.i. tangencialni indukcijski količnik, ki ga uporabimo pri definiciji osnovnih parametrov. Poenostavljena oblika rotorja v obliki enotne ravnine, tako ne zadosča več pri analizi omenjenih pojavov. Disk se tako razdeli na kolobarje enakovrednih sirin, kar omogoča ovrednotenje vpliva rotacije zračnega toka na rotor.

Ob upostevanju tangencialnega zračnega toka, ki nastane pri obremenitvi za samim rotorjem turbine, zapisemo enačbo za tangencialni indukcijski količnik, ki je razmerje hitrosti zračnega vrtinca in hitrosti rotorja.

(1.24)

Tokovno cev razdelimo na kolobarje z debelino dr, na razdalji r od osi. Povrsina tega dela je:

Sedaj lahko zapisemo impulz sile za primer povrsine kolobarja.

(1.26)

Sledi vrtilni moment za dano povrsino:

(1.27)

Moč, ki jo ustvarja rotor, je produkt vrtilnega momenta po celotni dolzini in kotne hitrosti.

(1.28)

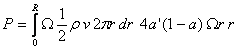
Na koncu zapisemo glede na (1.21) se izkoristek rotorja:

(1.29)

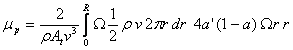
Uporaba teorije Betzove meje in teorije o ohranitvi gibalne količine velja samo za določen interval vrednosti aksialnega indukcijskega količnika. Problem nastane za a≥0.5, saj je tisti trenutek hitrost zračnega vrtinca za turbino 0 ali celo negativna. V tem primeru je količnik sunka sile η_I=1 in doseze celo vrednost 2, kar je iz praktičnega vidika nemogoče, saj definira učinkovitost gibalne količine rotorja in kot tak ne more preseči vhodne količine energije. Taksni pogoji nastanejo pri ekstremno obremenjenih turbinah, z velikimi vrtilnimi momenti, velikimi vrednostih hitrostnih stevil ali v primeru direktnega natekanja turbulentnega zračnega toka na rotor. Natančnejsi vzrok je v turbulentnosti zračnega vrtinca za rotorjem turbine, ki se mesa s prostim zrakom, kar pospesi zračni tok na izstopu rotorja. Za optimalne razmere pri maksimalni moči turbine, takrat je a=1/3, kar je razvidno iz diagrama za idealno turbino po Betzu (1.2), ima η_I maksimalno vrednost pri 8/9. V primeru velikih indukcijskih količnikov, ko model o Betzovi meji ni več veljaven, poisčemo resitev z empiričnimi popravki po Glauertu.

Diagram (1.3)

Teorija elementa lopatice

Do sedaj podane teorije o gibalni količini temeljijo na srednji hitrosti aksialne in tangencialne smeri toka na povrsini lopatic rotorja in definirajo impulz sile ter navor na osnovah spremembe gibalne količine tekočine. Z njihovo pomočjo definiramo zgornjo mejo izkoristka moči za katerokoli lopatico, glede na hitrost prostega zračnega toka in pridobljeno moč, vendar pri tem ne upostevamo vpliva geometrije lopatic. Teorija elementa lopatic je metoda s katero analiziramo njihovo delovanje in lastnosti med gibanjem v zraku. Podajmo osnovo za izračun optimalne oblike lopatice za doseganje maksimalnih aerodinamičnih izkoristkov rotorja, ki jih pogojuje razmerje aerodinamičnih koeficientov C_v, C_u, torej oblika konture profila. Poudarek je na analizi sil, ki nastopajo v posameznih delih lopatice kot funkcija geometrije. Lopatica ima v vsakem segmentu prereza iz obodne strani proti korenu, za malenkost manjso hitrost ter spreminjajočo se konturo in naklon profila po celotni dolzini. V analizi je zato predvideno končno stevilo elementov v obliki prerezov, za določeno dolzino lopatice navadno od 10 do 20, ki ne vplivajo drug na drugega. Vse dele se ovrednoti in integralno sesteje kar privede do iskanih veličin vrtilnega momenta in moči. Za zaključek se vrednosti pomnozi s stevilom lopatic in določi s pomočjo numerične iteracije končno obliko rotorja

Z znanimi hitrostmi lahko definiramo sile delujoče na segment profila, iz slike (1.7). Vedeti je potrebno, da po definiciji delujeta sili vzgona in upora pravokotno ter vzporedno na relativno hitrost zračnega toka, kar upostevamo v enačbah (1.52, 1.53) z uporabo kotnih funkcij. Enačbi za sili vzgona in upora se za obravnavani element profila razlikujeta od (1.41) le za ustrezni dr.

(1.50)

(1.51)

Enačbi za normalno silo in silo vrtilnega momenta:

(1.52)

(1.53)

Ob upostevanju končnega stevila lopatic B, zapisemo enačbi za impulz sile v smeri normale in navora, ki delujeta na rotor. Navor je podan kot produkt tangencialne sile in radia.

(1.54)

(1.55)

Relativno hitrost lahko zapisemo po diagramu (), v obliki:

(1.56)

Sedaj lahko zapisemo zgornji enačbi z vstavljanjem enačb (1.55) in (1.30) v obliko, ki vsebuje parametre indukcijskih količnikov.

(1.56)

(1.58)

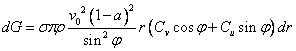
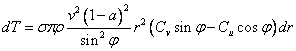
Celoten navor lopatice se izračuna z numerično integracijo navora od korena do konic lopatice, potek sledi v nadaljevanju. Moč rotorja lahko tako preliminarno določimo s produktom izračunanega navora in kotne hitrosti rotorja.

Teorija elementa in spremembe gibalne količine lopatice

Z zdruzitvijo teorij o ohranitvi gibalne količine in elementa lopatice preidemo h končni resitvi za preračun konstrukcije rotorja vetrne turbine, t.i. BEM teorije. Teorija povezuje učinek rotorja in geometrijo lopatic, kar je se posebej pomembno pri preliminarnem izračunu modela rotorja s končnim stevilom lopatic. Praktično gre za zdruzevanje enačb iz obeh teorij, kar poteka za primer enačbe sunka sile z izenačitvijo enačb za normalno silo iz teorije o gibalni količini in teorije elementa lopatice. Impulz sile torej zapisemo z uporabo enačb (1.26), (1.56) ter jih preuredimo v:

(1.59)

Zapisemo enačbo za navor elementa lopatice, z izenačenjem enačb (1.27) in (1.57).

(1.60)

Enačbo lahko zapisemo v lepsi obliki, brez hitrostnega stevila z uporabo enačbe ().

(1.61)

V praksi se za izračun indukcijskih faktorjev vstavlja parameter koeficienta upora v vrednost nič, kar je priblizek realnim vrednostim. S tem dosezemo izračun koeficientov neodvisno od karakteristik aerodinamičnih profilov. Zgornje enačbe lahko torej zapisemo kot:

(1.62)

(1.63)

(1.64)

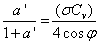
Z nekaj algebre, lahko iz predhodnih enačb izračunamo končne enačbe, ki jih uporabimo za izračun izkoristka rotorja.

(1.65)

(1.66)

(1.67)

(1.68)

Aerodinamični izkoristek rotorja poisčemo najprej z upostevanjem prispevkov moči posameznih elementov za določen radij, nato z integracijo vseh obročev po dolzini lopatice z uporabo enačbe (1.33) izračunamo izkoristek. Moč elementa vsake lopatice je bila podana v enačbi (1.34) in je za celoten rotor enaka:

(1.69)

Enačbo (1.34) preoblikujemo in uporabimo (1.57), v sledečo obliko:

(1.70)

Vstavimo enačbi (1.62) in (1.68) ter zapisemo enačbo za aerodinamični izkoristek rotorja v končni obliki:

(1.71)

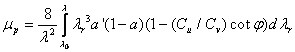
Alternativni izraz lahko zapisemo z nekaj algebre in z vstavljanjem enačb (1.65) in (1.66) v enačbo (1.70).

(1.72)

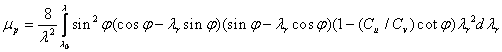
Enako lahko postopamo v primeru količnika sunka sile

(1.71)

Faktor izgube na konicah lopatic

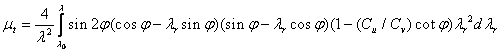
Teorija elementa in spremembe gibalne količine lopatice, v dani obliki predvidevata neskončno stevilo lopatic in tako ne uposteva vpliva stevila lopatic na rotor. Uvede se faktor izgube na konicah lopatic K in s tem nadgradi vse poglavitne enačbe iz teorije o BEM. Turbulentni tok nastaja na konicah lopatic in iztekajočem se robu po celotni dolzini lopatice. Do vrtinčenja prihaja, zaradi tendence natekajočega se zračnega toka z nizjim tlakom (spodnji del lopatice), k izenačenju tlaka. Tok se ukrivi v smeri nasprotne strani lopatice (visji tlak) in začne kroziti pod dodatnim vplivom prostega zračnega toka. Velikost vrtinčenja se proti konicam lopatic veča in je sorazmerna s tlakom, ki ima na obodu največjo velikost. Značilen turbulentni vrtinec horizontalnih vetrnih turbin, nastajajoč na obodu rotorja pusti sled se daleč za lopaticami in povzroča pri njihovem obratovanju aerodinamične izgube. Da bi se priblizali realnim tokovnim razmeram na rotorju, uvedemo korekcijski faktor K v obliki enačbe, ki velja v intervalu od 1 do 0 in predstavlja redukcijo hitrosti po celotni dolzini lopatice. Argument vrednosti kosinusa je v radianih.

(1.62)

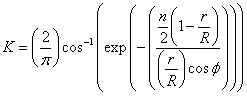
Kot smo ze omenili, korekcijski faktor uporabimo v prejsnjih enačbah in jih preoblikujemo.

(1.26)

(1.26)

(1.62)

(1.63)

(1.64)

(1.67)

(1.66)

(1.65)

(1.72)

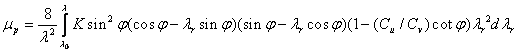
Enakovreden postopek se uporablja pri enostavnejsih izračunih, kjer izpustimo korekcijski faktor K in namesto njega uporabimo efektivni radij rotorja, ki nadomesti izgube. Določen je za velikost rotorja, ki je za 3% manjsi od načrtovanega.

Tokovne razmere

Učinek vetrne turbine je teoretično mogoče definirati s teorijo (BEM), ki zdruzuje teoriji o ohranitvi gibalne količine lopatic in elementa lopatice. Teorija temelji na Betzu, ki z meritvami natančno popisuje stanje turbin v praksi, kamor se tudi vrnemo kasneje. Kot je bilo ze omenjeno, je veljavnost metode omejena na maksimalne vrednosti indukcijskih faktorjev pri 0,5. Nad  to vrednostjo se ustvarjajo zapleteni tokovni vzorci, ki jih teorija ne predvidi in ni več veljavna. Delovanje turbine je v osnovi na ta način popisano s tokovnimi razmerami delovanja rotorja, za vse vrednosti indukcijskih količnikov. Količnik sunka sile η_I=1, je parameter, ki se uporablja za popis stanj. Podan je kot razmerje sunka sile in dinamične sile, ki sledi v enačbi:

(1.30)

Enačba popisuje tokovne razmere v diagramu (), in jih deli v stiri sklope. Kriterij delitve temelji na intervalu indukcijskega faktorja v relaciji s smerjo in velikostjo sunka sile.

Sodeč iz diagrama, lahko opazimo pri negativnih indukcijskih faktorjih (a<0), negativne vrednosti količnika sunka sile. V takem primeru je jasno, da rotor deluje, kot pogonska naprava. Nastaja aksialna sila usmerjena proti zračnemu toku, ki hkrati doda energijo zračnemu vrtincu za ravnino rotorja. Tipičen primer tovrstnega delovanja je letalski propeler, po katerem tokovno stanje tudi imenujemo. Vetrne turbine delujejo v območju stanja mlina na veter in turbulentnega vrtinca. Tokovno stanje mlina na veter je značilno pri običajnem delovanju turbine, za aksialne indukcijske faktorje manjse od 0,5. Večji indukcijski faktorji, bi ob predpostavki BEM teorije povzročili sorazmeren padec količnika sunka sile, vendar se v praksi izkaze, da poteka delovanje turbine pri aksialnih indukcijskih faktorjih med 0,5 in 1, pri visjih vrednostih za η_I, ki jih popisuje rdeča krivulja diagram (). Pogosto se za tokovno stanje intervala indukcijskih količnikov od 0,4 do 1, uporablja Glauert-ova empirična formula. Zadnji interval delimo na dva dela, stanje v neposredni blizini 1, ki ga imenujemo stanje obročev vrtinca, ko zrak obteka rotor in ne opravlja koristnega dela ter s premikom v desno, stanje zaviranja propelerja, ko rotor spremeni smer zračnega toka v nasprotno smer.

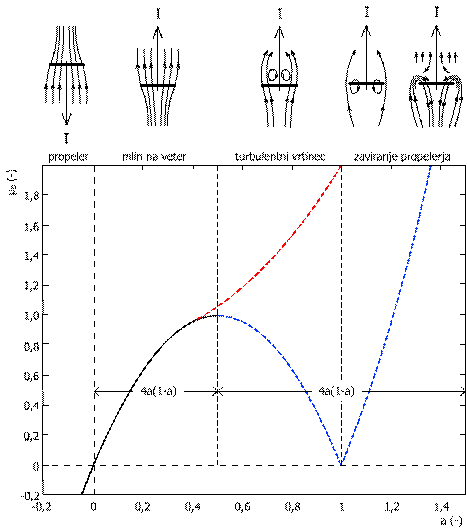
Diagram ()

Če se vrnemo na obratovanje rotorja v stanju turbulentnih vrtincev, kot smo omenili na začetku poglavja, poisčemo resitev v Glauertovih empiričnih relacijah med aksialnim indukcijskim faktorjem in količnikom sunka sile. Izračun poteka se vedno v okviru BEM teorije, kjer se omejimo na veljavnost indukcijskega faktorja na 0,4, ekvivalentna vrednost za η_I je 0,96. Enačbo, ki popisuje krivuljo količnika sunka sile v celotnem intervalu delovanja turbine lahko izrazimo tudi v obliki, ki vsebuje parametre delujočih sil na lopatico, po enačbi (1.56), iz poglavja o delovanju sil na infinitezimalni del lopatice.

(1.29)

Z znanim kriterijem določimo aksialni indukcijski faktor rotorja turbine z navadno enačbo (1.61). Za vrednosti , ki jih predvideva teorija, večje od 0,96, upostevamo empirične relacije po Glauertu in izgube na konicah lopatic, po enačbi:

(1.29)

Postopek izračunov se resuje s pomočjo ugibanj začetnih parametrov ter kasneje s stevilnimi računskimi operacijami, ki vsebujejo metode numeričnih resevanj enačb. Uvede se računalniski program, s katerim je moč na podlagi iteracijskega postopka optimizirati obliko rotorja.

Karakteristika rotorja

Lastnost individualnega rotorja definira specifična krivulja, ki jo določa nazivna moč turbine. Eden od parametrov moči rotorja je izkoristek, podan z aerodinamičnimi lastnostmi Betzove teorije in je merodajen argument učinka rotorja, enačba (). Povezava s hitrostnim stevilom nastane relevantna, pri spremembi relativne hitrosti vetra, kar lahko razberemo iz enačbe (), ki definira optimalni izkoristek rotorja pri vseh hitrostih. Razmerje je se posebej uporabno pri analizi učinka rotorja, saj gre za brezdimenzijska parametra, ki sta glede na lastnosti spremenljivk primerna za popis karakteristične krivulje, ne glede na način krmiljenja turbine. V praksi se pri dimenzioniranju uporablja karakteristična krivulja, za preliminarno določitev moči pri katerikoli kombinaciji hitrosti vetra in rotorja.

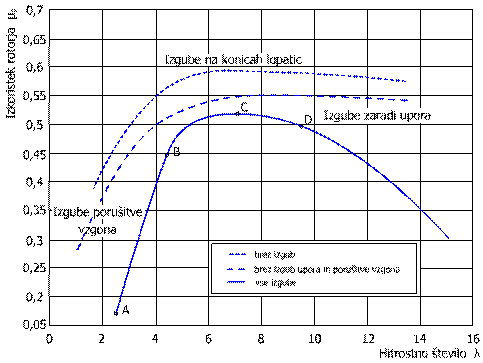
Diagram ()

Primer krivulje v diagramu (), je podan za hitrostna stevila z fiksnim vpadnim kotom, torej je rotor krmiljen s porusitvijo vzgona. Najopaznejsi del v diagramu je točka C, kjer je maksimalna vrednost izkoristka rotorja pri hitrostnem stevilu 5,2 glede na teoretično mejo bistveno nizja. Dejstvo je, da oblika lopatice ni idealna. Razlika v izkoristku nastane zaradi izgub na konicah lopatic in njihovem uporu. Na potek leve strani krivulje, če sledimo smeri obratovalnih točk ABC pri nizjih hitrostnih stevilih, vpliva torej porusitev vzgona lopatice, kar nakazuje črtkana krivulja. Vpadni kot se povečuje, ko se priblizujemo točki A. Na nasprotni strani krivulje CD, se vpadni kot zmanjsuje. Prevladuje vpliv upora, ki je posledica trenja na povrsini lopatice (kozni efekt). Značilno za rotorje s stalnim naklonom lopatic je v doseganju maksimalnih moči, na strani krivulje porusitve vzgona. Takrat nastanejo maksimalne vrednosti koeficientov vzgona za večji del lopatice.

Model rotorja vetrne turbine

Model vetrne turbine je bil predhodno dimenzioniran s pomočjo metode računalnisko podprte numerične simulacije toka fluida (CFD). Izvedba modela je bila prenesena v praktično obliko, kar je omogočalo vzporeden potek primerjave izmerjenih karakteristik in optimalne oblike z matematičnim modelom, po metodi BEM. Rotor je manjsih moči, s prenosom na izvedbo je predvidena moč 2kW in ima specifično obliko aerodinamičnega profila lopatic z oznako GOE417A, sledi v nadaljevanju. Meritve karakteristike modela so potekale na institutu KGH Godovič v laboratoriju za aerodinamiko, kjer se nahaja vetrovnik. Na temo je nastala diplomska naloga kolega Borisa Korosca z naslovom Eksperimentalno modeliranje aksialne turbine.

Zasnova

Zasnova rotorja je v enostavni obliki, z doseganjem sorazmerno visokih izkoristkov in je načrtovana za specifične pogoje obratovanja. Dane zahteve so izvedene z izvedbo rotorja s pasivnim krmiljenjem, kvalitetnimi materiali in primerno geometrijo lopatic. Enostavno obliko dosezemo z linearizacijo optimalne oblike lopatic. Tako omogočimo ravno obliko lopatice po vsej dolzini, na račun zmanjsanja aerodinamičnega izkoristka. Ravna oblika se izkaze kot prednost pri enostavnejsi izdelavi rotorja, in s tem povezano ekonomsko ravnotezje med masovno proizvodnjo ter zivljenjsko dobo celotne naprave. Tehnoloski proces izdelave je usmerjen k rezanju večjega stevila lopatic iz jeklene ali vlaknene poliesterske cevi, s pomočjo rezanja CNC krmiljenega stroja ali odrezovanja s stiskalnico. Aerodinamični profil je enostavne oblike in ima aerodinamično lastnost ukrivljene plosče. Oblika rotorja je podana s petimi lopaticami simetrično porazdeljenimi na razmaku 72°, togo vpetimi v pesto. Oblika, ki gre ponovno zaradi gostote rotorja, pri optimalnem stevilu treh lopatic, v skodo aerodinamičnemu izkoristku, na drugi strani znizuje vklopno hitrost turbine, saj k temu pripomore večji vrtilni moment rotorja. Turbina lahko na ta način obratuje pri nizjih hitrostih vetra. Rotor in posledično vrtilna frekvenca sta krmiljeni s porusitvijo vzgona in krmiljenjem gredi z elektroniko generatorja. Pogoj za tak način krmiljenja je v stalnem obratovanju turbine blizu porusitve vzgona, za kar ima posledico zopet nizji aerodinamični izkoristek. Moč turbine je odvisna od načina delovanja turbine za nazivne obratovalne pogoje in je funkcija krmiljenja turbine. Oba faktorja sta opisana v karakteristični krivulji rotorja. Obremenitve se pri načinu obratovanja s porusitvijo vzgona, po dosezeni nazivni moči povečujejo, kar je razvidno tudi iz karakteristične krivulje za enako moč vetra. Ves presezek energije se akumulira torej v konstrukciji, zato je potreben primeren preračun dinamičnih in statičnih napetosti konstrukcije, da ne prihaja do fizičnega odklona lopatic in nenačrtovanega obratovanja rotorja. Generator je pritrjen direktno na pesto, kar zmanjsa mehanske izgube in stevilo strojnih elementov. Predvidena obratovalna lokacija modela se nahaja v Postojni na visini 15m z absolutno nadmorsko visino 610m, iz katere izhajamo pri podatku za izračun gostote in hitrosti zraka. Značilna vremenska karakteristika je burja s sunki vetra, ki doseze hitrosti do 40m/s skozi vse leto. Turbina v končni izvedbi mora zagotavljati avtonomno preskrbo z električno energijo samostojne enodruzinske hise s stirimi člani. Potreba po električni energiji, za obratovanje običajnih gospodinjskih naprav je na mesečni ravni potrebno 290kWh, po podatkih statističnega urada RS, pri največji moči 2kW. Električna energija se shranjuje v akumulatorjih, za primer brezveterja ali zaloge električne energije in daje kvaliteto ter fleksibilnost sistemu. Vetrovne razmere so pomembna okolisčina za optimalno dimenzioniranje turbine in so specifične za dan primer. Zajem podatkov na lokaciji objekta vključuje parametre kot so povprečna hitrost vetra, smer vetra, odkloni od povprečne hitrosti v krajsih intervalih - sunki, dnevni, mesečni in letni odkloni ter spremembe po visini. Studija statistike se izvede pred dimenzioniranjem, po metodi Weibuillove verjetnostne porazdelitve.

Dimenzioniranje

Oblika rotorja definiramo glede na aerodinamične in trdnostne lastnosti, ki jih pogojuje izbira materiala in vplivi okolice na lopatice. Izbran rotor s petimi lopaticami, argumentirano v poglavju 3, je eden od vhodnih parametrov v izračunu končne geometrije. Izračun temelji na teoriji spremembe gibalne količine z upostevanjem zračnega vrtinca in teoriji elementa lopatice. Izračun končne oblike, torej analize geometrije poteka po sistemu iteracijskih zank, kar resujemo z numeričnimi metodami s pomočjo osebnega računalnika. Postopek je opisan v poglavju 3.3.1. Potrebni vhodni podatki so naklon in tetiva aerodinamičnega profila c, torej torzija lopatice, podatki za naklon alfa C_v in C_u, pri različnih Reynoldsonovih stevilih, ki morajo biti za veljavnost preračuna nad primernih vrednosti. Dva tipa profila S822 in S823 lahko razdelimo po celotni obliki profila se določi po Newtonovi interpolaciji za vsak posamezen segment. Porazdelitev se na razdalji korena in 75% lopatice. Preračuna se optimalna oblika porazdelitve profila v datotekah za 10ih segmentov v obliki numeričnih podatkov za x in y spremenljivke krivulje posameznega profila. Podoben program, s katerim je bila izvedena primerjava v diplomski nalogi, je prav tako namensko razvit za dimenzioniranje rotorjev vetrnih turbin in dostopen na spletu z imenom PROPID. Programa omogočata dva načina uporabe analize in dimenzioniranja. Pomeni, da je mogoče v načinu dimenzioniranja vstaviti vhodne podatke, kot so moč rotorja, hitrost vetra, itd., v tabelo ali datoteko, na kar z zagonom zaporedja algoritmov s programskim jezikom FORTRAN, po nekaj Newtonovih iteracijah v izhodni datoteki izpise parametre za zeljeno obliko rotorja.

Izbira profila

Ključen vpliv na karakteristiko rotorja pogojuje izbira aerodinamičnega profila lopatice. Kot ze rečeno ima model rotorja predefinirano obliko profila ukrivljene plosče, z oznako GOE417A. Potrebna je analiza in komentar izbranega profila v obliki primerjave namensko razvitih profilov vetrnih turbin. Po priporočilih laboratorija za obnovljive vire NREL^[7], se za turbine moči 2-20kW uporabljajo profili druzine, ki odgovarjajo pogoju razmerja tetive in sirine profila za vrednosti 10%-16% in jih uporabimo v primerjavi s profilom ukrivljene plosče. Gre za tipa profilov S822 in S823, ki omogočata večjo trdnost v čelni smeri lopatice in boljse krmiljenje s porusitvijo vzgona. Izbrana profila imata tudi lastnost neobčutljivosti na hrapavost povrsine, kar je pomembno pri krmiljenju s porusitvijo vzgona, glede na zazelene konstantne aerodinamične lastnosti rotorja. Karakteristike profilov so podane za oba tipa v obliki diagramov.

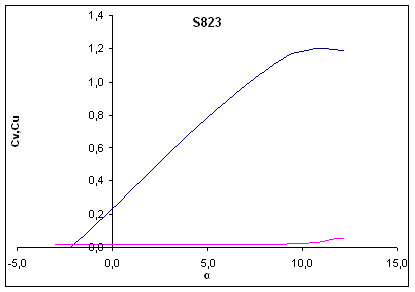
Diagram ()

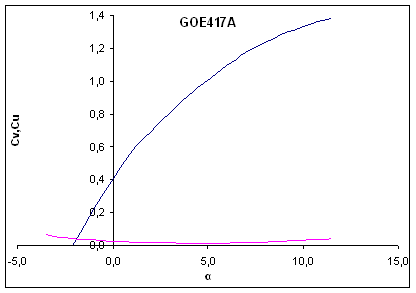
Diagram ()

Primerjalna diagrama obeh profilov sta podana za nazivne obratovalne vrednosti rotorja moči 2kW, kjer se vrednosti Reynoldsonovega stevila gibljejo pri 500000.

Iz diagramov je razvidno, da ima namensko razvit profil linearno narasčajočo karakteristiko in zvezen prehod v intervalu maksimuma, kar pripomore k lazjem krmiljenju frekvence in enakomernejsemu prehodu k porusitvi vzgona. Pri profilu ukrivljene plosče, je pri nizkih vpadnih kotih koeficient upora nekoliko visji, nato doseze minimum pri 5°. V primerjavi z optimalnim profilom ali profili razvitimi posebej za vetrne turbine, kjer se vrednosti v realnih pogojih priblizujejo 0, ugotovimo da gre za pomanjkljivost. Druga negativna lastnost, se kaze v mehanski trdnosti profila. Lopatica zaradi neugodne geometrije, ki ima lastnost vitkega elementa, pri visjih hitrostih obratovanja izgubi togost in se upogiba, kar se poslabsa aerodinamične lastnosti. Izbiro profila ukrivljene plosče posledično, kljub manjsim izkoristkom argumentiramo z enostavno, zatorej ekonomično tehnično resitvijo.

Optimalna geometrija

Dimenzioniranje optimalnega rotorja poteka na osnovi izbranega aerodinamičnega profila, z določitvijo geometrije zvitja in sirine lopatice po dolzini, pri nazivnem hitrostnem stevilu. S spremembo hitrostnega stevila prihaja do spremembe vrednosti aerodinamičnih izkoristkov, kar lahko uporabimo pri določanju maksimalnega izkoristka. Na začetku dimenzioniranja je zato potrebno določiti spekter relativnih kotov v relaciji z izkoristkom in nato poiskati ustrezno hitrostno stevilo. Iz enačbe () za aerodinamični izkoristek, lahko vidimo ključne parametre, potrebne za izračun: relativni kot toka, hitrostno stevilo, razmerje aerodinamičnih koeficientov in faktor izgube K. Z izbiro profila, določimo razmerje aerodinamičnih koeficientov, kjer je vrednost najmanjsa. Faktor izgube je odvisen od stevila lopatic in posledično relativnega kota in hitrostnega stevila. Da zadovoljimo zgornjim zahtevam, določimo optimalen relativni kot pri določenem hitrostnem stevilu. Relacijo dosezemo z odvajanjem enačbe (). Faktor izgube in člen aerodinamičnih koeficientov izpustimo, saj sta v zvezi neodvisna.

(1.29)

Po ureditvi dobimo enačbo za optimalen relativni kot zračnega toka v vsakem segmentu lopatice.

(1.29)

Lopatico lahko sedaj po dolzini razdelimo na N enakih segmentov. Izračunamo lokalno hitrostno stevilo () ter nato relativni kot zračnega toka.

(1.29)

Poisčemo faktor izgub na lopaticah K.

(1.62)

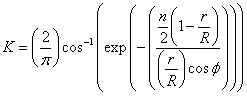
Sledi izračun sirine lopatice c, po enačbi ().

(1.65)

Vzgonski koeficient izberemo pri minimalni vrednosti γ_i (1.40). Porazdelitev zvitja je podana v enačbi (1.49), kjer vpadni kot določimo glede na nazivno vrednost koeficienta vzgona.

(1.49)

Na koncu izračunamo aerodinamični izkoristek rotorja in izrazimo integral z vsoto vseh segmentov lopatice po enačbi ()

(1.72)

Naveden postopek omogoča optimalen izračun geometrije lopatic za izbran profil in dolzino lopatic pri nazivnem hitrostnem stevilu. Z upostevanjem izkoristka, dobimo maksimalno moč, ki jo je mogoče pridobiti iz zraka, za katerokoli hitrost povprečnih vrednosti zračnega toka.

V glavnem je potek postopka za matematični izračun geometrije vsakokratnega rotorja turbine obrazlozen v zgornjem poglavju. Postopek izračuna v računalniskem programu poenostavi in prihrani čas pri ponovitvah računanja in optimiranja rotorja, zato je potek v tabelaričnem programu Ms Excel primerna resitev. Uporabljene so osnovne matematične operacije z absolutnim in relativnim sklicevanjem polj tako, da je izračun pri spremembi vstopnih podatkov avtomatičen. Tabela je razdeljena v tri sklope: Izbiro vstopnih parametrov, izračun oblike rotorja in izračun moči. Vstopne parametre nazivnih vrednosti vstavljamo v rumena polja, ob katerih so podane priporočene vrednosti, ki veljajo za dane vstopne podatke. Potrebni parametri so: nazivna moč, mehanski in aerodinamični izkoristek, nazivna hitrost prostega toka zraka in vrtilna frekvenca rotorja. Pri normirani moči turbine ob pogoju, da vstavimo predvideni mehanski izkoristek moči, izkoristek rotorja, lokalno gostoto zraka in nazivno hitrost zračnega toka, izračun izpise vrednost za preliminarno velikost rotorja. Izračun velikosti rotorja sluzi kot referenčna vrednost dolzine lopatice za načrtovano moč. Sledi izračun idealne oblike rotorja, ki se izrise grafično v diagramih c/(r/R) in β/(r/R), za relaciji sirine lopatice c skozi radij in naklon lopatice po njeni dolzini. Pri preračunu je potrebno določiti vrednosti vzgonskega količnika Cv, uporovnega količnika Cu in vpadnega kota α, ki ustrezajo najmanjsi vrednosti kvocienta Cu in Cv. Podatki iz meritev se navadno nahajajo v tabelarični obliki, ki sledi po vrstnem redu α, Cv in Cu, poljubnih α pri merjenih Reynoldsonovih stevilih. S pomočjo Excelove tabele AirfoilPrep, ki jo je moč dobiti na spletu, določimo iz podatkov vrednosti meritev načrtovanega profila, linearne interpolirane vrednosti α za interval 0,5°. Z vstavljenimi podatki se izrise diagram idealne oblike lopatice. Naslednja operacija je linearizacija ali preoblikovanje idealne oblike. Izvedena je za sirino in zvitje lopatice na poljubnem delu, ki je v tabeli označeni z vijoličasto barvo. Ponastaviti je potrebno enačbi za izračun koeficientov premice k in j ter določiti interval linearizacije za vijoličasta polja. Z določeno končno obliko lopatice preidemo na zadnji del preračuna, kjer z iterativnim postopkom določimo moč in izkoristek rotorja. Pri iterativnem postopku preračunavanja opazujemo stevilo iteracij in konvergiranje razlik indukcijskih količnikov. Podani sta dve metodi iteracije, za vrednost indukcijskega koeficienta a, ki je manjsa od 0,4 (rdeči stolpci), metoda 1 in metoda 2 za a>0,4, kjer Betzova teorija ne velja. V tabeli končnih podatkov ponastavimo reference na tabelo iteracije z zadovoljivimi vrednostmi. Izpise se izkoristek rotorja in posledično nominalna moč.

Linearizacija geometrije

Matematično definirana oblika optimalno oblikovanega rotorja, v praksi privede do tezav glede realizacije izvedbe geometrije lopatic. Uporabi se metoda linearizacije konture in zvitja lopatic tako, da je s tehnoloskega vidika izdelava praktično izvedljiva in preprosta. Na drugi strani, je tendenca spreminjanja oblike, da se sirine za posamezne segmente lopatic čim bolj priblizujejo optimalnim dimenzijam. S postopkom iteracije primerjamo različne variante lineariziranih oblik lopatic z enakimi aerodinamičnih lastnostmi in na ta način izberemo končno obliko, ki ima največji učinek. Linearizacija v preračunu je podana za zelen interval sklopov relativnih segmentov, navadno enega, po dolzini lopatice r/R. Linearizirano geometrijo popisuje enačba premice. Koeficient naklona premice, določimo z mejnimi vrednostmi intervala, za kar sta potrebni dve vrednosti in posledično enačbi. Enačba premice konture () in enačba premice zvitja ().

(1.43)

(1.43)

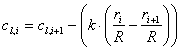
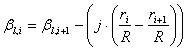
Spremembo krivulje prvotno analiziramo grafično s pomočjo primerjave diagrama optimalne in linearizirane oblike lopatice. Poudarek je na drugi polovici lopatice, proti konici, kjer se ustvarja največ moči, med r/R=0.5 in r/R=0.9. Na koncu izračunamo numerične vrednosti, ki jih ovrednotimo s primerjavo aerodinamičnih izkoristkov rotorjev.

Izvedba in opis

Meritveni model je enostavne izvedbe in ročne izdelave. Lopatice so odrezane iz aluminijaste cevi primerne velikosti, in zamaknjene iz osi glede na načrtovano zvitje. Profil ima tako obliko ukrivljene plosče. Konice lopatic so zaobljene, kot posledica manjsih aerodinamičnih izgub in manjsega hrupa. Robovi konture so ročno bruseni s čimer je dosezena zadovoljiva aerodinamika in kvaliteta povrsin, glede na izdelavo modela. Nosilci lopatic so pritrjeni z vijačno zvezo in so okrogle oblike, kar omogoča enostavno spreminjanje nastavnega kota s prirobnicami. Rotor sestavlja pet lopatic, dinamično uravnotezenih z razmakom 72° in togo vpetih v pesto. Pesto je prav tako iz aluminija, skonstruirano z metodo računalnisko podprtega načrtovanja (CAD) in izdelano s CNC krmiljeno struznico. Opisane komponente sestavljajo osnovne gabarite rotorja, premera 800mm in pesta 170mm, ki jih omejujejo dimenzije lopatic, slika (). Karakteristika rotorja je izmerjena pri hitrostnem stevilu 3,5 in frekvenci 910min^-1. Nominalna moč rotorja, ki se pretvori iz zračnega toka pri danih pogojih je 47W in aerodinamičnemu izkoristku 13,6%. Vrtilni moment, ki se med obratovanjem ustvarja znasa 0,49Nm. Po teoretičnih izračunih ima načrtovana karakteristika, kjer doseze rotor nominalno moč, pri hitrostnem stevilu 7. Predvideni aerodinamični izkoristek se takrat giblje pri 55%.

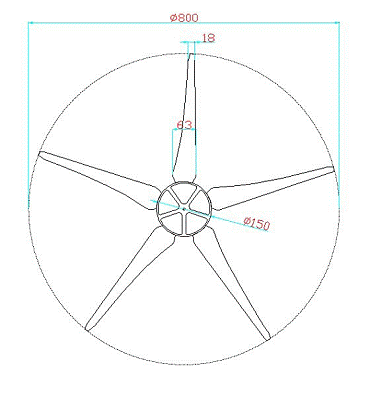
Slika ()

Matematični model rotorja je osnovan na geometriji meritvenega rotorja. Vstopni parametri so pridobljeni z izmerami geometrije lopatic in aerodinamičnega profila meritvenega rotorja. Meritve potekajo v vsakem segmentu posebej, v natančno določeni točki, ki jo definira srednja vrednost sirine odseka. Vrednosti meritev so podane v tabeli (), skupno dvajsetih segmentov, ki so razdeljeni skozi celotno dolzino lopatice. Popis parametrov sirine in naklona prerezov, definira osnovno formo lopatice. Aerodinamičen profil ima v vsakem segmentu obliko istega tipa (GOE417A) in tako poda aerodinamične lastnosti lopatice. Parametri meritev tvorijo karakteristiko oblike rotorja in sluzijo za vstopne podatke pri analizi.

Tabela ()

Preliminaren izračun moči

Na začetku izračuna je potrebno določiti parameter za gostoto zraka na lokaciji turbine. Po enačbi (), sledi izračun za povprečno vrednost temperature iz povprečnih vrednosti podatkov Hidrometeoroloskega zavoda Slovenije za kraj, primer Postojna: povprečna temperatura za obdobje od 1991-2005 je 9,2°C.

(2 . )

V enačbi je upostevana nadmorsko visina lokacije, kjer se naprava nahaja. Za nas primer je vstavljena vrednost za h enaka 610m. Podatki so podani v zavihku, lokalni podatki. Dobljen rezultat je vstavljen v enačbo za izkoristek rotorja (1.33). Enačbo se preoblikuje in izrazi polmer rotorja, ki sluzi zgolj kot ocena predvideni moči.

(1.33)

Pred tem se določi ostale manjkajoče podatke za nominalno moč, ki je v nasem primeru 177W ter nazivno hitrost vetra, 10,7m/s. Uposteva se vrednosti za mehanski izkoristek η_m, 0,9 in aerodinamični izkoristek rotorja η_p, 0,55.

Izračun hitrostnega stevila λ poteka po enačbi (). Prvo se izračuna kotno hitrost Ω po enačbi:

(1.32)

(1.32)

V naslednjem sklopu obravnavamo izračun idealne oblike lopatice. Po opisanem postopku iz poglavja 1.2.9 razdelimo lopatico na 20 enakih delov. Segmenti so v tabeli v stolpcu poz. označeni z indeksom od 1 do 20 in si sledijo v vrstnem redu, od oboda proti korenu. Izračunane vrednosti veljajo za sredisča odsekov. Rezultati in vstavljeni podatki v opisanem postopku, se nanasajo na skrajni segment označen z indeksom 1, ki se nahaja na obodu lopatice. Pred samim začetkom postopka je potrebno določiti glavne vstopne podatke. To so vrednosti za vpadni kot α, koeficiente vzgona in upora, C_l in C_d, pri zahtevanem Reynoldsonovem stevilu, v nasem primeru 200,000. Vrednosti se iz tekstovne datoteke uvozimo v Excel-ovo razpredelnico in razvrsti v stolpce za α, C_l in C_d. Podatke se prenese v tabelo podatkov AirfoilPrep v zavihek Interpolate, Original table, v padajočem vrstnem redu. Vrednosti y se postopoma vstavi za C_l in v naslednjem koraku C_d. Interpolacija steče preko makro ukaza Do Interpolation, za zeleno stopnjo vpadnih kotov α, ki so funkcija spremenljivke y. Preračun je veljaven ob pogoju, da vrednosti aerodinamičnih koeficientov ustrezajo, enakemu vpadnemu kotu. Podatke linearne interpolacije prenesemo nazaj v prvoten dokument, kjer se nahaja tabela označena z imenom Podatki aerodinamičnih profilov. Pri izbiri optimalnih vrednosti aerodinamičnih koeficientov sledimo pravilu, da je vrednost kvocienta C_d/C_l najmanjsa, enačba ().

(1.6)

V nasem primeru je vrstica vrednosti optimalnega vpadnega kota označena z rumeno barvo, zgolj za pomoč pri vstavljanju v ostale enačbe.

Izračun pričnemo s podajanjem vrednosti za relativno oddaljenosti sredisč segmentov r_i/R, po celotni dolzini lopatice:

(1.6)

Določimo polmer sredisča posameznega segmenta r_i, izhajamo iz enačbe ().

(1.6)

V nadaljevanju določimo hitrostno stevilo za vse segmente z enačbo:

(1.6)

ter iz dobljenih parametrov kot relativne hitrosti zračnega toka φ, ki je optimalen za vsak segment lopatice.

(1.6)

Naklon segmenta je nato izračunan z razliko izbranega vpadnega kota α in relativnega kota φ.

(1.6)

Določimo naklon lopatice β_1,0, ki je podan glede na referenčno izhodisče konice lopatice v prvem segmentu, s kotom odseka β₁. Vrednost za β_1,0 je ze izračunana v prejsnji enačbi in je v vsakem segmentu enaka 1,1°. Podatke uporabimo v enačbi (), ki popisuje zvitje ali torzijo lopatice β_t.

(1.6)

Izračunani parametri predstavljajo dobrsen del geometrije lopatice. Ostane se izračun sirine lopatice, ki se po dolzini spreminja zaradi ohranjanja vzgonskega količnika lopatice. Izbran vzgonski količnik pri vpadnem kotu 6°, znasa 0,9133. Enačba uposteva stevilo lopatic rotorja, kar je v nasem primeru 5. Ostali parametri so znani, zato sledi izračun enačbe:

(1.6)

Določimo se koeficient sirine c_i/R ter zaključimo z oblikovanjem lopatice.

(1.6)

Obliko idealne geometrije lopatice sedaj lahko grafično ponazorimo v obliki diagrama. Diagram () opisuje funkcijo odvisnosti sirine lopatice z relativno dolzino, c/(r/R). Vstavimo vrednosti za celoten interval odsekov, na abcisi parameter r_i/R in ordinati c_i. Ekstremna vrednost nastopi pri relativni dolzini lopatice 0,125, torej pri korenu, kjer je sirina največja.

\s

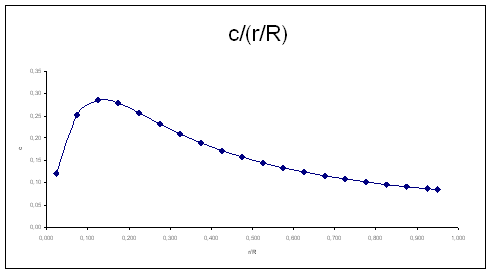
Diagram ()

Diagram () popisuje torzijo lopatice. Podobno, kot pri prejsnjem je parameter zvitja v relaciji z relativno dolzino lopatice. Iz diagrama je razvidno, da gre za eksponentno padajočo funkcijo, tako je kot zvitja največji pri korenu in pada proti konici lopatice k 0.

\s

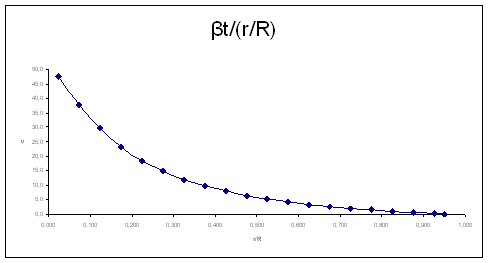
Diagram ()

V tabeli nam ostanejo se parametri, ki jih bomo kasneje uporabili v zadnjem delu izračuna, v sklopu iterativnega postopka. Za pomembnejsi parameter pri dimenzioniranju rotorja velja gostota rotorja, ki je v tabeli postavljen na skrajno mesto. Izračunamo jo z enačbo ():

(1.6)

Pri oceni moči rotorja, potrebujemo vrednosti indukcijskih količnikov, glede na dano obliko lopatice. Izračun aksialnega indukcijskega količnika za prvi segment,

(1.6)

sledi se tangencialni.

(1.6)

Veljavnost podatkov aerodinamičnega profila je pogojena z izbiro vrednosti pri ustreznem Reynoldsonovem stevilu. Velikost stevila je sorazmerna hitrosti. Torej je največja vrednost Reynoldsonovega stevila pri kotni hitrosti za največji radij, to je na obodu rotorja. Relativno hitrost za prvi segment izračunamo z vektorsko vsoto aksialne in tangencialne komponente hitrosti po enačbi ().

(1.6)

Reynoldsonovo stevilo za posamezen segment izračunamo pri vrednosti kinematične viskoznosti zraka η_z, 17,6 x 10^-5, ki ustreza temperaturi 9°C. Značilno linearno dimenzijo, ki je dana v izračunu, glede na dejansko vrednost krivulje oblike, poenostavimo z dolzino profila c_i. Izračun vrednosti je zato priblizen.

(1.6)

Nadaljujemo z rubriko linearizacije geometrije. Linearizacija poteka glede na določene kriterije, ki pogojujejo spreminjanje sirine in zvitja z radiem. V primeru modela s pomočjo grafične metode opredelimo interval linearizacije. Iz krivulje diagrama določimo začetno točko intervala, ta zdruzuje vrednosti obeh parametrov v stolpcu r_i/R in znasa 0,925 za c₂. Nato določimo se zadnjo točko intervala pri 0,575. Enačba premice je definirana s količnikom naklona premice k. Določen je z enačbo () s segmenti 1 in 10, ki mejijo na interval lineariziranih vrednosti. Za vrednost y in y₁ vstavimo torej 0,08 in 0,15, za x in x₁ pa 0,95 in 0,525 ter izračunamo količnik linearizacije sirine lopatice.

(1.6)

Količnik uporabimo v prvem segmentu za interval c₂ do c₉, po enačbi:

(1.6)

Ponovimo postopek linearizacije za argument β_t v intervalu od 0° do 8,7°. Izračunamo količnik premice j:

(1.6)

ter nato se naklon lopatice β_t

(1.6)

Tabela izračunov v rubriki analiza končne oblike rotorja, predstavlja končno obliko načrtovane lopatice. Njeno obliko definiramo v diagramih, ki sledijo.

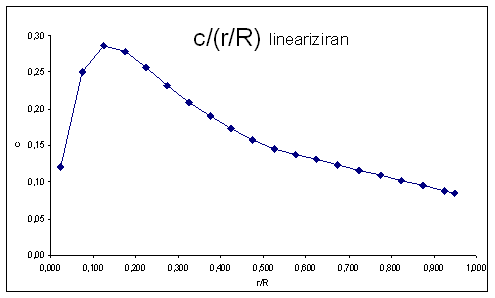
Diagram ()

\s

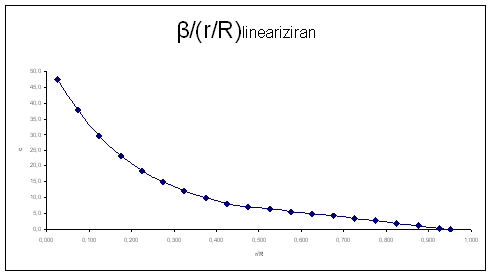
Diagram ()

Numerična iteracija

V zadnjem delu se ukvarjamo s preliminarnim izračunom moči rotorja. Parameter, ki popisuje aerodinamično izgubo med delovanjem rotorja se imenuje indukcijski faktor. Definiran je za aksialno in tangencialno smer natekanja zraka na lopatico. Dejansko vrednost je mogoče določiti z vstavljanjem ključnih podatkov ponovno v začetne enačbe v obliki zaključene zanke. Referenčna parametra sta indukcijska faktorja, zato se zaradi njunih sprememb temu ustrezno povečuje stevilo zank. Postopek imenujemo iteracija. Uporabljeni sta dve metodi. Prva metoda velja pri pogoju, da je aksialni indukcijski faktor manjsi od 0,4. V primeru, da je vrednost presezena, resujemo iteracijski postopek po metodi 2, kar se je izkazalo za resitev dimenzioniranja modela. Postopek je opisan za obe. Na začetku iteracije je potrebno določiti priblizno geometrijo rotorja, ki je namenjena zgolj kot osnova postopku iteracije, in je pridobljena na podlagi ugibanj ali rezultatov ze obstoječih izračunov. Dejanje izvedemo s prvo iteracijo in iz navedenega sklepamo, da sta potrebni vsaj dve iteraciji za pričakovan rezultat. V grobem smo preliminarne parametre ze določili na začetku izračuna in jih tudi vstavili v polja za vstopne podatke, označene z oranzno barvo. To so podatki za radij, hitrostno stevilo rotorja in stevilo lopatic. Ob njih se nahajajo priporočene vrednosti po katerih se orientiramo. Sedaj lahko pričnemo s prvo iteracijo po metodi 1. Parametri si sledijo po vrstnem redu, tako ustvarimo primerne pogoje za vse nadaljnje iteracije.

Metoda 1

Nastavimo predvideni kot relativne hitrosti za vsak segment posebej z enačbo():

(1.6)

Sledi ji izračun korekcijskega faktorja izgub na konicah lopatice:

(1.6)

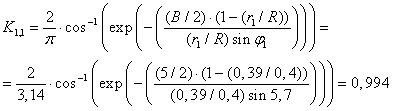
Ponovno izračunamo kot relativne hitrosti vetra:

(1.6)

Nadaljujemo z enačbo za dejanski vzgonski količnik:

(1.6)

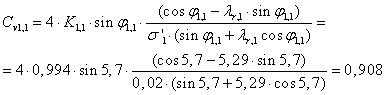
Vzgonskemu količniku pripada določen vpadni kot, ki se nahaja v tabeli s podatki o aerodinamičnih profilih. Ročno iskanje ustreznih vrednosti, bi bilo ob stalnem spreminjanju vrednosti vzgonskega količnika pri večjem stevilu iteracij zamudno. Vpeljana je funkcija VLOOKUP s katero za vsak segment poisčemo ustrezen kot α. Zahtevani argumenti, ki tvorijo enačbo so po vrstnem redu: sklicna vrednost Cv, matrika iskanih vrednosti α in Cv, zaporedna stevilka stolpca matrike sklicnih vrednosti in ukaz, ki poisče priblizno vrednost izračuna. Sedaj lahko zapisemo enačbo in izračunamo vpadni kot prvega segmenta s prvo iteracijo po metodi 1.

(1.6)

Izračunani parametri zadosčajo za izračun indukcijskega aksialnega in tangencialnega količnika.

(1.6)

(1.6)

Kriterij konvergence iteracije spremljamo s pomočjo spremembe indukcijskih faktorjev Δa in Δa'.

(1.6)

in

(1.6)

Sledi druga iteracija, ki se za malenkost razlikuje od prejsnje. Izpusčen je kot relativne hitrosti, ki je bil pri prvi iteraciji podan v prvem stolpcu zaradi izbire priporočenih začetnih vrednosti iteracije. Iteracijo zaključimo takrat, ko se spremembe indukcijskih količnikov tem bolj priblizajo ničli. V primeru modela moramo iteracijo zaključiti ze pri drugi ponovitvi zaradi pogoja, ki omejuje vrednost indukcijskega količnika na 0,4, konvergenca zaradi turbulentnega toka ni mogoča.

Metoda 2

V primerjavi s prejsnjo, se razlikuje z uvedbo nove enačbe za izračun parametra lokalnega koeficienta sunka sile Ct, s katerim je moč z empirično relacijo aksialnega indukcijskega faktorja po Glauertu, poiskati resitev v okviru teorije o spremembi gibalne količine lopatice. Torej se vedno velja pogoj, da ne sme indukcijski faktor preseči vrednosti 0,4, oziroma mora imeti koeficient sunka sile vrednost manjso od 0,96. Postopamo kot v primeru prve iteracije, metoda 1, diagram (). Ocenimo začetne parametre rotorja, izvedemo postopek iteracije z izbranim vpadnim kotom in pripadajočimi aerodinamičnimi koeficienti, zatem izračunamo Ct, določimo a in a' in uporabimo izračunane podatke geometrije pri oceni moči rotorja.

Diagram ()

Pri oceni vpadnega kota za posamezen segment, uporabimo enačbi () in (), iz prejsnje iteracije.

(1.6)

Poisčemo ustrezen količnik vzgona in upora:

(1.6)

(1.6)

Sedaj lahko izračunamo količnik sunka sile Ct:

(1.6)

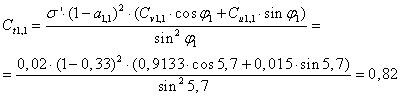
V primeru, da bi vrednost Ct presegla 0,96, bi bilo potrebno resevati parameter aksialnega indukcijskega faktorja po enačbi (), vendar to v nasem primeru ni bilo potrebno.

(1.6)

Resimo enačbi za izračun indukcijskih faktorjev, ki se od prejsnje metode razlikujeta po korekcijskem faktorju K.

(1.6)

(1.6)

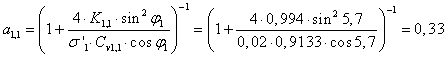
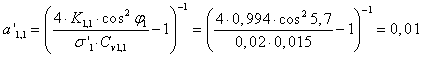
Končno lahko zaključimo z iteracijo in poisčemo tisti del, kjer se funkcija najbolj pribliza ničli. V nasem primeru je sprememba indukcijskih faktorjev najmanjsa pri peti iteraciji. Tabela z izračunanimi podatki je sedaj osnova pri izračunu izkoristka rotorja in je hkrati končna oblika lopatice pri danih pogojih. Za nadaljnjo optimizacijo rotorja, ko zelimo doseči večje izkoristke, z drugimi vstopnimi podatki, se celoten postopek ponovi, kar ima za posledico spremembo geometrije lopatic in s tem ponovna uporaba ene od metod iteracije.

Izkoristek rotorja je sestavljen iz vsote vseh segmentov lopatice rotorja. Za posamezen segment vstavimo podatke končne oblike lopatice, v enačbo ().

(1.6)

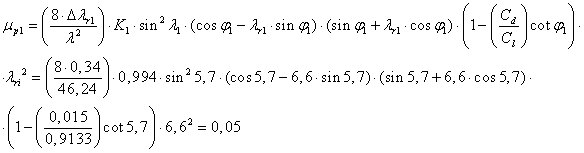
Z vsoto vseh segmentov izračunamo celoten izkoristek lopatice, oziroma rotorja.

(1.6)

Na koncu zapisemo se enačbo moči rotorja in upostevamo izračunan izkoristek.

(1.6)

Dobljen rezultat je maksimalna moč, ki jo lahko pridobimo iz vetra in je izračunana pri optimalnih obratovalnih pogojih za nazivni vpadni kot skozi celotno dolzino lopatice, pri specifičnem hitrostnem stevilu.

Karakteristična krivulja

V praksi je idealne pogoje ob spremenljivem zračnem toku, v daljsih časovnih intervalih, nemogoče doseči. Izkoristek rotorja se zato zmanjsa, kar definiramo v diagramu izkoristka rotorja pri različnih hitrostnih stevilih (). Krivulja je lastnost vsakega rotorja posebej. Izračunamo jo za interval obratovalnih hitrostnih stevil kar pomeni, da se pogoji delovanja spreminjajo ter s tem povezani parametri aerodinamičnih koeficientov, pri vsakem hitrostnem stevilu posebej. Preidemo v tabelo, ki je prirejena za izračun izkoristka rotorja pri konstantni geometriji in spreminjajočem se hitrostnem stevilu. Pri spremembi vstopnega veličine hitrosti zračnega toka, ostanejo parametri geometrije nespremenjeni, saj je glede na dinamične vplive iz okolice, učinek rotorja predmet modeliranja in zato konstanta. Ostali parametri v relaciji s hitrostjo imajo status odvisnih spremenljivk. Hitrostno stevilo se spreminja v obratnem sorazmerju s hitrostjo zračnega toka, zato poisčemo primerno hitrost, ki nam da ustrezen λ. Pri tem se uskladi relativna hitrost in definira Reynoldsonovo stevilo. Kot ze omenjeno se aerodinamični parametri spremenijo za vsako hitrostno stevilo posebej, zato je potrebno vstaviti v tabelo aerodinamičnih koeficientov podatke za primerno hitrost zračnega toka. Referenčni interval za izbiro parametra Re, se nahaja na zunanjem delu med 0,5 in 0,9 ri/R, kjer lopatica doprinese tudi največ moči. Z definiranimi aerodinamičnimi pogoji poisčemo bazo podatkov profila in jo vključimo v preračun. Postopek iteracije lahko sedaj steče za prvo hitrostno stevilo, za ostala je potrebno postopek ponoviti.

Primerjava

Pogoj za ustrezno primerjavo matematičnega modela z meritvenim, je v zagotovitvi identičnih vhodnih parametrov. Z izmerami geometrije referenčnega rotorja in posnemanjem razmer v vetrovniku, se tako ustvari matematični model popisan z numeričnimi vrednostmi, ki ustrezajo merilnim pogojem. Vrednosti geometrije rotorja in meritev iz vetrovnika podamo v tabeli () in ().

Tabela ()

Hitrost zračnega toka je bila omejena na trdnostne lastnosti rotorja, saj je zmogljivost vetrovnika omogočala opravljanje meritev pri večjih hitrostih, kot so bile izvedene. Izvedba generatorja električne napetosti, ki je sluzila kot zaznavalo merjenih veličin navora, el. toka in napetosti, ni dopusčala visje vrtilne frekvence. Inducirana napetost na el. motorju je bila visja od mozne, zagotovljene za zaviranje gredi rotorja. Iz tega razloga je turbina dosegla nizke vrednosti hitrostnega stevila in sorazmerno majhno moč. Karakteristike rotorjev lahko razberemo iz tabel () in (). Relevantna sta brezdimenzijska parametra, hitrostnega stevila in aerodinamičnega izkoristka, kar je temelj primerjave. Interval vrednosti je v primeru meritvenega modela nekoliko manjsi iz razlogov omenjenih na začetku. Prednost matematičnega modela je tako v moznosti napovedi karakteristike v celotnem razponu obratovanja. Porusitev vzgona nastopi pri hitrostnem stevilu 7, ko doseze izkoristek maksimalno vrednost, kar v primeru meritev ni bilo mogoče definirati. Maksimalne vrednosti aerodinamičnih izkoristkov pri omenjenih hitrostih znasajo 55% in 14%.

Tabela () in ()

\s

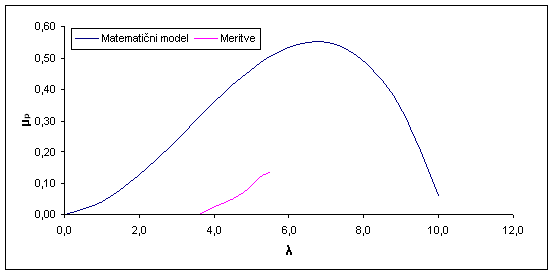
Diagram ()

Primerjavo karakteristik najlaze prikazemo v obliki diagrama, ki popisuje lastnosti obeh turbin. Prva ugotovitev in hkrati najbolj očitna je v nerazviti krivulji meritvene turbine. Nastane problem analize, tako da se osredotočimo zgolj na primerjavo učinka rotorja. Iz diagrama () je razvidno, da prihaja do občutnih neskladij med teoretično podanim rotorjem in meritvenim. Eden od vzrokov je zaradi upogiba lopatic in s tem spreminjanja aerodinamičnih lastnosti med samim obratovanjem. Deformacija prihaja do izraza pri večjih obremenitvah, torej pri visjih hitrostnih stevilih, kjer je analiza delovanja najvaznejsa. Ostali prav tako delujoči vplivi so mehanske izgube v lezajih, izgube generatorja električne napetosti, vpliv pesta na natok zraka na rotor,. Primerjavo učinka, lahko analiziramo v delovni točki, pri hitrostnem stevili 5,5, kjer sta vrednosti učinka 0,14 in 0,5. Razlika je za 0,36, kar je precej. Iz prakse vemo, da se gibljejo izkoristki večjih turbin pri vrednostih 0,4 in da so pri manjsih vrednosti se nizje. S tega stalisča je razlog za nesorazmerje tako v napaki izračunane vrednosti, kot tudi v meritvah. Boljse rezultate bi dosegli z meritvami večjega modela. Vpliv napak na izkoristek bi bili v tem primeru manjsi. Vse motnje na izvedbi in meritvah, bi tako lazje analizirali in optimirali potek eksperimentalnega modeliranja.

Zaključek

V nalogi sem se ukvarjal s postopkom aerodinamičnega dimenzioniranja aksialne vetrne turbine. Metoda, ki sem jo uporabil za popis modela, temelji na teoriji elementa in spremembe gibalne količine lopatice (BEM). Osnova delovanja tovrstnih rotorjev je Betzova meja, ki definira maksimalen učinek rotorja pri 59%. Postopek resevanja algoritmov je bil izveden v Ms Excelu in se je izkazal za fleksibilno resitev dimenzioniranja rotorjev. Poleg samega dimenzioniranja je bila izvedena tudi analiza ze obstoječe geometrije rotorja. Aplikacijo lahko uporabimo tako za modeliranje kot tudi za analizo lastnosti aerodinamike vetrnih turbin. Enostavno izračunamo karakteristiko rotorja za celoten interval obratovanja pri različnih aerodinamičnih lastnostih lopatice in jo grafično ponazorimo v obliki diagrama. Podobne obrazce za dimenzioniranje in analizo lahko izvedemo za različne tipe rotorjev, primer aksialnih ventilatorjev, v kateremkoli rezimu obratovanja.

Primerjava karakteristik meritev in matematičnega modela se ni izkazala za najbolj uspesno. Vzroki za to so najverjetneje v eksperimentalnem modeliranju vetrnih turbin, ki je v Sloveniji se v povojih. Boljse rezultate bi lahko dosegli z analizo in nadgradnjo samih meritev. Nato bi ji sledila ponovitev meritev na modelu. Veljavnost računalniskega programa bi lahko ovrednotili z meritvami različnih modelov vetrnih turbin. Napake v računalnisko podprti analizi, glede na visok izkoristek v izračunu, so predvidene v samem poteku izvajanja resevanja algoritmov. S teoretičnega stalisča metoda analize in dimenzioniranja ni sporna. Opravljene meritve na objektih se pokrivajo s teoretičnimi preračuni. Na njen pomen kaze tudi zgodovinsko ozadje izvedb v praksi, ki ima za seboj dolg spisek turbin, ki danes uspesno obratujejo. Rezultate matematičnega modela bi bilo potrebno primerjati z računalnisko podprto simulacijo fluidov ali drugimi namenskimi programi, ki temeljijo na teoriji BEM. Za izboljsavo meritvenega modela bi predlagal izvedbo lopatic iz karbonskih vlaken. Na ta način bi povečal kvaliteto meritev in poenostavil izdelavo testnih modelov. Za razvoj dokončnega modela izvedemo se analizo dinamične trdnosti. Določiti je potrebno mejo porusitve in optimirati nosilnost lopatice, s čimer bi zaključili proces razvijanja modela in presli na izvedbo prototipa.

Viri

John F. Falker, Nikolas Jenkins;    Wind energy technology

Siegfried Heier; Wind energy conversion systems

J.F.Manwell, J. G. McGowan, A. L. Rogers; Wind energy explained

Erich Hau; Wind turbines fundamentals, technologies, application, economics

UIUC Airfoil Data Site - https://www.ae.uiuc.edu/m-selig/ads.html

AirfoilPrep - https://wind.nrel.gov/

National renewably energy laboratory https://www.nrel.gov/wind/

[email protected]