La prueba de hipótesis sobre de igualdad de medias es uno de las aplicaciones más usadas por los investigadores en el campo de las ciencias sociales. El uso de software estadístico, como es el caso del SPSS, ofrece una variedad de procedimientos capaces de desempeñar de forma correcta este tipo de comparaciones.
Varios de estos procedimientos son bastante simples, diseñados expresamente para el manejo de este tipo de problemas, mientras otros son más generales, y necesariamente más complejos.
Para poder emplear adecuadamente cualquiera de estas opciones, los usuarios necesitan estar familiarizados con la estructura de los datos requerido por SPSS.
El SPSS, como la mayoría de los programas estadísticos, trabaja inicialmente sobre datos rectangulares (matrices de datos), donde las filas de la matriz rectangular representan los casos, mientras las columnas denotan las variables, como ya comentamos en el segundo capítulo.
De esta forma, la pregunta esencial que debemos resolver cuando nosotros vamos comparar dos o más medias es si estas representan a procesos de muestreos independientes o relacionados.
La segunda pregunta que deberemos resolver es si se quiere comparar las medias de dos o más de dos grupos de casos.
La estructuración para Muestreo 939e42j s Independientes Si la comparación deseada involucra a temas o datos independientes de muestreo, la estructura general seguirá el esquema general de una o más variables de agrupación para identificar qué tipo de datos representa, junto con los valores para la variable sobre la que nosotros deseamos comparar los grupos citados. Por ejemplo, supongamos que intentamos medir las diferencias en rendimiento académico de dos grupos de sujetos formados atendiendo a la condición del sexo. La estructuración apropiada de datos para una comparación de dos medias en estos dos grupos de casos sería:
|
GRUPO |
Y |
En otras palabras SPSS necesita un indicador de como hay que agrupar cada caso (en nuestro ejemplo esto es realizado por la variable llamada GRUPO), así como también el valor de la variable medida (en el ejemplo Y). Una vez que los datos son introducidos de acuerdo a este formato, cualquier de los procedimientos siguientes pueden usarse para obtener una prueba de la hipótesis nula sobre la igualdad de los dos grupos en la población:
T-TEST GROUPS=GRUPO /VAR=Y.(PRUEBA T PARA MUESTRAS INDEPENDIENTES)
ONEWAY Y BY GRUPO. (ANOVA DE UN FACTOR)
T-TEST GROUPS=GRUPO /VAR=Y.
Prueba T para muestras independientes

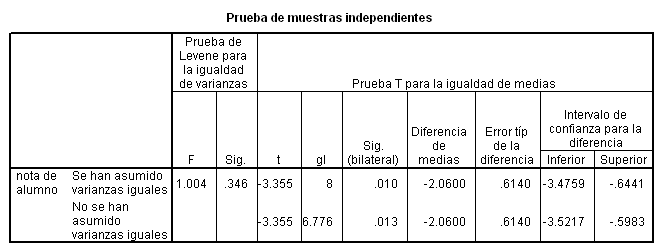
Observanción: el 0 no se encuentra en el intervalo de confianza, luego decimos que existe independencia.
ONEWAY Y BY GRUPO. (ANOVA DE UN FACTOR)

Para situaciones en que hay tres o más grupos se sigue la misma estructura, excepto que habrá más de dos valores para la variable GRUPO, y teniendo en cuenta además que no podemos usar el T-TEST como procedimiento para comparar más de dos de medias a un mismo tiempo.
Por ejemplo, supongamos el siguiente caso:
|
GRUPO |
Y |
Los procedimientos en SPSS que podriamos utilizar serían:
MEANS Y BY GRUPO/STATISTICS=ANOVA. (MEDIA...)
ONEWAY Y BY GRUPO. (ANOVA DE UN FACTOR)
MEANS Y BY GRUPO /STATISTICS=ANOVA.
Medias
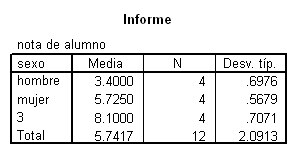
ONEWAY Y BY GRUPO. (ANOVA DE UN FATOR)

La estructuración para Muestreo 939e42j s Emparejados o Dependientes
Suponga que en vez de querer comparar las medias de dos o más grupos de casos independientes, nosotros ahora queremos hacer comparaciones entre las medidas tomadas sobre los mismos sujetos bajo diferentes o las mismas condiciones. A estas medidas repetidas en el tiempo, nosotros la identificaremos en este ejemplo como el factor TIEMPO.
La estructuración de datos es ahora diferente. Lo que representamos es una variable analizada en dos momentos distintos, y la forma de expresarlo es como si tuviesemos dos variables medidas para cada caso. Por ejemplo, podemos llamarlas TIEMPO1 y TIEMPO2, resultando una estructuración de datos semejante a la siguiente:
|
TIEMPO1 |
TIEMPO2 |
Los procedimientos MEANS, ONEWAY y ANOVA no son útiles a la hora de manejar este tipo de datos. La forma adecuada de indicarlo a hora es:
T-TEST PAIRS=TIEMPO1 TIEMPO2.
RELIABILITY VARIABLES=TIEMPO1 TIEMPO2
/STATISTICS=ANOVA.
MANOVA TIEMPO1 TIEMPO2
/WSFACTORS=TIEMPO(2).
T-TEST PAIRS=TIEMPO1 TIEMPO2.(PRUEBA T PARA MUESTRAS RELACIONADAS)


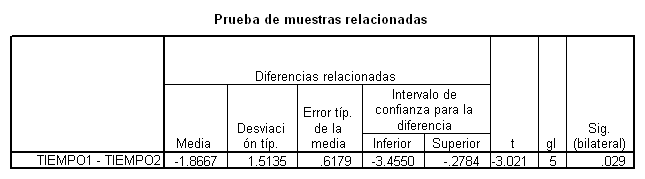
Si nos movemos en una comparación que involucre a más de dos medias relacionadas, no podríamos usar el procedimiento: T-TEST.
La estructura de los datos para más de dos medias relacionadas sería semejante a:
|
TIEMPO1 |
TIEMPO2 |
TIEMPO3 |
Siendo la sintaxis equivalente a:
RELIABILITY VARIABLES=TIEMPO1 TIEMPO2 TIEMPO3
/STATISTICS=ANOVA.
MANOVA TIEMPO1 TIEMPO2 TIEMPO3
/WSFACTORS=TIEMPO(3).
RELIABILITY
VARIABLES=TIEMPO1 TIEMPO2 TIEMPO3
/STATISTICS=ANOVA.
|
R E L I A B I L I T Y A N A L Y S I S - S C A L E (A L L) Analysis of Variance Source of Variation Sum of Sq. DF Mean Square F Prob. Between People 16.6383 5 3.3277 Within People 19.4867 12 1.6239 Between Measures 17.2800 2 8.6400 39.1541 .0000 Residual 2.2067 10 .2207 Total 36.1250 17 2.1250 Grand Mean 6.1500 Reliability Coefficients N of Cases = 6.0 N of Items = 3 Alpha = .9337 |
MANOVA
TIEMPO1 TIEMPO2 TIEMPO3
/WSFACTORS=TIEMPO(3).
|
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Tests of Between-Subjects Effects. Tests of Significance for T1 using UNIQUE sums of squares Source of Variation SS DF MS F Sig of F WITHIN CELLS 16.64 5 3.33 CONSTANT 680.81 1 680.81 204.59 .000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Tests involving 'TIEMPO' Within-Subject Effect. Mauchly sphericity test, W = .45846 Chi-square approx. = 3.11956 with 2 D. F. Significance = .210 Greenhouse-Geisser Epsilon = .64870 Huynh-Feldt Epsilon = .78113 Lower-bound Epsilon = .50000 AVERAGED Tests of Significance that follow multivariate tests are equivalent to univariate or split-plot or mixed-model approach to repeated measures. Epsilons may be used to adjust d.f. for the AVERAGED results. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. TIEMPO Multivariate Tests of Significance (S = 1, M = 0, N = 1 ) Test Name Value Exact F Hypoth. DF Error DF Sig. of F Pillais .97435 75.96058 2.00 4.00 .001 Hotellings 37.98029 75.96058 2.00 4.00 .001 Wilks .02565 75.96058 2.00 4.00 .001 Roys .97435 Note.. F statistics are exact. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Tests involving 'TIEMPO' Within-Subject Effect. AVERAGED Tests of Significance for TIEMPO using UNIQUE sums of squares Source of Variation SS DF MS F Sig of F WITHIN CELLS 2.21 10 .22 TIEMPO 17.28 2 8.64 39.15 .000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - |
La estructura de los datos para dos medias relacionadas o más y una o más independientes sería equivalente a:
|
GRUPO |
TIEMPO1 |
TIEMPO2 |
La única solución es utilizar la información dada por MANOVA, y esta información única será estrictamente válida bajo algunas suposiciones bastante severas. Siendo su sintaxis equivalente a:
MANOVA TIEMPO1 TIEMPO2 BY GRUPO(1,2)
/WSFACTORS=TIEMPO(2).
MANOVA
TIEMPO1 TIEMPO2 BY GRUPO(1,2)
/WSFACTORS=TIEMPO(2).
|
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Tests of Between-Subjects Effects. Tests of Significance for T1 using UNIQUE sums of squares Source of Variation SS DF MS F Sig of F WITHIN CELLS 7.05 6 1.17 GRUPO 9.00 1 9.00 7.66 .033 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Tests involving 'TIEMPO' Within-Subject Effect. Tests of Significance for T2 using UNIQUE sums of squares Source of Variation SS DF MS F Sig of F WITHIN CELLS .38 6 .06 TIEMPO 5.76 1 5.76 90.95 .000 GRUPO BY TIEMPO .09 1 .09 1.42 .278 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - |
|