'

(system) — сукупність об`єктів і відношень між ними, що утворюють єдине ціле в процесі системогенезу. Аналізуються, оцінюються, проектуються та керовані оптимально за алгоритмом ситемогенезу. Формалізований опис систем за алгоритмом системогенезу дозволяє порівнювати та класифікувати системи, віводячи та використовуючи основоположні базові критерії систем та системності.

», як наука все більше і більше розвивається через високу потр& 858j99i #1077;бу правильного прийняття рішень, вибір якого принесе як найбільшу користь.

В даній курсовій роботі досліджується система «Шахи», де розглядаються дуже цікаві і актуальні проблеми, відповідь на які допоможуть організаторам турнірів та тренерів отр& 858j99i #1080;мати правильну відповідь у прийнятті рішення. На

Вводиться п'ять аксіом і доводиться існування функції корисності. Дамо змістовне представлення цих аксіом. Позначимо через х, у, z різні результати процесу вибору, а через р, q вірогідність тих або інших результатів. Введемо визначення лотереї. Лотереєю називається гра з двома результатами: результатом х, що отр& 858j99i #1080;мується з вірогідністю р, і результатом у, отр& 858j99i #1080;муваним з вірогідністю 1-р (мал. 1).

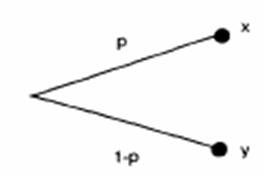Мал.1 Представлення лотереї

Прикладом лотереї є підкидання монети. При цьому, як відомо, з вірогідністю р=0,5 випадає орел або решка. Хай х=$10 і у=-$10 (тобто ми отр& 858j99i #1080;муємо $10 при випадінні орла і платимо стільки ж при випаданні решки). Очікувана (або середня) ціна лотереї визначається по формулі рх+(1-р)у. Приведемо аксіоми раціонального вибору.

Аксіома 1. Результати х, у, z належать безлічі А результатів.

Аксіома 2. Хай Р означає строгу перевагу (схоже на відношення > в математиці); R — нестрога перевага (схоже на відношення >= в математиці); I байдужість (схоже на відношення =). Ясно, що R включає Р і I. Аксіома 2 вимагає виконання двох умов:

1) зв'язаність: або xRy, або yRx, або те і інше разом;

2) транзитивності: з xRy і yRz виходить xRz.

Аксіома 3. Дві представлені на мал.2 лотереї знаходяться у відносній байдужості. Справедливість цієї аксіоми очевидна. Вона записується в стандартному вигляді як ((х, р, у)q, у) I (х, pq, у).

Мал. 2. Дві лотереї, що знаходяться відносно байдужості

Аксіома 4. Якщо х1у, то (х, р, z) I (у, р, z).

Аксіома 5. Якщо хРу, то хР(х, р, у) Ру.

Аксіома 6. Якщо xРyРz, то існує вірогідність р, така що у1(х, р, z). Всі приведені вище аксіоми досить прості для розуміння і здаються очевидними. У припущенні, що вони виконуються, була доведена наступна теорема: якщо аксіоми 1—6 задовольняються, то існує чисельна функція U, визначена на А (множина результатів) і така, що:

1) xRy тоді і лише тоді, коли U(x)> U(y);

2) U(x, р,у )= pU(x)+(l-p)U(y).

Функція U(x) вимірюється на шкалі інтервалів. Функція U(x) – єдина (наприклад, якщо U(x)> U(y), то і aU(x)> aU(y), де а — ціле позитивне число)

Із 166 учасників турніру,які подали заявки, для 62 більше підходять картонні дошки , а для решти – дерев’яні. Якщо буде закуплено картонні дошки, то, клубний внесок для проведення турніру складе

Необхідно знайти функцію корисності, оцінити середній очікуваний прибуток і на основі отр& 858j99i #1080;маних даних обрати кращу альтернативу для закупівлі

За 10 грн. є можливість додатково звернутися до експерта, який може проаналізувати хід шахового турніру, і визначити, які шахові фігури більш вигідніше застосувати. Провівши серію тестових досліджень, експерт може стверджувати, що на фігури потр& 858j99i #1110;бно витратити 14 грн., на закупівлі деревяних фігур можна зекономити 6 грн. , а на пластмасових −14.

Після проведення досліджень можна зробити висновок, що найкращим варіантом є закупівля дерев’яних дошок та пластмасових фігур, а послуги експерта не потр& 858j99i #1110;бні та не вигідні

ПРИЙНЯТТЯ РІШЕНЬ ЩОДО БУДОВИ НОВОГО НАВЧАЛЬНОГО КОРПУСУ УНІВЕРСИТЕТУ НА ОСНОВІ ІНДИВІДУАЛЬНОГО ВИБОРУ .

На практиці індивідуальні завдання ухвалення рішень вельми поширені в суспільстві. Візьміть фірми, компанії, банки. Не дивлячись на існування колегій, правлінь і рад, зазвичай є центральна фігура - ЛПР, що визначає курс, тактику і стратегію дій на майбутній період. Від прозорливості цього лідера, його особистих якостей залежить дуже багато що. Серед подібних якостей в успішних ЛПР обов'язково присутнє уміння домовлятися з людьми, переконувати їх в правильності і обґрунтованості своїх дій. Те ж саме ми бачимо в урядах, політичних партіях — там завжди висуваються лідери, і саме вони приймають основні рішення. Широка поширеність завдань індивідуального вибору, можливість врахувати колективні переваги, прістра­ стія і інтереси активних груп при вирішенні цих завдань роблять в даний час проблеми індивідуального вибору найбільш практично важливим класом завдань ухвалення рішень. Тому особливу увагу ми приділятимемо саме процесам ухвалення індивідуальних рішень.

Ø  проводити навчання у нинішньому корпусі (рішення );

Ø  орендувати додатково навчальний корпус на околиці міста (рішення );

Ø  орендувати додатково навчальний корпус у центрі міста (рішення );

Ø  купити додатковий навчальний корпус на околиці міста (рішення );

Ø  купити додатковий навчальний корпус у центрі міста (рішення ).

Ø 

Ø  набір учасників у кількості 90% від минулорічного набору (стан );

Ø  набір учасників у кількості, що дорівнює минулорічному набору (стан );

Ø  набір учасників у кількості, що на 10% більше за минулорічний набір (стан );

Ø  набір учасників у кількості, що на 20% більше за минулорічний набір (стан );

Ø  набір студентів у кількості, що на 25% більше за минулорічний набір (стан ).

Значення функції переваг рішень для станів задані в таблиці 6:

Таблиця 6. Значення функції переваг рішень для станів

 Таким чином за критерієм Гурвіца оптимальне рішення Y*=Y2,4,5

за критерієм максимуму середнього виграшу оптимальне рішення Y*=Y1,6.

Метод Дельфи отр& 858j99i #1080;мав назву від грецького міста Дельфи, що прославилося мудрецями, що жили там, – провісниками майбутнього.

Метод Дельфи – це багатотурова процедура анкетування. Після кожного туру дані анкетування допрацьовуються, отр& 858j99i #1080;мані результати повідомляються експертам з вказівкою розташування оцінок.

принципу більшості голосів – вибирається те рішення, яке має найбільше число прихильників;

принципу диктатора – за основу береться думка одного обличчя групи.

принципу Курний – використовується у тому випадку, коли коаліцій немає, тобто пропонується число рішень, рівне числу експертів. В цьому випадку необхідно знайти таке рішення, яке б відповідало вимозі індивідуальної раціональності без утиску інтересів кожного окремо;

принципу Парето – використовується при ухваленні рішень, коли всі експерти утворюють єдине ціле, одну коаліцію. В цьому випадку оптимальним буде таке рішення, яке невигідно міняти відразу всім членам групи, оскільки воно об'єднує їх в досягненні загальної мети;

принципу Еджворта – використовується в тому випадку, якщо група складається з декількох коаліцій, кожною з яких невигідно відміняти своє рішення. Знаючи переваги коаліцій, можна ухвалити оптимальне рішення, не завдаючи збитку один одному.

Ранжування – процедура впорядкування об’єктів, яку виконує експерт або ОПР. Якщо серед об’єктів немає однакових за показниками, які порівнюються, тобто немає еквівалентних об’єктів, то між об’єктами існує лише впорядкування строгого порядку.

Побудова узагальненої групової оцінки об’єктів відбувається шляхом обробки індивідуальних оцінок експертів. Найчастіше таку оцінку отр& 858j99i #1080;мують шляхом підсумовування індивідуальних оцінок із ваговими коефіцієнтами компетентності. Так само як і при індивідуальному виборі експертні оцінки можуть бути виражені у кількісній шкалі або в рангах. При вимірюванні в рангах на основі матриць попарних порівнянь об’єктів експертами складають узагальнену матрицю парних порівнянь, за якою й визначають групову оцінку пріоритетів об’єктів.

Вважаючи, що найбільш переважаюча альтернатива має ранг рівний 1, а найгірша − ранг 5, то маємо таке впорядкування об'єктів.

Так як Хкр більше ніж Хсп, то отр& 858j99i #1080;мане ранжування вважається статистично не значимим.