Двохетапні задачі стохастичного п 757g65h 88;ограмування

Недоліком розглянутих одноетапних задач стохастичного п 757g65h 88;ограмування є те, що в них лише фіксується факт можливих відхилень значень випадкових параметрів і усереднені розв’язки вибирають за умови, що відхилення значень від середнього рівня в будь-який бік небажане (зменшується величина дисперсії параметрів у обмеженнях або цільова функція — дисперсія мінімізується). У більшості реальних економічних задач має значення не лише величина відхилення, але також і його напрямок. Двохетапні задачі стохастичного п 757g65h 88;ограмування позбавлені зазначеного недоліку.

Розглянемо задачу стохастичного п 757g65h 88;ограмування в такій постановці:

(10.10)

(10.11)

(10.12)

виникає дефіцит. Позначимо його через

— питомі витрати на збереження надлишків та — питомі витрати, що п 757g65h 86;в’язані з дефіцитом . Отже, можна визначити штрафну функцію для і-го обмеження за результатом його виконання. Позначимо її через S, тоді:

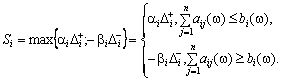
(10.13)

(10.14)

(10.15)

та можна розглядати як такі, що забезпечують виконання обмежень (10.11) як рівностей.

згідно з апріорною інформацією про стан зовнішнього середовища, який і визначає реалізацію випадкових параметрів. Значення вектора Х не задовольняє обмеження задачі для кожного та , що компенсують відхилення, які виникли за попереднім планом Х. Витрати на корекцію початкового п 757g65h 83;ану визначаються як

Детерміноване моделювання не дає змоги об’єднати два етапи: прийняття плану та його коректування. Перехід від детермінованих моделей до стохастичних, в яких використовуються випадкові величини, що саме і викликають необхідність корекції, уможливлює отримання математичних моделей, що об’єднують вищеназвані два етапи планування. Отже, в результаті розв’язу­вання двохетапних стохастичних задач отримують плани, що є стійкими за умов невизначеності і мінімізують загальні витрати на реалізацію і корекцію плану, тобто забезпечують загальний ефект від попереднього п 757g65h 83;ану та його корекції.

У моделях двохетапного стохастичного п 757g65h 88;ограмування відоб­ражаються найхарактерніші особливості планування за умов невизначеності:

вибір попереднього п 757g65h 83;ану з урахуванням його майбутнього коректування,

коректування попередньо вибраного п 757g65h 83;ану по мірі уточнення інформації.

Модель (10.13)—(10.15) — найпростіша двохетапна модель стохастичного п 757g65h 88;ограмування. У загальному випадку план-корекція вводиться в систему обмежень з допомогою матриці корекції загального вигляду, елементи якої можуть залежати від ω, тобто розглядається система нерівностей:

(10.16)

(10.17)

Попередній план Х вибирається до спостережень над ω. Коли ω стає відомим, то визначають план-корекцію Y у такий спосіб, щоб виконувались співвідношення (10.16), (10.17). При цьому ефект від плану-корекції дорівнює:

(10.18)

Оскільки з кожним планом-корекцією Y пов’язаний певний ефект, то при певному Х і спостереженому ω його краще за все вибирати з умови максимізації (10.18) за обмежень (10.16), (10.17). Позначимо такий план через і назвемо його опти тити, що існує при кожному Х і ω, у протилежному разі в (10.16) можна ввести штучні змінні Y

(10.19)

(10.20)

(10.21)

Y

(10.22)

(10.23)

(10.24)

. Задача (10.22)—(10.24) на відміну від (10.19)—(10.21) лінійна, однак, якщо в задачі (10.19)—(10.21) розв’язком є n-вимірний вектор Х, для пошуку якого можна застосувати чисельні методи, то в задачі (10.22)—(10.24) невідомими є і застосувати для розв’язування задачі чисельні методи можна лише за умови, якщо Ω — скінченна множина з невеликою кількістю елементів.

Розглянемо в загальному вигляді найпростішу стохастичну задачу з визначення оптимального п 757g65h 83;ану виробництва.

, а питомі витрати, що п 757g65h 86;в’язані зі зберіганням надлишку продукції та компенсацією дефіциту, — відповідно через та

та (що, як правило, виконується) отримуємо тривіальну відповідь:

Потрібно п 757g65h 77;ревезти однорідну продукцію від двох постачальників трьом споживачам. Обсяг продукції першого п 757g65h 86;стачальника a a

Відомі також витрати на перевезення одиниці продукції від кожного п 757g65h 86;стачальника до кожного споживача, що наведені в табл. 10.9 в умовних одиницях:

Якщо п 757g65h 86;пит на продукцію буде більшим, ніж її наявність, то необхідно буде сплатити штраф за недопостачання кожної одиниці продукції першому, другому та третьому споживачам обсягом відповідно 105, 169 і 86 ум. од., а якщо попит буде меншим, то необхідно буде зберігати надлишки, що п 757g65h 86;требуватиме додаткових витрат на одиницю продукції обсягом відповідно 40, 45 та 30

— обсяги перевезень продукції від і-го п 757g65h 86;стачальника до j-го споживача, а невідомі величини, що характеризують обсяги недопостачання та надлишки, — відповідно векторами

Тоді математична модель двохетапної задачі стохастичного п 757g65h 88;ограмування зведена до задачі лінійного п 757g65h 88;ограмування

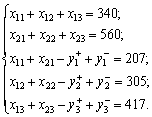
. Мінімальні витрати дорівнюють: F = 35 744 ум. од.

Одним із способів урахування випадкових процесів та явищ є застосування методів стохастичного п 757g65h 88;ограмування.

Головною метою використання стохастичних моделей і методів оптимального п 757g65h 83;анування є врахування всього діапазону можливих значень параметрів, що вивчаються, та імовірнісного характеру використаної інформації. Причини імовірнісного характеру вхідної інформації для економіко-математичних моделей відомі: наявність випадкових помилок при зборі даних, випадковість економічних процесів, вплив погодних умов на деякі галузі матеріального виробництва. Вивчення, а також практичне застосування стохастичних моделей дає змогу не лише підвищити наукову обґрунтованість та точність планових розрахунків, але також і розглянути ряд цікавих задач, розв’язування яких із застосуванням детермінованих моделей неможливе.

Однією з важливих переваг, що дає використання методів і моделей стохастичного п 757g65h 88;ограмування, є можливість знаходження оперативних та перспективних планів розвитку системи, що досліджується, які можна коригувати, причому в такому разі сумарні витрати на реалізацію плану та його п 757g65h 86;дальшу корекцію будуть мінімальними.

Необхідно зазначити, що більшість практично цікавих моделей стохастичного п 757g65h 88;ограмування має ряд особливостей, які не дають змоги застосовувати до них традиційні методи нелінійного п 757g65h 88;ограмування. Тому останнім часом інтенсивно розвиваються прямі методи стохастичного п 757g65h 88;ограмування, з допомогою яких стало можливим розв’язування подібних задач.

Сутність задач стохастичного п 757g65h 88;ограмування.

За якими ознаками можлива класифікація задач стохастичного п 757g65h 88;ограмування?

,

,

ва менший від попиту, або невиправданих витрат у протилежному разі.

Нехай введено такі позначення: ξ — випадковий попит на продукцію; С — ціна на реалізовану продукцію; g — питомі витрати на її виробництво; x — шуканий обсяг виробництва продукції.

Для виробництва двох видів виробів можна використати обладнання двох типів Затрати часу використання обладнання для виготовлення продукції є випадковими величинами. Собівартість одного виробу буде також випадковою величиною. Нехай щільності розподілів випадкових величин та відомі: розподілені за нормальним законом з математичними сподіваннями та середніми квадратичними відхиленнями а розподілені рівномірно на інтервалі .

N N N N

рактів становить не більше як 0,10, а ризик невиконання контракту не більший за 0,05.