Поняття „еластичність” попиту. Фактори і с 656g67g 90;упені еластичності попиту.
1. Поняття „еластичність” попиту. Фактори і с 656g67g 90;упені еластичності попиту
 |
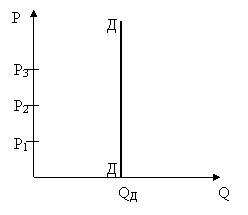Істотна зміна ціни призводить до незначної зміни величини попиту 0 > ЕРД < 1. В умовах жорсткого попиту вигідно підвищувати ціну, що веде до незначного зменшення покупок.
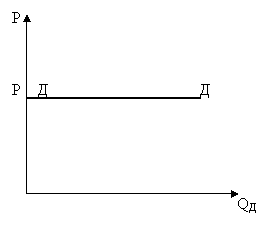
ЕРД>1. Для товарів еластичного попиту підвищення ціни призводить до скорочення загальної виручки від продажу. Ціну вигідно знижувати, якщо є можливість збільшити величину збуту, тоді загальна виручка від продажу зростає.
та абсолютно еластичний попити), але вони іноді дають корисні точки відліку в мікроекономічному аналізі.
,
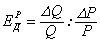де ∆Q ‑ зміна величини попиту;
∆Р ‑ зміна ціни;
.
 |
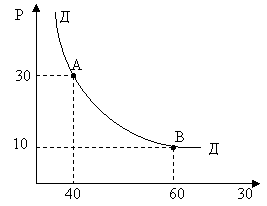∆Q = 60 - 40 = 20
Q = (40 + 60)/2 = 50
,
попит
нееластичний.
.
Наприклад, дана функція попиту QД = 300 - 2р. Визначимо коефіцієнт еластичності попиту в точці А, при Ра = 75.
QД = 300 – 2 • 75 = 150
(QД)' = -2
,
де ∆Q‑ зміна величини попиту;
∆І ‑ зміна доходу споживача.
Звичайно, ЕІД> 0 ,але для товарів Гіффена ЕІД < 0.
,
де 
‑
∆Qх ‑ зміна величини попиту на товар X;
∆Ру – зміна ціни товару У.
Якщо En = 0 , тоді дані товари незалежні. Якщо товари взаємозамінні, то En > 0, якщо En < 0, то товари взаємно доповнюють один одного. Таким чином, за величиною перехресної еластичності попиту можна судити про ступінь замінності або доповнюваності товару.
,
де ∆QS – зміна величини пропозиції;
∆Р – зміна ціни;
.
Для
миттєвого
періоду, коли
продукт вже
вироблено,
його
кількість є
величина
постійна, 
. Графічно
ця ситуація
показана на
рис. 2.22 (крива IS).
У
короткостроковому
періоді
пропозиція може
якоюсь мірою
пристосовуватися
до змін ціни
на певній
частині
кривої
пропозиції
(рис. 2.22 крива SS),
а 
. Однак при
цьому
можливості
виробництва
обмежені і в
міру
наближення
до гранично
можливого
обсягу (Q*)
еластичність
пропозиції
знижується,
добігаючи
нуля.
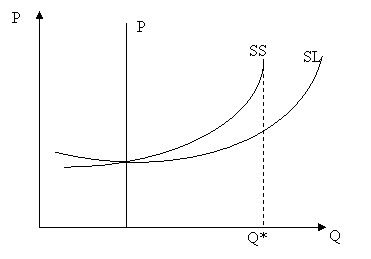У
довгостроковому
періоді
можливості
пристосування
розширюються,
а коефіцієнт
еластичності
зростає.
Обмеженість
пропозиції
при цьому,
зазвичай, не
відіграє
суттєвої
ролі (рис. 2.22
крива SL
Рис. 2.22 – Криві пропозиції у миттєвому періоді (IS), короткостроковому періоді (SS), довгостроковому періоді (SL)
а) 
;
б) ;
в) ;
г) 
.
Сучасна теорія виробництва склалася наприкінці XIX – початку XX ст. У явному вигляді виробнича функція була представлена в 1890р. англійським математиком А.Беррі, який допомагав А.Маршаллу при підготовці математичного додатку до “Принципів економікс”.
q = f(x),
де q - величина випуску (результат виробництва),
х - витрати фактора виробництва.
 |
q = f(x1,х2),
де q - величина випуску,
x1 і х2 - витрати факторів виробництва.
Виробничу функцію даного виду неможливо зобразити на площині, вона може бути подана у тривимірному просторі. Дві координати (х1 та x2) відкладаються на горизонтальних осях, а третя (q) – на вертикальній осі і відповідає випуску продукту. Розглянемо цю ситуацію на рис. 3.2.
а) б)
Графіком виробничої функції служить поверхня 'горба', що підвищується зростанням кожної з координат х1 і x2. При цьому графік на рис. 3.1 можна розглядати як вертикальний розріз 'горба' площиною, паралельною осі х1, що відповідає фіксованому значенню другої координати x2= x
Якщо горизонтальний переріз поверхні 'горба' зобразити окремо на площині з координатами х1 і x2, то буде крива, що об'єднує такі комбінації витрат ресурсів, які дозволяють отримати даний фіксований обсяг випуску продукту. Ця крива отримала назву ізокванти (isoquant) виробничої функції (рис.3.3).
 |
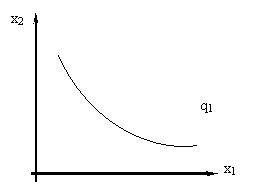або 
.
 |
q = f(x1, x2, …xn).
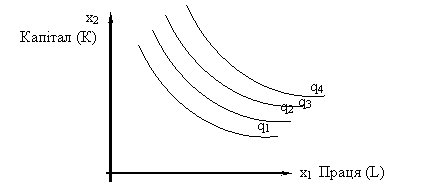
Усе, що було сказано про виробничу функцію двох аргументів, можна перенести і на функцію значного числа аргументів із застереженням: ізокванти цієї функції – не плоскі криві, а n-мірні поверхні. Проте ми і в подальшому аналізі будемо користуватися “плоскими ізоквантами” – в ілюстративних цілях, і як зручним способом аналізу у випадках, коли витрати двох ресурсів є змінними, а інші – постійними.
Яким чином буде змінюватися обсяг виробництва в міру того, як все більша і більша кількість змінних ресурсів буде приєднуватися до фіксованих ресурсів фірми? У найзагальнішій формі відповідь на це запитання дає закон спадної віддачі. Цей закон стверджує, що починаючи з певного моменту, послідовне приєднання одиниць змінного ресурсу (наприклад, праці) до незмінюваного фіксованого (наприклад, капіталу) дає зменшуваний додатковий (граничний) продукт з розрахунку на кожну наступну одиницю змінного ресурсу. (Закон уперше був сформульований у XVIII ст. французьким економістом А.Тюрго щодо сільського господарства і мав назву закону спадної родючості грунту'). Закон спадної віддачі не доводиться формально, він виведений емпіричним шляхом на підставі численних спостережень. Цей закон має універсальний характер, тобто застосовується до будь-якого виробництва.
Загальний продукт (ТР - Total product) – це загальна кількість виробленого продукту у натуральному вираженні, що зростає із збільшенням використання змінного фактора (рис. 3.6).
 |
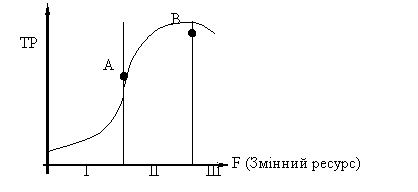На стадії І зростання випуску загального продукту випереджає зростання затрати змінного фактора F. На стадії II загальний продукт зростає повільніше, ніж затрати змінного ресурсу. На III стадії зростання затрат таке, що супроводжується зниженням обсягу виробництва.
Середній продукт (АР - averаge product). Якщо загальний продукт поділити нa використовуваний у його виробництві змінний ресурс F, отримаємо показник середнього продукту
.
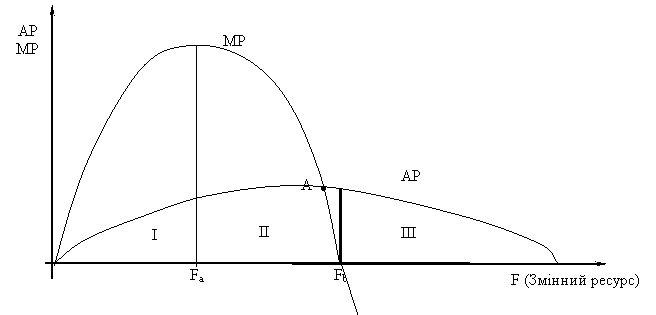
Граничний продукт (МР – marginal product) - це додатковий випуск продукції, що утворюється при додаванні одиниці змінного ресурсу. Визначається за формулою
.
Граничний продукт характеризує граничну продуктивність ресурсу. На графіку (рис.3.7) видно, що на І стадії крива МР зростає швидше за АР, що пояснюється методикою розрахунку цих показників. На II стадії граничний продукт (МР) убуває, а середній продукт (АР) зростає до точки свого максимуму (точка А), а потім убуває, але повільніше, ніж граничний продукт (МР). На III стадії граничний продукт (МР) набуває негативного значення.
фірми. Однак більшість ділових рішень приймається не в натуральних, а в грошових одиницях. Значить, нашим наступним кроком буде переформування обмежень, сполучених кривими продукту в грошовій термінології (ця проблема детально розглядається у темі 8).
,
ΔL – зміна розміру праці.
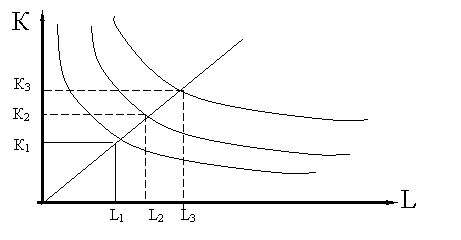
Граничну норму технологічного заміщення факторів виробництва можна розрахувати й через граничні продукти. Дійсно, якщо при зменшенні капіталу з К1 до К2 та зростанні кількості праці з L1 до L2 (рис. 3.8)
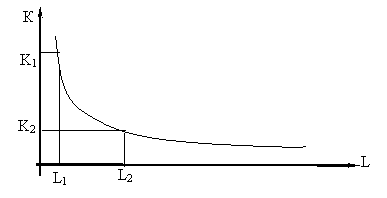
, тоді 
.
1) фактори виробництва можуть використовуватися лише у певній пропорції. У цьому випадку ізокванта матиме вигляд прямого кута, а MRTS дорівнюватиме нулю; 2)повне заміщення факторів виробництва. За такої умови ізокванта мала б вигляд прямої лінії з постійним нахилом, який дорівнює 1.
 |
а) 
;
б) 
;
в) 
;
г) 
.
а) U = f(x);
б) U = f(x1, x2, …xn);
в) U = U1(x1)+U2(x2)+…+Un(xn);
г) q = f(x).
|
