UNIVERSITATEA DIN ORADEA
FACULTATEA DE STIINTE ECONOMICE
SPECIALIZAREA MANAGEMENT
Modelul econometric pentru
Cifra de afaceri din industrie si
Productia industriala
Oradea, 2009
CUPRINS
|
|
Pagina |
|||
|
Introducere . |
|
|||
|
1. Ipoteze fundamentale |
|
|||
|
2. Determinarea estimatorilor de regresie liniara prin metoda celor mai mici patrate |
|
|||
|
3. Testarea validitatii modelului |
|
|||
|
3.1. Testarea validitatii modelului de regresie folosind metoda descompunerii variantei |
|
|||
|
3.2. Calcularea coeficientului de corelatie R2, a coeficientului de corelatie corectat si testarea reprezentativitatii lui |
|
|||
|
3.3. Teste si regiuni de incredere pentru coeficienti |
|
|||
|
3.3.1.Testarea validitatii estimatiei coeficientilor |
|
|||
|
3.3.2. Intervale de incredere pentru coeficienti |
|
|||
|
3.4. Testarea ipotezelor fundamentale referitoare la variabila 616d38g aleatoare ε |
|
|||
|
a) analiza legaturii dintre cele doua variabile (studiul aspectului norului de puncte) b) determinarea modelului c) determinarea estimatorilor de regresie liniara prin metoda celor mai mici patrate d) testarea validitatii modelului testarea validitatii modelului de regresie folosind metoda descompunerii variantei; calculul raportului de corelatie si testarea semnificatiei lui; inferenta statistica pentru parametrii modelului de regresie; testarea ipotezelor fundamentale referitoare la variabila 616d38g aleatoare ε ipoteza de homoscedasticitate ipoteza independentei ipoteza de normalitate e) Previziunea variabilei Y Pentru analiza
legaturii dintre variabilele Cifra de afaceri din industrie si Productia
industriala, am ales urmatorul model: unde: Yt = Cifra de afaceri din industrie din luna t Xt = Productia industriala din luna t εt = variabila reziduala T = numarul de observatii = 110 1. Ipoteze fundamentale
(i) xt si yt reprezinta valori numerice ale variabilelor X si Y rezultate prin observarea statistica, neafectate de erori sistematice; (ii) Y = Indicii valorici ai cifrei de afaceri din unitatile industriale pe total (piata interna si piata externa) , este variabila endogena aleatoare, pentru ca este functie de (iii) X = Indicii productiei industriale - lunari, pe activitati ale industriei - serie bruta , variabila explicativa, este considerata ca fiind o variabila determinista in model, nealeatoare;
(i) ε are o distributie independenta de timp, de speranta matematica nula, respectiv: E (εt) = 0, ( ) t = 0, 1, 2, ., T V
(εt) = E[εt - E(εt)]2
= altfel spus, modelul este homoscedastic. Dependent Variable: CA |
|
|
||
|
Method: Least Squares |
|
|
||
|
Date: 05/12/09 Time: 13:23 |
|
|
||
|
Sample: 2000M01 2009M02 |
|
|
||
|
Included observations: 110 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
PI |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
|
Mean dependent var |
|
|
|
Adjusted R-squared |
|
S.D. dependent var |
|
|
|
S.E. of regression |
|
Akaike info criterion |
|
|
|
Sum squared resid |
|
Schwarz criterion |
|
|
|
Log likelihood |
|
F-statistic |
|
|
|
Durbin-Watson stat |
|
Prob(F-statistic) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coefficientsa |
||||||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
||
|
B |
Std. Error |
Beta |
||||
|
|
(Constant) |
|
|
|
|
|
|
VAR00002 |
|
|
|
|
|
|
|
a. Dependent Variable: VAR00001 |
|
|
|
|||
3. Testarea validitatii modelului
Masura variatiei
Numarul gr. de libertate
Dispersii
corectate
Valoarea testului F
Fcalc
Fα;v1;v2
Varianta explicata de model, datorata factorului X
k = 1
Varianta
Reziduala, datorata factorilor neesentiali
T - k - 1= 108
Varianta
totala
T - 1=109
ANOVAb
Model
Sum of Squares
df
Mean Square
F
Sig.
Regression
0,000a
Residual
Total
a. Predictors: (Constant), VAR00002
b. Dependent Variable: VAR00001
Model Summary
Model
R
R Square
Adjusted R Square
Std. Error of the Estimate
0,759a
a. Predictors: (Constant), VAR00002
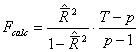
Se compara valoarea calculata a lui F cu cea tabelara. Regulile de decizie sunt urmatoarele:
- daca Fcalc < Ftab, ipoteza nula este cea care este acceptata, fapt echivalent cu inexistenta unei legaturi intre cele doua variabile la nivel de populatiei totala.
- daca Fcalc > Ftab, ipoteza nula este cea care se respinge, acceptandu-se cea alternativa.
Deoarece Fcalc = 142,56 > Ftab = 3,96, se accepta ipoteza H1 garantandu-se cu o probabilitate de 95%, ca intre cele doua variabile exista legatura la nivelul populatiei totale.
Coefficientsa
Model
Unstandardized Coefficients
Standardized Coefficients
t
Sig.
B
Std. Error
Beta
(Constant)
VAR00002
a. Dependent Variable: VAR00001
Valorile 
sunt:
3.3.2. Intervale de incredere pentru coeficienti
Ø Forma intervalului de incredere pentru coeficientul a al modelului este:
unde
- termenul liber
- abaterea medie patratica a coeficientului a
Se cunoaste = 2,755, = 0,227 si ttab
= 1,96, iar probabilitatea de garantare a rezultatelor este 95%, deci putem
face calculele:
Putem garanta deci, cu o probabilitate de 95%, ca valoarea coeficentului a, la nivelul populatiei totale, este cuprinsa intre 2,32 si 3,18.
Ø Forma intervalului de incredere pentru coeficientul b al modelului este:
unde
- termenul liber
- abaterea medie patratica a coeficientului b
Se cunoaste =-206,27, = 24,32 si ttab = 1,96, iar probabilitatea de garantare a
rezultatelor este 95%, deci putem face calculele:
Putem garanta deci, cu o probabilitate de 95%, ca valoarea coeficentului b, la nivelul populatiei totale, este cuprinsa intre -253,93 si -158,61.
3.4. Testarea ipotezelor fundamentale referitoare la variabila 616d38g aleatoare ε
Pe langa influenta factorilor esentiali, asupra marimii Cifrei de afaceri (Y) isi exercita influenta si alti factori, care sunt surprinsi prin variabila ε. Acesti factori ar putea fi: conditiile de mediu, concurenta, nivelul inclinatiei spre economisire a consumatorilor etc. .
3.4.1. Ipoteza de homoscedasticitate a variabilei reziduale
Pentru a verifica ipoteza de homoscedasticitate a erorilor
modelului 
se foloseste testul White; se pleaca de la
ecuatia
si se doreste sa se studieze daca intre ,
xt si xt2 exista o legatura. Daca intre aceste
variabile exista legatura, despre erorile modelului se spune ca sunt
heteroscedastice, daca nu - ele se numesc homoscedastice.
Existenta legaturii la nivelul esantionului este indicata de raportul de corelatie estimat, iar pentru generalizarea rezultatelor se emit ipotezele:
- daca 
,
ipoteza H0 se respinge, si se accepta ca fiind adevarata, cu o
probabilitate de 95%, ipoteza H1, ceea ce inseamna ca erorile sunt
heteroscedastice, acest lucru garantandu-se cu o probabilitate de 95%. In acest
caz modelul nu este valid, el neputand fi folosit la realizarea de previziuni.
|
White Heteroskedasticity Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
|
Probability |
|
|
|
Obs*R-squared |
|
Probability |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
||
|
Dependent Variable: RESID^2 |
|
|
||
|
Method: Least Squares |
|
|
||
|
Date: 05/12/09 Time: 13:24 |
|
|
||
|
Sample: 2000M01 2009M02 |
|
|
||
|
Included observations: 110 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
PI |
|
|
|
|
|
PI^2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
|
Mean dependent var |
|
|
|
Adjusted R-squared |
|
S.D. dependent var |
|
|
|
S.E. of regression |
|
Akaike info criterion |
|
|
|
Sum squared resid |
|
Schwarz criterion |
|
|
|
Log likelihood |
|
F-statistic |
|
|
|
Durbin-Watson stat |
|
Prob(F-statistic) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< DWcalc < d1
d1 DWcalc d2
d2 < DWcalc < 4 - d2
4 - d2 DWcalc 4 - d1
4 - d1 < DWcalc < 4
Autocorelare
pozitiva
Indecizie
Erorile sunt
independente
Indecizie
Autocorelare
negativa
Dependent Variable: CA
Method: Least Squares
Date: 05/12/09 Time: 13:23
Sample: 2000M01 2009M02
Included observations: 110
Variable
Coefficient
Std. Error
t-Statistic
Prob.
PI
C
R-squared
Mean dependent var
Adjusted R-squared
S.D. dependent var
S.E. of regression
Akaike info criterion
Sum squared resid
Schwarz criterion
Log likelihood
F-statistic
Durbin-Watson stat
Prob(F-statistic)
In cazul nostru, DWcalculat = 0,44 , se compara cu d1 si d2 din tabelul distributiei Durbin Watson. In cazul nostru d1=1,64 iar d2=1,69, si deoarece
0 < DWcalc = 0,44 < d1 = 1,64 , se garanteaza cu probabilitatea de 95% ca erorile modelului sunt autocorelate pozitiv, nefiind independente, deci modelul nu este valid.
3.4.3. Testarea normalitatii distributiei variabilei aleatoare ε
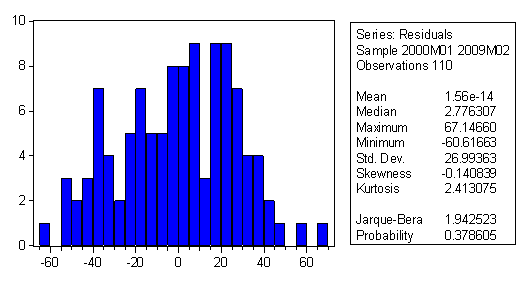
Verificarea ipotezei de normalitate a erorilor presupune compararea histogramei erorilor cu Clopotul lui Gauss. Se stie ca acesta este caracterizat prin doi parametri - coeficientul de asimetrie, = 0 respectiv coeficientul de boltire, = 3. Se spune despre erorile unui model econometric ca sunt distribuite normal daca intre valorile si ce caracterizeaza histograma erorilor si valorile standard ale Clopotului lui Gauss, 0 si 3, nu exista difernete semnificative din punct de vedere statistic. In cazul nostru aceste valori sunt coeficientul de asimetrie, Skewness, respectiv coeficientul de boltire, Kurtosis, Dupa cum se observa, histograma erorilor este simetrica, deoarece valoarea coeficientului de asimetrie este apropiat de zero, iar legat de boltire, histograma erorilor este mai plata decat Clopotul lui Gauss, intrucat < 3 (histograma erorilor este platicurtica).
Problema care se pune in acest moment este aceea de a verifica daca diferentele intre si valoarea standard = 0 respectiv respectiv valoarea standard =3, sunt semnificative din punct de vedere statistic sau nu. In acest scop se foloseste testul Jarque Bera. Se emit ipotezele:
H0: 
adica erorile sunt distribuite normal
H1: 
adica erorile sunt nu distribuite
normal
Pentru alegerea
ipotezei corecte, se determina valoarea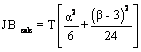 
,
care in cazul nostru este deja calculata: JB
calc = 1,94
Regulile de decizie sunt:
daca 
,
atunci ipoteza de normalitate a erorilor este acceptata.
daca 
,
atunci ipoteza de normalitate a erorilor este respinsa.
In cazul nostru JBcalc = 1,94 < tab , deci ipoteza acceptata este H0, adica erorile sunt distribuite normal. In consecinta, modelul este valid, deci poate fi folosit la realizarea de previziuni.
4. Previziunea variabilei Y
Modelul econometric este de forma:
CA = a ∙ PI + b + εt
Previziunea nu se poate face datorita faptului ca nu se indeplinesc urmatoarele conditii:
Presupunand ca modelul este valid dorim sa estimam valoarea la care va ajunge indicele cifrei de afaceri in luna martie 2009, daca valoarea indicelui productiei industriale este de 250%
CA = 2,75 ∙ PI - 206,27
PI = 250 %
atunci
CA
5. Concluzii
Previziunea modelului nu se poate face deoarece modelul nu este valid.
Bibliografie
https://statistici.insse.ro/shop/index.jsp?page=tempo3&lang=ro&ind=IND101B
https://statistici.insse.ro/shop/index.jsp?page=tempo3&lang=ro&ind=IND104E
Mester, I.T. - "Econometrie", Ed. Universitatii din Oradea, 2007
Mester, I. T.- "Statistica Economica", Ed. Universitatii din Oradea, 2007
https://ro.wikipedia.org/wiki/Cifra_de_afaceri
https://www.scribd.com/doc/7058766/Manual-an-1-Economie-Politica-Vol-1?autodown=pdf
https://facultate.regielive.ro/cursuri/management/managementul_productiei-5257.html
|
= 