UNIVERSITATEA DIN ORADEA
FACULTATEA DE STIINTE ECONOMICE
SPECIALIZAREA Management
Modelul econometric pentru agregatul monetar M2 in functie de importuri
Oradea, 2009
CUPRINS
|
|
Pagina |
|
Introducere . |
|
|
1. Ipoteze fundamentale |
|
|
2. Determinarea estimatorilor de regresie liniara prin metoda celor mai mici patrate |
|
|
3. Testarea validitatii modelului |
|
|
3.1. Testarea validitatii modelului de regresie folosind metoda descompunerii variantei |
|
|
3.2. Calcularea coeficientului de corelatie R2, a coeficientului de corelatie corectat si testarea reprezentativitatii lui |
|
|
3.3. Teste si regiuni de incredere pentru coeficienti |
|
|
3.3.1.Testarea validitatii estimatiei coeficientilor |
|
|
3.3.2. Intervale de incredere pentru coeficienti |
|
|
3.4. Testarea ipotezelor fundamentale referitoare la variabila aleatoare ε |
|
|
3.4.1. Ipoteza de homoscedasticitate a variabilei reziduale |
|
|
3.4.2. Ipoteza independentei valorilor variabilei reziduale εt |
|
|
3.4.3. Testarea normalitatii distributiei variabilei aleatoare ε |
|
|
4. Previziunea variabilei |
|
|
5. Concluzii |
|
|
Bibliografie |
|
Introducere
Dispunem de 50 observatii asupra marimii variabilelor agregatul monetar M2 si importuri, notate astfel:
Y - agregatul monetar M2 si X - importuri
|
Perioada |
Importuri (mil euro) |
Agregatul monetar M2 (mil euro) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obiectivele cercetarii noastre sunt:
Identificarea existentei legaturii intre cele doua variabile
Stabilirea intensitatii legaturii
Analiza formei legaturii
Determinarea parametrilor modelului
Daca modelul elaborat este valid cu ajutorul lui se vor putea realiza previziuni
Metodologia cercetarii presupune parcurgerea urmatorilor pasi:
a) analiza legaturii dintre cele doua variabile (studiul aspectului norului de puncte)
b) determinarea modelului
c) determinarea estimatorilor de regresie liniara prin metoda celor mai mici patrate
d) testarea validitatii modelului
testarea ipotezelor fundamentale referitoare la variabila aleatoare ε
ipoteza de homoscedasticitate
ipoteza independentei
ipoteza de normalitate
e) Previziunea variabilei Y
In scopul identificarii formei legaturii dintre cele doua variabile, vom reprezenta grafic norul de puncte:
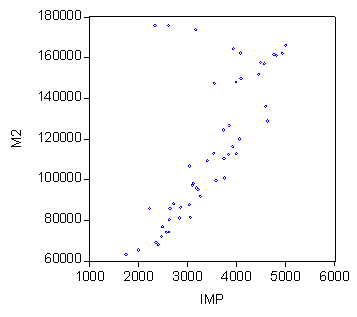
Analiza modului in care sunt dispuse punctele pe suprafata graficului permite studierea aspectelor legate de:
Ø Existenta legaturii - intre X si Y exista legatura deoarece punctele nu sunt imprastiate in planul xOy, ci se aduna sub forma unui nor.
Ø Sensul legaturii - legatura este directa deoarece atunci cand valorile lui X cresc, cresc si valorile lui Y.
Ø Forma legaturii - punctele sunt asezate in jurul unei liniiÒlegatura este liniara (de forma Y=aX+b).
Ø Intensitatea legaturii - fasia este de latime medie deci si legatura dintre cele 2 variabile este de intensitate medie
Pentru analiza legaturii dintre variabilele agregatul monetar M2 si importuri am ales urmatorul model:
![]()
unde:
Yt = valoarea agregatului monetar M2 din luna t
Xt = importurile din luna t
εt = variabila reziduala
1. Ipoteze fundamentale
H0 : Ipoteza de liniaritate: modelul este liniar in Xt
H1 : Ipoteze asupra variabilelor X si Y:
(i) xt si yt reprezinta valori numerice ale variabilelor X si Y rezultate prin observarea statistica, neafectate de erori sistematice;
(ii) Y este variabila endogena aleatoare, pentru ca este functie de
(iii) X, variabila explicativa, este considerata ca fiind o variabila determinista in model, nealeatoare;
H2 : Ipoteze asupra erorilor ε:
(i) ε are o distributie independenta de timp, de speranta matematica nula, respectiv:
E (εt) = 0, ( ) t = 0, 1, 2, ., T
V (εt) = E[εt - E(εt)]2
= ![]() =
= ![]()
altfel spus, modelul este homoscedastic.
(ii) Independenta erorilor. Doua erori εt si εt' sunt independente liniar intre ele, adica
![]()
respectiv
![]()
(iii) Variabila are o distributie normala.
H3 : Ipoteze privind variabila exogena X:
(i)
cov(xt, εt)
= 0, ![]() t - erorile sunt independente
de X;
t - erorile sunt independente
de X;
(ii) Se presupune ca pentru T ¥, primele doua momente empirice ale variabilei X sunt finite, respectiv
Speranta
matematica ![]()
Varianta
![]()
2. Determinarea estimatorilor de regresie liniara
prin metoda celor mai mici patrate
Coefficientsa
Model
Unstandardized Coefficients
Standardized Coefficients
t
Sig.
B
Std. Error
Beta
(Constant)
VAR00001
a. Dependent Variable: VAR00002
3. Testarea validitatii modelului
Testarea validitatii modelului presupune parcurgerea urmatoarelor etape:
Testarea validitatii modelului de regresie folosind metoda descompunerii variantei;
Calculul raportului de corelatie si testarea semnificatiei lui;
Inferenta statistica pentru parametrii modelului de regresie;
Verificarea ipotezelor modelului de regresie.
3.1. Testarea validitatii modelului de regresie folosind metoda descompunerii variantei
Dispersia totala verifica urmatoarea relatie:
![]()
Termenii relatiei se definesc prin:
![]() - varianta totala a variabilei Y determinata
de toti factorii sai de influenta;
- varianta totala a variabilei Y determinata
de toti factorii sai de influenta;
![]() - varianta fenomenului Y determinata numai de variatia
factorului X, considerat
factorul principal al variabilei Y, adica variatia lui Y explicata de modelul econometric;
- varianta fenomenului Y determinata numai de variatia
factorului X, considerat
factorul principal al variabilei Y, adica variatia lui Y explicata de modelul econometric;
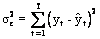 - variatia reziduala, sau variatia fenomenului
Y generata de catre factorii
nespecificati in model, acesti factori fiind considerati - in etapa de
specificare - drept factori cu influenta intamplatoare, neesentiali pentru a
explica variatia fenomenului Y
- variatia reziduala, sau variatia fenomenului
Y generata de catre factorii
nespecificati in model, acesti factori fiind considerati - in etapa de
specificare - drept factori cu influenta intamplatoare, neesentiali pentru a
explica variatia fenomenului Y
Sursa de variatie
Masura variatiei
Numarul gr. de libertate
Dispersii
corectate
Valoarea testului F
Fcalc
Fα;v1;v2
Varianta explicata de model, datorata factorului X
![]()
2,957E10
k = 1
![]()
![]()
Varianta
Reziduala, datorata factorilor neesentiali
![]()
3,037E10
T - k - 1 = 48
![]()
Varianta
totala
![]()
5,994E10
T - 1 = 49
![]()
Pe baza datelor din tabel se pot testa urmatoarele ipoteze:
H : s2Y/X s2 , cele doua dispersii sunt aproximativ egale, influenta factorului X nu difera semnificativ de influenta factorilor intamplatori.
H : s2Y/X s2 , influenta factorului X si a factorilor intamplatori - masurata prin cele doua dispersii - difera semnificativ si, deci, se poate trece la discutia similitudinii, a verosimilitatii modelului teoretic in raport cu modelul real.
|
ANOVAb |
||||||
|
Model |
Sum of Squares |
df |
Mean Square |
F |
Sig. |
|
|
|
Regression |
2,957E10 |
|
2,957E10 |
|
0,000a |
|
Residual |
3,037E10 |
|
6,327E8 |
|
|
|
|
Total |
5,994E10 |
|
|
|
|
|
|
a. Predictors: (Constant), VAR00001 |
|
|
|
|||
|
b. Dependent Variable: VAR00002 |
|
|
|
|||
Acceptarea ipotezei H0 este echivalenta cu respingerea modelului (modelul nu este valid).
Testarea semnificatiei dintre doua dispersii se face cu ajutorul distributiei teoretice Fisher-Snedecor, respectiv cu testul F.
Cunoscand cele doua valori, ![]() = , si Fα,v1,v2 = valoarea teoretica a variabilei F, preluata din tabelul repartitiei
Fisher - Snedecor, in functie de un prag de semnificatie α si un numarul
gradelor de libertate =
k; =
n-k-1, regula de
decizie se scrie:
= , si Fα,v1,v2 = valoarea teoretica a variabilei F, preluata din tabelul repartitiei
Fisher - Snedecor, in functie de un prag de semnificatie α si un numarul
gradelor de libertate =
k; =
n-k-1, regula de
decizie se scrie:
- se accepta H1 si se respinge H0 daca Fcalc >Fα, , deci modelul este valid.
3.2. Calcularea coeficientului de corelatie R2, a coeficientului de corelatie corectat si testarea reprezentativitatii lui
Coeficientul de corelatie R2 exprima rolul jucat de ansamblul variabilelor exogene asupra variabilei endogene. Cu cat valoarea acestuia este mai apropiata de 1, cu atat legatura dintre variabile este mai intensa.
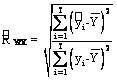
|
Model Summary |
||||
|
Model |
R |
|
Adjusted |
Std. Error of the Estimate |
|
|
0,702a |
|
|
|
|
a. Predictors: (Constant), VAR00001 |
|
|||
Efectuam calculele si obtinem:
![]()
Aceasta expresie nu tine cont de numarul observatiilor si nici de numarul variabilelor explicative din model. O valoare mai precisa a lui R2 , care tine cont de numarul observatiilor T = 50 si numarul variabilelor exogene p = 2 este urmatoarea (R2 corectat):
![]()
Testarea
reprezentativitatii lui ![]() :
:

Se compara valoarea calculata a lui F cu cea tabelara. Regulile de decizie sunt urmatoarele:
- daca Fcalc < Ftab, ipoteza nula este cea care este acceptata, fapt echivalent cu inexistenta unei legaturi intre cele doua variabile la nivel de populatiei totala.
- daca Fcalc > Ftab, ipoteza nula este cea care se respinge, acceptandu-se cea alternativa.
Intrucat Fcalc>Ftab rezulta ca se accepta ipoteza H1, deci intre cele doua variabile exista legatura.
3.3. Teste si regiuni de incredere pentru coeficienti
3.3.1.Testarea validitatii estimatiei coeficientilor
Pentru testarea validitatii estimatiei coeficientilor ai se utilizeaza testul Student. In general :
H0 : ai = 0, cu alternativa
H1 : ai ≠ 0
Daca 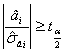 atunci H0 se respinge, iar
coeficientul ai este semnificativ diferit de 0.
atunci H0 se respinge, iar
coeficientul ai este semnificativ diferit de 0.
Valorile ![]() sunt
sunt ![]() 4,268, respectiv
4,268, respectiv ![]() =15036,448.
=15036,448.
Pentru parametrul a emitem ipotezele:
H0 : a = 0, cu alternativa
H1 : a ≠ 0
|
Coefficientsa |
||||||
|
Model |
Unstandardized Coefficients |
Standardized Coefficients |
t |
Sig. |
||
|
B |
Std. Error |
Beta |
||||
|
|
(Constant) |
|
|
|
|
|
|
VAR00001 |
|
|
|
|
|
|
|
a. Dependent Variable: VAR00002 |
|
|
|
|||
Dupa efectuarea calculelor, obtinem:
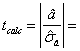
si stim ca ttab = 1,96
Comparam cele doua valori si tragem concluzia ca ipoteza adevarata este H1 cu o probabilitate de 95%, ceea ce inseamna ca valoarea coeficientului a in populatia totala difera semnificativ de 0.
Pentru parametrul b emitem ipotezele:
H0 : b = 0, cu alternativa
H1 : b ≠ 0
Dupa efectuarea calculelor, obtinem:
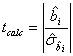
Comparam cele doua valori si tragem concluzia ca ipoteza adevarata este H0 cu o probabilitate de 95%, ceea ce inseamna ca valoarea coeficientului b in populatia totala nu difera semnificativ de zero.
3.3.2. Intervale de incredere pentru coeficienti
Forma intervalului de incredere pentru coeficientul a al modelului este:
![]()
unde ![]() - termenul liber
- termenul liber
![]() - abaterea medie patratica a coeficientului a
- abaterea medie patratica a coeficientului a
Se cunoaste ![]() = ,
= , ![]() = si ttab = 1,96, iar probabilitatea de garantare a
rezultatelor este 95%, deci putem face calculele:
= si ttab = 1,96, iar probabilitatea de garantare a
rezultatelor este 95%, deci putem face calculele:
P (20,814 ≤ a ≤ 37,544) = 95%
Putem garanta deci, cu o probabilitate de 95%, ca valoarea coeficentului a, la nivelul populatiei totale, este cuprinsa intre 20,814 si 37,544.
Forma intervalului de incredere pentru coeficientul b al modelului este:
![]()
unde ![]() - termenul liber
- termenul liber
![]() - abaterea medie patratica a coeficientului b
- abaterea medie patratica a coeficientului b
Se cunoaste ![]() = ,
= , ![]() = si ttab
= 1,96, iar probabilitatea de garantare a rezultatelor este 95%, deci putem
face calculele:
= si ttab
= 1,96, iar probabilitatea de garantare a rezultatelor este 95%, deci putem
face calculele:
P (- 14414,278 ≤ b ≤ 44528,598) = 95%
Putem garanta deci, cu o probabilitate de 95%, ca valoarea coeficentului b, la nivelul populatiei totale, este cuprinsa intre - 14414,278 si 44528,598.
3.4. Testarea ipotezelor fundamentale referitoare la variabila aleatoare ε
Pe langa influenta factorilor esentiali, asupra marimii agregatul monetar M2 (Y) isi exercita influenta si alti factori, care sunt surprinsi prin variabila ε. Acesti factori ar putea fi: exporturi, rata dobanzii, rata somajului, rata inflatiei, cursul de schimb, etc.
3.4.1. Ipoteza de homoscedasticitate a variabilei reziduale
Pentru a verifica
ipoteza de homoscedasticitate a erorilor modelului ![]() se foloseste testul White; se pleaca de la
ecuatia
se foloseste testul White; se pleaca de la
ecuatia
![]()
si se doreste sa se studieze
daca intre ![]() ,
xt si xt2 exista o legatura. Daca intre aceste
variabile exista legatura, despre erorile modelului se spune ca sunt
heteroscedastice, daca nu - ele se numesc homoscedastice.
,
xt si xt2 exista o legatura. Daca intre aceste
variabile exista legatura, despre erorile modelului se spune ca sunt
heteroscedastice, daca nu - ele se numesc homoscedastice.
Existenta legaturii la nivelul esantionului este indicata de raportul de corelatie estimat, iar pentru generalizarea rezultatelor se emit ipotezele:
![]() (modelul este homoscedastic)
(modelul este homoscedastic)
H1: ![]() (modelul este heteroscedastic)
(modelul este heteroscedastic)
Regulile de decizie sunt:
|
White Heteroskedasticity Test: |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic |
|
Probability |
|
|
|
Obs*R-squared |
|
Probability |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation: |
|
|
||
|
Dependent Variable: RESID^2 |
|
|
||
|
Method: Least Squares |
|
|
||
|
Date: |
|
|
||
|
Sample: 2005M01 2009M02 |
|
|
||
|
Included observations: 50 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
2.08E+09 |
3.78E+09 |
|
|
|
IMP |
|
|
|
|
|
IMP^2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
|
Mean dependent var |
6.07E+08 |
|
|
Adjusted R-squared |
|
S.D. dependent var |
1.63E+09 |
|
|
S.E. of regression |
1.62E+09 |
Akaike info criterion |
|
|
|
Sum squared resid |
1.23E+20 |
Schwarz criterion |
|
|
|
Log likelihood |
|
F-statistic |
|
|
|
Durbin-Watson stat |
|
Prob(F-statistic) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
daca ![]() ,
nu se poate respinge ipoteza H0, adica erorile sunt homoscedastice,
acest lucru garantandu-se cu o probabilitate de 95%.
,
nu se poate respinge ipoteza H0, adica erorile sunt homoscedastice,
acest lucru garantandu-se cu o probabilitate de 95%.
- daca ![]() ,
ipoteza H0 se respinge, si se accepta ca fiind adevarata, cu o
probabilitate de 95%, ipoteza H1, ceea ce inseamna ca erorile sunt
heteroscedastice, acest lucru garantandu-se cu o probabilitate de 95%. In acest
caz modelul nu este valid, el neputand fi folosit la realizarea de previziuni.
,
ipoteza H0 se respinge, si se accepta ca fiind adevarata, cu o
probabilitate de 95%, ipoteza H1, ceea ce inseamna ca erorile sunt
heteroscedastice, acest lucru garantandu-se cu o probabilitate de 95%. In acest
caz modelul nu este valid, el neputand fi folosit la realizarea de previziuni.
Asadar,
la nivel de esantion, raportul de corelatie inregistreaza valoarea ![]() , valoare
apropiata de zero. Acest fapt ne indica inexistenta unei legaturi intre
variabile la nivelul esantionului. Pentru a generaliza aceasta informatie la
nivelul populatiei totale, aplicam testul Fisher si emitem cele doua ipoteze:
, valoare
apropiata de zero. Acest fapt ne indica inexistenta unei legaturi intre
variabile la nivelul esantionului. Pentru a generaliza aceasta informatie la
nivelul populatiei totale, aplicam testul Fisher si emitem cele doua ipoteze:
![]() (modelul este homoscedastic)
(modelul este homoscedastic)
H1:
![]() (modelul este heteroscedastic)
(modelul este heteroscedastic)
Deoarece Fcalculat este mai mic decat Ftabelar= 3,92, nu se poate respinge ipoteza H0, adica erorile sunt homoscedastice, acest lucru garantandu-se cu o probabilitate de 95%.
3.4.2. Ipoteza independentei valorilor variabilei reziduale εt
Testul Durbin Watson se bazeaza pe modelul de regresie multifactorial
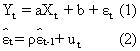
Erorile modelului (1), ![]() se considera a fi corelate de ordinul unu
daca, in general, intre doua erori oarecare succesive,
se considera a fi corelate de ordinul unu
daca, in general, intre doua erori oarecare succesive, ![]() si
si ![]() ,
exista o legatura ca si cea descrisa in relatia (2), adica in situatia in care
valoarea coeficientului , la nivelul populatiei
totale, difera semnificativ de zero. Verificarea independentei erorilor se
rezuma deci la testarea ipotezelor:
,
exista o legatura ca si cea descrisa in relatia (2), adica in situatia in care
valoarea coeficientului , la nivelul populatiei
totale, difera semnificativ de zero. Verificarea independentei erorilor se
rezuma deci la testarea ipotezelor:
H0: = 0 (erori independente, necorelate) cu alternativa
H1: ≠ 0 (erori dependente, corelate)
Pentru alegerea ipotezei corecte se determina statistica Durbin Watson:

Valoarea DWcalc, se compara cu doua valori teoretice, d1 si d2, citite din tabelul distributiei Durbin - Watson in functie de un prag de semnificatie , convenabil ales, ( = 0,05 sau = 0,01), de numarul de variabile exogene, k si de valorile observate T, T
Regulile de decizie ale testului sunt:
|
< DWcalc < d1 |
d1 DWcalc d2 |
d2 < DWcalc < 4 - d2 |
4 - d2 DWcalc 4 - d1 |
4 - d1 < DWcalc < 4 |
|
Autocorelare pozitiva |
Indecizie |
Erorile sunt independente |
Indecizie |
Autocorelare Negativa |
|
Dependent Variable: M2 |
|
|
||
|
|
|
|
||
|
|
|
|
||
|
Method: Least Squares |
|
|
||
|
Date:
|
|
|
||
|
Sample: 2005M01 2009M02 |
|
|
||
|
Included observations: 50 |
|
|
||
|
M2=C(1)*IMP+C(2) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
|
|
|
|
|
|
|
|
|
|
|
|
C(1) |
|
|
|
|
|
C(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R-squared |
|
Mean dependent var |
|
|
|
Adjusted R-squared |
|
S.D. dependent var |
|
|
|
S.E. of regression |
|
Akaike info criterion |
|
|
|
Sum squared resid |
3.04E+10 |
Schwarz criterion |
|
|
|
Log likelihood |
|
Durbin-Watson stat |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In cazul nostru, DWcalculat = , se compara cu d1 si d2 din tabelul distributiei Durbin Watson. In cazul nostru d1=1,64 iar d2=1,69 pentru probabilitatea de 95%. Deoarece 0 < DWcalc < d1 erorile sunt autocorelate pozitiv.
3.4.3. Testarea normalitatii distributiei variabilei aleatoare ε

Verificarea ipotezei de normalitate a erorilor presupune compararea histogramei erorilor cu Clopotul lui Gauss. Se stie ca acesta este caracterizat prin doi parametri - coeficientul de asimetrie, = 0 respectiv coeficientul de boltire, = 3. Se spune despre erorile unui model econometric ca sunt distribuite normal daca intre valorile si ce caracterizeaza histograma erorilor si valorile standard ale Clopotului lui Gauss, 0 si 3, nu exista difernete semnificative din punct de vedere statistic.
In cazul nostru aceste valori sunt coeficientul de asimetrie, Skewness, = 2,228 respectiv coeficientul de boltire, Kurtosis, = 8,032. Dupa cum se observa, histograma erorilor nu este simetrica, deoarece valoarea coeficientului de asimetrie nu este apropiata de zero, iar legat de boltire, histograma erorilor este mai ascutita decat Clopotul lui Gauss, intrucat > 3 (histograma erorilor este leptocurtica).
Problema care se pune in acest moment este aceea de a verifica daca diferentele intre = 2,228 si valoarea standard = 0 respectiv =8,032 respectiv valoarea standard =3, sunt semnificative din punct de vedere statistic sau nu. In acest scop se foloseste testul Jarque Bera.
Se emit ipotezele:
H0: εt~N(0,1) adica erorile sunt distribuite normal
H1: ![]()
![]()
![]() adica erorile sunt nu distribuite normal
adica erorile sunt nu distribuite normal
Pentru alegerea ipotezei corecte, se determina
valoarea 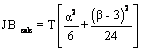 ,
care in cazul nostru este deja calculata: JB calc = 94,158.
,
care in cazul nostru este deja calculata: JB calc = 94,158.
Regulile de decizie sunt:
daca ![]() ,
atunci ipoteza de normalitate a erorilor este acceptata.
,
atunci ipoteza de normalitate a erorilor este acceptata.
daca ![]() ,
atunci ipoteza de normalitate a erorilor este respinsa.
,
atunci ipoteza de normalitate a erorilor este respinsa.
In cazul nostru JBcalc = 94,158 > tab= 5,99, deci ipoteza de normalitate a erorilor este respinsa. In consecinta, modelul nu este valid, deci nu poate fi folosit la realizarea de previziuni
4. Previziunea variabilei Y
M2 = a ∙ Imp + b + εt
Previziunea nu se poate face datorita faptului ca nu se indeplinesc urmatoarele conditii:
valoarea coeficientului b in populatia totala nu difera semnificativ de zero
ipoteza de independenta a erorilor (erorile sunt autocorelate pozitiv)
ipoteza de normalitate a erorilor (erorile nu sunt distribuite normal)
Presupunand ca modelul este valid, daca in mai 2009 valoarea importurilor ar ajunge la 3000 mil euro, atunci valoarea previzionata a agregatului monetar M2 ar fi de:
M2 = 29.17923 ∙ Imp + 15057.16
M2 = 29.17923 ∙ 3000 + 15057.16 = 102594.85 mil euro
5. Concluzii
Previziunea modelului nu se poate face deoarece modelul nu este valid.
Bibliografie
www.bnr.ro
www.insse.ro
|