Studierea unor functi 222h72c i din punct de vedere cantitativ si calitativ utilizand diverse procedee: majorari, minorari pe un interval dat, proprietatile algebrice si de ordine ale multimii numerelor reale in studiul calitativ local, utilizarea reprezentarii grafice a unei functii pentru verificarea unor rezultate si pentru identificarea unor proprietati

Explorarea unor proprietati cu caracter local si/ sau global ale unor functii utilizand continuitatea , derivabilitatea sau reprezentarea grafica .

OBIECTIVE OPERATIONALE :

Prin rezolvarea exercitiilor la tabla , elevii sa demonstreze ca

STRATEGII DIDACTICE :

Principii didactice :

Principiul participarii si invatarii active.
Principiul asigurarii progresului gradat al performantei.
Principiul conexiunii inverse ( feed - back )

Metode de invatamant :

conversatia
explicatia
exercitiul
descoperirea
expunerea

Forme de evaluare :

observatia
prin lucru individual

Forme de oganizare a clasei :

frontala
individuala

Resurse materiale :

didactice

Moment organizatoric

Activitatea profesorului

Activitatea elevului

conversatia

Saluta clasa.

Se rezolva unele probleme extradidactice aparute.

Noteza absentele

Elevul de serviciu prezinta lista elevilor care lipsesc.

Verificarea cunostintelor din lectia precedenta si reactualizarea celor necesare

comunicarii temei noi :

a) controlul

temelor date

elevilor pentru

acasa

Exercitiu individual

b) Verificarea cunostintelor din lectia

precedenta

- Enuntul teoremelor : criteriului raportului , lema lui Stolz - Cesaro si criteriul radicalului

Concomitent cu exercitiul din tema propune pentru un elev din clasa un exercitiu asemanator cu lucrul de acasa : Ex.

Profesorul verifica si apreciaza oral rezultatele obtinute.

Trei elevi enunta criteriul raportului ,lema lui Stolz - Cesaro si criteriul radicalului

Doi elevi rezolva exercitiu

Conversatia

Exercitiu

Dirijarea

invatarii

Def. Fie D R , D¹ Un punct x₀ ∈ se numeste punct

de acumulare pentru D daca oricare ar fi V V( x₀) avem :

( V) D ¹

Notam multimea punctelor de acumulare ale multimii D cu D^/ .

Def. Daca un punct apartine multimii D si nu este punct

de acumulare pentru D , atunci el se numeste punct izolat pentru D .

Expunere

Mai precis : a D este punct izolat pentru D daca exista

U V( a) a.i. ( U) D = ( vecinatatea U are in comun

cu multimea D cel mult punctul a ) .

Ex. 1. D = . In acest caz D^/ =

Rezolvare : Fie V = V

( V) D ¹ ( V contine toate numerele naturale mai mari sau egale cu 1+ [] ) .

Ex.2. D=[ 0 , 1) . In acest caz D^/ =[ 0 , 1] .

0 x₀ 1 2

- punctele interioare din x₀ ( 0 , 1 ) sunt evident punctele de acumulare pentru D .

- orice vecinatate a lui 1 si orice vecinatate a lui 0 are elemente

in comun cu D (deci 0 si 1sunt puncte de acumulare pentru D )

- punctul 2 este izolat pentru D : alegand V=(1,7; 2,3) V

avem V D = adica ( V) D =

Consideram functiile

f:R R , f(x) = x+3 si g: R R , g(x) = ln . Graficele lor ne sunt cunoscute din casa a-IX-a , respectiv a-X-a .

Graficul lui f Graficul lui g

Sa consideram numarul real x₀ = 0 . Observam pe grafice ca

atunci cand x se apropie foarte mult de x₀ = 0 , fara a atinge insa acest numar , valorile f(x) se apropie oricand de mult de

numarul =3 , iar valorile g(x) se apropie oricand de mult de

numarul = .Aceasta apropiere intuitiva a lui x catre x₀ ,

respectiv a lui f(x) catre sau a lui g(x) catre , o vom

descrie matematic cu ajutorul notiunii de vecinatate .

Un elev rezolva la tabla Ex. 2

Explicatie Descoperire

Def. Fie f : D R , D R , D¹ si x₀ D^/. Punctul

este limita functiei in x₀ daca V V( ) , U V( x₀) ,

astfel incat f(x) V pentru orice x D U , xx₀ .

Limita functiei in punctul x₀ se noteaza si se

citeste ,, limita cand x tinde la x₀ din f(x) ''

Teoreme de caracterizare a limitei unei functii

Criteriul

Definitia cu vecinatati a limitei unei functii este echivalenta are o transcriere in limbaj de inecuatii si inegalitati .

Fie x₀ si

O vecinatati oarecare U V( x₀) poate fi :

, cu , daca x₀ =

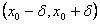cu , daca x₀ R .

O vecinatati oarecare V V ) poate fi :

, cu , daca

cu , daca R .

In aceste conditii definitia ,, cu vecinatati '' a limitei unei functii este echivalenta cu urmatoarele propozitii '

Cazul x₀ =

Û , astfel incat

f(x) < pentru orice x D , x <

Ex .1.

Intr-adevar , pentru , avem Û

Alegand . Atunci pentru orice avem

Expunere

Explicatie

Descoperire

Cazul x₀ R ;

Û , astfel incat

f(x) < pentru orice x D , x ¹ x₀ ,

Ex. 2.

Intr-adevar , pentru Û

Daca alegem avem x ,

Þ lnx <

Cazul x₀ =

Û , astfel incat

f(x) < pentru orice x D , x >

Ex. 3.

Teorema :Daca limita unei functii exista atunci ea este unica .

Un elev rezolva Ex. 3

Expunere

Descoperire

Intensificarea

retinerii si

asigurarea

trasferului

Ex1. Sa se determine celelalte 6 cazuri ale teoremelor de caracterizare a limitei unei functii

Ex2. Sa se arate ca

Trei elevi expune la tabla celelalte

cazuri ale teoremelor de caracterizare a limitei unei functii .

Un elev rezolva Ex. 2

Exercitiu comentat

Concluzii si realizarea feed-back-ului

Fac o scurta recapitulare a notiunilor care au fost utilizate in decursul lectiei si generalizez cu ajutorul elevilor notarea si comentarea activitatii elevilor pe parcurs.

Despre ce am vorbit astazi la lectie?

Enuntul teoremelor invatate ?

Se rezolva la tabla exercitii ca aplicatii la notiunile prezentate

Elevii raspund la intrebari .

- Elevii rezolva exercitiile de pe fisa de lucru .

Apoi prezinta la tabla

rezolvarea lor .

Conversatia

Descoperire

Asigurarea

transferului

Stabilesc tema pentru acasa (man.ex:1pag 110;din culegere ex: 2 pag 110).si de rezolvat exercitiile din fisa .Ofer indicatii cu privire la rezolvarea exemplelor ce ar putea prezenta dificultati.

Isi noteaza in caiete tema pe acasa

Conversatie

Limite de functii

Clasa a-XI - a A 2008-2009

Ex .1.

Rezolvare : Fie , f(x) = x³ Intr-adevar , pentru , avem f(x) < Û Û