Obiective:
Dupa parcurgerea acestui modul studentul va cunoaste:
modul de formulare al ipotezelor in cazul comparatiilor multiple
determinarea semnificatiei diferentelor si interpretarea acestora in cazul planurilor experimentale de baza
modul de formalizare a notiunii de comparatie
determinarea semnificatiei diferentelor si interpretarea lor in cazul planurilor experimentale factoriale.
4.1. MULTIMI SAU COLECTIVITATI DE k ESANTIOANE INDEPENDENTE
In capitolul dedicat inferentei statistice am avut in vedere studii experimentale ce cuprindeau cel mult 2 grupe, respectiv doua esantioane independente sau perechi .
In problemele de comparatie ce se puneau am luat in considerare cel mult doua esantioane aplicand criteriul z sau t .In capitolul de fata avem in vedere situatii mai complexe, in care intervin colectivitati sau multimi formate din k grupe, care ilustreaza adesea k situatii sau conditii.
Pe parcursul diverselor capitole s-au prezentat exemple si aplicatii .Acum le reluam si adaugam altele.
Exemplu:
Se instituie un experiment pentru a cunoaste efectul unor tranchilizante asupra activitatii de conducere auto. In acest scop se administreaza tranchilizante cu nume diferite sau doze diferite (5 mg, 10 mg, 15 mg, 20 mg) la patru loturi de persoane stabilite dupa regulile selectiei aleatoare. Se introduce si un grup de control, caruia nu i se administreaza nici un drog. Notam variabila independenta (administrarea unui tranchilizant) cu A si vom avea in studiu patru modalitati a1, a2, a3, a4, la care se adauga grupa de control a0. Avem, practic, un singur factor de variatie, prezent sub 5 modalitati. Nu facem nici o alta diferentiere a subiectilor, decat cea oferita de administrarea in doze diferite a drogului. Efectul fiecarui medicament aplicat se dezvaluie in diferentele sau variatiile aparute in comportamentul la volan. Acesta din urma il consideram printr-o fateta particulara: timpul de reactie (TR). Ne asteptam ca drogul in doze diferite sau purtand nume diferite sa diferentieze grupele cuprinse in studiu, sa apara deosebiri in ceea ce priveste TR intre grupele de experienta si cea de control. Sursele acestor deosebiri sau variatii sunt bine precizate.
In cadrul acestui exemplu avem de-a face cu un singur factor de variatie (A). Pentru a raspunde la intrebarea initiala, urmeaza sa se instituie in final comparatii multiple.
Exemplu:
Intr-o experienta de psihologie sociala s-a urmarit cum se modifica atitudinea oamenilor - intr-o problema data - sub influenta unor mijloace de convingere:
film
expunere orala
film + expunere orala
toate avand aceeasi tema. In acest scop s-au constituit, pe baza de selectie aleatoare, trei grupe de experienta potrivit celor 3 conditii amintite (a1, a2, a3 ),la care s-a adaugat o grupa de control (conditia a0).Experimentul in ansamblu cuprinde deci patru grupe aleatoare, fiecare avand in final o fizionomie particulara gratie procedurii experimentale urmate. La prima grupa s-a prezentat o expunere, la a doua s-a proiectat un film, la a treia grupa a avut loc o expunere insotita de un film, iar la grupa de control s-a aplicat cum se spune 'conditia zero'(nici o influenta). Variabila independenta o constituie mijlocul de convingere aplicat. Urmeaza sa se instituie anumite comparatii intre grupe dupa criterii bine determinate, in functie de factorul experimental pus in joc.
Modelul de analiza ramane in esenta acelasi ca in al doilea exemplu .Este vorba de un plan unifactorial sau un plan de baza.
Exemplu:
Se aplica un test - sa zicem Matrici Progresive - la 5 clase a VII-a din scoli generale diferite luate la intamplare. Se pune problema de a reuni datele de la 5 clase pentru a obtine o colectivitate mai numeroasa, numita colectivitate esantion de referinta, in vederea stabilirii unui etalon sau tabel de norme. Dupa cum se stie, orice test are atasat un barem sau etalon intocmit pe o colectivitate larga. acest barem de raportare poate fi o scala numerica sau o tipologie.
Trebuie sa ne asiguram ca grupele .respectiv clasele de elevi sunt omogene, pentru a putea 'amesteca' rezultatele . Deci nu este vorba de un experiment care sa induca efecte diferite, ci este vorba de aplicarea unui 'reactiv' identic (un test), cercetatorul fiind interesat sa obtina date deplin comparabile, pentru a fi contopite intr-un 'agregat' statistic unic.
Retinem ca grupele, respectiv clasele de elevi au fost luate ca atare, 858j91i ca grupuri natural intacte, in compozitia lor datorata hazardului. De asemenea, clasele testate au fost si ele luate la intamplare din scoli diferite, fara sa se acorde preferinta unui colectiv sau altul din anumite motive. Cele trei exemple prezentate au o nota comuna. In ele este vorba de colectivitati mai largi formate din cate 4-5 grupe. Fiecare grup sau esantion in parte constituie un esantion aleator, avand compozitia datorata hazardului. Vorbim deci de grupe independente . Intervine insa un nivel superior de integrare :colectivitatea mai larga sau multimea celor k grupe cuprinse in studiu. Nota de 'aleator' urmeaza a fi aplicata si la acest nivel. Vom avea deci colectivitati sau multimi de grupe independente spre deosebire de colectivitati de esantioane-perechi, despre care va fi vorba mai departe.
In toate exemplele date va fi vorba de multimi de grupe independente.
Acestea se incadreaza in doua categorii de situatii:
Situatii, ca in al treilea exemplu, in care nu numai fiecare grup in parte constituie un esantion aleator avand un numar de elemente, ci si grupele ca atare sunt luate la intamplare, alcatuind deci o colectie de grupe, un esantion aleator (de k grupe) extras dintr-o populatie de grupe.
Situatii cand fiecare grup in parte este un esantion aleator dar cele k grupe care compun multimea cuprinsa in studiu sunt alese sistematic, adica pe baza unui criteriu bine determinat(primele doua exemple). Fiind cele mai frecvente, ne ocupam in continuare numai de acestea.
Unitatile sau elementele ce compun grupele corespund cerintelor selectiei aleatoare. In schimb, la nivelul colectivitatii mai largi de k grupe nota 'aleatoare' nu mai este prezenta. Asupra fiecarei grupe se exercita o influenta bine determinata pe baza unui plan sistematic, astfel incat fiecare esantion prezinta o fizionomie aparte.
Problemele care se pun in cele doua situatii sunt diferite, de asemenea si tehnicile de lucru. La baza acestora se afla insa aceeasi metoda numita analiza de varianta, prescurtat ANOVA.
Dupa cum ne sugereaza insasi denumirea metodei, este vorba de o analiza a variatiei datelor, a imprastierii lor in jurul mediei .
Dispersia
sau imprastiere datelor in raport cu media o exprimam cu ajutorul diferentelor(
x-m). La nivelul grupului ar trebui
sa ne referim la suma abaterilor, adica ![]() ,operatie ce ne-ar duce la impas, deoarece suma algebrica a
abaterilor este zero. Se ia atunci
,operatie ce ne-ar duce la impas, deoarece suma algebrica a
abaterilor este zero. Se ia atunci ![]() 2,expresie pe care am numit-o suma patratelor(SP) si care ne indica variabilitatea grupului.
2,expresie pe care am numit-o suma patratelor(SP) si care ne indica variabilitatea grupului.
In orice cercetare de psihologie ne intereseaza sa desprindem influenta sau actiunea unor factori relevanti, factori cuprinsi in enuntul problemei initiale. Influenta unui factor se dezvaluie in efectele sau variatiile produse in campul studiat. In ansamblu se releva o anumita variabilitate sau dispersie a datelor inregistrate in functie de sursele precis reperate. Obiectul analizei il constituie suma efectelor (diferente, deosebiri, variatii) datorate fiecarui factor, la care se adauga efectele interactiunii lor(Matalon,1969).
Cu alte cuvinte, este vorba de analiza variabilitatii sau dispersiei datelor avand surse de variatie bine precizate. Evident se presupune ca efectele sau rezultatele se preteaza la masurare, la evaluare mai precisa.
4.2. PLANURI DE BAZA (CU UN SINGUR FACTOR DE VARIATIE)
Intr-o colectie de date numerice variabilitatea sau dispersia se releva dupa cum s-a aratat in imprastierea masuratorilor in raport cu media, ceea ce se exprima prin diferentele (x-m), mai exact prin suma acestor diferente sau abateri, adica S (x-m). Intrucat suma algebrica a abaterilor este zero, se ia S (x-m)2, expresie care s-a numit suma patratelor - prescurtat SP.
In cel de-al doilea exemplu amintit, este vorba de 4 grupe de experienta, carora li s-a administrat in esenta un tranchilizant purtand nume diferite. Se noteaza inabilitatile intalnite in comportamentul la volan sau intr-un test convenabil, sa zicem "timpul de reactie la alegere". Deci, variabila dependenta sau criteriul (x) ne apare sub forma aceluiasi indicator pentru toate grupele.
Pentru generalizare, consideram k grupe, avand datele aranjate intr-un tabel cu rubricile de mai jos (Tab. 4.1, dupa Faverge, 1963).
Notam variabila dependenta cu x si scriem valorile ei in prima coloana din tabel. Avem k grupe A, B, C, si notam grupe generica cu G iar efectivul ei cu ng.
Tabelul 4.1
|
x |
A |
B |
C |
G |
Total |
||
|
Efectiv Total |
na Ta |
ng Tg |
N = T = |
In coloanele rezervate fiecarei grupe se trec efectivele sau frecventele corespunzatoare valorilor x, precum si produsele fxx respectiv fxx2, in vederea totalizarii pe coloane:
S x = Tg, apoi S x2
Pentru fiecare grupa se poate determina o medie mg. Simbolul S indica o insumare in interiorul unei grupe, iar cu T, totalul celor N date pe intreaga colectie de masurari si cu m media acestora.
Semnul S indica o insumare ce priveste cele k grupe ca grupe, ceea ce inseamna totalul a k numere (cate unul de grupa).
Utilizand notatiile introduse, putem scrie pentru un element x al unui grup G:
x-m = (x-mg) + (mg-m)
ceea ce inseamna ca abaterea fata de media generala a unui rezultat din colectia totala se compune din abaterea sa fasa de media grupului respectiv; la ea se adauga diferenta dintre media grupului si media generala.
Pentru a inlesni intelegerea acestei egalitati se poate incerca o vizualizare (dupa Spence, Underwood, Duncan si Cotton, 1968). Presupunem ca avem 4 grupe care, fiind supuse influentei unui factor in grade diferite, prezinta in final rezultate net diferite astfel incat toti membrii primei grupe au obtinut cote mai mici decat membrii grupei a doua, iar aceasta, la randul ei, se situeaza integral sub nivelul intrunit de grupa a treia s.a.m.d.
Luand un element oarecare din grupul 2, pe care-l vom nota x2, abaterea sa fasa de media colectiei totale m se compune din doua cantitati (x2 - m2) si (m2-m). Figura 4.1. (dupa Spence, Underwood, Duncan si Cotton), releva in mod intuitiv acest lucru.
Ecuatia fundamentala a variabilitatii datelor, exprimata condensat prin suma patratelor, este urmatoarea:
SS (x-m)2 = SS (x-mg)2 + Sng (mg-m)2
ceea ce s-ar putea citi intr-un limbaj calitativ: variabilitatea totala se compune din variabilitatea interna a grupelor la care se adauga variabilitatea intergrupe. Intr-o formula mai curand mnemotehnica, s-ar putea scrie prescurtat:
SS = SS + SS sau SP = SP + SP
totala intra inter totala intra inter
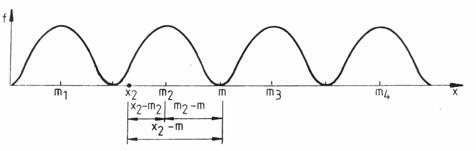
Fig. 4.1
Intr-un experiment exista de regula doua surse da variatie, de diferente sau deosebiri. Prima este variabilitatea interna a grupelor si tine de diversitatea surselor, a masuratorilor din interiorul fiecarui grup. Aceasta se poate numi variatia intragrup si este indicata de dispersia datelor in cadrul fiecarui grup A, B, C fata de media grupului respectiv mg; ea se poate scrie S (x-mg)2, iar pe ansamblu datelor SS (x-mg)2. A doua sursa o constituie variatia dintre grupe sau intergrupe si este indicata de modul de dispersie a mediilor de grup fata de media generala, mai corect de diferentele mg-m (luate de ng ori in cadrul fiecarui grup).
Aceasta se scrie: Sng (mg-m)2 sau SP inter. Variabilitatea totala pe ansamblu experimentului se divide in doua parti. variabilitatea datelor (subiectilor) in interiorul grupurilor si variabilitatea intergrupe. In experiment se manipuleaza variabilitatea intergrupe. Termenul de grup nu are aici nici un sens sociologic - asa cum s-a spus - ci unul statistic, fiind vorba de colectii de date sau masurari. In timp ce variabilitatea interna grupelor se atribuie hazardului, variabilitatea intergrupe este expresia actiunii factorilor modificati sau controlati in experiment.
Pentru a intelege mai usor distinctiile de mai sus se recurge la un exemplu (dupa Ray).
Se considera 2 grupe A si B avand efectivele egale: na = nb = 5 (Tab. 4.2)
Tabelul 4.2
|
A |
B |
|
Ta ma = 3 S(x -ma)2 = 10 |
Tb mb S (x - mb)2 |
Reunind grupele, media generala va fi 5, deoarece
T = Ta + Tb = 50,
iar
N = na + nb = 10.
Variabilitatea intragrup adica S (x-ma)2 este in fiecare grup egala cu 10, iar pe ansamblu:
SS (x-mg)2 = 10 + 10 = 20.
Variabilitatea intergrupe poate fi detasata daca eliminam variatia intragrupe, ceea ce se realizeaza prin inlocuirea fiecarui rezultat in parte in cadrul grupei prin media grupei respective. Asadar, elementele unei grupe G vor intra aici numai prin media si numarul lor. In consecinta rezulta tabelul 4.3.
Se observa ca totalurile nu se schimba; de asemenea, m, ma si mb raman neschimbate. Iese in relief variabilitatea intragrupe pe ansamblu.
Se constata, in cadrul grupei A, ca (ma - m) = 2 = constant iar na(ma-m)2 = 20. Tot asa, in cadrul grupei B, diferenta (mb-m) = 2 = constant, iar nb(mb-m)2 = 5 x 4 = 20 . Insumand pe cele doua grupe, variabilitatea va fi Sn(mg-m)2= 20 + 20 = 40.
|
A |
B |
|
Ta ma = 3 |
Tb mb |
|
m = 5 |
|
Inregistrand egalitatea, vom avea:
SS(x-m)2 = (10+10) + (20+20) = 20 + 40 = 60.
Revenind la termenii ecuatiei fundamentale, sa notam ca termenul SS (x-mg)2, adica SPintra se determina indirect, pentru a evita calculele laborioase - efectuand diferenta intre SΣ (x-m)2, adica Sptotala si Sng(mg-m)2, sau SPinter.
S-au propus formule de calcul pentru acesti termeni:
![]()
si
![]()
in care intervin efectivele fiecarui grup ng totalul datelor in cadrul fiecarui grup Tg, patratul totalurilor pe ansamblu T si suma patratelor valorilor Sx
Interesul formulelor de calcul este legat de prelucrarea manuala a datelor ori ca exercitiu preliminar, sau in absenta programelor de prelucrare statistica (actual, se utilizeaza calculatoarele).
H. Abdi (1987) propune o rutina de calcul in 7 puncte pentru calculul sumelor de patrate (SPtotala, SPintra si SPinter). Autorul introduce o noua notatie numita "numere in patrate" si anume AS, A si 1. cu A se noteaza numarul de modalitati ale variabilei independente A, iar cu S numarul de subiecti pe grupa, considerat a fi egal in cele k grupe. A ar fi numarul de grupe diferite din tabelul 4.1, iar S ar fi ng.
Iata suita de pasi cu valoare mnemotehnica:
Pasul 1: "Marele total" (T) adica SSx = x1 + x2 +
Pasul 2: AS = SSx = x12 + x22 +
Pasul 3: A = ![]() .
.
Pasul 4: 1 = ![]() (Pasul 1)2/N.
(Pasul 1)2/N.
Pasul 5: SPtotala = AS - 1 = (Pasul 2) - (Pasul 4).
Pasul 6: SPinter = A - 1 = (Pasul 3) - (Pasul 4).
Pasul 7: SPintra = AS - A = (Pasul 2) - (Pasul 3).
Pentru estimarea variantei intragrup ve si a variatiei intergrupe vg se preconizeaza expresiile:
![]() , care este
o estimare pentru ve
, care este
o estimare pentru ve
respectiv
![]() , o
estimare pentru ve + nvg
, o
estimare pentru ve + nvg
Expresiile de mai sus s-au numit patrate medii. Conventional, ele se pot nota PMintra si PMinter, pentru a pastra simetria cu notatiile precedente.
Se utilizeaza in continuare raportul Sn decor, notat cu F, care este catul dintre patratele medii:
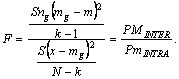
Valoarea acestui raport se interpreteaza cu ajutorul unui tabel special in functie de ipotezele sau intrebarile initiale ale cercetarii (Anexa 1.8.). Intreaga procedura presupune, pe de o parte, aspectul normal al distributiei, pe de alta parte, omogenitatea variatiei in populatia generala din care s-au extras grupele (esantioanele).
Exemplu (dupa Faverge, 1963):
La incheierea unei experiente, efectuata cu 5 clase paralele A, B, C, D si E, s-a dat aceeasi proba finala, pentru a vedea in ce masura factorul studiat influenteaza rezultatele.
Presupunem ca clasa E este clasa de control. In tabelul de comparatie (Tab. 4.4.) sunt date efectivele ng pe clase, apoi totalul Tg de raspunsuri exacte obtinut la proba respectiva in fiecare clasa si totalul patratelor acestor valori Sx
Tabelul 4.4
|
Clase |
A |
B |
C |
D |
E |
Total |
|
Nr. de elevi (ng) |
157 = N |
|||||
|
Totalul datelor (Tg) |
4784 = T |
|||||
|
Totalul patratelor (Sx2 |
= S Sx2 |
Calculam Sng(mg-m)2, adica SPinter pe baza formulei
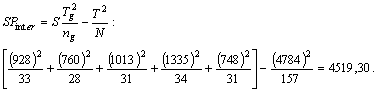
Apoi SS(x-m)2, adica SPtotala pe baza formulei![]()
![]()
Urmeaza sa se afle variabilitatea intragrup SPintra, scazand din variabilitatea totala pe cea intergrupe:
Sa aplicam pentru verificare rutina de calcul in 7 puncte propusa de Abdi:
P1: "Marele total" T = 4784.
P2: AS = Sx
P3:
A = ![]()
![]()
P4: ![]()
P5: SPtotala = AS - 1 = ![]()
P6: SPinter = A - 1 = Pasul 3 - Pasul 4 = 150294,18 - 145774,88 =
= 4515,30.
P7: SPintra = AS - A = Pasul 2 - Pasul 3 = 164040 - 150294,18 =
= 1374,82.
In continuare se pot determina patratele medii:
PM inter = ![]()
PMintra = ![]()
dupa care se calculeaza
raportul ![]()
In zilele noastre, intreaga procedura este rezolvata de programe de prelucrare statistica a datelor, rulate pe calculator. Parcurgerea intregului demers este utila pentru a fi in cunostinta de cauza.
Situand valoarea gasita prin calcul in tabelul Sn decor, facem un extras (Tab. 4.5). In prima linie a tabelului localizam numarul gradelor de libertate asociat numaratorului (n = k-1) iar in prima coloana reperam numarul gradelor de libertate asociat numitorului (n' = N-k). Prima valoare tabelara 2,49 corespunde pragului p = 0,05 iar cea de-a doua pragului p = 0,01. Valoare gasita prin calcul, adica 12,49, este mai mare decat se poate conchide ca diferentele sunt semnificative la pragul de p < 0,01. Ipoteza nula a egalitatii mediilor este infirmata, factorul de diferentiere avand deci efecte semnificative.
Tabelul 4.5
|
n n | |
Procedura urmata pana aici constituie un test global, o analiza de varianta globala - de unde prescurtarea "Fomnibus" - care nu ne spune de pilda intre ce grupe diferentele sunt semnificative; mai corect, care sunt modalitatile variabilei independente cu efecte sensibile sau altele - cu consecinte minore. In consecinta, nu ne vom opri doar la studiul global.
O mentiune este necesara. Testul F ne da un indiciu asupra efectului variabilei independente, dar el nu ne permite sa evaluam intensitatea acesteia.
4.3. FORMALIZAREA NOTIUNII DE COMPARATIE
Avand k grupe independente, se pune problema - dupa efectuarea analizei globale de varianta (Fomnibus) - sa facem comparatii perechi de grupe sau intre mai multe grupe; intervine deci un test de comparatie multipla. In limbaj tehnic se spune ca descompunem gradele de libertate ale sursei de variatie intre grupe.
De pilda, in experienta citata era vorba de administrarea de tranchilizante la 4 grupe diferite. Problema se pune de a testa efectele acestor droguri intre grupele de experienta luate doua cate doua, sau trei grupe in raport cu una, dar si cele patru grupe experimentale fata de grupa de control, care reprezinta situatia-martor. Asadar, in comparatiile ce vor fi facute avem in vedere nu numai perechi de medii (m1 cu m2, apoi m1 cu m3 sau m2 cu m3 s.a.m.d.), ci orice combinatie de medii (de ex.: m1, m2, m3, m4 in raport cu m5).
Adusa la forma sa abstracta, o comparatie intre perechi de medii poate fi notata cu ajutorul variabilei d (spre exemplu, d1 = m1 - m2, sau d2 = m1 - m3 etc.). Generalizand, o comparatie intre perechi de medii poate fi conceptualizata drept o combinatie liniara de medii sau o suma ponderata de medii, astfel incat suma ponderilor (coeficientilor) sa fie nula. Avand k grupe, vom avea k medii (mg) supuse comparatiei. Notam cu ag ponderile sau coeficientii cu care aceste medii sau grupe intra in diferite comparatii. Suma acestor coeficienti Sk(ag) trebuie sa fie zero. Simbolul d indica o comparatie, ceea ce reprezinta practic o suma ponderata de medii:
d = a1m1 + a2m2 + +akmk = Sk[(ag)(mg)],
in care a1 + a2 + + ak = 0.
Pentru exemplificare, sa luam o colectie de 3 grupe independente avand efectivele egale: ng = n = constant. In tabelul 4.6 sunt date comparatii prevazute intre medii (respectiv grupe) si coeficientii a cu care mediile respective intra in comparatie.
Dupa cum se observa, media necuprinsa in comparatie capata a = 0, ceea ce este firesc. In genere se evita numerele fractionale, desi sunt in principiu utilizabile. Daca am avea 5 grupe, respectiv 5 medii, si am dori sa testam combinatia m1 + m2 fata de m3 + m5 este de preferat sa se atribuie ponderilor (+3) + (+3) si (-2) + (-2), astfel incat S ag = +6 -6 = 0. Evident, atribuirea ponderilor comporta o parte de arbitrar, conditia fiind sa se obtina S ag = 0. In tabel se vede ca, de regula, grupele care se compara primesc coeficienti pozitivi, iar grupele cu care se compara capata coeficienti negativi. (Este vorba de o simpla indicatie de lucru).
Tabelul 4.6
|
Comparatii intre medii (grupe) |
Coeficienti |
||
|
a1 |
a2 |
a3 |
|
|
m1 cu m2 m1 cu m3 m2 cu m3 m1 cu m2 + m3 m2 cu m1 + m3 m3 cu m1 + m2 | |||
Avand o colectie de k grupe sunt posibile mai multe comparatii intre medii (grupe). Or, are sens sa fie facute comparatiile relevante. Anumite comparatii fiind facute, altele devin superflue.
Punand conditia ca efectivele ng sa fie egale ne dam usor seama ca grupele se deosebesc practic intre ele prin ∑x = Tg, astfel incat nu este necesar sa ducem calculele pana la determinarea mediilor.
In consecinta, in comparatiile pe care le facem vom utiliza totalurile Tg si ponderile corespunzatoare ag. Vom nota in cazul acesta comparatiile cu litera mare D si vom avea:
D = Sk [(ag) (Tg)].
Sa urmarim un exemplu (dupa Faverge, 1963)
Un experimentator doreste sa compare intre ele 4 sisteme de semnalizare A, B, C, D. In acest scop 40 de subiecti sunt repartizati - potrivit regulilor selectiei aleatoare - in patru grupe de cate zece si sunt supusi aceleiasi probe in care se inregistreaza numarul de erori comise de fiecare. In prima grupa se utilizeaza sistemul de semnalizare A, in a doua grupa sistemul B s.a.m.d. Date obtinute apar in tabelul 4.7.
Tabelul 4.7
|
Grupa |
A |
B |
C |
D |
|
Totalul erori (Tg) Totalul patrate (Sx2 |
Se pune intrebarea daca exista diferente de valoare intre cele patru sisteme de semnalizare.
Efectivele fiind egale (ng = n = 10), grupele se diferentiaza in functie de valorile Tg.
Se face distinctie intre comparatii prevazute la initierea experimentului si comparatii aposteriori sugerate de anumite 'denivelari' intre medii, constatate la incheierea cercetarii. Se cere - ca prim pas - indeosebi in cazul comparatiilor aposteriori, efectuarea unui test global (Fomnibus) si o valoare semnificativa F; in celalalt caz, testul F global nu este obligatoriu.
In experimentul amintit mai sus, la grupele A si D semnalizarea are la baza un suport grafic, iar la grupele B si C un suport numeric. Asadar, se pune problema de a compara grupele intre ele luate separat doua cate doua, dar si combinatia A + D si B + C. Aceasta din urma comparatie ar fi putut sa fie sugerata doar de diferentele constatate la sfarsitul experientei (aposteriori).
In calcule figureaza intotdeauna varianta intragrup (PMintra)astfel incat este util sa intocmim tabelul cu datele de baza pentru analiza globala de varianta (Tab. 4.8.).
Retinem din acest tabel patratul mediu intragrup (PMintra = 11,8), care va fi acelasi pentru toate comparatiile.
Tabelul 4.8
|
Sursa |
n |
Suma patratelor |
Patratele medii |
F |
|
Intergrupe Intragrupe Total |
2,9 s p |
Referindu-ne la combinatia A + D in raport cu B + C determinam valoarea comparatiei potrivit formulei enuntate:
D1
In continuare, cautam o estimare a variantei dintre grupele cuprinse in comparatie, deci un PMinter relativ la combinatia de grupe avute in vedere.
Formula de calcul pentru acest patrat mediu relativ la comparatia considerata este:
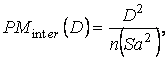
numarul gradelor de libertate v fiind 1 pentru fiecare comparatie particulara.
In exemplu:
D2
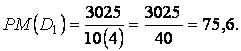
Calculam apoi raportul:
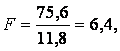
si situam valoarea calculata in tabelul F pentru v = 1 si v = N- k. Diferentele sunt semnificative.
Daca efectuam calculele pornind de la medii, notam comparatiile cu d, pastrand formula cunoscuta:
d = Sk [(ag) (mg)].
In estimarea variantei intergrupe, relativa la combinatia de medii considerata, intervine o mica modificare:
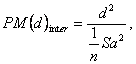
deoarece calculele sunt duse pana la medii.
In exemplu dat vom avea:
d
d
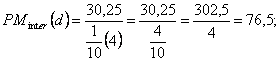
iar F = 75,6 : 11,8 = 6,4. Deci acelasi rezultat.
In continuare ne putem opri la comparatii intre perechi de grupe. Sa luam pentru exemplificare comparatiile D2 intre A si B, apoi D3 intre C si D:
D
![]()
![]()
D = 64 (- 1) + 108 (+ 1) = - 64 + 108 = 44,
![]()
![]()
Pentru comparatiile aposteriori, dupa un test global F se trece la comparatii multiple, fixandu-se un prag mai sever de semnificatie. Oricum. insa, un test de semnificatie nu se poate substitui in principiu unui experiment si atunci este cazul sa se procedeze mai curand la contravalidare, adica la repetarea experientei cu un lot de subiecti pentru verificare comparatiilor aposteriori.
Tehnica de analiza a datelor infatisata mai sus se refera la experiente cu o singura variabila independenta care prezinta modalitati diferite, reperate printr-o etichetare verbala diferita. Corespunzator acestor modalitati se constituie k grupe dupa regulile selectiei aleatoare. Practic, exista un factor de clasificare a grupelor, si anume variabila independenta cu modalitatile ei. Metoda de lucru consta in efectuarea - ca prim pas - a unei analize globale de varianta (Fomnibus), dupa care se instituie un test de comparatie multipla.
4.4. PLANUL BIFACTORIAL
Considerand un factor (A), modificat in experienta, si efectul acestei modificari (y) numit variabila dependenta, vom putea urmari legea de variatie a lui y in functie de A. Daca se introduce o a doua variabila independenta B - ca in primul exemplu prezentat la inceput - aceasta va actiona in combinatie cu A si va modifica eventual regula de variatie a lui y.
Un tip simplu de combinatie este cel aditiv, in care factorii actioneaza dupa relatia:
X = A + B.
In tabelul 4.9 este dat un exemplu cu 2 variabile independente A si B. Variabila A prezinta 3 modalitati sau niveluri, notate cu A1, A2 si A3. Variabila B prezinta doua niveluri: B1 si B2. In casutele tabelului apar rezultatele exprimate in valori medii; asadar, variabila dependenta sau criteriul apar condensate in cifre medii. La marginile tabelului s-au calculat, de asemenea, mediile pe linii si coloane. Pentru a ne da seama de modul de interactiune a celor doua variabile independente urmeaza sa intocmim un grafic, in care sa localizam pe abscisa nivelurile factorului A, iar pe ordonata vor apare datele variabilei dependente (y), trasand apoi curbe separate corespunzator modalitatilor B1, respectiv B2.
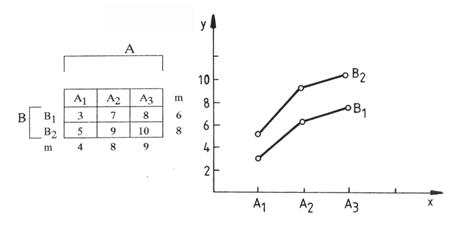
Tabelul 4.9
Fig. 4.2
Se poate observa ca cele doua curbe sunt paralele, ceea ce inseamna ca legea de variatie a fenomenului studiat (y), in conditiile factorului A, nu se modifica atunci cand intervin valorile asociate ale factorului B. Altfel spus, marimea efectelor unei variabile ramane constanta pentru toate conditiile celei de a doua variabile independente. In cazul acesta vorbim de o combinatie aditiva a influentei celor doi factori (Matalon, 1969).
Exista si moduri de combinare neaditiva, care pot fi, la randul lor diferite.
In tabelele 4.10 si 4.11 sunt date asemenea exemple. Este vorba, de asemenea, de cate doua variabile independente A si B, criteriul fiind exprimat in valori medii.
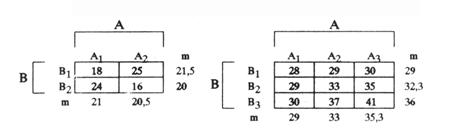
Tabelul 4.10 Tabelul 4.11
Intocmim in continuare graficele corespunzatoare, notand pe ordonata criteriul sau variabila dependenta - adica valorile din casutele tabelului - iar pe abscisa vom nota una din valorile independente (A sau B). In exemplele alese vom nota pe abscisa variabila A, care prezinta doua modalitati sau niveluri in tabelul si trei modalitati in experienta redata in tabelul
Se vede din figurile 2.3 si 2.4 ca variatia fenomenului studiat in functie de conditiile A se modifica atunci cand intervin si valorile asociate ale lui B. Curbele nu mai sunt paralele, deci ipoteza relatiei aditive nu mai sta in picioare. Vorbim atunci de o combinatie neaditiva sau interactiune.
Se observa ca in figura 2.4 curbele tind sa se indeparteze, trecand de la conditia B1 la conditia B3; influenta factorului A se amplifica in comparatie cu B2, dar mai ales cu B3. Interactiunea este mai puternica
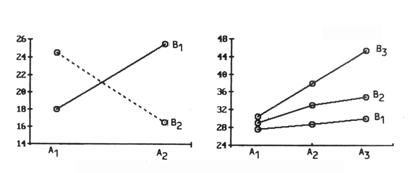
Fig. 4.4 Fig. 4.5
in exemplul redat in figura 4.4; influenta factorului A variaza in sens invers, dupa cum este asociata cu B1 sau cu B2. Concluziile ce ar putea rezulta din simpla considerare a rezultatelor marginale din tabelul 4.10. (mediile pe linii si pe coloane) pot fi inselatoare.
In termeni generali vorbim de interactiunea dintre 2 factori atunci cand legea de variatie a fenomenului studiat in functie de unul din factori nu ramane aceeasi in raport de modalitatile asociate celui de al doilea factor (Leplat, 1973). Cand in combinatie intervine un al treilea factor, modul de interactiune al celor trei variabile independente este mai greu de interpretat, iar ipotezele cu privire la formula lor de actiune conjugata devin mult mai complicate.
In planul factorial apare adeseori grupuri de control prin care se realizeaza conditia zero. Planurile factoriale pun in evidenta relatii mult mai complexe decat planurile de baza. Ca urmare, rezultatele obtinute pe baza lor au o mai mare validitate ecologica (= reflecta mai exact realitatea din afara laboratorului, in care traieste subiectul uman). Datele obtinute dintr-un experiment probeaza ipoteza care a stat la baza lui daca sunt semnificativ statistic (lucru dovedit prin testele statistice, ANOVA etc). La baza acestor teste se afla comparatiile intergrupale si cele intragrupale.
In cadrul planurilor factoriale se evidentiaza atat efectele fiecarei variabile studiate cat si efectul interactiunii acestora. Natura efectelor se poate constata prin diagrame de interactiune. De exemplu in cazul unui design factorial de tip 2X2 combinatiile posibile si modul lor de reprezentare grafica sunt prezentate in figura 4.6.
Figura 4.6 Tipuri de efecte in cadrul diagramelor de interactiune
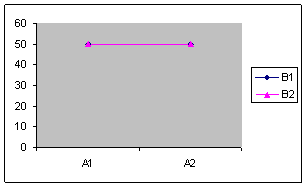 Design factorial 2X2 in care:
Design factorial 2X2 in care:
Efectul variabilei A nu este semnificativ
Efectul variabilei B nu este semnificativ
Efectul interactiunii AXB nu este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
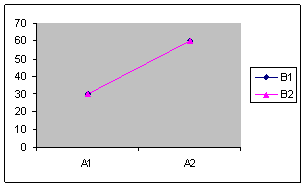 Design factorial 2X2 in care:
Design factorial 2X2 in care:
Efectul variabilei A este semnificativ
Efectul variabilei B nu este semnificativ
Efectul interactiunii AXB nu este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
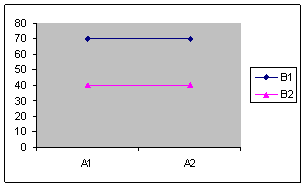
Design factorial 2X2 in care:
Efectul variabilei A nu este semnificativ
Efectul variabilei B este semnificativ
Efectul interactiunii AXB nu este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
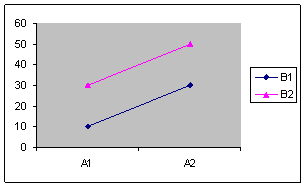
Design factorial 2X2 in care:
Efectul variabilei A este semnificativ
Efectul variabilei B este semnificativ
Efectul interactiunii AXB nu este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
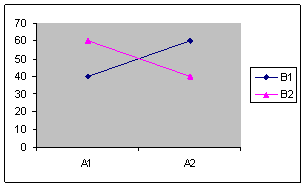
Design factorial 2X2 in care:
Efectul variabilei A nu este semnificativ
Efectul variabilei B nu este semnificativ
Efectul interactiunii AXB este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
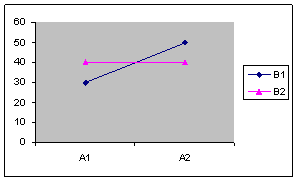 Design factorial 2X2 in care:
Design factorial 2X2 in care:
Efectul variabilei A este semnificativ
Efectul variabilei B nu este semnificativ
Efectul interactiunii AXB este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
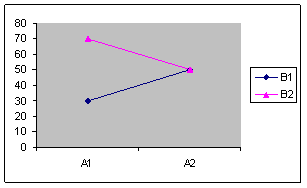
Design factorial 2X2 in care:
Efectul variabilei A nu este semnificativ
Efectul variabilei B este semnificativ
Efectul interactiunii AXB este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
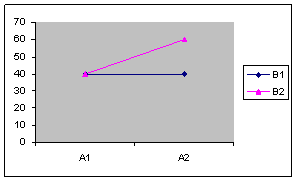 Design factorial 2X2 in care:
Design factorial 2X2 in care:
Efectul variabilei A este semnificativ
Efectul variabilei B este semnificativ
Efectul interactiunii AXB este semnificativ
|
A1 |
A2 |
Medie |
|
B1 | |||
|
B2 | |||
|
Medie |
In continuare prezentam tehnica de analiza a datelor pentru experiente cu doua variabile independente, deci cu doi factori de clasificare. Elementul nou care intervine este fenomenul de interactiune a variabilelor.
Exemplu (dupa I. Radu):
S-a initiat un experiment de instruire programata in care s-au utilizat, in grupuri paralele, programe liniare (PL) si programe ramificate (PR). De asemenea, s-a mentinut, pentru comparatie, in alte grupe, lectia orala clasica (LC). Pentru o urmarire diferentiata a efectelor, grupele au fost dihotomizate in functie de CI si anume: CI > m si CI < m. Asadar, avem doua variabile independente: A, metoda de instruire si B, nivelul de inteligenta (CI). Prima variabila prezinta trei modalitati (PL, PR si LC), iar a doua variabila are doua modalitati: CI > m si CI < m.
Datele de baza sunt condensate in tabelul 4.12
Tabelul 4.12.
|
Nivel de int. (B) |
Metoda de instruire |
Total |
||
|
PL (I) |
PR (II) |
LC (III) |
||
|
(I) CI > m |
Tg = 114 S x2 = 1116 | |||
|
(II) CI < m |
Tg = 88 Sx2 | |||
|
Total |
T = 489 S Sx2 |
|||
Efectivele grupelor au fost egale: ng = n = 12, iar N = 72, fiind vorba de 6 grupe.
O studiere globala a variabilitatii intergrupe nu prezinta in cazul acesta interes. Se impun comparatii intre coloane pentru a desprinde efectele principale ale modalitatilor variabilei A, apoi comparatii pe linii pentru a releva efectul esential al variabilei B in cele doua modalitati ale acestora, iar in final studierea interactiunii celor 2 variabile. Dupa cum se stie, in toate comparatiile intervine o estimare a variatie intragrup, care se determina indirect mai intai variabilitatea totala, apoi variabilitatea intergrupe, pentru a obtine - prin scadere - variabilitatea intragrup.
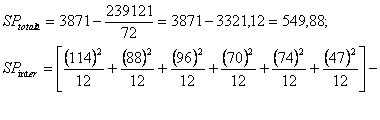
![]()
![]()
In continuare, variabilitatea intergrupe urmeaza sa o desfacem in cele trei componente amintite: pe o coloane pentru variabila A, pe linii pentru variabila B si apoi efectul combinatiei AxB.
Testand ipoteza nula relativ la coloane, vom considera fiecare coloana in parte ca formand un singur grup. La fel se va proceda in cadrul comparatiilor pe linii.
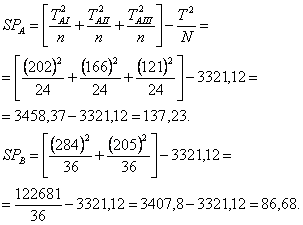
Variabilitatea datorata interactiunii se determina indirect prin scadere:
SPAxB = SPinter - SPA - SPB.
In cazul dat:
SPAxB = 224,19 - 137,23 - 86,68 = 0,28.
In continuare se afla patratele medii:
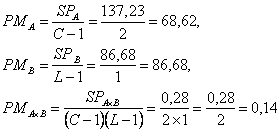
(C indica numarul de coloane din tabel, iar L arata numarul de linii)
La acestea adauga:
![]()
Urmeaza rapoartele F:
![]() (p
< 0,01);
(p
< 0,01);
![]() (p < 0,01);
(p < 0,01);
![]() (NS).
(NS).
Sumar.
In acest modul s-a prezentat problematica legata de comparatiile multiple. In prima parte pe baza unor exemple s-au delimitat variantele analizei de varianta in functie de tipul design-ului experimental utilizat. S-a discutat apoi modul de calcul in cazul planurilor experimentale de baza, in acest context fiind prezentata formalizarea notiunii de comparatie. In finalul capitolului s-a prezentat modul de calcul al semnificatiei diferentelor precum si interpretarea acestora in cazul planurilor factoriale.
Bibliografie
1. Abdi, H., Introduction au traitement statistique des donees experimentales, Grenoble, Presses Univ., 1987.
2. Faverge, J. M., Methodes statistiques en psychologie applique, t. II,Paris, P.U.F., 1963
3. Hazs, L.W., Statistics for Psychologist, New York, Holt Rinehart and Winston,1966.
4. Leplat, J., La methode experimentale en psychologie apliquee, in " Trataite de psychologie apliquee", (Reuchelin M.,dir.), t.2, Paris P.U.F., 1973.
5. Matalon, B., La logique des plans d'experiences, in G. et J. Lemaine (ed.) "Pszchologie sociale et experimentation", Paris, Mont-Bordas, 1969.
6. Radu, I., Insusirea unor cunostinte de matematica prin invatare programata. In 'Creativitate, modele, programare ", (Al.Rosca, red.), Bucuresti, Edit. Stiintifica, 1967.
7. Spence, J.,Underwood,B., Duncan,C., Cotton,J., Elementarz Statistics, New York, Appleton - Century - Crofts, 1968.
ANOVA este "acronimul" pentru analiza de varianta (acronim = cuvant format din initialele altor cuvinte)
|