METODE NEPARAMETRICE

Obiective

Dupa parcurgerea acestui modul studentul va cunoaste:

Conditiile de utilizare a probelor neparametrice

Procedura de comparatie in situatia esantioanelor independente prin utilizarea testului U

Procedura de comparatie in situatia esantioanelor perechi prin utilizarea testului Wilcoxon

Metodele statistice aplicate in mod curent in cercetarea psihologica presupun ca multimea datelor obtinute intr-o experienta sau ancheta se organizeaza dupa curba lui Gauss (in forma de clopot), urmand deci o lege normala de distributie. In acest caz expresia curbei de frecventa era:

in care л si e sunt doua numere a caror valoare este cunoscuta, m si s fiind doi parametri. Valorile celor doi parametri se determina plecand de la esantionul experimental. Aceasta cerinta a normalitatii variabilelor nu poate fi realizata intotdeauna. Cand se lucreaza cu grupe mici, deci cu multimi reduse de date, graficul sau histograma intocmita nu ne sugereaza de multe ori ipoteza unei distributii normale in colectivitatea mai larga. In asemenea cazuri, trebuie sa facem apel - in prelucrarea si interpretarea datelor - la metode sau probe care nu depind de forma distributiei. Este vorba de o serie de procedee cunoscute sub numele de 'metode statistice neparametrice'.

In cazul aplicarii acestor metode, evident nu se mai calculeaza m si s. Analizele se fac plecand de la medianele distributiilor. Calculele se fac adesea asupra rangurilor obtinute pe baza clasificarii datelor sau asupra semnelor acestor valori. In felul acesta intervine o anumita pierdere de informatie; metodele neparametrice raman insa singurele indicate in cazul scarilor ordinale si, in general, in cazul esantioanelor mai mici care nu permit ipoteza unei distributii normale in colectivitatea mai larga. Aceleasi procedee de lucru devin utilizabile si pentru ansambluri mai numeroase de date (esantioane mari), cand pierderea de informatie este neglijabila, deoarece calculele se simplifica foarte mult. Metodele neparametrice intervin ca tehnici de prelucrare in problemele de comparatie, cand vrem sa apreciem efortul unei experiente sau, in general, influenta unui factor bine precizat. Si in acest tip de probleme pot sa apara doua situatii:

. cand lucram cu grupe sau clase separate, independente, si

. cand avem de-a face cu grupe sau esantioane perechi.

In prima situatie se lucreaza de regula cu grupe sau clase paralele: grupe de experienta si de control, luate in compozitia lor data la intamplare. In a doua situatie este vorba de multe ori de aceeasi grupa comparandu-se datele inregistrate in pretest si posttest. Evident, rezultatele aceluiasi subiect in pre- si posttest formeaza perechi, iar efectul experientei intreprinse se apreciaza dupa diferentele calculate in doua esantioane diferite a caror compozitie este astfel reglementata incat fiecarui subiect dintr-o grupa sa ii corespunda un subiect din grupa paralela.

Identificarea celor doua situatii este esentiala pentru procedura de urmat. Pentru compararea a doua grupe (esantioane) independente ne folosim de testul U iar in cazul a doua esantioane perechi aplicam proba Wilcoxon.

3.1. COMPARAREA A DOUA ESANTIOANE INDEPENDENTE

3.1.1. Testul U (Mann - Whitney)

Cand se compara grupe sau clase de elevi diferite dupa schema: clasa experimentala (C_e) si clasa de control (C_c) atunci este indicat sa utilizam tehnica testului U preconizata de Mann si Whitney. Metoda se preteaza destul de bine la datele numerice rezultate din atribuirea de puncte, clasificari, note etc.

Testul U constituie una dintre cele mai puternice metode neparametrice. Acesta tine cont de rangul fiecarui rezultat in clasificarea generala si serveste la testarea ipotezei nule (Ho) potrivit carei cele doua grupe (esantioane) independente sunt extrase la intamplare din aceeasi colectivitate.

Exemplu (dupa I. Radu):

Intr-o experienta de instruire programata la clasa a VIII-a rezultatele la probele finale apar exprimate in notele de la 0 la 20. Clasa experimentala (C_e) are 27 elevi, iar clasa de control (C_c) tot 27 de elevi. Datele simplu ordonate sunt cuprinse in tabelul 3.1

Tabel 3.1

Tabel 3.2

Reprezentarea grafica da histograme asimetrice, astfel incat ipoteza distributiei normale in populatie nu este de sustinut. Intrucat intinderea variatiei este destul de mare (de la 0 la 20), este indicat testul U pentru evaluarea semnificatiei rezultatelor.

Conform Ho, se combina rezultatele celor doua grupe intr-un singur ansamblu, trecand apoi la clasificarea notelor in ordine crescatoare sau descrescatoare. In exemplul nostru vom folosi ordinea descrescatoare (Tab. 3.2).

Admitem in continuare ipoteza nula (Ho), considerand cele doua esantioane ca selectii intamplatoare din aceeasi colectivitate; in consecinta notele sau rezultatele lor nu trebuie sa difere in mod semnificativ. Daca este asa, suma rangurilor (R₁) atribuite datelor obtinute de grupul experimental ar trebui sa fie sensibil egala cu suma rangurilor (R₂) din grupul de control, adica R₁ = R₂ (sub Ho).

Pentru a calcula R₁, respectiv R₂, pentru fiecare nota se va face produsul dintre efectivul care a obtinut nota (in cadrul fiecarei clase) si rangul atribuit acestei note. In tabelul 3.3. este redat modul de calcul pentru exemplul ales de noi.

Totalul rangurilor atribuite (R₁ +R₂) trebuie sa fie egal cu N(N+1)/2, in care N = N₁ + N₂. In exemplul nostru R₁ + R₂ = (54x55)/2 = 1485.

Adunand cele doua sume obtinute in tabelul de mai sus, avem: 605 + 880 = 1485. Aceasta verificare este totdeauna utila. Pentru testul ipotezei nule se poate utiliza fie R₁, fie R₂; sunt de preferat datele relative la grupa mai putin numeroasa. Pentru usurarea calculelor se va determina de la inceput suma rangurilor (R) numai la unul din esantioanele date (la cel mai restrans).

Daca N₁ si N₂ sunt mai mari decat 8 se introduce o variabila U, care pe baza unor transformari conduce la raportul:

in care se recunoaste variabila normala redusa. Daca utilizam R₂, la numarator in loc de N₁/2 va apare N₂/2.

Pentru exemplu nostru, dupa efectuarea calculelor vom avea:

Ne referim la proprietatile distributiei normale, adica la trei repere fixe care sunt date in extrasul de mai jos.

Pentru valoarea | z | gasita avem p < 0,02. Rezulta deci ca ipoteza nula este infirmata (are sanse sa se confirme in mai putin de 2% din cazuri). In consecinta, admitem ipoteza specifica aflata la baza experimentului.

Tabel 3.3

Aplicarea metodei prezentate impune restrictia ca numarul rangurilor egale la diferite note sa nu fie prea mare.

Cand N₁, N₂ < 8, urmeaza sa se raporteze totalul rangurilor R₁ sau R₂ la datele inscrise intr-un tabel special intocmit de Mann si Whitney. Intrucat se acorda putin credit rezultatelor obtinute pe baza unor grupuri restranse (N < 8) nu este cazul sa expunem procedeul de lucru aplicat in aceste situatii

3.2 COMPARAREA A DOUA ESANTIOANE PERECHI

3.2.1. Proba Wilcoxon

Este o metoda neparametrica ce se aplica, esantioanelor perechi si tine seama nu numai de semnul diferentelor ci si de marimea acestora.

Se ordoneaza diferentele in valoare absoluta in ordine crescatoare si se atribuie ranguri: rangul 1 se atribuie celei mai mici diferente, rangul 2 celei care-i urmeaza etc. Se face apoi suma rangurilor corespunzatoare diferentelor pozitive (R+) si cea corespunzatoare diferentelor negative (R-). Ipoteza nula (Ho): se presupune ca nu exista motive sa fie superioara celeilalte (deci nu exista diferente intre esantioane0.

Cand R+ (sau R-) este anormal de mica, atunci se va conchide asupra diferentei semnificative.

Si aici se disting doua situatii, in functie de volumul esantionului:

a) N < 25; b) N > 25.

a) Cazul N < 25

Exemplu:

Un lot de 8 subiecti este testat in doua conditii experimentale (esantion - pereche) obtinandu-se cotele din tabelul 3.4, unde:

d sunt diferentele intre cotele obtinute in cele doua situatii experimentale;

r sunt rangurile corespunzatoare acestor diferente;

R+ = 22 si R- = 6

Tabelul 3.4.

Se retine suma rangurilor aflate in minoritate pe care o notam cu Rc.

Rc = R- = 6

Valoare lui Rc se raporteaza la datele cuprinse intr-un tabel special intocmit de Wilcoxon

(Tab. 3.5.):

Tabelul 3.5.

Acest tabel indica valoarea maxima pe care o poate lua Rc pentru a fi considerat semnificativ la pragul p = 0,05 si p = 0,01. N reprezinta numarul rangurilor.

Pentru N = 7 valoarea maxima admisa la p = 0,05 este 2. Intrucat Rc = 6, se considera ca ipoteza nula nu este infirmata.

b) Pentru N > 25, distributia valorilor R tinde spre o distributie normala si vom utiliza formula:

comparand valoarea gasita prin calcul cu cea oferita de tabelul legii normale reduse.

In aceasta formula R este suma rangurilor (R)

Cu ajutorul criteriului z se calculeaza probabilitatea ca valoare R obtinuta sa survina prin simpla intamplare.

Exemplu (dupa Faverge):

S-a efectuat un experiment de comunicare intre grupe. Diferentele A - B constatate la 32 grupe intre categoriile A si B se repartizeaza astfel:

Se pune intrebarea daca numarul de comunicari de tipul A difera semnificativ de cele de tip B? Se considera valorile absolute ale diferentelor in ordine crescanda (sau descrescanda) si se intocmeste o histograma:

Eliminam ca si la proba semnelor diferentele nule. Raman 30 de valori. Dintre acestea, 6 valori sunt egale cu 1, deci le atribuim rangul intermediar (mediu) de 3,5 s.a.m.d.

Calculam suma rangurilor (R ).

Luam in calcul R-, intocmind histograma corespunzatoare:

Suma rangurilor este:

R- = 2 x 19 212i86c ,5 + 3 x 15 + 3 x 9 212i86c ,5 + 3 x 3,5 = 123.

Se calculeaza si ceilalti termeni ai formulei:

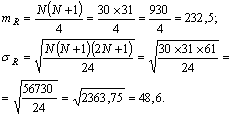
Deci

Valoarea | z | obtinuta este mai mare decat valoarea 1,9 212i86c 6 corespunzatoare pragului p = 0,02, deci se poate spune ca ipoteza nula este infirmata.

Sumar

In cadrul acestui modul s-au prezentat pe baza de exemple doua probe neparametrice in conditiile comparatiilor realizate pentru esantioane independente ,respectiv esantioane perechi. Astfel in situatia comparatiilor esantioanelor independente s-a prezentat testul Mann-Whitney (testul U), iar pentru situatia comparatiei esantioanelor perechi testul Wilcoxon.

Teme

S-a masurat la 10 baieti si la 10 fete de varste egale rapiditatea scrierii in numar de litere pe minut. Rezultatele sunt redate mai jos. In fiecare coloana apar rezultatele obtinute de un baiat si o fata de aceeasi varsta

Baieti: 84 9 212i86c 2 86 100 102 87 9 212i86c 6 88 9 212i86c 6 85

Fete : 88 9 212i86c 0 9 212i86c 2 107 9 212i86c 8 9 212i86c 5 102 88 9 212i86c 9 212i86c 89 212i86c

Datele prezentate permit sa se spuna ca baietii sunt mai rapizi ca fetele

In cadrul unui experiment efectuat in vederea evaluarii efectului unei metode de memorare s-a inregistrat numarul de raspunsuri corecte in cadrul probelor individuale date in posttest. Rezultatele au fost urmatoarele:

Grupul A: 12, 11, 12, 14, 7, 10, 12, 11, 12, 8, 14, 12, 8, 12, 11, 12, (Grup experimental)

Grupul B: 9 212i86c , 13, 12, 9 212i86c , 7, 10, 6, 9 212i86c , 7, 13, 7, 10, 12, 9 212i86c (Grup de control)

Se cere sa se verifice daca metoda prezentata conduce la rezultate diferite sau nu.

Bibliografie

Faverge,J. M., Methodes statistiques en psychologie applique, t. II,Paris, P.U.F., 19 212i86c 63

2. Plutchik, R., Foundation of Experimental Research, New York, Harper & Row Publisher, 19 212i86c 68.

3. Siegel, S., Psychometric Methods-Nonparametric Statistics for the Behavioral Sciences, New York, McGraw - Hill Book Company Inc., 19 212i86c 56.