APLICATII. CALCULUL PLACILOR PLANE
PLACI CIRCULARE. TEORIA INCOVOIERII AXIAL-SIMETRICE A PLACILOR CIRCULARE.
SOLUTIA LUI POISSON.
1.15.1 GENERALITATI. DEFINITII. CLASIFICARI.
IPOTEZE DE CALCUL.
|
z |
|
p=p(r) |
|
|
|
h |
|
z |
|
D |
|
reactiuni |
|
a. |
|
|
|
z |
|
b. |
|
reactiuni |
|
|
|
z |
|
z |
|
c. |

|
Fig.1.15.1. |
 1. Numim de obicei
"placa", modelul mecanic al unor elemente de rezistenta care au doua din
dimensiuni de acelas ordin de marime, iar a treia (grosimea h) mult mai mica in
comparatie cu primele doua. In constructia de masini exemple de elemente de
rezistenta care pot fi considerate din punct de vedere al raportului
dimensional ca niste placi, sunt numeroase: fundurile plane ale rezervoarelor,
capacele plane ale cilindriilor, flansele tevilor, diferite tipuri de diafragme
si dispozitive de etansare, pistoanele motoarelor cu ardere interna si ale pompelor,
peretii cutiilor paralelipipedice etc.
1. Numim de obicei
"placa", modelul mecanic al unor elemente de rezistenta care au doua din
dimensiuni de acelas ordin de marime, iar a treia (grosimea h) mult mai mica in
comparatie cu primele doua. In constructia de masini exemple de elemente de
rezistenta care pot fi considerate din punct de vedere al raportului
dimensional ca niste placi, sunt numeroase: fundurile plane ale rezervoarelor,
capacele plane ale cilindriilor, flansele tevilor, diferite tipuri de diafragme
si dispozitive de etansare, pistoanele motoarelor cu ardere interna si ale pompelor,
peretii cutiilor paralelipipedice etc.
A. Din punct de vedere geometric o placa este caracterizata prin
a) forma si dimensiunile suprafetei mediane, prin care vom intelege locul geometric al punctelor aflate la distanta egala de ambele suprafete exterioare ale placii.
Din acest punct de vedere vom deosebi:
-placi curbe-daca suprafata mediana este o suprafata curba (simetrica sau stramba).
-placi plane-daca suprafata mediana este un plan: dupa forma conturului din plan al placii vom intalni: placi plane circulare, dreptunghiulare, triunghiulare, eliptice, inelare etc.
b) grosimea "h" a placii, constanta sau variabila masurata pe normala la suprafata mediana
a).materialul din care este confectionata -care se presupune ca este omogen, izotrop si asculta de legea lui Hooke.
b).sarcinile aplicate placii care se presupun ca au o simetrie axial-radiala si ele mai pot fi
-o presiune
normala pe suprafata placii distribuita dupa o lege oarecare p=p(r) [N/m
![]() ]
(fig.1.15.1.a),
]
(fig.1.15.1.a),
-forte perpendiculare pe planul placii, uniform distribuite pe contururi circulare, cu centrele pe axa de simetrie [N/m] (fig .b),
-momente cu efect de incovoiere uniform distribuite tot pe contururi circulare (pentru a pastra simetria axiala a incarcarii) [Nm/m],
-forte concentrate actionand in centrul de simetrie [N].
c)
![]() modul de fixare (rezemare) care poate fi rigid, elastic sau dupa o lege
modul de fixare (rezemare) care poate fi rigid, elastic sau dupa o lege
oarecare, cu margini libere sau articulate etc.
d)fortele
interioare sau eforturile sectionale care sunt cele cunoscute de la grinzi N,
T, M
![]() ,
cu deosebirea ca in cazul placilor, "toate fortele interiore se masoara pe
unitatea de lungime a sectiuni prin placa" (N[N/m], T[N/m], M
,
cu deosebirea ca in cazul placilor, "toate fortele interiore se masoara pe
unitatea de lungime a sectiuni prin placa" (N[N/m], T[N/m], M
![]() [N/m]).
[N/m]).
2. Ipoteze. Parametrii de incovoiere ai unei placi (in general) depind foarte mult de grosimea placii in comparatie cu celelalte dimensiuni ale sale. De aceea, din acest punct de vedere, se obisnuieste sa se vorbeasca de trei categorii de placi: 1)placi suptiri avand deformatii mici; 2) placi subtiri cu deformatii mari; 3) placi groase.
Noi ne vom ocupa numai cu studiul placilor subtiri avand deformati mici, pentru care -pe baza ipotezelor pe care le vom enunta -se poate dezvolta o teorie aproximativa cu rezultate destul de multumitoare. Celelalte categorii de placi au dezvoltate teorii specifice, destul de dificile, pentru care recomandam bibliografia, (pentru placile groase nici nu exista un studiu sistematic si o solutie generala).
|
r |
|
z |
|
D |
|
w=w(r) |
|
z |
|
p(r) |
|
h |
|
. |
|
. |
|
conditii:
|
|
Fig.1.15.2
|
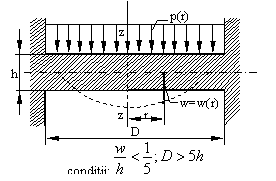
 Sa consideram o placa circulara de grosime constanta h,
rezemata intr-un mod oarecare si incarcata cu un sistem de sarcini
axial-simetrice; datorita simetriei starea de deformatie si de tensiune a placii
va fi simetrica in raport cu axa ei centrala z-z si cu planul median care, in
urma deformatiei, va deveni o suprafata de rotatie numita "suprafata elastica a
placii" (fig.1.15.2).
Sa consideram o placa circulara de grosime constanta h,
rezemata intr-un mod oarecare si incarcata cu un sistem de sarcini
axial-simetrice; datorita simetriei starea de deformatie si de tensiune a placii
va fi simetrica in raport cu axa ei centrala z-z si cu planul median care, in
urma deformatiei, va deveni o suprafata de rotatie numita "suprafata elastica a
placii" (fig.1.15.2).
IPOTEZA a I-a. Se accepta ca deplasarile w ale punctelor planului
median al placii pe directia axei z, in orice punct al sau, sunt cu mult mai
mici decat grosimea h a placii, astfel incat
![]() Aceasta ipoteza ne permite sa consideram ca
planul median al placii se deformeaza fara sa se intinda, respectiv ca deplasarile
radiale ale punctelor lui se pot neglija (ipoteza se aseamana cu cea de la
grinzile drepte, cand - la demonstrarea formulei lui Navier - am presupus ca
fibrele din planul neutru nici nu se lungesc nici nu se scurteza, desi se
deformeaza, acceptand ca sagetile grinzii sunt mult mai mici decat sectiunea
inaltimi transversale).
Aceasta ipoteza ne permite sa consideram ca
planul median al placii se deformeaza fara sa se intinda, respectiv ca deplasarile
radiale ale punctelor lui se pot neglija (ipoteza se aseamana cu cea de la
grinzile drepte, cand - la demonstrarea formulei lui Navier - am presupus ca
fibrele din planul neutru nici nu se lungesc nici nu se scurteza, desi se
deformeaza, acceptand ca sagetile grinzii sunt mult mai mici decat sectiunea
inaltimi transversale).
Daca aceasta ipoteza nu este satisfacuta problema se complica deoarece pe de o parte nu mai apar deformatii foarte mici (care uneori pot fi neglijate), ci deformatii finite, iar pe de alta parte reactiunile de pe conturul de reazem influenteaza la randul lor asupra sagetilor placii, atunci cand deplasarea punctelor din planul placii este impiedicata de legaturi. Asemenea placi care nu satisfac aceasta ipoteza se numesc uneori placi de grosime mica sau rigiditate mica, de tipul membranelor.
IPOTEZA a II-a, este cunoscuta sub numele de "ipoteza Kirchhoff " sau ipoteza " nestrambarii normalei " - si este intr-o anumita forma - o generalizare la cazul corpurilor de tip placa a cunoscutei ipoteze a sectiunilor plane a lui Bernoulli de la grinzi. Ea spune ca: " punctele care se afla inainte de deformatia placii pe o normala oarecare la planul median al sau, raman dupa deformatie tot pe o dreapta care este insa normala la suprafata elastica a placii,(la planul mediu deformat ) ".
|
Fig.1.15.3 |
Evident ca ipoteza este perfect valabila numai in cazul incovoierii pure axial-simetrice a placii: in relitate, in cazul incovoierii cercetate de noi prin forte normale pe suprafata (incovoiere simpla) placii, au solicitari de forfecare in sectiunile paralele cu planul median ceea ce face ca normalele initial drepte sa se strambe putin. Intocmai ca la grinzile drepte si in calculul placilor se neglijeaza acest efect si rezultatele obtinute pentru incovoierea pura se utilizeaza si pentru incovoierea simpla. Transpusa intr-o forma pe care o vom utiliza mai departe, privita deci sub un aspect mai global, aceasta ipoteza ne spune ca sectiunile cilindrice coaxiale cu conturul - in starea neancarcata a placii - se transforma in urma deformatiei in suprafete conice. Astfel, generatoarele unei sectiuni initial cilindrice devin generatoarele unui con circular al carui varf se gaseste pe axa de simetrie "z" a placii (fig.1.15.3). Aceasta ipoteza denumita uneori si "ipoteza cinematica" sau "ipoteza elementului liniar" (care isi pastreaza lungimea in urma deplasarilor) permite sa se reduca problema spatiala a teoriei elasticitatii la o problema plana, respectiv la determinarea eforturilor si deplasarilor punctelor din planul median, care sunt functie numai de doua coordonate (ceea ce este un avantaj esential).
IPOTEZA a III-a. Este cunoscuta sub numele "ipoteza statistica" si se
refera la starea de tensiune a placii. Intocmai ca la grinzile drepte unde se
neglija interactiunea straturilor paralele cu planul neutru si la placi se
considera ca tensiunile normale din actiunile paralele cu planul median (
![]() ) sunt neglijabile in comparatie cu tensiunile normale din sectiunile perpendiculare pe planul median. Se
accepta deci tot o lipsa de interactiune intre straturile orizontale ale
placii, paralele cu planul median desi in realitate exista o presiune reciproca
intre aceste straturi: in consecinta fiecare asemenea strat infinit suptire al
placii poate fi considerat ca lucrand independent, aflandu-se intr-o stare
plana de tensiune. Aceasta ipoteza este aplicabila numai pentru placile la care
raportul dintre grosimea h a placii si diametrul este mai mic decat 1/5 (D>5h). Daca nu este satisfacuta aceasta conditie placa se
considera "groasa". Ipoteza are in special
implicatii matematice deoarece simplifica legea lui Hooke generalizata in care
se neglijeaza termenii
) sunt neglijabile in comparatie cu tensiunile normale din sectiunile perpendiculare pe planul median. Se
accepta deci tot o lipsa de interactiune intre straturile orizontale ale
placii, paralele cu planul median desi in realitate exista o presiune reciproca
intre aceste straturi: in consecinta fiecare asemenea strat infinit suptire al
placii poate fi considerat ca lucrand independent, aflandu-se intr-o stare
plana de tensiune. Aceasta ipoteza este aplicabila numai pentru placile la care
raportul dintre grosimea h a placii si diametrul este mai mic decat 1/5 (D>5h). Daca nu este satisfacuta aceasta conditie placa se
considera "groasa". Ipoteza are in special
implicatii matematice deoarece simplifica legea lui Hooke generalizata in care
se neglijeaza termenii
![]() considerati mici, tensiunile
considerati mici, tensiunile
![]() intrand in categoria tensiunilor secundare.
intrand in categoria tensiunilor secundare.
1.15.2. STUDIUL STARII DE DEFORMATII
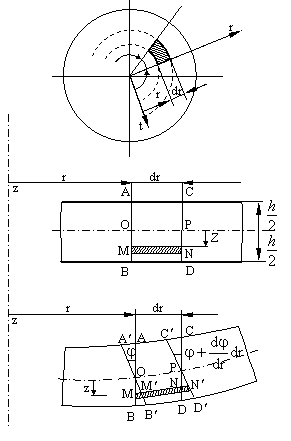
1.Ipotezele adoptate simplifica foarte mult problema studiata si ne dau o imagine foarte clara despre geometria starii deformate a placii in conditile incarcarii axial-simetrice pe baza unei corelati gemetrice simple se pot determina deformatiile in orice punct al placii, introducand o anumita variabila specifica problemei. Vom adapta un sistem de coordonate polare (v.fig.1.15.4); vom face o sectiune radiala prin placa si vom fixa atentia asupra unui element de suprafata cu lungimea dr (ABCD), aflat la distanta r de axa z. Din planul acestui element vom examina ce se intampla cu segmentul MN (de lungime initiala dr ) care se afla la distanta z de planul median.
|
|
|
r |
|
dr |
|
r |
|
t |
|
z |
|
r |
|
dr |
|
A |
|
C |
|
O |
|
P |
|
M |
|
N |
|
Z |
|
|
|
|
|
B |
|
D |
|
z |
|
r |
|
dr |
|
A |
|
|
|
|
|
C |
|
N |
|
|
|
|
|
M |
|
z |
|
B |
|
|
|
D |
|
|
|
|
|
|
|
O |
|
P |
|
Fig.1.15.4 |
 2.In conformitate
cu prima ipoteza (v.fig.1.15.1) punctele O si P care apartineau planului median
al placii inainte de deformatie, raman in suprafata mediana deformata, si tot
la distantele initiale r si r+dr de axa y. Dupa cea de-a doua ipoteza
(Kirchhoff) segmentul AOB care era paralel cu axa z si normal la planul median
- inainte de incarcare si deformarea placii - se roteste cu un anumit unghi
2.In conformitate
cu prima ipoteza (v.fig.1.15.1) punctele O si P care apartineau planului median
al placii inainte de deformatie, raman in suprafata mediana deformata, si tot
la distantele initiale r si r+dr de axa y. Dupa cea de-a doua ipoteza
(Kirchhoff) segmentul AOB care era paralel cu axa z si normal la planul median
- inainte de incarcare si deformarea placii - se roteste cu un anumit unghi
In acest sens se definesc
- deformatia specifica radiala (
![]() )
reprezentand lungirea specifica in directia razei a unui element de lungime
)
reprezentand lungirea specifica in directia razei a unui element de lungime
![]() ,
dispus radial. Dupa deformatia placii elementul MN ocupa pozitia M'N' astfel
incat lungirea lui totala va fi:
,
dispus radial. Dupa deformatia placii elementul MN ocupa pozitia M'N' astfel
incat lungirea lui totala va fi:
![]()
![]() =M'N'-MN=(M'N'-M'N)-(MN-M'N)=NN'-MM'=
=M'N'-MN=(M'N'-M'N)-(MN-M'N)=NN'-MM'=
![]()
![]() (1.15.2.1)
(1.15.2.1)
-deformatia specifica circumferentiala (
![]() )
reprezentand lungirea specifica a unei fibre inelare care trece initial prin
punctul M inainte si dupa deformatia placii. Inainte de deformatia placi
punctul M se afla pe un cerc cu raza r avand lungimea circunferintei 2
)
reprezentand lungirea specifica a unei fibre inelare care trece initial prin
punctul M inainte si dupa deformatia placii. Inainte de deformatia placi
punctul M se afla pe un cerc cu raza r avand lungimea circunferintei 2
![]() r;
dupa deformatia placii punctul M trece intr-o noua pozitie M' care se gaseste
pe un cerc de raza r+MN'=r+z
r;
dupa deformatia placii punctul M trece intr-o noua pozitie M' care se gaseste
pe un cerc de raza r+MN'=r+z
![]() ,
cu lungimea circumferintei2
,
cu lungimea circumferintei2
![]() .
.
Lungirea totala a aceste circum ferintei este deci:
![]() . Rezulta deci lungirea specifica pe directia
circumferintiala,
. Rezulta deci lungirea specifica pe directia
circumferintiala,
![]() in punctul M:
in punctul M:
![]() (1.15.2.2)
(1.15.2.2)
1.15.3. ASPECTUL FIZIC. EXPRIMAREA TENSIUNILOR
CU AJUTORUL FUNCTIEI
![]() .
.
![]()
In conformitate cu cea de-a treia
ipoteza (v.fig.1.15.1) privind absenta tensiunilor normale in sectiunile
paralele cu planul median (
![]() =0),
legea lui Hooke generalizata obtine o forma mult mai simpla; tinand cont ca
deformatiile specifice
=0),
legea lui Hooke generalizata obtine o forma mult mai simpla; tinand cont ca
deformatiile specifice
![]() si
si
![]() le
corespund ca directie tensiunile normale
le
corespund ca directie tensiunile normale
![]() si
si
![]() se
obtine:
se
obtine:
![]()
![]()
(1.15.3.1)
Din aceste relatii se deduce (ca o
consecinta a modelului de deformatie acceptat) ca tensiunile normale sunt nule
in plan median (z=0) si variaza proportional cu distanta z de la planul median;
ele sunt deci tnsiuni de intindere sub planul median (pentru z>0) si de
compresiune in cealalta parte a planului. Evident ca aceasta distributie de
tensiuni depinde si de modul de rezemare si de incarcare a placii. Aceste
tensiuni nu pot fi inca calculate deoarece functia
![]() (r)
este necunoscuta.
(r)
este necunoscuta.
1.15.4. ASPECTUL STATIC. RELATII INTRE EFORTURI SI
TENSIUNI
|
D |
|
|
|
|
|
|
|
E |
|
|
|
|
|
G |
|
|
|
C |
|
|
|
D |
|
B |
|
F |
|
|
|
Tr
|
|
|
|
A |
|
z |
|
A |
|
E |
|
|
|
|
|
|
|
G |
|
H |
|
|
|
|
|
B |
|
|
|
F |
|
z |
|
dz |
|
z |
|
Fig.1.15.5 |
 1.15.4.1. TENSIUNI.
1.15.4.1. TENSIUNI.
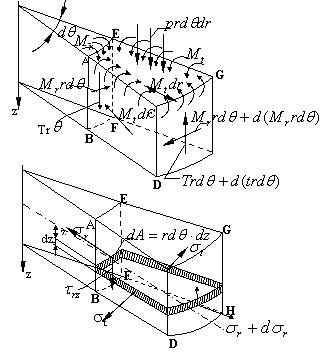
Pentru studiul starii de tensiune vom decupa din placa un
element de volum prismatic ABCDEFHG cu ajutorul a patru suprafete de sectionare:
dupa plane radiale care contin axa z si care fac intre ele unghiul infinit mic
d
![]() ;
doua suprafete cilinrdice concentrice coaxiale cu axa z, cu razele r si r+dr
(fig.1.15.5).
;
doua suprafete cilinrdice concentrice coaxiale cu axa z, cu razele r si r+dr
(fig.1.15.5).
Sa cercetam ce tensiuni sunt posibile sa apara pe suprafetele acestui element de volum tinand cont de ipotezele adoptate si de cazul particular simetric (geometric si mecanic) pe care-l studiem.
I.In "sectiunile radiale"
(suprafetele ABCD si EFHG ) datorita simetriei geometrice si simetriei
incarcarii exterioare, nu este posibila aparitia tensiunilor tangen tiale
deoarece deformatia placii se face astfel incat nu apar deformatii unghiulare
(altfel spus suprafetele ABCD si EFHG nu luneca una in raport cu cealalta, nici
in directia axei z nici in directia axei r). Inseamna ca pe aceste elemente de
suprafata apar numai "ten siunile normale circumferen tiale"
![]() care sunt aceleasi in
toate sectiunile radiale aflate la distante r de axa z.
care sunt aceleasi in
toate sectiunile radiale aflate la distante r de axa z.
II. In "sectiunile periferice" (ABEF si CDGE) care se inscriu dupa
deformatie pe niste suprafete conice care luneca una in raport cu cealalta,
este posibila aparitia unor tensiuni tangentiale de tipul
![]() -dirijate paralele cu axa z -care sunt rezultatul modului
de deformatie al placii. Apar de asemenea "tensiuni normale radiale"
-dirijate paralele cu axa z -care sunt rezultatul modului
de deformatie al placii. Apar de asemenea "tensiuni normale radiale"
![]() . Aceste tensiuni sunt evident constante (au aceias
valoare) in tote punctele elementului de suprafata circumferential aflat la un
anumit nivel z=const. de planul neutru, deoarece o ipoteza de neuniformitate ar
contrazice simetria axiala.
. Aceste tensiuni sunt evident constante (au aceias
valoare) in tote punctele elementului de suprafata circumferential aflat la un
anumit nivel z=const. de planul neutru, deoarece o ipoteza de neuniformitate ar
contrazice simetria axiala.
III. Sa mai precizam ca nu este posibila aparitia unor tensiuni tangentiale
![]() deoarece nu exista dualele lor din
sectiunile radiale
deoarece nu exista dualele lor din
sectiunile radiale
![]()
Am reprezentat aceste tensiuni pe elementul de volum din fig.1.15.5.b.
1.15.4.2. EFORTURI SECTIONALE
Sa punem acum in evidenta eforturile N,T,Mi care solicita acest element de volum si care apar ca rezultantele fortelor interioare pe fetele lui.
|
P |
|
r |
|
r |
|
dr |
|
r+dr |
|
Fig.1.15.6 |
 I.Pe sectiunea periferica ABEF fortele tangentiale
elementare de forma
I.Pe sectiunea periferica ABEF fortele tangentiale
elementare de forma
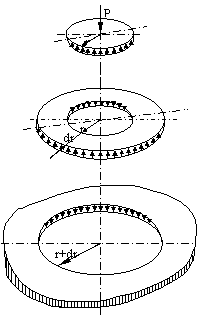
Sa stabilim sensul pozitiv pentru forta taietoare; pentru acasta vom decupa din placa in mod succesiv o serie de cilindri concentrici, avand aceas axa centrala z -ca in fig.1.15.6. -si vom pune in evidenta fortele taietoare care actioneaza pe suprafetele cilindrice de sectionare, stabilindu-le sensul pe baza principiului actiunii si reactiunii.
Astfel pentru partea centrala a placii, -cilindrul de raza r -(fig.1.15.6.a) forta taietoare de pe suprafata exterioara va trebui sa echilibreze actiunea fortei exterioare distribuite si deci va avea sensul de jos in sus (contrar sensului pozitv al axei z). Rezulta atunci automat ca suprafata cilindrica al elementului inelar (fig. 1.15.6.b) forta taietoare este indreptata in sensul pozitiv al axei z (in jos); vom conveni sa consideram aceasta forta taietoare ca fiind pozitiva.
Pe suprafata cilindrica exterioara a inelului (de raza r+dr) conform principiului actiunii si reactiunii, forta taietoare pozitiva va fi indreptata spre partea negativa a axe z. Pe fig.1.15.5. s-au reprezentat fortele taietoare pozitive pe cele doua sectiuni periferice ale elementului de volum.
II. Tot in sectiunile periferice
actioneaza si niste momente incovoietoare radiale, de intensitate Mr
distibuite pe arcul rd
![]() care
sunt rezultatele momentelor fortelor inerioare normale de tipul
care
sunt rezultatele momentelor fortelor inerioare normale de tipul
![]() Rezulta deci ca momentul incovoietor care
actioneaza in suprafata ABEF este
Rezulta deci ca momentul incovoietor care
actioneaza in suprafata ABEF este
![]() ,
iar in suprafata infinit apropiata CDGH este
,
iar in suprafata infinit apropiata CDGH este
![]() (Momentele incovoietoare le-am indicat in fig.1.15.5 prin vectori cu dubla
sageata).
(Momentele incovoietoare le-am indicat in fig.1.15.5 prin vectori cu dubla
sageata).
III.
In sectiunile radiale, actioneaza momente incovoietoare circumferentiale a caror intensitate se noteaza cu Mt
si care se obtin evident ca rezultat al momentului fortelor interioare de
tipul
![]() .
Astfel in sectiunile ABCD si EFGH, actioneaza momentele incovoietoare Mtdr.
.
Astfel in sectiunile ABCD si EFGH, actioneaza momentele incovoietoare Mtdr.
Momentele incovoieri se considera pozitive daca pe grosimea placii, in punctele care corespund valorilor pozitive ale coordonatei z apar tensiuni normale de intindere.
IV. Ne putem pune evident problema daca pe fortele elementului de volum
considerat, ca rezultat al reducerii fortelor elementare normale
![]() si
si
![]() ,nu
actioneaza si niste eforturi sectionale normale N, in ideea ca torsorul de
reducere poate avea atat un vector moment, cat si un vector forta. Vom arata ca
in cazul in care am acceptat o distributie a tensiunilor de forma (1.15.3.1) aceste
forte normale sunt nule.
,nu
actioneaza si niste eforturi sectionale normale N, in ideea ca torsorul de
reducere poate avea atat un vector moment, cat si un vector forta. Vom arata ca
in cazul in care am acceptat o distributie a tensiunilor de forma (1.15.3.1) aceste
forte normale sunt nule.
Astfel
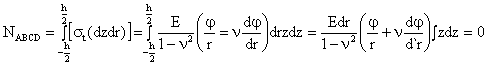
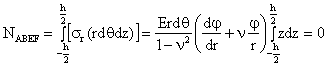
1.15.4.3. RELATII DE ECHIVALENTA INTRE EFORTURI SI TENSIUNI
Urmarim explicitarea aceluias principiu al egalitatii dintre momentele fortelor elementare interioare, in raport cu urma in planul sectiunii a suprafetei neutre si eforturile sectionale privite ca solicitari exterioare. Putem astfel scrie (integrand pe toata grosimea placii)

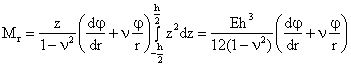
Analog:

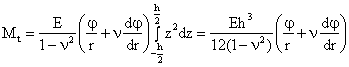
Se introduce notatia
![]() [daNm] (1.15.4.1)
[daNm] (1.15.4.1)
Aceasta marime se numeste "rigiditatea la incovoierea cilindrica a placii Cu aceasta notatie expresiile precedente devin:
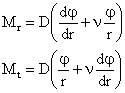 (1.15.4.2)
(1.15.4.2)
OBSERVATII:
1.Din aceste relatii se poate obtine expresia unghiului de rotatie
![]() al
normalei in functie de intensitatile momentelor incovoietoare:
al
normalei in functie de intensitatile momentelor incovoietoare:
![]() (1.15.4.3.)
(1.15.4.3.)
2. Introducand relatiile (4.4.2) in (4.3.2) se poate obtine:
 (1.15.4.4)
(1.15.4.4)
Aceste relati seamana formal cu
cunoscuta formula a lui Navier si evidenteaza distributia simetrica a
tensiunilor normale pe grosimea placii, care obtin valori maxime la suprafata
placii, (pemtru z=
![]() ):
):
![]() (1.15.4.5)
(1.15.4.5)
1.15.5 ECUATIILE DE ECHILIBRU ALE ELEMENTULUI
DE VOLUM AL PLACII
|
r |
|
dr |
|
|
|
|
|
A |
|
p |
|
|
|
C |
|
D |
|
|
|
|
|
B |
|
|
|
G |
|
E |
|
|
|
A |
|
C |
|
|
|
|
|
|
|
|
|
|

|
Fig.1.15.7 |
 Consideram
din nou elementul de placa caruia ii aplicam pe langa eforturile sectionale
(T,Mr,Mt) si fortele exterioare provenind - de exemplu -
din actiunea unei presiuni normale pe suprafata exterioara a placii,
distribuita dupa o lege oarecare p=p(r). Elementul de volum fiind infinit mic se poate presupune ca
presiunea p [daN/c2] a fortelor super ficiale este constanta, iar
forta concentrata rezulta ta, echivalenta din punct de vedere static avand
valoarea pdA=prd
Consideram
din nou elementul de placa caruia ii aplicam pe langa eforturile sectionale
(T,Mr,Mt) si fortele exterioare provenind - de exemplu -
din actiunea unei presiuni normale pe suprafata exterioara a placii,
distribuita dupa o lege oarecare p=p(r). Elementul de volum fiind infinit mic se poate presupune ca
presiunea p [daN/c2] a fortelor super ficiale este constanta, iar
forta concentrata rezulta ta, echivalenta din punct de vedere static avand
valoarea pdA=prd
In fig.1.15.7 s-a desenat din nou elemen tul de volum in doua vederi pentru a scrie mai usor ecuatiile de echilibru, care sunt:
I.Proiectia tuturor fortelor dupa axa z:
Trd
![]() -[Trd
-[Trd
![]() +d(Trd
+d(Trd
![]() )]+prd
)]+prd
![]() dr=0
dr=0
de
unde: (1.15.5.1):
![]()
Dar, deoarece marimea d
![]() nu variaza cu
raza, putem simplifica cu d
nu variaza cu
raza, putem simplifica cu d
![]() si
prima ecuatie de echilibru se poate scrie:
si
prima ecuatie de echilibru se poate scrie:
![]() (1.15.5.2)
(1.15.5.2)
II. Suma momentelor tuturor fortelor aplicate elementului in raport cu axa
![]()
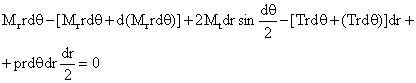
In aceasta ecuatie ce doi termeni pr d
![]() dr
dr
![]() si
si
![]() se pot neglija ca
infiniti mici de ordin superior fata de restul termenilor, astfel incat ecuatia
precedenta devine (pentru sin
se pot neglija ca
infiniti mici de ordin superior fata de restul termenilor, astfel incat ecuatia
precedenta devine (pentru sin
![]()
![]()
Impartind cu
dr d
![]()
![]() avand in final
avand in final
![]() (1.15.5.3)
(1.15.5.3)
Celelalte ecuatii de echilibru, datorita conditiilor de simetrie sunt satisfacute in mod identic.
1.15.6.ECUATIA DIFERENTIALA A PLACILOR CIRCULARE
IN FUNCTIA REZOLVATA
![]()
Starea de echilibru a placii este guvernata de cele doua ecuatii diferentiale (1.15.5.2) si (1.15.5.3) care contin trei functii necunoscute: T= T(r); Mr=Mr(r); Mt=Mt(r). Problema este deci static nedeterminata, insa dupa metodologia generala a unor astfel de probleme, tinand cont de celelalte aspecte (geometric si fizic) se poate reduce numarului necunoscutelor la una singura.
Practic, se procedeaza astfel:
|
P |
|
F |
|
F |
|
T |
|
|
|
T |
|
|
|
r |
|
r |
|
Fig.1.15.8 |
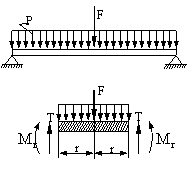
 I.In
primul rand integrand ecuatia (1.15.5.2), in conditiile in care se cunoaste
functia incarcarii p=p(r) se poate determina intensitatea fortei taietoare T ca
functie de raza T=T(r). In mod concret insa, aceasta marime se determina mult
mai simplu din examinarea echilibrului partii cilindrice centrale a placii
avand raza curenta r (v.fig.1.15.8).
I.In
primul rand integrand ecuatia (1.15.5.2), in conditiile in care se cunoaste
functia incarcarii p=p(r) se poate determina intensitatea fortei taietoare T ca
functie de raza T=T(r). In mod concret insa, aceasta marime se determina mult
mai simplu din examinarea echilibrului partii cilindrice centrale a placii
avand raza curenta r (v.fig.1.15.8).
Pentru generalizarea problemei,
in fig.1.15.8 am mai introdus si o forta concentrata F actionand in centrul
placii. Scriind suma proiectiilor
fortelor dupa axa z, rezulta:
![]()
de unde, pentru p=const,(incarcare uniform distribuita):
![]() [daN/m] (1.15.6.1)
[daN/m] (1.15.6.1)
II. Procedand astfel inseamna
ca functia T(n) se poate determina intotdeauna in mod independet de celelalte
necunoscute ale problemei. Rezulta deci ca ecuatia diferentiala de echilibru (1.15.5.3)
contine numai doua functii necunoscute Mr si Mt. Punand
insa in locul acestora expresiile lor (1.15.4.2), se obtine o ecuatie
diferentiala cu o singura funtie necunoscuta
![]() (r),
care este unghiul de rotire al normalei la planul median al razei, functie de
raza. Se poate considera ca in acest caz functia
(r),
care este unghiul de rotire al normalei la planul median al razei, functie de
raza. Se poate considera ca in acest caz functia
![]() joaca rolul unei "functii rezolvante" analoaga
functie de tensiune a lui Airy (v.vol.II,pag.191), deoarece cu ajutorul ei
putem rezolva toate problemele privind starea de tensiune si de deformatie a
placii. Considerand ca grosimea h a placii, deci si rigiditatea sa D sunt
constante, se obtine succesiv
joaca rolul unei "functii rezolvante" analoaga
functie de tensiune a lui Airy (v.vol.II,pag.191), deoarece cu ajutorul ei
putem rezolva toate problemele privind starea de tensiune si de deformatie a
placii. Considerand ca grosimea h a placii, deci si rigiditatea sa D sunt
constante, se obtine succesiv

![]()
Aceasta este ecuatia diferentiala a placilor circulare (obtinuta si rezolvata de S.D.Poisson in 1929), care se integreaza usor daca vom observa ca poate fi pusa sub forma;
![]()
Identitatea ultimelor doua expresii se poate verifica cu usurinta dezvoltand prin diferentiere parte stanga a relatiei (1.15.6.3).
Printr-o
dubla integrare din relatia (1.15.6.3) se obtine expresia unghiului de rotatie
![]() (r):
(r):
![]()
![]()
![]()
![]()
![]() (1.15.6.4)
(1.15.6.4)
unde C1 si C2 sunt constante de integrare care se determina pentru fiecare caz particular in parte punand conditiile la limita specifice.
1.15.7. CALCULUL DEPLASARILOR.
FUNCTIA REZOLVANTA w(r).
De multe ori in locul unghiului de rotatie al normalei
![]() se alege ca
necunoscuta unica a problemei sageata w(r). De altfel legatura analitica dintre
cele doua marimi pentru placile de mare rigiditate pe care le studiem (cu
deplasari mici) se stabileste cu usurinta; urmarind fig.1.15.9. daca notam cu w
deplasarea punctelor placii aflate pe un cerc de raza r, se poate scrie
se alege ca
necunoscuta unica a problemei sageata w(r). De altfel legatura analitica dintre
cele doua marimi pentru placile de mare rigiditate pe care le studiem (cu
deplasari mici) se stabileste cu usurinta; urmarind fig.1.15.9. daca notam cu w
deplasarea punctelor placii aflate pe un cerc de raza r, se poate scrie
![]() (1.15.7.1)
(1.15.7.1)
De aici:
![]() (1.15.7.2)
(1.15.7.2)
C3 fiind constanta de integrare care se determina de obicei din conditia ca deplasarile w pe contururile de rezemare ale placii sa fie nule.
|
|
|
|
|
w |
|
r |
|
z |
|
|
 |
|
Fig.1.15.9 |

Daca se lucreaza direct cu aceste variabile, momentele incovoietoare pentru o unitate de lungime de placa vor fi
 (1.15.7.3)
(1.15.7.3)
iar ecuatia de echilibru a elementului de volum:
![]() (1.15.7.4)
(1.15.7.4)
In cazurile in care placa are mai multe portiuni pentru care functia T=T(r)
are forme diferite, integrarea se efectueaza pentru fiecare dintre aceste
portiuni pe domeniile unde functia T(r) si derivatele ei sunt continui. In
aceste cazuri numarul constantelor de integrare creste deoarece in procesul de
rezolvare expus expresia unghiului
![]() de pe fiecare
portiune contine cate doua constante de
integrare independente de aceea
numarul total de constante ce urmeaza a fi determinate este egal cu dublul
numarului de portiuni.
de pe fiecare
portiune contine cate doua constante de
integrare independente de aceea
numarul total de constante ce urmeaza a fi determinate este egal cu dublul
numarului de portiuni.
Ecuatia (1.15.7.4) se poate scrie sub forma echivalenta:
![]() (1.15.7.5)
(1.15.7.5)
1.15.8. CONDITII LA LIMITA PENTRU DETERMINAREA
CONSTANTELOR DE INTEGRARE
Rezolvarea unei probleme de
placa circulara revine, din punct de vedere matematic, la determinarea unei
functii
![]() (r)
care sa satisfaca ecuatia diferentiala
(r)
care sa satisfaca ecuatia diferentiala
(1.15.6.2) si anumite conditii la limita sau conditii de rezemare pe conturul placii. Trebuie sa observam insa ca determinare constantelor C1 si C2 din (1.15.6.4) este independenta de calculul lui C3 din (1.15.7.2).
Intocmai ca la grinzi si aici avem doua categorii de conditii la limita
I. Conditii de rezemare, care pot fi
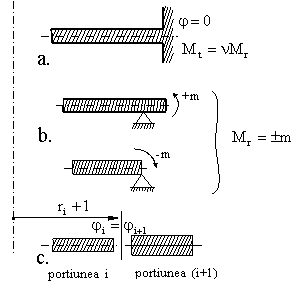
1.Pe un contur incastrat al
placii, trebuie sa avem
![]() =0
si w =0. Tot aici,intre intensitatile momentelor incovoietoare, in conformitate
cu (1.15.4.3) trebuie sa avem satisfacuta relatia de legatura Mt=
=0
si w =0. Tot aici,intre intensitatile momentelor incovoietoare, in conformitate
cu (1.15.4.3) trebuie sa avem satisfacuta relatia de legatura Mt=
![]() Mr
(fig.1.15.9).
Mr
(fig.1.15.9).
|
|
|
|
|
a. |
|
+m |
|
-m |
|
|
|
|
|
b. |
|
|
|
|
|
portiunea i |
|
portiunea (i+1) |
|
c. |
|
. |
|
Fig.1.15.10 |
 2.Pe
marginea libera (din punct de vedere al rezemarii) sau pe o margine articulata,
pe care nu sunt aplicate cupluri exterioare, trebuie sa admitem Mr=0.
Daca pe aceste margini se aplica un cuplu exterior uniform distribuit de
intensitate
2.Pe
marginea libera (din punct de vedere al rezemarii) sau pe o margine articulata,
pe care nu sunt aplicate cupluri exterioare, trebuie sa admitem Mr=0.
Daca pe aceste margini se aplica un cuplu exterior uniform distribuit de
intensitate
3.La placile care nu au orificiu central, constanta C2 este nula deoarece unghiul de rotatie, din conditii de simetrie, la r=0 este nul atunci din (1.15.6.4) rezulta C2=0.
II. Conditii de continuitate
Acestea
se pun in situatia in care placa are sau mai multe portiuni de rigiditate
diferita, sau mai multe domenii concentrice pe care functia T=T(r) are forme
analitice diferite. In acest caz integrarea se efectueaza pentru fiecare din
aceste domenii in mod separat, ceea ce face sa creasca numarul constantelor de
integrare care vor fi egale cu dublul numarului de domenii (deoarece expresia
unghiului
![]() de pe fiecare portiune contine cate doua
constante de integrare independente) -conditiile de continuitate exprima faptul
ca suprafata elastica a placii este o suprafata continua, fara zone de
discontinuitate sau variatii brusce ale parametrilor geometrici care o
caracterizeaza. Transpusa analitic, aceasta constatare fizica, se scrie astfel:
de pe fiecare portiune contine cate doua
constante de integrare independente) -conditiile de continuitate exprima faptul
ca suprafata elastica a placii este o suprafata continua, fara zone de
discontinuitate sau variatii brusce ale parametrilor geometrici care o
caracterizeaza. Transpusa analitic, aceasta constatare fizica, se scrie astfel:
-la
contactul portiunilor cilindrice i si i+1, de raza comuna ri+1
(v.fig.1.15.10), din conditia de continuitate a deplasarilor avem
![]() ;
;
-din
conditia de egalitate a fortelor interioare
![]() ,
i=1,2,...,n
,
i=1,2,...,n
Aceasta conditie este echivalenta cu egalitatea
derivatelor unghiurilor de rotatie pe contururile comune portiunilor
![]()
-Evident ca pentru determinarea constantelor de integrare C3i se scrie egalitatea sagetilor pe razele comune ale portiunilor considerate wi=wi+1.
Pe cazurile concrete ce le vom studia in continuare se va intelege mai bine modul de formulare a conditiilor la limita si de determinare a constantelor de integrare.
1.15.9. CERCETAREA STARII DE TENSIUNE A PLACII
1.Vom completa rezultatele obtinute
pana acum privind starea de tensiune a
placii. Am stabilit distributia tensiunilor normale pe grosimea placii in
sectiunile ei radiale (
![]() )
si coaxiale (
)
si coaxiale (
![]() )
-rel.1.15.4.4 -rezultat al ipotezelor de deformabilitate pe care le-am
acceptat. Pentru a avea o imagine completa a starii de tensiune trebuie sa
stabilim si legea de distributie a tensiunilor tangentiale
)
-rel.1.15.4.4 -rezultat al ipotezelor de deformabilitate pe care le-am
acceptat. Pentru a avea o imagine completa a starii de tensiune trebuie sa
stabilim si legea de distributie a tensiunilor tangentiale
![]() pe grosimea placii in sectiuinile ei coaxiale. In sectiunile radiale am aratat
ca tenisunile tangentiale sunt nule din motive de simetrie. Aceste tensiuni
le-am figurat pe elementul de volum din fig.1.15.5.
pe grosimea placii in sectiuinile ei coaxiale. In sectiunile radiale am aratat
ca tenisunile tangentiale sunt nule din motive de simetrie. Aceste tensiuni
le-am figurat pe elementul de volum din fig.1.15.5.
2. Ne propunem deci sa calculam
tensiunile tangentiale
![]() .
Pentru aceasta vom folosi un rationament
similar cu cel de la stabilirea formulei lui Juravski). Consideram elementul de
volum din placa ABCDEFGH (fig.1.15.11), pe care-l sectionam cu un plan paralel
cu planul median la distanta z de acesta; pe portiunea inferioara astfel
izolata figuram tote tensiunile (fig.1.15.11.b), in suprafata de sectionare
1234 actionand, prin dualitate,
.
Pentru aceasta vom folosi un rationament
similar cu cel de la stabilirea formulei lui Juravski). Consideram elementul de
volum din placa ABCDEFGH (fig.1.15.11), pe care-l sectionam cu un plan paralel
cu planul median la distanta z de acesta; pe portiunea inferioara astfel
izolata figuram tote tensiunile (fig.1.15.11.b), in suprafata de sectionare
1234 actionand, prin dualitate,
![]() =
=
![]() .
.
Scriem, ca o ecuatie de echilibru a acestui element de volum ca suma proiectiilor tuturor fortelor dupa axa r, este nula, deci:

|
|
|
A |
|
E |
|
dr |
|
C |
|
G |
|
r |
|
z |
|
suprafata mediana |
|
4 |
|
H |
|
2 |
|
D |
|
B |
|
1 |
|
3 |
|
F |
|
|
|
|
|
z |
|
|
|
|
|
1 |
|
3 |
|
F |
|
B |
|
2 |
|
|
|
4 |
|
H |
|
|
|
D |
|
|
|
|
|
|

|
Fig.1.15.11 |

Reducand
tensiunii asemenea, considerand ca
![]() si simplificand cu
dr
si simplificand cu
dr
![]() se obtine
se obtine
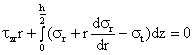
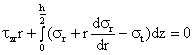
Dar
![]() (v.1.15.4.4)
(v.1.15.4.4)

![]()
Se obtine:
 (1.15.9.2)
(1.15.9.2)
Dar folosind ecuatia (4.6.2) putem exprima tensiunea
![]() cu
ajutorul fortei taietoare T
cu
ajutorul fortei taietoare T
|
|
|
|
|
z |
|
z |
|
. |
|
. |
|
h |
|
distributia
|

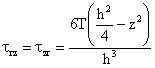 (1.15.9.3)
(1.15.9.3)
|
S Fig.1.15.12 |
 Relatia obtinuta ne arata ca
tensiunile tangentiale sunt distribuite parabolic pe grosimea placii (fig.1.15.12),
intocmai ca la grinzile drepte de sectiune dreptunghiulara. Ele sunt nule
pe suprafetele superioara si inferioara a placi (
Relatia obtinuta ne arata ca
tensiunile tangentiale sunt distribuite parabolic pe grosimea placii (fig.1.15.12),
intocmai ca la grinzile drepte de sectiune dreptunghiulara. Ele sunt nule
pe suprafetele superioara si inferioara a placi (
![]() (1.15.9.4)
(1.15.9.4)
3. Putem sa examinam acum starea de tensiune intr-o serie de puncte caracteristice pe grosimea placii.
-in punctele situate pe suprafetele exterioare ale placii, precum si in suprafata mediana are loc o stare de tensiune biaxiala; in planul median, deoarece tensiunile normale sunt nule aceasta stare biaxiala este de forfecare pura. In toate celelalte puncte ale placii datorita tensiunilor tangentiale din sectiunile cilindrice coaxiale are loc o stare triaxiala de tensiune.
-daca pe suprafata placii actioneaza o presiune exterioara, atunci si pe suprafata incarcata a placii are loc o stare de tensiune triaxiala.
-sectiunile radiale ale placii
reprezinta una din suprafetele principale, deoarece pe ele nu lucreaza tensiuni
tangentiale. De aceea tensiunea circumferentiala
![]() este
intotdeauna o tensiune normala principala. Celelalte doua tensiuni normale
principale se pot calcula cu relatia cunoscuta
este
intotdeauna o tensiune normala principala. Celelalte doua tensiuni normale
principale se pot calcula cu relatia cunoscuta
![]()
-pe suprafata neancarcata a placii cele trei tensiuni principale sunt
![]()
Daca suprafata placii este incarcata cu
presiunea p [daN/cm2] tensiunile
principale vor fi
![]()
PLACI DREPTUNGHIULARE. TEORIA INCOVOIERII
PLACILOR DREPTUNGHIULARE.
ECUATIA SOPHIE-GERMAIN
1.16.1. STABILIREA ECUATIEI DIFERENTIALE A SUPRAFETEI
ELASTICE A PLACII. ECUATIA LUI SOPHIE-GERMAIN.
|
. |
|
x |
|
a |
|
w |
|
b |
|
W(x,y) |
|
|
|
b |
|
z |
|
u |
|
|
|
a |
|
y |
|
w |
|
c |
|
W(x,y) |
|
|
|
z |
|
c |
|
v |
|
|
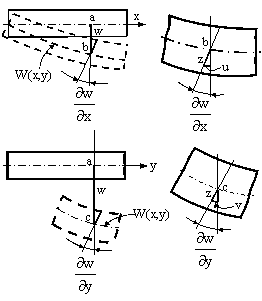
|
Fig.1.16.1 |
 1.Calculul
placilor dreptunghiula re de grosime constanta poate fi facut dupa aceeas metodologie ca la
placile circulare studiind aspectul static, geometric si fizic. Vom adapta o
metoda mai generala pornind de la ecuatile teoriei elasticitati in spatiu
introducand in acesta ipotezele enumerate la inceputul capitolului. Se evita in
felul acesta calculul eforturilor sectionale, deter minand direct tensiunea cu
ajutorul functiei w(x,y)
1.Calculul
placilor dreptunghiula re de grosime constanta poate fi facut dupa aceeas metodologie ca la
placile circulare studiind aspectul static, geometric si fizic. Vom adapta o
metoda mai generala pornind de la ecuatile teoriei elasticitati in spatiu
introducand in acesta ipotezele enumerate la inceputul capitolului. Se evita in
felul acesta calculul eforturilor sectionale, deter minand direct tensiunea cu
ajutorul functiei w(x,y)
2. Vom nota -in mod similar- cu w sageata suprafetei mediane, adica distanta pe verticala dintre punctul luat de planul median inainte de deformatie si pozitia acelui punct de pe suprafata elastica. Datorita faptului ca se admite ca un segment rectiliniu de lungime egala cu grosimea placii normal pe suprafata mediana isi pastreaza lungimea, deplasarea w-cu exactitate care merge pana la infinitii mici de ordin superiori- va fi aceeasi pentru toate punctele care apartin acestui element rectiliniu. Cu alte cuvinte deplasarile punctelor de pe placa care sunt paralele cu axa Oz si care in cazul unei placi groase sunt functii de trei coordonate W(x,y,z) in cazul placilor subtiri de care ne ocupam vor fi functii numai de doua coordonate, deci toate punctele planului median capata numai deplasari verticale.
Aceasta ecuatie a fost stabilita de Sophie-Germain in 1815. Ea este atribuita si lui Lagrange care a obtinut-o in 1811 cand examina memoriul prezentat Academiei de Stinte franceze de Sophie-Germain.
Punctele placii care nu apartin planului median vor avea evident si deplasari dupa axele x si y pe care le vom nota cu u si v.
3. Ecuatile geometrice. Se stabilesc urmarind fig.1.16.1 din care rezulta imediat ca
![]() (1.16.1)
(1.16.1)
Daca tinem cont de relatiile :
![]()
rezulta imediat:
![]() (1.16.2)
(1.16.2)
Acestea sunt ecuatiile geometrice ale problemei.
4. Ecuatile fizice
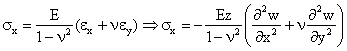
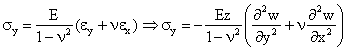
![]() (1.16.3)
(1.16.3)
|
0 |
|
y |
|
z |
|
dz |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
suprafata mediana |
 Aceste
ecuati ne arata ca tensiunile
Aceste
ecuati ne arata ca tensiunile
Trebuie sa remarcam insa ca pe fetele elmentului pot aparea de data aceasta
si tensiuni tangentiale
![]() (fig.1.16.2)
(fig.1.16.2)
|
Fig.1.16.2 |

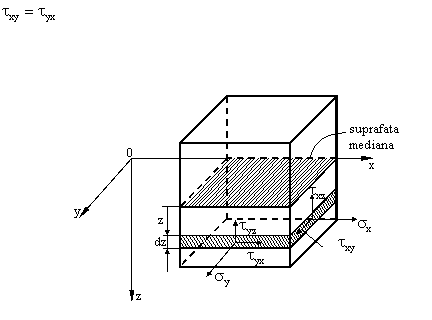
5. Sa transformam acum ecuatile statice in care nu tinem cont de fortele masice
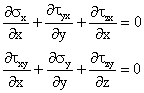
 (1.16.4)
(1.16.4)
Integrand ultimele ecuatii se obtine:

Determinarea
functiilor
![]() si
si
![]() se
face impunand conditii la limita care sa exprime faptul ca pe fetele placii nu
actioneaza sarcini tangentiale deci pentru z
se
face impunand conditii la limita care sa exprime faptul ca pe fetele placii nu
actioneaza sarcini tangentiale deci pentru z
![]() avem
avem
![]() .
Se obtine evident:
.
Se obtine evident:
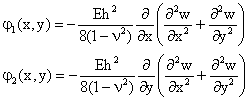
Rezulta atunci:
 (1.16.5)
(1.16.5)
Rezulta de aici ca aceste tensiuni variaza parabolic pe grosimea placii (este o generalizare a formulei lui Juravsky de la grinzi).
Trebuie sa remarcam ca toate tensiunile care pot sa apara in placa date de (1.16.3) si (1.16.5) se pot obtine din ecuatia suprafetei elastice a placii w(x,y) prin simple ecuati de derivare. Deci, intocmai ca functia Airy, ecuatia suprafetei elastice joaca rolul unei "functii rezolvante".
6. Pentru a gasi aceasta ecuatie sa
facem apel la conditile la limita pe care nu le-am utilizat inca si anume:
pentru z=h/2 avem
![]() iar
pentru z=-h/2 avem
iar
pentru z=-h/2 avem
![]() .
Asta inseamna ca am presupus ca placa noastra este incarcata cu sarcini
transversale aplicate pe suprafata ei exterioare. Insa la acelasi rezultat se
ajunge daca presupunem ca sarcina se aplica pe suprafata inferioara sau pe
suprafata mediana.
.
Asta inseamna ca am presupus ca placa noastra este incarcata cu sarcini
transversale aplicate pe suprafata ei exterioare. Insa la acelasi rezultat se
ajunge daca presupunem ca sarcina se aplica pe suprafata inferioara sau pe
suprafata mediana.
In acest sens trebuie sa gasim
expresia lui
![]() pe care o scoatem din cea de-a treia ecuatie
de echilibru static
pe care o scoatem din cea de-a treia ecuatie
de echilibru static

Introducem (1.16.5) si obtinem
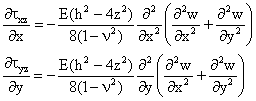
Avem astfel:

Prin integrare obtinem:
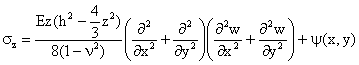 (1.16.6)
(1.16.6)
Aplicam conditiile la limita
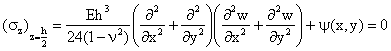
 (1.16.7)
(1.16.7)
Insumand ultimele expresii rezulta
![]() (1.16.8)
(1.16.8)
![]() Inlocuind aceste rezultate in (1.16.8) rezulta:
Inlocuind aceste rezultate in (1.16.8) rezulta:

Daca
notam rigiditatea la incovoiere a placii
![]() relatia precedenta devine:
relatia precedenta devine:
![]() (1.16.9)
(1.16.9)
Scrisa cu ajutorul operatorului Laplace
![]() (1.16.9)
(1.16.9)
Aceasta este ecuatia diferentiala fundamentala a teoriei incovoierii unei placii plane de grosime mijlocie solicitate numai de forte transversale, dedusa in sistemul cartezian de coordonate cunoscuta sub numele de ecuatia lui Sophie-Germain.
Observatii.
I.Ecuatia stabilita este adevarata nu numai pentru placile dreptunghiulare ci in general pentru orice placa daca se respecta ipotezele pe care le-am formulat.
|
|
|
|
|
p |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
p |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
-p |
|
|
|
|
|
p |
|
a. |
|
b. |
|
c. |
 II.Conform (1.16.6)
tensiunea
II.Conform (1.16.6)
tensiunea
|
Fig.1.16.3 |

1.16.2. CONDITIILE PE CONTUR (LA LIMITA)
1. Din punct de vedere matematic
rezolvarea unei probleme de placi plane revine la determinarea unei functii
w(x,y) care sa satisfaca ecuatia diferentiala (1.16.9) si anumite conditii la
limita (pe conturul placii). Astfel spus aceasta este o problema tip Cauchy
pentru ecuatia Sophie-Germain. Ne reamintim ca o functie
![]() care satisface o ecuatie
diferentiala de tipul
care satisface o ecuatie
diferentiala de tipul
![]() se
numeste functie armonica, iar functia care satisface ecuatia (omogena)
se
numeste functie armonica, iar functia care satisface ecuatia (omogena)
![]() f=0 se numeste functie biarmonica. Se observa de altfel ca
orice functie armonica
f=0 se numeste functie biarmonica. Se observa de altfel ca
orice functie armonica
![]() este
in acelasi timp si o functie biarmonica. Astfel integrala ecuatiei (1.16.9) se
poate scrie sub forma: w=f(x,y)+ f(x,y) unde functia f(x,y) este integrala particulara a
ecuatiei (1.16.9) care in general poate fi determinata intotdeauna iar
este
in acelasi timp si o functie biarmonica. Astfel integrala ecuatiei (1.16.9) se
poate scrie sub forma: w=f(x,y)+ f(x,y) unde functia f(x,y) este integrala particulara a
ecuatiei (1.16.9) care in general poate fi determinata intotdeauna iar
![]() (x,y)
este o functie biarmonica care de obicei nu este greu de ales. Totusi nu orice
functie biarmonica care satisface ecuatia diferentiala (1.16.9) constituie o
solutie a problemei examinate; unica solutie este doar aceea care satisface
totodata si conditiile la limita date, iar o altfel de functie nu mai este usor
de aflat! Tocmai in aceasta consta dificultatea principala a rezolvarii
problemelor legate de placi. Din acest motiv suntem nevoiti a ne multumi de
obicei cu solutii aproximative, obisnuite prin metoda diferentelor finite sau
sa cautam solutia sub forma unor serii trigonometrice infinite sau sa utilizam
teoria functiilor de variabila complexa etc. Fac exceptie placile circulare
incarcate simetric pentru care ecuatia (1.16.9) transformata in sistemul de
coordonate polare se rezolva prin cuadraturi; o alta exceptie cunoscuta o
constituie placa eliptica incastrata pe contur si incarcata cu presiunea p
uniform repartizata pentru care ecuatia suprafetei elastice se poate scrie
exact.
(x,y)
este o functie biarmonica care de obicei nu este greu de ales. Totusi nu orice
functie biarmonica care satisface ecuatia diferentiala (1.16.9) constituie o
solutie a problemei examinate; unica solutie este doar aceea care satisface
totodata si conditiile la limita date, iar o altfel de functie nu mai este usor
de aflat! Tocmai in aceasta consta dificultatea principala a rezolvarii
problemelor legate de placi. Din acest motiv suntem nevoiti a ne multumi de
obicei cu solutii aproximative, obisnuite prin metoda diferentelor finite sau
sa cautam solutia sub forma unor serii trigonometrice infinite sau sa utilizam
teoria functiilor de variabila complexa etc. Fac exceptie placile circulare
incarcate simetric pentru care ecuatia (1.16.9) transformata in sistemul de
coordonate polare se rezolva prin cuadraturi; o alta exceptie cunoscuta o
constituie placa eliptica incastrata pe contur si incarcata cu presiunea p
uniform repartizata pentru care ecuatia suprafetei elastice se poate scrie
exact.
2.Asadar conditiile la limita pentru functia w trebuie sa fie date in functie de modul de rezemare al placii. Vom examina cateva conditii de contur importante, in cazul unei placi dreptunghiulare.
Daca una din marginile placii este
incastrata, atunci sunt impiedicate deplasarile punctelor acestei margini,
normale la planul placii, cat si rotatia acestei margini. (astfel spus
intelegem ca planul tangent la suprafata mediana deformata de-a lungul acestei
margini va coincide cu pozitia initiala a planului median al placii ). Admitand
ca marginea incastrata este rectilinie si normala pe axa y si este data de
ecuatia x = a, conditiile la limita se scriu:
![]() ,
,
![]() (1.16.10)
(1.16.10)
|
. |
|
y |
|
x=a |
|
x |

|
Fig.1.16.4 |
 Daca
marginea x = a a unei placi este simplu rezemata ( fig.1.16.4), atunci
deplasarile marginii normale pe planul placii sunt impiedicate, deci w = 0; in
acelasi timp aceasta margine se poate roti liber, deci momentul incovoietor in
lungul acestei margini trebuie sa fie nul (
Daca
marginea x = a a unei placi este simplu rezemata ( fig.1.16.4), atunci
deplasarile marginii normale pe planul placii sunt impiedicate, deci w = 0; in
acelasi timp aceasta margine se poate roti liber, deci momentul incovoietor in
lungul acestei margini trebuie sa fie nul (
In particular, daca este vorba de o
margine rectilinie normala pe axa Ox, conditiile la limita se scriu:
![]() ,
,
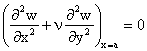
(1.16.11)
Dar cum in
lungul marginii simplu rezemate w=0, deci si
![]() , relatiile precedente se utilizeaza sub o forma
echivalenta:
, relatiile precedente se utilizeaza sub o forma
echivalenta:
![]()

care nu contin coeficientul lui Poisson.
Aceste conditii pot fii exprimate si
in tensiuni: sectiunea de rezemare putandu-se roti liber inseamna ca in ceasta
sectiune de rezemare atat tensiunile normale
![]() , cat si tensiunile tangentiale
, cat si tensiunile tangentiale
![]() paralele cu axa
Oy trebuie sa fie nule (tensiunile paralele cu axa Oz pot si trebuie sa existe
intrucat ele sustin placa). Din punct de vedere analitic dupa (1.16.3) aceasta
revine la:
paralele cu axa
Oy trebuie sa fie nule (tensiunile paralele cu axa Oz pot si trebuie sa existe
intrucat ele sustin placa). Din punct de vedere analitic dupa (1.16.3) aceasta
revine la:
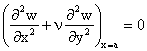
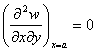
Daca insa este greu de ales ecuatia w = f (x,y) care
sa satisfaca toate conditiile la limita fara exceptie, atunci conditiile la
limita pot fi putin atenuate, renuntand de exemplu la conditia obligatorie ca
![]() si impunand numai ca suma acestor tensiuni pe
grosimea placii sa se reduca la un sistem de tensiuni autoechilibrate (cu
alte cuvinte conditiile la limita ar urma sa fie satisfacute numai sub forma integrala ).
si impunand numai ca suma acestor tensiuni pe
grosimea placii sa se reduca la un sistem de tensiuni autoechilibrate (cu
alte cuvinte conditiile la limita ar urma sa fie satisfacute numai sub forma integrala ).
Daca marginea unei placi, de exemplu
marginea x = a este nerezemata, atunci este logic sa admitem ca in aceasta
suprafata nu apar nici un fel de tensiuni, adica
![]()
Tinand cont de expresiile acestor tensiuni, conditiile se transcriu sub forma:
 ,
,
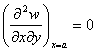
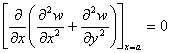
Deoarece conditiile la limita pot fii satisfacute mai usor sub forma integrala decat in fiecare punct al conturului de rezemare uneori este indicat ca formulele tensiunilor sa fie transformate, exprimandu-le prin integralele lor care ne duc la eforturile sectionale. De aceia pe o margine libera nu avem nici momente incovoietoare, nici momente de rasucire si nici forta taietoare, verticale, adica:
![]()
![]()
![]()
Sub aceasta forma conditiile pentru o margine libera au fost exprimate de Poisson; mai tarziu Kirchhoff a aratat ca aceste trei conditii sunt prea multe pentru o margine libera si ca doua conditii ar fii suficiente pentru a determina complet deplasarile w. De aceia conditiile precedente se scriu intr-o forma echivalenta:
 ;
;
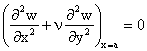
|