Eurocodul

Eurocodul

Introducere

Acest document (EN 1994-1-1:2004), Eurocodul 4: Proiectarea structurilor compozite din metal-beton; Partea 1-1 Reguli generale si reguli pentru cladiri, a fost intocmita de catre Comisia Tehnica CEN/TC 250 „Eurocoduri pentru structuri”, al carui secretariat a fost asigurat de catre BSI.

Acestui Standard European i se va conferi titlul de standard national, fie prin publicarea unui text identic fie prin aprobare, la cel tarziu Iunie 2005, si standardele nationale similare vor fi retrase pina la cel tarziu Martie 2010.

Acest document anuleaza ENV 1994-1-1:1992.

CEN/TC 250 este responsabil pentru toate Eurocodurile pentru structuri.

Conform regulilor interne ale CEN/CENELEC, organizatiile nationale de standardizare din urmatoarele tari trebuie sa implementeze acest Standard European: Austria, Belgia, Cipru, Republica Ceha, Danemarca, Estonia, Finlanda, Franta, Germania, Grecia, Ungaria, Islanda, Irlanda, Italia, Letonia, Lituania, Luxemburg, Malta, Olanda, Norvegia, Polonia, Portugalia, Slovacia, Slovenia, Spania, Suedia, Elvetia si Marea Britanie.

Istoric al programului Eurocod

In 1975, Comisia Comunitatii Europene a aprobat un program de actiune in domeniul constructiilor, bazat pe articolul 95 al Tratatului. Obiectivul programului era eliminarea obstacolelor tehnice pentru cooperare economica si armonizarea specificatiilor tehnice.

In cadrul programului de actiune, Comisia a luat initiativa de a stabili un set de reguli tehnice armonizate pentru proiectarea constructiilor, care in prima faza vor servi drept alternativa la regulile nationale in vigoare in Statele Membre si in cele din urma sa le inlocuiasca.

Pentru cincisprezece ani, Comisia, cu ajutorul unei Comisii de Indrumare alcatuita din Reprezentanti ai Statelor Membre, a condus dezvoltarea programelor Eurocodurilor, care a condus la prima aparitie a codurilor Europene in anii 1980.

In 1989, Comisia si Statele Membre ale UE si EFTA au decis, pe baza unei intelegeri intre Comisie si CEN sa transfere pregatirea si publicarea Eurocodurilor catre CEN printr-o serie de Mandate, in scopul de a le conferi pe viitor statutul de Standarde Europene (EN). Aceasta leaga de facto Eurocodurile de prevederile tuturor Directivelor Consiliului. si/sau Deciziile Comisiei care se ocupa de standardele Europene (ex.: Directiva Consiliului 89/106/EEC privind produsele pentru constructii – CPD – si Directivele Consiliului 93/37/EEC, 92/50/EEC si 89/440/EEC privitoare la lucrarile si serviciile publice si Directivele EFTA similare initiate in vederea reglementarii pietei interne).

Programul de Eurocod-uri pentru Structuri cuprinde urmatoarele standarde care constau in general dintr-un numar de parti:

Acordul dintre Comisia Comunitatilor Europene si Comitetul European de Standardizare (CEN) referitoare la lucrarile pentru EUROCOD-uri pentru calculul cladirilor si lucrarilor civile ingineresti (BC/CEN/03/89).

Standardele Eurocod recunosc responsabilitatea autoritatilor in fiecare Stat Membru si a pastrat intact dreptul lor de a determina valorile referitoare la probleme de reglementare a sigurantei la nivel national acolo unde acestea continua sa varieze de la Stat la Stat.

Statutul si domeniul de aplicare al Eurocod-urilor

Statele Membre ale UE si EFTA recunosc ca Eurocod-urile servesc drept documente de referinta pentru urmatoarele scopuri:

ca un mijloc de a demonstra conformitatea lucrarilor pentru cladiri si a lucrarilor civile ingineresti cu cerintele esentiale ale Directivei Consiliului 89/106/EEC, in mod particular Cerinta Principala N°1 – Rezistenta mecanica si stabilitate – si Cerintta Principala N°2 – Siguranta la foc;

ca o baza pentru specificarea contractelor pentru lucrari de constructie si servicii ingineresti inrudite;

ca un cadru pentru armonizarea specificatiilor tehnice privind produsele pentru constructii (EN-uri si ETA-uri).

Eurocod-urile, atat cat privesc lucrarile de constructie, au o legatura directa cu Documentele Iterpretative² la care se refera articolul 12 al CPD, desi au o natura diferita decat standardele de materiale armonizate³. Totusi, aspectele tehnice care apar din folosirea Eurocod-urilor trebuie sa fie considerat in mod adecvat de catre Comisia Tehnica CEN si/sau Grupurile de lucru EOTA care lucreaza la standardele de produse in vederea realizarii unei compatibilitati depline a acestor specificatii tehnice cu Eurocod-urile.

Standardele Eurocod prevad reguli de calcul structural comune pentru folosirea zilnica pentru calculul intregii structuri si a produselor componente care au atat o natura traditionala cat si inovativa. Forme sau conditii de calcul neobisnuite ale constructiilor nu sint acoperite in mod specific si o apreciere mai experta a lucrurilor este ceruta din partea proiectantului in astfel de cazuri.

Standardele Nationale care implementeaza Eurocod-urile

Standardele Nationale care implementeaza Eurocod-urile vor contine textul intreg al Eurocod-ului (incluzand toate anexele), asa cum a fost publicat de catre CEN, care poate fi precedat de o pagina de titlu National si o introducere Nationala si poate fi urmata de o anexa Nationala.

Anexa Nationala poate numai sa contina informatii despre acei parametri care sint lasati liberi in Eurocod, la alegerea fiecarei natiuni, cunoscuti si ca Parametrii Determinati la nivel National, si care vor fi folositi pentru calculul cladirilor si a lucrarilor ingineresti care se vor executa in tara respectiva, ex.:

- valori si/sau clase unde sint date alternative in Eurocod

- valori care se folosesc acolo unde in Eurocod este dat doar un simbol

- date specifice nationale (geografice, climatice, etc.), ex.: harta incarcarilor din zapada,

- procedeul care trebuie folosit atunci cand in Eurocod se dau procedee alternative.

Anexa Nationala poate de asemenea sa mai contina:

- decizii despre folosirea anexelor informative si

_____ _______ ______ _____________

Conform Art.3.3 al CPD, cerintelor esentiale (ER-uri) li se va da o forma concreta in documente interpretative pentru crearea

legaturilor necesare dintre cerintele esentiale si mandatele pentru armonizarea EN-urilor si a ETAG-urilor/ETA-urilor.

Conform ART.12 al CPD documentele interpretative vor:

a) da o forma concreta cerintelor esentiale prin armonizarea terminologiei si a principiilor de tehnici de baza si indicarea

claselor sau nivelurilor pentru fiecare cerinta acolo unde este necesar;

b) indica metode de corelare a acestor clase sau niveluri de cerinte cu specificatiile tehnice, ex.: metode de calculare si de

demonstratie, reguli tehnice pentru calculul proiectelor, etc;

c) servi drept referinta pentru stabilirea standardelor armonizate si a indicatiilor pentru aprobarile tehnice Europene.

Eurocod-urile joaca, de facto, un rol similar in domeniul de aplicare al ER 1 si a unei parti a ER 2.

- referinte pentru informatii suplimentare ne-contradictorii si care sa ajute proiectantul in aplicarea Eurocod-ului.

Legaturi intre Eurocod-uri si prescriptiile tehnice armnonizate pentru produse

(EN-uri, ETA-uri)

Exista nevoia unei consecvente intre specificatiile tehnice armnonizate pentru materiale si regulile tehnice pentru lucrari⁴. Mai mult, toate informatiile care insotesc Marca CE a produselor de constructie

care se refera la Eurocod-uri vor mentiona foarte clar care Parametrii Determinati la nivel National au fost luati in considerare.

Informatii suplimentare specifice EN 1994-1-1

EN 1994-1-1 descrie Principiile si cerintele pentru siguranta, functionalitate si durabilitate a structurilor compozite din otel si beton, impreuna cu prevederile specifice pentru cladiri. Este bazat pe un concept al starilor limita folosit in legatura cu o metoda a factorilor partiali.

Pentru proiectarea structurilor noi, se intentioneaza sa se foloseasca EN 1994-1-1, pentru aplicare directa impreuna cu alte Parti din EN 1994, Eurocod-urile EN 1990 – 1993 si Eurocod-urile EN 1997 si 1998.

EN 1994-1-1 serveste si ca document de referinta pentru celelalte CEN TC-uri in materie de aspecte structurale.

EN 1994-1-1 se intentioneaza sa se foloseasca de catre;

- comitete care schiteaza alte standarde pentru proiectarea structurilor si a standardelor inrudite privind produsele, testarea si executia;

- clientii (ex.: pentru formularea cerintelor specifice in functie de nivelurile de siguranta si de durabilitate);

- proiectanti si constructori;

- autoritati relevante;

Valorile numerice pentru factorii partiali si alti parametri de siguranta sint recomandate ca valori de baza care prevad un nivel acceptabil de siguranta. Valorile au fost alese considerand ca se aplica un nivel corespunzator de manopera si de organizare a proiectului. Cand EN 1994-1-1 este folosit ca document de baza de catre alte CEN/TC-uri aceeasi valoare trebuie sa se foloseasca.

Anexa Nationala pentru EN 1994-1-1

Acest standard furnizeaza valori cu mentiuni care sa indice acolo unde este cazul ca sa se ia decizii la nivel national. Totusi Standardul National care implementeaza EN 1994-1-1 trebuie sa aibe o anexa Nationala care sa contina toti Parametrii Determinati la nivel National care se folosesc la proiectarea cladirilor si a lucrarilor ingineresti care se executa in tara respectiva.

Deciziile nationale sint permise in EN 1994-1-1 prin urmatoarele clauze:

6.4.3(1)(h)

Vezi Art. 3.3 si Art. 12 al CPD, cat si clauzele 4.2,4.3.1 si 5.2 al ID 1.

B.2.5(1)

B.3.6(5)

Capitolul 1 Generalitati

Domeniul de aplicare

Domeniul de aplicare al Eurocodului 4

(1) Eurocodul 4 se aplica la proiectarea structurilor si elementelor compozite pentru cladiri si lucrari de inginerie civila. Eurocodul 4 corespunde principiilor si cerintelor de siguranta si functionalitate a structurilor, principiile care stau la baza proiectarii si a verificarii sint date in EN 1990 – Bazele proiectarii structurilor.

(2) Eurocodul 4 se ocupa doar de cerintele pentru rezistenta, functionalitate, durabilitate si rezistenta la foc a structurilor compozite. Alte cerinte, ex.: privind izolarea fonica si termica, nu sint luate in considerare.

(3) Eurocodul 4 se doreste a se folosi impreuna cu:

EN 1990 Eurocod: Bazele proiectarii structurilor.

EN 1991 Eurocod 1: Actiuni asupra structurilor

EN-uri, hEN-uri, ETAG-uri, ETA-uri pentru produse de constructie relevante pentru structuri compozite.

EN 1090 Executia structurilor din metal si din aluminiu

EN 13670 Executia structurilor din beton

EN 1992 Eurocod 2: Proiectarea structurilor din beton

EN 1993 Eurocod 3: Proiectarea structurilor din metal

EN 1997 Eurocod 7: Proiectarea geotehnica

EN 1998 Eurocod 8: Proiectarea structurilor antiseismice, cand structurile compozite sint construite in regiuni seismice.

(4) Eurocodul 4 este impartit in diverse parti:

Partea 1-1: Reguli generale si reguli pentru cladiri

Partea 2-2: Proiectarea structurilor impotriva focului

Partea 3-3: Poduri

Domeniul de aplicare al Partii 1.1 din Eurocodul 4

(1) Partea 1-1 a Eurocodului 4 da o baza generala pentru proiectarea structurilor compozite impreuna cu regulile specifice pentru cladiri.

(2) Urmatoarele subiecte sint analizate in Partea 1-1:

Capitolul 1: Generalitati

Capitolul 2: Bazele proiectarii

Capitolul 3: Materiale

Capitolul 4: Durabilitate

Capitolul 5: Analiza structurala

Capitolul 6: Stari limita de rezistenta

Capitolul 7: Stari limita ale exploatarii normala

Capitolul 8: Noduri de cadre compozite pentru cladiri

Capitolul 9: Placi compozite cu tabla profilata, pentru cladiri

Normative de referinta

Urmatoarele normative contin prevederi care, prin referintele din acest text, constituie prevederi ale acestui standard European. Pentru referintele datate, modificari ulterioare sau revizuiri ale oricaror din aceste publicatii nu se iau in considerare. Totusi, partile implicate in semnarea acordurilor bazate pe acest standard european sint incurajate sa cerceteze posibilitatea aplicarii celor mai recente editii a normativelor indicate mai jos. Pentru referintele nedatate, ultima editie a normativului la care se face referire se considera in vigoare.

Standarde generale de referinta

EN 1090-2 ¹   Executia structurilor de metal si de aluminiu – Reguli tehnice pentru executia

structurilor de metal

EN 1990:2002  Principii de baza pentru proiectarea structurala.

Alte standarde de referinta

EN 1992-1-1 ¹  Eurocode 2: Proiectarea structurilor din beton: Reguli generale si reguli

pentru cladiri

EN 1993-1-1 ¹ Eurocode 3: Proiectarea structurilor din metal: Reguli generale si reguli

pentru cladiri

EN 1993-1-3 ¹  Eurocode 3: Proiectarea structurilor din metal: Profile subtiri si table

formate la rece

EN 1993-1-5 ¹  Eurocode 3: Proiectarea structurilor din metal: Elemente structurale plate

EN 1993-1-8 ¹  Eurocode 3: Proiectarea structurilor din metal: Proiectarea nodurilor

EN 1993-1-9 ¹  Eurocode 3: Proiectarea structurilor din metal: Rezistenta la oboseala a structurilor

din metal

EN 10025-1:2002  Produse laminate la cald pentru structuri din metal: Conditii generale de livrare.

EN 10025-2:2002  Produse laminate la cald pentru structuri din metal: Conditii tehnice de livrare

pentru oteluri ne-aliate

EN 10025-3:2002  Profile din otel laminate la cald pentru structuri din metal: Conditii tehnice de

livrare pentru profile laminate din oteluri normalizate, sudabile, cu granulatie fina.

EN 10025-4:2002  Profile din otel laminate la cald pentru constructii: Conditii tehnice de livrare

pentru profile laminate termo-mecanic din oteluri sudabile, cu granulatie fina.

EN 10025-5:2002  Profile din otel laminate la cald pentru constructii: Conditii tehnice de livrare

pentru oteluri cu rezistenta imbunatatita la coroziunea atmosferica.

EN 10025-6:2002  Profile din otel laminate la cald pentru constructii: Conditii tehnice de livrare

pentru table din otel cu limita de curgere inalta, in stare imbunatatita (in conditii

de calire si calmare)

EN 10147:2000  Table si platbanda de otel pentru constructii cu limita de curgere inalta, pentru

indoirea la rece: Conditii tehnice de livrare pentru oteluri laminate termo-mecanic.

EN 10149-2:1995 Table laminate la cald din otel pentru constructii cu limita de curgere inalta, pentru

indoire la rece: Conditii tehnice de livrare pentru oteluri laminate normalizate.

Va fi publicat

EN 10149-3:1995 Table laminate la cald din otel pentru constructii cu limita de curgere inalta, pentru

indoirea la rece: Conditii tehnice de livrare pentru oteluri laminate normalizate.

Ipoteze

(1) In plus fata de ipotezele generale ale EN 1990 urmatoarele ipoteze se aplica:

-cele date in clauzele 1.3 din EN 1992-1-1 si EN 1993-1-1.

Diferente intre principii si reguli de aplicare

(1) Se aplica regulile din EN 1990, 1.4.

1.5 Definitii

1.5.1 Generalitati

(1) Se aplica termenii si definitiile date in EN 1990, 1.5, EN 1992-1-1, 1.5, si EN 1993-1-1, 1.5.

1.5.2 Termeni si definitii aditionali folosite in acest standard

1.5.2.1 Element compozit

un element structural cu componente de beton si otel structural sau otel format la rece legate prin conectori de forfecare astfel incat sa se limiteze lunecarea longitudinala intre beton si otel si separarea unei componente de cealalta.

1.5.2.2 Conectori de forfecare

o legatura dintre beton si componentele de otel a unui element compozit care are o suficienta rezistenta si rigiditate pentru a permite ca cele doua componente sa fie proiectate ca parti ale aceluiasi element structural.

1.5.2.3 Comportare compozita

comportare care apare dupa ce legatura de forfecare devine efectiva in urma intaririi betonului.

1.5.2.4 Grinda compozita

un element compozit supus predominant la incovoiere

1.5.2.5 Stalp compozit

un element compozit supus predominant la compresiune sau compresiune cu incovoiere

1.5.2.6 Placa compozita

un planseu in care foile de tabla profilata sint folosite mai intai drept cofraje temporare si mai apoi in combinatia structurala cu betonul intarit si actioneaza drept armatura in planseul final.

1.5.2.7 Cadru compozit

un cadru structural in care unele sau chiar toate elementele sint elemente compozite si majoritatea celor ramase sint elemente structurale din metal.

1.5.2.8 Nod compozit

un nod intre un element compozit si un alt element compozit, element din metal sau beton armat, in care armatura este luata in considerare in proiectarea pentru rezistenta si rigiditatea nodului.

1.5.2.9 Structura sau element sprijinite

o structura sau un element la care greutatea elementelor de beton se aplica elementelor de metal care sint sprijinite pe deschidere, sau sint sprijinite independent pina cand elementele de beton sint capabile sa preia eforturi.

1.5.2.10 Structura sau element nesprijinite

o structura sau un element la care greutatea elementelor de beton se aplica elementelor de metal care sint nesprijinite pe deschidere.

1.5.2.11 Rigiditate la incovoiere nefisurat

rigiditatea E_a I₁ unei sectiuni transversale a unui element compozit unde I₁ este momentul de inertie a sectiunii, echivalente, efectiva de metal calculata in ipoteza ca betonul intins este nefisurat.

1.5.2.12 Rigiditate la incovoiere fisurat

rigiditatea E_a I₂ unei sectiuni transversale a unui element compozit unde I₂ este momentul de inertie a sectiunii, echivalente, efectiva de metal calculata neglijand betonul intins dar incluzand armatura.

1.5.2.13 Precomprimare

procesul de aplicare a eforturilor de comprimare asupra partii din beton a unui element compozit, realizata prin tendoane sau prin deformatii impuse controlate.

1.6 Simboluri

Pentru obiectul acestui standard urmatoarele simboluri se aplica.

Litere mari latine

Capitolul 2 Bazele proiectarii

2.1 Cerinte

(1) Proiectarea structurilor compozite trebuie sa fie in coformitate cu regulile generale date in EN 1990

(2) Prevederile suplimentare pentru structurile compozite date in acest capitol vor fi de asemenea luate in considerare.

(3) Cerintele de baza ale EN 1990, Capitolul 2 sint considerate a fi satisfacute pentru structuri compozite cand se aplica in acelasi timp umatoarele:

- calculul la stari limita in legatura cu metoda factorului partial in conformitate cu EN 1990

- actiuni in conformitate cu EN 1991,

- combinatii de actiuni in conformitate cu EN 1990 si,

- rezistente, durabilitate si functionalitate in conformitate cu acest Standard.

2.2 Principiile proiectarii la stari limita

(1)P Pentru structuri compozite, vor fi considerate etapele relevante in derularea executiei

Variabile de baza

2.3.1 Actiuni si influente ale mediului

(1) Actiunile care se folosesc in calcul sint date in sectiunile corespunzatoare din EN 1990

(2)P La verificarea tablei de otel folosita drept cofraj, se va lua in calcul efectul de arcuire (o crestere a grosimii betonului datorita deformarii tablei)

2.3.2 Proprietatile materialelor si produselor

(1) Daca actiunile cauzate de comportarea in timp a betonului nu sint altfel date in Eurocode 4, ele vor fi considerate conform EN 1992-1-1.

2.3.3 Clasificarea actiunilor

(1)P Efectele contractiei si curgerii lente a betonului si a variatiilor neuniforme de temperatura produc forte interne in sectiuni si eforturi longitudinale si de curbura in elemente; efectele care apar in structuri static determinate si in structuri static nedeterminate cand nu se ia in considerare compatibilitatea deformatiilor, vor fi clasificate ca efecte de ordin primar.

(2)P In structuri static nedeterminate efectele de ordin primar din contractii, curgere lenta, temperatura sint asociate cu efectele aditionale ale altor actiuni astfel incat efectele totale sint compatibile; acestea vor fi clasificate ca efecte secundare si vor fi considerate drept actiuni indirecte.

2.4 Verificari prin metoda coeficientilor partiali de siguranta

2.4.1 Valori de calcul

2.4.1.1 Valori de calcul ale actiunilor

(1) Pentru precomprimare prin deformatii controlate impuse, ex. prin presare pe reazeme, coeficientul partial _p de siguranta trebuie specificat pentru starile limita de rezistenta, luand in considerare efectele favorabile si nefavorabile.

Nota: Valorile lui _p pot fi date in Anexa Nationala. Valoarea recomandata pentru ambele

efecte, favorabil si nefavorabi; este 1,0

2.4.1.2 Valori de calcul ale proprietatilor materialelor sau produselor

(1)P In afara cazului in care o estimare superioara a rezistentei este ceruta, factori partiali vor fi folositi pentru a micsora rezistenta caracteristica sau nominala.

(2)P Pentru beton, un factor partial _C, se va aplica. Rezistenta de calcul la compresiune va fi data de :

unde valoarea caracteristica f_ck va fi obtinuta din EN 1992-1-1, 3.1 pentru beton normal si din EN 19992-1-1, 11.3 pentru beton usor.

Nota: Valoarea lui _C este cea folosita in EN 1992-1-1

(3)P Pentru armatura de otel, un factor partial _s , se va aplica.

Nota: Valoarea lui _s este cea folosita in EN 1992-1-1

(4)P Pentru otelul folosit la structura, tablele de otel si dispozitivele de prindere, factori partiali _M , se vor aplica. In afara cazului in care este specificat altfel, factorul partial pentru otelul folosit la structura

se va considera _M0.

Nota: Valorile lui _M sint cele folosite in EN 1993

(5)P Pentru legatura de forfecare, un factor partial _V , se va aplica.

Nota: Valoarea lui _V poate fi data in Anexa Nationala. Valoarea recomandata pentru _V este 1,25.

(6)P Pentru forfecare longitudinala in planseele compozite ale cladirilor, un factor partial _VS , se va aplica.

Nota: Valoarea lui _VS poate fi data in Anexa Nationala. Valoarea recomandata pentru _V este 1,25.

(7)P Pentru verificari la oboseala a dornurilor cu cap, factorii partiali _Mf si _Mf,s se vor aplica.

Nota: Valoarea lui _Mf este cea folosita in sectiunile relevante din EN 1993. Valoarea lui _Mf,s poate fi data in Anexa Nationala. Valoarea recomandata pentru _Mf,s este 1,0.

2.4.1.3 Valori de calcul ale datelor geometrice

(1) Datele geometrice pentru sectiuni transversale si sisteme pot fi luate din standardele de produse hEN sau din desenele de executie si tratate ca valori nominale.

2.4.1.4 Rezistente de calcul

(1)P Pentru structuri compozite, rezistentele de calcul vor fi determinate in conformitate cu EN 1990, relatia (6.6a) sau relatia (6.6c).

2.4.2 Gruparea actiunilor

(1) Expresiile generale pentru combinatii de actiuni sint date in EN 1990, Capitolul 6.

Nota: Pentru cladiri, regulile privind combinatiile pot fi date in Anexa Nationala a Anexei A din EN 1990.

2.4.3 Verificarea echilibrului static (ES)

(1) Expresia de baza pentru verificarea echilibrului static al cladirilor, asa cum este descrisa in EN 1990, Tabelul A1.2(A), se aplica de asemenea situatiilor de calcul echivalente cu verificarea echilibrului static, ex.: pentru proiectarea ancorarilor sau verificarea ridicarii reazemelor la grinzi continue.

Capitolul 3 Materiale

3.1 Beton

(1) In afara cazului in care sint altfel prevazute in Eurocode 4, proprietatile se obtin din EN 1992-1-1, 3.1 pentru beton normal si din EN 1992-1-1, 11.3 pentru beton usor.

(2) Aceasta parte din EN 1994 nu reglementeaza proiectarea structurilor compozite cu betoane avand clase de rezistenta mai mici decat C20/25 si LC20/22 si mai mari decat C60/75 si LC 60/66.

(3) Contractia betonului trebuie determinata luand in considerare umiditatea mediului, dimensiunile elementului si compozitia betonului.

(4) Acolo unde actiuni compuse se iau in calcul, la cladiri, efectele contractiei proprii pot fi neglijate in determinarea eforturilor si a deformatiilor.

Nota: Experienta a aratat ca valorile efortului de contractie date in EN 1992-1-1 pot da efecte ale contractiei

exagerate in structuri compozite. Valorile pentru contractia betonului pot fi date in Anexa Nationala.

Valorile recomandate sint date in Anexa C.

3.2 Armatura din otel pentru beton

(1) Proprietatile armaturilor se obtin din EN 1992-1-1,3.2.

(2) Pentru structuri compozite, valoarea de calcul a modulului de elasticitate Es poate fi luata egala cu valoarea armaturii rigide data in EN 1993-1-1, 3.2.6.

3.3 Otel structural

(1) Proprietatile otelului structural se obtin din EN 1993-1-1, 3.1 si 3.2.

(2) Regulile din aceasta parte a EN 1994 se aplica otelului folosit la structura cu rezistenta nominala de curgere care nu depaseste 460 N/mm².

3.4 Dispozitive de conectare

3.4.1 Generalitati

(1) Pentru stabilirea cerintelor privind suruburile si sudurile, trebuie consultat EN 1993-1-8.

3.4.2 Conectori tip dornuri cu cap pentru lunecare

(1) Trebuie consultat EN 13918.

3.5 Tabla metalica cutata pentru placi compozite

(1) Proprietatile se obtin din EN 1993-1-1, 3.1 si 3.2.

(2) Regulile din aceasta parte a EN 1994 se aplica proiectarii planseelor compozite cu foi de tabla profilata fabricate din otel in conformitate cu EN 10025, table metalice formate la rece si in conformitate cu EN 10149-2 sau EN 10149-3 sau foi de tabla galvanizata in conformitate cu EN 10147.

Nota: Valoarea minima a grosimii nominala t poate fi data in Anexa Nationala. Valoarea recomandata este 0,70 mm.

Capitolul 4 Durabilitate

4.1Generalitati

(1) Prevederile relevante care sint date in EN 1990, EN 1992 si EN 1993 trebuiesc aplicate.

(2) Detaliile legaturilor de forfecare trebuie sa fie in conformitate cu 6.6.5

4.2 Tabla metalica cutata pentru placi compozite

(1)P Suprafetele de tabla expuse vor fi protejate adecvat sa reziste in conditii atmosferice specifice.

(2) Stratul de zinc, daca este specificat, trebuie sa indeplineasca conditiile din EN 10147 sau din standardele specifice in vigoare.

(3) Un strat de zinc cu o masa totala de 275 g/m² (incluzand ambele fete) este suficient pentru planseele interioare intr-un mediu ne-agresiv dar aceasta prevedere poate sa varieze in functie de conditiile de exploatare.

Capitolul 5 Calculul structural

5.1 Modelarea structurii pentru calcul

5.1.1 Modelarea structurii si ipoteze de baza

(1)P Modelarea structurii si ipotezele de baza se vor lua in conformitate cu EN 1990, 5.1.1 si va anticipa comportarea sectiunilor transversale, elementelor, nodurilor si reazemelor. 

(2) Capitolul 5 se aplica structurilor compozite in care cele mai multe elemente structurale si noduri sint fie compozite sau din otel structural. Acolo unde comportarea structurala este in mod esential aceea a unei structuri din beton armat sau beton precomprimat, cu doar cateva elemente compozite, analiza globala se face in conformitate cu EN 1992-1-1.

(3) Analiza planseelor compozite cu tabla profilata de otel la cladiri trebuie facuta in conformitate cu Capitolul 9.

5.1.2 Modelarea nodurilor

(1) Efectele comportarii nodurilor asupra distributiei fortelor interne si a momentelor in structura, si asupra deformatiilor structurii, pot in general sa fie neglijate dar unde astfel de efecte sint semnificative (ca de exemplu cazul nodurilor semi-continui) trebuie luate in considerare, vezi Capitolul 8 si EN 1993-1-8.

(2) Pentru a identifica cazurile in care trebuiesc considerate efectele comportari nodurilor in analiza, trebuie facuta o diferenta intre cele trei modele de noduri dupa cum urmeaza, vezi 8.2 si EN 1993-1-8, 5.1.1:

- simple, in care nodul poate fi considerat ca nu transmite momente incovoietoare;

- continui, in care rigiditatea si/sau rezistenta nodului permite continuitatea totala a elementelor care se iau in considerare in calcul;

- semi-continui, in care comportarea nodului trebuie luata in considerare in calcul.

(3) Pentru cladiri, cerintele diferitelor tipuri de noduri sint date in Capitolul 8 si in EN 1993-1-8.

5.1.3 Interactiunea sol-structura

(1)P Trebuie luata in considerare deformatia caracteristica a reazemelor atunci cand devine semnificativa.

Nota: EN 1997 ofera indrumare in calcularea interactiunii sol-structura.

5.2 Stabilitate structurala

5.2.1 Efectele geometriei deformate a structurii

(1) Efectele actiunilor pot in general fi determinate folosind fie:

- analiza de ordinul I, folosind geometria initiala a structurii

- analiza de ordinul II, luand in considerare influenta deformatiilor asupra structurii.

(2)P Efectele geometrie deformate (efecte de ordinul II ) trebuie sa fie luate in considerare daca duc la marirea efectelor actiunilor sau modifica in mod semnificativ comportarea structurala.

(3) Analiza de ordinul I poate fi folosita daca marirea fortelor interne relevante sau a momentelor cauzate de catre deformatiile date de analiza de ordinul I este mai mica de 10%. Aceasta conditie se considera a fi indeplinita daca urmatorul criteriu este indeplinit:

unde:

_cr este factorul prin care incarcarea de calcul se mareste pentru a cauza instabilitatea

elastica

(4)P In determinarea rigiditatii structurii, tolerante corespunzatoare trebuiesc admise pentru

fisurarea si curgerea lenta a betonului si pentru comportarea nodurilor.

5.2.2 Metode de calcul

(1) Cadrele plane de tipul grinda-stalp pot fi verificate pentru modul de cedare forfecare de nivel prin calcul de ordinul I daca este satisfacut criteriul (5.1) pentru fiecare etaj. In aceste structuri _cr poate fi calculat folosind expresia data in EN 1993-1-1, 5.2.1(4), cu conditia ca forta axiala de compresiune in grinzi nu este semnificativa si tolerante corespunzatoare sint admise pentru fisurarea betonului, vezi 5.4.2.3, curgerea lenta a betonului, vezi 5.4.2.2 si pentru comportarea nodurilor, vezi 8.2 si EN 1993-1-8, 5.1.

(2) Efecte de ordinul II pot fi incluse indirect prin folosirea analizei de ordin I cu amplificare corespunzatoare.

(3) Daca efectele de ordin II din elemente individuale si imperfectiunile in elementele principale sint luate in intregime in calcul in analiza globala a structurii, nu sint necesare verificari individuale de stabilitate ale elementelor.

(4) Daca efectele de ordin II din elemente individuale sau unele imperfectiuni (ex.: pentru flambaj lateral cu/si torsiune sau incovoiere) nu sint luate in intregime in considerare, in calculul global al structurii, stabilitatea elementelor individuale trebuie verificata pentru efectele care nu au fost incluse in calculul global.

(5) Daca calculul global neglijeaza efectele de torsiune laterala, rezistenta unei grinzi compozite la flambaj lateral cu torsiune poate fi verificata folosind pct.6.4.

(6) Pentru stalpi compoziti si elemente compozite comprimate, stabilitatea la incovoiere poate fi

verificata folosind una din urmatoarele metode:

(a) prin calcul global in conformitate cu 5.2.2(3), cu verificarea rezistentei sectiunilor transversale

conform cu 6.7.3.6 si 6.7.3.7, sau

(b) prin analiza elementului individual in conformitate cu 6.7.3.4, luand in considerare momentele de

la capete si fortele din analiza globala a structurii incluzand efecte globale de ordinul II si

imperfectiuni globale acolo unde este cazul. Analiza elementului trebuie sa tina cont de efectele

de ordinul II in element si de imperfectiunile principale ale elementului, vezi 5.3.2.3, cu verificarea

rezistentei sectiunii transversale in conformitate cu 6.7.3.6 sau 6.7.3.7, sau

(c) pentru elemente in compresiune axiala, prin folosirea curbelor de flambaj care iau in considerare

efectele de ordin II in element si imperfectiunile elementului, vezi 6.7.3.5. Aceasta verificare

trebuie sa ia in considerare fortele de capat din calculul global al structurii incluzand efectele

globale de ordin II si imperfectiunile globale cand este cazul, si trebuie sa se bazeze pe o

lungime de flambaj egala cu lungimea sistemului.

(7) Pentru structuri in care stalpii sint din otel structural, stabilitatea poate fi verificata prin verificari ale elementelor bazate pe lungimi de flambaj, in conformitate cu EN 1993-1-1, 5.2.2(8) si 6.3.

5.3 Imperfectiuni

5.3.1 Principii de baza

(1)P Tolerante corespunzatoare trebuie sa fie incorporate in calculul structural pentru acoperirea efectelor imperfectiunilor, incluzand eforturi reziduale si imperfectiuni geometrice cum ar fi: lipsa de verticalitate, lipsa de liniaritate, lipsa planeitatii, lipsa preciziei la imbinari si a excentricitatilor minore inevitabile prezente in nodurile structurii neincarcate.

(2)P Forma imperfectiunilor considerate va lua in considerare modul de flambare elastica a structurii sau a elementului in planul de flambare considerat, in cea mai defavorabila directie si forma.

5.3.2 Imperfectiuni la cladiri

5.3.2.1Generalitati

(1) Imperfectiuni geometrice echivalente, vezi 5.3.2.2 si 5.3.2.3, trebuiesc folosite, cu valori care sa reflecte posibilele efecte ale imperfectiunilor globale si locale, doar daca efectele imperfectiunilor locale nu sint incluse in formulele rezistentelor pentru proiectarea elementului, vezi 5.3.2.3

(2) In cadrul unei analize globale, imperfectiunile elementelor in elemente compozite comprimate pot fi neglijate acolo unde, conform 5.2.1(2), poate fi folosita analiza de ordin I. Acolo unde trebuie folosita analiza de ordinul II, imperfectiunile elementelor pot fi neglijate in cadrul analizei globale daca:

unde:

este definit la 6.7.3.3 si calculata pentru elementul considerat articulat la ambele capete

N_pl,Rk este definit la 6.7.3.3

N_Ed este valoarea de calcul a fortei normale

(3) Imperfectiunile elementelor trebuiesc luate in considerare intotdeauna atunci cand se verifica stabilitatea pe lungimea unui element in conformitate cu 6.7.3.6. sau 6.7.3.7.

(4) Imperfectiunile din interiorul elementelor comprimate din otel trebuiesc considerate in conformitate cu EN 1993-1-1, 5.3.2 si 5.3.4

5.3.2.2 Imperfectiuni globale

(1) Efectele imperfectiunilor trebuiesc admise in conformitate cu EN 1993-1-1, 5.3.2

5.3.2.3 Imperfectiuni ale elementelor

(1) Valori de calcul pentru imperfectiuni initiale echivalente pentru stalpi compoziti si elemente compozite comprimate trebuiesc luate din Tabelul 6.5

(2) Pentru grinzi compozite libere in lateral efectele imperfectiunilor sint incorporate in formula data pentru momentul capabil la flambaj, vezi 6.4.

(3) Pentru elemente de otel efectul imperfectiunilor este incorporat in formulele date pentru rezistenta la flambaj, vezi EN 1993-1-1, 6.3

5.4 Calculul efectelor actiunilor

5.4.1 Metode de calcul global

5.4.1.1 Generalitati

(1) Efectele actiunilor pot fi calculate prin calcul global elastic, chiar si acolo unde rezistenta sectiunii se bazeaza pe rezistenta ei plastica sau ne-lineara.

(2) Calculul global elastic trebuie folosit pentru starile limita de exploatare, cu corectii corespunzatoare pentru efectele ne-lineare cum ar fi fisurarea betonului.

(3) Calculul gobal elastic trebuie folosit pentru verificari la starea limita de oboseala

(4)P Efectele forfecarii in acelasi plan si a flambajului local trebuiesc luate in considerare daca acestea influenteaza semnificativ calculul global.

(5) Efectele flambajului local a elementelor de otel asupra alegerii metodei de calcul pot fi luate in considerare prin clasificarea sectiunilor transversale, vezi 5.5.

(6) Efectele flambajului local a elementelor de otel asupra rigiditatii poate fi ignorata in sectiuni compozite normale. Pentru sectiuni din clasa 4, vezi EN 1993-1-5, 2.2.

(7) Efectele asupra analizei globale a alunecarilor in gaurile pentru suruburi si deformatii similare ale pieselor de legatura trebuiesc considerate.

(8) Daca analiza ne-liniara nu este folosita, efectele lunecarii si separarii betonului de metal in calculul fortelor interne si a momentelor pot fi neglijate la contactul dintre metal si beton unde este prevazuta o legatura de forfecare in conformitate cu 6.6.

5.4.1.2 Latimea efectiva a talpilor tinand cont de deformatiile de forfecare

(1)P Pentru luarea in considerare a deformatiilor din forte taietoare, la stabilirea flexibilitatii talpilor se poate apela la o metoda de calcul riguroasa sau utilizand latimi efective ale talpilor definite in continuare.

(2) Efectele deformatiilor de forfecare in talpile de otel trebuiesc considerate in conformitate cu EN 1993-1-1, 5.2.1(5).

(3) Latimea efectiva a talpilor de beton trebuie sa fie determinata in conformitate cu urmatoarele prevederi

(4) Cand se foloseste calculul global elastic, o latime efectiva constanta poate fi considerata in fiecare deschidere. Aceasta valoare poate fi luata ca valoarea b_eff,1 la mijlocul deschiderii pentru o deschidere sprijinita la ambele capete, sau valoarea b_eff,2 pe reazemul unei console.

(5) La mijlocul deschiderii sau la un reazem intern, latimea efectiva totala b_eff,2, vezi Figura 5.1, poate fi determinata ca si:

unde:

b₀ este distanta dintre centrele conectorilor de forfecare

b_ei este valoarea latimii efective a talpii de beton pe fiecare parte a inimii si se ia egala cu

L_e/8 dar nu mai mare decat latimea geometrica efectiva b_i. Valoarea b_i trebuie luata ca

distanta de la conectorul de forfecare la un punct situat la jumatatea distantei dintre

doua inimi adiacente, masurate pe linia mediana a talpii de beton, cu exceptia ca linga

o latura libera, distanta b_i este distanta pina la latura libera. Lungimea L_e trebuie luata

drept distanta aproximativa intre punctele in care momentul incovoietor este egal cu 0.

Pentru grinzi compozite continui tipice, unde dimensionarea este guvernata de

infasuratoarea de momente din diverse cazuri de incarcari, si pentru console, L_e poate

fi considerat ca in Fig. 5.1

(6) Latimea efectiva la un reazem de capat poate fi determinata astfel:

cu :

unde:

b_ei este latimea efectiva, vezi (5), a ultimei deschideri si L_e este deschiderea echivalenta

a ultimei deschideri conform Figurii 5.1

(7) Distributia latimii efective intre reazeme si regiunile din mijloc se pot considera asa cum sint aratate in Figura 5.1.

(8) La cladiri, acolo unde distributia de momente incovoietoare este influentata de rezistenta sau de rigiditatea la rotire a unui nod, aceasta trebuie luata in considerare pentru determinarea lungimii L_e.

(9) Pentru calculul structurilor cladirilor, b₀ trebuie sa fie luata egala cu zero iar b_i masurata din centrul inimii.

5.4.2 Calcul liniar elastic

5.4.2.1 Generalitati

(1) Aproximari trebuiesc admise pentru efectele fisurarii betonului, curgerii lente si contractarii betonului, etapele constructiei si precomprimare.

Legenda:

1 L_e = 0,85 L₁ pentru b_eff,1

2 L_e = 0,25 (L₁+ L₁)pentru b_eff,2

3 L_e = 0,70 L₂ pentru b_eff,1

4 L_e = 2L₃ pentru b_eff,2

Figura 5.1: Deschiderile echivalente, pentru latimea activa a talpii de beton

5.4.2.2 Curgerea lenta si contractia

(1)P Aproximari adecvate trebuiesc admise pentru efectele curgerii lente si contractiei betonului.

(2) Cu exceptia elementelor care au ambele talpi compozite, efectele curgerii lente poate fi luata in considerare folosind raportul modular n_L pentru beton. Rapoartele modulare depinzand de tipul de incarcare (indice L) sint date de :

unde:

n_o este raportul modular E_a/ E_cm pentru incarcare de scurta durata

E_cm  este modulul secant de elasticitate al betonului pentru incarcarea de scurta durata

conform EN 1992-1-1, Tabelul 3.1 sau Tabelul 11.3.1;

f_t  este coeficientul de curgere lenta f (t,t₀) conform EN 1992-1-1,3.1.4 sau 11.3.3,

depinzand de varsta betonului (t) la momentul considerat si de varsta (t₀) in momentul

incarcarii.

_L  este multiplicator pentru curgerea lenta depinzand de tipul de incarcare, care se ia 1,1

pentru incarcari permanente si 0,55 pentru efectele primare si secundare ale

contractarii si 1,5 pentru precomprimarea prin impunerea deformatiilor

(3) Pentru incarcarile permanente asupra structurilor compozite turnate in mai multe etape o valoarea medie t₀ trebuie folosita pentru determinarea coeficientului de curgere lenta. Aceasta ipoteza trebuie luata si pentru precomprimare cu deformatii impuse daca tot betonul din deschiderile principale in momentul precomprimarii este mai vechi de 14 zile.

(4) Pentru contractie, varsta la care se considera aplicarea incarcarii trebuie in general luat la o zi.

(5) Acolo unde se folosesc plansee prefabricate sau unde precomprimarea planseului de beton se realizeaza inainte ca legatura de forfecare sa intre in lucru, coeficientul de curgere lenta si valorile de contractie se iau din momentul in care se realizeaza conclucrarea compozita.

(6) Unde distributia de momente incovoietoare la t₀ este in mod semnificativ modificata de curgerea lenta, de exemplu in grinzi continui cu structura mixta avand atat deschideri compozite cat si necompozite, efectele secundare in functie de timp datorita curgerii lente trebuiesc considerate, cu exceptie in cazul analizei globale la starea limita de rezistenta pentru elemente care au toate sectiunile transversale in Clasa 1 sau 2. Pentru efectele secundare in functie de timp raportul modular poate fi determinat cu ajutorul unui multiplicator pentru curgerea lenta _L egal cu 0,55.

(7) Efectele primare si secundare cauzate de contractie si de catre curgerea lenta a talpilor de beton trebuiesc luate in considerare in mod corespunzator. Efectele curgerii lente si a contractiei pot fi neglijate la calcul pentru verificari la starile limita de rezistenta altele decat la oboseala, pentru elemente compozite cu toate sectiunile transversale in Clasa 1 sau 2 si pentru care nu sint necesare aproximari la flambaj lateral cu torsiune; pentru stari limita de exploatare, vezi Capitolul 7. 

(8) In regiunile in care planseul de beton se presupune ca se fisureaza, efectele primare datorita contractiei pot fi neglijate in calcularea efectelor secundare.

(9) In stalpi compoziti si elemente comprimate, trebuie sa se tina cont de efectele curgerii lente in conformitate cu 6.7.3.4(2).

(10) Pentru conlucrari compozite duble cu ambele talpi nefisurate (ex.: in cazul precomprimarii) efectele curgerii lente si a contractiei trebuiesc determinate cu metode mai precise.

(11) Pentru simplificari in structuri care satisfac expresia (5.1) sau 5.2.2(1), care nu sint in principal folosite la depozitare si nu sint precomprimate prin deformatii impuse controlate, efectele curgerii lente a betonului in grinzile compuse pot fi luate in considerare prin inlocuirea ariei de beton A_c cu aria echivalenta de otel A_c/n atat pentru incarcarea de scurta durata cat si pentru incarcarea de lunga durata, unde n este un raport modular nominal corespunzator unui modul de elasticitate pentru beton E_c,eff egal cu E_cm/2.

5.4.2.3 Efectele fisurarii betonului

(1)P Aproximari adecvate trebuie admise pentru efectele fisurarii betonului.

(2) Urmatoarea metoda poate fi folosita pentru determinarea efectelor fisurarilor in grinzi compozite cu talpi de beton.

Infasuratoarea fortelor interne si a momentelor pentru combinatiile caracteristice, vezi EN 1990, 6.5.3, incluzand efectele pe termen lung trebuiesc calculate folosind rigiditatea la incovoiere E_aI₁ a sectiunilor nefisurate. Aceasta este denumita drept „ calcul fara fisuri ”. In regiuni unde efortul din fibra extrema intinsa de beton datorita infasuratorii din efectele globale depaseste de doua ori rezistenta f_ctm sau f_1ctm , vezi EN 1992-1-1, Tabelul 3.1 sau Tabelul 11.3.1, rigiditatea trebuie redusa la valoarea E_aI₂ , vezi 1.5.2.12. Aceasta distributie a rigiditatilor poate fi folosita pentru starile limita de rezistenta si pentru starile limita de exploatare. O noua distributie a fortelor interne, a momentelor si deformatiilor este determinata apoi daca este cazul, prin recalcul. Aceasta este denumita „calcul la fisurare”.

(3) Pentru grinzi compozite continui cu talpi de beton deasupra sectiunii de metal si ne-precomprimate, incluzand grinzile in cadre care preiau forte orizontale prin contravantuiri, urmatoarea metoda simplificata poate fi folosita. Acolo unde toate rapoartele lungimilor deschiderilor continui adiacente (scurte/lungi) intre reazeme sint de cel putin 0,6, efectul fisurarii poate fi luat in calcul prin folosirea rigiditatii la incovoiere E_aI₂ pentru peste 15% din deschidere de fiecare parte a reazemului intern si prin folosirea valorii nefisurate E_aI₁ in rest.

(4) Efectul fisurarii betonului asupra rigiditatii la incovoiere a grinzilor compozite si a elementelor comprimate trebuiesc determinate in conformitate cu pct. 6.7.3.4.

(5) La cladiri, contributia betonului inglobat al unei grinzi poate fi determinata prin folosirea valorii medii a rigiditatilor betonului inglobat fisurat si nefisurat. Aria betonului comprimat poate fi determinata din distributia efortului plastic.

5.4.2.4 Stadii si ordinea de executie

(1)P O analiza corespunzatoare trebuie facuta pentru a tine cont de efectele construirii in etape, incluzand acolo unde este necesar efecte separate ale actiunilor aplicate armaturii rigide si in intregime sau partial elementelor compozite.

(2) Efectele etapelor de construire pot fi neglijate in calculul la starile limita de rezistenta altele decat de oboseala, pentru elemente compozite unde toate sectiunile transversale sint in Clasa 1 sau 2 si in care nu sint necesare aproximari pentru flambaj lateral cu torsiune.

5.4.2.5 Efectele temperaturii

(1) Efectele datorate temperaturii trebuiesc considerate in conformitate cu EN 1991-1-5.

(2) Efectele temperaturii pot fi neglijate in analiza la starile limita de rezistenta altele decat de oboseala, pentru elemente compozite unde sectiunile transversale sint de Clasa 1 sau 2 si in care nu sint necesare tolerante pentru flambaj lateral cu torsiune.

5.4.2.6 Pre-comprimare prin deformatii impuse controlat

(1)P Acolo unde este prevazuta precomprimare prin deformatii controlate impuse (ex.: presare pe reazem), efectele devierilor posibile de la valorile prevazute ale deformatiilor impuse si a rigiditatilor asupra momentelor interne si a fortelor trebuie sa fie luate in considerare pentru calculul la starile limita de rezistenta si exploatare.

(2) Doar daca nu este folosita o metoda mai precisa pentru determinarea momentelor interne si a fortelor, valorile caracteristice ale actiunilor indirecte datorita deformatiilor impuse pot fi calculate cu valorile caracteristice sau nominale ale proprietatilor materialelor si ale deformatiilor impuse, daca deformatiile impuse sint controlate.

5.4.3 Calcul global neliniar

(1)P Calculul neliniar poate fi folosit in conformitate cu EN 1992-1-1, 5.7 si EN 1993-1-1, 5.4.3.

(2)P Comportarea legaturii de forfecare trebuie luata in considerare.

(3)P Efectele deformarii geometriei structurii trebuiesc luate in considerare in conformitate cu pct. 5.2.

5.4.4 Calcul liniar-elastic cu redistributie limitata

(1) Tinand cont de faptul ca efectele de ordinul II nu se iau in considerare, calculul liniar elastic cu redistribuiri limitate poate fi aplicat grinzilor continui si cadrelor pentru verificari la stari limita altele decat oboseala.

(2) Distributia momentelor incovoietoare data de un calcul liniar elastic global conform 5.4.2 poate fi redistribuit intr-un mod care satisface echilibrul si care tine cont de efectele comportarii inelastice a materialelor si a tuturor tipurilor de flambaj.

(3) Momentele incovoietoare obtinute cu un calcul liniar elastic pot fi redistribuite :

a) in grinzi compozite cu legaturi de forfecare totale sau partiale asa cum sint date in (4) - (7);

b) in elemente de metal in conformitate cu EN 1993-1-1, 5.4.1(4);

c) in elemente de beton supuse in principal la incovoiere in conformitate cu EN 1992-1-1, 5.5;

d) in grinzi partial incastrate fara planseu de beton sau compozit, in conformitate cu (b) sau

(c), cazul cel mai defavorabil.

(4) Pentru verificari la stari limita de rezistenta altele decat oboseala, momentele incovoietoare elastice in grinzile compozite pot fi modificate conform (5) - (7) acolo unde:

- grinda este un element compozit continuu, sau parte a unui cadru care preia incarcari

orizontale prin contravantuiri,

- grinda este legata cu noduri rigide si de rezistenta totala, sau cu un astfel de nod si un nod

articulat

- pentru o grinda compozita partial incastrata, fie este stabilita capacitatea de rotire ca fiind

suficienta pentru gradul de redistribuire adoptat, fie contributia betonului inglobat in

compresiune este neglijata atunci cand se calculeaza momentul capabil in sectiunile unde

momentul incovoietor este redus,

- fiecare deschidere are o inaltime uniforma si

- nu sint necesare aproximari pentru flambaj lateral cu torsiune.

(5) Acolo unde (4) se aplica, momentele incovoietoare in grinzile compozite determinate prin calcul liniar elastic global pot fi modificate astfel:

- prin reducerea momentelor negative maxime cu valori care sa nu depaseasca procentele

date in Tabelul 5.1, sau

- numai in grinzi cu toate sectiunile transversale in Clasa 1 sau 2, prin marirea momentelor

negative maxime cu valori care nu depasesc 10%, pentru calcul elastic neliniar fara fisurare

sau 20% pentru calcul elastic liniar cu fisurare, vezi 5.4.2.3.

- doar daca este verificata capacitatea de rotire si aceasta permite o valoare mai mare.

Tabelul 5.1: Limitari ale redistribuirilor momentelor negative, procente din valoarea initiala a momentelor incovoietoare care trebuiesc reduse

(6) Pentru marci de otel mai mari decat S355, redistribuirea este posibila doar pentru grinzile care au toate sectiunile transversale in Clasa 1 si Clasa 2. Redistribuirea prin reducerea momentelor maxime negative nu trebuie sa depaseasca valoarea de 30% pentru un calcul fara fisurare si 15% pentru un calcul cu fisurare, doar daca nu este demonstrat ca o valoare mai mare este permisa de catre capacitatea de rotire.

(7) Pentru sectiuni transversale compozite in Clasa 3 sau 4, limitarile date in Tabelul 5.1 referitoare la momentele incovoietoare folosite in calcul, se aplica elementelor compozite. Momentele aplicate elemetelor de otel nu trebuie redistribuite.

5.4.5 Calcul global rigid-plastic

(1) Calculul rigid-plastic global poate fi folosit pentru verificari la stari limita de rezistenta altele decat oboseala, unde efectele de ordin II nu trebuiesc considerate si cu conditia ca:

- toate elementele si nodurile cadrului sint din otel sau compozite,

- otelul satisface EN 1993-1-1, 3.2.2,

- sectiunile transversale ale elementelor de otel satisfac EN 1993-1-1, 5.6 si

- nodurile sint capabile sa sustina momentele plastice capabile pentru a asigura o suficienta

capacitate la rotire.

(2) In grinzile si stalpii cladirilor, in mod normal, nu este necesar sa se considere efectele plastifierii alternate.

(3)P Acolo unde este folosit calculul plastic-rigid global, la fiecare articulatie plastica:

a) sectiunea transversala a armaturii rigide sa fie simetrica fata de un plan paralel cu planul

inimii sau inimilor;

b) proportiile si legaturile elementelor de otel trebuie astfel alese incat flambajul lateral cu

torsiune sa nu apara;

c) legaturi laterale ale talpii comprimate trebuiesc prevazute la toate articulatiile la care poate

sa apara rotirea plastica sub orice caz de incarcare;

d) capacitatea de rotire va fi suficienta, atunci cand se tine cont de compresiunea axiala din

element sau nod, pentru a permite rotirea necesara a articulatiei si

e) acolo unde cerintele de rotatire nu sint calculate, toate elementele continand articulatii

plastice vor avea sectiuni transversale de Clasa 1 in zona articulatiilor plastice

(4) In grinzile compozite ale cladirilor, capacitatea de rotire poate fi considerata ca fiind suficienta atunci cand:

a) marca de otel nu depaseste S355,

b) contributia betonului inglobat in compresiune este neglijata cand se calculeaza momentul

capabil de calcul,

c) toate sectiunile transversale din zona articulatiilor plastice sint in Clasa 1; si oricare din

celelalte sectiuni transversale sint in Clasa 1 sau 2,

d) fiecare nod grinda-stalp a fost aratat ca are o capacitate de calcul la rotire suficienta, sau sa

aiba un moment capabil de calcul de cel putin 1,2 ori mai mare decat momentul capabil

plastic de calcul al grinzii,

e) deschideri adiacente nu difera in lungime mai mult de 50% din cea mai mica deschidere

f) deschiderile de capat nu depasesc 115% din lungimea deschiderilor adiacente

g) in orice deschidere in care mai mult de jumatate din incarcarea totala de calcul pentru acea

deschidere se concentreaza pe o lungime de 1/5 din deschidere, atunci in orice zona a

articulatiei plastice unde planseul de beton este in compresiune, nu trebuie sa fie in compresiune mai mult de 15% din inaltimea elementului; aceasta nu se aplica si atunci cand se arata ca articulatia va fi cea din urma care se va forma in acea deschidere si

h) talpa de otel in compresiune este legata lateral in zona articulatiei plastice.

(5) Doar daca nu se verifica in alt fel, ar trebui considerat ca stalpii compoziti nu au capacitati de rotire.

(6) Acolo unde sectiunea transversala a unui element de otel variaza in lungul lungimii, se aplica EN 1993-1-1, 5.6(3).

(7) Acolo unde legaturi sint cerute prin (3)(c) sau 4(h), ele ar trebui amplasate astfel incat distanta in lungul elementului de la articulatiile plastice la legaturi sa nu depaseasca jumatate din inaltimea sectiunii de metal.

5.5 Clasificarea sectiunilor transversale

5.5.1 Generalitati

(1)P Sistemul de clasificare definit in EN 1993-1-1, 5.5.2 se aplica sectiunilor transversale ale grinzilor compozite.

(2) O sectiune compozita trebuie sa fie clasificata conform clasei cea mai defavorabila ale elementelor de otel comprimate. Clasa unei sectiuni compozite depinde in mod normal de directia momentului incovoietor in acea sectiune.

(3) Un element comprimat de otel rezemat prin alipirea lui la un element de beton poate fi plasat intr-o clasa mai favorabila, cu conditia ca imbunatatirea comportarii rezultata sa fie stabilita.

(4) Pentru clasificari, distributia efortului plastic trebuie folosita cu exceptia zonelor dintre Clasele 3 si 4, unde distributia elastica a eforturilor trebuie folosita luand in considerare etapele de construire si a efectelor curgerii lente si a contractiei. Pentru clasificare, valorile de calcul ale rezistentelor materialelor trebuiesc folosite. Betonul intins trebuie neglijat. Distributia eforturilor trebuie determinata pentru sectiunea transversala bruta a inimii de metal si a talpilor.

(5) Pentru sectiuni transversale din Clasa1 si 2 cu bare intinse, armatura folosita pe latimea sectiunii trebuie sa apartina clasei de ductilitate B sau C, vezi EN 1992-1-1, Tabelul C.1. In plus pentru o sectiune al carui moment capabil este determinat conform 6.2.1.2, 6.2.1.3 sau 6.2.1.4, trebuie prevazuta o arie minima de armatura A_s pe latimea activa a talpii de beton astfel incat sa fie satisfacuta urmatoarea conditie:

cu:

unde:

A_c este aria activa a talpi de beton;

f_y este valoarea nominala a rezistentei la curgere a armaturii rigide in N/mm²;

f_sk este rezistenta caracteristica la curgere a armaturii;

f_ctm  este rezistenta medie la intindere a betonului, vezi EN 1992-1-1, Tabelul 3.1 sau

Tabelul 11.3.1;

k_c este un coeficient dat in 7.4.2;

d este egal cu 1,0 pentru sectiuni transversale din Clasa 2, si egal cu 1,1 pentru sectiuni

transversale din Clasa 1, sectiuni in care se produc rotiri ale articulatiilor plastice.

(6) Plasele sudate nu trebuiesc incluse in sectiunea activa doar daca nu a fost demonstrat ca au suficienta ductilitate, cand se folosesc in plansee de beton, pentru a se evita ruperea.

(7) In calculul global pentru etapele de construire, trebuie luata in considerare clasa sectiunii de otel in etapa considerata.

5.5.2 Clasificarea sectiunilor compozite fara inglobare cu beton

(1) O talpa metalica comprimata impiedicata sa flambeze prin alipirea lui la o talpa de beton prin conectori de forfecare poate fi considerata ca facand parte din Clasa 1 daca distantele dintre conectori sint conform 6.6.5.5.

(2) Clasificarea celorlalte talpi de metal si inimi comprimate din grinzi compozite fara inglobare cu beton trebuie sa fie in conformitate cu EN 1993-1-1, Tabelul 5.2. Un element care nu satisface limitele de incadrare in Clasa 3 trebuie incadrat in Clasa 4.

(4) Sectiuni transversale care au inimi in Clasa 3 si talpi in Clasele 1 sau 2 pot fi tratate ca o sectiune activa din Clasa 2 cu o inima activa in conformitate cu EN 1993-1-1, 6.2.2.4.

5.5.3 Clasificarea sectiunilor compozite avand inglobare cu beton

(1) O talpa de otel a unei sectiuni compozite avand inglobare cu beton in conformitate cu pct. (2) de mai jos poate fi clasificata in conformitate cu Tabelul 5.2.

(2) Pentru inima unei sectiuni inglobate cu beton, betonul care este inglobat trebuie sa fie armat, legat mecanic de sectiunea de metal, si sa fie capabil sa previna flambajul inimii si al oricarei parti a talpii comprimate catre inima. Trebuie considerat ca cerintele de mai sus sint satisfacute daca:

a) betonul care inglobeaza inima este armat cu bare longitudinale si etrieri, si /sau plasa sudata,

b) cerintele pentru raportul b_c/b date in Tabelul 5.2 sint indeplinite,

c) betonul dintre talpi este fixat de inima in conformitate cu Figura 6.10 prin sudarea etrierilor de inima sau cu bare de 6 mm diametru prin gauri si/sau dornuri cu un diametru mai mare decat 10mm sudate de inima si

d) distantarea longitudinala a dornurilor pe fiecare fata a inimii sau a barelor prin gauri nu este mai mare de 400 mm. Distanta dintre fata interna a fiecarei talpi si cel mai apropiat rand de piese nu este mai mare decat 200mm. Pentru sectiuni de metal la care inaltimea minima este de cel putin 400mm si doua sau mai multe randuri de piese, o aranjare alternanta a dornurilor si/sau a barelor prin gauri poate fi folosita.

(3) O inima de otel din Clasa 3 incastrata in beton in conformitate cu pct.(2) de mai sus poate fi reprezentata printr-o inima activa cu aceeasi sectiune transversala din Clasa 2.

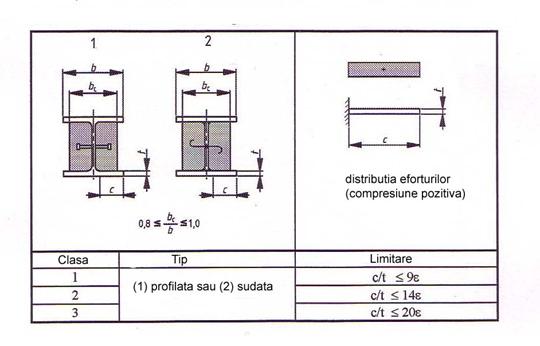
Capitolul 6 Stari limita ultime

Grinzi

Grinzi pentru cladiri

(1)P Grinzile compozite sunt definite in 1.5.2. Tipurile de sectiuni ale grinzilor compozite cu placi de beton armat sau compozite sunt aratate in Figura 6.1. Grinzile compozite cu inglobare partiala in beton armat sunt grinzile la care inima sectiunii de otel este inglobata in beton armat iar intre componentele de beton armat si otel se prevad conectori.

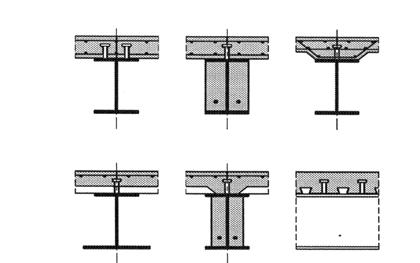
Figura 6.1 Tipuri de sectiuni compozite

(2) Eforturile sectionale capabile de calcul la incovoiere si /sau la forta taietoare verticala se vor determina in conformitate cu 6.2 pentru grinzi compozite cu sectiuni din otel fara inglobare in beton armat si cu 6.3 pentru grinzi compozite cu sectiuni din otel cu inglobare partiala in beton

(3)P In cazul grinzilor compozite se vor verifica capacitatile de :

rezistenta a sectiunilor critice (6.2 si 6.3);

rezistenta la flambaj prin torsiune laterala (6.4);

rezistenta la flambajului la forta taietoare (6.2.2.3) si la forte transversale aplicate inimii (6.5);

rezistenta la lunecare longitudinala (6.6);

(4)P Sectiunile transversale critice sunt :

sectiunile de moment incovoietor maxim pozitiv ;

sectiunile de reazem;

sectiunile supuse la forte sau reactiuni concentrate;

puncte in care are loc o modificare brusca a sectiunii alta decat cea datorata fisurarii betonului;

(5) O sectiune care se modifica brusc se va considera critica in cazul in care raportul intre momentul capabil maxim si cel minim este mai mare de 1,2.

(6) Pentru verificarea capacitatii de rezistenta la lunecare longitudinala, lungimea critica reprezinta lungimea interfatei intre doua sectiuni critice.Pentru aceasta verificare sectiunile critice pot fi si:

capetele libere ale consolelor;

in cazul grinzilor cu sectiune variabila, sectiunile se aleg astfel incat raportul dintre momentele capabile plastice (la incovoiere dupa aceeasi directie) a oricaror sectiuni adiacente sa nu depaseasca 1,5.

(7)P Notiunile de „conectare totala” si de „conectare partiala” se aplica numai grinzilor la care capacitatea de rezistenta la incovoiere a sectiunilor critice se determina folosind calculul plastic.

O deschidere a unei grinzi, sau a unei console, are o conectare totala in cazul in care majorarea numarului de conectori nu conduce la marirea rezistentei la incovoiere a elementului.In celelalte cazuri conectarea se considera partiala.

NOTA – Limitele utilizarii conectarii partiale sunt date in 6.6.1.2.

Latimea efectiva a placii pentru verificarea sectiunilor transversale

(1) Latimea efectiva a placii din beton pentru verificarea sectiunilor transversale se va determina in conformitate cu 5.4.1.2 tinandu-se cont de distributia latimii efective intre zonele de reazem si zonele din camp.

2) In cazul cladirilor se poate considera o latime efectiva constanta pe toata zona de moment pozitiv a fiecarei deschideri. Aceasta valoare poate fi considerata egala cu valoarea b_eff,1 din mijlocul deschiderii. Aceeasi ipoteza se aplica pe intreaga zona de moment negativ de o parte si de alta a unui reazem intermediar. Aceasta valoare se poate lua cu valoarea b_eff,2 de pe reazemul respectiv.

Eforturile sectionale capabile ale grinzilor compozite

Momentul capabil la incovoiere

Generalitati

(1)P Momentul capabil de calcul la incovoiere se va determina pe baza unui calcul rigid-plastic numai in cazul in care sectiunea compozita este in Clasa 1 sau 2 si nu se folosesc armaturi pretensionate.

(2) Calculul elastic si neliniar al momentului capabil la incovoiere se poate aplica sectiunilor de orice clasa.

(3) Pentru calculul elastic si neliniar se considera ca sectiunea transversala compozita ramane plana daca conectarea si armatura transversala se proiecteaza in conformitate cu 6.6 considerand distributiile cele mai judicioase ale fortei de lunecare longitudinale de calcul.

(4)P Rezistenta la intindere a betonului se va neglija in calcul.

(5) In cazul in care sectiunea de otel a elementului compozit este curba in plan , se va tine cont de efectele curburii .

Momentul capabil plastic M_pl,Rd al unei sectiuni compozite

(1) In calculul M_pl,Rd se vor considera urmatoarele ipoteze:

a)      exista o interactiune totala intre otelul structural , armatura si beton;

b)      sectiunea efectiva de otel este solicitata la rezistenta ei de calcul la curgere f_yd din intindere sau compresiune;

c)      ariile efective ale armaturii longitudinale intinse sau comprimate sunt solicitate la rezistenta de calcul la intindere sau compresiune;

d)      aria efectiva de beton comprimata rezista la un efort unitar de 0,85f_cd, constant pe toata inaltimea zonei comprimate, unde f_cd, este rezistenta cilindrica de calcul la compresiune a betonului.

Distributiile caracteristice ale eforturilor unitare in domeniul plastic sunt indicate in Figura 6.2.

Figura 6.2 : Exemple de distributii plastice ale eforturilor unitare in cazul unei grinzi compozite cu placa din beton armat si conectare totala la moment incovoietor pozitiv si negativ

(2) Pentru sectiuni compozite din otel structural S420 sau S460 ,in cazul in care inaltimea zonei comprimate a placii depaseste 15% din inaltimea totala a elementului, momentul capabil de calcul M_Rd se va considera βM_pl,Rd unde β este factorul de reducere indicat in Figura 6.3. Pentru valori

x_pl /h mai mari decat 0.4 , momentul capabil la incovoiere se va determina din 6.2.1.4 sau 6.2.1.5.

(3) In cazul calculului rigid-plastic, armatura intinsa va respecta conditiile din 5.5.1(5)

(4)P In cazul cladirilor, tabla cutata din zona comprimata a sectiunii se va neglija in calcul.

(5) In cazul cladirilor, tabla cutata din zona intinsa a sectiunii efective se considera solicitata la rezistenta de curgere de calcul f_yp,d.

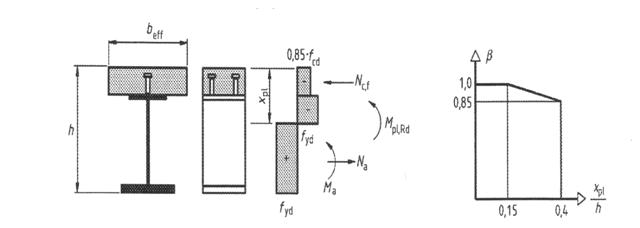
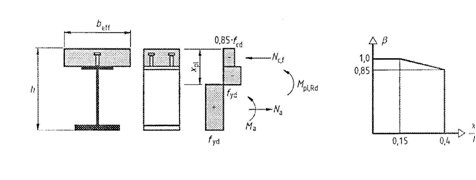
Figura 6.3 Coeficientul de reducere β pentru M_pl,Rd

Momentul capabil plastic al sectiunilor cu conectare partiala

(1) In zonele de moment pozitiv ale grinzilor compozite se poate folosi conectarea partiala in conformitate cu 6.6.1 si 6.6.2.2.

(2) In cazul in care nu se apeleaza la alte metode mai exacte momentul capabil plastic negativ se va determina conform 6.2.1.2 iar conectarea se va dimensiona pentru a asigura curgerea armaturii intinse .

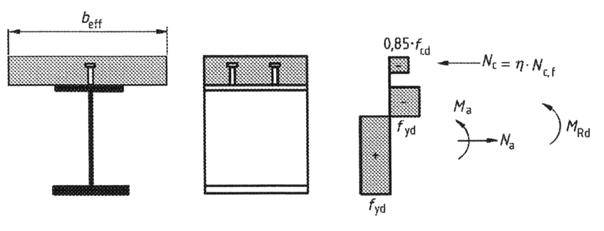
Figura 6.4 Distributia plastica a eforturilor unitare in cazul incovoierii pozitive si a conectarii partiale

(3) Momentul capabil al sectiunii critice a grinzii M_Rd se va determina in cazul conectorilor ductili printr-un calcul rigid plastic conform cu 6.2.1.2, considerand insa o valoare redusa a fortei de compresiune din beton N_c in locul fortei N_cf data de 6.2.1.2(1)(d). Raportul η = N_c/N_cf reprezinta gradul de conectare. Pozitia axei neutre din placa va fi determinata de noua forta N_c , vezi Figura 6.4. Cea de a doua axa neutra din sectiunea de otel poate fi folosita pentru clasificarea inimii.

Legenda

1 calcul plastic

2 metoda simplificata

Figura 6.5 Relatia intre M_Rd si N_c (in cazul conectorilor ductili)

(4) Relatia intre M_Rd si N_c data in (3) este exprimata cantitativ de curba convexa ABC din Figura 6.5 unde M_pl,a,Rd si M_pl,_Rd sunt momentele capabile plastice la incovoiere pozitiva numai a sectiunii din otel si respectiv a sectiunii compozite cu conectare totala.

(5) Prin metoda data in(3) , se poate obtine o valoare acoperitoare pentru M_Rd folosind variatia liniara AC din Figura 6.5 :

M_Rd = M_pl,a,Rd + (M_pl,Rd – M_pl,a,Rd ) (6.1)

6.2.1.4 Momentul capabil neliniar la incovoiere

(1)P In cazul in care momentul capabil la incovoiere al sectiunii compozite se determina printr-un calcul neliniar, se vor lua in considerare relatiile efort unitar -deformatii specifice ale materialelor.

(2) Se va presupune ca sectiunea compozita ramane plana si ca deformatia specifica a armaturilor intinse si comprimate este aceeasi cu cea medie a betonului inconjurator cu care conlucreaza.

(3) Eforturile unitare din betonul comprimat se va determina din curbele efort unitar -deformatie specifica date in EN 1992-1-1,3.1.7.

(4) Eforturile unitare din armatura se vor determina din diagramele biliniare date in EN 1992-1-1,3.2.7.

(5) Eforturile unitare din otelul structural comprimat sau intins se vor determina din diagramele biliniare date in EN1993-1-1,5.4.3(4) tinandu-se cont si de modul de executie (cu sau fara sprijiniri).

(6) Pentru sectiuni compozite de Clasa 1 si 2 cu placa de beton comprimata, momentul capabil neliniar la incovoiere M_Rd se va determina functie de forta de compresiune din beton N_c utilizand relatiile simplificate (6.2) si (6.3) si asa cum este aratat in Figura 6.6:

M_Rd = M_a,Ed + (M_el,Rd – M_a,Ed ) pentru N_c ≤ N_c,el (6.2)

M_Rd = M_el,Rd + (M_pl,Rd – M_el,Rd ) pentru N_c,el ≤ N_c ≤ N_c,f (6.3)

cu:

M_el,Rd = M_a,_Ed + k M_c,Ed (6.4)

unde:

M_a,Ed este momentul incovoietor de calcul aplicat sectiunii de otel inainte de faza compozita;

M_{c,E d} este momentul incovoietor aplicat sectiunii compozite;

k este factorul pentru atingerea efortul unitar limita conform 6.2.1.5(2); in cazul unei executii fara sprijiniri , se va tine cont de etapele de executie;

N_c,_el este forta de compresiune din placa de beton corespunzatoare momentului M_el,Rd.

Pentru sectiuni la care se aplica 6.2.1.2 (2), in expresia (6.3) si in Figura 6.6 se va inlocui M_pl,Rd cu valoarea redusa β M_pl,Rd.

(7) In cazul cladirilor M_el,Rd se poate determina simplificat utilizind 5.4.2.2(11).

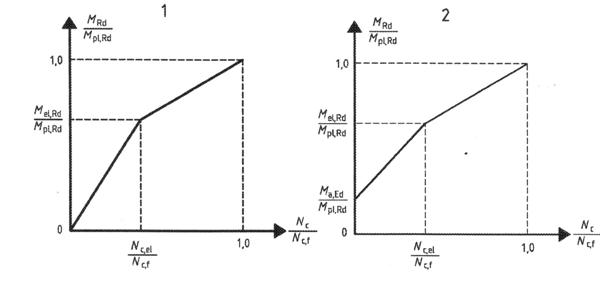
Legenda

1 executie cu sprijininiri

2 executie fara sprijiniri

Figura 6.6 Relatia simplificata intre M_Rd si N_c pentru sectiuni cu placa din beton comprimata

6.2.1.5 Momentul capabil elastic la incovoiere

(1) Eforturile unitare se vor calcula prin metoda elastica, utilizand latimea efectiva a talpii din beton in conformitate cu 6.1.2. Pentru sectiunile din Clasa 4 , se va determina sectiunea efectiva de otel conform EN 1993-1-5,4.3.

(2) In calculul momentului capabil elastic la incovoiere pentru sectiunea efectiva , eforturile unitare limita se vor considera:

- f_cd in betonul comprimat;

- f_yd in otelul structural intins sau comprimat

- f_sd in armatura intinsa sau comprimata. Armatura comprimata din placa se poate neglija .

(3)P Eforturile unitare rezultate din actiunile aplicate numai asupra structurii din otel se vor adauga eforturilor unitare din faza compozita.

(4) Daca nu se utilizeaza o metoda mai exacta , efectul curgerii lente se va considera in calcul prin utilizarea coeficientului de echivalenta in conformitate cu 5.4.2.2.

(5) La sectiuni la care betonul intins se considera fisurat, eforturile datorate efectelor initiale (izostatice) ale contractiei pot fi neglijate.

Forta taietoare verticala capabila

Domeniul de aplicare

Paragraful 6.2.2 se aplica grinzilor compozite cu sectiunea din otel laminata sau sudata cu inima plina, care poate fi rigidizata.

Forta taietoare verticala capabila plastica

(1) Forta taietoare verticala capabila V_pl,Rd se va lua egala cu forta taietoare capabila a sectiunii din otel V_pl,a,Rd cu exceptia cazului in care se determina valoarea contributiei la forta taiatoare a componentei din beton armat.

(2) Forta taietoare capabila plastica V_pl,a,Rd a sectiunii din otel se va calcula in conformitate cu EN 1993-1-1,6.2.2.

Forta taietoare capabila la flambaj

(1) Forta taietoare capabila la flambaj V_b,Rd a unei inimi de otel fara inglobare in beton se va determina conform EN 1993-1-1,6.2.6

(2) Contributia placii din beton nu se ia in considerare decat in cazul in care se utilizeaza o metoda de calcul mai exacta decat cea din EN 1993-1-5,5 si se dimensioneaza conectarea de lunecare la forta verticala respectiva.

Incovoierea cu forta taietoare verticala

(1) In cazul in care forta taietoare verticala V_Ed depaseste jumatate din forta taietoare capabila V_Rd

data de valoarea minima intre V_pl,Rd din 6.2.2.2 si V_b,Rd din 6.2.2.3, se va tine cont de influenta fortei taietoare asupra momentului capabil.

(2) Pentru sectiuni de Clasa 1 sau 2, influenta fortei taietoare verticale asupra momentului capabil la incovoiere se va considera printr-o reducere a rezistentei de calcul a otelului inimii (1-ρ) f_y asa cum se arata in Figura 6.7 unde:

ρ = (2V_Ed / V_Rd – 1)² (6.5)

si V_rd este forta taietoare capabila respectiva , determinata conform 6.2.2.2 sau 6.2.2.3.

(3) Pentru sectiuni in Clasa 3 sau 4, se aplica EN 1993-1-5, 7.1 folosind eforturile unitare calculate pentru sectiunea compozita.

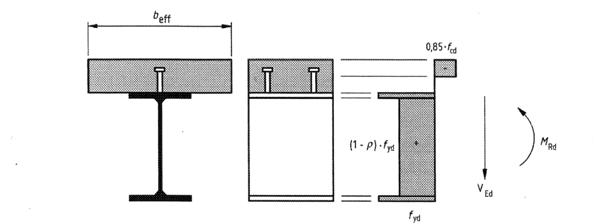
Figura 6.7 : Distributia eforturilor unitare plastice modificate de efectul fortei taietoare verticale

6.3 Eforturi sectionale capabile ale grinzilor compozite cu inglobare partiala in beton a sectiunii din otel

6.3.1 Domeniul de aplicare

(1) Grinzile din otel cu inglobare partiala in beton au fost definite in 6.1.1(1).Din sectiunea efectiva a unei grinzi compozite cu inglobare partiala poate sa faca parte si o placa din beton armat sau compozita conectata de sectiunea de otel . Tipurile de sectiuni de otel cu inglobare partiala sunt aratate in Figura 6.8.

(2) Articolul 6.3 se aplica sectiunilor cu inglobare partiala de Clasa 1 sau 2 in conditiile in care se asigura ca raportul d/t_w nu este mai mare decat 124ε .

Figura 6.8 : Tipuri de sectiuni de grinzi din otel cu inglobare partiala in beton

(3) In cazul in care nu sunt date alte precizari in 6.3, se aplica prevederile generale din EN 1994-1-1

6.3.2 Momentul capabil la incovoiere

(1) Intre sectiunea de otel si betonul ce inglobeaza inima se va asigura o conectare totala conform 6.6.

(2) Momentul capabil la incovoiere se va determina printr-un calcul plastic. Armatura comprimata din betonul de inglobare se poate neglija. In Figura 6.9 sunt aratate cateva exemple de tipuri de distributii plastice de eforturi unitare .

(3) Pentru determinarea compresiunii in placile din beton armat sau compozite care fac parte din sectiuni efective compozite se poate utiliza conectarea partiala.

(4) In cazul conectarii partiale cu conectori ductili, momentul capabil plastic al grinzii se va calcula conform 6.3.2.(2) si 6.2.1.2.(1), dar cu utilizarea unei valori reduse a fortei de compresiune in placa din beton sau compozita N_c ca in 6.2.1.3(3),(4) si (5).

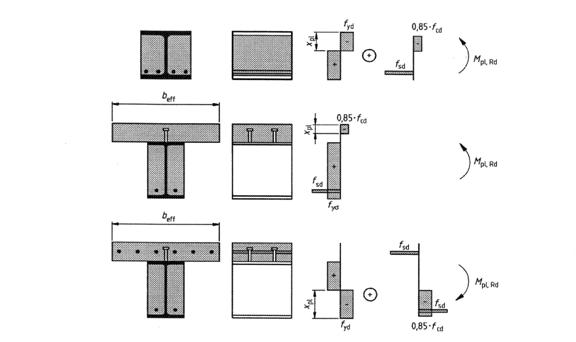
Figura 6.9 : Exemple de distributii plastice pentru sectiuni efective

6.3.3 Forta taietoare verticala capabila

(1) Forta taietoare verticala capabila a sectiunii din otel V_pl,a,Rd se va determina printr-un calcul plastic conform 6.2.2.2(2).

(2) Contributia betonului armat ce inglobeaza inima va fi luata in calcul la determinarea fortei taietoare capabile a sectiunii daca se utilizeaza etrieri ca in Figura 6.10. Intre betonul de inglobare si sectiunea din otel se va prevede o conectare corespunzatoare.Daca etrierii betonului de inglobare sunt deschisi , se vor suda la intreaga capacitate de rezistenta de inima. In celelalte situatii se va neglija contributia etrierilor la forta taietoare.

(3) Daca nu se utilizeaza un calcul mai exact, distributia fortei taietoare totale V_Ed intre V_a,Ed care actioneaza asupra sectiunii din otel si respectiv V_c,Ed care actioneaza asupra betonului armat de inglobare, se considera in aceeasi proportie cu distributia intre cele doua componente a momentului capabil la incovoiere M_pl,Rd.

(4) Forta taietoare capabila a betonului armat ce inglobeaza inima va tine cont de fisurarea betonului si se va verifica conform EN 1992-1-1,6.2 si a altor cerinte corespunzatoare din acest Standard.

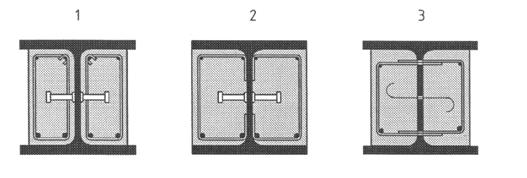
Legenda

1 etrieri inchisi

2 etrieri deschisi sudati de inima

3 etrieri care trec prin inima

Figura 6.10 ; Dispozitia etrierilor

6.3.4 Incovoierea cu forta taietoare verticala

(1) In cazul in care forta taietoare de calcul a sectiunii de otel V_a,Ed este mai mare decat jumatate din forta taietoare capabila plastica V_pl,a,Rd , se va tine cont de efectul acesteia asupra momentului capabil plastic la incovoiere.

(2) Influenta fortei taietoare asupra momentului capabil la incovoiere va fi exprimata ca in 6.2.2.4(2) cu urmatoarele modificari. In relatia (6.5) , pentru a calcula reducerea rezistentei otelului in zona inimii se va inlocui raportul V_Ed/V_pl,Rd cu V_a,Ed /V_pl,Rd . Dupa aceasta inlocuire , momentul capabil redus se va calcula conform 6.3.2.

Flambajul prin incovoiere si rasucire laterala a grinzilor compozite

6.4.1 Generalitati

(1) O talpa a unei grinzi de otel solidarizata conform 6.6 prin conectori de o placa de beton sau compozita se considera stabila lateral daca se impiedica instabilitatea laterala a placii din beton.

(2) Toate celelalte talpi comprimate se vor verifica la stabilitate laterala.

(3) Pentru sectiunea de otel se vor aplica metodele din EN 1993-1-1,6.3.2.1-6.3.2.3 si in general din 6.3.4. considerand eforturile sectionale care se aplica sectiunii compozite , si efectul secventei de executie conform 5.4.2.4,

(4) In cazul grinzilor compozite ale cladirilor cu sectiuni transversale in Clasa 1,2,3 ,constante pe lungimea grinzii, se va folosi metoda data in 6.4.2.

6.4.2 Verificarea la flambaj prin incovoiere si rasucire laterala a grinzilor compozite continue cu sectiuni transversale in Clase 1 , 2 si 3.

(1) Momentul capabil de flambaj prin deversare laterala in cazul grinzilor compozite continue (sau in cazul unei grinzi de cadru compozita pe toata lungimea ei) cu o sectiune transversala constanta in Clasa 1,2 sau 3 se va considera:

M_b,Rd = χ_LT M_Rd (6.6)

unde:

χ_LT este factorul de reducere pentru flambajul prin deversare laterala care depinde de

zveltetea relativa

M_Rd este momentul capabil la incovoiere negativa pe reazemul intermediar respectiv ( sau la nodul grinda -stalp)

Valorile factorului de reducere χ_LT se pot obtine din EN 1993-1-1,6.3.2.2 sau 6.3.2.3.

(2) Pentru sectiuni transversale de Clasa 1 sau 2, momentul M_Rd se va determina conform 6.2.1.2 pentru grinzi a caror moment capabil la incovoiere se bazeaza pe un calcul plastic, conform 6.2.1.4 pentru grinzi a caror moment capabil la incovoiere se bazeaza pe un calcul neliniar , sau conform 6.3.2 pentru grinzi cu inglobare partiala in beton, f_yd se determina utilizand coeficientul partial de siguranta γ_M1 dat in EN 1993-1-1,6.1(1).

(3) Pentru sectiuni transversale de Clasa 3, M_Rd se va determina utilizand relatia (6.4) , respectiv ca momentul capabil elastic minim care determina fie atingerea efortul unitar de intindere f_sd in armatura, sau a efortului unitar de compresiune f_yd in fibra inferioara extrema a sectiunii din otel ; f_yd se va determina utilizand coeficientul partial de siguranta γ_M1 dat in EN 1993-1-1,6.1(1).

(4) Zveltetea relativa se va calcula cu relatia:

= (6.7)

unde:

M_Rk este momentul capabil al sectiunii compozite calculat cu rezistente caracteristice;

M_cr este momentul critic elastic pentru flambaj prin deversare laterala determinat pe reazemul intermediar in care momentul este cel mai mare.

(5) In cazul in care aceeasi placa este conectata de una sau mai multe grinzi de otel aproximativ paralele cu grinda compozita considerata si sunt indeplinite conditiile 6.4.3(c),(e) si (f), la calculul momentului critic elastic M_cr se va folosi modelul „cadrului U continuu invers „ ce se formeaza. Acest model considera ,asa cum se arata in Figura 6.11 , deplasarea laterala a talpii inferioare care conduce la incovoierea inimii si la o rotire a talpii superioare careia i se opune incovoierea placii din beton armat.

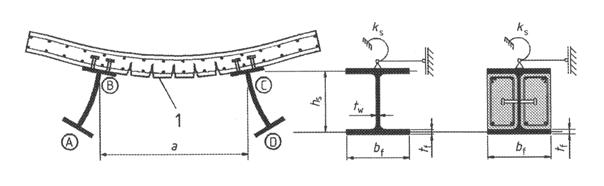
Legenda

1 fisuri

Figura 6.11 : Cadrul U invers rezistent la flambajul prin torsiune laterala

(6) Pentru modelul cadrului U, pentru rigiditatea la torsiune a grinzii de otel pe unitatea de lungime k_s , la nivelul talpii superioare a sectiunii de otel , se considera urmatoarea relatie:

k_s = (6.8)

unde:

k₁ este rigiditatea la incovoiere a placii fisurate din beton armat sau compozite pe directia transversala grinzii , care se va considera:

k₁ = α (EI)₂/ a (6.9)

in relatia lui k₁ , α = 2 in cazul unei grinzi marginale , cu sau fara consola , si α = 3 pentru o grinda interioara. In cazul un planseu cu 4 sau mai multe grinzi paralele, se

va considera pentru o grinda interioara α = 4.

a este distanta intre grinzile paralele

k₂ este rigiditatea la incovoiere a inimii de otel, care se va considera:

k₂ = (6.10)

pentru o grinda de otel fara inglobare in beton

unde:

ν_a este coeficientul lui Poisson pentru otel , h_s si t_w sunt definite in Figura 6.11

(7) Pentru o grinda de otel cu inglobare partiala in beton conform 5.5.3(2), rigiditatea la incovoiere k₂ va tine cont de inglobare si se va calcula cu:

k₂ = (6.11)

unde:

n este coeficientul de echivalenta pentru efecte de lunga durata in conformitate cu 5.4.2.2, si

b_c este latimea inglobarii de beton, vezi Figura 6.8

(8) In modelul de cadru-U invers , se va tine cont in calculul lui M_cr de efectul favorabil al rigiditatii la torsiune Saint Venant G_aI_at al sectiunea de otel ,

(9) Pentru o grinda cu inglobare partiala in beton armat fie cu etrieri deschisi sudati de inima , fie cu etrieri inchisi, la rigiditatea de torsiune a grinzii de otel se adauga rigiditatea inglobarii. Aceasta rigiditate la torsiune suplimentara se va considera G_c I_ct /10 unde G_c este modului de deformatie al betonului care se va considera 0,3E_a/n ( unde n este coeficientul de echivalenta pentru efecte de lunga durata), iar I_ct este constanta Saint Venant la torsiune a inglobarii de beton , considerand-o nefisurata si de latime egala cu latimea totala a inglobarii.

6.4.3 Verificarea simplificata fara calcul

(1) O grinda continua (sau o grinda de cadru care este compozita pe toata lungimea ei) de sectiune transversala de Clasa 1, 2 sau 3 se va proiecta fara contrafise laterale daca sunt satisfacute urmatoarele conditii:

a)      Lungimea deschiderilor alaturate nu difera mai mult de 20% din deschiderea minima.Cand exista o consola , lungimea ei nu depaseste cu mai mult de15% lungimea deschiderii adiacente.

b)      Incarcarea pe fiecare deschidere este uniform distribuita, si incarcarea permanenta de calcul depaseste 40% din incarcarea totala.

c)      Talpa superioara a elementului de otel este conectata la o placa din beton armat sau compozita conform 6.6.

d)      Aceeasi placa este de asemenea conectata la alta grinda suport aproximativ paralela cu grinda compozita considerata, pentru a forma un cadru U invers asa cum este ilustrat in Figura 6.11.

e)      Daca placa este compozita, ea reazema intre cele doua elemente ale cadrului U inversat considerat.

f)        La fiecare reazem al grinzii de otel, talpa inferioara este impiedicata lateral si inima ei este rigidizata. In celelalte zone inima grinzii poate ramane nerigidizata.

g)      Daca elementul de otel are o sectiune transversala IPE sau HE fara inglobare in beton si inaltimea ei nu depaseste limitele date in Tabelul 6.1.

h)      Daca grinda de otel are inglobare partiala in beton conform 5.5.3(2) si inaltimea ei h nu depaseste cu mai mult de 200mm pentru otel de pana la S355 si cu mai mult de 150mm pentru otel S420 si S460 limitele date in tabelul 6.1.

Nota: Prevederile pentru alte tipuri de sectiuni de otel vor fi incluse in Anexe Nationale

Tabelul 6.1 : Inaltimea maxima pentru elemente de otel fara inglobare in beton pentru care se aplica paragraful 6.4.3.

6.5 Forte transversale aplicate inimilor

6.5.1 Generalitati

(1) Regulile date in EN 1993-1-5, 6 pentru determinarea rezistentei de calcul ale inimilor rigidizate sau nerigidizate solicitate la forte transversale prin intermediul talpii se aplica si in cazul talpilor necompozite, si in zonele adiacente ale inimii ale grinzilor compozite.

(2) Daca forta transversala actioneaza in combinatie cu o incovoiere cu forta axiala, rezistenta va fi verificata conform EN 1993-1-5, 7.2.

(3) La un reazem intermediar al unei grinzi cu o inima in Clasa 2 in conformitate cu 5.5.2(3), vor fi prevazute rigidizari transversale cu exceptia cazului in care s-a verificat ca inima nerigidizata are suficienta rezistenta la voalare si flambaj.

6.5.2 Voalarea inimilor indusa de talpi

(1) Pentru voalarea inimii se aplica EN 1993-1-5,8 in care aria A_fc se considera egala cu valoarea minima dintre aria talpii necompozite si aria echivalenta de otel a talpii compozite considerand coeficientul de echivalenta pentru incarcari de scurta durata.

6.6 Conectarea la lunecare

6.6.1 Generalitati

6.6.6.1 Bazele proiectarii

(1) Articolul 6.6 se aplica grinzilor compozite si dupa caz si altor elemente compozite.

(2)P Pentru preluarea lunecarii longitudinale dintre beton si otelul structural se vor prevede conectori de lunecare si armatura transversala si se va ignora efectul aderentei naturale intre cele doua componente.

(3)P Conectorii de lunecare vor avea suficienta capacitate de deformatie pentru a asigura orice redistributie a fortelor de luncare considerate in calcul.

(4)P Conectorii de lunecare ductili sunt conectorii cu suficienta capacitate de deformare care sa justifice comportarea ideal plastica a conexiunii in structura considerata.

(5) Un conector de lunecare se poate considera ductil daca capacitatea caracteristica de deformatie de lunecare δ_uk este cel putin 6mm

Nota : O evaluare a δ_uk este data in Anexa B

(6)P Cand pentru aceeasi deschidere a unei grinzi se vor folosi doua sau mai multe tipuri de conectori de lunecare se va tine cont de orice diferenta semnificativa in proprietatile lor de incarcare-deformatie de lunecare.

(7)P Conectorii de lunecare trebuie sa fie capabili sa previna separarea elementului de beton de cel de otel cu exceptia cazurilor in care separarea este impiedicata prin alte mijloace.

(8) Pentru a preveni separea placii , conectorii de lunecare vor fi dimensionti sa reziste la o forta ultima de intindere perpendiculara pe planul talpii de otel , de cel putin 0.1ori capacitatea ultima de rezistenta la lunecare a conectorului. Daca este necesar conectorii de lunecare vor fi prevazuti cu dispozitive de ancorare suplimentare.

(9) Conectorii de lunecare tip dornuri cu cap conform 6.6.5.7 se considera ca asigura rezistenta la desprindere, daca conectorul nu sunt solicitati la intindere directa.

(10)P Se va evita lunecarea longitudinala si despicarea placii de beton determinata de fortele concentrate aplicate de conectori,

(11) Conditia de la 6.6.1.1.(10) este satisfacuta daca detalierea conectarii este in conformitate cu prevederile din 6.6.5 si armatura transversala in conformitate cu 6.6.6.

(12) In cazul in care se utilizeaza o alta metoda de conectare intre elementul de otel si elementul din beton decit cea cu conectori de lunecare prevazuta in 6.6 ,comportarea considerata in proiectare a acestei conectari se va baza pe teste si va fi sustinuta de un model conceptual. Proiectarea elementului compozit in acest caz se va conforma proiectarii unui element similar care utilizeaza conectori de lunecare ca in 6.6 proiectare uzuala in prezent.

(13) In cazul cladirilor , numarul de conectori de lunecare trebuie sa fie cel putin egal cu valoarea obtinuta din impartirea fortei de lunecare totala la starea limita ultima , determinta conform cu 6.6.2, la forta de lunecare capabila de calcul a unui conector P_Rd . Pentru conectori de lunecare tip dornuri cu cap , forta capabila de calcul va fi determinata conform relatiei 6.6.3 sau 6.6.4 dupa caz.

(14)P Conectarea partiala poate fi folosita la grinzile cladirilor din Clasa 1 sau 2. Numarul de conectori de lunecare va fi determinat prin teoria conectarii partiale si considerand capacitatea de deformare a conectorilor .

6.6.1.2 Limitele utilizarii in cazul grinzilor compozite a conectarii partiale la lunecare

(1) Dornurile cu cap cu o lungime totala dupa sudura de 4 ori mai mare decat diametrul tijei , si cu o tija de diametru nominal mai mare decat 16mm si mai mic de 25 , se pot considera ca fiind ductili in cadrul urmatoarelor limite ale gradului de conectare, care este definit de raportul η = n / n_f

Pentru sectiuni de otel cu talpi egale :

L_e ≤ 25: η ≥ 1 - ( ) ( 0,75 - 0,03L_e ), η ≥ 0,4 (6.12)

L_e > 25: η ≥ 1 (6.13)

Pentru sectiuni de otel avand talpa inferioara cu o arie de trei ori mai mare decat aria talpii superioare:

L_e ≤ 20: η ≥ 1 - ( ) ( 0,30 - 0,015L_e ), η ≥ 0,4 (6.14)

L_e > 20: η ≥ 1 (6.15)

unde:

L_e este distanta in metri intre punctele de moment zero in zona de moment pozitiv ; pentru grinzi continue curente, L_e se considera a fi cea din Figura 5.1;

n_f este numarul de conectori de lunecare in cazul conectarii totale determinat conform 6.6.1.1(3) si 6.6.2.2(2);pentru lungimea L_e a grinzii

n este numarul de conectori de lunecare prevazut pe aceeasi lungime.

(2) Pentru sectiuni de grinzi avand aria talpii inferioare depasind cu mai putin de trei ori aria talpii superioare , limita pentru η se va determina din expresia (6.12) - (6.15) prin interpolare liniara.

(3) Conectorii de lunecare tip dornuri cu cap pot fi considerati ductili pentru un domeniu mai larg de deschideri decat cele date (1) mai sus daca:

(a)        conectorii dupa sudura au o lungime mai mare decat 76mm si o tija cu diametrul

nominal de 19mm,

(b)       sectiunea transversala de otel I sau H a grinzii este laminata sau sudata si are talpi egale,

(c)        placa compozita are tabla cutata care descarca perpendicular pe grinda si nervurile din beton sunt continue in dreptul grinzii.

(d)       exista cate un conector in fiecare cuta a tablei cutate, plasat in centrul cutei sau

alternativ de o parte si de alta a centrului pe toata lungimea deschiderii.

(e)        pentru tabla cu b₀ / h_p ≥ 2 si h_p ≤ 60 mm, cu notatiile din Figura 6.13 si

(f)         forta N_c se calculeaza cu metoda simplificata data in fig 6.5.

Cand aceste conditii sunt indeplinite , raportul η va satisface cerintele:

L_e ≤ 25: η ≥ 1 - ( ) ( 1 - 0,04L_e ), η ≥ 0,4 (6.16)

L_e > 25: η ≥ 1 (6.17)

Nota: Cerintele din 6.6.1.2 sunt determinate pentru o distributie uniforma a conectorilor.

6.6.1.3 Distantele intre conectorii de lunecare ai grinzilor

(1)P Conectorii de lunecare se vor distribui in lungul grinzii corespunzator cu distributia fortei de lunecare ,astfel incat sa transmita lunecarea longitudinala si sa prevena separarea intre beton si grinda de otel,

(2) La console si in zonele de moment negativ ale grinzilor continue , armatura intinsa se va dispune in conformitate cu distantele intre conectori si va fi corespunzator ancorata.

(3) Conectorii de lunecare ductili se vor distribui uniform pe lungimea dintre sectiunile critice definite in 6.1.1 asigurand ca:

- toate sectiunile critice de pe deschidere sunt in Clasa 1 sau in Clasa 2

- η satisface limitele date in 6.6.1.2 si

- momentul capabil la incovoiere al sectiunii compozite nu depaseste de 2.5 ori momentul capabil plastic al sectiunii de otel

(4) Daca momentul capabil plastic la incovoiere depaseste de 2.5 ori momentul capabil al sectiunii din otel, sunt necesare verificari suplimentare pentru a se determina daca conectarea este adecvata

in punctele situate aproximativ la mijlocul distantei dintre sectiuni critice consecutive .

(5) Numarul necesar de conectori de lunecare pot fi distribuiti in conformitate cu forta de lunecare longitudinala determinata in domeniul elastic pentru incarcarea considerata, intre sectiunea de moment maxim pozitiv si reazemul adiacent sau si sectiunea de moment maxim negativ. In acest caz nu sunt necesare verificari suplimentare ale conectarii.

6.6.2 Forta de lunecare longitudinala in grinzi

6.6.2.1 Grinzi la care eforturile sectionale capabile se calculeaza in domeniul elastic sau neliniar

(1) Daca se aplica calculul elastic sau neliniar , forta de lunecare longitudinala va fi determinata in conformitate cu articolele 6.2.1.4 sau respectiv 6.2.1.5.

6.6.2.2 Grinzi la care eforturile sectionale capabile se calculeaza in domeniul plastic

(1)P Forta de lunecare longitudinala totala se va determina in conformitate cu capacitatea de rezistenta la incovoiere considerand diferenta de forta normala in beton sau in otel pe lungimea critica.

(2) Pentru conectarea totala se fac referiri corespunzatoare in 6.2.1.2, sau 6.3.2.

(3) Pentru conectare partiala se fac referiri corespunzatoare in 6.2.1.3, sau 6.3.2.

6.6.3 Conectori tip dornuri cu cap utilizate in cazul placilor monolite din beton armat sau in betonul armat de inglobare

6.6.3.1 Forta de lunecare capabila de calcul

(1) Forta de lunecare capabila de calcul a unui dorn cu cap sudat automat in conformitate cu EN14555 se va determina ca valoarea minima intre :

P_Rd = (6.18)

sau

P_Rd = (6.19)

cu:

α = 0,2 pentru 3 ≤ h_sc/d ≤ 4 (6.20)

α = 1 pentru h_sc/d > 4 (6.21)

unde:

este coeficient partial de siguranta ;

d este diametrul tijei dornului, 16mm ≤ d ≤ 25mm ;

f_u este rezistenta la intindere ultima a materialului dornului dar nu mai mare de 500N/mm² ;

f_ck este rezistenta caracteristica cilindrica la compresiune a betonului la varsta respectiva beton cu densitate mai mare de 1750kg/m³ ;

h_sc este inaltimea totala a dornului

Nota : Valoarea pentru poate fi data in Anexa Nationala . Valoarea recomandata este 1,25.

(2) Gulerul de sudura va respecta cerintele din EN 13918.

(3) Paragraful (1) nu se aplica in cazul in care conectorii de lunecare sunt dispusi astfel incat fortele de despicare actioneaza in directia grosimii placii.

6.6.3.2 Influenta intinderii asupra fortei de lunecare capabile

(1) In cazul in care conectorii de lunecare sunt solicitati direct la forte de intindere care se adauga forfecarii , trebuie calculata forta de intindere de calcul aferenta unui conector F_ten .

(2) Daca F_ten ≤ 0.1P_Rd , unde P_Rd este rezistenta de calcul definita in 6.6.3.1, forta de intindere poate fi neglijata.

(3) Daca F_ten > 0.1P_Rd , conectarea nu face obiectul EN 1994.

6.6.4 Forta de lunecare capabila a dornurilor cu cap folositi la placile compozite cu tabla cutata

6.6.4.1 Tabla cutata are nervurile paralele cu grinda de reazem

(1) Dornurile sunt amplasate intr-o regiune in care betonul are forma unei nervuri de ingrosare, vezi Figura 6.12.In cazul in care tabla cutata este continua peste grinda, latimea nervurii b_o este latimea cutei asa cum este data in Figura 6.12. Inaltimea nervurii se va considera h_p, inaltimea totala a tablei neglijand amprentele.

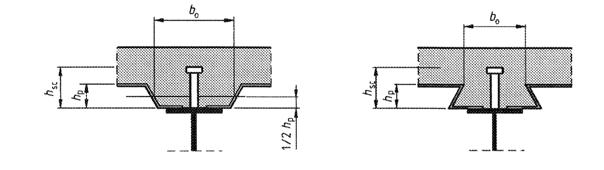
Figura 6.12 : Grinda cu tabla cutata avand nervurile paralele cu grinda

(2) Forta de lunecare capabila de calcul se va considera forta capabila a dornului cu cap in cazul placii din beton, vezi 6.6.3.1 multiplicata cu factorul de reducere k_l din urmatoarea expresie

k_l = 0,6 (6.22)

unde:

h_sc este inaltimea totala a conectorului, dar mai mica decat h_p + 75mm

(3) In cazul in care tabla nu este continua peste grinda si nu este corespunzator ancorata de aceasta, latura respectiva a nervurii si armarea ei vor satisface 6.6.5.4.

Nota: Metodele de ancorare corespunzatoare a tablei se pot da in Anexele Nationale

6.6.4.2 Tabla cutata avand nervurile perpendiculare pe grinzii de reazem

(1) Considerandu-se satisfacute conditiile date in (2) si (3), forta de lunecare capabila de calcul se va considera egala cu valoarea determinata pentru placile din beton armat, in conformitate cu 6.6.3.1 ( cu conditia ca f_u sa nu fie considerat mai mare de 450N/mm²) multiplicata cu un factor de reducere k_t dat de relatia :

unde:

n_r este numarul de conectori de lunecare dintr-o cuta aflata la intersectia cu grinda, mai mic ca 2 ,iar celelalte simboluri sunt definite in Figura 6.13.

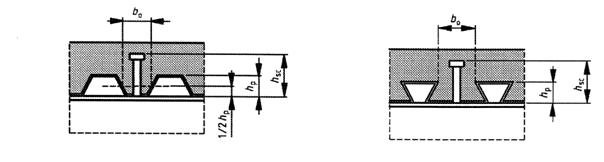
Figura 6.13 : Grinda cu tabla cutata avand nervurile perpendiculare pe grinda

(2) Factorul k_t nu se va considera mai mare decat valoarea corespunzatoare k_t,max data in tabelul 6.2

(3) Valorile lui k_t date in (1) si (2) se aplica in urmatoarele conditii:

conectorii de lunecare sunt plasati in cute avand o inaltime h_p mai mica de 85mm si o latime b_o mai mare decat h_p si

pentru sudura patrunsa prin tabla, diametrul conectorului nu va fi mai mare de 20mm, sau

pentru cazul in care se prevad gauri in tabla, diametrul conectorilor va fi mai mic de 22mm.

Tabelul 6.2 : Limita superioara k_t,max a factorului de reducere

6.6.4.3 Incarcarea biaxiala a conectorilor de lunecare

(1) In cazul in care conectorii de lunecare asigura efectul compozit in acelasi timp pentru grinda si pentru placa compozita, combinatia de forte care actioneaza asupra conectorului va satisface urmatoarea relatie:

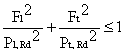
(6.24)

unde:

F_l este forta longitudinala determinata de actiunea compozita a grinzii

F_t este forta tansversala determinata de actiunea compozita a placii , vezi capitolul 9;

P_l,Rd , P_t,Rd sunt fortele corespunzatoare capabile de forfecare ale conectorului.

6.6.5 Detalierea conectarii de lunecare si influenta executiei

6.6.5.1 Rezistenta la separare

(1) Suprafata conectorului care preia fortele de separare (de exemplu, intradosul capului conectorului) nu trebuie sa fie la o distanta mai mare de 30mm de armatura inferioara, vezi Figura 6.14

6.6.5.2 Acoperirea cu beton si turnarea betonului

(1)P Alcatuirea conectarii se va realiza astfel incat betonul sa se poata compacta adecvat in jurul bazei conectorului.

(2) Daca este necesara, acoperirea cu beton a conectorului va avea valoarea minima din conditiile :

a)          mai mare decat 20mm, sau

b)          o valoare mai mica decit cea recomandata pentru armatura de EN 1992-1-1, in Tabelul 4.4.

(3) Daca acoperirea nu este necesara , fata superioara a conectorului va fi la acelasi nivel cu suprafata superioara a placii din beton armat.

(4) In executie , rata si secventa betonarii, vor urmari ca betonul maturizat partial sa nu fie avariat de actiunea compozita limitata care are loc la deformarea grinzii de otel solicitata de operatiile succesive de betonare. De cate ori este posibil , nu se vor impune defomatii conectorilor pana cand betonul nu atinge o rezistenta cilindrica de cel putin 20N/mm².

6.6.5.3 Armarea locala a placii

(1) In cazul in care conectorii de lunecare sunt langa o margine longitudinala de placa , se va prevede , o armatura transversala in conformitate cu 6.6.6 ancorata in betonul dintre marginea placii si randul adiacent de conectori.

(2) Pentru a preveni despicarea placii de beton cauzata de conectori , se vor aplica urmatoarele recomandari suplimentare in cazul in care distanta de la marginea placii la axul primului rand de conectori este mai mica de 300mm:

a)      se va dispune o armatura transversala sub forma de bucla care trece in jurul conectorilor,

b)      in cazul in care se folosesc dornuri cu cap, distanta de la marginea placii din beton la axul celui mai apropiat conector va fi mai mare de 6d, unde d este diametrul nominal al conectorului , iar barele in forma de bucla vor avea diametrul de cel putin 0.5d si,

c)      barele se vor amplasa cat mai jos cu putinta asigurandu-se totusi o acoperire suficienta la partea de jos.

(3)P La marginea unei console compozite, se va asigura o armare locala suficienta pentru a transfera fortele conectorilor la armatura longitudinala.

6.6.5.4 Alte tipuri de nervuri de ingrosare decat cele formate de tabla cutata

(1) Cand intre intradosul placii din beton si sectiunea de otel se foloseste o nervura de ingrosare din beton, laturile nervurii de ingrosare se vor afla in exteriorul liniilor duse la 45° de la limita exterioara a conectorului, vezi Figura 6.14.

Figura 6.14 : Detalii ale conectarii

(2) Acoperirea cu beton a conectorului de la exteriorul nervurii de ingrosare nu va fi mai mica de 50mm.

(3) Barele armaturii transversale din nervura de ingrosare vor fi suficiente pentru a satisface cerintele 6.6.6 si se vor amplasa la o distanta libera mai mare de 40mm fata de suprafata conectorului care se opune tendintei de separare.

6.6.5.5 Distanta intre conectorii de lunecare

(1)P In situatia in care se considera in calcul ca stabilitatea sectiunii de otel sau a elementului de beton este asigurata de conectarea intre cele doua , distanta intre conectori va fi sufcient de mica pentru ca aceasta ipoteza sa fie valabila.

(2) In cazul in care o talpa de otel comprimata aflata intr-o clasa inferioara, trece in Clasa 1 sau 2 datorita conectarii cu o placa de beton sau compozita, distanta intre axele conectorilor pe directia compresiunilor nu va depasi urmatoarele limite:

- in cazul in care placa este in contact pe toata lungimea grinzii : 22 t_f

- in cazul in care placa nu este in contact pe toata lungimea (exemplu placii compozite avand cutele transversale grinzii :15t_f

unde:

t_f este grosimea talpii

f_y este rezistenta nominala de curgere a talpii in N/mm²

Distanta libera intre marginea talpii comprimate si cel mai apropiat rand de conectori de lunecare nu va fi mai mare decat 9t_f .

(3) In cazul cladirilor distanta maxima intre centrele conectorilor nu va fi mai mare decat de 6 ori grosimea placii sau 800mm.

6.6.5.6 Dimensiunile talpii de otel

(1)P Grosimea unei placi din otel sau a unei talpi pe care se sudeaza un conector de lunecare va fi suficienta pentru a asigura o sudura corespunzatoare si un transfer corespunzator al fortei intre conector si talpa fara ruperi locale sau deformatii excesive.

(2) Distanta e_D intre marginea conectorului si marginea talpii grinzii pe care se sudeaza , nu va fi mai mica de 20 mm , vezi Figura 6.14.

6.6.5.7 Conectori de lunecare tip dornuri cu cap

(1) Inaltimea totala a conectoului nu va fi mai mica decat 3d, unde d este diametrul tijei.

(2) Capul va avea un diametru mai mare decat 1,5d si o inaltime mai mare de 0,4d.

(3) Pentru elementele intinse si solicitate la oboseala, diametrul conectorului sudat nu va depasi de 1,5 ori grosimea talpii pe care se sudeaza, cu exceptia cazului in care se exista determinari experimentale care stabileasc rezistenta la oboseala a conectorului.

(4) Distanta intre conectori de lunecare pe directia forfecarii nu va fi mai mica de 5d ; distanta pe directie transversala directiei de forfecare nu va fi mai mica de 2,5d in placi din beton armat si 4d in celelalte cazuri.

(5) Cu exceptia situatiei in care conectorul este amplasat deasupra inimii , diametrul conectorului sudat nu va fi mai mare decat de 2.5 ori grosimea placii pe care se sudeaza cu exceptia cazului in care exista determinari experimentale ale rezistentei la forfecare a conectorului.

6.6.5.8 Conectori de lunecare tip dornuri cu cap folositi cu planseele cu tabla cutata la cladiri.

(1) Inaltimea nominala a conectorului nu se va extinde cu mai putin de 2d peste cota superioara a tablei cutate, in care d este diametrul tijei.

(2) Latimea minima a cutei care se va umple cu beton nu va fi mai mica de 50mm.

(3) In situatia in care datorita pozitionarii panourilor de tabla cutata conectorii de lunecare nu pot fi dispusi in centrul cutei, ei se vor amplasa alternativ pe cele doua parti ale cutei , pe toata lungimea deschiderii.

6.6.6 Lunecarea longitudinala a placilor din beton armat

6.6.6.1 Generalitati

(1)P Pentru a se preveni cedarea prematura la lunecare longitudinala sau despicarea longitudinala in placa din beton armat se va prevedea armatura transversala .

(2)P Efortul unitar de calcul la lunecare longitudinala pentru orice suprafata potentiala de rupere din placa ν_Ed nu va depasi rezistenta la lunecare a suprafetei considerate.

(3) Lungimea suprafetei de lunecare b-b indicata in Figura 6.15 se va lua egala cu 2h_sc plus diametrul capului conectorului pentru un singur rand de conectori sau dispusi in sah, sau egala cu (2h_sc+s_t) plus diametrul capului pentru conectori dispusi perechi, unde h_sc este inaltimea conectorului si s_t este distanta transversala intre centrele conectorilor.

(4) Forta de lunecare longitudinala de calcul pentru unitatea de lungime a grinzii care apare la suprafata de lunecare se va determina conform 6.6.2 si va fi in conformitate cu calculul si distanta dintre conectori.

Se va tine deasemenea cont de variatia fortei de lunecarii longitudinala pe latimea placii din beton.

(5) Pentru fiecare tip de suprafata de lunecare considerata , efortul unitar de calcul de lunecare longitudinala ν_Ed se va determina din lunecarea longitudinala pe unitatea de lungime a grinzii, tinand cont de numarul de planuri de lunecare si de lungimea suprafetei de lunecare.

6.6.6.2 Forta capabila de lunecare longitudinala

(1) Forta capabila de calcul la lunecare a talpii din beton (planurile de lunecare a-a ilustrate in Figura 6.15) se va determina conform EN 1992-1-1, 6.2.4.

(2) In absenta unui calcul mai riguros, rezistenta la lunecare al oricarei suprafete potentiale de rupere la lunecare in talpa sau in nervura de ingrosare din beton se va determina din EN 1992-1-1,6.2.4(4). Pentru o suprafata de lunecare care trece la limita conectorilor ( de exemplu suprafata b-b din Figura 6.15), dimensiunea h_f se va considera lungimea suprafetei de lunecare.

(3) Armatura transversala efectiva pe unitatea de lungime A_sf / s_f din EN 1992-1-1, va fi cea indicata in Figura 6.15, in care A _b, A _t si A_bh sunt ariile armaturilor pe unitatea de lungime a grinzii, armaturi ancorate in conformitate cu EN 1992-1-1, 8.4 (pentru armatura longitudinala)

(4) In cazul in care se foloseste o combinatie de elemente prefabricate si monolite de beton, rezistenta la lunecare longitudinala se va determina in conformitate cu EN 1992-1-1,6.2.5. 

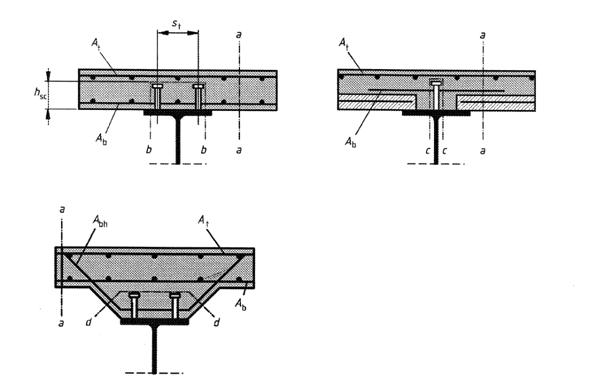
Figura 6.15 : Suprafetele caracteristice potentiale de rupere la lunecare

6.6.6.3 Armatura transversala minima

(1) Aria minima a armaturii se va determina in conformitate cu EN 1992-1-1,9.2.2.(5) folosind definitii similare cu armatura transversala.

6.6.6.4 Lunecarea longitudinala si armatura transversala a grinzilor

(1) In cazul in care se foloseste tabla cutata si supafata de lunecare trece prin grosimea placii ( de exemplu suprafata a-a din Figura 6.16), dimensiunea h_f se va considera grosimea betonului de deasupra tablei.

(2) In cazul in care tabla cutata se utilizeaza cu nervurile transversal grinzii si rezistenta conectorului se determina folosind factorul de reducere k_t ca in 6.6.4.2 , nu este necesara considerarea suprafetelor de tipul b-b din Figura 6.16.

(3) Pentru suprafetele de tip c-c din Figura 6.16 inaltimea tablei nu va fi inclusa in hf cu exceptia cazurilor in care exista verificari experimentala.

(4) In cazul in care tabla cutata are conlucrari mecanice sau de frecare , directia cutelor este transversala grinzii si tabla cutata trece continuu peste grinda, contributia tablei cutate la armarea transversala pentru suprafete de tipul a-a se va lua in considerare prin inlocuirea relatiei (6.21) din EN1992-1-1,6.2.4(4) prin:

(A_sf f_yd / s_f ) + A_pe f_yp,d > ν_Ed h_f / cotθ (6.25)

unde :

A_pe este aria efectiva a sectiunii transversale a tablei cutate pe unitatea de lungime a grinzii, vezi 9.7.2.(3); pentru tabla cu gauri , se va folosi aria neta;

f_yp,d este rezistenta de curgere a tablei.

Figura 6.16 Tipuri de suprafete potentiale de rupere la lunecare cand se foloseste tabla cutata

(5) In cazul in care tabla cutata transversala grinzii este discontinua peste talpa superioara a grinzii de otel, si conectorii de lunecare sunt sudati de talpa grinzii direct prin panourile de tabla cutata in relatia (6.25) termenul A _p f_yp,d se va inlocui cu:

P_pb,Rd /s cu conditia P_pb,Rd /s ≤ A _p f_yp,d (6.26)

unde:

P_pb,Rd este rezistenta la compresiune locala a conectorului sudat prin tabla conform 9.7.4;

s este distanta longitudinala intre centrele conectorilor cu rol in ancorarea tablei cutate.

(6) In cazul utilizarii tablei cutate, cerinta pentru armatura minima se raporteaza la aria de beton de deasupra tablei.

6.7 Stalpi si elemente compozite comprimate

6.7.1 Generalitati

Capitolul 6.7 se aplica pentru proiectarea stalpilor si elementelor compozite comprimate cu sectiuni inglobate in beton si tevi rectangulare si circulare umplute cu beton,vezi Figura 6.17.

Figura 6.17 : Tipuri de sectiuni de stalpi compoziti si notatii

(2)P Acest capitol se aplica stalpilor si elementelor compozite comprimate cu otel de grad de la S235 la S420 si beton de greutate normala de clasa C20/25 la C50/60.

(3) Acest capitol se aplica stalpilor izolati si stapilor sau elementelor compozite comprimate din structuri in cadre cu celelalte elemente grinzi compozite sau grinzi din otel.

(4) Indicele de contributie al otelului δ trebuie sa indeplineasca urmatoarea conditie:

0,2 ≤ δ ≤ 0,9 (6.27)

unde:

δ este definit in 6.7.3.3(1)

(5) In cazul stalpilor sau a elementele compozite comprimate se vor verifica in orice sectiune capacitatile de:

rezistenta a elementului conform cu 6.7.2 sau 6.7.3,

rezistenta la flambaj local conform cu (8) si (9) mai jos,

transfer al incarcarii conform cu 6.7.4.2 si

rezistenta la lunecare intre componentele de otel si beton conform cu 6.7.4.3.

(6) Pentru calcul sectiunilor exista doua metode :

o metoda generala in 6.7.2 a carui domeniu include elemente cu sectiuni nesimetrice si neuniforme pe lungimea stalpului ;

o metoda simplificata in 6.7.3 pentru elemente cu dubla simetrie si sectiuni uniforme pe lungimea stalpului.

(7) Pentru elementele compozite solicitate la momente incovoietoare si la forte normale rezultate din actiuni independente, coeficientul partial de siguranta γ_F se va reduce cu 20%. in cazul eforturilor sectionale care conduc la cresterea capacitatii de rezistenta

(8)P Se va considera in calcul influenta flambajului local al sectiunii de otel asupra capacitatii de rezistenta .

(9) Efectul flambajului local se poate neglija pentru sectiuni de otel cu inglobare totala in beton conforma cu 6.7.5.1(2), si pentru alte sectiuni pentru care nu sunt depasite valorile maxime date in tabelul 6.3

Tabelul 6.3 : Valori maxime (d/t), (h/t) si b/t_f cu f_y in N/mm²

Sectiunea transversala	Max(d/t), max(h/t),si max(b/t)
Sectiuni din tevi circulare de otel umplute cu beton	max( d/t) =90
Sectiuni din tevi rectangulare de otel umplute cu beton	max( h/t) =52
Sectiuni I cu inglobare partiala in beton	max( b/tf) =44

6.7.2 Metoda generala de proiectare

(1)P Calculul pentru stabilitatea structurala va tine cont de efectele de ordinul doi inclusiv de eforturile reziduale,imperfectiunile geometrice, instabilitatea locala, fisurarea betonului,curgerea lenta si contractia betonului , curgerea otelului structural si al armaturii.Calculul va asigura ca instabilitatea nu va avea loc pentru cea mai defavorabila combinatie de actiuni la starea limita ultima si ca nu se vor depasi capacitatile de rezistenta ale sectiunilor individuale solicitate la incovoiere , forte longitudinale si forte taietoare.

(2)P Efectele de ordinul doi se vor considera in orice directie in care poate apare cedarea, daca ele afecteaza semnificativ stabilitatea structurala.

(3)P Eforturile sectionale se vor determina printr-un calcul elasto-plastic.

(4) Sectiunile plane se considera ca raman plane. Intre componentele de otel si beton se considera o actiune compozita totala pana la rupere.

(5)P Rezistenta la intindere a betonului se va neglija.Se va considera in calcul influenta rigidizarii betonului intins intre fisuri asupra rigiditatii la incovoiere.

(6)P Contractia si curgerea lenta se vor considera in calcul daca reduc semnificativ stabilitatea structurala.

(7) Curgerea lenta si contractia se pot ignora in mod simplificat daca crestera momentelor de incovoiere de ordinul intai nu este mai mare de 10%.

(8) In calculele neliniare se vor folosi urmatoarele relatii σ-ε :

pentru betonul comprimat din EN 1992-1-1,3.15;

pentru otelul armaturii din EN 1992-1-1,3.2.7;

pentru otelul structural din EN 1993-1-1,5.4.3(4).

(9) Imperfectiunile initiale echivalente ale elementelor pot fi utilizate simplificat in conformitate cu Tabelului 6.5 in locul efectului eforturilor reziduale si a imperfectiunilor geometrice.

6.7.3 Metoda simplificata de proiectare

6.7.3.1 Generalitati si domeniul de aplicare al metodei

(1) Acesta metoda simplificata se limiteaza la elementele cu sectiuni transersale cu dubla simetrie si constante pe lungimea elementului , sectiuni laminate sau sudate.Metoda simplificata nu se aplica daca elementul de otel este realizat din doua sau mai multe sectiuni neconectate.Zveltetea relativa definita in 6.7.3.3 va indeplini urmatoarea conditie:

≤ 2,0 (6.28)

(2) Pentru o sectiune transversala cu inglobare totala in beton, vezi Figura 6.17a, limitele maxime ale acoperirii cu beton care se pot utiliza in calcul sunt:

max c_z = 0,3h max c_y = 0,4b (6.29)

(3) Armatura longitudinala care se poate utiliza in calcul nu va depasi 6% din aria de beton.

(4) Raportul intre inaltimea si latimea sectiunii compozite va fi cuprinsa intre limitele 0,2 si 5,0.

6.7.3.2 Eforturi sectionale capabile

(1) Forta de compresiune capabila plastica N_pl,Rd a sectiunii compozite se va calcula sumand fortele capabile plastice la compresiune ale componentelor:

N_pl,Rd = A_a f_yd + 0,85 A_c f_cd + A_s f_sd (6.30)

Relatia (6.30) se aplica sectiunilor de otel cu inglobare totala sau partiala in beton.Pentru sectiunile umplute cu beton coeficientul 0,85 se va inlocui cu 1,0.

(2) Momentul capabil la incovoiere al unei sectiuni comprimate si curba corespunzatoare de interactiune se vor calcula considerand blocuri de eforturi unitare ca in Figura 6.18, tinindu-se cont de forta taietoare de calcul, V_Ed in conformitate cu (3). Rezistenta la intindere a betonului se va neglija.

Figura 6.18 : Curba de interactiune pentru compresiune si incovoiere uniaxiala

(3) Influenta fortei taietoare asupra momentului capabil la incovoiere cu forta axiala se va lua in considerare cand se determina curba de interactiune, daca forta taietoare V_a,_Ed aplicata sectiunii de otel depaseste 50% din forta taietoare capabile V _pl,a,Rd a sectiunii de otel vezi 6.2.2.2.

In cazurile in care V_a,Ed > 0,5 V_pl,a,Rd , influenta fortei taietoare asupra momentului capabil de calcul la incovoiere cu compresiune se va considera in calcul prin utilizarea unei rezistente de calcul a otelului redusa (1-ρ)f_yd in zona de forta taietoare conform cu 6.2.2.4(2) si Figura 6.18.

Forta taietoare V_a,Ed nu va depasi forta taietoare capabila a sectiunii de otel determinata conform 6.2.2. Forta taietoare capabila a componentei din beton armat V_c,Ed se va verifica conform cu

EN 1992-1-1,6.2.

(4) V_Ed se poate distribui in cazul in care nu se foloseste o metoda mai riguroasa intre V_a,_Ed actionand asupra sectiunii de otel si V_c,Ed actionand asupra sectiunii de beton astfel:

V_a,Ed = V_Ed (6.31)

V_c,Ed = V_Ed - V_{a, Ed} (6.32)

unde :

M_pl,a,Rd este momentul capabil plastic al sectiunii de otel si

M_pl,Rd este momentul capabil plastic al sectiunii compozite.

Se poate considera in mod simplificat ca V_Ed actioneaza numai asupra sectiunii de otel.

(5) Curba de interactiune se poate inlocui simplificat printr-o diagrama poligonala ( linia punctata din Figura 6.19). Figura 6.19 arata un exemplu de distributii plastice ale eforturilor unitare pe o sectiune total inglobata pentru punctele de la A la D. N_pm,Rd se va considera 0,85 f_cd A_c pentru sectiunile cu inglobare totala sau partiala in beton, vezi Figurele 6.17(a) - (c), si f_cd A_c pentru sectiunile umplute cu beton , vezi Figurile 6.17(d) - (f).

Figura 6.19 : Curba de interactiune simplificata si distributiile de eforturi unitare corespunzatoare.

(6) In cazul tevilor umplute cu beton de sectiune circulara , se va tine cont de cresterea rezistentei betonului determinata de confinare in conditiile in care zveltetea relativa definita la 6.7.3.3 nu depaseste 0,5 si e/d < 0,1, unde e este excentricitatea incarcarii egala cu M_Ed / N_Ed si d este diametrul exterior al stalpului.Forta axiala capabila plastica la compresiune se poate calcula in aceste conditii cu relatia urmatoare:

N_pl,Rd = η_a A_a f_yd + A_c f_cd ( 1+ ) + A_s f_sd (6.33)

unde:

t este grosimea peretelui tevii din otel.

Pentru elemente cu e = 0 valoarea η_a = η_ao si η_c = η_co sunt date de relatiile urmatoare:

η_ao = 0,25( 3 + 2 ) (dar ≤1,0) (6.34)

η_co = 4,9 - 18,5 + 17 ² (dar ≥ 0) (6.35)

Pentru elemente incovoiate si comprimate cu 0 < e/d ≤ 0,1 , valorile η_a si η_c se vor determina din (6.36) si (6.37), unde η_ao si η_co sunt date de (6.34) si (6.35):

η_a = η_ao + (1- η_ao )(10 e/d) (6.36)

η_c = η_co( 1-10 e/d) (6.37)

Pentru e/d > 0,1 , η_a = 1,0 si η_c = 0 .

6.7.3.3 Rigiditatea efectiva la incovoire , indicele de contributie al otelului, zveltetea relativa

(1) Indicele de contributie al otelului δ se defineste ca:

(6.38)

unde:

N_pl,Rd este forta axiala capabila plastica la compresiune definita in 6.7.3.2(1).

(2) Zveltetea relativa pentru planul de incovoiere considerat este data de :

= (6.39)

unde:

N_pl,Rk este valoarea caracteristica a fortei capabile plastice la compresiune data de (6.30) daca ,in l loc de rezistente de calcul se folosesc rezistente caracteristice;

N_cr este forta normala critica elastica pentru modul de flambaj semnificativ , calculat cu rigiditatea efectiva (EI)_eff determinata in conformitate cu (3) si (4).

(4) Pentru determinarea zveltetei relative si a fortei critice elastice N_cr , valoarea caracteristica a rigiditatii efective la incovoiere (EI)_eff a sectiuni stalpului compozit se va calcula din:

(E I)_eff = E_a I_a + E_s I_s + K_e E_cm I_c (6.40)

unde:

K_e este un factor de corectie care se va lua 0,6.

I_a , I_c si I_s sunt momentele de inertie ale sectiunii de otel structural, sectiunii nefisurate de beton,si respectiv al armaturii pentru planul de incovoiere considerat.

(4) Se va tine cont de influenta efectelor de lunga durata asupra rigiditatii elastice efective la incovoiere.Modului de elasticitate al betonului E_cm se va reduce la o valoare efectiva E_c,eff in conformitate cu urmatoarea relatie:

E_c,eff = E_cm (6.41)

unde:

φ_t este coeficientul de curgere lenta conform cu 5.4.2.2(2);

N_Ed este forta normala totala de calcul;

N_G,Ed este fractiunea permanenta din forta normala .

6.7.3.4 Metode de calcul si imperfectiunile elementelor

(1) Pentru verificarea elementelor , calculul se va baza pe un calcul linear elastic de ordinul doi.

(2) Pentru determinarea eforturilor sectionale ,valoarea rigiditatii efective la incovoiere (EI)_eff,II se va determina cu urmatoarea expresie:

(EI)_eff,II = K_o ( E_a I_a + E_s I_s + K_e,II E_cm I_c ) (6.42)

unde :

K_e,II este un factor de corectie care se va lua 0,5;

K_o este un factor de calibrare care se va considera 0,9.

Efectele de lunga durata se vor lua in considerare in conformitate cu 6.7.3.3(4).

(3) Efectele de ordinul doi nu se vor considera cand se aplica 5.2.1(3) si in cazul in care incarcarea critica elastica se determina cu rigiditatea la incovoiere (EI)_eff,II in conformitate cu (2)

(4) Influenta imperfectiunilor structurale si geometrice se vor lua in calcul prin imperfectiunile geometrice echivalente.Imperfectiunile echivalente pentru stalpii compoziti sunt date in Tabelul 6.5, unde L este lungimea stalpului.

(5) Pe lungimea stalpului , efectele de ordinul doi se vor considera prin multiplicarea momentului de calcul de ordinul unu M_Ed printr-un factor k dat de:

k = , ≥ 1,0 (6.43)

unde:

N_cr,eff este forta normala critica pentru axa respectiva, rigiditatea efectiva la incovoiere

corespunzatoare data in 6.7.3.4(2) si o lungime efectiva egala cu lungimea stalpului;

β este un factorul echivalent al distributiei de momente dat in Tabelul 6.4.

6.7.3.5 Eforturi sectionale capabile la compresiune axiala

(1) Elementele se vor verifica utilizand calculul de ordinul doi conform cu 6.7.3.6 tinand cont de imperfectiunile elementelor

(2) Pentru elementele comprimate axial valoarea de calcul a fortei normale N_Ed va satisface relatia simplificata:

(6.44)

unde :

N_pl,Rd este forta normala capabila plastica a sectiunii compozite in conformitate cu 6.7.3.2(1), dar

cu f_yddeterminat utilizand factorul partial de siguranta γ_M1 dat de EN 1993-1-1,6.1(1);

c este factorul de reducere pentru modul de flambaj respectiv dat in EN 1993-1-1,6.3.1.2

functie de zveltetea relativa corespunzatoare

Curbele de flambaj care se refera la sectiunile compozite sunt date inTabelul 6.5 unde ρ_s este

A_s/ A_c.

Tabelul 6.4 Factorul β pentru determinarea momentelor in teoria de ordinul doi.

6.7.3.6 Eforturi sectionale capabile la compresiune si incovoiere uniaxiala

(1) Folosind curba de interactiune determinata in conformitate cu 6.7.3.2(2)-(5) se va verifica urmatoarea relatie:

(6.45)

unde:

M_Ed este valoarea maxima a momentelor de la extremitati si de pe lungimea stalpului, calculate conform 6.7.3.4, incluzand daca este necesar imperfectiunile si efectele de ordinul doi ;

M_pl,N,Rd este momentul capabil plastic la incovoiere cu forta normala N_Ed calculat cu relatia

μ_d M_pl,Rd , conform Figurii 6.18.

M_pl,Rd este momentul capabil plastic la incovoiere pura, pentru punctul B din Figura 6.19.

Pentru otel de grade intre S235 si S355 inclusiv , coeficientul α_M se va considera 0,9 iar pentru grade S420 si S460 va avea valoarea de 0,8.

Tabelul 6.5 Curbe de flambaj si imperfectiuni pentru stalpi compoziti

(2) Valoarea μ_d = μ_dy sau μ_dz, vezi Figura 6.20, se refera la momentul capabil plastic M_pl,Rd pentru planul de incovoiere considerat. Valorile μ_d mai mari ca 1,0 se vor folosi numai in cazul in care momentul M_Ed depinde direct de actiunea fortei normale N_Ed , de exemplu cand momentul M_Ed rezulta dintr-o excentricitate a fortei normale N_Ed. In alte cazuri este necesara o verificare suplimentara in conformitate cu 6.7.1(7).

Figura 6.20 : Calculul la compresiune cu incovoiere biaxiala

6.7.3.7 Compresiune si incovoiere biaxiala

(1) Pentru stalpi compozii sau elemente comprimate cu incovoiere biaxiala valorile μ_dy si μ_dz din Figura 6.20 se vor calcula conform cu 6.7.3.6 separat pentru fiecare axa. Imperfectiunile se vor considera numai in planul in care se asteapta sa se produca cedarea.Daca nu este evident care plan este critic, verificarea se va face in ambele planuri.

(2) Pentru compresiune si incovoiere biaxiala se vor satisface urmatoarele conditii de verificare a stabilitatii pe lungimea stalpului si la extremitati :

(6.46)

(6.47)

unde:

M_pl,y,Rd si M_pl,z,Rd sunt momentele capabile plastice la incovoiere in planurile respective de incovoiere;

M_y,Ed si M_z,Ed sunt momentele de calcul la incovoiere care includ efectele de ordinul doi si imperfectiunile conform cu 6.7.3.4;

μ_dy si μ_dz sunt definite in 6.7.3.6;

α_M = α_M,y si α_M = α_M,z sunt date in 6.7.3.6 (1).

6.7.4 Conectarea si transferul incarcarii

6.7.4.1 Generalitati

(1)P In regiunile de transfer al incarcarilor de la elementele conectate la capetele stalpului si al incarcarilor aplicate pe lungimea acestuia , se vor lua masuri pentru a se asigura distributia momentelor si a fortelor taietoare si axiale intre otel si beton considerand rezistenta la lunecare la interfata intre beton si otel. Se va asigura o cale definita clar de transmitere a incarcarilor , care sa nu presupuna deplasri relative de lunecare la interfata care sa invalideze ipotezele presupuse in calcul.

(2)P In cazul in care stalpii compoziti si elementele comprimate sunt solicitate la forte taietoare importante, ca de exemplu de forte concentrate tranversale si momente la extremitati,se vor lua masuri de a se asigura transferul eforturilor unitare tangentiale longitudinale corespunzatoare acestor forte la interfata intre otel si beton.

(3) Pentru stalpi incarcati axial si elemete comprimate, nu este necesar sa se considere lunecarea longitudinala in afara zonelor de transfer a incarcarilor.

6.7.4.2 Transferul incarcarilor

(1) In zonele de transfer a incarcarilor si in zonele de schimbare a sectiunii, se vor prevede conectori de lunecare daca rezistenta la forecare τ_Rd la interfata intre otel si beton data in 6.7.4.3, este depasita. Fortele de lunecare se vor determina din variatia rezultantelor eforturilor unitare ale sectiunii de otel sau beton armat pe zona de transfer a incarcarilor.Daca incarcarile se transmit numai sectiunii din beton, se vor considera in calcul valorile determinate in domeniul elastic tinand cont de curgerea lenta si de contractie.In celelalte cazuri fortele de la interfata se vor determina printr-un calcul elastic sau plastic care determina cazul cel mai sever.

(2) In absenta unei metode mai exacte , lungimea de transfer a incarcarilor nu va depasi 2d sau L/3 , unde d este dimensiunea transversala minima a sectiunii stalpului si L este lungimea stalpului.

(3) Pentru stalpii sau elementele comprimate compozite la care incarcarile se transmit prin placi de capat , nu sunt necesari conectori de lunecare daca intreaga suprafata a interfetei dintre sectiunea de beton si placa de capat este in permanenta comprimata in conditiile in care se tine cont de curgerea lenta si contractie. In alte cazuri, transferul incarcarii se va verifica conform (5) . Pentru tevi umplute cu beton de sectiune circulara se va tine cont de efectul de confinare daca sunt satisfacute conditiile date in 6.7.3.2(6) si folosind valorile η_a si η_c pentru egala cu zero.

(4) In cazurile in care conectori de lunecare sunt sudati de inima sectiunii I sau a unei sectiuni similare total sau partial inglobate in beton, se va tine cont de fortele de frecare care se dezvolta din impiedicarea expansiunii laterale a betonului de catre talpile adiacente ale sectiunii din otel.Aceaste forte se adauga la fortelor capabile de calcul ale conectorilor.Fortele rezistente suplimentare din frecare se considera a fi egale cu μ P_Rd / 2 pe fiecare talpa si fiecare rand orizontal de conectori de lunecare asa cum este aratat in Figura 6.21, in care μ va fi egal cu 0,5.

P_Rd este forta capabila unui singur conector conform 6.6.3.1.In absenta unor rezultate experimentale mai favorabile lumina intre talpi nu va depasi valorile date in Figura 6.21.

(5) Daca sectiunea transversala este partial incarcata ( ca de exemplu in Figura 6.22a), incarcarile se vor distribui cu o panta 1:2,5 , pe grosimea t_e a placii de capat. Eforturile unitare din beton se vor limita la aria efectiva de transfer a incarcarii, pentru sectiuni din tevi umplute cu beton conform cu (6) iar pentru toate celelalte sectiuni conform EN 1992-1-1,6.7.

Figura 6.21 Forte de frecare suplimentare la stalpii compoziti prin folosirea dornurilor cu cap

(6) Daca betonul din tevile umplute circulare sau rectangulare este incarcat numai partial, de exemplu prin gusee trecute prin tevi sau prin intermediul unor rigidizari asa cum este aratat in Figura 6.22, rezistenta locala la compresiune a betonului σ_c,Rd generata sub gusee sau rigidizari de eforturile sectionale , se va determina cu:

σ_c,Rd = , ≤ f_yd (6.48)

unde

t este grosimea peretelui tevii,

a este diametrul tevii sau latimea sectiunii patrate

A_c este aria sectiunii de beton a stalpului;

A₁ este aria incarcata de sub guseu, vezi Figura 6.22;

η_cL =4,9 pentru tevi circulare si 3.5 pentru tevi rectangulare

Raportul A_c / A₁ nu va depasi valoarea de 20. Sudurile intre gusee si teava de otel se vor calcula conform EN1993-1-8,Capitolul 4.

(7) Pentru sectiunile din teava circulara umpluta cu beton, armatura longitudinala se va lua in considerare la calculul capacitatii de rezistenta a stalpului,chiar daca armatura nu este sudata sau in contact direct cu placile de capat in conditiile in care:

- nu este necesara verificarea la oboseala,

- distanta intre armatura si placile de capat nu depaseste 30 mm, vezi Figura 6.22(a).

(8) Armatura transversala va respecta EN 1992-1-1, 9.5.3, In cazul sectiunilor de otel cu inglobare partiala in beton, betonul va fi ancorat prin armatura transversala in conformitate cu Figura 6.10.

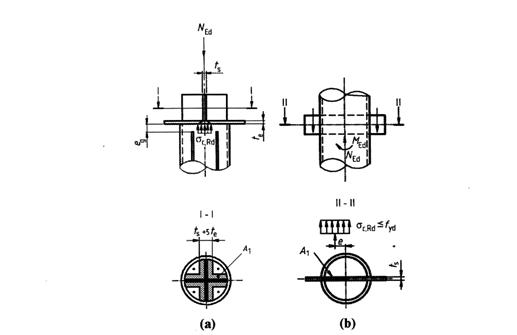
Figura 6.22 : Sectiuni din teava circulara partial inglobata in beton

(9) In cazul transferului incarcarii numai prin intermediul sectiunii transversale de otel sau de beton , pentru sectiunile de otel cu inglobare totala in beton , armatura transversala se va dimensiona pentru lunecarea longitudinala care rezulta din transmiterea fortei normale (N_c1 din Figura 6.23) de la partea de beton direct conectata prin conectori de lunecare la partile de beton fara conectare directa ( in Figura 6.23, sectiunea A-A; aria hasurata din afara talpilor din Figura 6.23 se va considera ca nu este conectata direct).Calculul si dispunerea armaturii transversale se va baza pe un model de grinda cu zabrele considerand un unghi de 45° intre biela comprimata de beton si axa elementului.

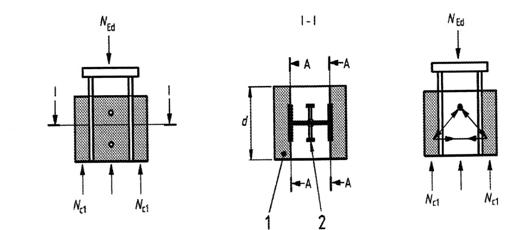
Legenda:

neconectata direct

conectata direct

Figura 6.23 Ariile de beton conectate si neconectate direct pentru calculul armaturii transversale

6.7.4.3 Lunecarea longitudinala in afara zonelor de transfer al incarcarilor

(1) In afara zonelor de transfer al incarcarilor , se va verifica forta de lunecare longitudinala la interfata intre beton si otel cauzata de forte taietoare si / sau momente. Conectorii de lunecare se vor dispune, pe baza distributiei eforturilor unitare de lunecare longitudinala de calcul cand acestea depasesc rezistenta la lunecare .

(2) In absenta unei metode mai riguroase , pentru a determina eforturile de lunecare la interfata ,se va utiliza calculul elastic, considerand efectele de lunga durata si fisurarea betonului.

(3) Pentru se pot considera valorile din Tabelul 6.6 in conditiile in care se asigura ca suprafata de otel in contact cu betonul nu este vopsita, acoperita cu ulei, grasime si nu este acoperita cu rugina sau cruste.

Tabelul 6.6 : Rezistenta la lunecare

(4) Valoarea data in Tabelul 6.6 pentru sectiuni de otel cu inglobare totala in beton se aplica sectiunilor cu o acoperire minima de 40mm si avand o armare longitudinala si transversala in concordanta cu 6.7.5.2. Pentru acoperiri mai mari si o armatura corespunzatoare , se pot folosi valori mai ridicate pentru . In cazul in care alte valori nu sunt verificate experimental, se pot folosi in cazul sectiunilor din otel cu inglobare totala in beton valori egale cu β_c in care β_c este dat de relatia :

(6.49)

unde :

c_z este valoarea nominala a acoperirii de beton , vezi Figura 6.17a;

c_z,min = 40mm este acoperirea minima cu beton

(5) In cazul sectiunilor I cu inglobare partiala in beton se vor folosi intotdeauna conectori de lunecare cand sunt solicitate la forta taietoare determinata din incovoierea dupa axa minora ,din incarcari laterale sau momente la extremitati. Cand in calculul fortei taietoare capabile nu se conteaza numai pe sectiunea otelului structural , armatura transversala care contribuie la forta taietoare capabila a sectiunii de beton V_c,Ed din 6.7.3.2(4) se va suda sau va trece prin inima sectiunii de otel.

6.7.5 Prevederi constructive

6.7.5.1 Acoperirea cu beton a profilelor de otel si a armaturii

(1)P Sectiunile de otel vor avea o acoperire minima cu beton armat pentru a se asigura transferul in siguranta al fortelor de aderenta, protectia la coroziune a otelului si impotriva despicarii betonului.

(2) Acoperirea cu beton a talpi de otel a unei sectiuni cu inglobare totala in beton nu va fi mai mica de 40mm , si 1/ 6 b unde b este latimea talpii.

(3) Acoperirea armaturii din otel beton va fi in concordanta cu EN 1992-1-1, Capitolul 5.

6.7.5.2 Armatura longitudinala si transversala

(1) Armatura longitudinala a stalpilor cu inglobare totala in beton care contribuie la momentul capabil la incovoiere a sectiunii nu va fi mai mica decat 0,3% din sectiunea de beton. In sectiunile din teava umpluta cu beton nu este in general necesara o armatura longitudinala daca nu se cere asigurarea rezistentei la foc.

(2) Armatura longitudinala si transversala din stilpii cu cu inglobare totala sau partiala in beton se va proiecta si detalia in concordanta cu EN 1992-1-1,9.5.

(3) Lumina dintre barele de armatura longitudinala si sectiunea de otel se poate reduce pana la 0 fata de cea impusa in (2) . In acest caz , perimetrul efectiv de aderenta c va fi considerat jumatate sau un sfert din perimetrul barei , asa cum este aratat in Figura 6.24 a) si respectiv b)

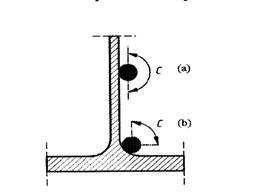
Figura 6.24 : Perimetrul efectiv c al unei bare de armatura

(4) Pentru elemente cu inglobare partiala sau totala in beton , in cazul unor conditii de mediu in clasa X20 conform EN 1992-1-1, Tabelul 4.1, si cand armatura longitudinala se neglijeaza in calcul, se prevede o armatura minima cu diametru 8mm la o distanta de 250mm, si o armatura transversala de 6mm la distanta de 200mm.Se poate utiliza ca varianta plasa sudata de diametru 4mm

6.8 Oboseala

6.8.1 Generalitati

(1)P Rezistenta la oboseala a structurilor compozite se va verifica in situatiile in care structurile sunt solicitate la fluctuatii repetate ale eforturilor unitare.

(2)P Proiectarea la starea limita de oboseala va asigura, cu un nivel acceptabil de probabilitate, ca pe toata durata proiectata de exploatare , structura nu va ceda sau nu va necesita reparatii ale avariilor din oboseala .

(3) In cazul conectorilor de lunecare tip dornuri cu cap , solicitati la combinatia caracteristica de incarcari , forta maxima de lunecare longitudinala a unui conector nu va depasi 0,75P_Rd , unde P_Rd este determinat conform 6.6.3.1.

(4) La cladiri nu se ia in considerare oboseala otelulul structural, a armaturii, a betonului si a conectorilor in cazul in care pentru otel se aplica conditiile din EN 1993-1-1,4(4) si pentru beton nu se aplica conditiile din EN 1992-1-1,6.8.1.

6.8.2 Coeficienti partiali pentru evaluarea oboselii

(1) Coeficientii partiali de siguranta pentru rezistenta la oboseala _Mf sunt dati in EN 1993-1-9,3 pentru elementele de otel si in EN 1992-1-1, 2.4.2.4 pentru beton si armatura.Pentru conectorii la lunecare , se aplica coeficientul partial γ _Mf,s.

Nota: Valoarea γ_Mf,s se va da in Anexa Nationala .Valoarea recomandata pentru γ_Mf,s este 1,0.

(2) Pentru incarcarile de oboseala se vor aplica coeficienti partiali γ_Ff.

Nota: Factorii partiali de siguranta γ_Ff pentru diferite tipuri de incarcari de oboseala se vor da in Anexa

Nationala.

6.8.3 Rezistenta la oboseala

(1) Rezistenta la oboseala pentru otel structural si suduri se va determina din EN 1993-1-9,7

(2) Rezistenta la oboseala a armaturii din otel-beton nepretensionata si pretensionata se va considera din EN 1992-1-1. Pentru beton se aplica EN 1992-1-1, 6.8.5.

(3) Curba rezistentei la oboseala a unui conector tip dorn cu cap sudat automat conform 6.6.3.1 este aratata in Figura 6.25 si este data pentru beton de greutate normala de relatia :

unde:

este rezistenta la oboseala corespunzatoare ariei sectiunii tijei dornului,calculata cu diametrul nominal al tijei.

este valoarea de referinta pentru 2milioane de cicluri cu

m este panta curbei rezistentei la oboseala, cu valoarea m = 8

N_R este numarul de cicluri in intervalul de eforturi unitare

(4) Pentru conectori inglobati in beton usor cu o clasa de densitate in concordanta cu EN 1992-1-1,11, rezistenta la oboseala se va determina conform (3) dar dupa inlocuirea cu si a

cu unde este dat in EN 1992-1-1.11.3.2.

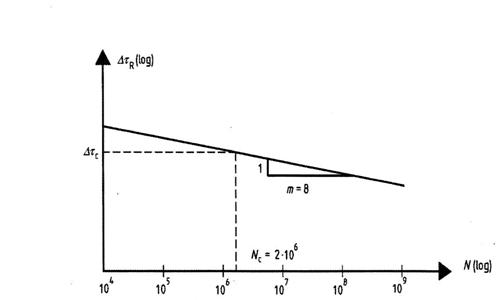
Figura 6.25 Curba rezistentei la oboseala pentru donuri cu cap in placi monolite din beton armat.

6.8.4 Eforturi sectionale si incarcari de oboseala

(1) Eforturile sectionale se vor determina printr-un calcul elastic global al structurii in concordanta cu 5.4.1 si 5.4.2 si pentru combinatiile de actiuni date in EN 1992-1-1,6.8.3.

(2) Eforturile sectionale maxime si minime rezultate din combinatiile conform (1) se definesc ca M_Ed,max,f si M_Ed,min,f .

(3) Incarcarea de oboseala se va obtine din capitolele corespunzatoare din EN 1991.In situatia in care nu se specifica incarcarea de oboseala , se poate utiliza EN 1993-1-9, Anexa A.1.

Cand se considera potrivit se poate folosi raspunsul dinamic al structurii sau efecte de impact.

6.8.5 Eforturi unitare

6.8.5.1 Generalitati

(1) Calculul eforturilor unitare se va baza pe 7.2.1.

(2) Pentru determinarea eforturilor unitare in zone fisurate, se va lua in calcul efectul rigidizarii la intindere a betonului asupra eforturilor unitare din armatura.

(3) Daca nu se verifica printr-o metoda mai riguroasa, efectul rigidizarii la intindere asupra eforturilor unitare ale armaturii se va considera in calcul conform 6.8.5.4.

(4) Daca nu se utilizeaza o metoda mai riguroasa , se va neglija efectul rigidizarii la intindere in calculul eforturilor unitare din otelul structural .

6.8.5.2 Beton

(1) Pentru determinarea eforturilor unitare in componentele de beton se va aplica EN 1992-1-1,6.8.

6.8.5.3 Otel structural

(1) In cazul in care momentele M_Ed,max,f si M_Ed,min,f determina eforturi unitare de intindere in placa de beton , eforturile unitare ale otelului structural pentru aceste momente incovoietoare se vor determina pe baza momentului de inertie I₂ conform cu 1.5.2.12.

(2) In cazul in care momentele M_Ed,max,f si M_Ed,min,f sau numai M_Ed,min,f determina compresiuni in placa de beton , eforturile unitare ale otelului structural pentru aceste momente se vor determina cu proprietatile sectiunii transversale nefisurate.

6.8.5.4 Armatura

(1) In cazul in care momentul M_Ed,max,f determina eforturi unitare de intindere in placa de beton ,si nu se utilizeaza o metoda mai riguroasa , efectul rigidizarii la intindere al betonului asupra efortului unitar σ_s,max,f in armatura corespunzator acestui moment se vor determina din relatiile de la (7.4) la (7.6) din 7.4.3(3). In ecuatia (7.5) din 7.4.3(3) , in locul factorului 0,4 se va folosi factorul 0,2.

(2) In cazul in care chiar si momentelul M_Ed,min,f determina eforturi unitare de intindere in placa de beton, intervalul de eforturi unitare Δσ este dat in Figura 6.26 iar efortul σ_s,min,f din armatura corespunzator M_Ed,min,fse va determina din :

σ_s,min,f = σ_s,max,f (6.51)

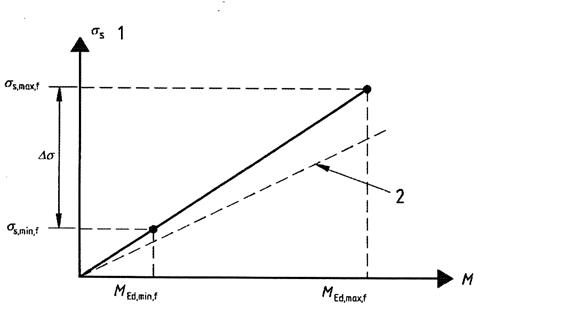
Legenda

placa intinsa

sectiune complet fisurata

Figura 6.26 : Derminarea σ_s,max,f si σ_s,min,f in zone fisurate

(3) In cazul in care momentele M_Ed,max,f si M_Ed,min,f sau numai M_Ed,min,f determina compresiuni in placa de beton , eforturile unitare in armatura corespunzatoare acestor momente incovoietoare se vor determina cu proprietatile sectiunii transversale nefisurate.

6.8.5.5 Conectori de lunecare

(1)P Lunecarea longitudinala pe unitatea de lungime se va calcula printr-un calcul elastic.

(2) In elemente in care are loc fisurarea betonului se va tine cont de efectul rigidizarii la intindere printr-un model corespunzator. Pentru simplificare , fortele de lunecare longitudinale la interfata dintre otelul structural si beton se vor determina utilizand proprietatile sectiunii nefisurate.

6.8.6 Domeniul eforturilor unitare

6.8.6.1 Otelul structural si armatura

(1) Intervalul de eforturi unitare se va determina din eforturile unitare obtinute in concordanta cu 6.8.5.

(2) In cazul in care verificarea la oboseala se bazeaza pe domeniul eforturilor unitare echivalente de avariere, intervalul Δσ_E se va determina in general din :

Δσ_E = λ Φ‌│σ_max,f + σ_min,f │ (6.52)

unde :

σ_max,f si σ_min,f sunt eforturile unitare maxime si minime conform 6.8.4 si 6.8.5;

λ este factorul echivalent de avariere

Φ este factorul echivalent de avariere din impact.

(3) In cazul in care un element este supus actiunii combinate a efectelor globale si locale se vor considera separat aceste efecte .Daca nu se utilizeaza o metoda mai precisa ,amplitudinile constante ale eforturilor unitare echivalente determinate de efectele globale si locale se vor combina utilizand:

Δσ_E = λ_glob Φ_glob ‌Δσ_E,glob + λ_loc Φ_loc ‌Δσ_E,loc (6.53)

in care indicii 'glob' si 'loc' se refera la efectele globale si respectiv locale.

(4) Pentru otelul structural Δσ_E se va considera ca intervalul de eforturi unitare Δσ_E2 definit in

EN 1993-1-9,1.3 iar pentru armatura ca intervalul Δσ_s,equ dat in EN 1992-1-1, 6.8.5.

(5) Factorul echivalent de avariere λ este definit pentru elemente de otel in EN 1993-1-9,6.2 , si pentru armatura din otel in capitolele corespunzatoare din EN 1992

(6) In cazul in care pentru λ nu se specifica o valoare , factorul echivalent de avariere se va determina conform EN 1993-1-9, anexa A , utilizand panta curbei corespunzatoare a rezistentei la oboseala.

6.8.6.2 Conectori de lunecare

(1) Pentru verificarea conectorilor de lunecare tip dorn cu cap pe baza intervalului eforturilor unitare nominale, intervalul constant de eforturi tangentiale pentru 2 milioane de cicluri este dat de :

= λ_v Δt (6.54)

unde :

λ_v este factorul echivalent de avariere care depinde de spectrul si panta m ale curbei rezistentei la oboseala

este intervalul de eforturi unitare tangentiale datorate incarcarii de oboseala , raportata la aria sectiunii transversale a tijei conectorului utilizand diametrul nominal d al tijei.

(2) Amplitudinea echivalenta constanta a intervalului de eforturi unitare tangentiale in cazul conectorilor de lunecare sudati sau de alte tipuri se va calcula in concordanta cu EN 1993 1993-1-9,6.

(3) In cazul in care nu se specifica pentru cladiri o valoare pentru λ_v , factorul echivalent de avariere se va determina in concordanta cu EN 1993-1-9, anexa A utilizand panta corespunzatoare a curbei rezistentei la oboseala a conectorului ,data in 6.8.3.

6.8.7 Evaluarea oboselii pe baza domeniului eforturilor unitare nominale

6.8.7.1 Otel structural , armatura si beton

(1) Evaluarea oboselii pentru armatura va respecta EN 1992-1-1, 6.8.5 sau 6.8.6.

(2) Verificarea betonului comprimat se va realiza conform EN 1992-1-1, 6.8.7.

(3) Evaluarea oboselii otelului structural va urmari EN 1993-1-9, 8.

6.8.7.2 Conectori de lunecare

(1) Pentru conectori dornuri cu cap sudati de o talpa comprimata in toate combinatiile semnificative de actiuni ( vezi 6.8.4 (1) ) , evaluarea oboselii se va face prin verificarea criteriului:

(6.55)

unde

este definit in 6.8.6.2(1)

este valoarea de referinta a rezistentei la oboseala pentru 2 milioane de

cicluri in concordanta cu 6.8.3.

(2) In cazul in care efortul unitar maxim in talpa de otel pe care se sudeaza conectorul este de intindere pentru combinatia cea mai semnificativa de incarcari, se va verifica in orice sectiune interactiunea intre intervalul eforturilor tangentiale in sudura dornurilor si intervalul eforturilor normale in talpa de otel utilizand urmatoarele relatii de interactiune .

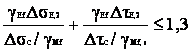
unde:

este intervalul de eforturi unitare in talpa determinat in concordnta cu 6.8.6.1;

este valoarea de referinta a rezistentei la oboseala data in EN 1993-1-9,7 pentru

categoria 80 si

intervalele de eforturi unitare si sunt definite in (1).

Relatia (6.5.6) se va verifica pentru urmatoarele situatii :valoarea maxima a cu valoarea corespunzatoare si valoarea maxima a cu valoarea corespunzatoare . Cu exceptia cazului in care rigidizarea betonului la intindere se ia in calcul printr-o metoda mai riguroasa, criteriul de interactiune se va verifica pentru intervalele de eforturi unitare determinate atat pentru proprietatile sectiunii fisurate cat si pentru cele ale sectiunii nefisurate.

Capitolul 7 Starile limita ale exploatarii normale

7.1 Generalitati

(1)P O structura din elemente compozite va fi proiectata si executata astfel ca toate starile limita relevante ale exploatarii normale sa fie satisfacute, conform principiilor din 3.4.EN 1990.

Verificarea starilor limita ale exploatarii normale se va baza pe criteriile din EN 1990, 3.4(3).

Starile limita ale exploatarii normale pentru placi compozite alcatuite din tabla cutata se vor verifica conform Sectiunii 9.

7.2 Eforturi unitare

7.2.1 Generalitati

(1)P Calculul eforturilor unitare pentru grinzi in starea limita a expolatarii normale va lua in considerare urmatoarele efecte, acolo unde acestea sunt relevante:

- variatia eforturilor de forfecare;

- curgerea lenta si contractia betonului;

- fisurarea betonului si sporul de rigiditate la intindere a betonului;

- ordinea de executie,

- flexibilitate sporita provocata de o semnificativa interactie incompleta datorita lunecarii

conexiunii la forfecare;

omportarea inelastica a otelului si betonului, daca exista;

torsiune si distorsiune impiedicata, daca exista.

(2) Variatia eforturilor de forfecare va fi luata in considerare conform 5.4.1.2.

(3) Daca nu se foloseste o metoda mai exacta, efectele curgerii lente si contractiei pot fi luate in considerare folosind rapoartele modulare, conform 5.4.2.2.

(4) In sectiuni fisurate, efectele primare ale contractiei pot fi neglijate cand se verifica eforturile unitare.

(5)P In calculul sectiunilor, se va neglija rezistenta la intinderea betonului.

(6) Se va lua in considerare influenta consolidarii la intindere betonului intre fisuri asupra eforturilor unitare in armatura si in otelul de precomprimare. Daca nu se folosesc metode mai exacte, eforturile unitare in armaturi se vor determina conform 7.4.3.

(7) Influentele consolidarii la intindere asupra eforturilor unitare din armatura rigida pot fi neglijate.

(8) Efectele interactiunii incomplete pot fi ignorate, daca se prevede o conectiune de forfecare totala si daca, in cazul unei conexiuni de forfecare partiala la cladiri, se aplica 7.3.1.(4).

7.2.2. Limitari ale eforturilor unitare la cladiri

(1) Limitarea eforturilor unitare nu este ceruta la grinzi daca, in starea limita ultima, nu se cere o verificare la oboseala si nu se aplica precomprimarea prin cable si/sau prin deformatii controlate impuse (de exemplu tensionarea reazemelor).

(2) Pentru stalpi compoziti in cladiri in mod normal nu se aplica limitari ale eforturilor unitare.

(3) Daca sunt necesare, se aplica limitarile eforturilor unitare in beton si armatura, precizate in EN 1992-1,7.2.

7.3 Deformatii la cladiri

7.3.1 Sageti

(1) Sagetile datorita incarcarii aplicate numai pe elementul de metal se vor calcula conform EN 1993 -1-1.

(2) Sagetile datorita incarcarilor aplicate pe elementul compozit se vor calcula folosind calcul elastic, conform sectiunii 5.

(3) Nivelul de referinta pentru sageata verticala δ_max a grinzii neproptite este fibra superioara a grinzii compozite. Numai cand sageata poate afecta aspectul cladirii se va lua ca nivel de referinta intradosul grinzii.

(4) Efectele interactiunii incomplete pot fi neglijate daca:

a)      proiectarea conexiunii de forfecare este conform 6.6,

b)      fie daca sunt folositi nu mai putin de jumatate din numarul de conectori de forfecare necesari pentru o conectare de forfecare totala, fie fortele rezultate dintr-o comportare elastica si care actioneaza pe conectorii de forfecare in starea limita a exploatarii normale nu depasesc P_Rd si

c)      in cazul unei placi nervurate cu nervuri transversale fata de grinda, inaltimea nervurilor nu depaseste 80mm.

(5) Efectul asupra sagetii al fisurarii betonului in zonele de momente negative va fi luat in considerare adoptand metodele de calcul precizate in 5.4.2.3.

(6) Pentru grinzi avand sectiuni critice de clasele 1, 2 sau 3 se poate folosi urmatoarea metoda simplificata. La fiecare reazim intermediar in care σ_ct depaseste 1,5 f_ctm sau 1,5 f_lctm, dupa caz, momentul incovoietor determinat printr-un calcul nefisurat definit in 5.4.2.3(2) se multiplica cu coeficientul de reducere f1 din fig.7.1, iar sporuri corespunzatoare se fac asupra momentelor incovoietoare din deschiderile adiacente. Curba A se va folosi numai pentru deschideri interioare, daca incarcarile pe unitate de lungime sunt egale in toate deschiderile, iar deschiderile nu difera cu mai mult de 25%. In caz contrar, se va folosi valoarea limita inferioara aproximativa f₁ = 0.6 (linia B).

(7) Pentru calculul sagetilor grinzilor nesprijinite se poate lua in considerare influenta curgerii locale a otelului rigid in dreptul unui reazim, prin multiplicarea momentului incovoietor la reazim, determinat conform metodelor prezentate in clauza de fata cu un coeficient de reducere suplimentar, dupa cum urmeaza:

- f₂ = 0.5 daca f_y se atinge inaintea intaririi placii de beton;

- f₂ = 0.7 daca f_y se atinge dupa intarirea placii de beton.

Aceasta se aplica la determinarea sagetii maxime, dar nu pentru contrasageata.

Fig. 7.1: Coeficientul de reducere al momentului incovoietor pe reazim.

(8) Daca nu se solicita in mod special de catre client, efectul curburii datorita contractiei betonului de greutate normala nu este necesar sa fie inclus, daca raportul deschiderii catre inaltimea totala a grinzii nu este mai mare de 20.

7.3.2 Vibratii

(1) Proprietatile dinamice ale grinzilor de planseu vor satisface criteriile din EN 1990, A1.4.4.

7.4 Fisurarea betonului

7.4.1 Generalitati

(1) Pentru limitarea deschiderii fisurilor se aplica la structuri compozite consideratiile generale din EN 1992-1-1, 7.3.1(1)-(9). Limitarea deschiderii fisurilor depinde de clasele de expunere, conform EN 1992-1-1,4.

(2) O estimare a deschiderii fisurilor se poate obtine din EN 1992-1-1, 7.3.4, in care efortul unitar σ_s trebuie calculat considerand efectele consolidarii la intindere. σ_s poate fi determinat conform 7.4.3(3), daca nu se foloseste o metoda mai precisa.

(3) Ca o alternativa simplificatoare si conservativa, limitarea fisurii la o deschidere acceptabila poate fi obtinuta prin asigurarea unei armari minime, definita la 7.4.2, iar distantele intre bare sau diametrele sa nu depaseasca limitele definite la 7.4.3.

(4) Cand grinzile in cladiri sunt proiectate ca simplu rezemate, desi placa este continua iar controlul deschiderii fisurilor nu are importanta, armarea longitudinala introdusa in latimea efectiva a placii de beton, conform 6.1.2, nu va fi mai mica decat:

- 0.4% din aria de beton pentru executie cu sprijinire

- 0.2% din aria de beton pentru executie fara sprijinire.

Armarea in grinda proiectata ca simplu rezemata se va prelungi cu o lungime de 0.25L de fiecare parte a unui reazim interior, sau 0.5L adiacenta unei console, in care L este lungimea deschiderii, respectiv lungimea consolei. Nu se va tine seama de orice fel de tabla cutata. Distanta maxima intre bare va fi conform 9.2.1(5), pentru o placa compozita sau conform EN 1992-1-1, 9.3.1.1(3), in cazul unei placi de beton masive.

7.4.2 Armarea minima

(1) Daca nu se foloseste o metoda mai precisa conform EN 1992-1-1, 7.3.2(1), in toate sectiunile fara precomprimare prin cable supuse unei intinderi semnificative datorita constrangerilor din deformatii impuse (adica efectele primare si secundare ale contractiei), in combinatie sau nu cu efectele incarcarii directe, armarea minima necesara A_s pentru placilegrinzilor compozite este data de:

A_s = k_s k_c k f_ct,eff A_ct /σ_s (7.1)

In care:

f_ct,eff este valoarea medie a rezistentei la intindere a betonului efectiva la varsta cand este de

asteptat ca fisurile vor incepe sa apara. Valorile f_ct,eff pot fi considerate a fi f_ctm,

conform EN 1992-1-1, Tabel 3.1, sau f_lctm, din Tabelul 11.3.1, dupa cum este cazul,

admitand drept clasa de rezistenta a betonului cea de la varsta cand se presupune ca are

loc fisurarea. Daca varsta betonului la fisurare nu poate fi stabilita cu un grad de

confidenta ca fiind sub 28 zile, se va adopta o rezistenta minima de intindere de 3 N/mm².

k este un coeficient ce tine seama de efectul eforturilor unitare neuniforme si autoechilibrate,

coeficient care poate fi luat cu valoarea 0.8;

k_s coeficient care tine seama de efectul de reducere a fortei axiale a placii de beton, datorita

fisurarii initiale si a lunecarii locale a conexiunii de forfecare, coeficient ce poate fi luat cu

valoarea 0.9;

k_c coeficient care tine seama de distributia de eforturi unitare pe sectiune, imediat inainte de

fisurare si este dat de:

k_c = 1/ [1 + h_c/( 2z₀ )] + 0.3 ≤ 1.0 (7.2)

h_c este grosimea talpii din beton, excluzand orice nervuratii;

z₀ este distanta verticala intre centrele de greutate ale talpii nefisurate de beton si al sectiunii

nefisurate compozite, calculata folosind raportul modular n₀ pentru incarcari de scurta

durata.

σ_s este efortul unitar maxim admis in armatura, imediat dupa fisurare. Acseta se poate

considera ca fiind rezistenta de curgere caracteristica f_sk. O valoare inferioara, dependenta

de dimensiunea barelor, ar putea fi totusi necesara pentru satisfacerea limiteelor prescrise

ale deschiderii fisurilor. Aceasta valoare este data in tabelul 7.1.

A_ct este aria zonei intinse (cauzata de incarcarea directa si efectele primare ale contractiei).

Imediat inaintea fisurarii sectiunii transversale. Pentru a simplifica, se poate folosi aria

sectiunii de beton din interiorul sectiunii efective.

(2) Diametrul maxim al barelor pentru armarea minima se poate modifica la valoarea Ø, data de:

Ø = Ø* f_ct,eff / f_ct,0 (7.3)

In care:

Ø* este diametrul maxim al barelor precizat in Tabelul 7.1;

f_ct,0 este o rezistenta de referinta cu valoarea de 2.9 N/mm².

Tabelul 7.1 Diametre maxime pentru bare cu adeziune inalta

(3) Cel putin jumatate din armatura minima necesara trebuie amplasata intre jumatatea inaltimii placii si fata supusa la cea mai mare deformatie specifica de intindere.

(4) La determinarea armaturii minime in talpile din beton cu grosimi variabile perpendicular pe directia grinzii, se va folosi grosimea locala.

(5) La cladiri, armarea minima conform (1) si (2) se va amplasa acolo unde, sub gruparile caracteristice de actiuni, eforturile unitare sunt de intindere.

(6) La cladiri, armarea minima longitudinala inferioara pentru inglobarea in beton a inimii unui profil metalic dublu T se va determina din expresia (7.1), luand k_c = 0.6 si k = 0.8.

7.4.3 Controlul fisurarii datorita incarcarilor directe

(1) Daca s-a introdus cel putin armarea minima prevazuta in 7.4.2 , limitarea deschiderii fisurilor la valori acceptabile se poate realiza in general limitand distantele intre barele de armatura sau diametrele barelor. Diametrele maxime ale barelor de armatura si distantele maxime intre bare depind de efortul unitar σ_s in armatura si deschiderea de fisura admisa prin proiect.

(2) Eforturile sectionale se vor determina prin calcul in domeniul elastic, conform Sectiunii 5, luand in considerare efectele fisurarii betonului. Eforturile unitare in armaturi se vor determina luand in considerare consolidarea betonului la intindere intre fisuri. Daca nu se foloseste o metoda mai precisa, eforturile unitare se pot calcula conform (3).

(3) In grinzi compozite in care placa de bewton se presupune ca este fisurata si nu precomprimata prin cable, eforturile unitare in armaturi cresc datorita efectelor consolidarii la intindere a betonului

Tabelul 7.2 Distante maxime intre bare cu adeziune inalta

intre fisuri, in comparatie cu eforturile unitare bazate pe o sectiune compozita in care se neglijeaza betonul. Eforturile unitare de intindere in armatura σ_s din incarcari direct aplicate se pot calcula din:

σ_s = σ_s,0 + ∆σ_s (7.4)

cu notatiile:

∆σ_s = 0.4 f_ctm / [ α_st ρ_s ] (7.5)

α_s = A I / A_a I_a (7.6)

in care:

σ_s,0 este efortul unitar in armatura provenit di eforturile sectionale aplicate pe sectiunea

compozita, cu neglijarea betonului intins;

f_ctm este rezistenta medie la intindere a betonului pentru beton normal, considerata a fi

f_ctm din EN1992-1-1, Tabelul 3.1 sau pentru beton usor ca f_lctm din Tabelul 11.3.1;

ρ_s este coeficientull de armare ρ_s = A_s / A_ct ;

A_ct este aria efectiva a talpii de beton din zona intinsa; pentru simplitate, se poate folosi

aria sectiunii de beton din cadrul latimii efective;

A_s este aria totala a tuturor randurilor de armaturi longitudinale din interiorul ariei efective

A_ct

A, I sunt aria si respectiv momentul de inertie ale sectiunii compozite efective, cu

neglijarea betonului din zona intinsa precum si a tablei cutate, daca exista;

A_a, I_a sunt aria si respectiv momentul de inertie ale sectiunii de otel.

(4) La cladiri fara precomprimare prin cable, gruparea cvasi-permanenta de actiuni se va folosi in mod normal pentru determinarea σ_s .

Capitolul 8 Noduri de cadre compozite pentru cladiri

8.1. Domeniul de aplicare

(1) Nodul compozit este definit la 1.5.2.8. Cateva exemple sunt aratate in figura 8.1. Alte noduri in cadre compozite trebuie proiectate conform EN 1992-1-1 sau EN 1993-1-8, dupa cum este cazul.

(2) Capitolul 8 se ocupa de noduri supuse predominant la incarcari statice. Se suplimenteaza sau se modifica EN 1993-1-8.

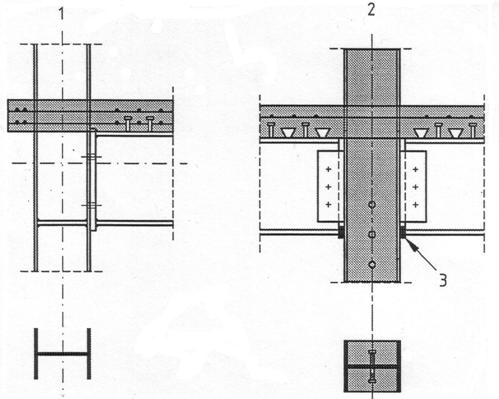
Legenda

1 configuratie unilaterala

2 configuratie bilaterala

3 placa de contact

Figura 8.1 : Exemple de noduri compozite

8.2 Calcul, modelare si clasificare

8.2.1 Generalitati

(1) Prevederile din EN1993-1-8, 5 referitoare la noduri ce leaga sectiuni H sau I se aplica cu modificarile din 8.2.2 si 8.2.3 de mai jos.

8.2.2 Calcul global elastic

(1) Daca rigiditatea rotationala Sj se ia ca avand valoarea Sj,ini/η conform EN 1993-1-8, 5.1.2, valoarea coeficientului de modificare a rigiditatii η pentru o conexiune placa-contact se va lua cu valoarea 1.5.

8.2.3 Clasificarea nodurilor

(1) Nodurile se vor clasifica conform EN 1993-1-8, 5.2, luand in considerare comportarea compozita.

(2) La clasificare, se vor lua in considerare directiile eforturilor sectionale.(forte si momente).

(3) Fisurarea si curgerea lenta in elementele ce se conecteaza pot fi neglijate.

8.3 Metode de calcul

8.3.1 Bazele si domeniul de aplicare ale metodelor

(1) EN 1993-1-8, 6 poate fi folosit la proiectarea nodurilor compozite intre grinzi si stalpi precum si la proiectarea innadirilor, daca partea de otel rigid a nodului se afla in domeniul de aplicare al acestei sectiuni.

(2) Proprietatile structurale ale componentelor acceptate in proiectare se vor baza pe incercari sau pe metode analitice sau numerice confirmate prin incercari.

Nota: Proprietatile componentelor sunt precizate in 8.4 si Anexa A de mai jos precum si in EN 1993-1-8, 6.

(3) La determinarea proprietatilor structurale ale unui nod compozit, un rand de bare de armatura poate fi tratat intr-un mod similar cu un rand de suruburi solicitate la intindere intr-o imbinare metalica, daca proprietatile structurale sunt cele ale armaturii.

8.3.2 Rezistenta

(1) Nodurile compozite trebuie proiectate pentru a rezista la forta taietoare verticala, conform prevederilor corespunzatoare din EN 1993-1-8.

(2) Momentul rezistent de proiectare al unui nod compozit cu conexiune de forfecare totala se va determina prin analogie cu prevederile pentru noduri in constructii metalice precizate in EN 1993-1-8, 6.2.7, luand in considerare contributia armaturii.

(3) Rezistenta componentelor se vor determina conform 8.4 de mai jos si conform EN 1993-1-8, 6.2.6, dupa cum este cazul.

8.3.3 Rigiditatea la rotire

(1) Rigiditatea rotationala a unui nod se va determina prin analogie cu prevederile pentru noduri in constructii metalice din EN 1993-1-8, 6.3.1, luand in considerare contributia armaturii.

(2) Valoarea coeficientului ψ, vezi EN 1993-1-8, 6.3.1(6), se poate lua 1.7, pentru un nod cu placa de contact.

8.3.4 Capacitatea de rotire

(1) Influenta fisurarii betonului, consolidarii in intindere si deformatia conexiunii de forfecare se vor lua in considerare la determinare capacitatii rotationale.

(2) Capacitatea rotationala a unui nod compozit se poate demonstra cu date experimentale. Se va lua in considerare variatiunile posibile ale proprietatilor materialelor fata de valorile caracteristice specificate. Demonstrarea experimentala nu este necesara daca se folosesc detalii pe care experienta la demonstrat ca poseda proprietati adecvate.

(3) Ca alternativa, se pot folosi metode de calcul, daca acestea sunt fundamentate prin incercari.

8.4 Rezistenta componentelor

8.4.1 Domeniul de aplicare

(1) Rezistenta urmatoarelor componente de baza ale nodurilor se vor determina conform 8.4.2 de mai jos:

- armatura longitudinala intinsa;

- placa metalica de contact comprimata.

(2) Rezistent’a componentelor identificate in EN 1993-1-8 trebuie luata cum este definita acolo, cu exceptia celor precizate la 8.4.3 mai jos.

(3) Rezistenta inimilor inglobate in beton ale sectiunilor stalpilor metalici trebuie determinata conform 8.4.4 de mai jos.

8.4.2 Componentele de baza ale nodului

8.4.2.1 Armaturile longitudinale din otel beton la intindere

(1) Latimea efectiva a talpii de beton va fi determinata pentru sectiunea transversala din dreptul conexiunii, conform 5.4.1.2.

(2) Se admite ca aria efectiva a armaturii longitudinale intinse este solicitata la valoarea limitei de curgere de proiect fsd.

(3) Acolo unde apar incarcari neechilibrate se poate folosi un model biela-tirant pentru verificarea transmiterii fortelor din placa de beton in stalp

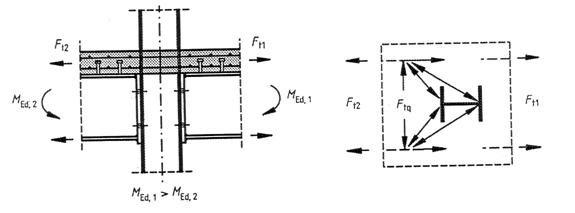
Figura 8.2: Model biela-tirant

(4) In cazul unei configuratii unilaterale proiectata ca un nod compozit, armatura efectiva longitudinala intinsa a placii trebuie ancorata suficient cu mult dincolo de deschiderea grinzii, pentru a permite dezvoltarea rezistentei de proiectare la intindere.

8.4.2.2 Placa metalica de contact la compresiune

(1) Daca inaltimea sau latimea placii de contact depaseste dimensiunea corespunzatoare a talpii comprimate a sectiunii de metal rigid, dimensiunea efectiva se va determina considerand repartitia la 45⁰ prin placa de contact.

(2) Se presupune ca aria efectiva a placii de contact comprimata

Inima stalpului solicitata la compresiune transversala

(1) Pentru o conexiune de placa de contact, latimea efectiva a inimii stalpului in compresiune b_eff,c,wc va fi determinata admitand repartitia la 45^o, prin placa de contact.

Componente armate

Panoul inimii de stalp la forfecare

(1) Cand inima stalpului metalic este inglobata in beton, vezi Figura 6.17b, rezistenta de forfecare de proiectare a panoului, determinata conform EN 1993-1-8, 6.2.6.1 poate fi sporita pentru a tine seama de inglobare.

(2) In cazul unui nod unilateral sau al unui nod bilateral in care inaltimile grinzilor sunt similare, rezistenta la forfecare de proiectare a betonului de inglobare a panoului inimii stalpului V_wp,c,Rd se va determina folosind relatia:

V_wp,c,Rd = 0.85 ν A_c f_cd sin θ (8.1)

cu notatiile:

A_c = 0.8 (b_c- t_w) (h – 2 t_f) cos θ (8.2)

θ = arctg [(h - 2t_f) / z ] (8.3)

In care:

b_c este latimea betonului inglobat;

h este inaltimea sectiunii stalpului;

t_f este grosimea talpii stalpului;

t_w estee grosimea inimii stalpului;

z este bratul de parghie, vezi EN 1993-1-8, 6.2.7.1 si Figura 6.15.

(3) Coeficientul de reducere ν, care tine seama de efectul compresiunii longitudinale in stalp asupra rezistentei de proiectare a panoului inimii stalpului la forfecare, se va determina dupa relatia:

ν = 0.55 [(1 + 2 (N_ed/ N_pl,Rd))] ≤ 1.1 (8.4)

in care:

N_ed este forta axiala de compresiune in stalp;

N_pl,Rd este rezistenta de proiectare plastica a sectiunii transversale a stalpului, inclusiv

Inglobarea, vezi 6.7.3.2.

8.4.4.2 Inima stalpului la compresiune transversala

(1) Daca inima stalpului metalic este inglobata in beton, rezistenta de proiectare a inimiistalpului la compresiune, determinata conform EN 1993-1-8, 6.2.6.2 poate fi sporita pentru a tine seama de inglobare.

(2) Rezistenta de proiectare a betonului de inglobare a inimii stalpului la compresiune transversala

F_c,wc,c,Rd se determina din relatia:

F_c,wc,c,Rd = 0.85 k_wc,c t_eff,c ( b_c - t_w )f_cd (8.5)

In care:

t_eff,c este lungimea efectiva a betonului , determinata in mod analog cu latimea efectiva

b_eff,c,wc definita in EN 1993-1-8, 6.2.6.2.

(3) Daca betonul de inglobare este supus unui efort unitar de compresiune longitudinal, efectul sau asupra rezistentei betonului de inglobare la compresiune transversala poate fi luat in considerare prin amplificarea valorii F_c,wc,c,_Rd cu un coeficient k_wc,c dat de:

k_wc,c = 1.3 + 3.3 ( σ_com,c,Ed / f_cd ) ≤ 2.0 (8.6)

in care:

σ_com,c,Ed este efortul unitar longitudinal de compresiune in betonul de inglobare datorit

fortei axiale N_Ed .

In absenta unei metode mai exacte, σ_com,c,Ed se poate determina din contributia relativa a betonului de inglobare la rezistenta plastica a sectiunii stalpului la compresiune N_pl,Rd , vezi 6.7.3.2.

Capitolul 9 Placi compozite cu tabla cutata la cladiri

9.1 Generalitati

9.1.1 Domeniul de aplicare

(1)P Aceasta sectiune se ocupa de placi compozite de planseu, cu deschideri numai in directia cutelor. Sunt incluse de asemenea placile in consola. Se aplica la proiecte de structuri de cladiri, unde incarcarile aplicate sunt predominant statice, inclusiv cladiri industriale, ale caror plansee pot fi actionate de incarcari mobile.

(2)P Domeniul de aplicare este restrictionat la tabla cutata, avand cute la intervale mici.

Nota: Tabla cutata cu cute dese este definita printr-o limita superioara a raportului b_r/b_s, vezi

Figura 9.2. Valoarea limitei poate fi data in Anexa Nationala. Valoarea recomandata

este 0.6.

(3)P La structuri la care incarcarea aplicata este in mare masura repetitiva sau se aplica abrupt, producand efecte dinamice, se adamit placi compozite, dar se va acorda o atentie sepciala la proiectarea de detaliu, pentru ca efectul de conlucrare sa nu se deterioreze in timp.

(4)P Placile supuse la incarcari seismice nu sunt excluse, cu conditia sa se defineasca o metoda de proiectare corespunzatoare pentru situatiile seismice, in proiectul respectiv sau sa se dea in alt Eurocod.

(5) Placile compozite pot fi folosite pentru a oferi legaturi laterale ale grinzilor metalice si pot actiona ca diafragme rezistente la actiuni orizontale, dar in prezentul Standard nu se dau reguli specifice. In ce priveste efectul de diafragma al tablei cutate actionand ca un cofraj, se aplica regulile date in EN 1993-1-3, 10.

Definitii

Tipuri de conectori de forfecare

Tabla cutata va fi capabila sa transmita forfecari orizontale la interfata intre tabla si beton; adeziunea pura intre tabla cutata si beton nu se considera efectiva in comportarea compozita. Comportarea compozita intre tabla cutata si beton va fi asigurata prin una sau mai multe din urmatoarele mijloace, vezi Figura 9.1:

a)        inclestare mecanica data de deformatiile profilului (indentari sau embose);

b)       inclestare de frecare pentru profile de forma coada de randunica;

c)        ancoraje de capat date de dornuri sudate sau alte tipuri de conectori locali, intre beton si tabla cutata, numai in combinatie cu (a) sau (b);

d) ancoraje de capat prin deformarea cutelor la capatul tablei cutate, numai in combinatie cu

(b).

Alte mijloace nu se exclud, dar nu intra in sfera acestui standard.

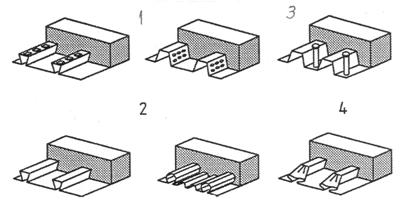
Legenda

1 inclestare mecanica

2 i nclestare de frictiune

3 ancorare de capat prn prin dornuri sudate

4 ancorare de capat prin deformarea cutelor

Figura 9.1: Forme de inclestare tipice in placi compozite

9.1.2.2 Conectare integrala si conectare partiala la forfecare

O deschiderea a unei placi are o conexiune de forfecare totala daca un spor de rezistenta al conexiunii de forfecare longitudinala nu sporeste rezistenta de proiectare la incovoiere a elementului. In caz contrar, conexiunea este partiala.

9.2 Prevederi pentru detaliere

9.2.1 Grosimea si armarea placii

(1)P Inaltimea totala a placii compozite h nu va fi mai mica de 80mm. Grosimea betonului h_c deasupra suprafetei superioare a tablei cutate nu va fi mai mica de 40mm.

(2)P Daca placa lucreaza compozit impreuna cu grinda sau este folosita ca diafragma, inaltimea totala nu va fi mai mica de 90mm iar h_c nu va fi mai mic de 50mm.

(3)P Se va prevedea armatura longitudinala si transversala in grosimea h_c a betonului.

Cantitatea de armatura pe ambele directii nu va fi mai mica de 80 mm²/m.

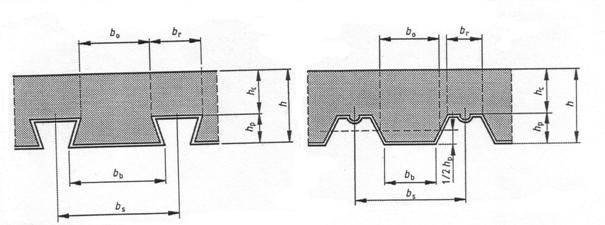
Figura 9.2: Dimensiunile tablei cutate si ale placii

(5) Distanta intre barele de armatura nu va depasi 2h sau 350mm, care valoare este mai mica.

9.2.2. Agregate

(1)P Dimensiunea nominala a agregatelor depinde de dimensiunea cea mai mica a elementului structural in care se toarna beton si nu va depasi cea mai mica valoare din:

0.40 h_c , vezi Figura 9.2;

b₀ / 3 , in care b₀ este latimea medie a cutelor (in cazul cutelor coada de randunica latimea minima, vezi Figura 9.2;

31.5 mm (sita C 31.5).

9.2.3 Cerinte de rezemari

(1)P Lungimea rezemarii va fi astfel incat se evite deteriorarea placii si a reazemului; fixarea tablei pe reazem sa se faca fara deteriorarea reazemului si prabusirea sa nu poata sa se intample ca rezultat al unei deplasari accidentale in timpul montajului.

(2) Lungimile de rezemare l_bc si l_bs indicate pe Figura 9.3 vor fi nu mai mici decat urmatoarele valori:

pentru placi compozite rezemate pe metal sau pe beton: l_bc = 75 mm si l_bs = 50 mm;

pentru placi compozite rezemate pe alte materiale: l_bc = 100 mm si l_bs = 70 mm.

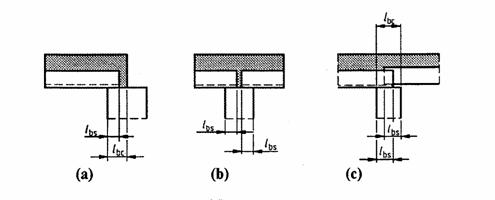
Nota: suprapunerea unor profile cutate este nepractica.

Figura 9.3: Lungimi minime de rezemare

9.3 Actiuni si efectele lor

9.3.1 Situatii prevazute in proiectare

(1)P Toate situatiile relevante pentru proiectare precum si starile limita corespunzatoare vor fi considerate in proiectare, pentru asigurarea unor grade adecvate de siguranta si de comportare in exploatare.

(2)P Se vor lua in considerare urmatoarele situatii:

a)      Tabla cutata considerata cofraj pierdut. Este necesara verificarea comportarii tablei cutate

cand actioneaza ca un cofraj pentru betonul proaspat. Se va tine seama de efectul spriji-

nirilor, daca acestea exista.

b)      Placa compozita: Este necesara verificarea placii planseului, dupa ce comportarea

compozita a inceput si eventualele sprijiniri au fost indepartate.

9.3.2 Actiuni asupra tablei cutate intrebuintata drept cofraj.

(1) Se vor lua in considerare urmatoarele incarcari in calculul tablei cutate considerata cofraj pierdut:

greutatea betonului si a tablei cutate;

incarcari de executie , cuprinzand aglomerarea locala a betonului in timpul executiei conform EN 1991-1-6, 4.11.2;

incarcari din depozitari, daca exista;

efectul de „baltire” (sporirea grosimii betonului datorita deformatiei tablei cutate).

(2) Daca sageata centrala δ a tablei cutate sub greutate proprie plus greutatea betonului umed, calculata in starea limita de exploatare, este mai mica de 1/10 din grosimea placii, efectul de baltire poate fi ignirat la proiectarea tablei cutate. Daca aceasta limita este depasita, efectul va fi luat in considerare.Se poate admite in proiectare ca grosimea nominala a betonului sporeste pe intreaga deschidere cu 0.7δ.

9.3.3 Actiuni asupra placii compozite

(1) Incarcarile si dispunerea lor vor fi conform EN 1991-1-1.

(2) In verificarile de proiectare pentru starea limita ultima, se poate admite ca intreaga incarcare actioneaza asupra placii compozite, daca aceasta ipoteza se face si pentru proiectarea la forta taietoare longitudinala.

9.4 Calculul eforturilor sectionale

9.4.1 Tabla cutata intrebuintata drept cofraj

(1) Proiectarea tablei cutate considerata cofraj pierdut va fi in conformitate cu EN 1993-1-3.

(2) Redistributia plastica a momentelor incovoietoare nu se admite daca se folosesc reazeme provizorii.

9.4.2 Calculul placii compozite

(1) Se vor folosi urmatoarele metode de calcul la starile limita ultime:

a)        calcul elastic linear cu sau fara redistributie;

b) calcul global rigid-plastic, cu conditia demonstrarii ca sectiunile unde sunt necesare rotiri

plastice poseda suficienta capacitate rotationala;

c) calcul elasto-plastic, considerand proprietatile nellineare ale materialelor.

(2) Pentru calculul in starile limita ale exploatarii normale se vor folosi metode de calcul lineare.

(3) Daca efectele fisurarii betonului se neglijeaza in calculul pentru starile limita ultime, momentele incovoietoare la reazemele intermediare se pot reduce optional cu pana la 30%, introducand sporuri corespunzatoare momentelor pozitive din deschiderile adiacente.

(4) Se poate folosi calculul plastic fara verificarea directa a capacitatii rotationale la starea limita ultima, daca se foloseste otel beton de clasa C conform EN 1992-1-1, Anexa C iar deschiderea nu depaseste 3.0m.

(5) O placa continua poate fi proiectata ca o serie de placi pe o singura deschidere. Se va introduce o armare nominala pe reazemele intermediare conform 9.8.1.

9.4.3 Latimea efectiva a placii compozite in cazul incarcarilor concentrate punctuale si lineare

(1) Daca placa suporta incarcari concentrate punctuale sau lineare, acestea se vor considera distribuite pe o latime efectiva, daca nu se efectueaza un calcul mai exact.

(2) incarcarile concentrate punctuale saui lineare paralele cu deschiderea placii se vor considera distribuite pe o latime b_m, masurata imediat deasupra cutelor tablei, vezi Figura 9.4, data de relatia:

b_m = b_p + 2( h_c + h_f) (9.1)

Legenda

1 finisaj

2 armatura

Figura 9.4: Distributia incarcarii concentrate

(3) Pentru incarcari concentrate lineare perpendiculare pe deschiderea placii, se va folosi expresia (9.1) in care b_p va fi considerat ca fiind lungimea incarcarii concentrate lineare.

(4) Daca h_p/h nu depaseste valoarea 0.6, latimea placii considerata a fi efectiva pentru calculul global si pentru rezistenta poate fi determinata pentru simplitate cu expresiile (9.2) pana lai (9.4):

a) pentru incovoiere si forta taietoare longitudinala:

- pentru placi cu o deschidere si pentru panourile exterioare ale placilor continue:

b_em = b_m + 2 L_p (1 – L_p/L) ≤ latimea placii (9.2)

- pentru deschiderile interioare ale placilor continue

b_em = b_m + 1.33 L_p (1 – L_p/L) ≤ latimea placii (9.3)

b) pentru forta taietoare verticala:

b_ev = b_m + L_p (1 – L_p/L) ≤ latimea placii (9.4)

in care:

L_p este distanta de la centrul incarcarii pana la reazemul cel mai apropiat;

L este lungimea deschiderii.

(5) Daca incarcarile nominale aplicate nu depasesc valorile de mai jos, se poate introduce o armare nominala transversala fara calcul:

incarcare concentrata: 7.5 kN;

- incarcare distribuita: 5.0 kN/m² .

Armatura nominala transversala va avea o sectiune transversala d enu mai putin de 0.2% din aria betonului structural peste nervuri, si se va extinde peste o latime nu mai mica de b_em asa cum a fost calculata in clauza de fata. Se vor prevedea lungimi de ancoraj minime dincolo de aceasta lungime, conform EN 1992-1-1. Armarea introdusa din alte motive poate satisface in intregime sau partial regula de fata.

(6) Daca onditiile din (5) nu sunt satisfacute, se va determina distributia de momente incovoietoare din incarcari lineare sau punctuale si se va calcula armatura transversala adecvata conform EN 1992-1-1.

9.5 Verificarea tablei cutate intrebuintata drept cofraj la starile limita ultime

(1) Verificarea tablei cutate ca un cofraj pierdut la starile limita ultime se va efectua conform EN 1993-1-3. Se va da atentie corespunzatoare efectului emboaselor sau indentatiilor asupra rezistentelor de proiectare.

9.6 Verificarea tablei cutate intrebuintata drept cofraj la starile limite de exploatare

(1) Proprietatile sectiunilor se vor determina conform EN 1993-1-3.

(2) Sageata δ_s a tablei cutate sub greutate proprie plus greutatea betonului umed exclusiv incarcarea din executie nu va depasi δ_s,max .

Nota: Valorile pentru δ_s,max pot fi precizate in Anexa Nationala. Valoarea recomandata este L/180, in care L este deschiderea efectiva intre reazeme (in context sprijinirile se considera reazeme).

9.7 Verificarea placilor compozite la starile limita ultime

9.7.1 Criteriu de proiectare

(1)P Valorile de proiectare ale eforturilor sectionale nu vor depasi valorile de proiectare ale rezistentelor pentru starile limita ultime relevante.

9.7.2 Incovoierea

(1) In cazul conexiunii totale la forfecare, rezistenta la incovoiere M_Rd a oricarei sectiuni transversale va fi determinata prin teoria plastica conform 6.2.1.2(1), dar cu limita de curgere de proiectare a elementului metalic (tabla cutata) luata cea pentru tabla cutata f_yp,d.

(2) In incovoierea negativa, contributia tablei cutate va fi considerata numai daca tabla cutata este continua si cand, pentru faza de executie, redistributia momentelor prin plastificarea sectiunilor transversale de reazem nu a fost folosita.

(3) In determinarea sectiunii efective A_pe a tablei cutate, latimea emboaselor si indentarilor in tabla va fi neglijata, daca prin incercari nu s-a demonstrat ca o mai mare sectiune este efectiva.

(4) Efectul voalarii locale a zonelor comprimate ale tablei cutate va fi luat in considerare folosind latimi efective care nu vor depasi dublul valorilor limitative precizate in EN 1993-1-1, Tabelul 5.2 pentru inimi metalice de Clasa I.

(5) Momentul rezistent pozitiv al unei sectiuni transversale cu axa neutra deasupra tablei cutate va fi calculat din distributia de eforturi din Figura 9.5.

Legenda

1 axa centrelor de greutate ale sectiunii tablei cutate

Figura 9.5: Distributia eforturilor la incovoiere pozitiva, daca axa neutra se afla deasupra tablei cutate

(6) Momentul rezistent pozitiv al unei sectiuni transversale cu axa neutra in cadrul tablei cutate va fi calculat din distributia de eforturi din Figura 9.6.

Legenda

1 axa centrelor de greutate ale sectiunii tablei cutate

2 axa neutra in plastic a sectiunii tablei cutate

Figura 9.6: Distributia eforturilor la incovoiere pozitiva, daca axa neutra se afla in cadrul tablei cutate

Pentru simplificare, z si respectiv M_pr se pot determina cu urmatoarele exepresii:

z = h – 0.5h_c – e_p + (e_p – e) N_cf / (A_pc f_ypd) (9.5)

M_pr = 1.25 M_pa [1 – N_cf / ( A_pc f_ypd)] ≤ M_pa (9.6)

(7) Daca se neglijeaza contributia tablei cutate, momentul rezistent negativ al unei sectiuni trans-versale se va calcula din distributia de de eforturi din Figura 9.7.

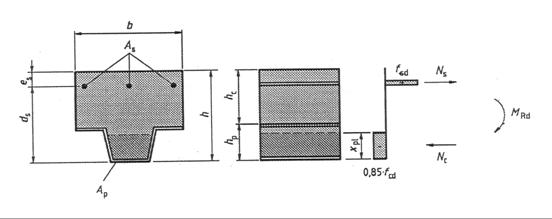
Figura 9.7: Distributia de eforturi la incovoiere negativa

9.7.3 Lunecarea longitudinala la placi fara ancoraje la capete

(1)P Prevederile prezentei clauze 9.7.3 se aplica placilor compozite cu inclestare mecanica sau cu frictiune (tipurile (a) si (b) definite in 9.1.2.1).

(2) Rezistenta de proiectare la lunecare longitudinala se va determina prin metoda m-k, vezi (4) si (5) mai jos, sau prin metoda conexiunii partiale definita in (7)-(10). Metoda conexiunii partiale se va folosi numai pentru placi compozite cu o comportare ductila la lunecare longitudinala.

(3) Comportarea la lunecare longitudinala se poate considera ductila, daca incarcarea de rupere depaseste incarcarea ce cauzeaza o lunecare constatata de capat de 0.1mm cu mai mult de 10%. Daca incarcarea naxima se atinge pentru o sageata la jumatatea deschiderii ce depaseste L / 50, incarcarea de rupere se va considera a fi cea ce a cauzat sageata de L / 50 la jumatatea deschiderii.

(4) Daca se foloseste metoda m-k, va trebui aratat ca forta taietoare maxima verticala de proiectare V_Rd pentru o latime de placa b nu depaseste rezistenta la forta taietoare de proiectare V_l,Rd determinata cu expresia urmatoare:

V_l,Rd = (b d_p/ γ_vs ) [ ( m A_p/b L_s) + k ] (9.7)

In care:

b , d_p sunt in mm;

A_p este sectiunea nominala transversala a tablei cutate in mm²;

m, k, sunt valori de proiectare ale coeficientilor empirici in N/mm2 obtiniti din incercari ale

placilor ce respecta cerintele de baza ale metodei m-k;

L_s este deschiderea de lunecare in mm, definita la (5) mai jos;

γ_vs este coeficientul de siguranta partial pentru starea limita ultima.

Nota 1: Valoarea γ_vs se poate preciza in Anexa Nationala. Valoarea recomandata este 1.25.

Nota 2: Se poate admite ca metoda de incercare descrisa in Anexa B respecta cerintele de baza ale metodei m-k.

Nota 3: I n expresia (9.7), se foloseste sectiunea nominala A_p deoarece aceasta este valoarea folosita in mod

normal in evaluarea incercarilor de determinare a parametrilor m si k.

(5) La proiectare, L_s se va lua :

L/4 in cazul unei incarcari uniform distribuite pe toata deschiderea;

distanta intre forta concentrata si cel mai apropiat reazem in cazul a doua forte concentrate egale si simetrice;

in cazul altor distributii de incarcari, inclusiv l combinatiile de incarcari distribuite si forte concentrate asimetrice, se va face o evaluare bazata pe rezultate de incercari sau pe urmatorul calcul aproximativ. Deschiderea de calcul pentru forta taietoare se va calcula ca momentul maxim impartit prin forta taietoare verticala maxima adiacenta reazemelor pentru deschiderea respectiva.

(6) Daca placa compozita se proiecteaza continua, se permite folosirea unei deschideri echivalente isostatice in scopul determinarii rezistentei. Lungimea deschiderii se va lua:

0.8L pentru deschideri interioare;

0.7L pentru deschideri marginale.

(7) Daca se foloseste metoda conexiunii partiale, trebuie demonstrat ca, in oricare sectiune trans-versala, momentul incovoietor de proiectare M_Ed nu depaseste rezistenta de proiectare M_Rd .

(8) Rezistenta de proiectare M_Rd se va determina conform 9.7.2(6) dar cu N_cf inlocuit prin:

N_c = τ_u,Rd b L_x ≤ N_cf (9.8)

si

z = h – 0.5x_pl – e_p + (e_p – e) ( N_c / A_pe f_yp,d ) (9.9)

in care:

τ_u,Rd este rezistenta de proiectare la forfecare (τ_u,Rk / γ_Vs ) _;

L_x este distanta sectiunii transversale considerate la reazemul cel mai apropiat.

Nota 1: Valoarea γ_Vs se va defini in Anexa Nationala. Valoarea recomandata este1.25.

Nota 2: Metoda de incercare data in Anexa B se poate admite ca satisface cerintele de baza pentru determinarea lui τ_u,Rd .

(9) In expresia (9.8), N_c se poate spori cu cantitatea μR_Ed daca τ_u,Rd se determina luand in cons-derare rezistenta suplimentara longitudinala la forfecare cauzata de reactiunea din reazem, in care:

R_Ed este reactiunea din reazem;

μ este un coeficient nominal.

Nota: Valoarea pentru μ poate fi data in Anexa Nationala. Valoarea recomandata este 0.5.

(10) In metoda conexiunii partiale, se poate lua in considerare armatura inferioara suplimentara.

9.7.4 Lunecarea longitudinala la placi cu ancoraje la capete

(1) Daca nu se demonstreaza prin incercari existenta unei contributii la rezistenta la forfecare longitudinala din partea altor dispozitive de forfecare, ancorajul de capat de tip (c) definit la 9.1.2.1 va fi proiectat la starea limita ultima pentru intreaga forta de intindere in tabla cutata.

(2) Rezistenta de proiectare la forfecare longitudinala a placilor cu ancoraje de capat de tip (c) sau (d) definite in 9.1.2.1 se poate deterrmina prin metoda conexiunii partiale descrisa in 9.7.3 (7), cu Nc sporit cu rezistenta ancorajului de capat.

(3) Rezistenta de proiectare P_pb,Rd a unui dorn cu bulb, sudat pe tabla cutata si folosit ca ancoraj de capat trebuie admis ca cea mai mica rezistenta dintre rezistenta de proiectare a dornului conform 6.6.4.2 sau rezistenta tablei cutate, determinata cu expresia urmatoare:

P_pb,Rd = k_φ d_d0 t f_yp,d (9.10)

cu notatia:

k_φ = 1 + a / d_d0 ≤ 6.0 (9.11)

in care:

d_d0 este diametrul sudurii inelare, care se poate lua de 1.1 ori diametrul tulpinii dornului;

a este distanta de la centrul dornului la capatul tablei cutate, dar nu mai mica de 1.5 d_d0;
t este grosimea tablei cutate.

9.7.5 Forta taietoare verticala

(1) Rezistenta la forta taietoare verticala V_v,Rd a unei placi compozite pe o latime egala cu distanta intre centrele nervurilor se va determina conform EN 1992-1-1, 6.2.2.

9.7.6 Strapungerea

(1) Forta rezistenta la strapungere V_p,Rd a unei placi compozite sub o forta concentrata se va determina conform EN 1992-1-1, 6.4.4; perimetrul critic se va determina ca in Figura 9.8.

9.8 Verificarea placilor compozite la starile limita de exploatare

9.8.1 Controlul fisurarii betonului

(1) Deschiderea fisurilor in zonele de momente negative ale placilor continue se vor verifica conform EN 1992-1-1, 7.3

(2) Daca placile continue sunt proiectate ca simplu-rezemate conform 9.4.2 (5), sectiunea transversala a armaturii anti-fisurare peste nervuri nu va fi mai mica de 0.2% din sectiunea transversala a betonului de deasupra nervurilor in cazul unei executii fara sprijiniri si 0.4% din aceasta sectiune transsversale pentru o executie cu sprijiniri.

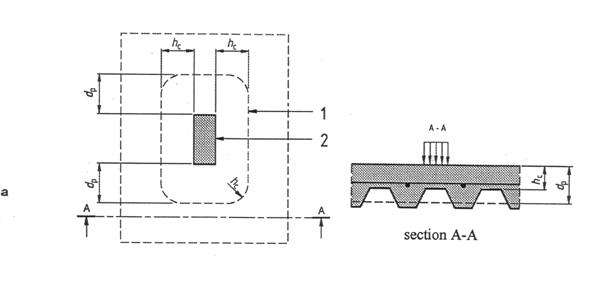
Legenda

1 perimetrul critic c_p

2 aria incarcata

Figura 9.8: Perimetrul critic pentru calculul la poansonare

9.8.2 Sageti

(1) Se aplica EN1990, 3.4.3.

(2) Sagetile datorite incarcarilor aplicate numai tablei cutate se vor calcula conform EN 21993-1-3 Capitolul 7

(3) Sagetile datorite incarcarilor aplicate pe elementul compozit se vor calcula folosind calculul elastic conform Sectiunii 5, cu neglijarea efectelor contractiei.

(4) Se poate renunta la calculul deplasarilor daca ambele conditii de mai jos sunt satisfacute:

raportul deschidere/ inaltime nu depaseste limitele din EN 1992-1-1, 7.4 pentru beton slab

solicitat si

conditia (6) de mai jos pentru neglijarea efectelor lunecarii de capat este satisfacuta.

(5) Pentru o deschidere interioara a unei placi continue, in care conexiunea de forfecare este ca cele definite in 9.1.21(a), (b) sau (c), deplasarile se pot determina folosind urmatoarele aproximatii:

momentul de inertie se poate admit ca fiind media valorilor pentru sectiunea fisurata si nefisurata;

pentru beton, se poate folosi o valoare medie a raportului modular atat pentru efectele de lunga durata cat si pentru cele de scurta durata.

(6) Pentru deschideri marginale, nu trebuie tinut seama de lunecarea de capat, daca incarcarea de corespunzand lunecarii initiale la incercare(definita ca incarcarea ce provoaca o lunecare de capat de 0.5mm) depaseste de 1.2 ori incarcarea de exploatare.

(7) Daca lunecarea de capat depaseste 0.5mm la o incarcare mai mica decat de 1.2 ori incarcarea de exploatare, fie se vor prevedea ancore de capat sau se vor calcula deplasarile incluzand efectul lunecarii de capat.

(8) Daca influenta legaturii de forfecare intre tabla cutata si beton nu este cunoscuta printr-o verificare experimentala a unui planseu compozit cu ancoraje de capat, proiectarea se va simplifica considerand un arc cu un tirant intins. In acest model, lungirile si scurtarile vor da deplasarile de care se va tine seama.

Anexa A (informativa)

Rigiditatile componentelor nodurilor

A.1 Domeniul de aplicare

(1) Rigiditatile urmatoarelor componente de baza ale nodurilor se vor determina conformA.2.1 de mai jos:

armatura longitudinala intinsa;

placa metalica de contact comprimata.

(2) Coeficientii de rigiditate k_i sunt definiti in EN 1993-1-8, expresia (6.27). Rigiditatea componentelor identificate in acel Standard pot fi luate asa cum sunt date acolo, cu exceptia celor definite in A.2.2 de mai jos.

(3) Rigiditatea inimilor inglobate in beton ale sectiunilor stalpilor se va determina conform A.2.3 de mai jos.

Influenta lunecarii conexiunii de forfecare asupra rigiditatii nodului se poate determina conform A.3.

A.2 Coeficienti de rigiditate

A.2.1 Componente de baza ale nodului

A.2.1.1 Armaturi longitudinale din beton armat intinse

(1) Coeficientul de rigiditate k_s,r pentru un rand r se poate obtine din Tabelul A.1.

Tabelul A.1: Coeficienti de rigiditate k_s,r

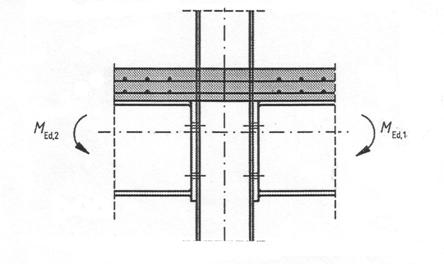
Figura A.1: Noduri cu momente incovoietoare

A.2.1.2 Placa metalica de contact comprimata

(1) Coeficientul de rigiditate poate fi considerat infinit

A.2.2 Alte componente ale nodurilor compozite

A.2.2.1 Panoul inimii stalpului forfecat

(1) Un panou nerigidizat intr-un nod cu o conexiune tip placa metalica de contact, coeficientul de rigiditate k₁ se poate lua ca fiind de 0.87 ori valoarea din EN 1993-1-8, Tabelul 6.11.

A.2.2.2 Inima stalpului la compresiune transversala

(1) Intr-o inima nerigidizata si o conexiune cu placa de contact, coeficientul de rigiditate k₂ se poate determina din relatia:

k₂ = 0.2 b_eff,c,wc t_wc / d_c (A.1)

in care:

b_eff,c,wc este latimea efectiva a inimii stalpului in compresiune, vezi 8.4.3.1.

Alti termeni sunt definiti in EN 1993-1-8, 6.

A.2.3 Componente armate

A.2.3.1 Panoul inimii stalpului forfecat

(1) Daca inima stalpului metalic este inglbata in beton, vezi Figura 6.17b, rigiditatea panoului poate sporita pentru a tine seama de inglobare. Suplimentul k_1,c ce se adaoga la coeficientul de rigiditate k₁ se poate determina din relatia:

k_1,c = 0.06 (E_cm / E_a) (b_c h_c / β z ) (A.2)

in care:

E_cm este modulul de elasticitate al betonului;

z este bratul de parghie, vezi EN 1993-1-8, Figura 6.15.

A.2.3.2 Inima stalpului la compresiune transversala

(1) Daca inima stalpului metalic este inglbata in beton, vezi Figura 6.17b, rigiditatea inimii stalpului la compresiune se poate spori pentru a tine seama de inglobare.

(2) In cazul unei conexiuni cu placa de contact, suplimentul k_2,c ce se adaoga la coeficientul de rigi-ditate k₂ se poate determina din relatia:

k_2,c = 0.13 (E_cm/ E_a) (t_eff,c b_c / h_c) (A.3)

in care:

t_eff,c este grosimea efectiva a betonului, vezi 8.4.4.2(2).

(3) In cazul unei conexiuni cu placa de capat, suplimentul k_2,c se poate determina din:

k_2,c = 0.5 (E_cm/ E_a) (t_eff,c b_c / h_c) (A.4)

A.3 Deformatia conectarii de forfecare

(1) Influenta lunecarii asupra rigiditatii nodului se poate determina prin relatiile (2)-(5) de mai jos, daca nu se tine seama de deformatia conexiunii la forfecare printr-o metoda mai exacta.

(2) Coeficientul de rigiditate k_s,r , vezi A.2.1.1, se poate multiplica prin coeficientul de reducere k_slip:

k_slip = 1 / ( 1 + E_s k_s,r / K_sc ) (A.5)

cu notatiile:

K_sc = N l / [ ν – (ν -1) h_s / (1+ ξ) d_s ] (A.6)

ν = ^½   (A.7)

ξ = (E_a I_a) / (d_s² E_s A_s ) (A.8)

in care:

h_s este distanta intre barele de armatura intinse si centrul zonei comprimatei, vezi

EN 1993-1-8, Figura 6.15, pentru centrul zonei comprimate;

d_s este distanta intre barele de armatura intinse si centrul de greutate al sectiunii metalice

a grinzii;

I_a este momentul de inertie al ariei sectiunii metalice a grinnzii;

l este lungimea grinzii cu momente negative adiacente nodului; intr-un cadru

contravantuit, aceasta lungime se poate considera ca 15% din lungimea deschiderii;

N este numarul de conectori de forfecare distribuiti pe lungimea l ;

k_sc este rigiditatea unui conector individual.

(3) Rigiditatea conectorului k_sc poate fi considerata ca fiind 0.7P_Rk /s , in care:

P_Rk este rezistenta caracteristica a conectorului la forfecare;

s este lunecarea determinata din incercari de impingere, conform Anexei B, la o

incarcare 0.7 P_Rk.

(4 In mod alternativ, in cazul unei placi monolite clasice sau a unei placi compozite la care coeficientul de reducere k_t este unitar, vezi 6.6.4.2, se pot adopta urmatoarele valori pentru k_sc :

- pentru dornuri cu diametrul 19mm prevazuti cu bulbi: 100 kN/mm

- corniere trase la rece cu inaltimea 80100 mm: 70 kN/mm.

(5) In cazul unui nod compozit cu mai mult de un singur rand de armaturi considerate efective in intindere, se aplica (2) de mai sus, daca randurrile de armaturi sunt reprezentate de un singur rand echivalent sub aspectul ariei transversale si sub aspectul pozitiei fata de centrul compresiunii si fata de centrul sectiunii de metal al sectiunii metalice a grinzii.

Anexa B (informativa)

Incercari standard

B.1 Generalitati

(1) In prezentul Standard, se dau reguli pentru:

a) incercari pe conectori de forfecare in capitolul B.2 si

b) incercari pe placi compozite de planseu in capitolul B.3.

Nota: Aceste proceduri pentru incercari standard se cuprind datorita absentei Directivelor pentru ETA. Cand

asemenea Directive se vor elabora, prezenta Anexa se va retrage.

B.2 Incercari asupra conectorilor de forfecare

B.2.1 Generalitati

(1) Daca regulile de proiectare in 6.6 nu sunt aplicabile, proiectarea se va baza pe incercari executate astfel incat sa ofere informatii asupra proprietatilor conectorilor necesare pentru proiectare in confor-mitate cu prezentul Standard.

(2) Variabilele ce trebuie cercetate cuprind geometria si proprietatile mecanice ale placii de beton, ale conectorilor de forfecare si ale armaturii.

(3) Rezistenta la incarcari, altele decat oboseala, poate fi determinata prin incercari de impingere in con-formitate cu cerintele prezentei Anexe.

(4) Pentru incercari la oboseala, probele vor fi de asemenea pregatite conform prezentei Anexe.

B.2.2 Organizarea incercarilor

(1) Daca conectorii de forfecare se folosesc in grinzi T cu placa de beton de grosime constanta sau cu vute ce respecta 6.6.5.4, se vor executa incercari standard de impingere. In alte situatii, se vor executa incercari specifice de impingere.

(2) In cazul incercarilor standard de impingere, dimensiunile probei, sectiunea metalica si armatura vor fi ca in Figura B.1. Nisa in placa de beton este optionala.

(3) Incercarile specifice de impingere se vor efectua astfel incat placile si armaturavor fi dimensionate corespunzator in raport cu grinzile pentru care incercarea este proiectata. In particular:

a)      lungimea l a fiecarei placi trebuie corelata cu intervalul longitudinal al conectorilor in structura compozita;

b)      latimea b a fiecarei placi nu va depasi latimea efectiva a placii grinzii;

c)      grosimea h a fiecarei placi nu va depasi grosimea minima a placii grinzii;

d)      daca o vuta in grida nu se incadreaza in 6.6.5.4 , placile probei supuse la impingere vor avea aceleasi vute si armare ca si grinda.

B.2.3 Pregatirea probelor

(1) Fiecare din cele doua placi se vor turna in pozitie orizontala, asa cum se toarna placile compozite in practica.

(2) Se va evita adeziunea intre talpile grinzii metalice si beton, ungand talpa sau prin alte metode corespunzatoare.

(3) Probele pentru incercarea prin impingere se vor intari in aer.

(4) Pentru fiecare cantitate de beton ce se toarna in probele de incercare la impingere, se vor realiza minimum patru specimene (cilindri sau cuburi) pentru determinarea rezistentei pe cilindru. Aceste probe se vor pastra odata cu probele de incercare. Rezistenta betonului f_cm se va determina ca valoare medie.

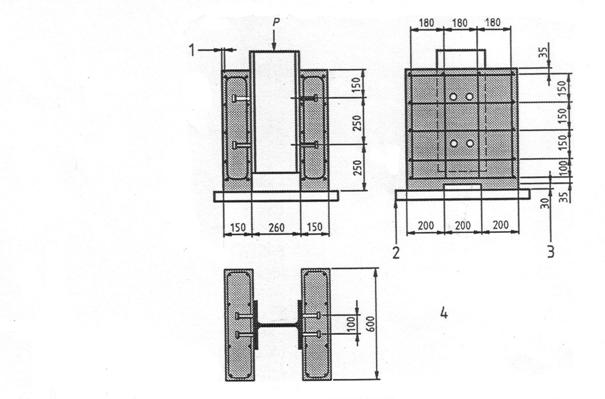
Legenda

acoperire 15mm

rezemare pe mortar sau ipsos

nisa este optionala

armare cu bare cu profil periodic Ø 10mm de inalta adeziune cu 450 ≤ f_ck ≤ 550 N/mm² ; sectiune profil metalic HE 260B sau 254 x 254 x 89 kg UC

Figura B.1: Proba pentru incercare standard de impingere

(5) Rezistenta la compresiune fcm a betonului la momentul incercarii va fi 70% ± 10% din rezistenta f_ck a betonului grinzii pentru care se face incercarea. Cerinta se poate satisface folosind beton de calitatea specificata dar efectuand incercarea mai curand de 28 zile de la turnarea probelor.

(6) Se vor determina limita de curgere, rezistenta de rupere la intindere si elongatia maxima a unei probe reprezentative a materialului conectorului de lunecare.

(7) Daca pentru placa se foloseste tabla cutata, rezistenta la intindere si limita de curgere a tablei cutate se va obtine din incercari pe cupoane taiate din tabla cutata folosita in incercare.

B.2.4 Procedura de incercare

(1) Incarcarea se va aplica la inceput in trepte pana la 40% din inarcarea de rupere asteptata si apoi se vor executa 25 de cicluri intre 5% si 40% din inarcarea de rupere asteptata.

(2) Se vor aplica apoi trepte de incarcare astfel ca ruperea sa nu aibe loc in mai putin de 15 minute.

(3) Lunecarea longitudinala intre fiecare placa de beton si profilul metalic se va masura continuu in timpul incarcarii sau la fiecare treapta de incarcare. Lunecarea se va masura cel putin pana cand incarcarea a scazut sub 20% din incarcarea maxima.

(4) Separatia transversala intre profilul laminat si fiecare placa se va masura cat mai aproape de de fiecare grup de conectori.

B.2.5 Evaluarea incercarii

(1) Daca se efectueaza trei incercari pe probe nominal identice iar devierea oricarui rezultat individual de incercare nu depaseste 10% din valoarea medie a tuturor incercarilor, rezistenta de proiectare se poate determina dupa cum urmeaza:

- rezistenta caracteristica P_Rk be va consideraca valoarea minima de rupere (impartita prin

numarul de conectori) redusa cu 10%;

- rezistenta de proiectare P_Rd se va calcul cu relatia:

P_Rd = ( f_u / f _ut ) (P_Rd / γ_V ) ≤ ( P_Rk / γ_V ) (B.1)

In care:

f_u este rezistenta ultima minim specificata a materialului conectorului;

f_ut este rezistenta ultima actuala a materialului conectorului in proba incercata; iar

γ_V este coeficientul partial de siguranta pentru conexiunea de forfecare.

Nota: Valoarea γ_V este data in Anexa Nationala. Valoarea recomandata este 1.25.

(2) Daca devierea fata de medie depaseste 10%, se vor efectua cel putin inca trei incercari de acelasi tip. Evaluarea incercarilor se va face atunci conform EN 1990, Anexa D.

(3) Daca conectorul este compus din doua elemente separate, unul rezistand la forfecare longi-tudnala iar celalalt la tendinta fortelor de separare a placii de grinda metalica, legaturile care rezista la separare vor fi suficient de rigide si de rezistente astfel ca separarea in incercari de impingere, masurata cand conectorii sunt supusi la 80% din incarcarea ultima, este mai mica decat jumatate din deplasarea placii fata de grinda.

(4) Capacitatea de lunecare δ_u a unei probe va fi considerata lunecarea maxima masurata la nivelul incarcarii caracteristice, cum rezulta in Figura B.2. Capacitatea caracteristica de lunecare δ_uk va fi considerata valoarea minima de incercare δ_u redusa cu 10% sau determinata prin evaluare statistica din toate rezultatele incercarilor. In acest ultim caz, capacitatea de lunecare caracteristica va fi determinataconform EN 1990, Anexa D.

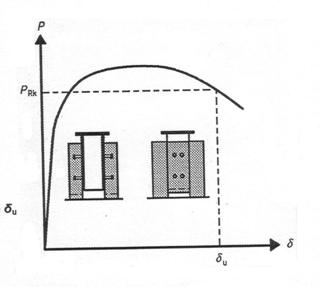
Figura B.2: Determinarea capacitatii de lunecare δ_u

B.3 Incercarea placilor compozite

B.3.1 Generalitati

(1) Incercarile ce se efectueaza conform prezentei sectiuni trebuie folosite la determinarea coeficientilor m si k sau a valorii τ_u,Rd care sunt necesare la verificarea rezistentei la forfecare longitudinala, cum s-a aratat in Capitolul 9.

(2) Din diagramele forta-deplasare, comportarea la forfecare longitudinala se clasifica ca fiind casanta sau ductila. Comportarea se admite a fi ductila daca este conforma cu 9.7.3 (3). In caz contrar, comportarea este casanta.

(3) Variabilele ce se cerceteaza cuprind: grosimea si tipul tablei cutate, calitatea otelului, finisajul tablei cutate, densitatea si calitatea betonului, grosimea placii si lungimea deschiderii de forfecare L_s.

(4) Pentru a reduce numarul de incercari necesare pentru o cercetare completa, rezultatele obtinute dintr-o serie de incercari pot fi de asemenea folosite pentru alte valori ale variabilelor, dupa cum urmeaza:

pentru grosimi ale tablei cutate t mai mari decat cea incercata;

pentru beton cu rezistenta specifica f_ck nu mai mica decat 0.8f_cm, in care f_cm este valoarea medie a rezistentei betonului la incercari;

la tabla cutata avand o limita de curgere f_yp nu mai mica decat 0.8f_ypm, in care f_ypm este valoarea medie a rezistentei de curgere in incercari.

B.3.2 Organizarea incercarilor

(1) Incercarile se vor efectua pe placi simplu rezemate.

(2) Dispozitia incercarii va fi conform Figurii B.3 sau echivalenta.

(3) Pe proba se vor aplica doua incarcari concentrate lineare egale, plasate la L/4 si 3L/4 de la rezemul din stanga.

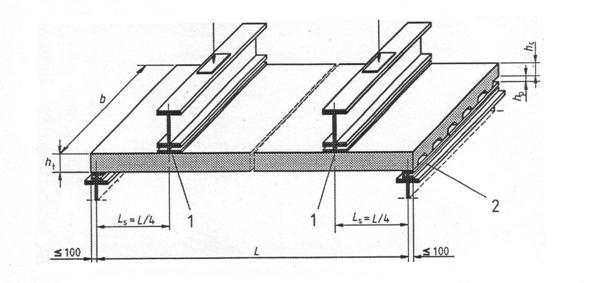
Legenda

1 foaie de neopren su echivalent

2 placa de repartitie la reazim ≤ 100mm x b x 10mm (min.) ( tipica pentru toate placile de repartitie)

Figura B.3: Dispozitia incercarii

(4) Distanta intre axele rezemelor si capatul placii nu va depasi 100mm.

(5) Latimea placilor de reazem si a incarcarilor lineare nu va depasi 100mm.

(6) Daca incercarile folosesc la determinarea coeficientilor m si k, pentru orice variabila cercetata se vor efectua doua grupuri de cate trei incercari (indicate in Figura B.4 prin zonele A si B) sau trei grupuri de cate doua incercari. Pentru probele din regiunea A, deschiderea de forfecare va fi cat mai lunga posibil dar totusi conducand la rupere prin forfecare longitudinala, pe cand pentru probele din zona B va fi cat mai scurta posibil dar totusi conducand la rupere prin forfecare longitudinala, dar nu mai putin de 3 h_t.

(7) Daca incercarile se folosesc pentru determinarea valorii τ_u,Rd , pentru fiecare tip de tabla cutata sau tratament se vor efectua nu mai putin de patru incercari pe probe de aceiasi grosime h_t fara armatura suplimentara sau ancoraje de capat. Intr-un grup de trei incercari, deschiderea de forfecare va fi cat mai lunga posibil dar totusi conducand la rupere prin forfecare longitudinala iar in ultima incercare ramasa cat mai scurta posibil dar totusi conducand la rupere prin forfecare longitudinala, dar nu mai mica de 3 h_t. Ultima incercare cu deschiderea de forfecare scurta se foloseste numai pentru a clasifica comportarea conform B.3.1(2).

B.3.3 Pregatirea probelor

(1) Suprafata tablei cutate va fi in forma „cum s-a laminat”, nefacandu-se nici o incercare de a imbunatati adeziunea prin degresarea suprafetelor.

(2) Forma si ambosarile tablei cutate vor reprezenta cu acuratete tabla folosita in practica. Interaxul si adancimea amboaselor nu vor devia de la valorile nominale cu mai mult de 5% si respectiv 10%.

(3) In zona intinsa a placii, se vor monta piese de favorizare a fisurarii pe intreagalatime a placii incercate sub incarcari aplicate. Piesele de favorizarea fisurarii se vor extinde cel putin pana la adancimea tablei cutate. Aceste piese de inducere a fisurarii sunt introduse pentru a defini mai bine lungimea deschiderii de forfecare L_s si a elimina rezistenta la intindere a betonului.

(4) Se permite introducerea de legaturi restrictive la inimile exterioare ale tablei cutate , spre a se comporta ca si cum ar lucra in placi mai late.

(5) Latimea b a placii ce se incearca nu va fimai mica decat de trei ori grosimea totala, 600mm, si latimea acopeririitablei cutate.

Probele vor fi turnate in situatia total rezemata. Aceasta este cea mai defavorabila situatie pentru modul de rupere prin distrugerea adeziunii prin forfecare.

Se pot introduce plase de armaturi in placa, de exemplu pentru a arma placa in timpul trans-portului, contra contractiei, etc. Daca se introduce, se va amplasa astfel incat sa lucreze la compresiune la momente pozitive.

Daca intr-o serie se cerceteaza o aceiasi variabila, betonul pentru toate probele respective va fi din acelasi amestec si tratat ulterior in aceleasi conditii.

Pentru fiecare grup de placi ce vor fi incercate intr-un interval de 48 ore, se vor preleva la turnarea placilor un numar de patru probe de beton, pentru determinarea rezistentelor pe cilindru sau cub. Rezistenta betonului f_cm a fiecarui grup trebuie considerata a fi valoarea medie, daca deviatia fiecarei probe fata de valoarea medie nu depaseste 10%. Daca devierea rezistentei la compre-siune depaseste 10% , rezistenta betonului se va considera a fi valoarea maxima observata.

Rezistenta la intindere si limita de curgere a tablei se vor obtine din incercari pe cupoane taiate din tabla cutata folosita drept cofraje pentru placile ce se incearca.

8.3.4 Procedura de incarcare pentru incercari

(1) Procedura de incarcare are scopul de reprezenta incarcarea aplicata pe o perioada de timp. Este gandita in doua etape: o incercare initiala, in care placa este supusa incarcarii ciclice; apoi, intr-o incercare ulterioara, placa este solicitata pana la rupere sub o incarcare crescatoare.

(2) Daca se executa doua grupe de cate trei incercari, una din cele trei probe din fiecare grup va fi supusa incarcarii statice fara incarcare ciclica, pentru a determina nivelul incarcarii ciclice pentru celelalte doua.

(3) Incercarea initiala: placa va fi supusa la o incarcare ciclica, care variaza intre o valoare inferioara nu mai mare de 0.2W_t si o valoare superioara nu mai mica de 0.6W_t, in care W_t este valoarea masurata a incarcarii de rupere, obtinuta in incercarea preliminara statica conform (2).

(4) Incarcarea se va aplica 5000 de cicluri intr-o perioada de nu mai putin de 3 ore.

(5) Incercarea ulterioara: dupa terminarea incercarii initiale, placa va fi supusa unei incercari staticein care incarcarea aplicata va creste progresiv, astfel ca ruperea sa nu aibe loc in mai putin de 1 ora. Incarcarea de rupere W_t este incarcarea maxima aplicata pe placa la rupere plus greutatea placii compozite si a sinelor de distributie.

(6) In cazul incercarii ulterioare, incarcarea se va aplica fie controland valoarea incarcarii fie a deplasarilor.

B.3.5 Determinarea valorilor de calcul pentru m si k

(1) Daca comportarea este ductila, vezi 9.7.3(3), forta de forfecare reprezentativa experimentala V_t se va lua de 0.5 ori valoarea incarcarii de rupere W_t definita in B.3.4. Daca comportarea este casanta, valoarea se va reduce cu un factor de 0.8.

(2) Rezistenta caracteristica la forfecare se va calcula ca fractilul de 5% din toate rezultatele incercarilor V_t, folosind un model statistic corespunzator si desenand o linie de regresie lineara carac-teristica, precum se arata in Figura B.4.

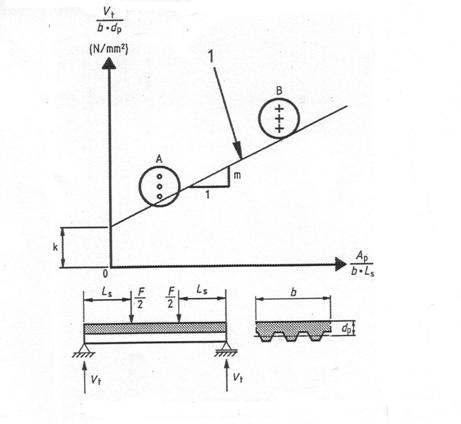
Legenda

1 Relatia de proiectare pentru rezistenta la forfecare longitudinala

Figura B.4: Evaluarea rezultatelor incercarilor

(3) Daca se realizeaza doua grupuri de trei incercari iar devierea oricarui rezultat individual intr-un grup nu depaseste 10%, relatia de proiectare se poate determina conform Anexei D din EN 1990 sau dupa cum urmeaza:

Din fiecare grup, valoarea caracteristica se va lua cea minima redusa cu 10%. Relatia de

proiectare se formeaza trasand o linie dreapta prin aceste valori caracteristice pentru grupurile

A si B.

B.3.6 Determinarea valorilor de calcul pentru τ_u,Rd

(1) Diagrama partiala de interactiune reprezentata in Figura B.5 va fi determinata folosind valorile masurate ale dimensiunilor si rezistentelor betonului si tablei striate. Ca rezistenta a betonului, se poate folosi valoarea medie f_cm dintr-un grup, cum este specificat in B.3.3(9):

(2) Se va determina momentul incovoietor maxim M in sectiunea transversala de sub forta concen-trata datorita incarcarii aplicate, greutatii proprie a placii si a sinelor de distributie. Calea A →B→C in Figura B.5 va da o valoare η pentru fiecare incercare si o valoare τ_u din relatia:

τ_u = η N_cf / [ b ( L_s + L₀ ) ] (B.2)

in care:

L₀ este lungimea in consola.

(3) Daca in proiectare se va tine seama de rezistenta suplimentara la forfecare longitudinala data de reactiunea reazemului , in conformitate cu 9.7.3(9), τ_u se va determina din:

τ_u = (η N_cf – μ V_t ) / [ b ( L_s + L₀ ) ] (B.3)

in care:

μ este valoarea default a coeficientului de frecare ,care se ia 0.5;

V_t este reactiunea din reazem la incarcarea de rupere experimentala.

(4) Rezistenta caracteristica la forfecare τ_u,Rk se va calcula ca fractila de 5% din valorile experimentale, folosind un model statistic corespunzator conform EN 1990, Anexa D.

Figura B.5: Determinarea gradului conexiunii de forfecare din M _incercare

(5) Rezistenta de proiectare la forfecare τ_u,Rd rezulta din rezistenta caracteristica τ_u,Rk impartita prin coeficientul partial de siguranta γ_Vs .

Nota: Valoarea γ_Vs poate fi precizata in Anexa Nationala. Valoarea recomandata este 1.25.

Anexa C (informativa)

Contractia betonului la structuri compozite in cladiri

(1) Valoarea nominala totala a deformatiei specifice libere de contractie se poate lua ca mai jos, daca nu este esential un contol precis al profilului in timpul executiei sau contractia este de asteptat ca va capata valori exceptionale:

in medii uscate (exterioare sau interioare in cladiri dar excluzand elemente umplute cu beton):

325 x 10 ^-6 pentru beton normal

500 x 10 ^-6 pentru beton usor

in alte medii si in cazul elementelor umplute cu beton

200 x 10 ^-6 pentru beton normal

300 x 10 ^-6 pentru beton usor.

Bibliografie

EN 1991-1-5: Actiuni asupra constructiilor: Actiuni termice (urmeaza a fi publicat)

EN 1991-1-6: Actiuni asupra constructiilor: Actiuni in timpul executiei (urmeaza a fi publicat)

EN 13670 Cerinte pentru executia constructiilor de beton (urmeaza a fi publicat)

EN ISO 13918:1998 Sudare – Dornuri si ferule ceramice pentru sudura cu arc (ISO 13918: 1998)

EN ISO 14555: 1998 Sudare – Sudarea cu arc a materialelor metalice (ISO 14555: 1998).