MǍSURAREA PARAMETRILOR R,X,Z

MǍSURAREA PARAMETRILOR R,X,Z

4.1. ELEMENTE GENERALE

Parametrii electrici ai unui circuit dipolar sau multipolar caracterizeazǎ proprietǎtile unor elemente ale circuitului de a disipa sau absorbi energie electromagneticǎ sub diferite forme (electricǎ, magneticǎ, termicǎ), energie dependentǎ de constructia elementului (dimensiuni, materiale, formǎ), de curentul electric care îl parcurge ori de tensiunea electricǎ la care este supus (frecventǎ, mǎrime, formǎ), precum si de alti factori de mediu sau de exploatare (temperaturǎ, presiune, umiditate, radiatii).

Elementele dipolare de circuit sunt caracterizate, fie de rezistenta R, dacǎ sunt parcurse de curenti continui, fie de impedanta Z, dacǎ sunt parcurse de curenti alternativi. Pentru mǎrimi alternative sinusoidale, utilizarea calcului în complex simplificǎ metodele de calcul ale circuitului.

4 ELEMENTE DE CALCUL ÎN COMPLEX SIMPLIFICAT A

MǍRIMILOR SINUSOIDALE

a. Mǎrimi alternative

O mǎrime sinusoidalǎ (armonicǎ) este o functie de timp având expresia:

(4.1)

în care y se numeste valoare instantanee a mǎrimii sinusoidale, Y_max se numeste valoare maximǎ sau de vârf, Y este denumitǎ valoarea efectivǎ, f se numeste pulsatia mǎrimii (f fiind frecventa), iar reprezintǎ faza initialǎ a mǎrimii sinusoidale, care depinde de valoarea initialǎ y(0), a mǎrimii sinusoidale:

Între mǎrimea efectivǎ si mǎrimea de vârf existǎ relatia . Pentru mǎrimile alternative, se mai definesc doi factori: factorul de formǎ k_f si factorul de vârf k_v, cu ajutorul relatiilor:

Pentru mǎrimile sinusoidale, acesti factori au valorile: k_f = 1,11; k_v =

b. Transformarea complexǎ directǎ si inversǎ

Pentru mǎrimile sinusoidale de forma (4.1), se poate stabili o corespondentǎ biunivocǎ între multimea functiilor sinusoidale y(t) si multimea numerelor complexe , corespondentǎ definitǎ de transformarea directǎ

(4.4)

si de transformarea inversǎ

(4.5)

în care operatorul "Im" semnificǎ partea imaginarǎ a unui numǎr complex. Din relatia (4.4), se constatǎ o proprietate fundamentalǎ a transformǎrii mǎrimilor sinusoidale în mǎrimi complexe, aceea cǎ modulul mǎrimii complexe este egal cu valoarea efectivǎ a mǎrimii sinusoidale:

(4.6)

Reprezentarea în complex prezintǎ avantajul cǎ transformǎ ecuatiile integro-diferentiale liniare cu coeficienti constanti, care caracterizeazǎ circuitele de curenti si tensiuni armonice, în ecuatii algebrice liniare de gradul întâi, satisfǎcute de imaginile în complex ale acestor tensiuni si curenti.

Derivarea, în complex simplificat, este echivalentǎ cu înmultirea imaginii complexe cu j, iar integrarea este echivalentǎ cu împǎrtirea imaginii cu j

c. Impedanta complexǎ

Dacǎ un element dipolar este alimentat la tensiunea altenativǎ de valoare instantanee , atunci el absoarbe curentul alternativ de valoare instantanee . Dipolul este caracterizat de impedanta Z, rezistenta R si reactanta X, ale cǎror valori sunt:

(4.7)

în care este defazajul dintre tensiune si curent.

Mǎrimile Z, R si X nu sunt independente. Ele verificǎ relatia:

(4.8)

În Fig. 4.1 se prezintǎ triunghiul impedantelor unui dipol, în perfectǎ concordantǎ cu relatiile (4.7).

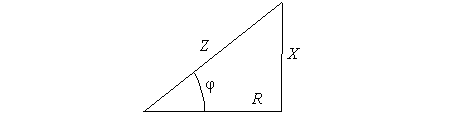
Fig. 4.1. Triunghiul impedantelor unui circuit de c.a.

Impedanta complexǎ se defineste cu relatia directǎ:

(4.9)

Relatia inversǎ de determinare a modului si fazei impedantei, pornind de la impedanta complexǎ, este:

4.1.2. METODE DE MǍSURARE A PARAMETRILOR R, X, Z

Rezistenta electricǎ a rezistoarelor sau bobinelor se mǎsoarǎ în curent continuu, la fel ca si rezistentele de izolatie sau ale dielectricilor condensatoarelor. În curent alternativ sinusoidal se mǎsoarǎ impedanta si componentele sale modulul si argumentul, sau partea realǎ si partea imaginarǎ.

Metodele de mǎsurare ale parametrilor R, X, Z se pot grupa în trei categorii: metode directe, metode de punte si metode indirecte

Metodele directe utilizeazǎ aparate construite special pentru a indica mǎrimea R, X (L sau C) si Z.

Metodele de punte folosesc puntile de mǎsurare de c.c. simple sau duble si punti de c.a. Aceste metode sunt precise si se folosesc în combinatie cu elemente speciale pentru detectarea echilibrului puntii;

Metodele indirecte constau în utilizarea unor relatii de calcul în care apar mǎrimi mǎsurate direct (tensiuni, curenti, puteri). În aceastǎ categorie se înscriu metodele industriale, metoda comparatiei si metoda substitutiei.

4.2. MǍSURAREA REZISTENŢELOR

Mǎsurarea rezistentelor se poate face prin toate cele trei metode generale enuntate în paragraful 4.1.2.

MǍSURAREA REZISTENŢELOR PRIN METODE DIRECTE

Mǎsurarea prin metode directe a rezistentelor se efectueazǎ prin utilizarea unor aparate speciale numite ohmmetre sau megohmmetre (dupǎ cum limita maximǎ a domeniului de mǎsurare este mai micǎ, respectiv mai mare decât 10⁴ . 10⁵ Ω), care indicǎ direct valoarea rezistentei mǎsurate.

Ohmmetrele se compun dintr-o sursǎ de tensiune continuǎ si un dispozitiv magnetoelectric cu bobinǎ simplǎ sau cu bobine încrucisate (de tip logometric), cele logometrice având avantajul de a da indicatii neinfluentate de variatiile tensiunii sursei de alimentare.

Ohmmetrele cu bobinǎ simplǎ pot fi cu schemǎ serie (Fig. 4.2.a), utilizate pentru mǎsurarea rezistentelor relativ mari (peste 10 . 100 Ω), sau cu schemǎ derivatie, care se folosesc pentru mǎsurarea rezistentelor mici (Fig. 4.2.b).

Ohmmetrul cu schemǎ serie are conectatǎ rezistenta de mǎsurat R_x, în serie cu microampermetrul magnetoelectric. Curentul prin miliampermetru este dat de relatia:

(4.11)

în care R_o este rezistenta internǎ a microampermetrului, R₁ este un rezistor cu rezistenta reglabilǎ si E este t.e.m. a sursei. Din relatia (4.11) se poate deduce deviatia aparatului:

(4.12)

în care K₁ si K₂ sunt doi termeni care pot fi considerati constanti. Scala aparatului este neuniformǎ (hiperbolicǎ), fiind gradatǎ invers. Mǎsurarea rezistentei se face astfel: se aduce la zero indicatia aparatului prin reglarea lui R_1, rezistenta de mǎsurat fiind scurtcircuitatǎ de intrerupǎtorul K_x. În acest fel se compenseazǎ, la fiecare mǎsurare, scǎderea tensiunii E a sursei. Pentru extinderea domeniului de mǎsurare se foloseste rezistenta R₂, care poate avea mai multe trepte.

a.                                              b.

Fig. 4.2. Ohmmetru: a - schema serie; b - schema derivatie.

Ohmmetrul cu schemǎ paralel are conectatǎ rezistenta de mǎsurat R_x, în paralel cu microampermetrul magnetoelectric. Conform regulii divizorului de curent, curentul prin miliampermetru este dat de relatia:

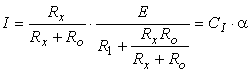(4.11)

Deviatia aparatului are expresia:

(4.12)

în care K₁ si K₂ sunt douǎ constante, dacǎ tensiunea sursei este constantǎ. si pentru acest tip de ohmmetru, scala este tot neuniformǎ, dar gradatǎ în sensul normal. Înainte de efectuarea mǎsurǎrii se aduce la zero indicatia aparatului, cu rezistenta de mǎsurat scurtcircuitatǎ. Exactitatea ohmmetrelor cu o singurǎ bobinǎ este relativ scǎzutǎ, în cele mai bune situatii se poate ajunge la o exactitate de 0,5.

Megommetrele se construiesc pe baza instrumentului magnetoelectric de tip logometric (Fig. 3.4). În paragraful 3.1.2.c, s-a prezentat principiul de functionare al megommetrului, care are si el tot scarǎ hiperbolicǎ (relatia 3.19').

4.2.2. MǍSURAREA REZISTENŢELOR PRIN METODE DE PUNTE

Mǎsurarea rezistentelor cu ajutorul puntilor de c.c. este una dintre cele mai vechi metode de mǎsurare cu precizie ridicatǎ. Aceste punti derivǎ din puntea simplǎ Wheatstone si acoperǎ un interval foarte larg de valori de la 10^-6 Ω, la 10¹⁰ Ω, cu exactitǎti de la 1 - 2 % în cazul puntilor portabile si pânǎ la 0,001 %, în cazul unor punti speciale de laborator.

a. Puntea Wheatstone echilibratǎ

Este formatǎ din patru noduri, având pe laturi rezistentele R₁, . , R₄, pe o diagonalǎ sursa exterioarǎ de tensiune si pe cealaltǎ diagonalǎ un indicator de zero (galvanometru, detector electronic de nul). Cu puntea Wheatstone se mǎsoarǎ rezistente de valori medii, cuprinse între 1Ω si 1MΩ. În Fig. 4.3.a se prezintǎ schema puntii.

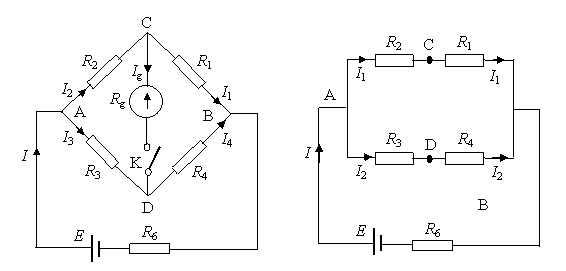
Fig. 4.3. Puntea Wheatstone: a - schema completǎ; b -schema la realizarea echilibrului.

Principiul metodei de punte constǎ în echilibrarea acesteia, adicǎ în anularea curentului din diagonala galvanometrului. În acest caz, I_g = 0 ceea ce conduce la egalarea potentialelor punctelor C si D: V_C = V_D. Asta înseamnǎ cǎ schema puntii se deseneazǎ ca în Fig. 4.3.b si din egalitatea V_C = V_D se poate scrie: R₂I₁ = R₃I₂ si R₁I₁ = R₄I₂, din care rezultǎ:

(4.13)

Relatia (4.13) se numeste relatia puntii Wheatstone echilibrate. Din aceastǎ relatie se poate determina rezistenta necunoscutǎ, de exemplu, R₁, astfel:

(4.14)

în care rezistenta R₄ este o rezistentǎ variabilǎ (cu 3 pânǎ la 6 decade), care se reglezǎ pânǎ când se realizeazǎ echilibrul puntii.

Manipularea puntii se reduce la variatia rezistentei R₄ pânǎ când curentul prin galvanometru se anuleazǎ. Deviatia galvanometrului este proportionalǎ cu curentul I_g:

α = S_I·I_g (4.15)

în care S_I este sensibilitatea galvanometrului. Curentul I_g se calculeazǎ aplicând teoremele lui Kirchhoff schemei din Fig. 4.3.b. Dupǎ efectuarea calculelor se obtine (a se vedea problema 4.1):

în care A si B sunt douǎ mǎrimi independente de R₄, care au expresiile:

Din a doua expresie (4.16) se vede cǎ pentru R₄ = 0, deviatia α este negativǎ si pentru R₄ = ∞, deviatia este pozitivǎ. Existǎ deci o valoare de echilibru R_4e pentru care deviatia se anuleazǎ. Deoarece rezistenta R₄ este variabilǎ în trepte este putin probabil sǎ se gǎseascǎ o rezistentǎ pentru care α = 0. De cele mai multe ori se gǎsesc douǎ valori vecine si , pentru care deviatiile α' si α" corespunzǎtoare au semne contrare. În acest caz, valoarea rezistentei de echilibru se obtine prin interpolare (metoda coardei) si este datǎ de expresia:

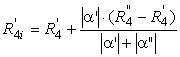(4.18)

în care cele douǎ deviatii s-au luat în valoare absolutǎ.

Sensibilitatea puntii se calculeazǎ calculând limita raportului dintre variatia Δα a deviatiei galvanometrului si variatia relativǎ ΔR₄/R₄ care a produs-o:

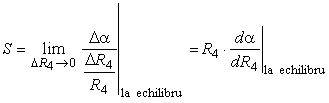(4.19)

Ţinând seama de expresia deviatiei α datǎ de relatia (4.16), prin derivare în raport cu R₄ se obtine expresia generalǎ a sensibilitǎtii puntii:

Întereseazǎ valoarea maximǎ a sensibilitǎtii, care se obtine prin derivarea expresiei (4.20), considerând variabile doar rezistentele R₂, R₃ si R₄, obtinându-se relatiile lui Heaviside:

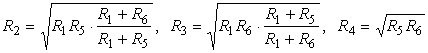
Înlociund relatiile (4.21) în (4.20) se obtine expresia sensibilitǎtii maxime:

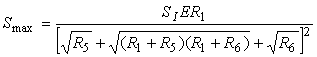
care nu-si schimbǎ valoarea la inversarea diagonalelor puntii.

Sensibilitatea puntii se mai poate mǎri prin mǎrirea sensibilitǎtii S_I a galvanometrului sau prin mǎrirea tensiunii E a sursei, care nu trebuie sǎ depǎseascǎ valoarea de 20 V.

Eroarea relativǎ maximǎ de mǎsurare a rezistentei R_x cu puntea se calculeazǎ, dupǎ o metodǎ asemǎnǎtoare cu aceea din problema 2.4, gǎsindu-se:

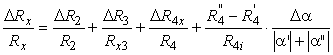(4.23)

în care sunt erorile relative constructive ale rezistentelor puntii, cuprinse uzual între (0,001 . 0,1) %.

b. Puntea dublǎ Thomson (Kelvin)

Se foloseste pentru mǎsurarea rezistentelor mici si foarte mici cuprinse în intervalul (1 . 10^-6) Ω. În puntea dublǎ rezistentele de contact sau ale firelor de legǎturǎ sunt plasate într-un circuit exterior, evitându-se influenta lor în circuitul de mǎsurare. Schema puntii este prezentatǎ în Fig. 4.4.a.

a. b.

Fig. 4.4. Puntea dublǎ: a - schema completǎ; b - schema transfiguratǎ.

Dacǎ în schema din Fig. 4.4.a se face transfigurarea triunghiului cu vârfurile în nodurile 1, 2, 3, într-o stea, se gǎseste Fig. 4.4.b, echivalentǎ cu o punte Wheatstone simplǎ. În Fig. 4.4.b rezistentele transfigurate r_x, r_N, r_g au expresiile:

(4.24)

Se echilibreazǎ puntea Wheatstone din Fig. 4.4.b (galvanometrul G indicǎ valoarea zero, caz în care avem relatia de echilibru:

Se înlocuiesc rezistentele r_x si R_N din (4.24) în (4.25) si se gǎseste relatia:

(4.26)

Uzual, puntile duble se construiesc cu R₁/R₂ = R₃/R₄, astfel încât relatia (4.26) devine:

relatie asemǎnǎtoare cu aceea a puntii Wheatstone simplǎ. Pentru cǎ la bornele rezistoarelor R_x si R_N, cǎderile de tensiune sunt mici, în mǎsurǎri pot interveni erori datorate tensiunilor termoelectromotoare. Aceste erori se compenseazǎ prin repetarea mǎsurǎrilor pentru aceiasi curenti cu sensul inversat (se schimbǎ polaritatea sursei de alimentare a puntii) si adoptarea mediei aritmetice a celor douǎ determinǎri.

c. Puntea pentru rezistente mari (puntea megohm)

Dacǎ se mǎsoarǎ rezistente mai mari de 1MΩ, puntea Wheatstone se modificǎ prin introducerea unei rezistente suplimentare si includerea unui generator de nul cu rezistentǎ de intrare foarte mare, realizat cu amplificatoare de c.c. (Fig. 4.5.a). Aceastǎ schemǎ poate mǎsura rezistente mari în intervalul (10⁶ . 10¹²) Ω.

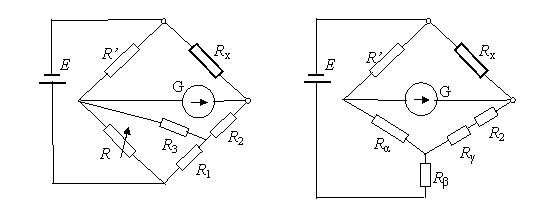
a. b.

Fig. 4.5. Puntea megohm: a - schema initialǎ; b - schema transfiguratǎ.

În puntea din Fig. 4.5.a se face transfigurarea în stea a triunghiului format de rezistentele R, R₁, R₃, obtinându-se schema unei punti simple (Fig. 4.5.b), în care rezistentele echivalente au expresiile:

(4.27)

Relatia de echilibru a puntii din Fig. 4.5.b este:

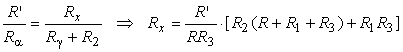(4.28)

Se constatǎ cǎ elementul variabil R este situat în latura opusǎ rezistentei de mǎsurat R_x si cǎ dacǎ acest element tinde la zero rezistenta R_x tinde la infinit, putând fi deci foarte mare. Tensiunea aplicatǎ rezistentelor poate lua valori foarte mari ajungând chiar pânǎ la 1000 V.

d. Punti neechilibrate

Puntea Wheatstone poate fi utilizatǎ în regim dezechilibrat, în scopul mǎsurǎrii unor variatii mici ΔR_x de rezistentǎ, în raport cu o valoare de echilibru R_xo. Este cazul puntilor tensometrice prezentate pe larg în paragraful 2.2.2.a, cu ajutorul cǎrora se determinǎ eforturile mecanice din piesele metalice, folosind mǎrcile tensometrice.

4.2.3. MǍSURAREA REZISTENŢELOR PRIN METODE INDIRECTE

a. Metoda ampermetrului si voltmetrului

Se mai numeste metoda industrialǎ si constǎ în determinarea, în c.c., a rezistentei electrice, prin mǎsurarea tensiunii U de la bornele rezistentei si a curentului I care trece prin rezistentǎ, calculul rezistentei fǎcându-se cu relatia:

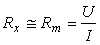(4.29)

Relatia (4.29) ar fi corectǎ dacǎ se presupune cǎ ampermetrul are rezistenta R_A nulǎ si voltmetrul are rezistenta R_V infinitǎ. În realitate, aceastǎ situatie idealǎ nu se întâlneste si de aceea relatia (4.29) este afectatǎ de erori sistematice de metodǎ.

Pentru a reduce aceste erori se fac corectii, dependente de metoda aplicatǎ. Astfel, pentru rezistente mici, se aplicǎ metoda aval si pentru rezistente mari se aplicǎ metoda amonte. În Fig. 4.6. se prezintǎ schema de montaj pentru mǎsurarea industrialǎ a unei rezistente. Rezistorul R_p este montat potentiometric, pentru reglarea tensiunii si Rezistorul R_o este montat în serie pentru reglarea curentului. Dacǎ se aleg corespunzǎtor valorile rezistentelor, unul din cele douǎ rezistoare din Fig. 4.6 poate lipsi.

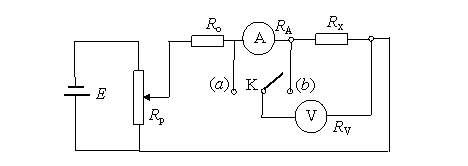
Fig. 4.6. Mǎsurarea rezistentei prin metode industriale:

(a) - metoda amonte; (b) - metoda aval.

Metoda amonte constǎ în conectarea voltmetrului la bornele rezistentei de mǎsurat, înseriatǎ cu ampermetrul [comutatorul K pe pozitia (a)]. Relatia de calcul (corectatǎ) a rezistentei este urmǎtoarea:

(4.30)

Metoda aval constǎ în conectarea voltmetrului la bornele rezistentei de mǎsurat [comutatorul K pe pozitia (b)]. Relatia de calcul (corectatǎ) a rezistentei este urmǎtoarea:

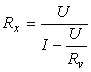(4.31)

Eroarea absolutǎ sistematicǎ de metodǎ, în cazul metodei industriale, se calculeazǎ ca diferentǎ între valoarea rezistentei aproximative, calculatǎ cu relatia (4.29), si valoarea corectatǎ, calculatǎ cu relatiile (4.30) sau (4.31), astfel:

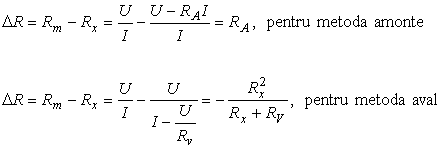(4.32)

ultima relatie obtinându-se tinând cont cǎ: 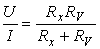. Se constatǎ cǎ în cazul ideal R_A = 0, respectiv R_V = ∞, erorile sistematice date de (4.32) sunt nule.

b. Metoda de comparatie

Principiul metodei constǎ în compararea a douǎ rezistente, putin diferite, montate fie în serie, fie în paralel. În Fig. 4.7 se prezintǎ schema de montaj pentru mǎsurarea rezistentei R_x prin metoda comparatiei tip serie, în care R_o este o rezistentǎ etalon, iar R_h este o rezistentǎ de reglaj. Se mǎsoarǎ cu voltmetrul V tensiunea la bornele rezistoarelor R_x si R_o de valori U_x, respectiv U_o, curentul fiind mentinut la aceeasi valoare cu ajutorul reostatului de reglaj R_h. Deoarece curentul se mentine constant la mǎsurarea celor douǎ tensiuni, rezistenta R_x se calculeazǎ cu relatia:

(4.33)

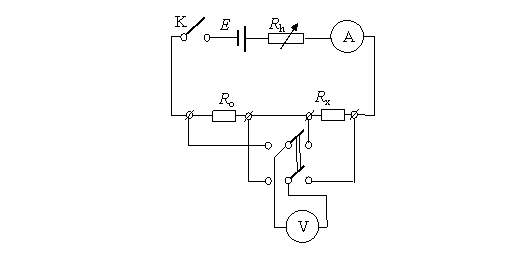
Fig. 4.7. Schema serie bazatǎ pe metoda comparatiei.

c. Metoda subtitutiei

Metoda permite determinarea cu precizie a rezistentei. Rezistenta de precizie R_o, reglabilǎ, se substituie rezistentei de mǎsurat R_x, în schema în care aceasta din urmǎ a fost mǎsuratǎ. Pǎstrând neschimbate conditiile anterioare, se variazǎ rezistenta R_o pânǎ când se obtin aceleasi deviatii la aparatele de mǎsurat, situatie în care R_x = R_o.

4.3. MǍSURAREA IMPEDANŢELOR

Mǎsurarea impedantelor se realizeazǎ în curent alternativ, prin metode directe, metode de punte si metode indirecte, ca si mǎsurarea rezistentelor. Din multitudinea de metode de mǎsurare a impedantelor se vor descrie cele mai folosite.

METODE DIRECTE DE MǍSURARE A IMPEDANŢELOR

Mǎsurarea prin metode directe a impedantelor se efectueazǎ prin utilizarea unor aparate speciale numite impedantmetre, inductantmetre sau capacimetre, dupǎ cum mǎsoarǎ direct impedanta (modulul si faza sau cele douǎ componente rectangulare), inductivitatea sau capacitatea.

a.      Capacimetrul

Capacimetrul este constituit dintr-un generator G, în dinti de fierǎstrǎu (Fig. 4.8) de frecventǎ joasǎ (50 . 120) Hz, care furnizeazǎ tensiunea prin condensatorul de mǎsurat C_x, la borna inversoare a unui amplificator operational, în montaj derivator.

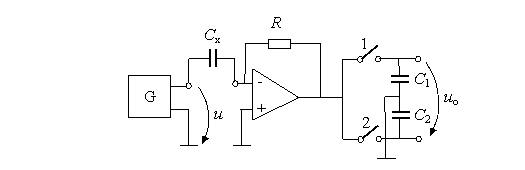
Fig. 4.8. Capacimetru.

La iesirea amplificatorului se culege tensiunea u_o, dreptunghiularǎ, de amplitudine proportionalǎ cu C_x si cu suma pantelor de crestere m₁ si descrestere m₂ a tensiunii în dinti de fierǎstrǎu:

(4.34)

Tensiunea u_o este stocatǎ de condensatoarele C₁ si C₂, prin intermediul comutatoarelor 1 si 2 (porti cu tranzistoare comandate), care conduc pe rând, în timpul palierului crescǎtor, respectiv descrescǎtor al semnalului de intrare. Capacimetrul are avantajul cǎ este independent de deriva amplificatorului operational si de caracteristicile semnalului de intrare. Domeniul de mǎsurare începe de la 0,01 pF si se terminǎ la circa 2000 μF.

b. Inductantmetru

Schema unui inductantmetru este prezentatǎ în Fig. 4.9. Curentul dat de generatorul G trece prin rezistenta R, de mare valoare, pentru obtinerea unui curent constant, apoi parcurge inductanta L_x de mǎsurat. Tensiunea U_L de la bornele inductantei are valoarea:

(4.35)

deoarece curentul prin aparat are valoare constantǎ. Aparatul are scalǎ liniarǎ si poate mǎsura inductivitǎti între 10 μH si 100 H, cu o exactitate între 0,5% si 3%.

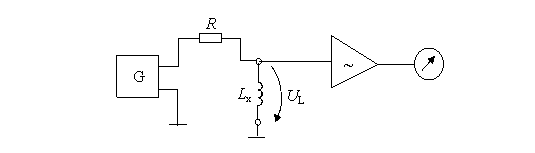
Fig. 4.9. Inductantmetru.

c. Impedantmetru (Z - metrul)

Impedantmetrele (Z - metrele) mǎsoarǎ fie modulul impedantei, fie modulul si faza (sau componentele ortogonale). O schemǎ bloc generalǎ a unui impedantmetru vectorial este prezentatǎ în Fig. 4.10. Amplificatorul A este comandat de sesizorul de curent I care sesizeazǎ curentul prin impedanta Z_x si regleazǎ automat amplificarea prin A astfel încât curentul rǎmâne constant independent de valoarea impedantei de mǎsurat. Tensiunea de la bornele lui Z_x, proportionalǎ cu aceastǎ impedantǎ, este preluatǎ de amplificatorul U si transmisǎ indicatorului |Z‌‌_x|, gradat în Ohmi. Semnalele de la blocurile U si I sunt

limitate si aplicate fazmetrului φ, de tip cu trecere prin zero, care indicǎ unghiul de defazaj al impedantei si-l afiseazǎ. Aparatul cu reglarea constantǎ a curentului se foloseste pentru impedante cu |Z‌‌_x| < 1000 Ω. Pentru impedante pentru care |Z‌‌_x| > 1000 Ω se foloseste un aparat similar, dar cu mentinerea constantǎ a tensiunii.

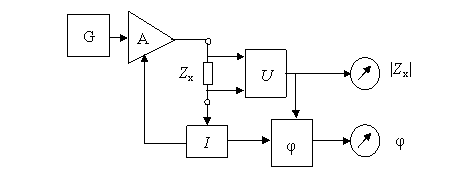
Fig. 4.10. Impedantmetru vectorial.

Impedantmetrul are exactitate micǎ de ordinul a 2 % pentru modulul impedantei si de 6 grade pentru defazaj. Domeniul de frecvente este mare fiind cuprins între 5 Hz si 500 kHz.

MǍSURARE A IMPEDANŢELOR PRIN METODE DE PUNTE

Puntile pentru mǎsurarea impedantelor sunt punti de c.a. si provin tot din puntea Wheatstone, prin înlocuirea rezistentelor din laturile sale cu impedante, iar indicatorul de nul este de c.a.

a. Puntea simplǎ în curent alternativ

În Fig. 4.11 se prezintǎ schema generalǎ a puntii de c.a. Conditia de echilibru se deduce prin analogie cu puntea Wheatstone de c.c. si se scrie astfel:

(4.36)

Fig. 4.11. Puntea simplǎ de c.a.

Se scrie impedanta complexǎ sub forma (4.9) punându-se în evidenta fie componentele acesteia R si X, fie modulul Z si argumentul φ. Exprimând impedantele complexe cu relatia (4.9), relatia complexǎ (4.36) este echivalentǎ cu urmǎtoarele douǎ relatii reale:

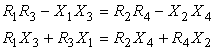(4.36')

Dacǎ se exprimǎ impedanta complexǎ în functie de modul si argument, relatia complexǎ (4.36) este echivalentǎ cu relatiile:

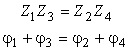(4.36")

Deoarece conditia de echilibru a puntii de c.a. se exprimǎ cu ajutorul a douǎ relatii, rezultǎ din echilibrul puntii se pot determina douǎ mǎrimi. Realizarea echilibrului se poate face prin variatia a douǎ sau mai multor mǎrimi din celelalte 6 care intervin în ecuatiile de echilibrul (4.36') sau (4.36").

Existǎ foarte multe scheme de punti de c.a., în functie de natura si modul de conectare ale impedantelor din laturile puntii. Aplicatii practice prezintǎ un numǎr de 6 . 8 punti de c.a.

Echilibrarea puntilor trebuie sǎ fie convergentǎ, rapiditatea convergentei fiind o calitate deosebitǎ. Puntile la care componentele mǎsurate R_x si X_x se echilibreazǎ independent au convergenta maximǎ si sunt de preferat. Sunt punti la care conditiile de echilibru nu depind de frecventǎ. Acestea sunt foarte eficiente deoarece sursele lor nu mai trebuie sǎ fie riguros sinusoidale.

b. Tipuri particulare de punti simple de c.a.

Se vor prezenta câteva tipuri de punti de c.a. cu aplicabilitate practicǎ la mǎsurarea capacitǎtilor si inductantelor.

Puntea Sauty serie are schema electricǎ prezentatǎ în Fig. 4.12. Elementele variabile ale puntii sunt rezistenta R_o si capacitatea C_o, din laturile 3 si 4.

Deducerea conditiilor de echilibru se poate face aplicând puntii relatia (4.36), cu folosirea impedantelor complexe:

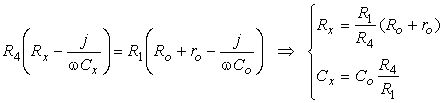(4.37)

Cu ajutorul puntii Sauty se poate calcula si tangenta unghiului de pierderi a condensatorului C_x, în functie de tangenta unghiului de pierderi a condensatorului C_o, folosind relatia:

(4.38)

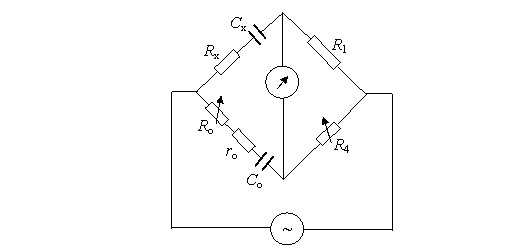
Fig. 4.12. Puntea Sauty serie.

Puntea Schering serie, ca si puntea Sauty serie, serveste la mǎsurarea capacitǎtii condensatoarelor. Puntea Schering este destinatǎ mǎsurǎrii în înaltǎ tensiune a cablurilor, izolatoarelor, materialelor izolante, înfǎsurǎrilor de înaltǎ tensiune ale transformatoarelor electrice si a condensatoarelor de înaltǎ tensiune, la frecventa industrialǎ de 50 Hz. Alimentarea puntii se face de la un transformator de înaltǎ tensiune. Tensiunea înaltǎ se aplicǎ în întregime condensatoarelor C_x si C_o, pe rezistentele R₁ si R₄ revenind o tensiune redusǎ, nepericuloasǎ, prin punerea la masǎ a punctului comun al celor douǎ rezistente.

Relatiile de echilibru ale puntii Schering sunt urmǎtoarele:

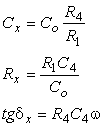(4.39)

Fig. 4.13. Puntea Schering serie.

Puntea Maxwell - Wien este o punte pentru mǎsurarea inductivitǎtilor cu factor de calitate Q, de valori mici si medii. Schema puntii se dǎ în Fig. 4.14.

Fig. 4.14. Puntea Maxwell - Wien.

Relatiile de echilibru ale puntii Maxwell - Wien sunt date de expresiile:

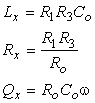(4.40)

Puntea Owen serie este o punte pentru mǎsurarea inductivitǎtilor cu factor de calitate Q, de valori mari. Schema puntii este arǎtatǎ în Fig. 4.15.

Relatiile de echilibru ale puntii Owen serie sunt date de expresiile:

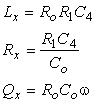(4.41)

Fig. 4.15. Puntea Owen serie.

Mǎsurarea inductivitǎtilor mutuale se poate face cu o punte obisnuitǎ de mǎsurare a inductivitǎtilor. Se procedeazǎ astfel: se mǎsoarǎ inductivitǎtile proprii totale ale celor douǎ bobine cuplate mutual, odatǎ cuplate în serie aditional si a doua oarǎ cuplate în serie diferential. Inductivitǎtile totale mǎsurate în cele douǎ cazuri au expresiile:

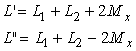(4.42)

Inductivitatea mutualǎ M_x se calculeazǎ scǎzând relatiile (4.42) si împǎrtind rezultatul la 4:

Existǎ si punti de c.a. speciale cu ajutorul cǎrora se poate mǎsura inductivitatea mutualǎ. Este cazul puntii Carey - Foster [ ]. De asemenea existǎ o mare varietate de punti de c.a. cu transformatoare. Acestea au avantajul cǎ influenta capacitǎtilor parazite este mai micǎ decât la puntile obisnuite [ ].

MǍSURARE A IMPEDANŢELOR PRIN METODE INDIRECTE

Metodele indirecte de mǎsurare a impedantelor se aseamǎnǎ cu cele folosite pentru mǎsurarea rezistentelor. Ele pot fi metode industriale (ampermetru - voltmetru - wattmetru), de compensatie, de zero si de rezonantǎ, ultimile douǎ fiind folosite în domeniul frecventelor înalte.

a. Mǎsurarea parametrilor R, X, Z prin metoda industrialǎ

Aceastǎ metodǎ constǎ în mǎsurarea puterii consumate de impedantǎ, a tensiunii la borne si a curentului absorbit. Schema de montaj este prezentatǎ în Fig. 4.16 si este o schemǎ aval, pentru ca tensiunea aplicatǎ impedantei sǎ fie mǎsuratǎ direct. Se noteazǎ cu P, U si I indicatiile celor trei aparate din schemǎ.

Dacǎ se neglijeazǎ consumul propriu al aparatelor de mǎsurare, parametrii R, X, Z se calculeazǎ cu ajutorul relatiilor aproximative:

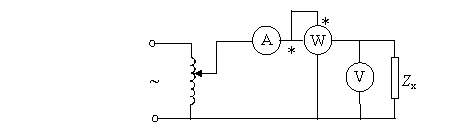
Fig. 4.16. Mǎsurarea parametrilor R, X, Z prin metoda industrialǎ.

În cazul în care nu se mai poate neglija consumul aparatelor de mǎsurare, se noteazǎ cu R_wU, R_V rezistentele bobinelor de tensiune ale wattmetrului si respectiv voltmetrului. Se noteazǎ cu R_e, rezistenta lor echivalentǎ (conectate în paralel), datǎ de relatia:

În aceastǎ situatie, relatiile care dau valorile parametrilor R, X si Z si care tin seama si de consumul aparatelor sunt urmǎtoarele (a se vedea problema 4.4):

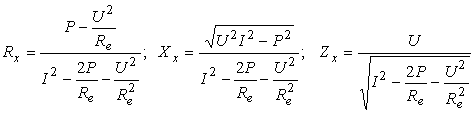
b. Mǎsurarea inductivitǎtilor si capacitǎtilor prin metoda industrialǎ

Mǎsurarea mǎrimilor L si C se poate face la frecventa industrialǎ de 50Hz, cu ajutorul unui ampermetru si al unui voltmetru, fiind necesarǎ si existenta unei surse de c.c. pentru mǎsurarea rezistentei, conform schemei din Fig. 4.17. Se considerǎ cǎ bobina are si rezistentǎ (notatǎ cu R_x). În Fig. 4.17 cu Z_x s-a notat fie bobina realǎ care se mǎsoarǎ, caracterizatǎ de parametrii R_x si L_x, fie condensatorul, caracterizat de capacitatea C_x.

Mǎsurǎtorile se desfǎsoarǎ astfel:

i) dacǎ se mǎsoarǎ inductivitatea unei bobine reale (cu rezistentǎ), se mǎsoarǎ mai întâi rezistenta R_x a bobinei, în c.c., cu relatia R_x = U_cc/I_cc, în care U_cc, I_cc sunt valorile tensiunii si curentului continuu, mǎsurate cu comutatorul K₁ pe pozitia din dreapta, apoi se mǎsoarǎ si impedanta Z_x a bobinei, în c.a., cu relatia Z_x = U_ca/I_ca, în care U_ca, I_ca sunt valorile alternative ale tensiunii si curentului, mǎsurate cu comutatorul K₁ pe pozitia din stânga, determinându-se dupǎ aceea, prin calcul, reactanta X_x, apoi inductivitatea L_x astfel:

în care f este frecventa tensiunii alternative, mǎsuratǎ cu frecventmetrul F.

ii) dacǎ se mǎsoarǎ capacitatea C_x a unui condensator, împedanta Z_x va fi înlocuitǎ de acest condensator. Se pune comutatorul K₁ pe pozitia din dreapta, se mǎsoarǎ reactanta capacitivǎ X_x, apoi se calculeazǎ capacitatea astfel:

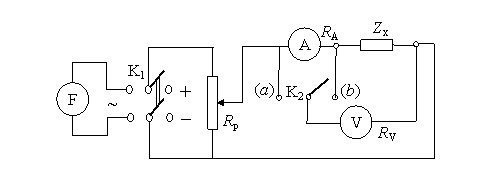
Fig. 4.17. Mǎsurarea mǎrimilor R si X (L sau C) prin metoda ampermetrului

si voltmetrului în c.c. si c.a: (a) - amonte; (b) - aval.

(4.47)

Relatiile (4.46) si (4.47) servesc la mǎsurarea indirectǎ a parametrilor unei bobine reale, respectiv ai unui condensator considerat fǎrǎ pierderi, în cazul în care se neglijeazǎ consumurile proprii ale aparatelor de mǎsurare. În aceste cazuri se poate folosi, fie metoda amonte [K₂ pe pozitia (a)], fie metoda aval [K₂ pe pozitia (b)].

În cazul în care se iau în seamǎ consumurile aparatelor, relatiile (4.46) si (4.47) se corecteazǎ. Fie R_A si R_V rezistentele ampermetrului, respectiv voltmetrului din schemǎ. Pentru mǎsurarea inductivitǎtii L_x se folosesc relatiile exacte:

(

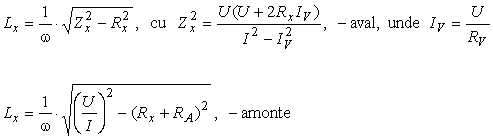Prima relatie se aplicǎ în cazul în care inductivitatea se mǎsoarǎ prin metoda aval, iar a doua relatie pentru metoda amonte. Relatiile exacte pentru mǎsurarea capacitǎtii sunt urmǎtoarele:

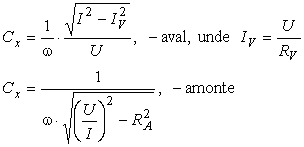
Prima relatie se aplicǎ în cazul în care capacitatea se mǎsoarǎ prin metoda aval, iar a doua relatie pentru metoda amonte.

În cazul mǎsurǎrii capacitǎtilor, metoda ampermetrului si voltmetrului se poate aplica numai la condensatoare cu capacitatea C ≥ 1μF, deoarece în caz contrar, la frecventa industrialǎ, curentul absorbit este prea mic si nu poate fi mǎsurat direct.

c. Mǎsurarea inductivitǎtii mutuale prin metoda industrialǎ

O metodǎ simplǎ de mǎsurare a inductivitǎtii mutuale o constituie conectarea bobinei 1 la sursa de tensiune alternativǎ, mǎsurarea curentului I₁ care o parcurge (Fig. 4.18), simultan cu conectarea la bornele bobinei 2 a unui voltmetru si mǎsurarea tensiunii induse U₂.

Fig. 4.18. Mǎsurarea inductivitǎtii mutuale prin metoda industrialǎ.

Inductivitatea mutualǎ se calculeazǎ cu relatia [ ]:

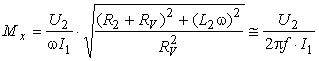
în care R₂ si L₂ω sunt rezistenta si reactanta bobinei secundare 2. Aproximatia din (4.50) se referǎ la faptul cǎ voltmetrul nu mǎsoarǎ t.e.m. E₂ indusǎ în secundar, ci tensiunea U₂ la bornele secundarului, mai micǎ decât E₂.

4.4. PROBLEME APLICATIVE

PROBLEMA 4.1.

Pentru puntea Wheatstone de c.c. a cǎrei schemǎ se prezintǎ în Fig. 4.3.a, sǎ se calculeze expresia generalǎ a curentului I_g prin diagonala verticalǎ a puntii, în functie de rezistentele R_k ale puntii si de t.e.m. E care o alimenteazǎ.

Solutie

Pentru reteaua datǎ de puntea din Fig. 4.3.a, se pot aplica teoremele lui Kirchhoff (teorema întâi în nodurile A, B, C si teorema a doua pe ochiurile ACD, CBD si ADBA), rezultând ecuatiile:

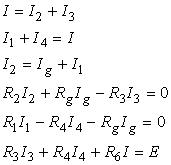
Se eliminǎ curentii I, I₂ si I₃ prin metoda substitutiei si se obtine sistemul:

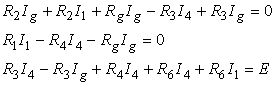
Dupǎ rezolvarea sistemului de mai sus printr-o metodǎ oarecare se obtine expresia curentului I_g:

în care A si B sunt douǎ mǎrimi independente de R₄, care au expresiile:

Se constatǎ cǎ s-au obtinut aceleasi relatii cu (4.16) si (4.17).

PROBLEMA 4.2.

În Fig. 4.19.a se prezintǎ schema electricǎ a puntii Anderson de c.a. Sǎ se gǎseascǎ relatiile de echilibru ale puntii si sǎ se arate cum se poate echilibra aceastǎ punte.

Solutie

Puntea Anderson se utilizeazǎ la mǎsurarea inductivitǎtii bobinelor de joasǎ frecventǎ.

a. b.

Fig. 4.19. Puntea Anderson: a - schema electricǎ; b - schema transfiguratǎ.

Pentru a deduce relatiile de echilibru ale puntii se face transfigurarea triunghiului C - R₂ - r, într-o stea echivalentǎ, cu impedantele complexe Z_α, Z_β, Z_γ, date de relatiile:

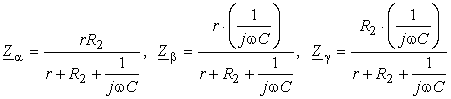
Pentru puntea transfiguratǎ din Fig. 4.19.b, relatiile de echilibru se deduc ca si la o punte obisnuitǎ de c.a., cu relatiile (4.36), care capǎtǎ forma:

,

Dupǎ înlocuirea impedantele complexe Z_α, Z_β, Z_γ, si separarea pǎrtilor reale si imaginare, se obtin relatiile echivalente:

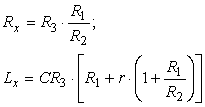
care reprezintǎ relatiile de echilibru ale puntii Anderson. Adesea se alege R₁ = R₂, caz în care relatiile de echilibru capǎtǎ o formǎ mai simplǎ:

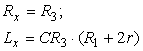
Echilibrul puntii se realizeazǎ în douǎ etape: mai întâi se alimenteazǎ puntea în c.c. si se regleazǎ R₃, pânǎ la echilibru; apoi se alimenteazǎ puntea în c.a. si se regleazǎ r pânǎ la obtinerea echilibrului. Din ultimile relatii de echilibru, obtinute pentru R₁ = R₂, se deduce faptul cǎ nu se pot mǎsura cu puntea Anderson inductivitǎti de valoare mai micǎ decât valoarea L_min = CR₃R₁, obtinutǎ pentru r = 0.

PROBLEMA 4.3.

În Fig. 4.20, se prezintǎ o bobinǎ realǎ (de parametrii R si L), înseriatǎ cu o rezistentǎ aditionalǎ R₁. Montajul este alimentat la o tensiune sinusoidalǎ de frecventǎ f = 50 Hz. Cunoscând valoarea rezistentei R₁ = 5 , precum si valorile efective ale tensiunilor indicate de cele 3 voltmetre: U₁ = 50 V, U₂ = 121 V,  U₃ = 149 V, sǎ se determine parametrii R si L ai bobinei, neglijând consumul voltmetrelor.

Solutie

Curentul prin bobinǎ are valoarea I = U₁/R₁ = 50/5 = 10A. Impedanta bobinei este datǎ de expresia:

Din triunghiul ABC (Fig. 4.20.b), conform teoremei cosinusului, rezultǎ:

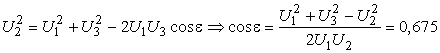
În Fig. 4.20.b, se proiecteazǎ fazorul tensiunii U₃ pe directia fazorului curentului I si rezultǎ relatia:

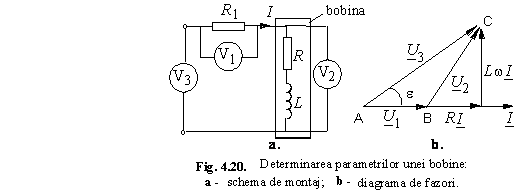
Prin rezolvarea sistemului de mai sus, se deduc valorile parametrilor bobinei: R = 5,06 si X = 0,0349 H.

PROBLEMA 4.4.

Pentru schema de montaj aval din Fig. 4.16, privind mǎsurarea parametrilor R_x, X_x, Z_x, sǎ se deducǎ expresii care sǎ tinǎ seama de consumul aparatelor de mǎsurare, în functie de R_wU, R_V, R_e care sunt rezistentele bobinelor de tensiune ale wattmetrului, voltmetrului si respectiv rezistenta lor echivalentǎ, datǎ de relatia (4.45). Se cunosc U, I si P, mǎsurate de cele 3 aparate din schemǎ.

Solutie: Schema de montaj din Fig. 4.16, admite o schemǎ echivalentǎ prezentatǎ în Fig. 4.21.a.

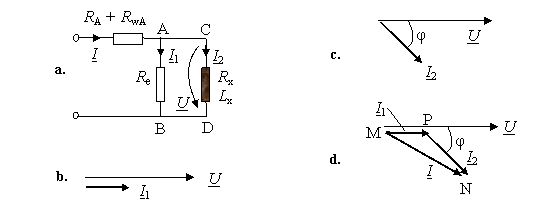
Fig. 4.21. Asupra determinǎrii de relatii exacte, luând în seamǎ consumul aparatelor

din Fig. 4.16: a- schema echivalentǎ; b - diagrama fazorialǎ a circuitului rezistiv AB;

c - diagrama fazorialǎ a circuitului CD; d - diagrama fazorialǎ a întregului circuit;

Din diagrama de fazori prezentatǎ în Fig. 4.21.d se aplicǎ teorema cosinusului în triunghiul MNP si se gǎseste:

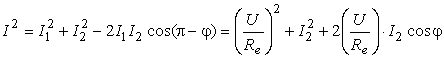
Deoarece curentul I₁, prin cele 2 bobine de tensiune ale wattmetrului si voltmetrului este foarte mic, putem scrie în relatia de mai sus, în termenul cu minus, cǎ si cǎ , astfel încât aceasta devine:

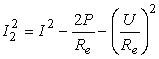
Rezistenta R_x se calculeazǎ mai precis cu relatia:

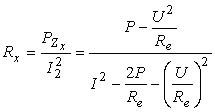
în care reprezintǎ puterea activǎ pierdutǎ efectiv în impedanta Z_x, iar I₂ curentul care trece efectiv prin Z_x. Impedanta Z_x si reactanta X_x se calculeazǎ astfel:

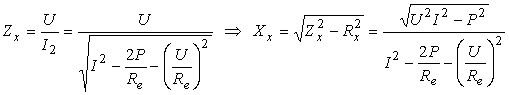
adicǎ tocmai relatiile (4.45').

PROBLEMA 4.5.

O bobinǎ realǎ (consideratǎ a avea si rezistentǎ) este alimentatǎ la o tensiune sinusoidalǎ, prin intermediul unui montaj, care contine un ampermetru, un voltmetru si un wattmetru, în montaj aval, indicând: I = 4A, U = 120 V, P = 160 W. Sǎ se determine rezistenta R_x si reactanta X_x ale bobinei, consideratǎ circuit R - X serie în douǎ ipoteze : a. neglijând consumul aparatelor ; b. tinând seama de consumul aparatelor stiind cǎ R_w = 5000 Ω si R_V = 10000 Ω ; c. erorile relative care se fac la punctul a, în raport cu punctul b.

Solutie: a. Dacǎ nu se tine seama de consumul aparatelor, impedanta bobinei este Z_x = U/I = 30 . Rezistenta bobinei este R_x = P/I² = 10 iar reactanta acesteia are valoarea .

b.      Dacǎ se tine seama de consumul aparatelor avem:

,

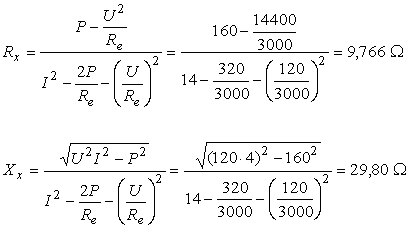
c. erorile relative care se fac la punctul a, în raport cu punctul b. se calculeazǎ cu relatiile :
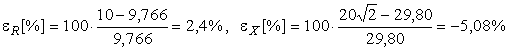