56.       Se cere sa se prezinte schema de constructie a unui tahimetru autoreductor DAHLTA  020 Carl Zeiss Jena, precizandu-se piesele sale componente si axele principale.

            Solutie : fig.nr.1.56

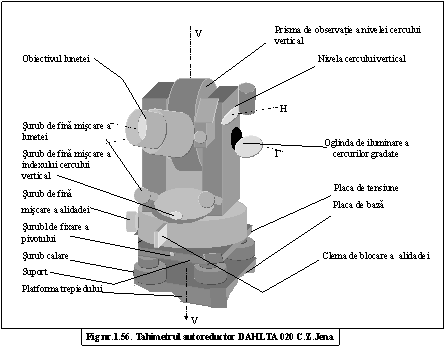
Axele constructive ale acestui tip de aparat sunt aceleasi ca in cazul teodolitului (fig.nr.1.41).

Caracteristicile aparatului sunt:

-   &n 232c24c bsp;   &n 232c24c bsp; luneta da imagine dreapta;

-   &n 232c24c bsp;   &n 232c24c bsp; microscopul cu scarita (similar cu microscopul teodolitului Theo 020) asigura o precizie de 1^c;

-   &n 232c24c bsp;   &n 232c24c bsp; la aparat se poate atasa o planseta speciala care permite atat schitarea la scara a planimetriei cat si  curbele de nivel prin care se reprezinta relieful terenului masurat;

-   &n 232c24c bsp;   &n 232c24c bsp; planul reticular este compus dintr-o parte mobila (ce serveste la masurarea diferentelor de nivel) si o parte fixa neceara vizarii si determinarii distantelor).

57.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Cum se inregistreaza citirile pe mira Dahlta, pentru calcularea diferentelor de nivel si a distantelor?

            Solutie: fig.nr.1.57.

            Citiri:

-   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp; la firul distanta C_d

-   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp; la firul de cote cu constanta

      k₁ = + 10 : C_Z

-   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp; la firul de cote cu constanta

      k₂ = + 20 : C_Z

58.       Daca din punctul de statie 47 (Z₄₇ = 321,432 m) s-a vizat mira instalata in punctul 48 si s-au inregistrat valorile prezentate in fig.nr.1.57 se cere sa se calculeze distanta orizontala dintre cele doua puncte si cota absoluta a reperului 48.

            Solutie;

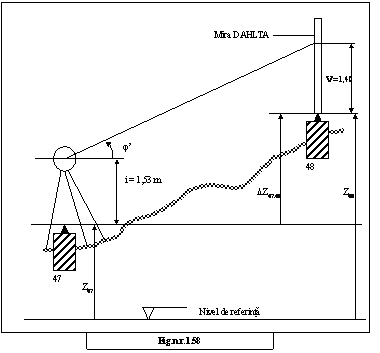
Distanta orizontala : D_47.48 = C_{d .}

Deci D_47.48 = 40,20 m;

Diferenta de nivel:

DZ_47.48 = (i - v) + h_m                                                    (2.58)

            h = C_Z1 x 10 = 2,78 m                                                 (3.58)

            h = C_Z2 x 20 = 2,78 m

                       h₁ + h₂

            h_m  = ------------ = 2.78 m                                          (4.58)

Deci, D_47.48 = + 2,91 m;

            Cota absoluta va fi: Z₄₈ = D₄₇ + DZ_47.48 ;                       (5.58)

ð   &n 232c24c bsp; Z₄₈ = 324,342 m.

59.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Sa se schiteze schema de constructie a tahimetrului B.R.T. 006 Carl Zeiss Jena. Se vor reprezenta piesele principale si secundare.

            Aparatul reduce automat distantele la orizont, permitand inregistrarea directa a distantelor orizontale.

60.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Care sunt operatiile prin care se inregistreaza o distanta orizontala cu ajutorul tahimetrului - telemetru B.R.T.006?

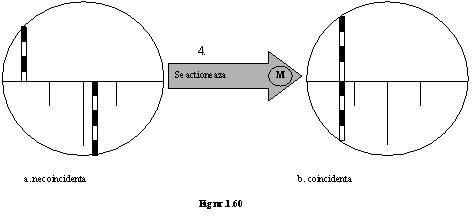
            Solutie: 1. se centreaza, caleaza aparatul in punctul de statie; 2. se fixeaza in punctul vizat un jalon sau de la caz la caz un semnal sau o mira de vizare; 3.(fig.nr.1.60.a): se vizeaza semnalul; 4.se inregistreaza pe scara distantelor valoarea b (baza variabila); 5. Se calculeaza distanta orizontala.

61.       In punctul de statie 28 ( Z₂₈ = 328,561 m) s-au inregistrat prin vizarea jalonului din reperul 61 urmatoarele valori: L = 43,21 m , DD = 1,24 m (corectia de reducere la orizont). S-a stabilit unghiul de panta al terenului j = 15^g 57^c. Se cere sa se calculeze distanta orizontala si cota punctului 61.

            Solutie:

            D = L - DD (1.61)

            Deci

            D = 43,21 - 1,24 = 41,97 m.

DZ'_28.61  = L² - D²                                                      (2.61)

            sau

DZ"_28.61  = Dtgj

            Vor rezulta:

DZ'_28.61  = 10,277 m;

DZ"_28.61  = 10,474 m

DZ' +  DZ"

DZ_28.61  = ----- ----- ----  (4.61)

            deci, DZ_28.61  = 10,376 m.

            Cota punctului 61:

            Z₆₁  =  Z₂₈  + DZ_28.61    (5.61)

            Z₆₁  = 338,937 m.

F.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Probleme de planimetrie

a.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Masurarea directa a distantelor

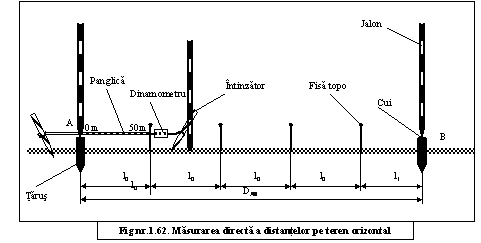
62.       In cadrul unei lucrari topografice, s-a masurat prin metoda directa, distanta orizontala dintre doua puncte A si . Sa se calculeze aceasta distanta, daca se cunosc urmatoarele date ale masuratorii:

            l₀  = 50 m (lungimea nominala a panglicii utilizate);

            l₁  = 28,43 m (distanta inregistrata pe ultima panglica);

            n  = 4 (numarul de panglici aplicate);

            terenul este orizontal (j ≤ 5^g).

Se va intocmi si schita corespunzatoare masuratorii.

Din figura prezentata (fig.1.62) rezulta:

            D_AB  = n . l₀  + l₁   (1.62)

            In acest caz: D_AB  = 4 x 50 + 28,43 = 228,43 m.

63.       Punctele topografice C si D se gasesc pe un teren inclinat, sub o panta cunoscuta (j). Cunoscand datele masuratorii, sa se calculeze D_CD  si sa se intocmeasca schita corespunzatoare.

Se dau:                         l₀ = 25 m;

                                     l₁  = 14,71 m;

                                     n  = 3;

j = 9^g21^c.

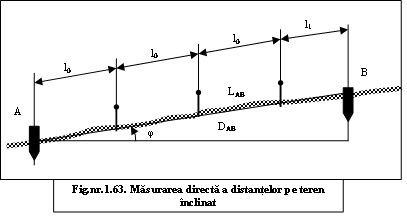
Observatie: instrumentele utilizate sunt aceleasi, ca in cazul precedent.

            Din schita:         L_AB  = n . l₀  + l₁         (1.63)

                                    D_AB = L_ABcosj

            Inlocuind datele problemei:

                                    L_AB  = 3 x 25 + 14,71 = 89,71 m;

                                    D_AB  = 89,71cos9^g21^c = 88,77 m.

64.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Sa se determine distanta orizontala dintre punctele 21 si 22 aflate pe un aliniament sub pantele succesive  j j si j - cunoscute. Se cunosc:

l₀  = 50 m;

n₁ = 2;                          n₂ = 1;                          n₃ = 3;

l₁  = 12,36 m;               l₂  = 16,52 m;               l₃  = 21,53 m;

j = 16^g31^c.                 j = 12^g52^c.                j =  7^g67^c.

Se calculeaza distantele inclinate:

L₁  = n₁ . l₀  + l₁  = 2 . 50 + 12,36 = 112,36 m;

L₂  = n₂ . l₀  + l₂  = 1 . 50 + 16,52 =   66,52 m;

L₃  = n₃ . l₀  + l₃  = 3 . 50 + 21,53 = 171,53 m.

Distantele orizontale corespunzatoare vor fi:

D₁  = L₁ . cosj = 112,36 . cos 16^g31^c = 108,69 m;

            D₂  = L₂ . cosj =   66,52 . cos 12^g52^c =   65,24 m;

            D₃  = L₃ . cosj = 171,53 . cos   7^g67^c = 170,29 m.

            Distanta totala D_21.22 va fi suma distantelor partiale:

            D_21.22  = D₁ + D₂ + D₃  = 108,69 = 65,24 + 170,29 = 344,22 m.

65.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  La masurarea prin metoda corecta a unei distante s-au obtinut urmatoarele valori:

l₀  = 50 m;

l₁  = 12,47 m;

n   = 7;

j = 12^g51^c;

l_r   = 50,007 m (lungimea reala a panglicii);

F_et = 3 daN/ mm² (forta de intindere la etalonare);

F_r  =  3 daN/ mm² (forta de intindere la masurare);

t₀   = 20ºC ( temperatura la etalonarea panglicii);

t₁   = 28ºC ( temperatura din timpul masuratorii);

A_sect = 10 mm² (aria sectiunii transversale a panglicii).

Sa se calculeze distanta orizontala aplicandu-se si corectiile necesare.

Solutie:

Calculul lungimii orizontale consta din urmatoarele etape:

-   &n 232c24c bsp;   &n 232c24c bsp; se determina distanta inclinata L:

L = n . l₀ + l₁ = 7 . 50 + 12,471 = 362,471 m         (1.65);

-   &n 232c24c bsp;   &n 232c24c bsp; se calculeaza corectia de etalonare, conform relatiei:

                      L

C_e = (l_r - l₀) ------                                                   (2.65)

                       l₀  

C_e = (50,007 - 50) ----------- = 0,051 m

-   &n 232c24c bsp;   &n 232c24c bsp; se aplica lungimii L, corectia de etalonare:

L' = L + C_e                                                             (3.65);

L' = 362,471 + 0,051 = 362,522 m;

-   &n 232c24c bsp;   &n 232c24c bsp; se determina corectia de temperatura:

                L'

C_t = Dl_t ------                                                                    (4.65)

               l₀

Dl_t = l₀ a (t₁ - t₀)                                                   (5.65)

deci :          Dl_t = 50 . 0.0115 (28 - 20) = 4,5 mm;

                   C_t  = 4,6 ------------ = 33,4 mm = 0,033 m

                    corectam apoi lungimea L':

                    L" = L' + C_t ;                                                       (6.65)

                    L" = 362,522 + 0,033 = 362,555 m;

-   &n 232c24c bsp;   &n 232c24c bsp; calculul corectiei de intindere se face cu relatia:

         L"( F_r   -  F_et )

C_p = ----- ----- -------                                      (7.65)

                     E . A_sect (cm²)

in cazul problemei C_p = ----- ----- ------- = 0,002 m

-   &n 232c24c bsp;   &n 232c24c bsp; lungimea inclinata corecta va fi:

      L''' = L" + C_p                                                   (8.65)

      L''' = 362,555 + 0,002 = 362,557 m.

Distanta orizontala corespunzatoare , se va calcula asa cum se cunoaste, din relatia:

                  D = L''' . cos j

            Deci, in final D = 362,557 cos 12^g51^c = 355,579 m.

b.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Masurarea indirecta a distantelor

66.       Sa se determine distanta orizontala intre punctele 43 si 44, daca s-au inregistrat prin masurare indirecta tahimetrica urmatoarele valori:

            C_S  = 1951 + n (m)                   i = 1,472 m (inaltimea instrumentului);

            C_M= 1472                                j = 0^g  (unghiul de panta);

            C_J  = 0993 - n (mm)                 K = 50 (constanta stadimetrica).

·   &n 232c24c bsp;    se verifica citirile pe mira

                      C_S + C_J

C_M = ------------- 3) mm                               (1.66)

           pentru acest caz:

1472 = ----- ----- ----- = 1472 (mm)

·   &n 232c24c bsp;    se constata ca se inregistreaza direct distanta orizontala ( j = 0^g).

·   &n 232c24c bsp;    se calculeaza distanta orizontala : d = K . H = K(C_S - C_J)   (2.66);

·   &n 232c24c bsp;    deci D = 50 (1,951 - 0,993) = 47,900 m.

67.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Punctele 61 si 62 sunt situate pe un teren inclinat. La masurarea prin metoda tahimetrica a distantei dintre aceste puncte s-au obtinut valorile:

C_S    = 2652 - n (mm)               i   = 1,537 m;

C_M  = 1537  (mm)                                j = 9^g61^c + n^c

C_J  =   0422 (mm)                                K = 100

Sa se calculeze distanta orizontala D_61.62  :

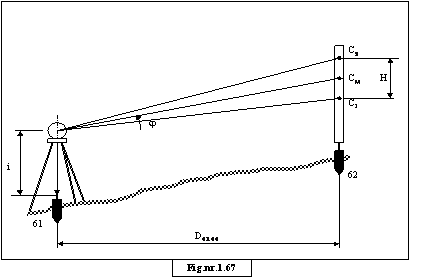
·   &n 232c24c bsp;    Se verifica citirile:

----- ----- ----- = 1537 (mm)

·   &n 232c24c bsp;    Se calculeaza distanta orizontala:

D = KHcos²j

·   &n 232c24c bsp;    In acest caz:

D = 100 (2,652 - 0,422) cos²9^g61^c = 217,957 m

68.   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;  Prin metoda paralactica - cu baza la capat s-a inregistrat un unghi orizontal paralactic de 7^g31^c + n^c diferenta directiilor orizontale corespunzatoare capetelor bazei). Daca viza pe baza s-a efectuat la inaltimea instrumentului si unghiul de panta masurat este nul - care este valoarea distantei orizontale dintre aparat si baza?

Solutie;

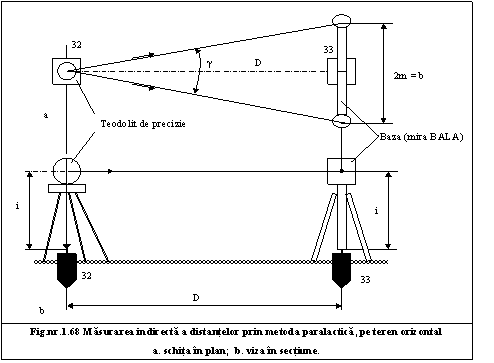
Din fig.nr. 1.68 se observa ca :

       g           D

ctg----- = --------     si  (b = 2m)

       2           b

g

de unde D = ctg -----     (m)

^g 1^c

deci D = ctg ---------- = 17,399 m

69.       Care este distanta orizontala dintre punctele 76 si 77 daca g ^g 1^c n^c si unghiul de inclinare al vizei este j ^{g c} n^c ?

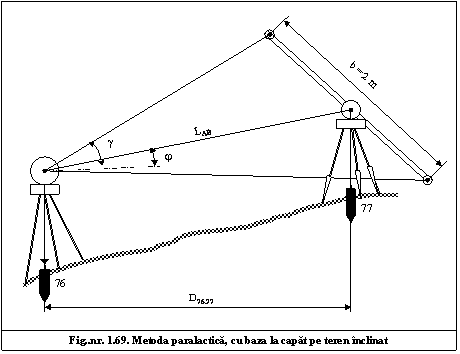
In acest caz:

 g           L

ctg ----- = --------     si                                                    (1.69)

       2            b

g

deci  L = ctg -----     (m)

^g 1^c

L = ctg ---------- = 8,86 m

iar D = Lcosj  (2.69) de unde D = 8,86 . cos ^g14^c => D = 8,82 m.

70.       In fig.nr.1.70 se prezinta modul cum s-a masurat distanta orizontala dintre punctele A si B, prin metoda paralactica cu baza la mijloc. Avand la dispozitie datele masuratorii sa se determine D_AB.

            Se cunosc: g = 4^g17^c, g = 4^g21^c, j = 0^g; j = 0^g; b = 2m.

            Din figura:

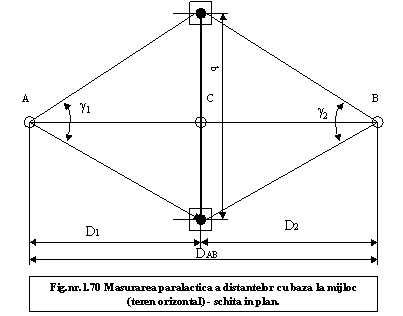
g

            D₁ = ctg-----                                                                (1.70)

g

            D₂ = ctg-----                                                                (2.70)

            D_AB = D₁ + D₂                                                             (3.70)

            Deci:  

        4^g17^c                   4^g21^c

D_AB = ctg  --------  + ctg ---------

2   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp;   &n 232c24c bsp; 

D_AB = 30,522 + 30,232 = 60,754 m