Elementele topografice ale terenului. Natura unghiurilor topografice. Azimute si orientari
Puncte topografice sunt puncte din teren, materializate sau nu, care caracterizeaza pozitia si forma detaliilor topografice (obiecte naturale sau artificiale din teren), sau concura la determinarea pozitiei altor puncte topografice. Ptr a fi reprezentate pe planuri si harti elementele ce sunt masurate pe teren, este necesar sa descompunem terenul in elemente liniare si unghiulare masurabile. Aceasta operatiune se numeste geometrizarea terenului si consta in alegerea pct. caracteristice de pe teren in asa fel incat prin unirea lor linia franta care rezulta sa dea cat mai exact forma terenului.
Elementele topografice ale terenului in plan vertical.
Sectionand terenul in plan vertical vom avea urmatoarele elemente liniare si unghiulare :
Aliniament AB - o linie sinuasa , ce urmareste linia terenului natural, si rezulta din intersectia terenului cu planul vertical ;
Distanta inclinata LAB - este linia dreapta ce uneste pct. A si B ;
Distanta redusa la orizont DAB - este proiectia in plan orizontal a distantei inclinate si este distanta ce o vom reprezenta pe harti si planuri ;
Unghiul de panta aAB - este unghiul facut de linia terenului natural cu proiectia sa in plan orizontal, este un unghi vertical.
Unghiul zenital ZAB - este unghiul facut de verticala locului cu linia naturala a terenului si este tot un unghi vertical ;
Cotele pct. A si B - HA si HB - sunt distantele pe verticala de la planul de nivel zero la planurile orizontale ce trec prin pct. A si B.
Diferenta de nivel - este distanta verticala intre suprafetele de nivel a doua pct. A si B . Poate fi pozitiva sau negativa , in functie de altitudinea pct. si sensul considerat.
Profil topografic - este reprezentarea grafica in plan a liniei de intersectie intre suprafata terenului si o suprafata verticala ce trece prin doua sau mai multe pct. date.
Panta terenului - este inclinarea dreptei ce uneste doua pct. A si B fata de orizontala, exprimata prin raportul dintre diferenta de nivel si distanta orizontala a celor 2 pct.
Suprafata de nivel - este o suprafata normala in orice punct al ei la directia gravitatii. Suprafata de nivel zero este aproximativ suprafata de echilibru a marilor si oceanelor; se foloseste ca suprafata de referinta a altitudinilor (cotelor) in nivelment .
Elementele topografice ale terenului in plan orizontal
Unghiul orizontal wAB - este unghiul diedru dintre planele verticale ce trec prin doua aliniamente AB si AC.
Distanta redusa la orizont DAB
Orientarea topografica qAB - este unghiul orizontal facut de directia nord geografic si directia AB masurat in sensul acelor de ceasornic, de la nord spre aliniamentul dat ;
In mod conventional se defineste orientarea directa qAB si orientarea inversa qBA. Cele 2 orientari difera cu 200g, adica :
qBA = qAB g
daca qAB > 200g atunci qBA = qAB - 200g
Coordonate rectangulare - individualizeaza poz. in plan orizontal a pct. topografice prin abcisa Y si ordonata X a proiectiei pct. in planul de referinta. Orientarea axei OX din suprafata de referinta este de regula directia nord. Coordonatele rectangulare XA si YA se mai numesc si coordonate absolute plane.
Coordonate relative - sunt lungimile proiectiilor pe axele OX si OY a distantei orizontale intre 2 pct. Se pot calcula din elementele masurate , cand se noteaza dC dU sau din coordonate absolute si se noteaza DC DY .
Coordonate polare - sunt o dist. orizontala DSP numita raza polara si un unghi orizontal wp numit unghi polar care definesc pozitia unui pct. P fata de un alt pct. S si o directie de referinta .Cunocsand orientarea de referinta qSA si coordonatele rectangulare ale pct. S, se pot calcula coordonatele absolute ale lui P.
Coordonate echerice- sunt coordonatele rectangulare intr-un sistem local in care axa abciselor este materializata in teren. Elementele care individualizeaza poz. pct. se masoara direct in valoare orizontala, ordonata fiind lungimea perpendicularei, iar abcisa distanta de la un capat al axei pana la piciorul perpendicularei.
2. Harti si planuri - utilizare; extragerea informatiilor planimetrice, extragerea informatiilor altimetrice . Scara hartilor si planurilor.
Planul topografic- este o reprezentare grafica conventionala a unor portiuni restranse ale suprafetei topografice, proiectate pe un plan orizontal, micsorata la o anumita scara si care prin detaliile pe care le contine reda in mod fidel suprafata topografica respectiva, fara sa se tina seama de curbura pamantului.
Harta- este o reprezentare grafica conventionala, micsorata la o anumita scara, in care este reprezentata intreaga suprafata a pamantului sau numai portiuni din ea si in constructia careia se tine seama de curbura pamantului.
![]()
Scara numerica- este raportul constant dintre distanta ,,d" de
pe plan dintre doua puncte si distanta orizontala ,,D" dintre aceleasi doua
puncte din teren, ambele fiind exprimate in aceleasi unitati de masura. Relatia
matematica de exprimare a scarii numerice este:
Valorile scarilor numerice sunt STAS, astfel ca putem avea unrmatoarele tipuri de scari:

Problemele ce se pot rezolva cu ajutorul scarii numerice sunt urmatoarele:
Pe un plan la scara 1/2000 s-a masurat o dist. de 20 cm. Ce valoare are aceasta distanta pe teren?
Cat reprezinta pe un plan la scara 1/1000 dist. din teren de 150 m?
Ce scara are planul ptr. care dist. din teren de 500m are pe plan 100 cm?
1.Se dau: d = 20cm, ![]()
Se cere: D
Conform relatiei numerice
pentru scara: ![]() ,
,
rezulta D = d*n sau D=20cm * 2000=40000cm=400m
Se dau: D=150m, ![]()
Se cere: d
Conform relatiei numerice pentru scara: ![]() ,
,
rezulta ![]()
![]()
3. Se dau: D=500m, d=100cm
Se cere: n
Conform relatiei numerice pentru scara: ![]() ,
,
Rezulta n = ![]() , deci scara este 1/500
, deci scara este 1/500
Se va putea calcula oricare din cele trei necunoscute functie de celelalte doua, astfel:
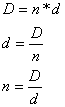
Atentie! D si d se exprima in aceiasi unitate de masura.
Cu cat numitorul este mai mic, scara este mai mare.
Adica, scara 1/200 este mai mare decat scara 1/10 000.
Scara grafica - fiecarei scari numerice ii corespunde o scara grafica, ce constituie o reprezentare grafica a scarii numerice. Dupa felul de construire a scarii grafice, se deosebesc:
scara grafica simpla sau liniara- asigura o precizie de 1/10 din baza.
Sacra grafica transversala sau compusa- asigurao precizie de 1/100 din baza.
Scarile grafice se folosesc atat ptr. determinarea distantei de pe harti si planuri, cat si in transpunerea unor distante masurate pe plan sau harta.
![]()
Precizia grafica a scarii - reprezinta
valoareacorespondenta din teren a valorii erorii de raportare sau citire de pe
plan si se exprima prin relatia:
Pg- precizia grafica
n - numitorul scarii;
Precizia grafica (Pg)este un parametru care permite stabilirea scarii la care trebuie intocmit un plan, in functie de marimea detaliilor care trebuie reprezentate.
Planuri topografice
planul topografic de baza al tarii este tiparit in trei culori si realizat intr-un singur sistem de proiectie la scarile : 1/2000 ; 1/5000 ; 1/10000 ;
planul topografic special se realizeaza ptr. diverse cerinte economice si poate fi realizat la scari ce variaza intre 1/100 pana la 1/1000.
harti la scari mici - 1/25000 pana la 1/100000 servesc ptr. studii de detaliu.
harti de ansamblu - sunt realizate la scari medii 1/200000 pana la 1/1000000 servesc ptr. studii generale;
harti geografice - sunt realizate la scari mici incepand cu 1/1000000 si mai mici servesc ptr. studierea generala a unei tari sau zone geografice.
Extragerea informatiilor planimetrice
1.Determinarea coordonatelor geografice: latitudine si longitudine
2. Determinarea coordonatelor rectangulare
3. Determinarea distantei dintre doua puncte de pe plan
4. Determinarea orientarii
5. Determinarea cotelor punctelor
6. Determinarea pantei unei drepte dintre doua puncte pe plan
1.Determinarea coordonatelor geografice: latitudine si longitudine
Pentru rezolvarea acestei probleme trebuie ca foaia de harta sa contina caroiaj geografic. In acest caz pentru a afla coordonatele geografice ale oricarui punct de pe harta se va proceda astfel:
se vor duce paralele din punct la caroiajul geografic pana ce-l intersecteaza pe acesta;
se va citi valoarea latitudinii si longitudinii din coltul de S-V al hartii;
se adauga la valorile citite minutele intregi care sunt din coltul unde s-a facut citirea pana la intersectia cu paralelele trasate anterior;
se masoara pe harta lungimea unui minut de latitudine si a unuia de longitudine;
se calculeaza cresterile de coordonate prin interpolare si se adauga la valorile citite. Cresterile de coordonate vor fi in secunde.
2. Determinarea coordonatelor rectangulare
Determinarea coordonatelor rectangulare se face in functie de caroiajul rectangular trasat pe foaia de harta. Etapele urmarite in rezolvarea problemei sunt urmatoarele:
incadram punctul intr-un carou trasat pe harta;
citim coordonatele X, Y ale colturilor caroului respectiv;
ducem perpendiculare din punct pe laturile caroului;
masuram in milimetri distantele de pe latura caroului din coltul cel mai apropiat pana la intersectia cu perpendicularele;
se transforma distantele masurate tinand cont de scara;
se aduna cresterile de coordonate la coordonatele colturilor caroului fata de care s-a facut masuratoarea;
se va tine cont de deformatia foii de harta calculand
coeficientul de deformatie k. ![]() , unde lteoretic este lungimea laturii caroului
teoretica si lreal este lungimea laturii caroului masurata pe harta.
Acest coeficient se aplica cresterilor de coordonate masurate pe harta.
, unde lteoretic este lungimea laturii caroului
teoretica si lreal este lungimea laturii caroului masurata pe harta.
Acest coeficient se aplica cresterilor de coordonate masurate pe harta.
3. Determinarea distantei dintre doua puncte de pe plan
Distanta se poate determina prin trei metode:
3.1
folosind scara numerica a hartii: ![]() unde D se calculeaza
in metri iar d se masoara in milimetri
unde D se calculeaza
in metri iar d se masoara in milimetri
3.2 folosind scara grafica a hartii ( simpla si transversala)
3.3 folosind coordonatele rectangulare calculate la punctul 2 cu relatia:
![]()
Precizia grafica ptr. o eroare e = +/- 2mm ;
d. Determinarea orientarii si a unghiurilor orizontale.
Orientarea unei directii reprezinta unghiul format de directia nordului geografic cu directia respctiva, masurat in sens orar. Unghiul de orientare al unei directii se poate determina pe harta prin doua procedee:
folosind coordonatele rectangulare care definesc directia respectiva :
![]()
avand in vedere reducerea la primul
cadran
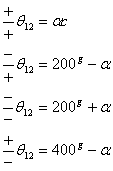
unde a este unghiul calculat prin arctg fara a tine seama de semnele raportului.
- folosind raportul circular gradat in grade centisimale
axa OX este verticala, OY este orizontala ;
originea unghiurilor este axa OX, iar sensul pozitiv numit sens direct topografic este cel orar. Ptr. aflarea valorii si a semnului functiilot trigonometrice cand se dau unghiuri in diferite cadrane sau calculului unghiurilor din intreg cercul cand cunoastem semnul si valoarea functiilor, este necesar sa aplicam reducerea unghiurilor la primul cadran. Cadranul in care se afla orientarea calculata depinde de semnalele ambelor cresteri de coordonate.
Mod de lucru cu raportul : se duce o paralela din pct. A la directia geografica nord si se asaza centrul raportorului in A, astfel ca valoarea 0 sa coincida cu directia nordului. Se masoara direct pe raportor valoarea orientarii directiei AB.
Determinarea unor elemente de altimetrie.
a. Determinarea cotelor punctelor
Cota unui punct se va determina cu ajutorul curbelor de nivel. In acest caz putem avea doua situatii:
A) punctul se afla pe curba de nivel - caz in care cota acestuia va fi cota curbei de nivel
B) punctul se afla intre
doua curbe de nivel - cota se va calcula prin interpolare. Se va duce linia de
cea mai mare panta ( linia ce este perpendiculara pe ambele curbe) si se va
masura lungimea acesteia D, precum si lungimea dreptei de la punct la curba ce
are cota cea mai mica dintre cele doua d. Se calculeaza apoi cresterea de
coordonate cu relatia: ![]() , unde E este echidistanta curbelor de nivel. Se va avea
grija ca cele doua distante sa fie masurate in milimetri. Cota punctului va fi:
cota curbei fata de care s-a facut masuratoare plus diferenta de nivel
determinata anterior.
, unde E este echidistanta curbelor de nivel. Se va avea
grija ca cele doua distante sa fie masurate in milimetri. Cota punctului va fi:
cota curbei fata de care s-a facut masuratoare plus diferenta de nivel
determinata anterior.
Diferenta de nivel intre doua puncte este diferenta cotelor celor doua puncte:
DH12= H2-H1
b. Determinarea diferentei de nivel intre 2 pct.
Cunoscand cotele a 2 pct. A si B se poate determina diferenta de nivel intre cele 2 pct.
DH = HB - HA
c. Determinarea unghiului vertical (de inclinare) al unei drepte de pe plan
Cunoscand distanta orizontala si diferenta de nivel, se poate calcula unghiul vertical( de inclinare) al dreptei respective, prin relatia:
![]()
d. Determinarea pantei liniei intre 2 pct. de pe plan
Tangenta unghiului de inclinare a reprezinta chiar panta liniei ce uneste cele 2 pct. de pe plan.
Avem :
![]()
P % = 1000 * tga
Panta se mai poate exprima si pe cale grafica , folosind graficul de panta.
3.Profilul topografic dupa o linie trasata pe un plan sau harta cu curbe de nivel. In lucrarile de studiu pe harta, se ridica problema reproducerii configuratiei naturale a terenului pe un anumit aliniament. Pe planuri sau harti cu curbe de nivel, aceasta problema se rezolva construind profilul topografic al terenului pe o anumita directie dorita. Ptr. a reprezenta terenul dintre doua puncte, se ia de regula scara inaltimilor de 10, 20, 25 de ori mai mare decat scara lungimilor.
Se unesc punctele A si B cu o linie dreapta si se numeroteaza toate punctele unde linia taie curbele de nivel;
Se considera scara lungimilor egala cu scara planului, iar scara inaltimilor de 10 ori mai mare;
Pe axa orizontala se alege o origine care se atribuie punctului A;
Se iau in compas distantele intre punctul A si punctele de intersectie ale dreptei AB cu curbele de nivel si se transpun pe axa orizontala, din aceste puncte ridicandu-se verticale;
Pe axa verticala a profilului se aseaza cotele punctelor la scara inaltimilor, pornind de la un plan de referinta care sa permita reprezentarea punctului de cea mai mica cota;
Avand pe aliniamentul AB toate punctele de cota cunoscuta, se duc drepte orizontale din aceste valori reprezentate pe scara verticala, pana ce acestea intersecteaza verticalele ridicate din punctele corespondente;
Unind punctele de intersectie obtinute , rezulta profilul topografic al terenului pe directia AB. In general, la intocmirea profilului topografic nu se mai construieste scara inaltimilor, valoarea cotelor raportandu-se direct pe verticalele ridicate din punctele caracteristice, eliminandu-se astfel incarcarea nejustificata a graficului.
4.Graficul de panta, constructia si utilizarea lui.
Graficul de panta este o scara care permite determinarea grafica pe un plan sau harta a pantei unei linii numai intre doua curbe de nivel. Graficul de panta se deseneaza pe marginea foii de plan sau harta, in functie de echidistanta E a curbelor de nivel si a numitorului scarii. In constructia graficului de panta se pleaca de le formula pantei, luandu-se un sistem de axe rectangulare, apoi pe una din axe la intervale arbitrare se noteaza valorile pantei sau ale unghiului de panta a. Din aceste puncte se ridica perpendiculare de lungime d = D Þ D = 100 * E ale caror extreme se unesc, obtinandu-se graficul
n p
de panta. Fig. 1.13 pag. C-19 .
Folosirea graficului de panta se face astfel: se ia intre varfurile compasului sau distantierului segmentul ,,di'' intre 2 curbe de nivel pe directia liniei careia dorim sa-i aflam panta. Aceasta distanta di se transpune pe graficul de panta astfel ca o gheara a compasului sa fie asezata pe axa pantei, iar celalalt varf sa fie pe grafic, citindu-se prin aproximare panta acestei linii pe axa pantei. Graficul de panta se poate construi ptr. orice forma de exprimare a pantei unei linii ( a, p% , p% ), folosind una din axele sistemului rectangular ptr. forma de exprimare a pantei, iar cealalta axa ptr. distante.
5. Principiul de trasare a unei linii de panta data.
Ptr. trasarea unei linii de panta constanta intre 2 puncte se folosesc curbele de nivel, adica la gasirea unor distante ,,di" pe plan, astfel ca omoloagele lor Di din teren sa aiba panta p% egala cu cea impusa. Cand punctele A si B se afla intre 2 curbe de nivel, se vor calcula distantele d1 si d3 de la punctul respectiv pana la prima curba de nivel, iar intre curbele de nivel se vor calcula o distanta d2 , numita si pas de proiectare, toate corespuzand pantei p% impuse. Se calculeaza d1, d3, d3 dupa formulele de mai jos :
d1 - distanta de la punctul A la prima curba de nivel:
d2- pasul de proiectare;
d3 - distanta de la ultima curba de nivel la punctul B.
d1 = 100 * DH A-C1 d2 = 100 * E * 1 ; d3 = 100 * DHC2 - B * 1
p% n p% n p% n
Cum procedam :
Ptr. a trasa linia de panta constanta pe plan, se ia in compas distanta d1 si cu varful compasului A se descrie un arc de cerc care va intersecta prima curba de nivel in doua puncte. Aceste puncte unite cu punctul A dau directii care respecta conditia de panta impusa. Cu varful compasului in aceste puncte si cu dist. d2 se descriu 2 arce de cerc care intersecteaza curba de nivel urmatoare in 4 puncte, obtinandu-se 4 variante care respecta conditia data. Mergand in continuare cu d2 in compas, variantele se dubleaza mereu, pana la ultima curba, din care cu d3 in compas se face inchiderea pe punctul B. Este bine ca proiectarea liniei de panta constanta impusa sa se porneasca din ambele puncte A si B, facandu-se jonctiunea lor pe traseul dintre A si B
6. Reprezentarea pe harti si planuri a reliefului prin curbe de nivel. Echidistanta. Clasificarea curbelor de nivel.
Metoda curbelor de nivel este metoda cea mai utilizata ptr. reprezentarea reliefului pe planuri si harti topografice, ptr. ca exprima orografia terenului, facilitand determinarea si interpretarea diverselor elemente ale reliefului pe plan ( altitudinea punctelor, panta, aria si volumul formelor de relief). Curbele de nivel sau izohipsele sunt proiectiile orizontale ale liniilor sinuoase ce unesc punctele de aceeasi cota, ele rezulta prin intersectarea imaginara a suprafetei topografice cu plane orizontale si echidistante. Valoarea c. de n. se exprima printr-un nr. intreg sau zecimal rotund. Acestea se exprima printr-un nr. intreg de metri in cazul scarilor uzuale, respectiv in metri si fractiuni rotunde de metri in cazul scarilor mari, pe terenuri sese. Cotarea c .de n. se face in functie de inaltimea planului orizontal imaginar de sectionare a reliefului. Ptr. ca reprezentarea reliefului sa se faca in mod unitar, planele orizontale imaginare se traseaza la distante egale pe verticala.
Distanta verticala dintre planele orizontale care determina 2 c. de n. consecutive se numeste echidistanta naturala sau numerica se noteaza cu E. Valoarea echidistantei naturale se alege in functie de accidentatia terenului, de scara planului sau hartii si de scopul lucrarii ptr. care se intocmeste planul. Ptr. terenuri accidentate, reprezentate pe planuri sau harti intocmite la scari mici , se alege o echidistanta mare ( 10,20, 40, 50, 100m); ptr. terenuri cu relief usor ondulat, reprezentate pe planuri intocmite la scari mari, se alege o echidistanta mica ( 1, 2, 5m) . Ptr. lucrari de irigatii sau desecari, care se executa pe terenuri cu relief ses, se alege o echidistanta foarte mica ( 0,10 ; 0,20 ; 0,25 ; 0,50 m). Stabilirea echidistantei naturale este determinata de echidistanta grafica, data de distanta orizontala de pe plan sau harta dintre 2 c. de n. succesive. Echidistanta grafica , notata cu e, nu poate fi mai mica de 0,2mm, ptr. a nu se confunda o c. de n. cu cealalta.
In functie de echidistanta , c. de n. sunt de mai multe feluri, desenandu-se cu diferite tipuri si grosimi de linii:
c. de n. normale - se traseaza la echidistanta normala ,,E", aleasa in functie de scara hartii sau a planului si in functie de accidentatia terenului. Se reprezinta printr-o linie subtire si continua.
c. de n. principale - sunt c. de n. normale ingrosate care se traseaza la cote rotunde. Pe ele se fac inscriptiile care indica valoarea c. de n.
c. de n. ajutatoarea - se traseaza prin linii intrerupte la echidistanta E/2, intre curbele normale.
c. de n. accidentale- se traseaza cu linie punctata la echidistanta E /4, intre curbele normele. Ultimele 2 categorii de c. de n. se folosesc la reprezentarea reliefului, in teren plan, cu variatii altimetrice reduse ale suprafetei topografice. Pe planurile si hartile topografice policrome, c. de n. precum si cifrele ce reprezinta valorile acestora se deseneaza si se scriu in culoare sepia( maro). Cifrele se vor inscrie cu baza orientata spre vale, pe portiunea respectiva c. de n. intrerupandu-se; valoarea curbei trebuie sa poate fi citita cu usurinta pe directiile sud si est ale planului sau hartii. Intrucat reprezentarea reliefului se suprapune reprezentarii planimetrice, c de n. se intrerup la marginea constructiilor, soselelor, rapelor; Acolo unde c. de n. sunt mai apropiate terenul are panta mai abrupta si invers, cand c. de n. sunt rare, terenul are panta mica. Linia cea mai scurta dintre 2 c. de n, perpendiculara pe acestea, se numeste linie de cea mai mare panta.
7. Sisteme de coordonate folosite in topografie. Suprafete de referinta.
Un pct. de pe supr. terestra poate fi definit de trei tipuri de coordonate:
coordonate geografice jA si lA - latitudine si longitudine
coordonate rectangulare X,Y,Z
coordonate polare D si q - distanta redusa la orizont si orientarea ;
Coordonatele rectangulare - individualizeaza poz. in plan orizontal a pct. topografice prin abcisa Y si ordonata X a proiectiei pct. in planul de referinta. Orientarea axei OX din supr. de referinta este de regula directia nord.
Coordonatele rectangulare XA si YA se mai numesc si coordonate absolute plane.
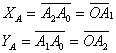
Coordonate relative - sunt lungimile proiectiilor pe axele OX si OY a distantei orizontale intre 2 pct. Se pot calcula din elementele masurate , cand se noteaza dC dU sau din coordonate absolute si se noteaza DC DY .
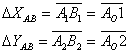
Se pot calcula din elemente masurate, cand se noteaza dX, dY, sau din coordonate absolute si se noteaza DX, DY:
![]()
![]()
Cu ajutorul coordonatelor relative se pot calcula coordonatele rectangulare ale unui punct daca se cunosc coordonatele altui punct:
![]()
Coordonate polare - sunt o dist. orizontala DSP numita raza polara si un unghi orizontal wp numit unghi polar care definesc pozitia unui pct. P fata de un alt pct. S si o directie de referinta .
Cunoscand orientarea de referinta qSA si coordonatele rectangulare ale pct. S, se pot calcula coordonatele absolute ale lui P.
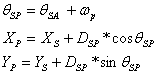
Coordonate echerice- sunt coordonatele rectangulare intr-un sistem local in care axa abciselor este materializata in teren. Elementele care individualizeaza poz. pct. se masoara direct in valoare orizontala, ordonata fiind lungimea perpendicularei, iar abcisa distanta de la un capat al axei pana la piciorul perpendicularei.
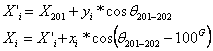
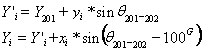
Pozitia unui pct. pe suprafata pamantului se exprima prin coordonatele lui geografice longitudinea l si latitudinea j precum si prin cota z. In planul de proiectie adoptat, pozitia pct. se noteaza cu x si y si precizeaza departarile in plan fata de axele sistemului cartezian adoptat.
Coordonatele geografice sunt latitudinea si longitudinea
Latitudinea j este unghiul format de normala la elipsoid cu planul ecuatorului. Putem vorbi de latitudine nordica sau sudica in functie de poz. punctului intr-una din cele 2 emisfere.
Longitudinea l este unghiul diedru dintre meridianul geodezic ce trece prin pct. si meridianul de origine al elipsoidului de referinta. Meridianul de origine 0 este ales conventional cel ce trece prin observatorul astronomic Greenwich, de langa Londra. Longitudinile se considera pozitive spre est si negative spre est.
Suprafete de referinta.
Aceste supr. sunt folosite aproape exclusiv ptr. definirea teoretica si realizarea practica a retelelor de nivelment si a a retelelor gravimetrice. Ptr. retelele planimetrice utilizarea acestor suprafete este extrem de limitata. Valoarea fortei de gravitatie variaza pe supr. globului datorita variatiei celor 2 forte din care rezulta. Intr-un pct. directia gravitatii este materializata de directia firului cu plumb. Suprafata pe care o intersecteaza aceasta directie sub un unghi drept se numeste suprafata de nivel.
Geoidul a fost considerat suprafata de nivel zero si a fost denumit de catre Listing in 1873. Uzual geoidul este definit ca suprafata medie a marilor linistite prelungita pe sub continente.
Elipsoidul de referinta- in raport cu geoidul, elipsoidul de referinta poate ocupa o poz. oarecare. In caz general verticala V la supr. geoidului G, care trece print-un pct. oarecare P situat pe supr. pamantului S, nu coiuncide cu normala N la supr. elipsoidului E care trece prin acest pct. ci formeaza cu acesta un unghi oarecare u, denumit unghi de deviatie a verticalei. Ptr. aducerea retelelor devtriangulatie pe supr. elipsoidului de referinta s-au propus mai multe metode ;
Metoda proiectarii - in aceasta metoda se procedeaza la aducerea elementelor masurate ( unghiuri, directii, lungimi, ) pe supraffat elipsoidului prin aplicarea unor corectii. Exista 2 posibilitati in acest sens::
Metoda Pizzetti- introduce complicatii insemnate prin faptul ca presupune cunoasterea curburilor verticale.
Sfera de raza medie ( sfera Gauss) - aceasta suprafata este des folosita in calculele dezice din reteaua de ordin superior.
Planul si sistemul de proiectie.
In retelele de triangulatie de indesire, nr. pct. este extrem de mare, fiind necesar sa se treaca la o suprafata plana, prin adoptarea unbui sistem de proiectie cartografica.
In tara noastra este folosit din 1951 sistemul de proiectie conforma Gauss - Kruger, avandu-se ca baza elipsoidul Krasovski.
Din 1971 s-a introdus un nou sistem de proiectie denumit sistem de proiectie stereografica 1970, cu elipsoid de referinta Krasovski.
In situatii speciale ptr. zone mai mici se poate folosi si un plan local de proiectie la care se raporteaza reteaua geodezica considerata.
In 1970 a fost adoptata in Romania Proiectia Stereografica 1970 si sistemul de cote referit la Marea neagra, ptr. executarea lucrarilor geodezice, topografice, fotogrametrice si cartografice.
|
Nume |
PROIECTIE STEREOGRAFICA CU PLAN SECANT 1970 |
|
Elipsoid |
KRASOVKI 1942 |
|
Punctul central al proiectiei |
Este situat la N de Fagaras |
|
Coordonatele originii sistemului de referinta |
X=500.000,000; Y=500.000,000 |
|
Deformatia in punctul central al proiectiei | |
|
Sisteme de cote |
MAREA NEAGRA |
8. Marcarea la sol a punctelor topografice. Descrierea topografica a punctelor. Operatia de fixare in pamant sau in zidaria constructiilor a marcilor geodezice sau topografice, poarta denumirea de marcare. Punctele geodezice din reteaua de sprijin si unele puncte din reteaua de ridicare se marcheaza in mod permanent. Unele puncte din reteaua de ridicare, care sevesc numai ptr. desfasurarea operatiilor de masuratori de teren, neavand o semnificatie deosebita ptr. definirea pozitiei detaliilor topografice se marcheaza in mod provizoriu. Tot in mod provizoriu se marcheaza si punctele importante noi, pana la definitivarea lucrarilor de marcare permanenta.
Marcarea provizorie se face cu tarusi de lemn, repere mobile, vopsea sau creta, in functie de situatie. In extravilan ptr. marcarea punctelor de statie sau a altor puncte importante, se folosesc tarusi din lemn de esenta tare, cu lungimea de 30 - 40cm si grosimea de 4 - 5 cm, cu sectiunea patrata sau rotunda. Partea inferioara se ascute, iar la partea superioara se poate executa o tesitura proaspata ptr. inscrierea numarului. Capatul superior trebuie sa fie taiat perpendicular pe lungime, iar centrul se marcheaza printr-un cui, sau semn in cruce, desenat cu creionul. Marcarea temporara in intravilan pe trotuare, carosabilul stazilor asfaltate, betonate sau pavate, terase, soclurile unor constructii, garduri se poate realiza prin semne desenate cu vopsea, var, creta, notand alaturi si nr. punctului respectiv. Reperele mobile ( numite si saboti sau broaste de nivelment) se utilizeaza ptr. marcarea provizorie a pct. De legatura la ridicarile nivelitice. Ptr. marcarea de foarte scurta durata a unor pct. se pot folosi fisele ( vergele metalice cu inel).
Marcarea permanenta a pct. se face prin borne, marci, buloane metalice si stalpi de lemn. Bornele servesc ptr. marcarea permanenta a punctelor din extravilan. Ele sunt confectionate din beton, beton armat sau piatra cioplita avand dimensiuni reglementate prin standarde. Bornele au forma unui trunchi de piramida cu bazele patrate. Punctul matematic al bornei este materializat printr- un bulon metalic, incastrat in centrul bazei mici sau print-o crestatura in forma de cruce. Unele pct. de hotar dintre localitatile vecine sunt materializate prin borne de hotar din beton armat, avand fixate la partea superioara o placa din fonta, cu inscriptia hotar. In topografia silvica, dar si in cea agricola, in locul bornelor pot fi folositi stalpi din lemn de esenta tare, in jurul carora se construieste o movila de pamant.
In intravilan, punctele topografice sunt marcate permanent prin buloane metalice batute in trotuar sau carosabil, avand o crestatura sau un pct. excavat in centrul capului superior, situat la suprafata. Ptr. marcarea permanenta a reperelor nivelitici se folosesc marci de nivelment confectionate din fonta, incastrate pe capul bornelor geodezice sau in zidul unor cladiri, cu cel putin 50 cm deasupra nivelului terenului. Bornele kilometrice de pe marginea soselelor, CF, si canalelor pot servi ca pct. de nivelment sau planimetrie.
9. Semnalizarea pct. topografice. Conditiile semnalelor topografice. Punctele de la sol sau din apropierea solului, trebuie sa fie semnalizate ptr. a asigura vizibilitatea reciproca pe deasupra vegetatiei sau altor obstacole de pe teren. Semnalizarea poate fi de scurta durata( provizorie) sau de lunga durata (permanenta). Semnalizarea provizorie se realizeaza cu ajutorul jaloanelor. Jalonul este un semnal portabil, confectionat din lemn usor, cu o lungime de 2m, grosimea de 4-5cm, si cu sectiunea octogonala, hexagonala sau triunghiulara. La capatul inferior este armat cu un sabot metalic de forma conica care usureaza fixarea prin infigere in pamant. Ptr. a fi vizibile de la distanta, jaloanele se vopsesc in 2 culori ( rosu si alb), pe portiuni alternative cate 20cm. In intravilan sau pe terenuri betonate sau care nu permit fixarea prin infigere in pamant, jaloanele se sprijina de ziduri, arbori, se tin cu mana pe durata limitata a masuratorilor sau se sprijina cu ajutorul unor trepiede ori prin legarea de alte 2 jaloane oblice. Pe langa semnalizarea prov. a pct. cu ocazia ridicarilor topografice, jaloanele se utilizeaza si ptr. vizualizarea unor trasee rectilinii ( jalonarea aliniamentelor, la pichetarea unor experiente, trasarea de unghiuri drepte). Semnalizarea permanenta a pct. din reteaua de sprijin si a celor de indesire se realizeaza cu balize, piramide sau semnale pe arbori. Balizele topografice se construiesc din lemn, cu inaltimea de 3 -6 m putand fi formate din 2 sau 3 parti: corpul ,fluturele si cutia. Corpul balizei este un pilon din lemn de brad, cu sectiunea patratica sau rotunda de 8 cm grosime sau din teava din metaL. Fluturele este fixat la partea superioara, fiind confectionat din 4 scandurele sau fasii de tabla cu lungimea de 40 - 80 cm si latimea de 17 - 20 cm, dispuse in cruce, vopsite alternativ in alb si negru.
Semnalele pe arbori sunt fluturi montati pe un corp fixat pe arbori in pozitie centrica sau excentrica fata de borna. Piramidele la sol sefolosesc ptr. semnalizarea unor pct. mai importante si sunt semnale in forma de piramida, avand o inaltime de 4 -7 m, cu 3 sau 4 picioare, din lemn sau teava metalica, pe care se fixeaza corpul cu fluturele asemanator cu al balizelor topografice sau o cutie de scanduri, vopsita in culoare neagra numita pop. Piramide cu poduri se folosesc ptr. semnalizarea unor pct. geodezice situate la distante mari in zone de ses. Aceste piramide au inaltimi mar, fiind construite cu unul sau 2 poduri ori etaje.
Conditiile semnalelor topografice.
sa se deosebeasca net de obiectele inconjuratoare, ca forma si colorit;
sa fie stabil si solid; stabilitatea piramidelor simple sau cu poduri trebuie sa permita masurarea unghiurilor pe vant de tarie medie, iar pilastrul sa nu faca atingerea cu piramida semnal;
la construirea piramidelor se impune ca vizele din centrul pilastrului, catre punctele alaturate, sa nu treaca la mai putin de 10 cm de stalpii de baza sau balustrade;
excentritatea proiectiei cilindrului de vizare a piramidelor si a centrului pilastrului fata de centrul bornei sa nu fie mai mare de 0,5 m.
Cand balizele sunt construite exact deasupra pct. stationabile, ptr. a fi temporar demontabile, se introduc intr-o cutie de lemn, formata din 4 scanduri sau intr-o teava mai groasa in lungime de 60 - 100 cm, fixata in pamant. Pe timpul cat se stationeaza cu aparatele topografice in pct. de statie, baliza este scoasa din cutie, urmand a fi reintrodusa inainte de plecarea din statie, dupa ambalarea aparatului. Corpul balizei poate fi montat si definitiv, in poz. excentrica fata de pct. matematic.
Inaltimea semnalelor se stabileste incat sa existe vizibilitate reciproca cu semnalele vecine atat in momentul construirii lor, cat si in perspectiva.
Trebuie sa se tina seama de inaltimea maxima ce poate fi atinsa de diferite obstacole de pe aliniamentele dintre semnale, cum ar fi constructii si arbori din parcuri, paduri, plantatii etc..
10. Geometrizarea liniilor de teren. - este operatia de selectare judicioasa a unui nr. minim de puncte topografice care sa aproximeze cu suficienta fidelitate liniile in cea mai mare parte sinuase din teren, atat in plan orizontal cat si in plan vertical, cu o linie poligonala, respectiv suprafetele ondulate ale terenului cu o suprafata poliedrica. Fig. 1.1 C.3
Densitatea pct. de detaliu este cu atat mai mare cu cat scara planului, accidentatia si sinuozitatea terenului sunt mai mari. Conditia care se impune este ca abaterea maxima f a liniei poligonale de la linia din teren sa fie mai mica de 0,2 mm la scara planului. In plan vertical, ptr. redarea reliefului, in functie si de accidentatia terenului, se aleg pct. la cel mult 3 -4 cm la scara planului.
Puncte topografice ( caracteristice) si ridicarea topografica a acestora . Semne conventionale.
Punctele topografice sunt pct. din teren, materializate sau nu, care caracterizeaza pozitia si forma detaliilor topografice ( obiecte naturale sau artificiale din teren), sau concura la determinarea pozitiei altor pct. topografice. Deoarece detaliile topografice ale terenului sunt compuse din elemente geometrice simple: pct., linii, planuri, care toate la rindul lor sint definite prin pct. rezulta ca ridicarea in plan consta in alegerea in mod judicios a pct. caracteristice, atit ca numar, cit si ca pozitie. Din pct. de vedere planimetric si altimetric, pct. si liniile caracteristice ale detaliilor topografice sint: un colt parcela, o incrucisare de drumuri, pct. de schimbare de directie ale limitelor si traseelor rectilinii, talvegul vailor, schimbare si sfarsit de panta, virful mamelonului, fundul gavanului.
11. Corectiile ce se aplica lungimilor masurate direct pe teren cu benzi de otel.
Corectia de etalonare - Daca la compararea si etalonarea benzii au aparut abateri fata de valoriile nominale ale panglicii acestea trebuie luate in considerare. Corectia de etalonare ptr. o lungime de banda se defineste prin relatia : ce = l r - ln
lr - lungimea reala rezultata dupa etalonarea benzii;
ln - lungimea nominala inscriptionata pe banda de otel;
Ptr. lungimea intregului aliniament masurat rezulta corectia totala de etalonare: Ce = ( Ltotal /l n )ce ;
Lungimea totala corectata se obtine cu relatia: L corectat = L total + Ce
Corectarea lungimii masurate poate fi realizata si prin aplicarea unui coeficient de etalonare, care se calculeaza: k = ( lr / ln ) ;
lungimea corectata fiind data de relatia : L corectat = L total K ;
Corectia de tensiune sau de intindere - benzile de otel fiind elastice, lungimea lor variaza in functie de forta de intindere in timpul masurarii. Corectia ptr. o lungime de panglica datorata variatiei fortei de intindere fata de cea la etalonare se calculeaza cu relatia:
CF = ( lF - ln) = [ ( 1000 ln) / ( S . E ) ] ( F - Fo);
ln - lungimea nominala a panglicii;
lF - lungimea panglicii in timpul masurarii;
E - modulul de elasticitate a otelului 2,1 10 4 kg / mm 2 ;
S - suprafata sectiunii transversale a panglicii;
Corectia totala ptr. o lungime masurata va fi :
CF = ( L total / ln ) cF ;
Iar lungimea totala corectata se va obtine :
Lcorectat = L total + C F ;
- Corectia de temperatura - Functie de temperatura in timpul procesului de masurare lungimea benzii va fi : lt = [ l + a ( t - te )] unde in timpul procesului de masurare temperatura este diferita de cea
lt - lungimea benzii in timpul masurarii;
le - lungimea benzii la etalonare ;
a - coeficientul de dilatare a otelului a = 0,0115 mm / 1 C / 1 m liniar;
t - temperatura in timpul masurarii;
te - temperatura in timpul etalonarii;
Rezulta corectia de temperatura ptr. o lungime de panglica:
ct = Dlt = lt - le = lc [ l + a ( t - te) ] - le = le a ( t - to ) ; Semnul corectiei este dat de diferenta ( t - to) . Ptr. reducerea efectului variatiei temperaturii asupra lungimii masurate, se recomanda ca masuratorile sa se execute pe timp de stabilitate termica si folosirea de termometre de contact ptr. determinarea temperaturii panglicii.
12. CONDITIILE GEOMETRICE ALE AXELOR UNUI TEODOLIT. NIVELA TORICA DE LA TEODOLIT.
Conditiile geometrice ale axelor:
a) VV sa fie verticala. Prin calare se realizeaza VV NN. Neindeplinirea acestei conditii conduce la eroarea de inclinare a axei principale de rotatie a teodolitului.
b) rO OO (axa de vizare sa fie perpendiculara pe axa secundara). Neindeplinirea acestei conditii conduce la eroarea de colimatie.
c) OO VV (axa secundara trebuie sa fie orizontala). Neindeplinirea acestei conditii conduce la eroarea de inclinare a axei secundare.
d) linia indec3ilor de la cercul vertical sa fie intr-un plan orizontal sau vertical, care contine axa OO de basculare a lunetei. Neindeplinirea acestei conditii conduce la eroarea de index.
Nivelele sunt dispozitive care servesc la orizontalitatea sau verticalizarea de drepte sau planuri, cat si la masurarea unor unghiuri mici de panta.
Nivela torica de la teodolite serveste la calarea definitiva (fina) a instrumentului.
Partile constructive ale unei nivele torice sunt:
- fiola de sticla
- fereastra
- surub de rectificare
- suport (alidada)
- articulatie
- reperii nivelei
- gradatiile nivelei (la 2 mm)
- bula de aer
Elementele caracteristice ale unei nivele torice sunt:
13. Cercul orizontal al teodolitului. Modul de masurare a unghiurilor cu el. Planul de vizare azimutal al teodolitului.
Cercul orizontal - serveste la masurarea directiilor ( unghiurilor) orizontale. El se compune din:
cerc gradat denumit limb, are diametrul de 70 - 100 mm la teodolitele de precizie medie si si pana la 250 mm la teodolitele de precizie ridicata.
un cerc denumit cerc alidat sau alidada, pe care se sprijina suprastructura teodolitului si se afla indicii de citire;
Ptr. masurarea corecta a unghiurilor orizontale limbul trebuie sa fie orizontal si sa ramana fix, iar alidada cu indicii de citire trebuie sa fie centrica cu cercul gradat si sa execute miscari de rotatie in jurul axei comune VV. Ptr. masurarea unui unghi orizontal w = AOB se vizeaza punctul A si se citesc in dreptul indicilor de citire diametral opusi valoarea directiilor CA si C'A.,se roteste cercul alidad pana cand luneta se afla pe directia punctului B. Indicii de citire vor executa aceeasi miscare de rotatie ca cercul alidad si luneta, in dreptul lor efectuandu-se lecturile CB si CB pe cercul orizontal gradat.
Ptr. verificare trebuie ca CA = CB + 200g 2ec si CB = CB + 200g 2ec cu ec - eroarea de citire. Unghiul orizontal se calculeaza din diferenta citirilor efectuate. w = CB - CA ; respectiv w = CB - CA ;
Valoarea cea mai probabila a unghiului w va fi media aritmetica : w w w ) / 2 ; Fig. 2.17. B - 25
Cercurile orizontale trebuie sa indeplineasca urmatoarele coditii:
cercul gradat sa fie orizontal si fixat in timpul masurarii unghiurilor;
cercul alidad sa fie orizontal si centric cu cercul gradat.
14. Cercul vertical al teodolitului . Modul de masurare a unghiurilor verticale . Planul de vizare zenital al teodolitului
Se construieste din acelasi material ca si cercul orizontal, iar modul de gradare se face asemanator. Cercul vertical are functia de masurare a unghiurilor verticale sau a celor zenitale.
Ptr. a masura unghiurile verticale, cercul vertical gradat ( limbul) trebuie sa se roteasca solidar cu luneta in jurul axei secundare a teodolitului OO, iar linia ce uneste indicii de citire trebuie sa fie riguros intr-un plan orizontal sau vertical . Cercul vertical gradat este astfel montat, incat linia ce uneste gradatiile 0 - 200g sa se gaseasca in acelasi plan cu axa de vizare a lunetei ( planul de vizare zenital). Cercurile verticale trebuie sa indeplineasca urmatoarele conditii constructive :
sa fie centric cu axa secundara a teodolitului OO ( axa de rotatie a lunetei) ;
limbul trebuie sa se roteasca solidar cu luneta;
cercurile sa se gaseasca intr-un plan vertical paralel cu axa principala de rotatie- VV - a teodolitului;
linia gradatiilor 0 - 200g sa se afle in acelasi plan cu axa de vizare - rO - a lunetei, planul de vizare zenital al teodolitului.
Indicii de citire sa se afle riguros intr-un plan orizontal sau vertical.
Spre deosebire de cercul orizontal, ptr, masurarea unui unghi vertical cercul gradat este mobil si indicii de citire sunt ficsi.
La un teodolit clasic masurarea unui unghi vertical se face ca si la cercul orizontal, executand citiri la cele 2 dispozitive de citire.
Masurarea unghiurilor verticale sau zenitale se face in felul urmator:
Se vizeaza pct. , se asigura orizontalitatea sau verticalitatea indecsilor de citire, aducand bula nivelei zenitale intre repere cu ajutorul surubului de basculare. Unghiul vertical se obtine direct, nu prin diferenta de 2 directii ca ptr. unghiul orizontal.
15. Microscopul cu scarita, principiul optic. Utilizarea lui la citirea pe limb a unghiurilor.
Aceste microscoape permit centralizarea citirilor efectuate la cercul orizontal si cel vertical. Acest microscop are pe reticul o scara gradata, a carei marime corespunde cu marimea aparenta a unei diviziuni a cercului gradat. Scarita este subdivizata intr-un nr. de parti egale, care permit executarea clara si simpla a citirilor.
Principiul microscopului cu scarita.
Obiectivul O1 care se afla tot timpul la aceeasi distanta fata de limb, formeaza o imagine reala micsorata si rasturnata. Ocularul O2 are rol de lupa si mareste imaginea formata de obiectiv. Distanta ,,p" fiind tot timpul constanta, inseamna ca si imaginea se va forma tot timpul in acelasi plan imagine. Scarita trebuie amplasata in planul imagine, astfel incat marimea ei sa corespunda cu imaginea unei diviziuni de pe limb. Fig. 2.21 B - 29 ;
( 1/ p) + ( 1 / p) = 1 / f 1 ; p = constant ; f = constant ; p = constant ;
Aproximatia de citire a unei scarite se stabileste cu relatia : a = 1 / n ;
1 - valoarea unei diviziuni de pe limb;
n - nr. de diviziuni al scaritei;
Ptr. a asigura aproximarea valorii PII toate scaritele sunt gradate in sens invers cresterii diviziunilor de pe limb.
16. Micrometrul optic cu coincidenta. Realizarea lui. Efectuarea citirilor.
Micrometrul optic cu coincidenta - permite coincidenta diviziunilor diametral opuse ale cercurilor gradate si efectuarea automata a mediei citirilor.
Realizarea lui
lamelele micrometrului optic
tamburul micrometrului
montura lamelelor
articulatia monturii
bratele oscilante( biele)
melcul ce actioneaza bratele
prisma deviatoare.
Efectuarea citirilor
se vizeaza si se puncteaza semnalul din teren
sec actioneaza de tamburul micrometrului pana la realizarea coincidentei diviziunilor diametral opuse
se citesc gradele de pe imaginea dreapta din stanga indicelui de citire
se numara diviziunile de la gradele de citire pana la gradele diametral opuse care difera cu 200g si se inmultesc cu 10c
minutele, zecile de secunde si secundele se culeg de pe tamburul micrometrului optic.
17. Nivela sferica, constructia si utilizarea ei . Verificarea si rectificarea nivelei sferice.
Serveste la calarea aproximativa a instrumentului; este mai putin precisa decat nivela torica.
Este formata dintr-o fiola de sticla de forma cilindrica , avand partea superioara sub forma de calota sferica. Fiola este umpluta cu eter sau alcool si este inchisa ermetic . Ea este montata intr-o cutie metalica de protectie, care la randul ei este prinsa prin trei suruburi de suport. Partea cea mai de sus a calotei sferice reprezinta pct. central al nivelei. Gradatiile unei astfel de nivele sunt cercuri concentrice cu centrul in pct. central si distantate intre ele la 2mm. Ptr. a lucra corect, diametrul bulei de aer trebuie sa fie cu 1 - 2 mm mai mic decat cel al cerculetului de reper.
Verificarea si rectificarea nivelei sferice O nivela sferica este rectificata atunci cand PNPN este paralel cu suportul " ss" .
Verificarea si rectificarea se face astfel:
se roteste suprastructura teodolitului pana cand nivela sferica se afla deasupra unui surub de calare;
se aduce bula de aer in cerculetul de reper prin actionarea suruburilor de calare;
se roteste alidada cu 200g in jurul axei VV ; daca bula de aer ramane in cerculetul de reper, atunci nivela sferica este rectificata. Daca bula de aer sufera o deplasare " d" din cerculetul de reper, atunci nivela trebuie rectificata.
rectificarea nivelei se realizeaza prin descompunerea deplasarii "d" pe 2 directii perpendiculare, una paralela cu suruburile de calare S1 S2 ( d1) si cealalta pe directia celui de al treilea surub de calare S3 ( d2) . Rectificarea se realizeaza separat pe fiecare directie in parte.
18. Reticulul lunetei. Reglarea lunetei. Punctarea semnalelor, precizia de vizare.
Reticulul lunetei este format dintr-o placa de sticla pe care sunt gravate foarte fin trasaturi numite fire reticulare. Notam intersectia firelor reticulare cu " r" si de aici deriva axa de vizare a lunetei " rO" care este data de pct. r si de centrul optic al obiectivului. Pe langa firele reticulare, reticulul mai poate prezenta trasaturi reticulare scurte, simetrice fata de firul reticular orizontal, denumite fire stadimetrice, care servesc la masurarea indirecta a lungimilor. La majoritatea reticulelor firul reticular vertical este doar pe jumatate un fir simplu, cealalta jumatate fiind formata din fire reticulare duble. Acest mod de gravare a firului reticular vertical sustine cele 2 metode de punctare - prin sectionare si prin incadrare.
Formarea imaginii in luneta - obiectul care se vizeaza va forma o imagine micsorata, reala si inversa intre ocular si focarul sau.
Marirea lunetei - este raportul dintre unghiul sub care se vede un obiect vizat prin luneta si unghiul sub care se vede acelasi obiect cu ochiul liber.
Reglarea lunetei se realizeaza in 2 etape :
a). Se indreapta luneta spre un fond deschis si se roteste de ocular pana cand imaginea firelor reticulare este clara, iar firele sunt bine conturate;
b). Se indreapta luneta spre obiectul din teren si se actioneaza de mansonul de focusare, pana ce imaginea obiectului din teren este clara, iar fenomenul de paralaxa nu apare prin deplasarea transversala a ochiului in fata ocularului.
Punctarea semnalelor - consta in aducerea centrului firelor reticulare pe pct. sau axa de simetrie a semnalului vizat. Ea se realizeaza in trei faze:
se indreapta luneta spre obiectul dorit folosind colimatorul montat deasupra lunetei. Se verifica aparitia obiectului in campul lunetei si se blocheaza miscarile teodolitului;
se actioneaza asupra surubului micrometric de deplasare a lunetei in plan vertical si se aduce firul reticular orizontal pe pct. caracteristic al semnalului.
din surubul micrometric ptr. miscarea lunetei in plan orizontal se aduce firul reticular vertical peste pct. vizat.
Precizia de vizare reprezinta spatiul conic vazut prin luneta sub unghiul w, limitat de diafragma reticulului;
Campul lunetei este invers proportional cu marirea lunetei.
Vizarea se face in trei faze (timp):
1.Vizarea aproximativa, care se face cu miscarile lunetei deblocate, prin suprapunerea colimatorului pe semnalul topografic din teren, dupa care se blocheaza miscarile generale in plan orizontal si vertical.
2.Punerea la punct a imaginii din luneta. Se incepe prin clarificarea imaginii reticulului prin intermediul ocularului, respectiv ajustarea ocularului la posibilitatile vizuale ale operatorului, pana ce imaginea firelor reticulare apare foarte clara si atat de neagra pe cat este de posibil. Apoi se realizeaza focusarea imaginii semnalului topografic din teren, actionand asupra surubului sau inelului de focusare.
3. Vizarea definitiva ( punctarea) consta in aducerea centrului r al reticulului pe semnalul vizat S actionand asupra suruburilor de miscare fina in plan orizontal si vertical.
Pozitiile lunetei ( poz. teodolitului sau ale cercului vertical) au fost alese prin conventie dupa cum urmeaza:
- pozitia I, in care cercul vertical se afla la stanga lunetei ( respectiv la stanga operatorului care vizeaza prin luneta) ; ptr. a diminua o eroare de constructie , prin conventie s-a stabilit ca in poz. I sensul de rotatie in plan orizontal al alidadei si al lunetei sa fie sensul acelor de ceasornic.
- pozitia a II a in care cercul vertical este situat in dreapta lunetei ; in acest caz s-a convenit ca sensul de rotatie in plan orizontal al alidadei si al lunetei sa fie in sensul trigonometric.
![]()
![]()

 Vizarea definitiva
Vizarea definitiva
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vizare aproximativa
19. Principiul masurarii optice a distantelor cu luneta topografica pe mire verticale .
Cand terenul este orizontal si axa de vizare este perpendiculara pe mira .
D = distanta dintre puncte ;
F = distanta focala a obiectivului ;
d = distanta dintre centrul optic al obiectivului si centrul de vizare al teodolitului;
D = distanta dintre focarul anterior al obiectivului si mira ;
D = D¢ + f + d ; f si d fiind constante, rezulta :
D = D¢ + K2 ; unde K2 poarta denumirea de constanta aditionala .
( h /H) = ( f /D ) deci D¢ = ( f / h ) h ;
Distantele dintre firele stadimetrice ale reticulului s-a notat cu " h". Rezulta ca raportul ( f /h ) este tot o constanta si va fi notat cu K1, purtand denumirea de constanta stadimetrica sau constanta multiplicatoare. Valoarea H este o marime variabila, in functie de distanta la care este amplasata mira fata de luneta si poarta denumirea de numar generator. Rezulta deci :
D = K1H + K2 ;
La lunetele moderne datorita montarii unei lentile analizatoare in spatele obiectivului, care are rol de lentile de focusare, constanta aditionala K2 = 0 , rezultand : D = K1 H
Numarul generator H, se determina cu ajutorul mirelor, prin efectuarea citirilor la firele stadimetrice si efectuand diferenta acestor citiri.
H = Cs - CJ ;
Unitatea de masura in care este exprimat numarul generator H, va genera o distanta exprimata in aceleasi unitati de masura.
Ptr. controlul citirilor pe mira se face si o lectura in dreptul firului reticular orizontal. Firele stadimetrice fiind simetrice fata de acest fir rezulta :
C¢m = ( Cs - Cj ) / 2 ;
Diferenta dintre media C¢m si citirea directa Cm nu trebuie sa difere la mai mult de 1 - 2 mm.
20. Principiul masurarii optice a distantelor cu luneta topografica pe mire verticale.
Cand terenul este inclinat si axa de vizare este la o inaltime oarecare pe mira . Aflarea distantei orizontale :
( H¢/ 2 ) = ( H / 2 ) cosa Þ H¢ = H cos a
L = K1 H¢ = K1 H cosa
D = L cosa = K1 H cos 2 a
Determinarea diferentei de nivel :
dh + s = I + D unde : i este inaltimea instrumentului in statie ;
s este inaltimea la care s-a vizat pe mira ;
dh este diferenta de nivel.
Masurarea distantelor pe cale indirecta cand terenul este inclinat D = D tg a
Rezulta : D = K1 H cos2 a tg a = K1 H sin a cos ;
dh = K1 H sin a cos a + ( I - s ) relatia se aplica cand viza este ascendenta.
Ptr. vize descendente se poate demonstra ca :
dh = K1 H sin a cos a + ( s - i) ;
Cand se vizeaza la inaltimea instrumentului pe mira instalata in punctul B, rezulta :
dh = K1 H sina cos a
21. Verificarea si rectificarea erorii de indice la cercul vertical al teodolitului. (a patra conditie geometrica a axelor teodolitului).
Se mai numeste si eroare de colimatie la cercul vertical.. Intervine la masurarea unghiurilor verticale si se datoreste urmatoarelor cauze:
a. necoincidenta dintre proiectia axei de vizare pe cercul vertical cu linia ce uneste gradatiile 0 -200.
b. indecsii de citire nu se afla intr-un plan orizontal sau vertical si deci nu asigura o linie de credinta orizontala sau verticala.
Prin medierea citirilor efectuate in cele 2 poz. ale lunetei, eroarea de index este eliminata.
Constatarea erorii
Se vizeaza un obiect indepartat bine vizibil in ambele poz. ale lunetei si se face citirea unghiurilor zenitale z' si z'' la cercul vertical. Suma celor 2 unghiuri zenitale trebuie sa fie egala cu 400g s s abaterea standard de masurare a unei directii zenitale ).
Cand suma unghiurilor zenitale nu satisface conditia de mai sus, inseamna ca exista o eroare de index.
Rectificarea erorii - se poate face in 2 moduri : cu nivela torica sau cu compensator.
In cazul nivelei torice - cu luneta in poz. a doua se va introduce la cercul vertical valoarea corecta 400g - z, din surubul de calare a nivelei torice zenitale. Se va constata ca nivela torica zenitala s-a decalat. Se va cala nivela torica zenitala integral din suruburile de rectificare a acestei nivele.
In cazul teodolitelor cu compensator la cercul vertical, valoarea corecta ptr. unghiul zenital in poz. a doua se va realiza la cercul vertical prin actionarea asupra surubului micrometric de miscare a lunetei in plan vertical. Daca privim spre luneta se va consata ca firul reticular orizontal s-a deplasat de pe pct. vizat. Refacerea punctarii corecte se va realiza din suruburile de rectificare al reticulului, dispuse in plan vertical.
Operatiile de verificare si eventual rectificare se va repeta prin vizarea altui semnal, pana cand eroarea de index e £ s sau z' si z''= 400 g s
Verificarea poz. juste a firelor reticulare - prin gravare este asigurata perpendicularitatea firelor reticulare. Firul reticular orizontal trebuie sa ocupe o poz. orizontala, iar cel vertical o poz. verticala. Este suficient sa se verifice poz. justa a unui singur fir reticular.
Daca aceasta conditie nu este indeplinita, rectificarea acestei erori se va realiza prin slabirea suruburilor coaxiale cu luneta, care fixeaza reticulul de tubul obiectiv, rotirea convenabila a intregului reticul si strangerea la loc a suruburilor.
22. Verificarea si rectificarea erorii de perpendicularitate a axei secundare ( 00) pe axa principala ( VV) la teodolite. (OOI VV). ( a treia conditie a axei teodolitului).
Eroarea de inclinare a axei de basculare a lunetei afecteaza masurarea unghiurilor orizontale, intrucat planul azimutal in care se misca axa de vizare, intersecteaza axa VV sub unghi ,, i " si nu contine aceasta axa.
Constatarea erorii - se face prin mai multe procedee numai dupa ce au fost indeplinite conditiile geometrice anterioare. Se vizeaza un pct. situat la inaltime pe un perete dintr-un pct. de statie apropiat ( cca. 20m) in ambele pozitii ale lunetei si se face proiectarea acestuia prin plonjarea lunetei pe o rigla situata in orizontul instrumentului. Daca conditia de perpendicularitate este indeplinita atunci citirile efectuate pe rigla in dreptul firului reticular vertical vor corespunde in limita erorii facute la punctarea pct. ( d £ 1 mm ).
Rectificarea erorii - se face din umerii lunetei, ridicand sau coborand unul din capetele axei de basculare a lunetei. La teodolitele moderne, prin montaj, aceasta eroare nu depaseste 20 cc.
23. Eroarea de colimatie la teodolite. Verificarea si rectificarea ei.( a doua conditie geometrica a axei teodolitului). ( conditia rO I OO).
Aceasta eroare se datoreaza descentrarii reticulului ( centrul firelor reticulare r nu se afla pe axa optico - geometrica a lunetei ). Prin rotirea lunetei in jurul axei secundare OO, axa de vizare rO nu mai descrie un plan perpendicular pe OO, ci un con a carui generatoare este rO.
Constatarea erorii : cu luneta aproximativ orizontala se vizeaza un pct. cat mai indepartat si bine vizibil in ambele pozitii ale lunetei si se fac citirile pe cercul orizontal. Daca citirile sunt egale 200g s (s = abaterea standard de masurare a unei directii), se poate cosidera ca eroarea nu exista. Daca egalitatea de sus nu este indeplinita , se considera ca eroarea exista si deci rO nu este perpendicular pe OO.
Prin medierea citirilor din ambele pozitii ale lunetei eroarea de colimatie este eliminata. Diferenta dintre valorile directiilor masurate in ambele poz. ale lunetei ( facand abstractie de cele 200g) reprezinta dublul erorii de colimatie . Valoarea erorii trebuie sa fie mai mica decat toleranta T = s
Rectificarea- cu luneta in poz. a 2 a se introduce la cercul orizontal valoarea justa ptr. directia considerata, rezultata din medierea citirilor in ambele poz. ale lunetei din surubul micrometric de miscare in plan orizontal. Privind prin luneta, se va constata ca firul reticular s-a deplasat de pe semnul vizat. Suprapunerea firului reticular vertical peste semnalul vizat se va realiza din suruburile de rectificare ale reticulului s1 si s2 dispuse in plan orizontal. Operatia de verificare si rectificare se va repeta , fie alegand alt semnal, fie modificand poz. originii limbului, pana cand e £ s
VV I NN- prima conditie geometrica a axelor teodolitului.
Verificarea si rectificarea ei.- se face prin calarea teodolitului, presupunand ca nivelele acestuia sunt verificate si rectificate. Cercurile orizontale orizontale fiind din constructie perpendiculare pe axa VV, inseamna ca prin orizontalitatea acestora se obtine automat verticalizarea axei VV.
Constatarea erorii - daca in urma calarii instrumentului se constata canivelele se deregleaza prin rotirea teodolitului in diferite poz. inseamna ca axa VV nu ramane verticala, desi calarea s-a facut corect si nivelele au fost rectificate.
Rectificarea - se face numai in ateliere specializate sau la uzinele construtoare. Eroarea de neverticalitate a axei VV nu se elimina prin metode de lucru. Din acest motiv :
operatia de calare trebuie facuta cu cea mai mare atentie
nivelele teodolitului trebuie verificate si rectificate iaintea masuratorilor.
Calarea instrumentului trebuie facuta cu maxima atentie. Ptr. evitarea decalarii instrumentului in timpul masuratorilor aparatul trebuie sa fie instalat in teren stabil si protejat contra influentelor radiatiilor solare.
24. Metode de masurare a unghiurilor orizontale. Masurarea unghiurilor verticale. In topografie unghiurile orizontale se masoara in scopul determinarii poz. planimetrice a pct. , iar unghiurile verticale servesc la determinarea poz. altimetrice si reducerea distantelor la orizont.
Unghiul orizontal (w AB ) este unghiul diedru format de 2 plane verticale care contin dreptele din teren . Poate fi masurat intre proiectiile ortogonale ale dreptelor .
Unghiul vertical ( a AB ) este unghiul format de axa de vizare cu un plan orizontal care contine axa de rotatie a lunetei. Unghiul de panta poate avea valori pozitive sau negative in functie de inclinarea axei de vizare.
Unghiul zenital ( z AB ) masoara inclinarea axei de vizare fata de zenit, indicii de citire fiind dispusi intr-un plan vertical, iar verticalizarea lor facandu-se automat cu ajutorul unui compensator.
Metode de masurare a unghiurilor orizontale .
Metoda simpla se utilizeaza ptr. masurarea unghiurilor izolate si are 2 variante
a. Procedeul prin diferenta citirilor
b. Procedeul cu zero in coincidenta - ung. se masoara in mod asemanator, cu deosebirea ca pe directia punctului A se va introduce la cercul orizontal gradatia zero ( diviziunea dispozitivului de citire se aduce in coincidenta cu diviziunea zero a limbului ). Inaintea vizarii pct. A, se introduce ,,zero" la cercul orizontal astfel incat citirea c¢A = 0 , operatiile urmatoare decurgand asemanator :
In poz. I : wAB¢ = c¢B - c¢A = c¢B - 0 = c¢B
In poz. a - II- a : wAB¢¢ = cB¢¢ - cA¢¢= c¢B - 200 ;
Unghiul rezulta ca diferenta a mediilor citirilor din cele 2 pozitii.
Metoda unghiurilor orizontale prin metoda in tur de orizont.
Masurarea unghiurilor prizontale prin metoda repetitiei .
Masurarea unghiurilor orizontale prin metoda reiteratiei.
25. Masurarea unghiurilor orizontale in statii ecentrice.
Centrarea directiilor - daca dintr-un pct. C nu este vizibilitate catre un pct. A din cauza unui obstacol, se stationeaza excentric in pct. E. Relatia de calcul a corectiei e este:
![]()
Corectia e
se aplica unghiului masurat si rezulta unghiul centrat.
unghiul ca diferenta intre cele 2 directii. Din
cauza obstacolului , se stationeaza excentric si se masoara unghiurile
directiilor si se determina corectiile
![]()
Semnal excentric - cand statia este centrica, dar semnalul este excentric, corectia se va determina cu relatia :
Metoda drumuirii este un procedeu de indesire a retelei geodezice in vederea ridicarii detaliilor topografice din teren.
Drumuirea este o linie poligonala franta, in care pozitia reciproca a punctelor este determinata prin masuratori de distante intre punctele de frangere si masuratori unghiulare in punctele de frangere ale traseului poligonal.
In functie de elementele de constrangere de care se dispune in teren, dar si a obiectivelor topografice care trebuie ridicate se pot face urmatoarele clasificari ale drumuirilor:
Clasificarea drumuirilor in functie de elementele de sprijin
Ø drumuire libera (neconstransa) - Cand in teren s-au efectuat doar masuratori pentru stabilirea pozitiei reciproce a punctelor din traseul poligonal.
Ø drumuire sprijinita la capete pe puncte de coordonate cunoscute - De cele mai multe ori insa, traseul poligonal se sprijina la capete pe puncte de coordonate cunoscute - drumuiri constranse sau drumuiri sprijinite, care permit ca punctele de drumuire sa fie determinate intr-un anumit sistem de coordonate.
Ø drumuire sprijinita la capete pe puncte de coordonate cunoscute si orientari cunoscute (pe lanturi cunoscute) - Controlul elementelor masurate devine si mai concludent daca in punctele de coordonate cunoscute pe care se sprijina drumuirea, se masoara suplimentar directii spre alte puncte de coordonate cunoscute, care fiecare reprezinta un alt element de control.
Ø drumuire cu punct nodal
Clasificarea drumuirilor dupa forma traseului poligonal :
- drumuiri intinse
- drumuiri inchise
In multe situatii, drumuirile se pot sprijini la capete pe puncte din alte drumuiri, constituidu-se in asa-numitele retele poligonale.
In aceasta situatie este justificata introducerea notiunii de 'ordinul drumuirii' si anume:
Traseul A - 201 - . - 206 - B - drumuire principala
Traseul 202 - 301 - . - 304 - C - drumuire secundara
Traseul 205 - 401 - . - 403 - 303 - drumuire tertiara
Ordine inferioare drumuirii tertiare nu sunt admise in instructiuni.
27. CONDITII DE PROIECTARE A DRUMUIRILOR PLANIMETRICE. OPERATII DE TEREN LA EXECUTIA UNEI DRUMUIRI PLANIMETRICE.
PROIECTAREA RETELELOR DE DRUMUIRI:
- Traseul drumuirilor se proiecteaza de regula de-a lungul arterelor de circulatie, cursurilor de apa, etc, intrucat laturile si punctele drumurii trebuie sa fie usor accesibile.
- Punctele de drumuire se amplaseaza in locuri ferite de distrugere, in care instalarea instrumentelor topografice se face cu usurinta.
- Intre punctele de drumuire invecinate trebuie sa existe vizibilitate perfecta, pentru ca directiile si lungimile sa se masoare fara dificultate.
- Punctele de drumuire se aleg in apropierea detaliilor care urmeaza sa fie ridicate.
Distanta intre punctele de drumuire este determinata de:
- conditiile concrete din teren,
- gradul de acoperire cu vegetatie sau cu constructii
- scopul ridicarii topografice
- aparatura topografica avuta in dotare
In situatia in care dispunem de aparatura clasica (teodolite, mire, panglici) se recomanda ca: - lungime medie latura de 100 - 150m
- lungime minima de 40 - 50 m
- lungime maxima 2000 - 3000 m.
In zone construite lungimea laturilor cat si lungimea drumuirii vor fi reduse in zone de extravilan.
OPERATII DE TEREN:
¾ marcarea punctelor de drumuire - se face de regula cu tarusi, in localitati cu tarusi metalici cherneruiti, iar in afara localitatilor cu tarusi de lemn.
¾ intocmirea schitelor de reperaj si descrierea topografica a punctelor.
¾ masurarea lungimii laturilor:
cu panglica se masoara laturile dus-intors, fiind admisa o toleranta intre
cele doua determinari de ![]()
Elemente cunoscute:
Ø Coordonatele punctelor 201, 202 (X,Y)
Ø Orientarile q q
1. Se calculeaza:
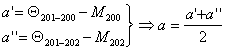
2. Calculul orientarilor pentru punctele radiate:
![]()
3. Calculul coordonatelor relative:
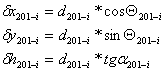
4. Calculul coordonatelor absolute:
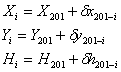
2. Metoda coordonatelor rectangulare (in terenuri cu panta a £ 5g )
Elemente cunoscute:
Ø Coordonatele punctelor 201, 202 (X, Y)
Ø Orientarea q
1. Se calculeaza:
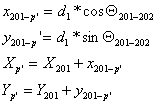
2. Calculul coordonatelor punctului P:
![]()
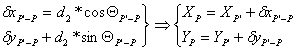
31. Efectuarea citirilor pe mire de nivelment ( centrimetrice si de invar).
Ptr. determinarea diferentelor de nivel, inaltimea axei de vizare a lunetei instrumentului fata de pct. marcat pe teren, se masoara pe rigle gradate, numite mire de nivelment.
Mirele centimetrice - lungimea este de 3m si pot fi intregi sau pliabile
lungimea 4m numai pliabile
capetele mirelor sunt protejate prin saboti metalici
verticalitatea lor intr-un pct. este realizata cu o nivela sferica
sunt vopsite in culori contrastante (fond alb- gradatii negre sau rosii)
inscrierea pe mira numai la metri si decimetri
diviziunile centrimetrice sunt vopsite
milimetri se aproximeaza
ptr. nivelment exista mire centrimetrice cu gradare pe ambele fete, originea de gradare a fetelor fiind diferita la talpa mirei, astfel incat citirile pe cele 2 fete sa difere mereu cu o constanta.
Sectiunea mirei este astfel aleasa ca sa nu se curbeze, iar eroarea de curbare sa fie cat mai mica.
Citirile pe mirele centimetrice se efectueaza obligatoriu la cele trei fire ale reticulului.
(Cfir sus + Cfir jos) = Cfir mijloc 1mm.
Mirele de invar - banda de invar este fixata la talpa mirei, iar la varf un resort intinde banda astfel ca tensiunea din banda sa ramana consatnta
coeficientul de dilatatie Ct = 0,0008 mm/1 /m
lungimea de d 3 sau 1,75 m numai dintr-o singura bucata
trasaturile pe mira au grosimea de 1mm ptr. benzile cu 2 scale si de 3mm ptr. benzile de invar cu o singura scala
distanta dintre trasaturi 5mm
eroarea de divizare a benzii de invar 0,001mm/1m
pe banda de invar se fac 2 randuri de diviziuni decalate la 2,5mm intre ele
originea celor 2 scale difera
mirele de invar se folosesc intotdeauna in pct. intermediare dintre reperi in combinatie cu broastele de nivelment
verticalizarea mirelor se face cu nivele sferice montate pe partea din spate a cutiei
Mirele sunt gradate in semidecimetri, avand gradatii atat pe cutie cat si pe banda de invar. Gradatiile pe banda de invar sunt din 5 in 5 mm, astfel incat 10 gradatii conduc la un semidecimetru inscris pe cutia mirei. Mirele de invar se folosesc numai la instrumente de nivelment geometric care au micrometre optice, care permit deplasarea optica a imaginii reticulului cu 5 mm.
La mirele de invar controlul citirilor se efectueaza prin efectuarea lecturilor pe 2 scale care au originea decalata. La mirele de fabricatie zeiss aceasta constanta este de 606500 astfel incat trebuie indeplinita conditia de control Cscala dreapta - 606500 = Cscala stanga 20 unitati de ultim ordin.
32. Instrumente de nivelment geometric cu compensator - din Leu
Nivelele cu compensator sau automate simplifica procesul de masurare, ridicand randamentul lucrarilor de teren. Orizontalizarea axei de vizare se realizeaza automat cu ajutorul unui compensator, dupa ce in prealabil aparatul a fost calat cu nivele sferica.
Dupa constructie compensatoarele pot fi de diferite tipuri, dar toate respecta aceleasi principii, bazandu-se pe principiul pendulului si refexiei.
Din pct. de vedere constructiv se distind trei categorii de compensatoare:
cu pendul
cu nivela
cu lichid
Precizia nivelelor cu orizontalizare automata a axei de vizare este determinata de puterea de marire a lunetei si de precizia compensatorului folosit.
In functie de precizia de masurare a dif. de nivel avem:
- nivele de precizie medie
- nivelele de precizie
- nivele de inalta precizie
Nivele cu compensatoare cu pendul - ptr. orizontalizarea automata a axei de vizare, s-au realizat diferite tipuri de compensatoare mecanice, care din punct. de vedere principial deplaseaza reticulul si de cmpensatoare optico - mecanice cu rol de schimbare a traseului unei raze orizontale ce vine de la obiectivul vizat in luneta nivelei din care se prezinta:
a. nivele automate cu compensatoare cu pendul, de precizie medie exemple:
nivela automata Ni 025 - Zeiss - este un instrument care realizeaza o eroare medie patratica de 2,5 mm/km de nivelment dublu. Instrumentul se manipuleaza usor, deoarece are o greutate mica, iar aspectul sau general este de corpul lunetei, de forma unei cutii paralepipedice, pe care este montata o nivela sferica cu ajutorul careia se efectueaza calarea aproximativa.
Parti componente:
- corpul lunetei cu obiectivul, reticulul, ocularul si sistemul de focusare cu surubul.
- compensatorul optic cu pendul, fixat in interiorul lunetei intre dispozitivul de focusare si placa reticulara , fiind format din 2 prisme triunghiulare fixate pe corpul pendului si o prisma pentagonala fixata in corpul lunetei. Pendulul este fixat print-o articulatie cu arc sub prisma fixa, fiind prevazut cu o greutate care la inclinari mici ale lunetei penduleaza sub actiunea gravitatiei in interiorul unui cilindru.
- orizontalizarea aproximativa se face cu ajutorul suruburilor de calare si a unei nivele sferice, fixata pe cutia lunetei, fiind prevazuta cu oglinda.
- cercul orizontal gradat permite masurarea unghiurilor orizontale cu o precizie de10c
- miscarea lunetei in plan orizontal este actionata de un surub fara sfarsit, care asigura deplasarea in jurul axului
constructia inferioara cuprinde: ambaza, suruburile de calare, placa de tensiune si placa de baza
- trepiedul
- nivela Ni 50 Zeiss - este o nivela usor manevrabila, cu imagine directa, fiind prevazuta cu un cerc gradat( 400g) sau 360 care permite masurarea unghiurilor cu o precizie de 0,1g 0,1
b. nivele automate cu compensatoare cu pendul de precizie exemple:
nivela automata Ni 30 Zeiss areo precizie superioara la executarea lucrarilor de nivelment geometric si tehnic ;
nivela automata Ni 40 Zeiss
c. nivele automate cu compensatoare cu pendul de inalta precizie exempla:
nivele automata koni 007 Zeiss- orizontalitatea axei de vizare se realizeaza print-o miscare de translatie, optica prin intermediul unui compensator format dintr- o prisma pendul, suspendat intr-o luneta periscopica. Parti componente:
corpul lunetei este fixat in poz. verticala, fiind protejat de carcasa, in care se gaseste:
- placa de sticla ptr. protectie, prisma pentagonala, lentila de focusare, obiectivul, reticulul si ocularul;
compensatorul optic cu pendulul format dint-o prisma pendulata, o prisma de reflexie
- orizontalizarea aproximativa se face cu ajutorul nivelei sferice
miscarea in plan orizontal este actionata prin clema de blocare si surubul micrometric
- cercul orizontal gradat cu ocularul microscopului de citire si partile optice componente
- tambur micrometric si surubul de fixare
- constructia inferioara cuprinde: ambaza, suruburi de calare, placa de tensiune si placa de baza
- trepiedul
- nivela automata Ni 002 zeiss
32. Instrumente de nivelment geometric cu comensator - din Masuratori Terestre
Principiul comensatorului - consideram un sistem optic, format dintr-o lentila convergenta L, cu axa Of si de distanta focala f, F fiind focarul imagine si ,,P" planul focal imagine.
Un pct. H la infinit formeaza imaginea in ,,h" planul focal, confundat cu F in centrul firelor reticulare. Daca se inclina sistemul optic cu un unghi a, noua axa a sistemului optic intersecteaza planul P in h' unde se formeaza imaginea lui H' si unde se afla firele reticulare. Prin rotire pct. r a descris un arc de raza f ajungand in r'. Planul focal ,,P" este perpendicular pe axa de vizare se roteste si el cu unghiul a
Daca sistemul optic este orizontalizat cu o nivela sferica unghiul a este mai mic:
d/a = f/b Þ b = (f/d) a
f/d = ct. Þb = c a
Valoarea c este constanta ptr. un instrument si se numeste amplificator unghiular sau putere de multiplicare a compensatorului si depinde de poz. pct. k in interiorul lunetei. Realizarea principiului de compensare poate fi obtinut pe 2 cai:
prin deplasarea centrului reticulului ,,r" pe directia razei orizontale si atunci este vorba de un compensator mecanic
prin devierea razei orizontale printr-un dispozitiv optic amplasat in pct. ,,k" astfel incat raza sa ajunga in centrul firelor reticulare, si atunci vorbim de un compensator optico - mecanic
Rezolvarea tehnica a acestor compensatoare se bazeaza pe principiul pendulului si reflexiei.
Nivelul Ni 007 de realizare a compensatorului - compensatorul este format dintr-o prisma pendul, suspendata intr-o luneta verticala si care realizeaza o translatie optica a liniei de vizare ca sa fie indeplinita conditia b = c a . Prisma este suspendata la distanta d = f/2 deci c =2.
Cand axa verticala a instrumentului este inclinata cu unghiul a si prisma se deplaseazacu o cantitate x/2, raza va fi deviata in total cu cantitatea x. Prisma pentagonala poate fi deplasata pe verticala cu ajutorul unui tambur, ca urmare raza va fi deplasata paralel pe o distanta de 5 mm, consituind astfel micrometrul optic al aparatului.
Precizia medie asigurata de Ni 007 pe dublu kilometru de nivelment cu micrometrul optic si mire de invar de 0,7 mm. Fara utilizarea micrometrului, cu blocarea acestuia la diviziunea 5 si cu mire centimetrice precizia este de 2mm pe dublu km de nivelment.
Nivelul Ni 025 si modul de realizare a compensatorului.
Principiul de compensare - prismele 3 si 5 ocupa prin pendulare ptr. inclinari mici ale lunetei aceeasi poz. ca si in cazul lunetei orizontale. Fascicolul care intra in luneta, inclinata cu unghiul a, este rabatut de prisma 3 cu un unghi 2 a si dupa o tripla reflexie in prisma fixa 4(prisma acoperis), este inca o data rabatut cu 2a de prisma 5. In total fascicolul este rabatut cu unghiul b a deci c = b a = 4. In consecinta d = f/4, iar compensatorul trebuie amplasat intre lentila de focusare si reticul.
Caracteristici:
marimea lunetei 20 x
distanta minima de vizare 1,5m
precizia 2,5 mm pe dublu km de nivelment
utilizabil numai ptr. mire centimetrice.
Nivelul automat cu olinda suspendata vertical. La jumatatea distantei focale d = f/2 se suspenda vertical o oglinda. Cand instrumentul este orizontal razele orizontale care vin de la H converg catre centrul reticulului r si sunt reflectate de oglinda in pct. r' simetric cu r in raport cu oglinda M.
Cand luneta s-a inclinat cu un unghi a, razele orizontale converg in r' din planul focal al obiectivului. Ele vor fi reflectate de oglinda M in pct. r' simetric cu r".
Caracteristici:
marirea lunetei este de 40x
destinat numai masuratorilor cu mire de invar
olinda pendulata de 0.2 mm pe dublu km de nivelment
oglinda pendulata are si rol de focusare
prin masurare in 2 poz. ale oglinzii pendulate sunt eliminate erori reziduale si se realizeaza uh orizont cvasi absolut de 1 secunda.
Modul de executare a lucrarilor:
Ptr. efectuarea masuratorilor instrumentul se instaleaza intr-un pct. al profilului in lung si apoi se vizeaza, la un alt pct. cunoscut, de obicei pct. precedent al profilului in lung si apoi se vizeaza succesiv la mirele tinute vertical in pct. caracteristice ale profilului transversal, pct. ce se aleg la distante egale in cazul terenurilor cu pante aproximativ uniforme sau la distante diferite in cazul cand panta terenului se schimba evident.
39. Elementele masurate in statie cand se efectueaza nivelment trigonometric la distanta mica.
Aceasta metoda de nivement se caracterizeaza prin aceea ca determinarea diferentei de nivel dintre puncte se realizeaza cu ajutorul distantei dintre pct. si unghiul vertical.
La executarea lui, unghiurile verticale se masoara cu ajutorul teodolitelor , iar distantele se masoara tahimetric sau se determina din coordonatele pct. daca acestea sunt cunoscute.
Principiul nivelmentului trigonometric consta in determinarea diferentei de nivel functie de distanta orizontala si unghiul vertical.
viza ascendenta
viza descendenta
Viza ascendenta .
Se dau : cota pct. de statie HA
Se masoara : unghiul vertical, inaltimea aparatului, distanta dintre pct. de statie si pct. nou.
Se calculeaza: cota pct. nou HB
Modul de lucru pe teren - se instaleaza teodolitul deasupra pct. de cota A ( se centreaza, se caleaza), se masoara ianltimea I a aparatului si apoi se vizeaza semnalul aflat pe pct. nou B, se citeste unghiul vertical( zenital z, sau de panta a
Modul de calcul
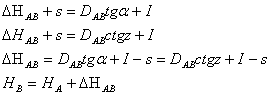
2. Viza descendenta
Se dau: cota pct. de statie HA
Se calculeaza : cota pct. nou HB
Modul de lucru pe teren - se instaleaza teodolitul deasupra pct. de cota cunoscuta A ( se centreaza, se caleaza), se masoara inaltimea aparatului si apoi se vizeaza semnalul aflat pe pct. nou B, se citeste unghiul vertical (zenital z, sau de panta a
Modul de calcul
![]()
Unghiul de panta este negativ, iar unghiul zenital este mai mare de 100g, fapt ce conduce la valori negative ptr. tangenta sau cotangenta.
Daca pct. B poate fi vizat la inaltimea aparatului termenii :'' I -s" si "s - I" devin zero, iar calculele se vor efectua :
![]()
40. Care sunt elementele (ipoteza) ce se urmaresc in cazul preciziei unei portei de nivelment trigonometric .
Marimile d si j se masoara cu anumite erori si astfel si dif. de nivel este afectata de o anumita eroare.
In cazul terenurilor orizontale , unghiul de inclinare este foarte mic, tgj tinde catre zero, iar cosj tinde spre 1, eroarea de distanta are un efect neinsemnat.
In cazul terenurilor inclinate, cand j tinde spre 50g, tgj tinde catre 1, iar cos2 practic este egal cu 0,5, rezulta ca eroarea de distanta intervine in marime naturala, iar efectul erorii naturale se dubleaza.
In cazul nivelmentului trigonometric la distante mari in relatiile de calcul al dif. de nivel intervin si alte marimi: inaltimea aparatului I si inaltimea semnalului S. Aceste elemente pot fi masurate cu o precizie destul de ridicata 1 cm, si astfel efectul eroriilor se poate neglijia.
Valorile coeficientului de refractie atmosferica in cazul vizelor inalte si nu prea lungi ( pana la 3-4 km) efectuate in timpul pranzului sunt destul de bine controlate.
In cazul vizelor lungi si in special al vizelor joase, duse din statii la sol, variatiile coeficientului de refractie atmosferica devin necontrolabile si afecteaza in mare masura precizia nivelmentului trigonometric.
Concluzii- Eroarea dif. de nivel creste direct proportional cu lungimea vizei si cu eroarea de masurare a unghiului de inclinare. Daca se urmaresc rezultatele de valoare se recomanda limitarea vizelor si masurarea unghiurilor cu atentie , in ambele poz. ale lunetei, facand citiri atat la firul nivelelor cat si la firele stadimetrice, folosind aparate de mare precizie.
41. Ponderea in nivelmentul trigonometric.
Nivelmentul trigonomeric se poate aplica pe toate terenurile , dar se utilizeaza de regula pe terenurile accidentate precum si ptr. determinarea dif. de nivel dintre pct. situate la distante mari ;
este mult mai expeditiv, deoarece dintr-o singura statie se pot determina diferente de nivel mari, pentru care la nivelmentul geometric ar trebui mai multe statii, care ii afecteaza precizia ;
pe terenuri framantate, avantajul nivelmentului trigonometric creste in cazul in care se executa concomitent cu ridicarile planimetrice.
Nivelmentul trigonometric se bazeaza pe principiul vizei inclinate, diferenta de nivel dintre puncte determinandu-se pe cale trigonometrica, in functie de unghiul vertical, masurat cu teodolitul sau tahimetrul, si de distanta dintre puncte, masurata direct sau determinata indirect pe cale stadimetrica sau prin calcul, din coordonate.
In cadrul metodei radierilor la distante mari pct. de intersectie inainte sau inapoi pot primi cote din mai multe parti. Cota medie, daca vizele sunt sensibil diferite se calculeaza ca o medie ponderata.
Ptr. calculul ponderilor , ce da eroarea medie a dif. de nivel rezulta ;
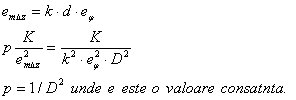
42. Tahimetre cu fire stadimetrice nereductoare - determinarea distantelor ???
43. Reducerea la orizont a distantelor in cazul masurarii lor cu tahimetrele.- din Masuratori
Ptr. masuratori topografice rapide se folosesc instrumentele tahimetrice, care efectueaza in acelasi timp atat ridicare planimetrica cat si ridicare altimetrica, deci cu aceleasi instrumente se masoara atat unghiurile cat si distantele.
Teodolitele tahimetru care folosesc mire verticale fac parte din categoria tahimetrelor de precizie medie. Aceste instrumente sunt tahimetre nereductoare, dist. orizontala si dif. de nivel determinandu-se prin calcul.
In principiu precizia ridicarilor tahimetrice este inferioara ridicarilor clasice, unde unghiurile se masoara cu teodolitul sau tahimetrul, iar distantele cu panglica.
Prin utilizarea tahimetrelor autoreductoare creste randamentul lucrarilor. Aceste aparate dau direct distantele reduse la orizont, precum si diferenta de nivel intre pct. de statie si pct. vizat.
In cazul ridicarilor tahimetrice curente, filosind principiul stadimetric al masurarii distantelor, se demonstreaza ca ptr. reducerea dict. la orizont si calculul diferentelor de nivel se folosesc relatiile :
- pentru reducerea la orizont a distantelor
![]()
- pentru diferentele de nivel
Dh = K . sina cosa + I - S
Dh = K . H . sinZ . cosZ + i - S
- pentru i = S
Dh = K . H . sina . cosa
Dh = K . H . sinZ . cosZ
in care :
a - unghiul vertical
Z - unghiul zenital
H - nr. generator interceptat pe mira intre firele stadimetrice
K - constanda stadimetrica K =100
i- inaltimea tahimetrului pana la axa de vizare
S - inaltimea semnalului vizat cu firul reticular orizontal.
Ptr. ca unghiul vertical a sau unghiul zenital Z sa fie masurate corect, se vizeaza intotdeauna la ialtimea aparatului pe stadie si ce citeste unghiula si Z apoi se face citirea nr. generator H.
Atat dist. redusa la orizont cat si dif. de nivel se poate calcula usor cu ajutorul tabelelor trigonometrice sau cu ajutorul tabelelor de coordonate topometrice.
43. Reducerea la orizont a distantelor in cazul masurarii lor cu tahimetre - luata din geodezie.
Relatia distantei D = K H este valabila numai in cazul cand viza este perpendiculara pe stadie, deci in terenuri orizontale. In cazul terenurilor inclinate viza nu cade perpendicular pe stadie si astfel nr. generator citit este mai mare decat cel corespunzator distantei inclinate L.
Ptr. a obtine distanta inclinata reala , nr. generator citit se inmulteste cu cosinusul unghiului de inclinare, adica H' = H cosj iar L = K H cosj. Ptr. obtinerea distantei reduse la orizont valoarea obtinuta se mai inmulteste inca odata cu cosj , adica :
D = L cosj = K H cos2
Reducerea distantelor in cazul stadiilor orizontale , care se tin intotdeauna perpendicular pe viza, indiferent de inclinarea terenului se face ca si in cazul masurarii distantelor pe cale directa cu relatia :
D = L cos.
44. Determinarea diferentelor de nivel in cazul masurarii unghiurilor verticale si a distantelor cu tahimetrele. ???/
45. Verificarea si determinarea constantelor tahimetrice.
Se recomanda ca verificarea constantei instrumentului sa fie realizata pe o baza de etalonare. Ptr. a efectua masuratori corecte de distanta constanta trebuie setata in instrument in meniul ,,Adj''.
Se realizeaza numai in atelierele de specialitate.
Verificarea si rectificarea nivelei sferice.
Se realizeaza ca la teodolit.
Se realizeaza ca la teodolit.
Erorile mici reziduale de inclinare a axei principale a instrumentului, datorita unei nivele torice putin dereglate sau a decalarii instrumentului in timpul masuratorilor, pot fi eliminate, intrucat majoritatea statiilor totale dispun de compensatoare biaxiale, care permit determinarea inclinarii axei principale de rotatie a instrumentului pe directia axei de vizare a lunetei si pe directia axei secundare OO.
Verificarea si rectificarea erorii de colimatie.
Verificarea si rectificarea erorii de index ( indice) la cercul vertical.
Se realizeaza ca la teodolit. Fiind o eroare sistematica valoarea ei poate fi setata in meniul ,,Adj" corectia fiind aplicata automat unghiurilor verticale masurate.
Verificarea poz. juste a firelor reticulare.
Se realizeaza ca la teodolit.
46. Porteea limita a unei linii tahimetrice. ????
47. Masurarea distantelor inclinate cu tahimetre, cand se utilizeaza mire orizontale.
se instaleaza in statie teodolitul de precizie, intr-o extremitate a distantei de masurat ;
se instaleaza in statie, la celalalt capat al distantei mira orizontala, se orizontalizeaza si se orienteaza perpendicular pe directia de vizare ;
se masoara cu teodolitul de precizie unghiul paralactic g dintre marcile de la extremitatile mirei, in cele 2 poz. ale lunetei ;
se determina distanta prin calcularea valorii ctg g
47. Masurarea distantelor inclinate cu tahimetre, cand se utilizeaza mire orizontale - din geodezie.
Ptr. masurarea distantelor se folosesc stadii, care se tin de obicei vertical sau orizontal. Verticalitatea respectiv orizontalitatea se poate asigura cu nivelele sferice. Ptr. citirea nr. generator (H) de pe stadie se folosesc firele stadimetrice din campul lunetei, cele orizontale, in cazul stadiilor tinute vertical si cele verticale in cazul stadiilor tinute orizontal. Stadiile orizontale sunt prevazute cu cate o catare care permite asezarea lor perpendiculara pe directia vizei.
48. Tahimetre autoreductoare - principiul
Tahimetrele autoreductoare utilizate astazi sunt instrumente care folosesc citirea centralizata a unghiurilor orizontale si verticale precum si a distantelor reduse la orizont si a diferentei de nivel, dupa diferite principii. Tahimetrele autoreductoare dau direct distanta orizontala de la aparat la mira.
Unele asigura aceeasi precizie ca si tahimetrele propiu-zise, iar altele asigura o precizie comparabila cu aceea a masuratorilor directe.
49. Tahimetre autoreductoare cu diagrama - principiul
Aceste tahimetre dau direct atat distanta redusa la orizont(d), cat si diferenta de nivel(DZ).
La tahimetrul autoreductor Dahlta, in campul lunetei, apare imaginea unei diagrame generata pe o placa de sticla optica. Diagrama contine:
firul reticular orizontal , firele distantei , firele ptr. diferentele de nivel si firul reticular vertical .
Firele curbe ptr. diferente de nivel pornesc de la intersectia firului reticular orizontal cu firul reticular vertical si sunt simetrice fata de firul reticular vertical. Sunt trasate o serie de curbe ptr. diferente de nivel negative. Aceste curbe au valori de 10, 20, 100 sau 10, 20,50,100 cu semnele adecvate. Curbele sunt desenate dupa legea calcului diferentelor de nivel:
DZ = KN sin 2 a , unde:
a - este unghiul de panta,
z - unghiul zenital.
Curbele ptr. distanta la Dahlta 020 zeiss - Jena sunt amplasate deasupra si dedesuptul firului reticular orizontal. Curba ptr. distanta amplasata deasupra are constanta stadimetrica 100, iar curba amplasata dedesupt are constanta stadimetrica 200. Curbele sunt desenate dupa legea reducerii distantei la orizont cu formulele:
d = KN cos2 a
d = KN sin2 z
Tahimetrul autoreductor are in dotare o mira speciala din pct. de vedere al gradatiilor, zero al mirei este amplasat la 1,40 m de la sol. De la acest reper pornesc gradatiile pozitive in sus si negative in jos.
Operatiile ptr. masurare ;
- se pune aparatul in statie ( se centreaza, se caleaza si se orienteaza aparatul pe directia nord magnetic)
se masoara inaltimea aparatului in statie
se vizeaza pe mira cu firul reticular orizontal la zero al mirei
- se citeste pe mira la intersectia firului reticular si firul de dist. - distanta redusa la orizont
se citeste pe mira la intersectia firului reticular vertical cu firul ptr.dif. de nivel- dif. de nivel
50. Tahimetre cu dubla imagine - principiul. (refractie) .
Principiul de constructie al tahimetrelor cu dubla imagine este urmatorul: in fata obiectivului se monteaza o pana de sticla , care acopera partea inferioara a campului lunetei, formand un sistem deviator. In aceste conditii unele raze vor trece prin luneta nedeviate, intalnind stadia orizontala intr-un punct. Alte raze vor intalni prisma deviatoare din partea inferioara a campului obiectivului si vor fi deviate intalnind stadia orizontala in alt punct. Devierea este in functie de unghiul format de cele doua fete ale penei. Deoarece unghiul de refractie este constant, rezulta ca distanta este proportionala cu segmentul pe mira orizontala dintre cele doua puncte. Ptr. ca sistemul sa fie reductor in constructia lunetei se introduc doua pene K1 si K2 de caracteristici identice.
Masurarea paralactica a distantelor- principiul.
Principiul de determinare paralactica a distantelor consta in masurarea unghiului orizontal sub care se vede o mira orizontala de lungime constanta, cu un teodolit de precizie. Se considera o mira orizontala AC si axa de rotatie OO a lunetei unui teodolit. Mira AC trebuie astfel orientata incat in planul AOC sa fie perpendiculara pe axa de vizare a lunetei. Proiectia lui AC in planul orizontal care trece prin punctul O este ac. Liniile de vizare OA si OC se proiecteaza in Oa si Oc, iar inaltimea OH a triunghiului isoscel AOC se proiecteaza in Oh.
Unghiul care se masoara cu teodolitul, este unghiul diedru aOc = y.
Prin urmare, este suficient sa gasim cotangenta unghiului de panta masurat cu un teodolit de precizie pentru a determina valoarea distantei D. Aceasta metoda de masurat nu necesita deci nici un instrument special, in afara de o mira prevazuta cu un colimator in centru , pentru asigurarea perpendicularitatii pe dreapta OH.
52. Ce erori intervin la masurarea paralactica a distantelor.
Erori la masurarea paralactica a unei distante :
Eroarea la masurare a distantei depinde de urmatoarele erori :
eroarea lungimii b a mirei
eroarea de masurare a unghiului g cu teodolitul
eroarea de perpendicularitate a mirei pe axa de vizare a teodolitului
eroarea de orizontalitate a mirei.
Influentele acestei erori se studiaza succesiv si independent una de cealalta.
53.Tahimetre telemerice-principiul .
Se deosebesc fundamental de tahimetrele propiu- zise si autoreductoare deoarece sunt construite cu baza in instrument si astfel nu este necesara o baza in al doilea punct al distantei de masurat, ci doar un semnal simplu, de ex. un jalon sau chiar obiectul vizat. Aceste tahimetre sunt construite in doua variante: cu baza variabila si unghi paralactic constant, si cu baza constanta si unghi paralactic variabil.
2.1.2. Operatii de teren
2.1.2.a. Marcarea si semnalizarea punctelor din reteaua de triangulatie locala a punctelor de indesire.
Marcarea in sol cu borne si in suprasol prin semnale se va face in puncte noi prin borne din piatra naturala sau din beton armat, respectiv prin semnale simple cu fluture sau prin semnale cu picioare.
2.1.2.b. Efectuarea masuratorilor unghiulare:
unghiurile orizontale vor fi masurate intre orele 600 - 1100; 1630 - 1930;
unghiurile verticale vor fi masurate intre orele 1100 - 1500;
- se vor masura dimineata punctele din partea de rasarit si dupa - amiaza cele de apus pentru a avea tot timpul soarele in spate;
se va intocmi la inceput un tur de orizont informativ in puncte, pentru a evita miscari suplimentare in cautarea punctelor;
se vor masura unghiurile prin metoda seriilor, respectand toate recomandarile si restrictiile prevazute;
se va stabili numarul de serii complete de masurare in fiecare punct si pe baza acestora se va stabili intervalul dintre originile seriilor:
![]()
q - numarul microscoapelor de citire ( = 2)
t - numarul seriilor
![]()
Pentru a se diminua erorile de perioada scurta ale gradatiilor limbului, se modifica intervalele calculate cu 10c.
Directiile in punctele retelei vor fi masurate cu teodolite de precizie (Wild T2, Theo 010A sau B, Wild T3).
La fiecare directie se va masura cu doua coincidente la micrometrul optic. Diferenta intre doua coincidente nu trebuie sa depaseasca 4cc.
Inchiderea unui
tur de orizont sa nu depaseasca ![]() , unde s = numarul de puncte vizate.
, unde s = numarul de puncte vizate.
Variatia intre diferitele directii reduse la origine sa nu depaseasca 15 - 20cc.
Seriile fiind cicluri de observatii independente, este permisa refacerea calarii instrumentului intre serii daca este nevoie.
Intr-o serie se admit maximum 8 vize.
Daca trebuie masurate mai mult de 8 directii dintr-o statie se vor forma doua grupe care sa contina 2 - 3 directii comune, de preferinta directia de origine sa fie comuna pentru cele 2 - 3 grupe.
Compensarea seriilor si stabilirea directiilor ce vor intra in compensare.
2.1.2.c. Efectuarea masuratorilor liniare asupra bazei retelei de triangulatie
Determinarea marimii liniare a bazei retelei de triangulatie se poate face prin:
masurarea directa;
masurarea cu aparatura electrooptica;
nivelmentul bazei;
determinarea lungimii bazei.
2.1.3. Operatii de calcul (Compensarea masuratorilor)
In esenta se urmareste o geometrizare a retelei de triangulatie, astfel incat figurile geometrice create sa satisfaca urmatoarele conditii:
suma unghiurilor in triunghiuri sa fie 200g;
suma unghiurilor in jurul unui punct sa fie 400g;
intre laturi si sinusurile unghiurilor opuse sa existe raporturi de perfecta egalitate.
Primele doua asigura conditii geometrice de baza, iar ultima asigura conditia de scara in reteaua creata. stiut fiind ca masuratorile noastre unghiulare si liniare sunt afectate de erori, conditiile amintite mai sus, vor fi satisfacute numai aproximativ, ceea ce impune efectuarea unor calcule de compensare.
Uzual sunt folosite doua metode de compensare a masuratorilor:
metoda masuratorilor conditionate;
metoda masuratorilor indirecte.
Principial, problema este de a gasi coordonatele unui punct nou P (x, y) prin vize date exclusiv din acest punct nou P spre trei puncte vechi A (x1, y1), B (x2, Y2) si C (x3, y3) - date prin coordonatele lor. Din masuratorile de teren se determina unghiurile a si b folosind metode precise de masurare.
Calculul coordonatelor punctului 2400
CAZUL II
Elemente necesare rezolvarii problemei
a) coordonatele punctelor vechi
|
Pct. |
X |
Y |
b)Unghiurile orizontale a b d
calculate din directiile masurate si compensate in statia 2400
|
PS |
PV |
Dir. mas. |
![]()
![]()
![]()
a = dir![]() - dir
- dir![]() = 311.9405 - 289.9870 =21.95
= 311.9405 - 289.9870 =21.95
b = dir![]() -dir
-dir![]() = 351.3485 - 311.9405 = 39.41
= 351.3485 - 311.9405 = 39.41
d = dir![]() - dir
- dir![]() = 15.2682 - 351.3485 = 63.92
= 15.2682 - 351.3485 = 63.92
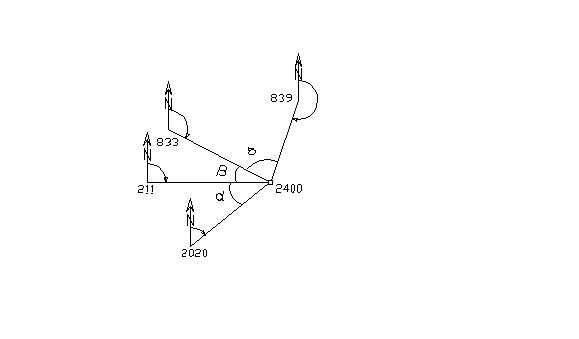
[a1] c) Schita
vizelor
Etape de calcul
1. Calculul orientarii![]()
![]()
![]()
Calculul orientarilor![]()
![]()
![]()
3. Calculul coordonatelor punctului 2400 prin intersectie inainte cu orientari
![]()
![]()
![]()
![]() 548316,365
548316,365
![]() 342096,098
342096,098
![]()
![]()
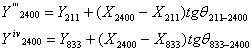
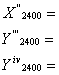
Pentru a rezolva problema sunt de parcurs doua etape:
In prima etapa, specifica retrointersectiilor, se vor gasi orientarile q q q ale vizelor AP, BP, CP.
In a doua etapa avand trei drepte de orientare cunoscuta si trecand fiecare prin cate un punct dat, se vor rezolva niste intersectii obisnuite (inainte).
Deci, doar prima parte a problemei este noua pentru a carei rezolvare se vor scrie cele trei ecuatii analitice, teoretice ale celor trei drepte care trec prin punctul P si respectiv A(x1, y1), B(x2, y2) si C(x3, y3).
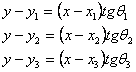 (1)
(1)
Se observa ca daca qAP q atunci:
![]() (2)
(2)
Se introduc relatiile (1) si (2) si obtinem:
 (3)
(3)
Sistemul (3) este un sistem de trei ecuatii cu trei necunoscute tgq, x si y
![]() (4)
(4)
Se iau primele 2 ecuatii din (3) si avem:
![]()
![]() (5)
(5)
un sistem de 2 ecuatii cu 2 necunoscute; din prima ecuatie rezulta
![]() (6)
(6)
pe care o inlocuim in ecuatia a doua din sistemul (5)
 (7)
(7)
Se face si in ecuatia a treia aceeasi substitutie:
![]() (8)
(8)
si apoi se iau ecuatia I si a III-a si se face substitutia de mai sus, va rezulta o ecuatie de acelasi tip cu ecuatia (7).
![]() (9)
(9)
Se imparte ecuatia (7) la ecuatia (9) si rezulta:
![]() (10)
(10)
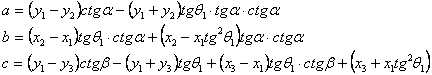
![]() (11)
(11)
grupand termenii dupa tgq vom avea
 (12)
(12)
![]() (13)
(13)
din relatia (13) se determina q1 si apoi q si q
Urmeaza determinarea orientarilor inverse qAP qBP qCP cu care se va intra in calculele unor intersectii inainte normale gasind astfel coordonatele punctului P.
67. Intersectia inapoi - metoda Collins - principiu.- din Masuratori
Printre metodele de rezolvare a retrointersectiilor este si aceea datorata lui Collins cunoscuta sub numele de metoda punctului ajutator.
Se dau coordonatele pct: 1 (x1, y1) , 2 (x2, y2) , 3 (x3,y3)
Pe teren se masoara unghiurile orizontale a si b din pct. P.
q este pct. ajutator a lui collins.
Din coordonatele pct. A si C se calculeaza qAC
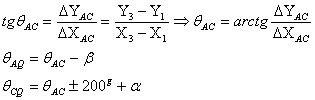
Din coordonatele pct. vechi A si C si cu orientarile qAQ si qCQ se vor calcula prin intersectie inainte coordonatele pct. ajutator Q (XQ , YQ ).
Din coordonatele pct. B si Q se determina qQB
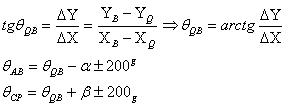
Cu coordonatele date ptr. punctele vechi A (X!, Y1) si C (X3, Y3) si cu orientarile calculate mai sus se poate calcula prin intersectie inainte punctul P.
67. Intersectia inapoi - metoda Collins - principiu.- din caiet
Se dau x,y ptr. 1,2,3 ,
Se cer x,y pentru pct. P.
Se masoara unghiuri orizontale a si b
Se duce un cerc prin 3 pct. doua de coordonate cunoscute pct. 1,3 si al treilea pct. necunoscut P. Se uneste pct. P cu pct. cunoscut 2 si se prelungeste dreapta pana ce intersecteaza cercul in pct. C denumit pct. lui Collins.
Avand orientarile de la pct. cunoscute catre pct. necunoscut s-a redus intersectia inapoi la mai multe intersectii inainte.
S-au masurat prin stationare in pct. P directii unghiulare orizontale catre pct. 1,2,3 ;
Se calculeaza punctul C ca intersectie inainte din triunghiul 13C
Calculam D13
Calculam g a b
Scriem teorema sinusului in triunghi
Calculam D1C si D3C
Calculam q si q1C, q3C
Calculam XC si YC
Calculam punctul P ca intersectie inainte din triunghiul C1P sau C3P
68. Intersectia inapoi - metoda punctelor duble - principiu. Hansen
Hansen a gasit o solutie de obtinere a unui pct. nou cand se pot viza numai doua pct. de coordonate cunoscute.
In cazul in care pe teren gasim numai 2 pct. vechi pentru a determina pct. nou P se mai materializeaza un al doilea pct. Q asfel incat distanta PQ sa fie 30% din distanta AB
- directia nou aleasa sa fie aproximativ paralela cu directia pct. cunoscute
Se dau : x,y ptr. A, B
Se cer x,y ptr.P
Pe teren stationam pe rand in pct. P si Q si masuram directii orizontale catre pct. vechi si catre celalalt pct. nou, si masuram distanta intre P si Q.
se vor masura directii Hz si distanta de la PQ
unghiuri orizontale intre directii vizate
aplicam teorema sinusurilor
calculam orientarile
69. Intersectia inapoi generalizata - principiu - xerox
70. Intersectia inapoi - metoda Casini - Martian - principiu.
Se dau : coordonatele pct. 1,2,3
Se masoara : unghiurile orizontale a si b
Se cere: sa se determine coordonatele pct. P.
Se traseaza doua cercuri prin pct. 12P si 23P, se duce din pct. 2 prin centrul cercurilor, diametrul si se obtin pct. A si B;
Latura AB este perpendiculara pe latura P2.
Ptr. a obtine coordonatele pct. A si B s-a unit pct. A cu pct. 1 si 2 obtinand triunghiul 12A, in care se observa ca unghiul din A subintinde acelasi arc ca unghiul a, iar unghiul din 1 este unghi drept, intrucat subintinde diametrul cercului;
Se determina unghiul g din pct. 2 cu formula :
g = 200g - ( 100g + a) = 100g - a
Cunoscand orientarile catre pct. cunoscute, din pct. necunoscut, intersectia inapoi s-a redus la mai multe intersectii inainte.
71. Metode de control la intersectia inapoi - metoda Casini - Martian - principiu - xerox
72. Intersectia inapoi - rezolvarea Marek - principiu. - din Masuratori
In zona sunt 2 pct. inaccesibile 1 si 2 de coordonate cunoscute spre care exista vizibilitate din pct. R pe care vrem sa-l determinam.
In apropiere se poate gasi un pct. S (necunoscut) care sa aibe vizibilitate reciproca cu R si spre pct. cunoscute 3 si 4.
Se masoara : a b g si d
Calculam :
a¢ g - a b¢ = 200g - b g¢ = 200g - g d = 200g - d
Se observa ca :
< A 21 = a¢ < A12 = b¢ < 34 B = g¢ < 43B = d
Calculul orientarilor :
q1-2 = din coordonate ; q1-A = q b¢ q2-A = q a¢
q3-4 = din coordonate ; q3-B = q d¢ q4-B = q g¢
Se calculeaza coordonatele pct. A si B prin intersectie inainte din 1 si 2, respectiv 3 si 4.
Se obtin XA, YA ; XB, YB .
Se determina qAB = qRS
qR1 = qRS - a ; qS-3 = qR-S 200g +g
qR2 = qRS - b qS-4 = qR-S 200g - d
Pct. R si S se determina prin intersectie inainte respectiv din 1 si 2 ; 3 si 4
Se obtin XR , YR ; XS , YS ;
Verificare :
Se calculeaza suprafata inchisa ARSB care trebuie sa fie zero.
Se calculeaza coordonatele punctului R prin intersectie inainte din 1 si S obtinandu- se aceleasi coordonate.
Intersectia inapoi - rezolvarea Marek - principiu- din Geodezie
Presupunem ca din pct. noi de determinat R si S exista vizibilitate reciproca si din fiecare, spre cate 2 pct. vechi ale retelei de sprijin 1 si 2 respectiv 3 si 4.
Determinarea coordonatelor pct. noi R si S se sprijina pe procedeul Collins.
Se duc cercurile 1,2 ,R si 3,4,S, se prelungeste dreapta RS obtinand pct. ajutatoare pe cerc A si B prin intersectii inainte, se determina mai intai coordonatele pct. A si B si in final ale pct. noi R si S.
Ptr. controlul calculelor se deduce din aceste coordonate suprafata ARSB, care trebuie sa fie nula , pct. fiind colineare.
se masoara unghiurile
se calculeaza orientarile dreptelor din coordonate
se calculeaza orientarile directiilor din pct. noi R si S
Coordonatele pct. noi R si S rezulta din intersectarea dreptelor corespunzatoar; 1R cu 2R respectiv 3S cu 4S;
Drept control pct. A,R,S si B trebuie sa fie colineare respectiv suprafata inchisa sa fie nula.
73. Intersectia liniara.
Pct. de coordonate cunoscute : A( XA,YA); B(XB,YB) ;
Masurat in teren : DAP ; DBP ;
Distantele pot fi masurate din pct. vechi spre pct. nou sau din pct. nou spre pct. vechi.
Se considera un cerc circumscris triunghiului ABP cu diametrul AB. Procedeul devine tot mai inexact cu cat pct. P se afla mai aproape de baza AB. Se remarca ca pct. P poate fi in stanga sau in dreapta bazei AB, rezolvarea matematica fiind acceasi.
Calcule :
Ptr. control trebuie sa fie indeplinite relatiile:
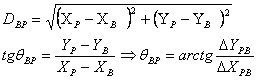
Se poate verifica in functie de semnul unghiului b, daca pct. este in stanga sau in dreapta bazei.
b qBP - qBA
In cazul in care s-a masurat suplimentar distanta DAB Intre pct. vechi, se poate calcula factorul de scara
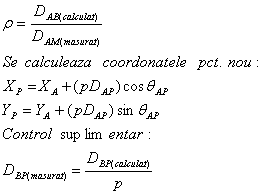
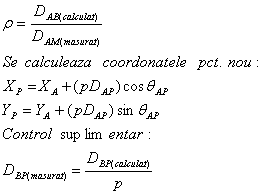
Transmiterea la sol a punctelor de triangulatie si indesire
Cazul cand punctele sunt stationabile- principiu. Sa presupunem ca avem un punct de triangulatie ,,P" de coordonate cunoscute situat pe terasa unei cladiri. Avem posibilitatea sa facem statie cu teodolitul in acest punct. Din acest punct P se observa inca cel putin 1-2 pct. de triangulatie mai indepartate. Pentru ca acest pct. sa serveasca la inchiderea drumuirilor, el trebuie transmis la sol. Se efectueaza urmatoarele operatii de teren:
-Se aleg la nivelul terenului punctele 1, 2, 3 astfel incat ele sa formeze cu punctul P doua triunghiuri aproximativ echilaterale si se borneaza aceste puncte;
Se stationeaza cu teodolitul in punctul P, in pct. 1, 2, 3 si se masoara cu precizia corespunzatoare indesirii triangulatiei, unghiurile;
Se masoara cu precizia corespunzatoare laturile celor doua triunghiuri;
La birou efectuam urmatoarele operatii:
Se determina in valorile lor orizontale, distantele prin aplicarea tuturor corectiilor( tensiune, etalonare, temperatura si reducere la orizont).
Se compenseaza unghiurile in cele doua triunghiuri- in triunghiul I sunt unghiurile masurate
a b g1' - 200g = W1
in triunghiul II unghiurile a b g2' - 200g = W2
ptr. Control
Se calculeaza orientarile din coordonatele pct. vechi;
Se calculeaza orientarile de la pct. P spre cele trei puncte de la sol;
Cu teorema sinusurilor se calculeaza lungimile laturilor;
Se calculeaza coordonatele pct-lor 1, 2, 3 prin radiere din P'(x, y);
Ca verificare trebuie sa gasim din coordonatele calculat e aceleasi distante;
74. Transmiterea la sol a pct. de triangulatie - cazul cand pct. sunt stationabile - principiu - de la Curs
Avem un pct. P de coordonate cunoscute.
Se materializeaza la sol 3 pct. astfel incat sa se formeze 2 triunghiuri aproximativ echilaterale.
Ptr. rezolvarea problemei e necesar sa vedem din pct. P minim 2 pct. de coordonate cunoscute.
Se dau : X,Y, ptr. P,A,B
Se cer : X,Y ptr. 1,2,3
Pe teren se stationeaza cu aparatul deasupra pct. P si vizam pe rand pct. A,1,2,3,B catre fiecare in parte masurand directiile unghiulare orizontale.
Se stationeaza pe rand in pct. noi 1,2,3 si masuram din fiecare pct. in parte directiile orizontale unghiulare catre pct. P si catre celelalte pct. noi, deasemeni vom masura si distantele intre pct. noi de la 1 la 2 si de la 2 la 3.
Calcule :
- Aplicam teorema sinusurilor in triunghiul 12P si in triunghiul P23
- Calculam orientari
- Verificare finala o facem calculand distanta D1 si D2 din coordonatele nou obtinute.
75. Transmiterea la sol a pct. de triangulatie si indesire - cazul cand pct. sunt nestationabile. Elemente cunoscute : coordonatele pct. P, T1, T2;
Elemente masurate :
Calculul unghiurilor g
Calculul lungimii laturilor triunghiurilor;
Calculul unghiurilor d
Calculul distantelor din coordonate;
Calculul orientarilor spre pct. noi;
Calculul coordonatelor pct. 1,2,3 ;
Control .
76. Transcalcularea geometrica - principiu.
Cand avem pct. de drumuire ptr. care se cunosc coordonatele intr-un sistem oarecare, iar pe laturile de drumuire s-au facut ridicari echerice.
Se doreste ca pct. de detaliu ridicate echeric sa obtina coordonate rectangulare in acelasi sistem cu drumuirea.
Avem 2 sisteme de axe de coordonateXOY si xoy.
Ptr, pct. 101 si 102 se cunosc coordonate din calculul si compensarea drumuirii A.B.
Ptr. pct. P1 se cunosc coordonatele echerice x si y.
Se cer coordonatele X1 si Y1 in sistemul in care a fost calculata drumuirea.
X1 = X0 + Y1 sina + x1 cosa Y1 = Y0 + y1 cosa - x1sina
X0 , Y0 - coordonatele originii
a - unghiul de rotatie a axelor de coordonate
x1, y1 - coordonate echerice ale pct. P1
X1, Y1, coordonatele topografice ale pct. P1 in sistemul drumuirii.
In cazul mai multor pct. vom avea a aI si se va lua media acestor valori egala cu unghiul mediu de rotatie al axelor.
c. Se calculeaza coeficientul mediu de deformatie. Calculand distanta din coordonatele topografice si geodezice intre aceleasi pct. vom avea :
![]()
Perechile de
distante nu sunt egale desi pe teren avem aceeasi distanta, ptr. ca :
pct. au fost determinate cu precizii diferite in cele 2 sisteme de axe de coordonate.
Datorita deformatiilor specifice sistemelor de proiectie, va trebui sa corectam coordonatele locale in asa fel incat sa obtinem distante egale cu cele obtinute din coordonate geodezice.
Aceasta corectare se face prin calcularea unui coeficient de mediu de deformatie cu care se inmultesc distantele din coordonatele sistemului local.
Se calculeaza mai multi coeficienti Ki obtinandu-se un coeficient Kmediu.
d.Calculul coordonatelor geodezice ale originii o a sistemului local . Coordonatele locale se inmultesc cu K( Kmediu)
Ptr. fiecare pct. cu coordonate duble va corespunde o pereche de coordonate Xo, Yo ale sistemului local
Se va lua media ptr. aceste coordonate Xo (mediu) si Yo(mediu)
d. Calculul coordonatelor geodezice ala pct. din sistem local
Se poate face calculul in serie din pct. in pct.
e. Calculul simplificat al coeficientilor Ksina si Kcosa
Ptr. fiecare pereche de pct. cu coordonate duble se obtin valori apropiate ptr. coeficienti K sin a si Kcosa, iar ptr. transcalculare se ia media acestora.
78. Transcalulari utilizand Teoria celor mai mici patrate.
Consideram n pct. de coordonate cunoscute in ambele sisteme XOY si xoy.
Presupunem ca mai avem j pct. care au coordonate numai in sistemul xoy si dorim sa determinam coordonatele acestor pct. in sistemul XOY. Pornind de la coordonatele de transcalcul cunoscute:
X = Xo + xKcosa + yKsina
Y = Yo + yKcosa - xKsina
Formulele pun in evidenta rototranslatia si coeficientul de scara.
K cosa = a ; K sina = b ; X0 = c ; Y0 = d ;
X = ax + by + c
Y = - bx + ay + d
In sistem avem 4 necunoscute deci la limita este nevoie de 2 pct. comune carev genereaza 4 ecuatii. Daca avem mai mult de 2 pct. comune atunci valorile a,b,c,d se deduc prin metoda celor mai mici patrate.
79. Aspecte privind precizia interioara si exterioara a retelelor de sprijin.
Eroarea medie a pct.
![]()
este o masura
a preciziei care este cel mai adesea preferata ptr. retelele de sprijin.
Ea descrie printr-o cifra precizia determinarii unui pct. si este univoc determinata, ea nemodificandu-si valoarea in cazul transformarilor spre deosebire de erorile medii mx si my ala coordonatelor.
In compensarile retelelor prin metoda observatiilor indirecte aceste erori se calculeaza ptr. fiecare pct. coeficienti de pondere Qxx si Qyy ptr. pct. noi se gasesc pe diagonala principala a matricei de cofactori.
In multe domenii, retelele de sprijin locale sunt prelucrate ca retele libere. Aici nu sunt pct. de sprijin vechi, neeronate, care sa determine originea, orientarea si factorul de scara.
Fiecare pct. din retea este considerat ca pct. nou.
In retelele libere se pot calcula eroriile medii ptr. toate pct. retelei.
Erorile medii de determinare al apct. in aceste retele sunt semnificativ mai mici decat intr-o retea constransa cu aceasi configuratie.
Erorile medii ale pct. cresc atunci cand se reduce nr. pct de constrangere , iar cand aceste constrangeri dispar in retea , erorile pct. devin brusc semnificativ mai mici.
a. Semnificatia geometrica a erorilor medii ala pct. in retele constranse .
In retelele constranse, ptr. eroarea unui pct. nou mp se pot da 2 explicatii:
- prima rezulta din diferenta coordonatelor dintre un pct. vechi si pct. nou.
Eroarea medie mPi a unui pct. nou este egala cu radicalul sumei erorilor medii patratice a diferentelor de coordonate dintre pct. Pi si un pct. vechi oarecare.
- cea de a doua semnificatie rezulta din legatura dintre un pct. vechi si pct. nou considerat exprimata prin coordonate polare DAi si qAi
Eroarea medie totala mPi este obtinuta ca fiind radical din suma erorilor distantei si orientariidintre pct. nou I un pct. vechi oarecare.
b. Semnificatia geometrica a erorii medii a unui pct. intr-o retea libera.
Semnificatia geometrica de la pct. a . nu se mai poate folosi neavand pct. vechi.
Eroarea medie a altitudinii unui pct. nou mHi intr- o retea libera este egala cu eroarea medie a dif. de nivel intre pct. respectiv si centrul de greutate a tuturor pct. din retea.
Retele planimetrice.
Intr-o retea planimetrica libera, eroarea medie mPi a unui pct. este egala cu radical din suma patratelor erorilor medii a cresterilor de coordonate dintre pct. considerat si centrul de greutate al retelei sau cu radical din suma patratelor erorilor distantei si a orientarii dintre pct. considerat Pi si centrul de greutate.
Concluzii :
eroarea medie totala a unui pct.are semnificatii total diferite in retele constranse si in retelele libere desi forma de exprimare este aceeasi;
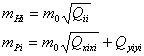
in retelele cu aceeasi configuratie prelucrate ca retea constransa si libera, comparatii intre erorile medii totale nu au sens, ele au semnificatii geometrice diferite ;
ptr. a scoate in evidenta aceasta deosebire mp este denumita in retelele constranse eroare medie exterioara a pct., iar in retelele libere eroare medie interioara a pct. ;
pe langa preciziile pct. in retelele locale se mai prezinta si precizia intregii retele, ptr. aceasta se foloseste media patratica a tuturor erorilor pct. np din retea :
comparatii intre aceste 2 marimi nu au sens, ele au semnificatii geometrice total diferite.
|