MISCARILE SATELITILOR ARTIFICIALI AI PAMINTULUI

MISCÃRILE SATELITILOR ARTIFICIALI AI PÃMÎNTULUI

11.1. NOÞIUNI GENERALE

Miºcãrile sateliþilor artificiali ai Pãmîntului sînt studiate în cadrul disciplinei cosmonauticã sau astrodinamicã, pe baza unor calcule foarte precise de mecanicã cereascã. Lansarea primului satelit artificial al Pãmîntului "Sputnik", a însemnat o nouã posibilitate, o nouã cale deschisã pentru umanitate, pentru explorarea spaþiului extraterestru.

Sateliþii artificiali, figura 11.1, au contribuit la rezolvarea unor problemele legate de:

-Conducerea navelor maritime ºi a aeronavelor spaþiale, pe cãile maritime sau aeriene de comunicþii.

-Determinarea poziþiei acestora ºi a elementelor de miºcare, cum sînt: viteza, acceleraþia, direcþia de deplasare.

-Avertizarea navelor asupra situaþiilor de avarie, catastrofe, determinarea poziþiei unde s-a produs aceasta ºi declanºarea acþiunilor de salvare.

-Extinderea comunicaþiilor ºi a transmisiunilor la mari distanþe, transmiterea informaþiilor meteorologice permanent, prevenirea echipajelor despre apariþia unor fenomene meteorologice sau hidrologice periculoase.

-Cercetarea suprafeþei terestre.

-Explorarea zonelor mari 949n1321j time, etc.

Folosirea sateliþilor artificiali porneºte de la o serie de proprietãþi ale acestora, cum sînt:

-acoperirea globalã,

-acþiunea rapidã,

-probabilitate mare de determinare a parametrilor de navigaþie cu erori mici, în orice zonã terestrã, indiferent de poziþia ºi timpul de miºcare a navelor maritime sau a aeronavelor,

-rezolvarea problemelor de navigaþie în orice fel de condiþii meteorologice, ziua sau noaptea, cu o mare precizie ºi într-un timp foarte scurt.

Pentru îndeplinirea acestor proprietãþi sistemul de navigaþie prin sateliþi artificiali, este alcãtuit din urmãtoarele pãrþi componente:

-Reþea de sateliþi artificiali, care evolueazã pe traiectorii calculate, dotaþi cu echipamente ºi aparate speciale.

Fig.11.1.

-Reþea terestrã de observare, unde se determinã informaþiile necesare pentru calculul efemeridelor sateliþilor de navigaþie.

-Centru terestru de calcul ºi monitorizare.

-Serviciu de timp care determinã momentul efectuãrii mãsurãtorilor cu mare precizie ºi transmite la bordul sateliþilor semnale de timp codificate.

-Reþea de mijloace de radiocomunicaþii, care asigurã transmiterea informaþiilor între sateliþi ºi elementele complexului terestru de navigaþie.

-Receptoare de radionavigaþie, care primesc informaþiile de la sateliþi, dispuse la bordul navelor maritime ºi aeronavelor.

Sateliþii artificiali utilizaþi în navigaþie se clasificã astfel:

1).Dupã caracterul acestora:

-Sateliþi pasivi, care nu au la bord aparaturã, aceºtia reprezintã un simplu mediu reflectant al undelor radio transmise de la sol.

-Sateliþi activi, care sînt dotaþi cu aparaturã de prelucrare a semnalelor, de orientare în spaþiu ºi de executare a comenzilor primite de la sol.

2).Dupã modul de transmitere a informaþiilor, sateliþii se clasificã astfel:

-Sateliþi cu rãspuns în timp real, atunci cînd staþiile de la sol asigurã vizibilitatea continuã a satelitului.

-Sateliþi cu memorie (cu rãspuns întîrziat), atunci cînd pe anumite porþiuni ale traiectoriei, acesta nu este vizibil de la sol ºi este necesar sã înregistreze toate informaþiile, pe care sã le transmitã ulterior.

3).Dupã forma traiectoriei, sateliþii pot sã aibã:

-Orbitã circularã, de aici rezultînd o miºcare circularã.

-Orbitã elipticã, de aici rezultînd o miºcare elipticã.

4).Dupã valoarea unghiului de înclinare a orbitei satelitului (i), faþã de Ecuatorul terestru, în funcþie de valorile acestui unghi, avem:

-pentru i = 0 , sateliþi ecuatoriali,

-pentru i = 90 , sateliþi polari,

-pentru valorile înclinãrii cuprinse între 10 , sateliþi obiºnuiþi.

5).Din punct de vedere al altitudinii, sateliþii se clasificã astfel:

-Sateliþi de joasã altitudine, pentru altitudini cuprinse între 1.000 ÷ 5.000 km.

-Sateliþi de medie altitudine, plasaþi între 5.000 ÷ 20.000 km.

-Sateliþi de mare altitudine, plasaþi între 20.000 ÷ 35.800 km.

Problemele principale ale sateliþilor artificiali ai Pãmîntului sînt urmãtoarele:

-lansarea ºi plasarea pe orbitã,

-funcþionarea satelitului,

-menþinerea legãturilor cu centrul de comandã de la sol,

-utilizarea acestuia pentru rezolvarea problemelor de navigaþie maritimã sau aerianã, comunicaþii, cercetare ºtiinþificã, explorarea spaþiului extraterestru, etc.

Dupã plasarea acestuia pe orbitã este foarte importantã studierea urmãtoarelor elemente, astfel:

-miºcarea neperturbatã a satelitului,

-perturbaþiile elementelor orbitale ale sateliþilor artificiali.

Pentru definirea parametrilor de lansare ai unui satelit artificial se considerã Pãmîntul ºi traiectoria elipticã a acestuia, figura 11.2. Studiul porneºte de la momentul plasãrii satelitului pe orbitã, al începutului miºcãrii de inerþie, pe baza soluþiei problemei a douã corpuri, care se atrag reciproc.

Astfel se considerã:

-T = centrul Pãmîntului.

-M = masa Pãmîntului.

-R = raza Pãmîntului.

-S_o = punctul iniþial de lansare.

-a = semiaxa mare a orbitei satelitului.

-Hs = înãlþimea punctului S_o, mãsuratã de la suprafaþa Pãmîntului.

Fig.11.2

Formula de calcul a distanþei de la centrul Pãmîntului, pînã la punctul iniþial de lansare, este urmãtoarea:

TS_o = r_o = R + Hs  (11.1)

-v_o = viteza iniþialã de lansare a satelitului (viteza cosmicã).

a = unghiul TS_ov_o, format între r_o ºi v_o.

-S = poziþia la un moment dat "t".

-A = poziþia apogeului orbitei satelitului.

-P = poziþia perigeului orbitei satelitului.

j = unghiul S_oTS, format între poziþiile S_o ºi S ale satelitului.

j_o = unghiul S_oTP, format între poziþiile S_o ºi P

Parametrii: H, v_o ºi a reprezintã condiþiile iniþiale sau parametrii de lansare pe orbitã ai corpurilor cereºti artificiale. Conform soluþiei matematice a problemei celor douã corpuri rezultã:

r = (11.2)

p = , (11.3)

e = , (11.4)

m = G M = 398.600 km³/ s²  . (11.5)

Elementele formulelor sînt urmãtoarele:

-r = raza vectoare.

-p = parametrul.

-e = excentricitatea orbitei.

m = parametrul gravitaþional al Pãmîntului.

-m = masa satelitului, care este neglijabilã în raport cu Pãmîntul.

-c = constanta ariilor.

-h = constanta energiilor.

În funcþie de viteza cosmicã, obiectul lansat poate sã fie:

-satelit, cu miºcarea pe cerc sau pe elipsã,

-navã interplanetarã, cu miºcarea pe parabolã sau pe hiperbolã.

11.2. MISCAREA CIRCULARÃ A SATELITULUI

Dacã în punctul S_o, viteza are valoarea primei viteze cosmice, care se obþine prin formula vitezei circulare (11.6) ºi de direcþia vitezei, care este situatã în planul orizontal al punctului S_o, unde: a p

vⁱ_o = (11.6)

În aceste condiþii obiectul lansat devine satelit artificial, care se va deplasa pe o orbitã circularã. Cu ajutorul formulei (11.6) se determinã faptul cã prima vitezã cosmicã descreºte cu înãlþimea. Pe baza acestei formule s-a întocmit tabelul 11.1.

TABELUL 11.1

Perioada de revoluþie sideralã a satelitului în miºcarea circularã se determinã cu ajutorul formulei (11.7).

T = [ 2p (R + H)] / vⁱ_o, (11.7)

Un satelit ipotetic care s-ar miºca la suprafaþa Pãmîntului (H = 0), adicã satelitul cu parametrii orbitali v_o = 7,91 km/s ºi T = 1,41 ore, se numeºte "satelitul zero" al Pãmîntului, iar valoarea de 7,91 km/s, reprezintã prima vitezã cosmicã.

Satelitul lansat la o înãlþime H = 35.870 km, care are parametrii orbitali urmãtori: v_o = 3,07 km/s ºi T = 24,00 ore, se numeºte satelit geostaþionar al Pãmîntului sau satelit geostaþionar. Acest satelit este denumit astfel datoritã faptului cã valoarea perioadei de revoluþie este egalã cu perioada de rotaþie a Pãmîntului ºi avînd înclinarea i = 0 , se vede nemiºcat de cãtre un observator terestru aflat la Ecuator.

În figura 11.2 este prezentatã proiecþia pe sfera cereascã a orbitei circulare a satelitului artificial al Pãmîntului, iar elementele de miºcare ale acestuia sînt studiate faþã de un sistem de referinþã Txyz.

Fig.11.2

11.3. MISCAREA ELIPTICÃ A SATELITULUI

ARTIFICIAL

Datoritã dificultãþilor de ordin tehnic, de realizare practicã a sateliþilor artificiali care sã evolueze pe o orbitã circularã, s-au realizat sateliþi care evolueazã pe orbite eliptice. Pornind de la condiþia (11.8):

v_o < , (11.8)

Folosind formula vitezei parabolice, se obþine ce-a de-a doua vitezã cosmicã, pentru înãlþimea H, denumitã ºi viteza de eliberare din apropierea Pãmîntului (11.9):

vⁱⁱ_o = = vⁱ_o,  (11.9)

Valoarea acestei viteze la suprafaþa terestrã, la H = 0, este: vⁱⁱ_o = 11,2 km/s.

Perioada de revoluþie a satelitului artificial pe elipsã, se obþine din legea a-III-a a lui Kepler, cu ajutorul relaþiei (11.10):

T = = 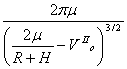, (11.10)

Miºcarea satelitului pe o orbitã elipticã se studiazã în raport cu un sistem de referinþã Txyz, al cãrui plan fundamental coincide cu planul Ecuatorului terestru, axa Tx fiind orientatã spre punctul vernal, figura 11.3. Dacã un obiect lansat în punctul S_o are o vitezã v_o > v^II_o, miºcarea se va efectua pe parabolã sau hiperbolã, iar obiectul se transformã în navã interplanetarã.

Fig.11.3

11.4. PERTURBAÞIILE ELEMENTELOR ORBITALE ALE SATELIÞILOR ARTIFICIALI AI PÃMÎNTULUI

Principalele perturbaþii care fac ca orbita realã a satelitului artificial al Pãmîntului sã fie mult mai complicatã, decît cea Keplerianã (neperturbatã), sînt urmãtoarele:

-Necentralitatea (anomaliile) cîmpului gravitaþional terestru, datoritã în principal turtirii Pãmîntului la poli.

-Rezistenþa atmosferei terestre.

-Forþele luni-solare, adicã acþiunea gravitaþionalã a Soarelui ºi Lunii.

-Presiunea radiaþiei solare.

-Alte cauze.

a).Efectul turtirii Pãmîntului la poli, adicã umflãtura ecuatorialã, este cauza cea mai importantã, care perturbã miºcarea satelitului. Considerînd cã satelitul se aflã în planul ecuatorial, la o înãlþime de 230 km, faþã de sol, adicã 6.608 km faþã de centrul Pãmîntului, acceleraþia perturbatoare datoratã turtirii Pãmîntului este de 1,40 cm/s², fiind de 656 de ori mai micã decît acceleraþia principalã, din cauza atracþiei terestre de la aceastã înãlþime,care este de 914 cm/s².

Aceastã perturbaþie se manifestã prin urmãtoarele fenomene:

-precesia orbitei satelitului,

-deplasarea liniei apsidale a orbitei.

1).Precesia orbitei satelitului reprezintã rotaþia planului satelitului în jurul axei polilor tereºtrii, în sens opus miºcãrii satelitului pe orbitã, figura 11.4. De aici rezultã o descreºtere a longitudinii nodului ascendent (W), dacã i < 90 , , înclinarea orbitei satelitului rãmîne constantã faþã de Ecuatorul terestru.

2).Deplasarea liniei apsidale sau deplasarea perigeului orbitei satelitului, în planul orbitei, avînd drept consecinþã creºterea sau descreºterea longitudinii perigeului (w), figura 11.5. Deplasarea perigeului este:

-maximã, pentru i = 0 ºi 180

-minimã, pentru i = 63

Înclinarea perigeului la valoarea lui i = 63 .₄, se numeºte înclinare criticã.

-pentru valorile lui i < 63 .₄, perigeul se deplaseazã pe orbitã în acelaºi sens cu miºcarea satelitului.

-pentru valorile lui i > 63 .₄, perigeul se deplaseazã în sens opus miºcãrii satelitului.

Pe baza determinãrilor fãcute pentru cunoaºterea perturbaþiilor sateliþilor artificiali ai Pãmîntului, datoritã necentralitãþii cîmpului gravitaþional terestru, s-au obþinut valori numerice foarte precise pentru turtirea Pãmîntului ºi pentru valorile cîmpului gravitaþional terestru.

Fig.11.4 Fig.11.5

b).Rezistenþa atmosferei terestre. Aceasta are un caracter diferit faþã de cel al turtirii Pãmîntului. Perturbaþia este cauzatã de ciocnirile dintre satelit ºi moleculele atmosferei terestre, avînd ca efect frînarea sau încetinirea miºcãrii satelitului în atmosfera terestrã. Teoretic, în zonele în care sînt plasaþi sateliþii artificiali, nu mai existã atmosferã, dar datoritã unor cauze complexe ºi în special furtunilor terestre, masele de aer ajung la altitudini foarte mari.

Acest fenomen se manifestã în special în zona perigeului orbitei, unde atmosfera este mai densã, astfel cã dupã fiecare trecere pe la perigeu, înãlþimea apogeului scade, dar înãlþimea perigeului rãmîne aproape constantã. Dimensiunile orbitei iniþiale eliptice se reduc, orbita se apropie de una circularã, elementele orbitale "a" ºi "e", descresc proporþional cu timpul, figura 11.6.

În acelaºi mod descreºte ºi perioada miºcãrii de revoluþie a satelitului artificial, pînã la o valoare criticã de cca. 87 de minute, dupã care satelitul intrã în straturile dense ale atmosferei, la cca.100-150 km, unde se încãlzeºte datoritã frecãrii cu aerul ºi apoi se dezintegreazã.

DEFINIÞIE: Durata miºcãrii satelitului artificial, din momentul plasãrii pe orbitã, pînã la

frînarea totalã în straturile dense ale atmosferei terestre, se numeºte

"durata vieþii" satelitului artificial al Pãmîntului.

De aici rezultã faptul cã, cu cît este mai înaltã orbita iniþialã a satelitului, cu atît este mai mare durata vieþii acestuia. Cunoaºterea perturbaþiilor sateliþilor artificiali, datoritã frînãrii atmosferice, oferã posibilitatea calculãrii densitãþii aerului la înãlþimile de deplasare ale acestora.

c).Forþele luni-solare, adicã acþiunea gravitaþionalã a Soarelui ºi Lunii, provoacã perturbaþii ale orbitelor sateliþilor artificiali, mai ales la sateliþii care au anumite caracteristici, cum sînt:

-excentricitãþi foarte mari ale orbitelor,

-mase mici ºi suprafeþe foarte mari (ale panourilor solare).

d).O altã cauzã a perturbaþiilor este datoratã presiunii radiaþiei solare, în special la sateliþii care au panouri solare cu suprafeþe mari.

Fig.11.6