Adsorbtia pe suprafete solide - Adsorbtia gazelor pe solide

Adsorbtia pe suprafete solide

Adsorbtia gazelor pe solide

Adsorbtia este fenomenul datorat fortelor de atractie exercitate de solid asupra moleculelor de gaz, ce au drept consecinta cresterea concentratiei moleculelor de gaze pe solid fata de interiorul gazului.

Adsorbtia este favorizata de presiuni ridicate si de temperaturi scazute si este de doua tipuri:

  Caracteristici:

- Adsorbtia fizica - temperaturi (T) mici

  - process reversibil

- caldura de adsorbtie mica 5 – 10 Kcal./mol

  - forte de interactiune Van der Waals intre gaz si solid (slabe)

  - process instantaneu

  - nespecific

  - exoterm

- Adsorbtia chimica - temperaturi mari – necesita energie de activare

  - process ireversibil

  - caldura de adsorbtie 10 – 100 kcal/mol

  - forte de atractie mari – legaturi chimice

  - proces exoterm

  - specific

Ecuatii ce descriu fenomenul de adsorbtie

Ec. FREUNDLICH

Ecuatie empirica ce da variatia adsorbtiei cu presiunea sau concentratia.

  = a*p1/n (1)

x = masa de gaz (moli)

m = masa de support (g)

p = presiunea de echilibru (atm)

a,n = constante ce depend de natura gazului si a solidului si se determina graphic./

Prin logaritmarea ec.(1) rezulta:

lg= lg a lg p (2) si rezulta a si n din grafic

lg    tg =

lg p

lg a 

Testarea valorilor experimentale

Daca valorile experimentale nu se inscriu pe dreapta data de ec.(2) rezulta ca nu e respectata ec.(1) FREUNDLICH .

  T = ct.

2) Ec. LANGMUIR   ----- ----- -----------

 

(3)

  p

a,b = constante pentru un anumit sistem si temperatura

Ecuatia (3) e stabilita considerind ca adsorbtia se face pina la o valoare limita corespunzatoare unui strat monomolecular de gaz pe suprafata S a adsorbantului.

La:

- p mici b*p<< 1(3’) = a*p (portiune liniara crescatoare)

- p mari b*p>> 1(3”) === ct.

= adsorbtia limita corespunzatoare formarii stratului monomolecular

Deci:

== =

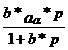si = (3’’’)

Testarea datelor experimentale si aflarea constantelor a si b:

Din (3) ; =

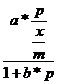
= =+*p

= +*p (4) =

Din (3’’’) = ; =

= = + *p

= + *p (5) a = *b

Din grafic:

  tg = =

 

= 

  p

Ec. (3’’’) se utilizeaza si sub forma :

(6)

= volumul corespunzator stratului adsorbit monomolecular.

Din (6) = = + (7)

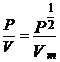sau + (8)

unde P^1/2 = presiunea corespunzatoare la V =

3) Ec. BRUNAUER, EMMET, TELLER (B.E.T.)

Considera ca adsorbtia se face in strat multimolecular.

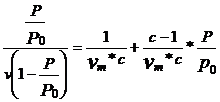(9), unde:

v = volumul de gaz adsorbit pe unitatea de masa de support la presiunea p

v_m = volumul de gaz adsorbit cind suprafata e acoperita cu un strat monomolecular

c = constant ace depinde de adsorbant

p = presiunea de lucru

p₀ = presiunea vaporilor saturanti

(10) unde E_m = caldura de adsorbtie la formarea v_m

  Ec = caldura de condensare a gazului in lichid

Din reprezentarea grafica, din panta dreptei si intercept v_m si c

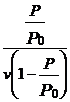
tg =

   

 

 

Putem calcula nr. de molecule adsorbite in stratul monomolecular :

=*N_A unde, N_A = numarul lui Avogadro; V_M = volum molar,

Notind= sectiunea eficace (suprafata ocupata de 1 molecula adsorbita) putem calcula suprafata de adsorbtie a suportului solid :

S = *N_A* (11)

4) Izostere de adsorbtie

Se obtin din reteaua de izoterme si constau in reprezentarea intr-o diagrama a variatiei P = f(T) la adsorbtie constanta (= const.)

  ₂>₁ 

    P 

  T₁<T₂<T_{3   2}

  T₁ = ct.

  T₂ = ct   ₁ 

 

T

  T₃ = ct  

P₁ P₂ P₃

P₁, T₁; P₂,T₁; P₃, T₃ .

(*) Se observa ca avem o variatie identica cu variatia presiunii de vapori a lichidelor cu temperatura ( ec. Clausius – Clapeyron).

Facind reprezentarea in coordonate log p = f se obtine:

lg P

lg P₂ ----- ----- ------

  tg = - tg(180 -) = Qa < 0

    (caldura de adsorbtie diferentiala)

lg P₁

 

Caldura de adsorbtie poate fi diferentiala sau integrala si este functie de gradul de acoperire al adsorbantului.

Pornind de la starea in care pe toata suprafata S (respectiv m grame adsorbent) se gasesc moli de substanta adsorbita si se mai adsorb dmoli in urma cresterii diferentiale a presiunii gazului, caldura diferentiala de adsorbtie este:

Qa = (12) , unde q = cantitatea totala de caldura masurata.

Caldura integrala de adsorbtie corespunde la o adsorbtie de moli de gaz pe o suprafata initial goala:

= d (13)

La echilibrul care se stabileste intre gazul_(liber) gazul_(adsorbit) trebuie sa avem :

= (14)

= potentialul chimic al gazului adsorbit

= potentialul chimic al gazului liber

= f ( T, ) (15) ; = f(T, P) (16)

Trebuie sa avem : d= d (17)

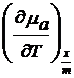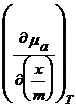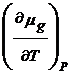dT + d() = dT + 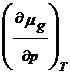dP (18)

dar = ct. ; d() = 0

Pentru un singur component gazos = G (19) si = -S (20) iar G = H –T*S (21).

Din (20) si (21) = -S = (22)

(18) devine:

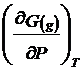-= * (19)

dar din (14) =    

si din (19) = G = ; iar =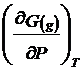

Deci (19) devine - = * (20)

Dar - = (21) si (20) rezulta:

  = - (22)

= caldura de adsorbtie si din cauza conditiei = ct., caldura diferentiala partial molara de adsorbtie, sau :

  = = constant (23)

sau formula integrata :

P₂> P₁ T₂ > T₁ < 0

Ec. (24) este similara ec. Clausius – Clapeyron pentru echilibrul LV aplicata pentru condensare.

ln P

ln P₂ ----- ----- ------

  tg = - tg(180 -) = Qa/RT

    Qa < 0

ln P₁ -------- ----- ------ ---------- fenomen exoterm deoarece in  cadranul II tg < 0

 

   

 

5) Izobare de adsorbtie

La p = ct. adsorbtia scade cu cresterea temperaturii (T) si anume in prima aproximatie exponential (graficul = f (T))

 

 

  P₂ > P₁

  P₂ = ct.

P₁ = ct.

  T

Se pleaca de la ecuatia (17) in care in acest caz dp 0 si rezulta :

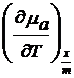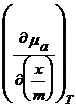dT + d() - 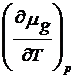dT = 0 (25)

Trebuie gasita valoarea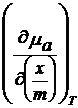

Se considera ca substanta (gazul) se comporta ideal:

= ⁰ + RT*ln() (26)

si 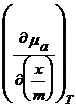= (27) si rezulta din (27) :

= (28)

Ec.(28) este similara ec. Clausius – Clapeyron pentru vaporizare sau izobarei de reactie van’t Hoff.

Daca se presupune ca nu depinde de T si (aproximatie grosolana pe un interval larg de temperatura) rezulta :

ln = - + const.

sau prin integrare :

ln = 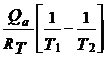(30)

Qa < 0 ca adsorbtia scade cu cresterea temperaturii (T).Din reprezentarea grafica se obtine Qa.

ln x/m

  tg = - Qa / R > 0 Qa < 0

ln (x/m)₂ -------- ----- ------ -

   

ln (x/m)₁ -------- ----- ------ ----------  

 

 

   

6) Adsorbtia din solutie pe suprafete solide

Respecta legea empirica a lui FREUNDLICH :

- la T = ct. = k* (31) , unde:

x = grame de substanta adsorbita

m = masa de adsorbant

C_ech = concentratia la echilibru

k,n = constante ce se determina din grafic

Testarea datelor experimentale si determinarea constantelor k si n:

Se logaritmeaza ec. (31) si rezulta:

lg = lg k + lg (32)

Ec. (32) se reprezinta grafic :

lg +

  + tg =

  +

  .

.

lg k

Daca punctele experimentale se inscriu pe o dreapta, este verificata ec. (32).

x se determina astfel :

x = (mol/l)* V(l) (33)

deci ec. (32) se mai poate scrie :

lg = lg k + lg (34)

unde V(l) = volumul solutiei in litri.