Matrici topologice
Dupa cum este bine cunoscut un graf chimic poate fi scris si sub forma unei matrici. Aceste matrici sunt de mai multe tipuri dintre care cele mai importante sunt : matricea de adiacenta, matricea distantelor etc. In cele ce urmeaza se prezinta explicit aceste matrici.
2.1. Matricea de adiacenta
Matricea de adiacenta reprezinta unul din cele mai importante moduri de codare a informatiilor structurale cuprinse intr-o molecula organica.
Elementele unei matrici de adiacenta (A(Gi)), aij, se definesc astfel [14, 49, 50] :

Se observa usor ca matricea de adiacenta este simetrica fata de diagonala principala. Valenta fiecarui varf este suma elementelor liniei sau a coloanei corespunzatoare varfului respectiv asa cum e descrisa in ec.(3) dar nu si in cazul legaturilor multiple.
![]()
in care n reprezinta numarul de varfuri si este egal cu ordinul matricii.
O relatie echivalenta cu cea anterioara este :
![]()
Matricea de adiacenta (A) contine toate informatiile necesare pentru a reconstrui un graf dar stocarea sa intr-un computer este impracticabila deoarece ocupa un spatiu prea mare [49]. Pentru a se evita utilizarea directa a lui A in literature de specialitate au fost raportate mai multe tipuri de coduri care usureaza stocarea intr-un computer si cu ajutorul carora se poate reconstrui matricea A. Cele mai importante coduri sunt: i)codul DAST [51] si codul de ,,granita''[52], coduri utilizate pentru codarea structurilor hidrocarburilor aromatice policiclice, ii)codul binar [53].
Pentru o mai usoara intelegere a constructiei matricii de adiacenta in Figura 17 este prezentata formula structurala, graful molecular specific si matricea de adiacenta pentru acidul D-lactic [54].
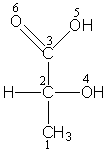

Figura 17 Formula structurala, graful molecular specific fara hidrogeni si matricea de adiacenta pentru acidul D-lactic
2.1.1. Versiunea compacta a matricei de adiacenta
Matricea de adiacenta este o matrice N×N simetrica care poate fi condensata intr-un numar binar (BIN) de N(N-1)/2 cifre. Numarul binar (BIN) poate fi transformat intr-un numar zecimal. BIN maxim este egal cu 2N(N-1) / 2 - 1 care in sistemul zecimal contine [N(N-1)/2·log2] + 1 ≈ [0.30· N(N-1)/2] + 1 cifre [49]. Pentru a construi versiunea condensata a acesteia se considera in partea superioara dreapta a lui A un triunghi ce contine doar 0 si 1 iar coloanele lui A pot fi exprimate ca un singur numar in sistemul binar. Pentru structura prezentata in Figura 18, numarul de intrari in BIN este N-1 si numerele zecimale corespunzatoare sunt BIN = (0, 1, 2, 0, 29, 6) [49].
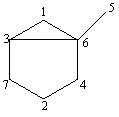
Figura 18. Structura utilizata ca exemplu in procesul de codare
Pentru structura prezentata in Figura 18, triunghiul superior al matricii de adiacenta A si codul binar (ultima linie separata ) sunt prezentate in Tabel 15315l1119p ul 1 [49, 53]. Valorile 0 cu exceptia diagonalei sunt omise pentru o mai buna intelegere a constructiei unei astfel de matrici.
Tabel 15315l1119p ul 1. Triunghiul superior al matricii de adiacenta A si codul binar (ultima linie separata ) pentru structura prezentata in Figura 18.
Informatiile continute in BIN sunt suficiente pentru a reface matricea A. Fiecare numar zecimal al lui A este transformat in echivalentul sau binar iar intrarile i ale lui BIN devin (i+1) coloane ale lui A. Conceptul de BIN este utilizat atat pentru grafurile aciclice cat si la cele ciclice. Matrice de adiacenta comprimata a fost utilizata cu succes si pentru codarea arborilor fizici [55, 56].
Valoarea minima in BIN este 0 iar valoarea maxima este 2i - 1 (i = 1, .., N-1). Aceste coduri BIN pot fi convertite intr-un singur numar A0. Pentru graful continand 7 varfuri (Figura 18, Tabel 15315l1119p ul 1) se obtine:
A0 = 64(32|16 + BIN(4)| + BIN(5)) + BIN(6) (5)
cu valoarea maxima pentru BIN: 26 = 64 si urmatoarele 25 = 32 etc.
A0 (6)
Pentru arborii fizici matricile de adiacenta pot fi codate printr-un vector linie numit matrice de adiacenta comprimata (CAM) [49]. CAM(i) este egal cu numarul de linii pentru ,,intrari'' diferite de 0 in (i+1) coloane ale lui A. Pentru usurinta calculelor a fost introdusa notatia prezentata in ecuatia 7 :
Xi = CAM (i+1) (7)
Pentru a exemplifica modul de codare BIN si CAM in Figura 19 este prezentat graful constitutional pentru 3-metihexan iar in ecuatiile 8 si 9 cele doua tipuri de codare.

Figura 19. Graful constitutional caracteristic 3-metihexanului
BIN: A0 = 16466887 (8)
0A = 6|5 + (X4 - 1)| + X5 - 1 (9)
Aplicand ecuatia 9 se obtine : 0A = 6|5 + (1-1)| + 6-1 = 7545. Procedeul de decodare a lui 0A = 7545 este prezentat in cele ce urmeaza:
(a) 545/6 = 90 (5) (b) 5+1 = 6 = X5 (c) 90/5 = 18 (0) (d) 0+1 = 1 = X4 (e) 18/4 = 4 (2)
(f) 2+1= 3 = X3 (g) 4/3 = 1 (1) (h) 1+1 = 2 = X2 (i) ½ = 0 (1) (j) 1+1 = 2 =X1
Dupa cum este bine cunoscut matricea de adiacenta si formele sale (forma compacta) precum si codarile acesteia au fost utilizate in multe studii QSAR /QSPR precum si la calculul de orbitali moleculari de tip Hückel [57].
2.2. Matricea distantelor
Pentru orice tip de graf un invariant important este reprezentat de matricea de distante D. Prin definitie elementele matricei D sunt reprezentate de cele mai mici cai (distantele dij) dintre oricare pereche de varfuri conectate [14, 18, 50, 58-68].
Istoria matricii D este succint prezentata de Mihalic [69] si tot Mihalic observa ca matricea de distante poate fi usor obtinuta din matricea de adiacenta [70], cu relatia :

unde Bi (G) reprezinta matricile care contin cele mai simple drumuri dintre vecinii de ordinul i. Ulterior F. S. Roberts construieste un algoritm similar [71] in timp ce Müller descrie un algoritm mai complex de constructie a matricii D din matricea de adiacenta A [72].
Pentru o mai usoara intelegere a constructiei matricei de distante in Figura 21 se prezinta formula structurala, graful constitutional si matricea de distante geometrice pentru 1-etil-2-metil-ciclopropan [62] respectiv 1-metil-2-propil-ciclobutan [64].
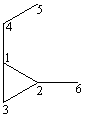
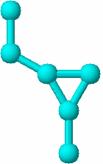

1-etil-2-metil-ciclopropan
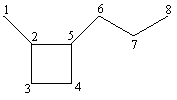
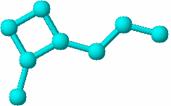

1-metil-2-propil-ciclobutan
Figura 21. Formula structurala, graful constitutional si matricea de distante pentru 1-etil-2-metil-ciclopropan respectiv 1-metil-2-propil-ciclobutan
O matricea de distante formala - care permite o descriere a structurii mai apropiata de chimie - se poate construi utilizand valorile propuse de Barysz si colaboratoriii acestuia [73]. In Tabel 15315l1119p ul 2 sunt prezentate valorile reale pentru cele mai uzuale legaturi intalnite in compusii organici precum si valorile legaturilor pentru izomerii de tip cis si trans (Figura 20) pentru care unghiul α dintre legaturi este de 1200 [65, 73].

Figura 20 Izomeri de tip cis si trans iar unghiul α dintre legaturi este de 1200
|
Tipul de legatura |
Distanta(dij) |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
|
Tabel 15315l1119p ul 2. Valorile celor mai uzuale legaturilor intalnite in compusii organici precum si ale izomerilor de tip cis / trans (Figura 20)
Pentru sisteme chimice mai complicate au fost dezvoltate o serie de programe pentru calculator care sunt capabile sa genereze matricile distantelor reale. Printre acestea doua din cele mai utilizate programe de mecanica cuantica capabile sa genereze o astfel de matrice se numesc MOPAC [74] respectiv WinMopac 7.21 [75].
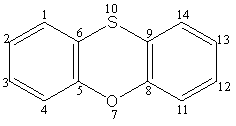
Pentru a obtine matricea de distante pentru fenoxatina, compus cu actiune antimicrobiala [76] , structura acestui compus este modelata cu ajutorul pachetului de programe Hyperchem [77]. Fisierul obtinut cu extensia .hin este transformat intr-un fisier cu extensia .mpn cu ajutorul programului BabelWin [78]. Pentru ca acest fisier sa poata fi utilizat de WinMopac sau Mopac, in scopul obtinerii matricei de distante se pot utiliza urmatoarele cuvinte cheie : THERMO ROT=1 GEO-OK mmok precise CHARGE=0 GNORM=0.1 BONDS VECTORS DENSITY a caror semnificatie se regaseste in referinta [74]. In Figura 22 sunt prezentate formula moleculara, graful constitutional si matricea de distante pentru fenoxatiina.
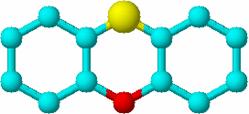
|
C1 |
C2 |
C3 |
C4 |
C5 |
C6 |
O7 |
C8 |
C9 |
S10 |
C11 |
C12 |
C13 |
C14 |
|
|
C1 | ||||||||||||||
|
C2 | ||||||||||||||
|
C3 | ||||||||||||||
|
C4 |
| |||||||||||||
|
C5 | ||||||||||||||
|
C6 | ||||||||||||||
|
O7 | ||||||||||||||
|
C8 | ||||||||||||||
|
C9 | ||||||||||||||
|
S10 | ||||||||||||||
|
C11 | ||||||||||||||
|
C12 | ||||||||||||||
|
C13 | ||||||||||||||
|
C14 |
Figura 22 Formula moleculara, graful constitutional si matricea distantelor reale pentru
fenoxatiina.
2.2.1. Transformarea matricilor de adiacenta in matrici de distante
Dupa cum s-a aratat in capitolul 2.2 in literature de specialitate exista o serie de lucrari care au ca subiect transformarea matricilor de adiacenta in matrici de distante [60, 70-72]. In esenta metoda de creare a matricilor D din matrici de adiacenta A este de a identifica un precedent adica un varf adiacent al unei muchii numerotate cunoscute si extinderea acestuia prin conexiunea prin intermediul unei alte muchii de varful imediat successor. Un exemplu concludent de constructie a matricei D din matricea A este prezentat in Figura 23 pentru 2-metilbutan si explicat in detaliu in referinta [60].
 Figura 23. Graful constitutional pentru
2-metilbutan (23a); matricea de
adiacenta A (23b); matricile de distante D
incomplete (23c, 23d); matricea de distante D completa (23e); graful 2-metilbutanului construit din matricea de adiacenta A (23f)
Figura 23. Graful constitutional pentru
2-metilbutan (23a); matricea de
adiacenta A (23b); matricile de distante D
incomplete (23c, 23d); matricea de distante D completa (23e); graful 2-metilbutanului construit din matricea de adiacenta A (23f)
Prima valoare necunoscuta din matricea D este a13 de la care se coboara in jos pana la valoarea 0 din diagonala principala. Miscarea orizontala spre stanga pana la valoarea a32 localizeaza varful imediat precedent pentru o muchie numerotata varf adiacent cu varful pentru care valoare necunoscuta este a13. Miscarea pe verticala are loc pana la primul vector orizontal identificat ca elemental a12 a carui valoare este 1. Varful caruia ii e caracteristica distanta a13 este adiacent cu varful caruia ii e caracteristica distanta a12. Suma valorilor a32 si a12 este 2, valoare care e atribuita lui a13. Deoarece matricile A si D sunt simetrice valoarea 2 pentru pozitia a13 este atribuita si lui a31. Valorile pentru a14 si a41 se determina in aceasi mod : i) a14 coboara vertical pana la a44; ii) a44 merge orizontal pana la a43 a varui valoare este 1; iii) a43 urca vertical pana la a13 a carui valoare este 2; iv) suma valorilor a43 si a13 reprezinta valoarea elementelor a14 si a41
(Figura 23, 23d). Valorile pentru a15 si a51 se determina in acealasi mod.
2.3. Matricea de distante reciproce
Pentru un graf molecular a fost definit un nou tip de matrice in care ponderea distantei dintre doi atomi descreste cu cresterea distantei globale [50, 79-81]. Acest nou tip de invariant se numeste matricea de distante reciproce. Pentru un graf G cu N varfuri matricea de distante reciproce RD(G) = RD este o matrice simetrica patrata N×N in care elementele (RD)ij sunt egale cu distanta reciproca intre varfurile i si j pentru elemente care nu se afla pe diagonala si egale cu 0 pentru elementele de pe diagonala.

In Figura 24 este prezentat graful molecular si matricea de distante reciproce in cazul 3-metilhexanului.
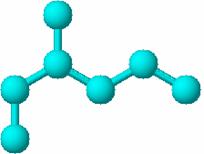

Figura 24. Graful molecular si matricea distantelor reciproce pentru 3-metilhexanului
Matricea RD a fost utilizata in constructia unor invarianti locali si indici topologici pentru codarea alcanilor [82, 83].
2.4. Matricea Detour
In anul 1969, F . Harary introduce in literatura matematica matricea Detour si matricea de distante pentru a descrie conectivitatea in grafurile directe [18] urmand ca mai tarziu cele doua matrici sa fie reamintite de catre Buckley si Harary in cartea despre conceptul de distanta in teoria grafurilor [84]. In literature chimica matricea Detour a fost introdusa in anul 1994 de catre Ivanciuc si Balaban [85] si independent in anul 1995 de catre Amic si Trinajstic [86].
In cazul uni graf G conectat (graful pentru care exista un drum intre fiecare pereche de varfuri ale sale), matricea Detour (G) este o matrice reala simetrica N×N in care valorile (i,j) sunt reprezentate de cea mai lunga cale dintre varfurile i si j [85-89].
Matricea Detour se poate defini utilizand ecuatia 12 :
![]()
unde lmax este cea mai lunga cale din graful G iar Bl este matricea auxiliara definita in ecuatia 13:

Pentru un graf complet matricea Detour are o forma foarte simpla in care elementele care nu se afla pe diagonala au valoarea egala cu gradul varfului iar elementele de pe diagonala sunt egale cu 0.
Asa cum s-a aratat in subcapitolul 2.2, distanta cea mai scurta dintre doua varfuri i si j se numeste distanta topologica (D)ij sau geodesica si reprezinta elemental principal pentru matricea de distante D [14, 18, 50, 58-68] iar distanta cea mai lunga dintre doua astfel de varfuri i si j se numeste distanta Detour ( )ij sau elongatie reprezinta elemental principal pentru matricea Detour [50, 85-89]. In ecuatiile 14 si 15 sunt definite din punct de vedere mathematic cele doua tipuri de matrici (D si

unde Ne, p(i,j) este numarul de muchii pe calea p(i,j) cea mai scurta /lunga.
In Figura 25 sunt prezentate comparative cele doua tipuri de matrici (D si ) pentru un graf ciclic [87].

25a 25b 25c
Figura 25. Matricile de distante (D, 25b) si Detour ( , 25c) pentru graful biciclic G (25a)
2.4.1. Polinomul si spectrul matricii Detour
Polinomul caracteristic pentru matricea Detour a unui graf G numit si polinom Detour, (G, x) se poate obtine cu ajutorul ecuatiei 16:
(G, x) = det |xI - (16)
unde I este o matrice simetrica N×N.
Coeficientii polinomului Detour se pot calcula cu ajutorul ecuatiei 17:
(G, x) = xN - c1xN-1 - .- cN-1x - cN = xN - n cnxN-n (17)
O cale mult mai usoara pentru calcului polinomului caracteristic este reprezentata de utilizarea metodei Le Verrier-Faddeev-Frame (LVFF) [90] modificata [91].
Pentru calculul coeficientilor cn se utilizeaza ecuatia 18 :
cn = (1 / n) i n)ii (18)
in care matricea diagonala ( n)ii este data de ecuatia 19 :
( n)ii = ( )ii(Bn-1)ii (19)
Bn este o matrice auxiliara si se poate calcula cu ajutorul ecuatiei 20:
(Bn)ii = ( n)ii - (cnI)ii (20)
In metoda LVFF pentru care n = N, ecuatia 20 devine:
(BN)ii = ( N)ii - (cNI)ii = 0 (21)
Pentru un graf complet cu N varfuri, polinomul Detour poate fi calculate cu ajutorul ecuatiei 22 :
π(KN ,x) = (x + d)N-1(x - d2) (22)
unde d reprezinta gradul unui varf in graful KN.
Mai multe detalii privind metode de calcul ale polinomului Detour se pot gasi in referintele [86, 87].
Spectrul pentru o matrice Detour, numit si spectru Detour contine un element pozitiv si N-1 elemente negative, aceasta distributie datorandu-se polinomului Detour si in principal a primului element din polinomul Detour care are semn negativ. Suma Elementelor din acest tip de spectru are valoarea 0.
Pentru grafurile ciclice prezentate in Figura 26, spectrul Detour este prezentat in Tabel 15315l1119p ul 3.
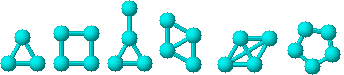
26a 26b 26c 26d 26e 26f
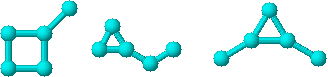
26g 26k 26l
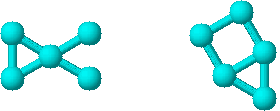
26m 26n
Figura 26. Grafuri ciclice pentru calculul spectrului Detour
|
Grafuri ciclice |
Spectrul Detour |
||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
|
|
26a | |||||
|
26b | |||||
|
26c | |||||
|
26d | |||||
|
26e | |||||
|
26f | |||||
|
26g | |||||
|
26k | |||||
|
26l | |||||
|
26m | |||||
|
26n | |||||
Tabel 15315l1119p ul 3. Spectrul Detour pentru grafurile ciclice prezentate in Figura 26
Balaban si Ivanciuc introduc in anul 1994 in literature de specialitate conceptul de matrice Detour / matricea distantelor [85] sau distanta maxima / distanta minima. Daca se combina triunghiul superior din matricea Detour cu cel inferior din matricea de distante se obtine o matrice Detour / Distanta ( / D) care este o matrice patrata N×N nesimetrica care poate fi definita astfel :

Pentru graful prezentat in Figura 25 (25a) matricea Detour / Distante [87] este prezentata in Figura 27.
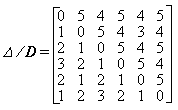
Figura 27. Matricea Detour / Distante pentru graful 25a prezentat in Figura 25
2.5. Matricea muchiilor adiacente
Matricea muchiilor adiacente a fost definita pentru prima data in literatura grafurilor chimice de catre D. H. Rouvray [92] si ulterior de catre N. Trinajstic [93]. E. Estrada descopera ca o serie de invarianti teoretici pentru un graf G, sursa importanta de noi descriptori moleculari, se pot obtine din matricea muchiilor adiacente [94]. Pentru un graf molecular G = (V, E) cu setul de varfuri V = si setul de muchii E = , matricea muchiilor adiacente are forma E = [gij]mxm [50, 92-97], in care m reprezinta numarul de muchii din graful G iar elementele gij sunt definite in ecuatia 24:
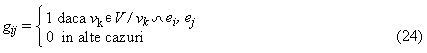
Cu alte cuvinte matricea muchiilor adiacente (E) este o matrice patratica simetrica in care elementele eij sunt egale cu 1 daca si numai daca muchiile i si j sunt adiacente si 0 in cazuri de neadiacenta [50, 92-97]. Gradul muchiilor (ek) se definesti cu ajutorul ecuatiei 25 [94]:
(ek) igik = jgjk (25)
Daca muchia ek este incidenta cu varfurile vi si vj atunci gradul muchiei ek poate fi exprimat cu ajutorul ecuatiei 26 [94]:
(ek) (vi) + (vj) (26)
Momentele spectrale pentru matricea E se pot defini cu ajutorul ecuatiei 27 [96-98]:
k k(G, E = tr(Ek) (27)
in care k(G, E reprezinta momentul spectral k pentru matricea E iar k este un exponent intreg.
2.6. Matricea Laplace
Pentru un graf G simplu matricea Laplace L =L(G) este o matrice reala simetrica si se defineste ca o matrice diferenta [50, 99-105] :
L = V - A (28)
unde A este matricea de adiacenta iar V este matricea de valenta (grad).
Matricea V este o matrice diagonala avant elementele definite cu ajutorul ecuatiei 29:
(V)ii = D(i) (29)
unde D(i) este gradul varfului i din graful G si se calculeaza dupa formula j(A)ij.
Matricea Laplace L =L(G) mai este numita intr-o serie de lucrari de specialitate matricea Kirchhoff [99], datorita rolului acestei matrici in Teorema Matricii Arbore (TMA), sau matricea de admitanta [100] denumire care isi are originea in teoria retelelor electrice. Majoritatea autorilor lucrarilor de specialitate au adoptat numele de matricea Laplace (L) deoarece este o matrice a unui operator discret Laplace [101].
Asa cum s-a amintit cea mai importanta utilizare a matricei L este in TMA [101] care este mentionata in cele ce urmeaza:
Teorema (TMA) : Daca i si j sunt doua varfuri ale unui graf G si Lij o submatrice a matricii Laplace obtinuta prin indepartarea liniei i si coloanei j atunci valoarea absoluta pentru determinantul matricei Lij este egal cu numarul de arbori cheie t(G) din graful G:
t(G) = |det(Lij)| (30)
In Figura 28 este prezentat formula si graful molecular pentru 3-etil-2,2,4-trimetilpentan si matricea Lapalce corespunzatoare [104].

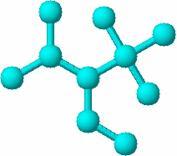

28a 28b 28c
Figura 28. Formula moleculara (28a), graful constitutional (28b) si matricea Laplace (28c) pentru 3-etil-2,2,4-trimetilpentan
2.6.1. Spectrul si polinomul matricii Laplace
Pentru un graf G cu N varfuri diagonalizarea matricei Laplace conduce la N valori proprii reale I = 1,.N. In cazul spectrului matricei L primului termen x1 prin conventie i se atribuie valoarea 0 iar termenii scad in ordinea urmatoare [103]:
0 = x1 ≤ x2 ≤...≤ xN-1 ≤ xN (31)
In cazul unor grafuri complete KN, spectrul Laplace este prezentat in ecuatia 32 [103] in timp ce pentru un graf regulat spectrul L este prezentat cu ajutorul ecuatiei 33 [103]:
(32)
xi (L) = D - xi(A) (33)
unde D este gradul varfului din graful regulat.
Mohar arata [105] ca spectrul Laplace are o serie de proprietati interesante. Cu ajutorul acestuia se pot calcula numarul de arbori cheie pe baza teoremei TMA:
![]()
In Figura 29 este prezentat spectrul Laplace (29b) pentru un graf complet (graful Kuratowski, 29a) [103] iar in Figura 30 graful (30a) si matricea Laplace (30b) pentru naftalina impreuna cu spectrul Laplace (30c) corespunzator si numarul de arbori cheie (30d) din respectivul graf [103].
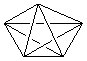
29a 29b
Figura 29. Graful Kuratowski (29a)
si spectrul
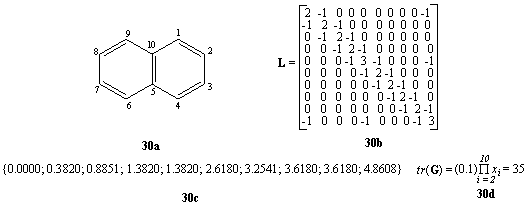
Figura 30. Graful (30a), matricea (30b) si spectrul Laplace (30c) pentru naftalina impreuna cu numarul de arbori cheie (30d) din respectivul graf
O alta proprietate importanta a spectrului Lapalce este aceea ca numarul de arbori cheie care deriva din respectivul spectru, in cazul unor grafuri ciclice, nu depinde de modul de imbinare a inelelor (liniara sau angulara).
In Tabel 15315l1119p ul 4 este prezentat spectrul Laplace si numarul de arbori cheie calculat cu ajutorul ecutiei 34 pentru cateva grafuri policiclice [103].
|
|
|
|
|
|
|
|
||||
|
tr =204 |
tr =204 |
tr =199 |
tr =161 |
tr =423381 |
Tabel 15315l1119p ul 4. Spectrul Laplace si numarul de arbori cheie calculat cu ajutorul ecutiei 34 pentru grafuri policiclice [103]
Polinomul (G, x) pentru matricea Laplace pentru un graf G este definit [101] cu ajutorul ecuatiei 35 :
(G, x) = det |xI - L| (35)
Forma coeficientilor polinomului Laplace se poate obtine fie cu ajutorul ecuatiei 36:
(G, x) = xN - c1xN-1 - .- cN-1x - cN = xN - n cnxN-n (36)
sau utilizand metoda Le Verrier-Faddeev-Frame (LVFF) [90] modificata [91].
Coeficientul cn din polinomul Laplace se poate calcula prin metoda LVFF cu ajutorul ecuatiei 37 [103]:
cn = (1/n) trLn (37)
unde matricea Ln este data de ecuatia 38:
Ln = LBn-1 (38)
Matricea auxiliara Bn-1 se poate defini cu ajutorul ecuatiei 39:
Bn-1 = Ln-1 - cn-1I (39)
In cazul metodei LVFF fiind o metoda iterativa, n = N-1 si matricii auxiliare prin conventie ii e atribuita valoarea 0.
BN-1 = LN-1 - cN-1I = 0 (40)
2.7. Matricea χ
Matricea a fost definita in literatura de specialitate pentru prima data de catre Hall [106]. Ulterior M. Randic redefineste matricea [107] in scopul obinerii unor noi invarianti care reprezinta sursa de constructie descriptorilor de conectivitate.
Acest tip de matrice se bazeaza pe matricea de adiacenta dar in locul valorilor 0 si 1 pentru elementele diferite de 0, valorile acestora sunt asimilate cu 1/√(m,n) in care m si n reprezinta valentele varfurilor implicate [50, 107].

Printr-o multiplicare matriciala uzuala se pot obtine puterile superioare ale matricii m
In Figura 31 este prezentat graful molecular (31a) si matricea (31b) in cazul 2, 2, 3-trimetilbutanului [107].
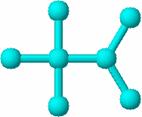
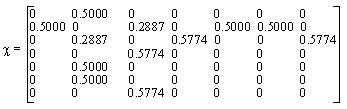
31a 31b
Figura 31. Graful molecular (31a) si matricea (31b) in cazul 2, 2, 3-trimetilbutanului
2.8. Matricea Cluj
Cu rezultatele introduse de indicii Szeged si utilizand o generalizare analoga a numerelor Ni,p ,se poate defini matricea Cluj, CJu [50, 108-111] prin ecuatia 42:
[CJu]ij = Ni,pk(i,j) = max | Vi,pk(i,j)| (42)
in care | Vi,pk(i,j)| este numarul de elemente al setului Vi,pk(i,j), maximum se face pe toate muchiile pk(i,j) iar :
Vi,pk(i,j) = ;| pk(i,j)| = min} (43)
k h = 1, 2,..
Setul Vi,pk(i,j) consta din cele i varfuri in concordanta cu calea pk(i,j) (conditia ph(i,j) pk(i,j) = ). Pentru structurile ciclice , prin definitie , elementele (ij) in matricea Cluj reprezinta max | Vi,pk(i,j)| . De fapt matricea Cluj, CJu reprezinta patratul unei serii de dimensiuni N N si este in general nesimetrica in raport cu diagonala. Matricile Cluj simetrice CJe si CJp [111] se definesc in aceeasi maniera cu matricile Szeged simetrice, SZe si SZp [50, 108-111] :
[CJe]ij = e[CJu]ij[CJu]ji (44)
[CJp]ij = p[CJu]ij[CJu]ji (45)
Prin analogie se poate deduce ca CJe reprezinta produsul Hadamard CJp si matricea de adiacenta A.
In Figura 32 este prezentat graful molecular (32a) si cele trei tipuri de matrici Cluj (32b, c, d) in cazul 2-metilciclohexanului.
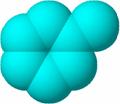

32a 32b 32c

32d
Figura 32. Graful molecular (32a) si cele trei tipuri de matrici Cluj (CJu-32b,CJp-c,CJe
-d) in cazul 2-metilciclohexanului
2.9. Matricea de rezistenta
O noua metrica in cazul grafurilor moleculare numita si distanta de rezistenta a fost definita de Klein si Randic [112]. Definirea are la baza teoria retelelor electrice si se considera ca o legatura simpla dintre doi atomi de carbon corespunde la 1W. Distanta dintre o pereche de varfuri vi si vj este definita (ecuatia 46) ca rezistenta electrica dintre varfuri [112-114].
d(w)ij = W (46)
In cazul grafurilor aciclice acest tip de distanta este tocmai distanta topologica dar pentru grafurile ciclice distanta de rezistenta este mai mica sau cel mult egala cu distanta topologica asa cum este definita in ecuatia 47:
d(w)ij ≤ W (47)
In Figura 33 este prezentata matricea de rezistenta W [113] pentru graful molecular 1-etil-2-metilciclobutan.

Figura 33. Matricea de rezistenta W pentru graful molecular 1-etil-2-metilciclobutan
2.10. Alte tipuri de matrici
2.10.1. Matricea Szeged
Acest tip de matrice a fost definit pentru prima data in literatura de specialitate de catre Diudea [109,115] prin utilizeaza elementele indicelui Szeged (Sz). Pentru un graf G cu N varfuri matricea Szeged Szp(w) = Szp(w, G) este o matrice patrata N×N si se poate defini cu ajutorul ecuatiei 48:
![]()
iar elementele nij se pot defini cu ajutorul ecuatiei 49:
nij (49)
in care w este schema ponderata utilizata la calculul distantelor din graful G.
Elementele matricii Szp sunt numere intregi. Un exemplu de matrice Szp este prezentat in Figura 34 pentru toluen [59]:
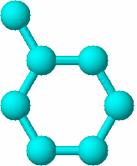

34a 34b
Figura 34.Graful molecular in cazul toluenului (34a) si matricea Szeged (34b) corespunzatoare
2.10.2. Matricea Szeged reciproca
Pentru un graf G cu N varfuri, matricea Szeged reciproca RSzp(w) = RSzp(w, G) este o matrice patrata N×N simetrica pentru care elementele sunt numere reale. Acest tip de matrice se poate defini cu ajutorul ecuatiei 50 [59]:
![]()
In Figura 35 este
prezentata matricea

Figura 35. Matricea Szeged reciproca in cazul grafului molecular caracteristic toluenului prezentat in Figura 34
2.10.3. Matricea distantelor complement
Dupa cum este bine cunoscut in cazul unei matrici de distante D, valoarea unui element ij este egala cu suma muchiilor pentru cea mai scurta cale dintre doua varfuri vi si vj ale unui graf G. Avand la baza aceasta definitie Randic defineste [116] pentru prima data matricea distantelor complement DC in cazul alcanilor. Matricea de distante complement DC(w) = DC(w, G) pentru un graf G cu N varfuri este o matrice simetrica patrata N×N care se poate defini [59, 117] cu ajutorul ecuatiei 51:
![]()
2.10.4. Matricea distantelor complement reciproca
Pentru un graf G cu N varfuri, matricea distantelor complement reciproca RDC(w) = RDC(w, G) este o matrice simetrica patrata N×N cu elemente reale care se poate defini [59, 117] cu ajutorul ecuatiei 52:
![]()
in care [DC(w)]ij reprezinta distanta complement dintre varfurile vi si vj, [DC(w)]ii reprezinta elementele diagonalei matricei iar w reprezinta schema de calcul pentru parametrii Vw caracteristici varfurilor si parametrii Ew caracteristici muchiilor.
In Figura 36 este prezentata matricea distantelor complement (36a) si a distantelor complement reciproca (36b) in cazul toluenului prezentat in Figura 34.
 Figura 36. Matricea distantelor
complement (36a) si a distantelor
complement reciproca (36b) in cazul
toluenului prezentat in Figura 34
Figura 36. Matricea distantelor
complement (36a) si a distantelor
complement reciproca (36b) in cazul
toluenului prezentat in Figura 34
2.10.5. Matricea distantelor complementare
O alta matrice in care valoarea elementelor corespunzatoare unei perechi de varfuri scade cu cresterea distantei dintre varfuri se numeste matricea distantelor complementare CD [59]. Acest tip de matrice este o matrice simetrica patrata N×N care poate fi definita cu ajutorul ecuatiei 53:
![]()
in care [D(w)]ij reprezinta distanta dintre varfurile vi si vj, d(w)max reprezinta distanta maxima dintre doua varfuri distincte din graf (diametrul grafului) iar d(w)min reprezinta distanta minima dintre doua varfuri distincte din graf (egala cu 1 pentru alcani si cicloalcani).
2.10.6. Matricea distantelor complementare reciproca
Matricea distantelor complementare reciproca (RCD(w) = RCD(w, G)) este o matrice simetrica patrata N×N definita [59] prin ecuatia 54:
![]() Pentru
graful caracteristic toluenului (Figura
34) in Figura 37 este prezentata
matricea distantelor complementare (37a)
si matricea distantelor complementare reciproca (37b).
Pentru
graful caracteristic toluenului (Figura
34) in Figura 37 este prezentata
matricea distantelor complementare (37a)
si matricea distantelor complementare reciproca (37b).

37a 37b
Figura 37. Matricea distantelor complementare (37a) si matricea distantelor complementare reciproca (37b) in cazul toluenului (Figura 34, 34a)
2.10.7. Matricea Wiener inversa
Acest tip de matrice RW(w) = RW(w, G) pentru un graf G cu N varfuri este o matrice simetrica patrata N×N cu elemente reale definita [59] prin ecuatia 55:
![]()
unde Vw(w)i este ponderea varfului vi, [D(w)]ij este distanta dintre varfurile vi si vj iar w este schema utilizata pentru calculul Vw si Ew.
2.10.8. Matricea Wiener inversa reciproca
Matricea Wiener inversa reciproca RRW(w) = RRW(w, G) pentru un graf G cu N varfuri este o matrice simetrica patrata N×N cu elemente reale definita [59, 118] cu ajutorul ecuatiei 56:
![]()
In Figura 38 este prezentata matricea Wiener inversa (38a) si matricea Wiener inversa reciproca (38b) in cazul grafului caracteristic toluenului (Figura 34, 34a).

38a 38b
Figura 38. Matricea Wiener inversa (38a) si matricea Wiener inversa reciproca (38b) in cazul grafului caracteristic toluenului (Figura 34, 34a)
2.10.9. Matricile combinatoriale
Matricea clasica de distante D reprezinta o sursa importanta de constructie a altor matrici cum ar fi: matricea de distante-delta DD si matricea de distante-cai Dp care au fost pentru prima data definite in literature de catre Diudea [119] conform ecuatiilor 57 si 58:

Elementele [DD]ij sunt reprezentate de numarul de ,,cai interne''(mai mari decat unitatea) incluse in cea mai mica distanta dintre varfurile vi si vj [113, 119] iar [Dp]ij reprezinta numarul total de ,,cai interne'' incluse in cea mai mica distanta dintre varfurile vi si vj [113, 119]. Se observa cu usurinta ca:
DD = Dp - D (59)
In Figura 38 sunt prezentate matricile combinatoriale DD (38a) si Dp (38b) in cazul grafului molecular caracteristic 1-etil-2-metilciclobutanului.

Figura 38. Matricile combinatoriale DD (38a) si Dp (38b) in cazul grafului molecular caracteristic 1-etil-2-metilciclobutanului
Matricea Dp este utilizata pentru calculul indicelui Hiper-Wiener iar matricea DD este utilizata la calcularea elementelor ,,non-Wiener'' in cazul indicelui Hiper-Wiener.
Pentru calculul polinomului caracteristic acestor tipuri de matrici se utilizeaza ecuatia 60:
Del(G, x) = det |xI - DD
Mai multe detalii privind privind polinomul si spectrul caracteristic matricilor combinatoriale sunt prezentate in referinta [120].
2.10.10. Matricea Hosoya
Randic defineste [121] in anul 1994 o noua matrice pentru un graf aciclic indirect conectat (arbore) numita matricea Hosoya Z = Z(T). Pentru un graf cu N varfuri acest tip de matrice este o matrice simetrica patrata N×N ale carei elemente zij se pot defini cu ajutorul ecuatiei 61 [121-123]:

in care : Z(T - pij) este indecele Hosoya pentru subgraful T - pij obtinut din arborele T prin indepartarea tuturor muchiilor de-a lungul caii pij ce conecteaza varfurile vi si vj.
Pentru o mai usoara intelegere a modului de constructie a acestui tip de matrice in Figura 39 este prezentata matricea Hosoya Z in cazul grafului molecular caracteristic 2-metilheptanului.
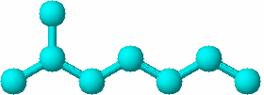

Figura 39. Matricea Hosoya Z in cazul grafului 2-metilheptanului
|